Treatment Effect Estimation with Disentangled Latent Factors

Let $t_{i}\in\{0,1\}$ denote a binary treatment where $t_{i}=0$ indicates the $i$-th individual receives no treatment (control) and $t_{i}=1$ indicates the individual receives the treatment (treated). We use $y_{i}(1)$ to denote the potential outcome of $i$ if it were treated, and $y_{i}(0)$ to denote the potential outcome if it were not treated. Noting that only one of the potential outcomes can be realized, and the observed outcome is $y_{i}=(1-t_{i})y_{i}(0)+t_{i}y_{i}(1)$. Additionally, let $\mathbf{x}_{i}\in\mathcal{R}^{d}$ denote the “as is” set of covariates for the $i$-th individual. When the context is clear, we omit the subscript $i$ in the notations.

Throughout the paper, we assume that the following three fundamental assumptions for treatment effect estimations (Rosenbaum and Rubin 1983) are satisfied:

The first goal of treatment effect estimation is estimating the average treatment effect (ATE) which is defined as: $ATE=\mathbb{E}[y(1)-y(0)]=\mathbb{E}[y|do(t=1)]-\mathbb{E}[y|do(t=0)]$, where $do(t=1)$ denote an manipulation on $t$ by removing all its incoming edges and setting $t=1$ (Pearl 2009).

The treatment effect for an individual $i$ is defined as $\tau_{i}=y_{i}(1)-y_{i}(0)$. Due to the counterfactual problem, we never observe $y_{i}(1)$ and $y_{i}(0)$ simultaneously and thus $\tau_{i}$ is not observed for any individual. Instead, we estimate the conditional average treatment effect $(\tau(x))$, defined as $\tau(\mathbf{x})\vcentcolon=\mathbb{E}[\tau|\mathbf{x}]=\mathbb{E}[y|\mathbf{x},do(t=1)]-\mathbb{E}[y|\mathbf{x},do(t=0)]$.

In this work, we propose the TEDVAE model (Figure 1) for estimating the treatment effects, where the observed pre-treatment variables $\mathbf{x}$ can be viewed as generated from three disjoint sets of latent factors $\mathbf{z}=(\mathbf{z}_{t},\mathbf{z}_{c},\mathbf{z}_{y})$. Here $\mathbf{z}_{t}$ are instrumental factors that only affect the treatment but not the outcome, $\mathbf{z}_{y}$ are risk factors which only affect the outcome but not the treatment, and $\mathbf{z}_{c}$ are confounding factors that affect both the treatment and the outcome.

On the one hand, the proposed TEDVAE model in Figure 1 provides two important benefits. The first one is that by explicitly modelling for the instrumental factors and adjustment factors, it accounts for the fact that not all variables in the observed variables set $\mathbf{x}$ are confounders. The second benefit is that it allows for the possibility of learning unobserved confounders that from their proxy variables.

On the other hand, our model diagram does not pose any restriction other than the three standard assumptions discussed in Section 3.1. To see this, consider the case where every variable in $\mathbf{x}$ itself is a confounder, i.e., $\mathbf{x}=\mathbf{x}_{c}$, then the generating mechanism in the TEDVAE model becomes $\mathbf{z_{c}}=\mathbf{x}$ with $\mathbf{z}_{t}=\mathbf{z}_{y}=\emptyset$ and the model in Figure 1 becomes identical to the widely used diagram for treatment effect estimation (Figure 2 in (Imbens 2019)).

With our model, the estimation of treatment effect is immediate using the back-door criterion (Pearl 2009):

For the estimation of the conditional average treatment effect, our result follows from Theorem 3.4.1 in (Pearl 2009) as shown in the following theorem:

An implication of Theorem 1 and 2 is that they are not restricted to binary treatment. In other words, our proposed method can be used for estimating treatment effect of a continuous treatment variable, while most of the existing estimators are not able to do so. However, due to the lack of datasets with continuous treatment variables for evaluating this, we focus on the case of binary treatment variable and leave the continuous treatment case for future work.

Theorems 1 and 2 suggest that disentangling the confounding factors allows us to exclude unnecessary factors when estimating ATE and CATE. However, keen readers may wonder since we already assumed unconfoundedness, doesn’t straightforwardly adjusting for $\mathbf{x}$ suffice?

Theoretically, it has been shown that both the bias (Abadie and Imbens 2006) and the variance (Hahn 1998) of treatment effect estimation will increase if variables unrelated to the outcome is included during the estimation. Therefore, it is crucial to differentiate the instrumental, confounding and risk factors and only use the appropriate factors during treatment effect estimation. In the next section, we propose our data-driven approach to learn and disentangle the latent factors using a variational autoencoder.

In the above discussion, we have seen that removing unnecessary factors is crucial for efficient and accurate treatment effect estimation. We have assumed that the mechanism which generates the observed variables $\mathbf{x}$ from the latent factors $\mathbf{z}$ and the decomposition of latent factors $\mathbf{z}=(\mathbf{z}_{t},\mathbf{z}_{c},\mathbf{z}_{y})$ are available. However, in practice both the mechanism and the decomposition are not known. Therefore, the practical approach would be to utilize the complete set of available variables during the modelling to ensure the satisfaction of the unconfoundedness assumption, and utilize a data-driven approach to simultaneously learn and disentangle the latent factors into disjoint subsets.

To this end, our goal is to learn the posterior distribution $p(\mathbf{z}|\mathbf{x})$ for the set of latent factors with $\mathbf{z}=(\mathbf{z}_{t},\mathbf{z}_{y},\mathbf{z}_{c})$ as illustrated in Figure 1, where $\mathbf{z}_{t},\mathbf{z}_{c},\mathbf{z}_{y}$ are independent of each other and correspond the instrumental factors, confounding factors, and risk factors, respectively. Because exact inference would be intractable, we employ neural network based variational inference to approximate the posterior $p_{\theta}(\mathbf{x}|\mathbf{z}_{t},\mathbf{z}_{c},\mathbf{z}_{y})$. Specifically, we utilize three separate encoders $q_{\phi_{t}}(\mathbf{z}_{t}|\mathbf{x})$, $q_{\phi_{c}}(\mathbf{z}_{c}|\mathbf{x})$, and $q_{\phi_{y}}(\mathbf{z}_{y}|\mathbf{x})$ that serve as variational posteriors over the latent factors. These latent factors are then used by a single decoder $p_{\theta}(\mathbf{x}|\mathbf{z}_{t},\mathbf{z}_{c},\mathbf{z}_{y})$ for the reconstruction of $\mathbf{x}$. Following standard VAE design, the prior distributions $p(\mathbf{z}_{t}),p(\mathbf{z}_{c}),p(\mathbf{z}_{y})$ are chosen as Gaussian distributions (Kingma and Welling 2014).

Specifically, the factors and the generative models for $\mathbf{x}$ and $t$ are described as:

with $p(x_{j}|\mathbf{z}_{t},\mathbf{z}_{c},\mathbf{z}_{y})$ being the suitable distribution for the $j$-th observed variable, $f_{1}$ is a function parametrized by neural network, and $\sigma(\cdot)$ being the logistic function, $D_{z_{t}},D_{z_{c}}$, and $D_{z_{y}}$ are the parameters that determine the dimensions of instrumental, confounding, and risk factors to infer from $\mathbf{x}$.

For continuous outcome variable $y$, we parametrize it as using a Gaussian distribution with its mean and variance given by a pair of disjoint neural networks that defines $p(y|t=1,\mathbf{z}_{c},\mathbf{z}_{y})$ and $p(y|t=0,\mathbf{z}_{c},\mathbf{z}_{y})$. This pair of disjoint networks allows for highly imbalanced treatment. Specifically, for continuous $y$ we parametrize it as:

where $f_{2}$, $f_{3}$, $f_{4}$, $f_{5}$ are neural networks parametrized by their own parameters. The distribution for the binary outcome case can be similarly parametrized with a Bernoulli distribution.

In the inference model, the variational approximations of the posteriors are defined as:

where $\hat{\mu}_{t},\hat{\mu}_{c},\hat{\mu}_{y}$ and $\hat{\sigma}_{t}^{2},\hat{\sigma}_{c}^{2},\hat{\sigma}_{y}^{2}$ are the means and variances of the Gaussian distributions parametrized by neural networks similarly to the $\hat{\mu}$ and $\hat{\sigma}$ in the generative model.

Given the training samples, the parameters can be optimized by maximizing the evidence lower bound (ELBO):

To encourage the disentanglement of the latent factors and ensure that the treatment $t$ can be predicted from $\mathbf{z}_{t}$ and $\mathbf{z}_{c}$, and the outcome $y$ can be predicted from $\mathbf{z}_{y}$ and $\mathbf{z}_{c}$, we add two auxiliary classifiers to the variational lower bound. Finally, the objective of TEDVAE can be expressed as

where $\alpha_{t}$ and $\alpha_{y}$ are the weights for the auxiliary objectives.

For predicting the CATEs of new subjects given their observed covariates $\mathbf{x}$, we use the encoders $q(\mathbf{z}_{y}|\mathbf{x})$ and $q(\mathbf{z}_{c}|\mathbf{x})$ to sample the posteriors of the confounding and risk factors for $l$ times, and average over the predicted outcome $y$ using the auxiliary classifier $q_{\omega_{y}}(y|t,\mathbf{z}_{c},\mathbf{z}_{y})$.

An important difference between TEDVAE and CEVAE lies in their inference models. During inference, CEVAE depends on $t$, $x$ and $y$ for inferencing $\mathbf{z}$; in other words, CEVAE needs to estimate $p(t|\mathbf{x})$ and $p(y|t,\mathbf{x})$, inference $\mathbf{z}$ as $p(\mathbf{z}|t,y,\mathbf{x})$, and finally predict the CATE as $\hat{\tau}(\mathbf{x})=\mathbb{E}[y|t=1,\mathbf{z}]-\mathbb{E}[t|y=0,\mathbf{z}]$. The estimations of $p(t|\mathbf{x})$ and $p(y|t,\mathbf{x})$ are unnecessary since we assume that $t$ and $y$ are generated by the latent factors and inferencing the latents should only depend on $\mathbf{x}$ as in TEDVAE. As we later show in the experiments, this difference is crucial even when no instrumental or risk factors are present in the data.

For evaluating the performance of CATE estimation, we use the Precision in Estimation of Heterogeneous Effect (PEHE) (Hill 2011; Shalit, Johansson, and Sontag 2017; Louizos et al. 2017; Dorie et al. 2019) which measures the root mean squared distance between the estimated and the true CATE when ground truth is available: $\epsilon_{\text{PEHE}}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(\hat{\tau}(\mathbf{x}_{i})-\tau(\mathbf{x}_{i}))^{2}}$ , where $\tau(\mathbf{x})$ is the ground truth CATE for subjects with observed variables $\mathbf{x}_{i}$.

For evaluating the performance of the average treatment effect (ATE) estimation, the ground truth ATE can be calculated by averaging the differences of the outcomes in the treated and control groups if randomized controlled trials data is available. Then, when comparing the ground truth ATE with the estimated ATE obtained from a non-randomized sample (observational sample or created via biased sampling) of the dataset, the performances can then be evaluated using the mean absolute error in ATE (Hill 2011; Shalit, Johansson, and Sontag 2017; Louizos et al. 2017; Yao et al. 2018) for evaluation: $\epsilon_{\text{ATE}}=|\hat{\tau}-\frac{1}{N}\sum\limits_{i=1}^{N}[t_{i}y_{i}-(1-t_{i})y_{i}]|$, where $\hat{\tau}$ is the estimated ATE, $t_{i}$ and $y_{i}$ are the treatments and outcomes from the randomized data. For both $\epsilon_{\text{ATE}}$ and $\epsilon_{\text{PEHE}}$, we use superscripts $tr$ and $te$ to denote their values on the training and test sets, respectively.

We first conduct experiments using synthetic datasets to investigate TEDVAE’s capability of inferring the latent factors and estimating the treatment effects. Due to the page limit, we only provide an outline of the synthetic dataset and provide the detailed settings in the supplementary materials.

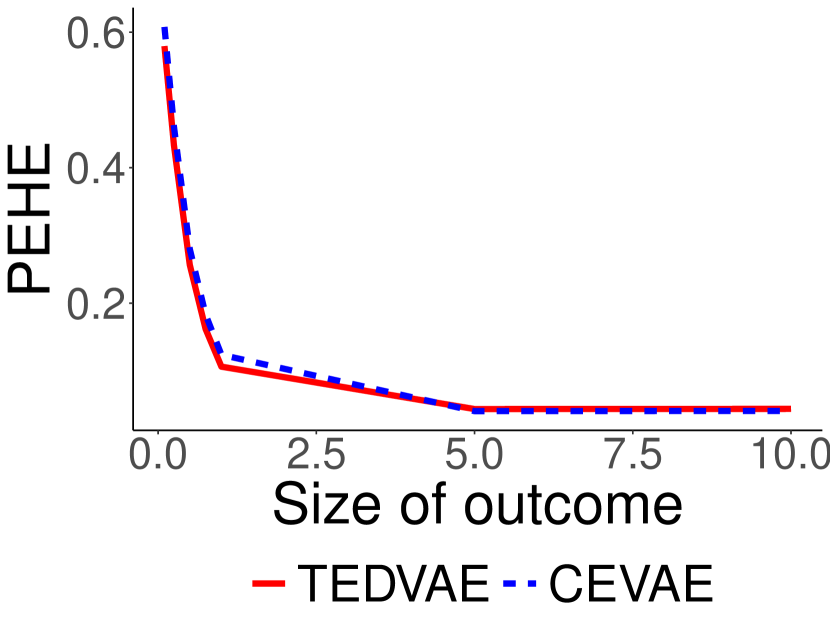
The first setting of synthetic datasets studies the benefit of disentangling the confounding factors from instrumental and risk factors, and are generated using the structure depicted in Figure 1. We illustrate the results in the first row of Figure 3. It can be seen that when the instrumental and risk factors exist in the data, the benefit of disentanglement is signficance as demonstrated by the PEHE curves between TEDVAE and CEVAE. When the proportions of the treated samples varies, the performances of CEVAE fluctuates severely and the error remains high even when the dataset is balanced; however, the PEHEs of TEDVAE are stable even when the dataset is highly imbalanced, and are always stays significantly lower than CEVAE. When the scales of outcome and CATE change, TEDVAE also performs consistently and significantly better than CEVAE.

The second setting for the synthetic datasets are designed to study how TEDVAE performs when the instrumental and risk factors are absent, and follow the same data generating procedure as in the CEVAE (Louizos et al. 2017). We illustrate the results of this synthetic dataset in the second row of Figure 3. Therefore, it is reasonable to expect that CEVAE would perform better than TEDVAE since the instrumental factors $\mathbf{z}_{t}$ and risk factors $\mathbf{z}_{y}$ do not exist. However, from the second row of Figure 3 we can see that TEDVAE either performs better than CEVAE, or performs as well as CEVAE using a wide range of parameters under this setting. This is possibly due to the differences in predicting for previous unseen samples between TEDVAE and CEVAE, where CEVAE needs to follow a complicated procedure of inferencing $p(t|\mathbf{x})$ and $p(y|t,\mathbf{x})$ first and then inferencing the latents as $p(z|t,y,\mathbf{x})$, whereas in TEDVAE this is not needed. These results suggests that the TEDVAE model is able to effectively learn the latent factors and estimate the CATE even when the instrumental and risk factors are absent. It also indicates that the TEDVAE algorithm is robust to the selection of the latent dimensionality parameters.

Next, we investigate whether TEDVAE is capable of recovering the latent factors of $\mathbf{z}_{t}$, $\mathbf{z}_{c}$, and $\mathbf{z}_{y}$ that are used to generate the observed covariates $\mathbf{x}$. To do so, we compare the performances of TEDVAE when setting the $D_{z_{t}}$, $D_{z_{c}}$ and $D_{z_{y}}$ parameters to 10 against itself when setting one of the latent dimensionality parameter of TEDVAE to $0$, i.e., setting $D_{z_{t}}=0$ and forcing TEDVAE to ignore the existence of $\mathbf{z}_{t}$. If TEDVAE is indeed capable of recovering the latent factors, then its performances with non-zero latent dimensionality parameters should be better than its performance when ignoring the existence of any of the latent factors. Figure 4 illustrates the capability of TEDVAE for identifying the latent factors using radar chart. Taking the Figure 4(a) as example, the $z_{t}$ and $\neg z_{t}$ polygons correspond to the performances of TEDVAE when setting the dimension parameter $D_{z_{t}}=5$ (identify $\mathbf{z}_{t}$) and $D_{z_{t}}=0$ (ignore $\mathbf{z}_{t}$). From the figures we can clearly see that the performances of TEDVAE are significantly better when the latent dimensionality parameters are set to non-zero, than setting any of the latent dimensionality to 0.

In this section, we use two benchmark datasets for treatment effect estimation to compare TEDVAE with the baselines.