Trapping and acceleration of spin-polarized positrons from $\gamma$ photon splitting in wakefields

Plasma-based wakefield accelerators have attracted worldwide attentions in recent years due to their capability of providing acceleration gradients three orders of magnitude higher than conventional radio-frequency accelerators Tajima and Dawson (1979); Chen et al. (1985); Nakajima et al. (1995). Over the past decades, the wakefield acceleration of electrons has been developed rapidly Esarey et al. (2009); Downer et al. (2018). This promises a new possibility for future electron-positron ($e^{-}e^{+}$) colliders with relatively compact size and low cost Leemans and Esarey (2009); Schroeder et al. (2010); Nakajima et al. (2019). To this end, trapping and acceleration of polarized positron beams are highly demanded on top of the advantage of high acceleration gradient for electrons in wakefields Artru et al. (2008); Clarke et al. (2008). However, generation, polarization, trapping and acceleration of such positron beams in plasma wakefields are still quite challenging.

Although plenty of schemes Esarey et al. (2009) have been proposed and studied for the effective trapping and acceleration of electrons in plasma wakefields Pukhov and Meyer-ter Vehn (2002); Lu et al. (2006), those schemes are not applicable for positrons since the transverse fields in nonlinear wakes usually defocus positrons, which makes continuous positron acceleration impossible. To overcome this issue, an amount of theoretical schemes have been proposed to simultaneously accelerate and focus positrons by using special driver or plasma structures, such as Laguerre-Gaussian laser pulses Vieira and Mendonça (2014), hollow electron beam drivers Jain et al. (2015), and finite-radius plasma columns Diederichs et al. (2019). But, unfortunately, in those studies the generation and injection of positrons have to be pre-provided. In recent FACET experiments, the positron accelerations have been demonstrated to run in a self-loaded plasma wakefield Corde et al. (2015) or a hollow plasma channel Gessner et al. (2016); Yakimenko et al. (2016). However, a pre-accelerated relativistic positron beam is also required and the beam polarization has not been studied yet.

Positrons are commonly polarized either via radiative process (Sokolov-Ternov effect) in a storage ring Sokolov and Ternov (1964); Baier and Katkov (1967); Baier (1972) or via high-energy polarized $\gamma$ photons interacting with a high $Z$-target (Bethe-Heitler pair production) Variola (2014). For the former the polarization time is rather long since the magnetic fields of a synchrotron are quite weak; for the latter the positron density is limited by the low photon luminosity Omori et al. (2006); Scott et al. (2011); Abbott et al. (2016). Recently, the state-of-the-art laser pulses with peak intensities up to $10^{22}$ W/cm² Gales et al. (2018); Shen et al. (2018); Yoon et al. (2019); Danson et al. (2019) enable to excite nonlinear quantum electrodynamics (QED) processes Ritus (1985); Xie et al. (2017) in laser-matter interaction Di Piazza et al. (2012); Sarri et al. (2015); Cole et al. (2018); Poder et al. (2018). And, polarized GeV-level positron beams can be created via employing asymmetric spin-resolved probabilities of nonlinear Breit-Wheeler (BW) pair production in a bichromatic Chen et al. (2019) or elliptically-polarized laser pulse Wan et al. (2020) (transverse polarization; the polarization of intermediate photons was not considered therein), or via the helicity transfer from polarized electrons (longitudinal polarization) Li et al. (2020a). However, in those methods the positron energies are limited by those of the scattering electrons via intermediate photons and impossible to achieve the level of hundreds of GeVs, and the beam qualities, such as the energy spread and emittance, are far worse than those of the beams from conventional accelerators, which severely restrict the applications in high-energy and particle physics (e.g. the polarized $e^{-}e^{+}$ collider Clarke et al. (2008)).

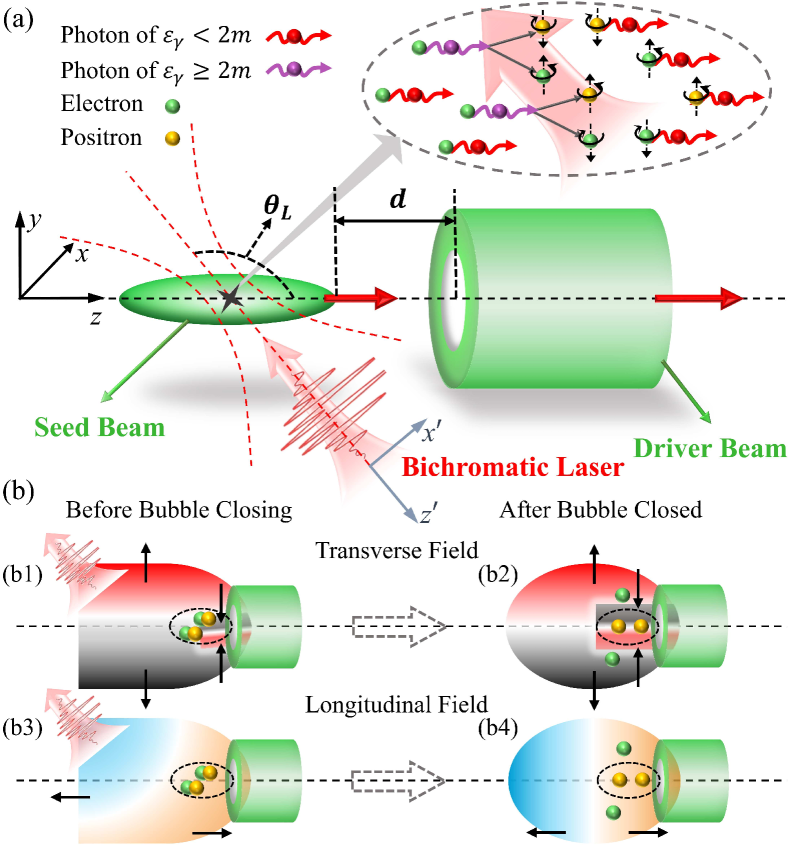
In this Letter, we propose a compact scheme to generate polarized positrons and inject them into plasma wakefields with further acceleration to high energies. The positron generation and polarization are studied quantum mechanically, while the bubble-recovery-based positron trapping and following acceleration and depolarization in wakefields semi-classically. The interaction schematic is shown in Fig. 1. A hollow electron beam working as a wake driver propagates into a low-density plasma and excites nonlinear wakefields (bubbles). Behind it, another copropagating seed electron beam collides with an ultra-intense linearly-polarized (LP) bichromatic laser pulse to emit abundant LP $\gamma$ photons via nonlinear Compton scattering, which could further decay into transversely polarized pairs through nonlinear BW process [see Fig. 1(a)] due to the asymmetric pair production and polarization probabilities in the laser positive and negative half cycles. We underline that in this study the polarization of intermediate $\gamma$ photons has been taken into account, otherwise the yield and polarization of the positrons will be remarkably overestimated. During the collision of the laser and seed beam, the wake structure driven by the driver beam is first destroyed and then gradually self-recovers at the downstream of the laser-seed-beam collision point. Some of the created high-energy polarized positrons can be trapped in the recovered wakefields [see Figs. 1(b1) and (b2)] and then accelerated by the wakefields [see Figs. 1(b3) and (b4)]. In our simulations over 70% positrons are finally injected into the wake and get further acceleration to an average energy beyond 1.2 GeV in 1 millimeter, with an average polarization exceeding 30%. The partial polarization of the positrons within the full width at half maximum (FWHM) of the energy spectrum can exceed 70% [see Fig. 2(c)]. The detailed injection and acceleration processes are discussed in the following.

We develope a Monte Carlo algorithm and implement it into two-dimensional QED particle-in-cell (PIC) code (benchmarked by EPOCH code Arber et al. (2015)) to describe the creation and polarization of the pairs quantum mechanically by using spin-resolved probabilities of nonlinear BW pair production sup , which are derived from the QED operator method Baier et al. (1973) in the local constant field approximation (valid at the invariant laser field parameter $a_{0}=|e|E_{0}/m\omega\gg 1$) Ritus (1985); Baier et al. (1998); Ilderton (2019); Di Piazza et al. (2019). To efficiently generate $\gamma$ photons and pairs requires the nonlinear QED parameters $\chi_{e}\equiv|e|\sqrt{-(F_{\mu v}p_{e}^{v})^{2}}/m^{3}\gtrsim 1$ (for electrons) and $\chi_{\gamma}\equiv|e|\sqrt{-(F_{\mu v}k_{\gamma}^{v})^{2}}/m^{3}\gtrsim 1$ (for $\gamma$ photons) Ritus (1985); Baier et al. (1998). Here, $F_{\mu v}$ is the field tensor, $p_{e}^{v}$ and $k_{\gamma}^{v}$ the 4-momenta of electron and $\gamma$ photon, respectively, $e$ and $m$ the electron charge and mass, respectively, and $E_{0}$ and $\omega$ the laser amplitude and frequency, respectively. Relativistic units with $c=\hbar=1$ are used throughout. The simulations of spin-resolved electron (positron) dynamics and photon emission and polarization follow the semi-classical algorithms in Refs. Li et al. (2019, 2020b); Wan et al. (2020). See more details of our simulation method in sup .

The simulation parameters of the laser pulse, electron beams and plasma are summarized as follows. A tightly-focused LP Gaussian bichromatic laser pulse propagates along $-z^{\prime}$ direction with $\theta_{L}=105^{\circ}$ and polarizes in $x^{\prime}-z^{\prime}$ plane, with wavelengths $\lambda_{1}=1\mu$m (period $T_{1}$) and $\lambda_{2}=0.5\mu$m, pulse durations $\tau_{1}=\tau_{2}=6T_{1}$, focal radii $w_{1}=w_{2}=2\mu$m, and peak amplitudes $a_{1}=4a_{2}\approx 67$ (corresponding to the peak intensities $I_{1}=4I_{2}\approx 6.15\times 10^{21}$ W/cm²). An unpolarized elliptical seed beam propagates along $+z$ direction, with an average energy $\varepsilon_{s,0}=4$ GeV, major axis $L_{maj}=7\mu$m, and minor axis $L_{min}=2\mu$m. A hollow driver beam is initially placed at the entrance of the plasma, with an average energy $\varepsilon_{d,0}=1$ GeV, outer radius $w_{out}=3\mu$m, inner radius $w_{in}=1.5\mu$m, and length $L_{h}=9\mu$m. The density, energy spread and angular divergence of the two electron beams are $n_{s,0}=n_{d,0}=0.1n_{c}$ with a Gaussian distribution (the critical density $n_{c}=1.1\times 10^{21}$ cm^-3 with respect to the laser pulse with wavelength of $\lambda_{1}$), $\Delta\varepsilon_{s,0}/\varepsilon_{s,0}=\Delta\varepsilon_{d,0}/\varepsilon_{d,0}=0.1$, and $\Delta\theta_{s}=\Delta\theta_{d}=0.1$ mrad, respectively. Here the delay distance of the two electron beams is $d=0\mu$m. More parameter scans for the driver beam size and other effects are shown in Fig. 4. The density of the background plasma (composed of $H^{+}$ and electrons) is $n_{p,0}=0.01n_{c}$. Note that the efficient excitation of a wakefield with central focusing fields for the positrons requires the driver beam satisfying $w_{in}/\sigma_{x}\geq 3$ and $k_{p}\sigma_{z}\leq 2$ Jain et al. (2015); Rosenzweig et al. (2004), where $\sigma_{x}$ and $\sigma_{z}$ are the transverse and longitudinal sizes of the driver beam and $k_{p}=2\pi/\lambda_{p}$ with $\lambda_{p}=\sqrt{\pi m/n_{p,0}e^{2}}$. Here we use $w_{in}/\sigma_{x}=3$ and $k_{p}\sigma_{z}\approx 1.8$, and the simulation domain is $60\lambda_{1}(x)\times 80\lambda_{1}(z)$ with grid resolutions d$x$ = d$z=\lambda_{1}/50$.

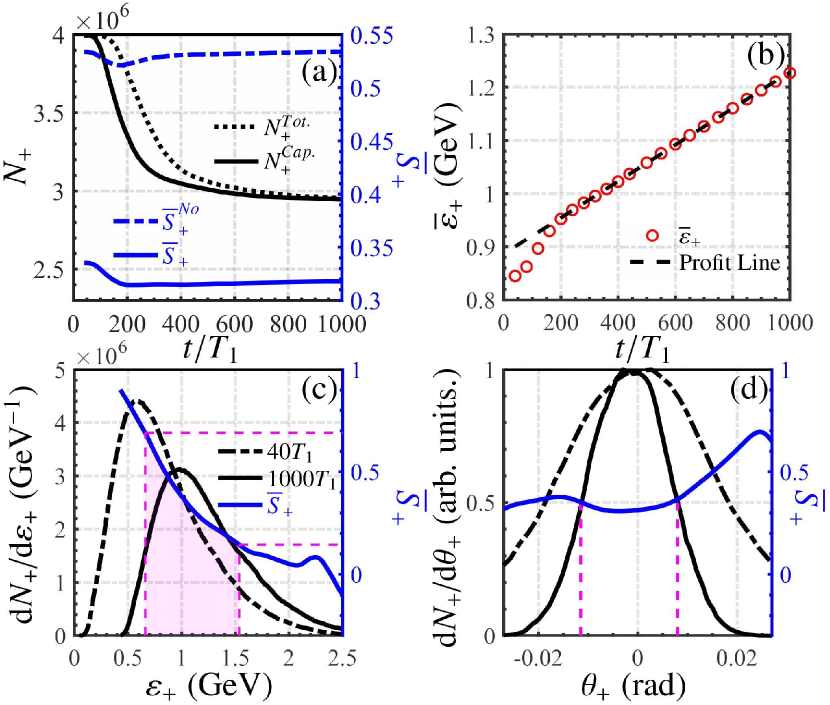
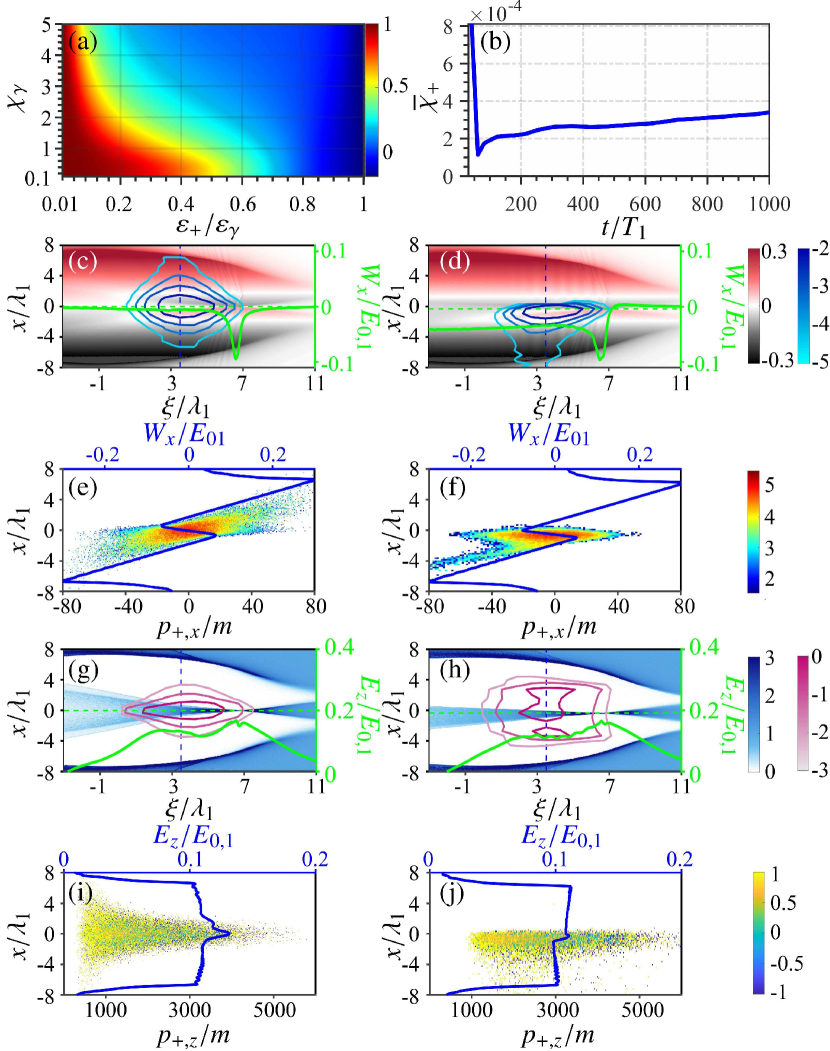
The main results of the positron trapping, acceleration and polarization are shown in Figs. 2 and 3. The pair production process is completed at the distance of $t_{i}\approx 40T_{1}$, where the bubble has not fully recovered yet, and nearly $4\times 10^{6}$ positrons are created with a yield ratio $N_{+}/N_{s}\approx 0.4\%$ (corresponding to a density of $n_{+}\sim 10^{-4}n_{c}$) and an average polarization (mainly along the magnetic field direction $y$) $\overline{S}_{+}\approx 33.52\%$ [see Fig. 2(a)]. As we mentioned before, if the polarization of intermediate $\gamma$ photons is artificially neglected as usual, $\overline{S}_{+}$ will be considerably overestimated by exceeding 68% [see the blue-dash-dotted line in Fig. 2(a), $\overline{S}_{+}^{No}\approx$ 53.5% at $t_{f}$]. Therefore we include this effects in our simulations and the analytical calculation of positron polarization is shown in Fig. 3(a). The polarization degree is inversely proportional to the positron energy, which affects the final polarization distribution of the accelerated positrons [see Fig. 2(c)]. Since in our case the QED parameter of the positron $\chi_{+}\propto a_{wake}\gamma_{+}[1-{\rm cos}(\theta_{L})]\ll 1$ [see Fig. 3(b)], the radiative depolarization effect is very weak, where $a_{wake}$ represents the invariant field parameter and $\gamma_{+}$ the Lorentz factor of positron. The depolarization effect derived from the spin procession in the wakefield govern by the Thomas-Bargmann-Michel-Telegdi equation Thomas (1926); A. (1927); Bargmann et al. (1959) is also quite weak Vieira et al. (2011); Wen et al. (2019). Consequently, the final positron polarization distribution mainly depends on the initial pair creation process and the conditions for the positron selection during the trapping and continuous acceleration processes. The last two processes rely on the wakefield structure. The positrons inherit transverse momenta $p_{+,x}$ from the seed electrons via intermediate $\gamma$ photons. During acceleration, the positrons with large-$p_{+,x}$ may escape from the central focusing region and are then expelled out of the bubble by the outer defocusing transverse field. The positrons with low-$p_{+,x}$ can be continuously trapped in the acceleration phase [see Figs. 3(c)-(f)]. Finally at $t_{f}=1000T_{1}$ about 74.12% positrons are accelerated with an average energy increase of about 350 MeV in a distance $\lesssim 1$ mm, reaching $\overline{\varepsilon}_{+}\approx 1.24$ GeV [see Fig. 2(b)], and the acceleration gradient is $G\approx 3.53$ GV/cm [see Figs. 3(g) and (h)]. The final average positron polarization is $\overline{S}_{+}\approx 31.77\%$, which is only slightly depolarized after acceleration [see Fig. 2(a)]. In the period of $200T_{1}\lesssim t\lesssim 1000T_{1}$ some high-energy positrons with low polarization gradually escape from the focusing region [see Fig. 3(j)], therefore, the polarization increases a little. At $t_{f}$ the positron polarization distribution around the peak area of the energy spectrum within the FWHM declines approximately from 70% to 15%. Such distribution provides a possible way to further increase the polarization by the energy-selection technique Alexander et al. (2009).

Besides the trapping ratio and polarization degree, the energy spread and divergence are also important factors for future applications. In Fig. 2(c), we find that the relative energy spread of the positrons decreases by about 26% after the wake acceleration compared to the instant of the pair creation $t_{i}$. While, the absolute energy spread does not increase during the acceleration, because the seed beam not only ‘provides’ the pairs but also flattens the local acceleration field [see Figs. 3(g)-(j)] assuring uniform acceleration and avoiding energy dispersion. The angular divergence of the positron beam is also improved by the focusing field to $\Delta\theta_{+}\approx 20$ mrad, which is about 50% lower than that at $t_{i}$ [see Fig. 2(d), the polarization is nearly uniform ($\overline{S}_{+}\approx 32.67\%$) within the FWHM labelled by the two dashed purple lines]. One can see that there is an asymmetric angular distribution at $t_{f}$ in Fig. 2(d). This is induced by the unbalanced plasma perturbations [indicated in Figs. 3(d) and (f)], originating from the laser incidence from one side.

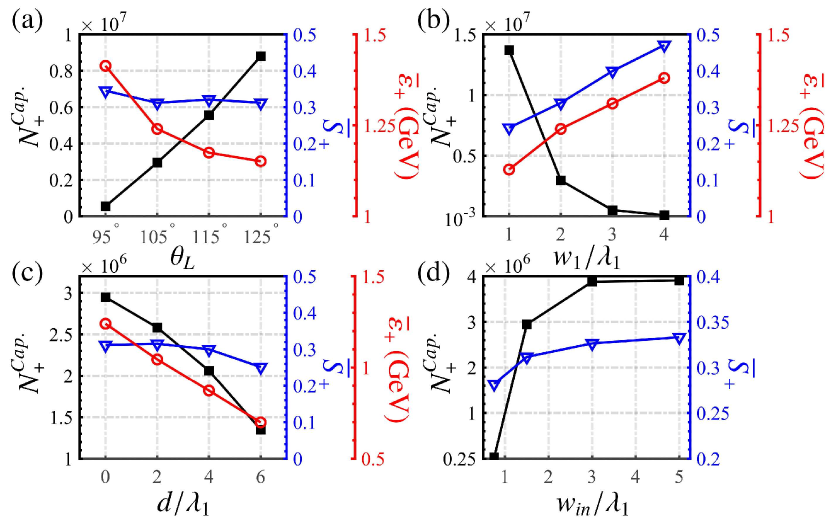
Finally, we study the impact of the initial parameters on the trapping, acceleration and polarization of the positrons in Fig. 4. As the collision angle $\theta_{L}$ increases from $95^{\circ}$ to $125^{\circ}$ [see the interaction scenario in Fig. 1], the probabilities of photon emission and pair production (determined by $\chi_{e}\propto a_{0}\gamma_{e}$[1-cos($\theta_{L}$)] and $\chi_{\gamma}\propto a_{0}k_{\gamma}$[1-cos($\theta_{L}$)], respectively) are both enhanced, thus, $N_{+}^{Cap.}$ increases. At the same time the average energy decreases due to $\overline{\varepsilon}_{+}\propto\sum\varepsilon_{\gamma}/N_{+}^{Cap.}\propto\sum\varepsilon_{s,0}/N_{+}^{Cap.}$. $\overline{S}_{+}$ decreases as well since the asymmetry of the spin-resolved pair production probabilities in the laser positive and negative half cycles is weakened and the radiative depolarization effect is enhanced [see Fig. 4(a)]. As the laser focal radius $w_{1}(w_{2})$ increases with a fixed laser energy $J$, the laser peak amplitude $a_{0}\propto\sqrt{J}/w_{1}$ and $N_{+}^{Cap.}\propto a_{0}^{2}\propto J/w_{1}^{2}$ decrease, and accordingly, $\overline{S}_{+}$ and $\overline{\varepsilon}_{+}$ are both enhanced [see Fig. 4(b)]. As the distance between the seed and driver beams $d$ rises up, more low-energy positrons with high polarization cannot enter the focusing region to be steadily accelerated (i.e. $N_{+}^{Cap.}$ and $\overline{S}_{+}$ both decrease), and the enhancement of the acceleration field by the seed beam [indicated in Figs. 3(g) and (h)] is weakened (i.e. $\overline{\varepsilon}_{+}$ decreases) [see Fig. 4(c)]. Thus, the condition of $d\lesssim\lambda_{p}/2$ should be satisfied. As the inner radius of the driver beam $w_{in}$ increases (more feasible in experiments), more plasma electrons converge into the hollow region to create a larger transverse size of the focusing region Jain et al. (2015); sup , therefore, more positrons can be trapped and the depolarization effect induced by the escape of high-polarization positrons is weakened (i.e. $\overline{S}_{+}$ increases) [see Fig. 4(d) and more details in Ref. sup ]. We underline that in our scheme the positrons are transversely polarized and can be used to investigate specific Triple Gauge Couplings and $W$-physics, and to test the validity of the standard model and discovering new physics Fleischer et al. (1994). In further, the arbitrary spin orientation can be realized through a proper spin rotator Moortgat-Pick et al. (2008).

In conclusion, utilizing both advantages of laser-driven QED process and plasma wakefield acceleration we have proposed a compact scheme for positron polarization, trapping and acceleration. Dense GeV positron beams with a spin polarization up to 70% and improved beam quality compared with the scheme of single laser-electron collision can be achieved. By using multi-staged wakefield acceleration with currently achievable laser facilities, this scheme also provides a possible way to generate highly-polarized positron beams with hundreds of GeVs energy for future compact research and application platforms of high-energy and particle physics.

Acknowledgement: This work was supported by National Natural Science Foundation of China (Grants No. 11991074, 11721091, 11874295, 11804269 and 11905169), the National Key R&D Program of China (Grant No. 2018YFA0404801), and the Science Challenge Project of China (Grants No. TZ2016099 and TZ2018005).