Transverse polarization of Lambda hyperons in hadronic collisions
Abstract
The transverse polarization of hyperon within reconstructed jets in hadronic collisions offers a complementary platform to probe the polarized fragmentation function . We illustrate that by performing a global analysis of the transverse polarization of hyperons produced in different kinematic regions and in different hadronic collisions, such as , , , and collisions, we can pin down the flavor dependence of which has been poorly constrained. Besides the single inclusive jet production, the -boson associated jet production supplements with more capability in removing ambiguities in the flavor dependence of .
I Introduction
Fragmentation functions (FFs) are nonperturbative quantities in calculating hadron production cross section in high energy reactions Collins:1981uw ; Metz:2016swz ; Chen:2023kqw ; Boussarie:2023izj , which are still not eligible for first-principle calculations in QCD. Usually, a global analysis of experimental data can provide vital information on FFs, which can then be used in making predictions for future experiments. On one hand, there is quite a lot of experimental data on the single inclusive hadron production in various high-energy collisions, which is sensitive to the collinear unpolarized FF . Therefore, quite a few studies Binnewies:1994ju ; Kretzer:2000yf ; Bourhis:2000gs ; deFlorian:2007aj ; deFlorian:2007ekg ; Albino:2008fy ; deFlorian:2014xna ; deFlorian:2017lwf ; Borsa:2021ran ; Borsa:2022vvp ; Borsa:2023zxk have extracted it with a global analysis. On the other hand, the transverse-momentum-dependent fragmentation functions (TMD FFs), especially the spin-dependent ones, are largely unknown due to limited data. Nonetheless, it has still attracted a lot of attention recently. Many phenomenological studies devoted to this topic Anselmino:2007fs ; Anselmino:2013vqa ; Anselmino:2013lza ; Anselmino:2015sxa ; Kang:2015msa ; Anselmino:2015fty ; Bacchetta:2001di ; Metz:2002iz ; Gamberg:2003eg ; Amrath:2005gv ; Bacchetta:2007wc ; Matevosyan:2012ga ; Lu:2015wja ; Yang:2016mxl ; Yang:2017cwi ; Wang:2018wqo ; Xie:2022lra . Furthermore, the QCD evolution Aybat:2011ge ; Echevarria:2014rua for the spin-dependent fragmentation functions has also been established at the leading twist, which paves the way for a global analysis of experimental data at different energy scales in the future. For a recent review of the general progress, see e.g. Metz:2016swz ; Chen:2023kqw ; Boussarie:2023izj .
The polarized FF , which is the partner in FFs of the famous Sivers function, induces the transverse polarization along the normal direction of the hadron production plane, i.e., along the direction with and being the three-momenta of the fragmenting parton and the produced hadron. Belle collaboration has measured the transverse polarization of in inclusive and semi-inclusive -annihilations Belle:2018ttu , which has been immediately followed by several phenomenological studies Anselmino:2019cqd ; DAlesio:2020wjq ; Callos:2020qtu ; Chen:2021hdn ; Li:2020oto ; Matevosyan:2018jht ; DAlesio:2021dcx ; Gamberg:2018fwy ; Gamberg:2021iat ; Yang:2021zgy ; Li:2021txj . A major issue emerges Chen:2021hdn in these studies: is the isospin symmetry of the polarized FF violated? The answer to this question is crucially important in understanding the fundamental properties of strong interaction. However, as confirmed in Refs. DAlesio:2022brl ; DAlesio:2023ozw , current experimental data from Belle alone cannot settle this issue. Therefore, it has been proposed that the future measurement of Lambda transverse polarization at the future electron-ion colliders (EIC) can ultimately test the isospin symmetry Chen:2021zrr . Similar studies have also been presented in Refs. Kang:2021kpt ; DAlesio:2023ozw . With the EIC experiment still at the horizon, we look for opportunities in experimental facilities that are currently available.
The concept of hadron within jet has been proposed Yuan:2007nd ; Bain:2016rrv ; Kang:2016ehg ; Kang:2017glf ; Kang:2020xyq ; Kang:2023elg , which makes it possible to study TMD FFs even in hadronic collisions. Recent works Kang:2020xyq ; DAlesio:2024ope have also constructed a framework to study in collisions. The relation between jet FFs and the conventional TMD parton FFs has been established. Preliminary results from the STAR collaboration have also been published Gao:2024dxl , which indicates the potential of studying spin effects in unpolarized hadronic collisions. Furthermore, hadronic collisions also provide an ideal platform to investigate the gluon FFs. As elaborated in Refs. Zhang:2023ugf ; Li:2023qgj , the longitudinal spin transfer of the gluon can be well constrained by measuring the longitudinal polarization correlation of two final state hadrons.
In this work, we investigate the Lambda transverse polarization in different hadronic collisions and demonstrate its potential of extracting the flavor dependence of the polarized FF. We benefit from the hadron within jet framework Yuan:2007nd ; Bain:2016rrv ; Kang:2017glf ; Kang:2020xyq ; Kang:2023elg ; DAlesio:2024ope and focus mainly on the phenomenological side. Therefore, we work at leading order (LO) in perturbative QCD and identify the TMD jet FFs with the TMD parton FFs. We perform a comprehensive calculation for the Lambda transverse polarizations in collisions. We demonstrate that the flavor components are quite different in different kinematic regions and in different hadronic collisions. Therefore, the current hadron colliders, such as RHIC, LHC and Tevatron, can significantly improve our understanding on the polarized FF. We also present our numerical results for the Lambda transverse polarization within -boson associated jets. The flavor component is different from that in the single inclusive jet production. Therefore, it provides a complementary channel to investigate the flavor dependence.
The jet FFs are in principle different from the parton FFs. However, as demonstrated in Kang:2016ehg ; Kang:2017glf ; Kang:2023elg , they can be matched to the latter. The matching coefficient is perturbatively calculable. Therefore, an extended universality has been established between parton FFs and jet FFs. At the LO accuracy, they are identical. Since the aim of this paper is to demonstrate the potential of hadron colliders for disentangling the flavor dependence of , we perform a LO calculation and leave a more accurate NLO global analysis for a future study when more experimental data are available. The LO calculation contains large uncertainties. For instance, the LO cross section strongly depends on the the choice of factorization and renormalization scales. However, in the context of flavor components, the scale dependence becomes negligible. A more precise next-to-leading order (NLO) calculation only provides a small correction and thus does not affect the qualitative conclusion. We present a comparison between LO and NLO results in Appendix B.
The rest of the paper is organized as follows. In Sec. II, we present the general formulas to calculate the jet production ratios and Lambda transverse polarization in hadronic collisions. In Sec. III, we present our numerical results for the production ratios and polarization in various reactions, and extensively explore the potential for flavor separation of . A summary is given in Sec. IV.
II General formulas
In this section, we first lay out the formulas for calculating hadron-within-jet cross section in hadronic collisions. Then, we present the Lambda transverse polarization with a Gaussian ansatz.
II.1 Differential cross sections
Since our goal is to investigate the potential of extracting the flavor dependence of the polarized FF in hadronic collisions, we first present the differential cross section of the single inclusive jet production with a given flavor in collisions. Although the flavor of a reconstructed jet in experiments is not well defined, we still employ this phrase since we have limited ourselves at the LO approximation. A jet is simply a parton at LO. The flavor dependent cross section is given by
| (1) |
where is the parton distribution function with the momentum fraction of the hadron carried by the parton and the factorization scale, and denote the rapidity and transverse momentum of parton which is also identified as the jet measured in experiments, and denotes the rapidity of unmeasured final state parton . The momentum fractions and can be calculated with and for massless partons. denotes the partonic cross section. To compare with the single inclusive jet cross section measured in the experiments, we have to sum over all possible “jet flavors” since current experimental instruments cannot distinguish jet flavors.
To quantify the flavor component of final state jets, we define the production ratio of a given jet flavor as
| (2) |
The cross section of hadron within jet production at the LO can be obtained by convoluting the above jet cross section with the corresponding jet FF Yuan:2007nd ; Kang:2017btw . We obtain
| (3) |
where is the momentum fraction of the parton carried by the final state hadron and is the transverse momentum of with respect to the jet momentum. Here is the Lambda mass and is the transverse spin vector of . is the unpolarized FF, and is the polarized FF.
II.2 Transverse polarization
The transverse polarization of final state hyperons along the direction is given by
| (4) |
Here indicates , and means .
Inserting Eq. (3) into Eq. (4), it is straightforward to obtain
| (5) |
Since this paper mainly focuses on the flavor dependence of the polarized FF , we neglect the QCD evolution effect for simplicity and take Gaussian ansatz for distribution, namely
| (6) | ||||
| (7) |
Here, is the Gaussian width which, as an approximation, is chosen the same between the unpolarized and polarized FFs. With the Gaussian ansatz and taking average over the magnitude of , the final expression for the Lambda polarization can be simplified to
| (8) |
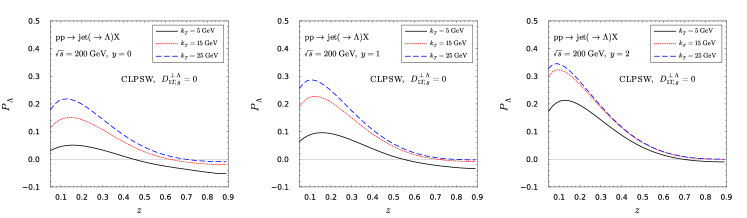
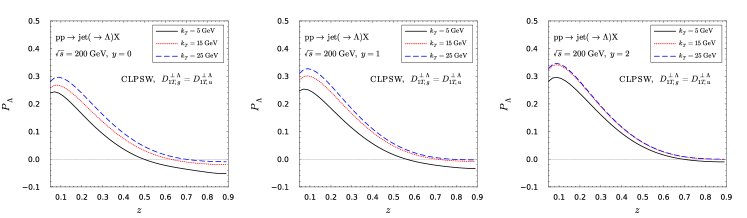
In the numerical calculation, we employ the DSV parametrization deFlorian:1997zj to provide the unpolarized Lambda FF and mainly employ the isospin symmetric CLPSW parametrization Chen:2021hdn for the polarized one . For comparison, we have also used the isospin violated DMZ DAlesio:2020wjq and CKT Callos:2020qtu parametrizations in some calculations.
Furthermore, in the hybrid factorization framework, the factorization scale of the initial state collinear parton distribution functions (PDFs) is usually chosen to be with being the transverse momentum of the jet in the lab frame. However, that of the final state TMD jet FFs is usually chosen to be with being the jet cone size. In the numerical evaluation, the DGLAP evolution of collinear PDFs has been taken care of by the CT18 PDF Hou:2019efy . The QCD evolution of the final state has been extensively investigated in Gamberg:2021iat ; Kang:2010xv . As discussed in Appendix C, this effect also does not change our conclusion. Therefore, we take the Gaussian ansatz for simplicity.
III Numerical results
In this section, we present our numerical predictions for the Lambda polarization in different hadronic collisions, namely , , , and photon-nucleus collisions. We make predictions for the single inclusive jet production process as well as the -boson associated jet production process. The flavor components in different processes vary quite a lot. Therefore, a global analysis of all those processes can eventually lay out the flavor dependence of the polarized fragmentation function.
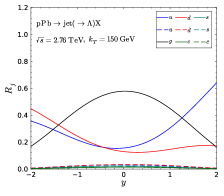
III.1 Single inclusive jet production in , and collisions
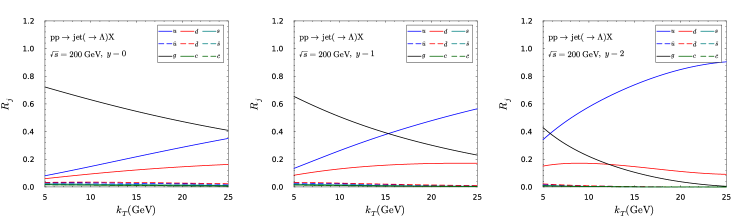
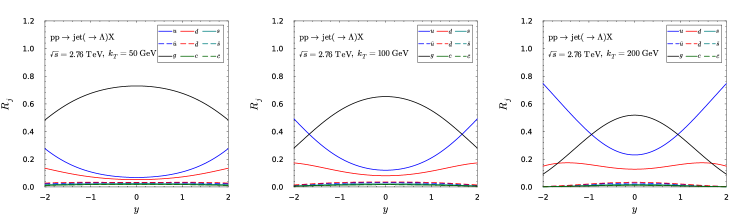
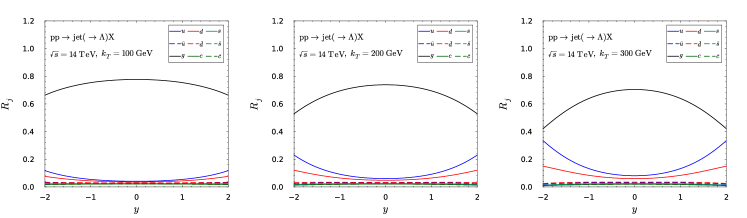
To demonstrate the potential of revealing the flavor dependence, we first calculate the production ratios of different flavor jets in collisions at the RHIC energy. The numerical results at the LO accuracy are presented as a function of jet in the upper panel of Fig. 1 and as a function of jet rapidity in the lower panel, where we employ CT18 PDFs Hou:2019efy . The qualitative feature is well-known: the valance quark contribution increases with increasing and increasing rapidity, while the gluon contribution decreases. The same feature is also exhibited at the LHC energies, as shown in Figs. 12 and 13 in the appendix. Therefore, by comparing the Lambda transverse polarization at different rapidities and jet transverse momenta, we obtain the power to extract the polarized gluon FFs which has been poorly constrained in previous studies DAlesio:2020wjq ; Callos:2020qtu ; Chen:2021hdn .
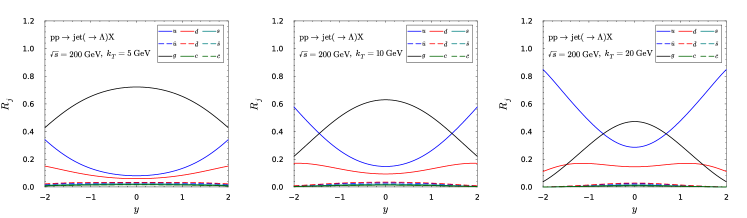
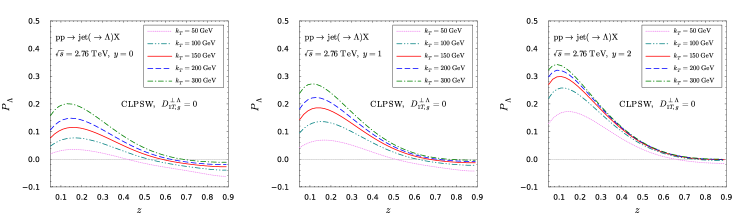
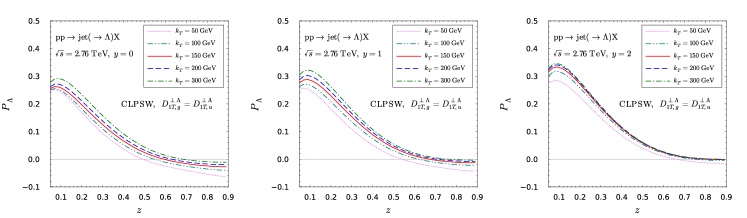
For instance, the CLPSW parametrization Chen:2021hdn is proposed to describe the Lambda transverse polarization in annihilation at LO. Therefore, the gluon fragmentation function is absent in the previous analysis. However, it is important in making predictions for the hadronic collisions, since they amount to a sizable contribution. In this study, we propose two extreme prescriptions. In the first prescription, we simply assume that the gluon does not contribute to the Lambda polarization by setting . In the second prescription, we assume that . The numerical results are shown in Fig. 2. The upper panel shows the results using the first prescription, while the lower panel shows those in the second prescription. The real case should deviate from these two simple prescriptions and might be somewhere in between. However, the difference between two panels demonstrates this process is indeed sensitive to the gluon FF. Therefore, it is plausible to extract the gluon FF. More numerical predictions for the LHC energies are presented in the appendix.
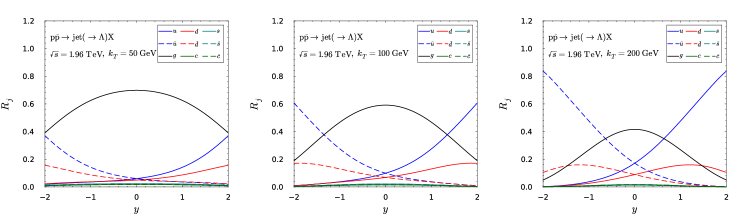
The second process we investigate is the single inclusive jet production in collisions. Unlike the case in collisions, the forward and backward directions are no longer symmetric in collisions. We show the production rate of different flavor jets as a function of rapidity in Fig. 3. It is apparent that there are more quark jets in the forward rapidity (proton-going direction) and there are more quark jets in the backward rapidity (antiproton-going direction). This forward-backward asymmetric enables us to examine the difference between quark and antiquark fragmentation functions. This point can be fully appreciated from the numerical results shown in Fig. 4. The CLPSW, DMZ and CKT parametrizations have parametrized the and fragmentation differently, so that the magnitude of forward-backward asymmetry also varies. Therefore, including the Tevatron experiment in the global analysis can cast more light on the flavor dependence of .
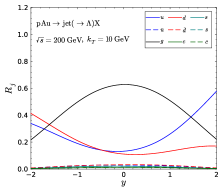
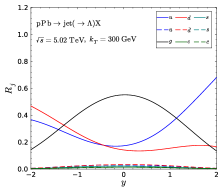
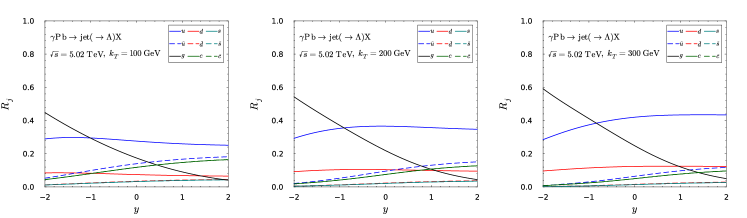
The last process we study in this subsection is the single inclusive jet production in collisions. Similar to the collisions, there is also a forward-backward asymmetry. However, in this process, we can study the difference between and quark fragmentation function. We present the production ratios of different flavor jets as a function of jet rapidity in Fig. 5, which clearly shows that there are more quark jets in the proton-going direction and more quark jets in the nucleus-going direction. For nuclear modified PDFs we take EPPS21 sets Eskola:2021nhw .
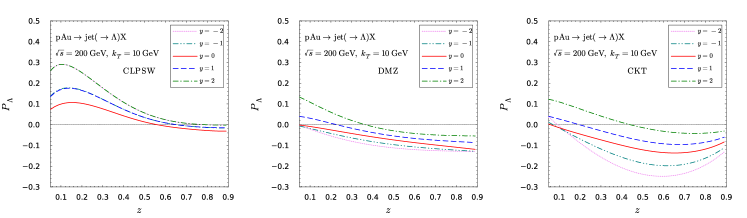
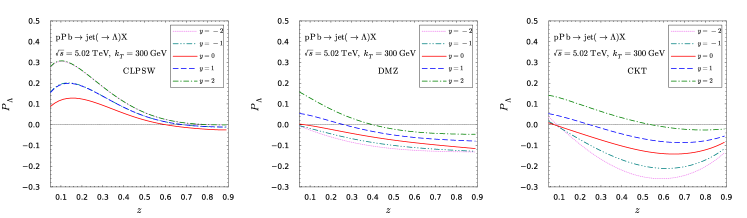
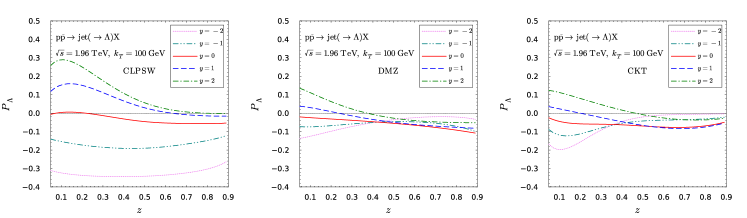
As underlined in the previous work Chen:2021hdn , the Lambda hyperon is an isospin singlet. The isospin symmetry requires . This requirement has been respected in the CLPSW parametrization, while it has been severely violated in the DMZ and CKT parametrizations. The answer to whether or not the isospin symmetry is violated in the hadronization process is vitally important for understanding strong interaction at the non-perturbative regime. We thus present the numerical results for the Lambda polarization at different rapidities in collisions in Fig. 6. Apparently, there is almost no difference between forward and backward rapidities in the isospin symmetric CLPSW parametrization. However, one can observe distinguish difference in the DMZ and CKT parametrizations. Therefore, future experimental measurements on this aspect can eventually clarify this issue.
To summarize, a global analysis of the Lambda transverse polarization in different kinematic regions in , , and collisions has great potential in pinning down the flavor dependence of the polarized fragmentation function .
III.2 -boson associated jet production
Besides the single-inclusive jet production, another important channel deserving study is the -boson associated jet production. Unlike the single-inclusive jet production dominated by strong interaction, this process is an electroweak process. The electroweak vertex modifies the production ratios of jets with different flavors. Therefore, the phenomenological study of this channel provides a complementary platform to investigate flavor dependence.
To be more specific, the process we consider is . Here, we only consider the prompt production for the final state photon or -boson. At LO, there are two partonic channels that contribute, namely and . Therefore, the gluon contribution is strongly suppressed at low jet and in the central rapidity.
Furthermore, for the photon associated jet production, the partonic cross sections are given by
| (9) | |||
| (10) |
Due to the factor, the quark contribution dominates in almost the whole kinematic region. However, as shown in Fig. 7, the gluon contribution is flat with increasing rapidity. This is a feature not expected in the single inclusive jet production where the gluon contribution is strongly suppressed in the forward rapidity. Therefore, this process provides with a fresh angle in the global analysis.
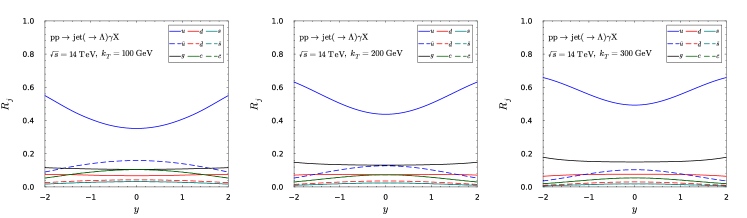
On the other hand, for the associated jet production, the partonic cross sections are given by
| (11) | |||
| (12) |
Here is the mass of -boson, is the Weinberg angle and . In this case, the contribution from quark is still important. However, it does not play the dominant role any more. As shown in Fig. 8, , and gluon contributions are, roughly speaking, equally important.
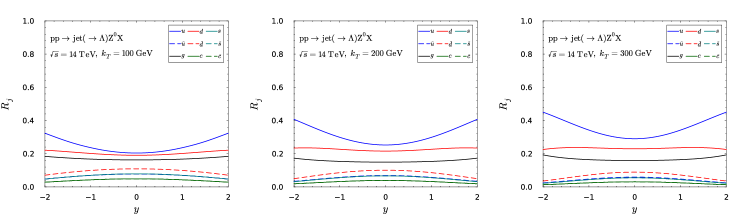
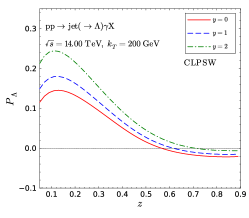
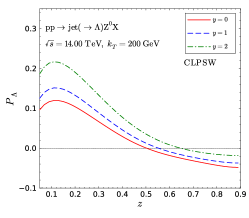
We present our numerical predictions for transverse polarization in the vecor boson associated jet production processes in collisions in Fig. 9. The left plot is the result for photon-jet production process and the right plot is that for -jet production. Both show that polarization can reach as large as .
III.3 Single inclusive jet production in photon-nucleus collisions
In the relativistic heavy-ion collisions, most of the hard scatterings come from the QCD events where both nuclei break up. However, since the large nucleus is accompanied by an enormous number of quasireal photons, it is also quite plausible that only one of the quasireal photons interact with the other nucleus in the peripheral nucleus-nucleus collisions. In this case, the projectile nucleus (the photon-providing one) does not break up and appears in the final state. The target nucleus (photon-striking one) breaks. In this work, we refer the photon-going direction as the forward direction.
According to the Equivalent Photon Approximation (EPA), we have the following collision
| (13) |
where the photon distribution of the projectile nucleus is given by Baltz:2007kq
| (14) |
Here, with being the light-cone momentum fraction carried by the quasireal photon. is the nuclear charge number, is the mass of the proton. and are the nucleus radiuses of the projectile and target nuclei. This process resembles SIDIS quite a lot. However, the photon in this process is almost onshell which is different from the case in SIDIS.
The partonic hard scatterings at LO are and with partonic cross sections given by
| (15) | |||
| (16) |
As shown in Fig. 10, the gluon contribution is very important in the backward rapidity. However, it becomes negligible in the forward rapidity. Therefore, this process also offers the optimal platform to investigate the gluon FFs.
We show our numerical predictions for Lambda transverse polarization in photon-nucleus collisions in Fig. 11. The results without gluon contribution are shown in the left panel, and those with gluon contribution are shown in the right panel. As expected, the difference between these two becomes sizable in the backward rapidity, registering the potential to probe the gluon FFs.
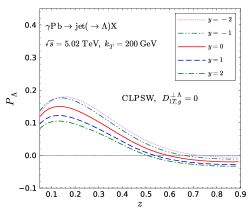
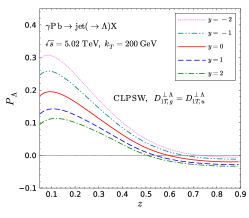
IV Summary
The flavor dependence of the polarized fragmentation function of remains ambiguous. While the dispute of isospin symmetry is expected to be ultimately solved Chen:2021zrr ; DAlesio:2023ozw by the future EIC experiment, the study of polarized gluon FF has to rely on other processes. Recent progress of hadron within jet Yuan:2007nd ; Bain:2016rrv ; Kang:2017glf ; Kang:2020xyq ; Kang:2023elg made it possible to investigate TMD FFs in hadronic collisions. In this paper, we demonstrate that the current hadron colliders which are still harvesting data have a great potential in constraining the flavor dependence and extracting the gluon polarized FF.
In this work, we perform a comprehensive study for the transverse polarization of Lambda hyperons produced in the single inclusive jet production and -boson associated jet production processes in , , and collisions. By comparing the Lambda transverse polarization in different kinematic regions and in different processes, we can gain information on the flavor dependence. Particularly, for the single inclusive jet production in collisions, the dominant contribution comes from gluon in the central rapidity, while the dominant contribution comes from quark in the forward rapidity. Therefore, by comparing the Lambda polarizations in forward and central rapidities, we can separate gluon FF from the quark FF. Similarly, in collisions, the dominant contribution arises from gluon as well in the central rapidity. However, quark dominates in the forward rapidity, while quark dominates in the backward rapidity. Such a forward-backward asymmetry allows us to separate quark FF from quark FF. A forward-backward asymmetry also appears in collisions, which allows us to test the isospin symmetry, i.e., the difference between and FFs. Furthermore, the flavor component of the -boson associated jet production is different from that of the single inclusive jet production. Therefore, it casts more light on the flavor dependence of the polarized FF.
As the complementary approach, we also study the Lambda transverse polarization in the photon-nucleus collisions. In this case, the gluon contribution varies significantly with the rapidity, which makes this process a novel probe to explore the polarized gluon FF.
Acknowledgements.
This work is supported in part by the National Natural Science Foundation of China (approval number 12375075, 11505080, 12005122), the Taishan fellowship of Shandong Province for junior scientists, the Shandong Province Natural Science Foundation under grant No. 2023HWYQ-011, No. ZR2018JL006, and No. ZR2020QA082, and the Youth Innovation Team Program of Higher Education Institutions in Shandong Province (Grant No. 2023KJ126).Appendix A Production ratios and polarization at LHC
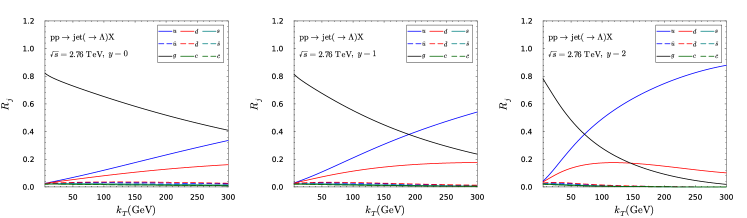
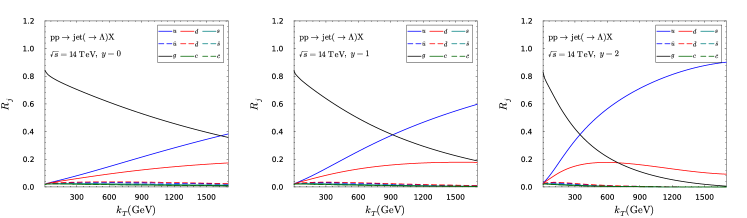
In this appendix, we present our predictions for the single inclusive jet production in collisions at LHC.
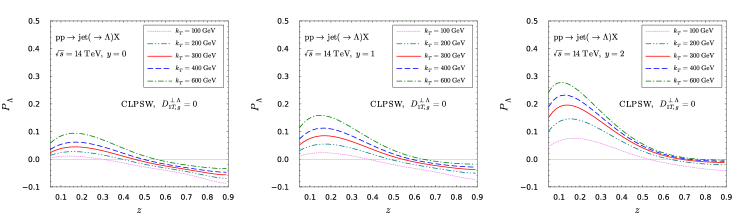
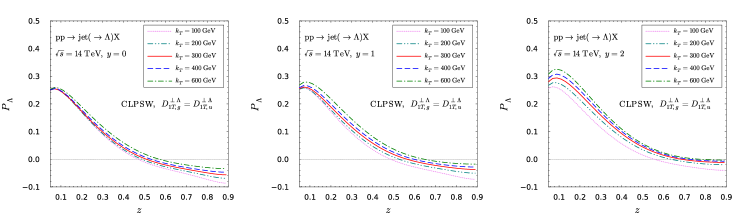
We first present the production ratios in Figs. 12 and 13 as functions of at fixed rapidity , and as functions of at fixed with at the LHC.
Then we present our numerical results for the Lambda transverse polarization at LHC in Fig. 14 and 15.
Appendix B Next-to-leading order correction
The leading-order calculation contains large uncertainties and is not sufficient for precision studies. However, the existing experimental data is still far from being accurate enough to constrain the polarized fragmentation function. Therefore, in this paper, we only present a general guideline on how to disentangle the flavor dependence of in current hadron colliders, and leave a more accurate next-to-leading order calculation for a future study when more experimental data with a higher precision is available. In this section, we simply demonstrate that the qualitative features obtained based on the leading order calculation is not affected by higher order corrections.
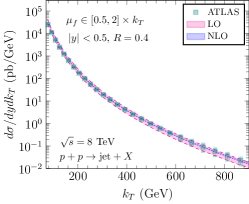
In Fig. 16, we first show the single inclusive jet production cross section at leading and next-to-leading orders in unpolarized pp collisions at TeV compared with the experimental data from the ATLAS collaboration ATLAS:2017kux at the LHC. We have varied the factorization/renormalization scales with being the jet transverse momentum to estimate the theoretical uncertainty. As expected, the scale dependence at the next-to-leading order is much smaller than that at the leading order. However, by properly choosing scales (for instance ), we can eliminate large logarithms in the next-to-leading order hard factor, and therefore minimize higher-order corrections. This way, even the leading order calculation can also describe the ATLAS data well.
Furthermore, we also present the leading and next-to-leading order jet flavor components as a function of jet transverse momentum in Fig. 17. We only present the relative contribution from , , , and gluon in Fig. 17. Contributions from the other partons are not shown explicitly since they are not of interest here. Clearly, the qualitative conclusion based on the leading order calculation remains unaltered at the next-to-leading order. Gluon jet still dominates at low and quark contribution significantly rises with increasing .
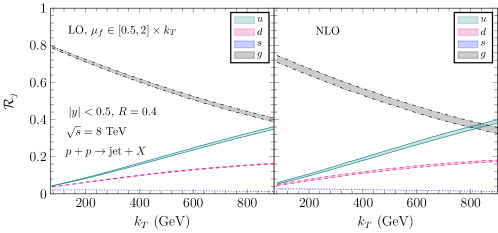
To summarize, the leading order calculation offers an intuitive and correct physical picture on the flavor component. The higher-order contribution is expected to provide minor correction to the flavor component and will not affect our conclusion.
Appendix C Collins-Soper Evolution of
In the hybrid factorization scheme, the jet fragmentation assumes the TMD factorization. Both the unpolarized jet fragmentation function and the polarized fragmentation function satisfy the Collins-Soper evolution equation. Here, we have already set all scales to be the same for simplicity. In the end, we arrive at
| (17) | |||
| (18) |
Here we have employed the -prescription to separate the perturbative and the non-perturbative regions, so that the scale with GeV-1.
The exact expressions for perturbative and non-perturbative Sudakov factors are taken from Ref. Gamberg:2021iat . The perturbative Sudakov factor remains the same for the polarized and unpolarized fragmentation functions. and are non-perturbative Sudakov factors that can only be extracted from experimental data. We note here that the non-perturbative Sudakov factor still contains large uncertainties, which can only be removed through a global analysis to the future experimental data.
is the collinear fragmentation function and therefore follows the DGLAP evolution equation. On the other hand, the QCD evolution of is a bit more involved. First, it is not a closed equation Kang:2010xv . The evolution kernel consists of a conventional DGLAP evolution part and also a twist-3 source term. The twist-3 source term is so far unknown. Second, even the conventional DGLAP evolution part also evolves the gluon polarized fragmentation function which is also not well constrained by the Belle experiment. At this stage of research, we have neglected the QCD evolution of the collinear function in the numerical evaluation and simply assume
| (19) |
with GeV being the factorization scale where has been extracted.
With the above configuration, we first present as a function of at different factorization scales in Fig. 18. Thanks to the Sudakov double and single logarithms, the broadening effect is quite strong at large factorization scale.
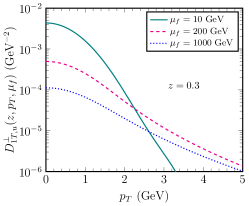
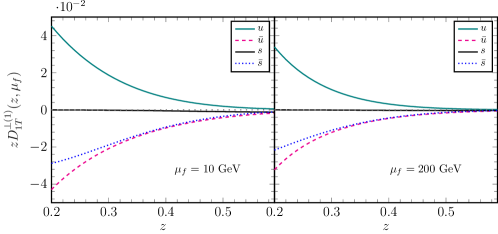
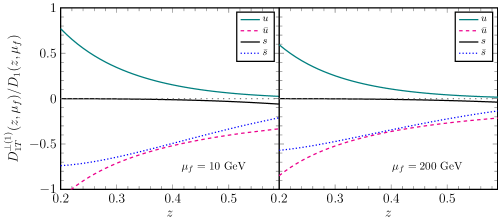
Since we have integrated over the in this research, it is intriguing to present the first moment of at different factorization scales as well. In contrast with Eq. (19), is defined as
| (20) |
where GeV. The numerical results are presented in Fig. 19. The QCD evolution affects the absolute magnitude of only by a little bit.
References
- (1) J. C. Collins and D. E. Soper, Nucl. Phys. B 194 (1982), 445-492 doi:10.1016/0550-3213(82)90021-9
- (2) A. Metz and A. Vossen, Prog. Part. Nucl. Phys. 91 (2016), 136-202 doi:10.1016/j.ppnp.2016.08.003 [arXiv:1607.02521 [hep-ex]].
- (3) K. B. Chen, T. Liu, Y. K. Song and S. Y. Wei, Particles 6 (2023) no.2, 515-545 doi:10.3390/particles6020029 [arXiv:2307.02874 [hep-ph]].
- (4) R. Boussarie, M. Burkardt, M. Constantinou, W. Detmold, M. Ebert, M. Engelhardt, S. Fleming, L. Gamberg, X. Ji and Z. B. Kang, et al. [arXiv:2304.03302 [hep-ph]].
- (5) J. Binnewies, B. A. Kniehl and G. Kramer, Z. Phys. C 65 (1995), 471-480 doi:10.1007/BF01556135 [arXiv:hep-ph/9407347 [hep-ph]].
- (6) S. Kretzer, Phys. Rev. D 62 (2000), 054001 doi:10.1103/PhysRevD.62.054001 [arXiv:hep-ph/0003177 [hep-ph]].
- (7) L. Bourhis, M. Fontannaz, J. P. Guillet and M. Werlen, Eur. Phys. J. C 19 (2001), 89-98 doi:10.1007/s100520100579 [arXiv:hep-ph/0009101 [hep-ph]].
- (8) D. de Florian, R. Sassot and M. Stratmann, Phys. Rev. D 75 (2007), 114010 doi:10.1103/PhysRevD.75.114010 [arXiv:hep-ph/0703242 [hep-ph]].
- (9) D. de Florian, R. Sassot and M. Stratmann, Phys. Rev. D 76 (2007), 074033 doi:10.1103/PhysRevD.76.074033 [arXiv:0707.1506 [hep-ph]].
- (10) S. Albino, B. A. Kniehl and G. Kramer, Nucl. Phys. B 803 (2008), 42-104 doi:10.1016/j.nuclphysb.2008.05.017 [arXiv:0803.2768 [hep-ph]].
- (11) D. de Florian, R. Sassot, M. Epele, R. J. Hernández-Pinto and M. Stratmann, Phys. Rev. D 91 (2015) no.1, 014035 doi:10.1103/PhysRevD.91.014035 [arXiv:1410.6027 [hep-ph]].
- (12) D. de Florian, M. Epele, R. J. Hernandez-Pinto, R. Sassot and M. Stratmann, Phys. Rev. D 95 (2017) no.9, 094019 doi:10.1103/PhysRevD.95.094019 [arXiv:1702.06353 [hep-ph]].
- (13) I. Borsa, D. de Florian, R. Sassot and M. Stratmann, Phys. Rev. D 105 (2022) no.3, L031502 doi:10.1103/PhysRevD.105.L031502 [arXiv:2110.14015 [hep-ph]].
- (14) I. Borsa, R. Sassot, D. de Florian, M. Stratmann and W. Vogelsang, Phys. Rev. Lett. 129 (2022) no.1, 012002 doi:10.1103/PhysRevLett.129.012002 [arXiv:2202.05060 [hep-ph]].
- (15) I. Borsa, M. Stratmann, D. de Florian and R. Sassot, Phys. Rev. D 109 (2024) no.5, 052004 doi:10.1103/PhysRevD.109.052004 [arXiv:2311.17768 [hep-ph]].
- (16) M. Anselmino, M. Boglione, U. D’Alesio, A. Kotzinian, F. Murgia, A. Prokudin and C. Turk, Phys. Rev. D 75 (2007), 054032 doi:10.1103/PhysRevD.75.054032 [arXiv:hep-ph/0701006 [hep-ph]].
- (17) M. Anselmino, M. Boglione, U. D’Alesio, S. Melis, F. Murgia and A. Prokudin, Phys. Rev. D 87 (2013), 094019 doi:10.1103/PhysRevD.87.094019 [arXiv:1303.3822 [hep-ph]].
- (18) M. Anselmino, M. Boglione, J. O. Gonzalez Hernandez, S. Melis and A. Prokudin, JHEP 04 (2014), 005 doi:10.1007/JHEP04(2014)005 [arXiv:1312.6261 [hep-ph]].
- (19) M. Anselmino, M. Boglione, U. D’Alesio, J. O. Gonzalez Hernandez, S. Melis, F. Murgia and A. Prokudin, Phys. Rev. D 92 (2015) no.11, 114023 doi:10.1103/PhysRevD.92.114023 [arXiv:1510.05389 [hep-ph]].
- (20) Z. B. Kang, A. Prokudin, P. Sun and F. Yuan, Phys. Rev. D 93 (2016) no.1, 014009 doi:10.1103/PhysRevD.93.014009 [arXiv:1505.05589 [hep-ph]].
- (21) M. Anselmino, M. Boglione, U. D’Alesio, J. O. Gonzalez Hernandez, S. Melis, F. Murgia and A. Prokudin, Phys. Rev. D 93 (2016) no.3, 034025 doi:10.1103/PhysRevD.93.034025 [arXiv:1512.02252 [hep-ph]].
- (22) A. Bacchetta, R. Kundu, A. Metz and P. J. Mulders, Phys. Lett. B 506 (2001), 155-160 doi:10.1016/S0370-2693(01)00388-4 [arXiv:hep-ph/0102278 [hep-ph]].
- (23) A. Metz, Phys. Lett. B 549 (2002), 139-145 doi:10.1016/S0370-2693(02)02899-X [arXiv:hep-ph/0209054 [hep-ph]].
- (24) L. P. Gamberg, G. R. Goldstein and K. A. Oganessyan, Phys. Rev. D 68 (2003), 051501 doi:10.1103/PhysRevD.68.051501 [arXiv:hep-ph/0307139 [hep-ph]].
- (25) D. Amrath, A. Bacchetta and A. Metz, Phys. Rev. D 71 (2005), 114018 doi:10.1103/PhysRevD.71.114018 [arXiv:hep-ph/0504124 [hep-ph]].
- (26) A. Bacchetta, L. P. Gamberg, G. R. Goldstein and A. Mukherjee, Phys. Lett. B 659 (2008), 234-243 doi:10.1016/j.physletb.2007.09.076 [arXiv:0707.3372 [hep-ph]].
- (27) H. H. Matevosyan, A. W. Thomas and W. Bentz, Phys. Rev. D 86 (2012), 034025 doi:10.1103/PhysRevD.86.034025 [arXiv:1205.5813 [hep-ph]].
- (28) Z. Lu and I. Schmidt, Phys. Lett. B 747 (2015), 357-364 doi:10.1016/j.physletb.2015.06.011 [arXiv:1501.04379 [hep-ph]].
- (29) Y. Yang, Z. Lu and I. Schmidt, Phys. Lett. B 761 (2016), 333-339 doi:10.1016/j.physletb.2016.08.053 [arXiv:1607.01638 [hep-ph]].
- (30) Y. Yang, Z. Lu and I. Schmidt, Phys. Rev. D 96 (2017) no.3, 034010 doi:10.1103/PhysRevD.96.034010 [arXiv:1706.03355 [hep-ph]].
- (31) X. Wang, Y. Yang and Z. Lu, Phys. Rev. D 97 (2018) no.11, 114015 doi:10.1103/PhysRevD.97.114015 [arXiv:1802.01843 [hep-ph]].
- (32) X. Xie and Z. Lu, Phys. Lett. B 842 (2023), 137973 doi:10.1016/j.physletb.2023.137973 [arXiv:2210.16532 [hep-ph]].
- (33) S. M. Aybat, J. C. Collins, J. W. Qiu and T. C. Rogers, Phys. Rev. D 85 (2012), 034043 doi:10.1103/PhysRevD.85.034043 [arXiv:1110.6428 [hep-ph]].
- (34) M. G. Echevarria, A. Idilbi and I. Scimemi, Phys. Rev. D 90 (2014) no.1, 014003 doi:10.1103/PhysRevD.90.014003 [arXiv:1402.0869 [hep-ph]].
- (35) Y. Guan et al. [Belle], Phys. Rev. Lett. 122 (2019) no.4, 042001 doi:10.1103/PhysRevLett.122.042001 [arXiv:1808.05000 [hep-ex]].
- (36) M. Anselmino, R. Kishore and A. Mukherjee, Phys. Rev. D 100 (2019) no.1, 014029 doi:10.1103/PhysRevD.100.014029 [arXiv:1905.02777 [hep-ph]].
- (37) U. D’Alesio, F. Murgia and M. Zaccheddu, Phys. Rev. D 102 (2020) no.5, 054001 doi:10.1103/PhysRevD.102.054001 [arXiv:2003.01128 [hep-ph]].
- (38) D. Callos, Z. B. Kang and J. Terry, Phys. Rev. D 102 (2020) no.9, 096007 doi:10.1103/PhysRevD.102.096007 [arXiv:2003.04828 [hep-ph]].
- (39) K. B. Chen, Z. T. Liang, Y. L. Pan, Y. K. Song and S. Y. Wei, Phys. Lett. B 816 (2021), 136217 doi:10.1016/j.physletb.2021.136217 [arXiv:2102.00658 [hep-ph]].
- (40) H. Li, X. Wang, Y. Yang and Z. Lu, Eur. Phys. J. C 81 (2021) no.4, 289 doi:10.1140/epjc/s10052-021-09064-1 [arXiv:2009.07193 [hep-ph]].
- (41) H. H. Matevosyan, A. Kotzinian and A. W. Thomas, JHEP 10 (2018), 008 doi:10.1007/JHEP10(2018)008 [arXiv:1808.00954 [hep-ph]].
- (42) U. D’Alesio, F. Murgia and M. Zaccheddu, JHEP 10 (2021), 078 doi:10.1007/JHEP10(2021)078 [arXiv:2108.05632 [hep-ph]].
- (43) L. Gamberg, Z. B. Kang, D. Pitonyak, M. Schlegel and S. Yoshida, JHEP 01 (2019), 111 doi:10.1007/JHEP01(2019)111 [arXiv:1810.08645 [hep-ph]].
- (44) L. Gamberg, Z. B. Kang, D. Y. Shao, J. Terry and F. Zhao, Phys. Lett. B 818 (2021), 136371 doi:10.1016/j.physletb.2021.136371 [arXiv:2102.05553 [hep-ph]].
- (45) Y. Yang, X. Wang and Z. Lu, Phys. Rev. D 103 (2021), 114011 doi:10.1103/PhysRevD.103.114011 [arXiv:2103.11348 [hep-ph]].
- (46) H. Li, X. Wang and Z. Lu, Phys. Rev. D 104 (2021) no.3, 034020 doi:10.1103/PhysRevD.104.034020 [arXiv:2104.12155 [hep-ph]].
- (47) U. D’Alesio, L. Gamberg, F. Murgia and M. Zaccheddu, JHEP 12 (2022), 074 doi:10.1007/JHEP12(2022)074 [arXiv:2209.11670 [hep-ph]].
- (48) U. D’Alesio, L. Gamberg, F. Murgia and M. Zaccheddu, Phys. Rev. D 108 (2023) no.9, 094004 doi:10.1103/PhysRevD.108.094004 [arXiv:2307.02359 [hep-ph]].
- (49) K. b. Chen, Z. t. Liang, Y. k. Song and S. y. Wei, Phys. Rev. D 105 (2022) no.3, 034027 doi:10.1103/PhysRevD.105.034027 [arXiv:2108.07740 [hep-ph]].
- (50) Z. B. Kang, J. Terry, A. Vossen, Q. Xu and J. Zhang, Phys. Rev. D 105 (2022) no.9, 094033 doi:10.1103/PhysRevD.105.094033 [arXiv:2108.05383 [hep-ph]].
- (51) F. Yuan, Phys. Rev. Lett. 100 (2008), 032003 doi:10.1103/PhysRevLett.100.032003 [arXiv:0709.3272 [hep-ph]].
- (52) R. Bain, Y. Makris and T. Mehen, JHEP 11 (2016), 144 doi:10.1007/JHEP11(2016)144 [arXiv:1610.06508 [hep-ph]].
- (53) Z. B. Kang, F. Ringer and I. Vitev, JHEP 11 (2016), 155 doi:10.1007/JHEP11(2016)155 [arXiv:1606.07063 [hep-ph]].
- (54) Z. B. Kang, X. Liu, F. Ringer and H. Xing, JHEP 11 (2017), 068 doi:10.1007/JHEP11(2017)068 [arXiv:1705.08443 [hep-ph]].
- (55) Z. B. Kang, K. Lee and F. Zhao, Phys. Lett. B 809 (2020), 135756 doi:10.1016/j.physletb.2020.135756 [arXiv:2005.02398 [hep-ph]].
- (56) Z. B. Kang, H. Xing, F. Zhao and Y. Zhou, JHEP 03 (2024), 142 doi:10.1007/JHEP03(2024)142 [arXiv:2311.00672 [hep-ph]].
- (57) U. D’Alesio, L. Gamberg, F. Murgia and M. Zaccheddu, Phys. Lett. B 851 (2024), 138552 doi:10.1016/j.physletb.2024.138552 [arXiv:2402.01612 [hep-ph]].
- (58) T. Gao, [arXiv:2402.01168 [hep-ex]].
- (59) H. C. Zhang and S. Y. Wei, Phys. Lett. B 839 (2023), 137821 doi:10.1016/j.physletb.2023.137821 [arXiv:2301.04096 [hep-ph]].
- (60) X. Li, Z. X. Chen, S. Cao and S. Y. Wei, Phys. Rev. D 109 (2024) no.1, 014035 doi:10.1103/PhysRevD.109.014035 [arXiv:2309.09487 [hep-ph]].
- (61) Z. B. Kang, A. Prokudin, F. Ringer and F. Yuan, Phys. Lett. B 774 (2017), 635-642 doi:10.1016/j.physletb.2017.10.031 [arXiv:1707.00913 [hep-ph]].
- (62) D. de Florian, M. Stratmann and W. Vogelsang, Phys. Rev. D 57 (1998), 5811-5824 doi:10.1103/PhysRevD.57.5811 [arXiv:hep-ph/9711387 [hep-ph]].
- (63) T. J. Hou, J. Gao, T. J. Hobbs, K. Xie, S. Dulat, M. Guzzi, J. Huston, P. Nadolsky, J. Pumplin and C. Schmidt, et al. Phys. Rev. D 103 (2021) no.1, 014013 doi:10.1103/PhysRevD.103.014013 [arXiv:1912.10053 [hep-ph]].
- (64) Z. B. Kang, Phys. Rev. D 83 (2011), 036006 doi:10.1103/PhysRevD.83.036006 [arXiv:1012.3419 [hep-ph]].
- (65) K. J. Eskola, P. Paakkinen, H. Paukkunen and C. A. Salgado, Eur. Phys. J. C 82 (2022) no.5, 413 doi:10.1140/epjc/s10052-022-10359-0 [arXiv:2112.12462 [hep-ph]].
- (66) A. J. Baltz, G. Baur, D. d’Enterria, L. Frankfurt, F. Gelis, V. Guzey, K. Hencken, Y. Kharlov, M. Klasen and S. R. Klein, et al. Phys. Rept. 458 (2008), 1-171 doi:10.1016/j.physrep.2007.12.001 [arXiv:0706.3356 [nucl-ex]].
- (67) M. Aaboud et al. [ATLAS], JHEP 09 (2017), 020 doi:10.1007/JHEP09(2017)020 [arXiv:1706.03192 [hep-ex]].