Transverse Cooper-Pair Rectifier
Abstract
Non-reciprocal devices are key components in modern electronics covering broad applications ranging from transistors to logic circuits thanks to the output rectified signal in the direction parallel to the input. In this work, we propose a transverse Cooper-pair rectifier in which a non-reciprocal current is perpendicular to the driving field, when inversion, time reversal, and mirror symmetries are broken simultaneously. The Blonder-Tinkham-Klapwijk formalism is developed to describe the transverse current-voltage relation in a normal-metal/superconductor tunneling junction, where symmetry constraints are achieved by an effective built-in supercurrent manifesting in an asymmetric and anisotropic Andreev reflection. The asymmetry in the Andreev reflection is induced when inversion and time reversal symmetry are broken by the supercurrent component parallel to the junction while the anisotropy occurs when the mirror symmetry with respect to the normal of the junction interface is broken by the perpendicular supercurrent component to the junction. Compared to the conventional longitudinal one, the transverse rectifier supports fully polarized diode efficiency and colossal nonreciprocal conductance rectification, completely decoupling the path of the input excitation from the output rectified signal. This work provides a formalism for realizing transverse non-reciprocity in superconducting junctions, which is expected to be achieved by modifying current experimental setups and may pave the way for future low-dissipation superconducting electronics.
Introduction.- As fundamental electronic components, diodes conduct current primarily in one direction, offering low (high) resistance in the forward (reverse) bias [1, 2]. The rectified current direction is usually parallel to the applied bias, which is dubbed as the longitudinal diode effect [Fig. 1(a)]. The longitudinal diodes play essential roles from consumer electronics and signal processors [1] to quantum sensing and computing [3]. New device architectures based on molecules [4], superconductors [Fig. 1(b)] [5, 6], and other quantum materials [7, 8] are being actively explored to achieve giant rectification [9, 10, 11] at low-energy consumption [12].
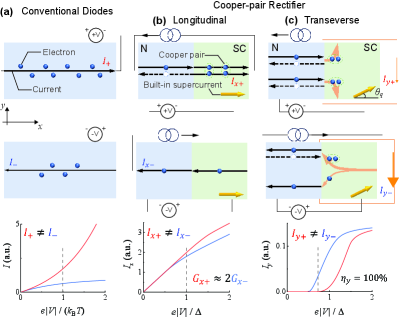
Beyond the longitudinal diodes, the recently revealed Hall rectifiers [13, 14, 15, 16] support output DC signals perpendicular to the input AC ones, leveraging the nonlinear Hall response of noncentrosymmetric quantum materials [15, 16, 17]. The decoupling between output and input direction enables a colossal Hall rectification effect, which can convert terahertz electromagnetic waves into DC output with high rectification efficiency and low-energy consumption [14].
In this work, we implement the concept of a transverse rectifier to the superconducting regime and propose a transverse Cooper-pair rectifier [Fig. 1(c)], where the Cooper-pair-dominated current is perpendicular to bias with a direction-selective magnitude. This transport effect is distinct from the longitudinal superconducting rectification [5, 6], and based on a mechanism different from single-electron nonlinear Hall rectifiers [13, 14, 15, 16]. Our proposed setup is a normal metal-superconductor (N-S) junction and, thus does not intrinsically require noncentrosymmetric quantum materials [13, 14, 15] or fluctuating Cooper pairs [16] as components. As a superconducting tunneling junction [18, 19, 20], our proposed rectifier is a low-dispassion cryogenic electronics device in low working bias (meV) and temperature (mK) conditions [21] with flexible external electromagnet knots and configurations. The device performance is featured by unidirectional Cooper-pair current and giant conductance rectification.
Symmetry constraints.- To characterize the transverse Cooper-pair rectifier, our work aims to develop a universal longitudinal and transverse current-voltage (-) relation, which can be conceptually explained through the symmetry constraints (Table 1). Generally, the linearized - relation of a two-dimensional tunneling junction with a bias along -direction is [22]
| (1) |
where is the longitudinal () and transverse () conductance in a unit of , denotes the direction of the incident electrons measured from -axis with , and is the direction-resolved transmission probability parallel/perpendicular to the bias. In semiconducting [1] and dissipative superconducting regime [23, 24], the breaking of inversion symmetry causes a longitudinal non-reciprocal current with due to the asymmetric conductance with respect to zero bias.
The further breaking of the mirror symmetry to the bias direction leads to the transverse rectification. The breaking of generates a transverse current, by destroying the initial equivalent contribution from the upward-going () and downward-going () modes [Fig. 1]. A non-zero is found due to the anisotropic transmission probability . This universal argument is valid for all tunneling Hall (transverse) currents in both non-superconducting [25] and superconducting junction [26, 27, 28, 29]. Accompanied by the breaking , the anisotropic and asymmetric transmission probability leads to the transverse rectification with .
The universal symmetry constraints above are specifically manifested in the Cooper-pair rectifier in an N-S junction. By developing the transverse current within the Blonder-Tinkham-Klapwijk (BTK) formalism [30], the transmission probabilities of the N-S junction is [31]
| (2) |
which contains the effect of (i) the retro-Andreev (electron-hole) reflection always contributing to current by forming Cooper pairs and (ii) the specular normal (electron-electron) reflection which reduces the longitudinal current because of the backscattering towards the N lead, but enhances the transverse one near the N-S interface.
The symmetry constraints can be achieved by an effective built-in unidirectional supercurrent [32, 33, 34, 35, 36], whose component parallel to biased direction break [37, 38] and the perpendicular one breaks . The time-reversal symmetry is also broken because of the unidirectional collective drifting motion [32]. The effective built-in unidirectional supercurrent is essential for superconducting non-reciprocity in both non-centrosymmetric superconductors [39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54] and Josephson junctions [55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94], whose origination is diverse including finite-momentum Cooper pairs [95, 96, 97] induced by Meissner effect [55], quantum interference effect [56, 60, 57, 58], vortex currents [59], the interplay between spin-orbit coupling and in-plane Zeeman field [61, 62, 63, 64, 65, 66, 68, 69, 67, 70, 71, 72, 73, 74, 75], and the non-zero net velocity between paired electrons in asymmetric helical states [76].
| Device | Conventional | Cooper-pair rectifier | |
|---|---|---|---|
| diode | longitudinal | transverse | |
| ✗ | ✗ | ✗ | |
| ✓ | ✓ | ✗ | |
BdG spectrum with built-in supercurrent.- In a microscopic picture, the effective built-in unidirectional supercurrent modulates the Bogoliubov-de Gennes (BdG) spectrum, leading to an anisotropic and asymmetric transmission probability. The mechanism is exhibited in Fig. 2.
To elaborate on the relation between built-in unidirectional supercurrent and the transmission probability, we first introduce this asymmetric and anisotropic BdG spectrum in an isotropic -wave superconductor. The Hamiltonian after a gauge transformation in Nambu space is [32, 98]
| (3) |
where is the superconducting gap coupling the electron-like and and hole-like quasiparticle with a Fermi level , momentum , and Cooper-pair drifting momentum [32].
The spectrum of the BdG quasiparticle,
| (4) |
with becomes asymmetric [Fig. 2(d)] and anisotropic [Fig. 2(f)], as the built-in supercurrent shifts dispersion centers of electrons (holes) from the origin [Fig. 2(c, e)] to () [Fig. 2(d, f)]. An anisotropy occurs because the original isotropic Fermi surfaces reduce to mirror-symmetric to the direction of the supercurrent. Subsequently, the symmetry between the electron and hole dispersions to is destroyed, resulting in an asymmetric BdG spectrum with an indirect gap.
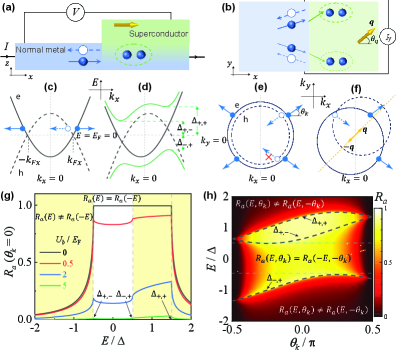
As exhibited in Fig. 2(d) and (h), the asymmetric and asymmetric BdG spectrum is characterized by four -dependent band edges
| (5) |
where the direction-selective Doppler energy shift [99, 100, 101, 102, 76, 103]
| (6) |
enhances/reduces the energy of states propagating parallel/anti-parallel to the built-in supercurrent. Thereby, the center of the band gap gains a -dependent shift from to at , resulting in an asymmetric and asymmetric BdG spectrum. Notably, BdG spectrum is gapless as with as the depairing momentum at zero-temperature [32, 35]. The effective built-in supercurrents in recent experiments are inherited from the proximity effect [55, 104], thereby do not have to obey the self-consistency equation [33, 34, 35, 32, 36].
Asymmetric and anisotropic Andreev reflection.- The configuration of the BdG spectrum implies that the Andreev reflection (AR) probability is asymmetric and anisotropic and eventually causes a non-reciprocal current in the N-S junction with a prioritized transport direction provided by the built-in supercurrent. By solving the quantum tunneling problem in the N-S junction, the AR probability for incident electrons with energy and direction is [31]
| (7) |
where , , , and . To obtain Eq. (7), the following assumptions are implemented. (i) Translational symmetry in direction is preserved. (ii) The effective mass and the Fermi level are shared by both the N and S sides. (iii) The interface tunnel barrier is the only boundary condition involved. (iv) Andreev approximation [105, 30] is considered, i.e. , . Thereby, the Fermi wave number mismatch between the N and S region is negligible, and the effect of the built-in supercurrent is revealed in the Dopper energy shift . Approximation (iv) is valid because quasiparticles with momentum nearly parallel to the interface () do not contribute significantly to both the longitudinal and transverse current. Thereby their effects in the - relation and related quantities will thus be negligible [106]. Our results are checked numerically [107] beyond the assumption (i-iv) and are qualitatively consistent with the analytical ones [31].
The asymmetric and anisotropic AR characterizing the direction-selective superconducting gap in the BdG spectrum are exhibited in Fig. 2(g) and (h). Asymmetry activated by manifests in even with finite interfacial barriers [Fig. 2(g)], since and are broken. AR dominates in the asymmetric energy window with Cooper-pair transferring, while exponentially decreases beyond this regime with increasing single-electron transmission. Furthermore, anisotropic embodying in is induced by , which breaks by providing a prioritized supercurrent orientation. Electrons with an incident direction closer to the supercurrent will confront a higher Doppler energy shift.
Remarkably, the symmetry constraints for the transverse Cooper-pair rectifier are met when the supercurrent deviates from the direction of the junction (). The simultaneous breaking of , , and manifesting in asymmetric and anisotropic AR, i.e. and . As a result, the transverse current occurs due to the imbalance AR between incident electrons with and , and of distinctive responses to the bias direction.
Non-reciprocal - relation and efficiency.- To investigate the currents in a biased N-S junction, we develop the non-reciprocal - relation by following the quasiparticle current argument in the BTK formalism [30, 108]. By considering electron and hole currents and the quasiparticle probability conservation, the - relation is [31]
| (8) |
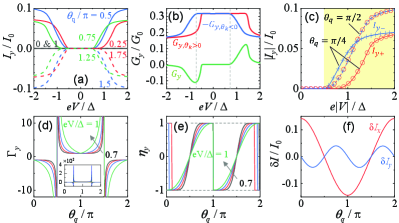
where , and is the width of the sample, and and are the Fermi-Dirac distribution between S and N sides, respectively. Eq. (1) is restored by linearized Eq. (8) in small bias and low-temperature conditions [31]. The transverse current occurs when is broken by [in Fig. 3(a)] due to the net contribution between anisotropic AR as the bias exceeds the regime [Fig. 2(g)].
A transverse Cooper-pair rectifier is found when and are further broken by . This device is characterized by a bias-direction-selective transverse current carrier, i.e. the forward-bias Cooper-pair current and reverse-bias single-electron current. This carrier alteration manifests in the differential conductance between opposite biases in Fig. 3(b). For positive bias (), Cooper pairs dominate the current in all directions, i.e. , resulting in . While negative bias, Cooper-pair transferring and single-electron transmission processes gain a direction-selective contribution to the current, i.e. , causing a non-zero .
High rectification efficiency is expected due to this bias-direction-selective Cooper pair transverse transport, which manifests in distinct two aspects. (i) The rectified conductance defined as
| (9) |
is divergent when [Fig. 3(d)], indicating that identical currents are driven regardless of the bias polarity [Fig. 3(c)]. (ii) A fully rectified current
| (10) |
is expected [Fig. 3(e)] when and , where
| (11) |
When the biases are around the superconducting gap, the transverse current is negligible due to the compensation Cooper-pair current flowing perpendicular to the junction under one bias and becomes finite stemming from the direction-selective current of Cooper-pairs and single electrons, as schematic in Fig. 1. These two aspects endow the transverse Cooper-pair diode beyond its longitudinal counterpart, whose diode efficiency is inherently constrained, as it necessitates the transfer of carriers (either Cooper pairs or single electrons) upon reversal of the bias.
The symmetry constrain (Table 1) is revealed in Eq. (11) and Fig. 3(f). The supercurrent component parallel to the junction direction () breaks both and and subsequently causes the longitudinal Cooper pair effect embodying in . While the transverse current difference is implying that the addition broken by the supercurrent component perpendicular to the junction direction ().
Discussions.- Experimentally, the transverse Cooper-pair rectifier can be realized in a four-terminal N-S junction with two normal metal probes [31]. For instance, such setup can be constructed in semiconducting [18, 19, 61, 62, 63, 64, 67, 65, 60, 66] or topological materials like Bi2Te3-NbSe2 hybrid structure [104]. One of the promising platforms is the InGaAs/InAs with Al as a proximate superconductor, where the effective built-in supercurrent is contorted by an external in-plane magnetic field interacting with spin-orbit coupling [109]. The mechanism for generating effective built-in supercurrent or Cooper-pair momentum is also compatible with topological surface states with in-plane Zeeman field and proximate superconductivity [77, 104], such as in NiTe2 [77] and Bi2Te3 [104].
As a proof-of-concept, we simulate [31] the non-reciprocal current and conductance of a four-terminal device via KWANT [110, 111]. The simulation results are consistent with the two-terminal model presented above. The numerical simulation also demonstrates that the transverse rectifications are robust against finite-thickness effects [112, 113], systematic inhomogeneous and disorders.
We remark that the transverse current in the Dirac system such as topological surface states may be helpful to distinguish the retro- and specular AR [114, 27]. Finally, transverse Cooper-pair diode operating in a dynamical regime [23, 24] remains an open question that can be investigated in future works.
Acknowledgements.
P.-H. Fu thanks Weiping Xu and Alessandro Braggio for inspiring discussions. P.-H. F. & Y. S. A. are supported by the Singapore Ministry of Education (MOE) Academic Research Fund (AcRF) Tier 2 Grant (MOE-T2EP50221-0019). C.H. L. is supported by Singapore’s NRF Quantum engineering grant NRF2021-QEP2-02-P09 and Singapore’s MOE Tier-II grant Proposal ID: T2EP50222-0003. J.-F. L. is supported by the National Natural Science Foundation of China (Grant No. 12174077) and the Joint Fund with Guangzhou Municipality under Grant No. 202201020238. Y. Xu is supported by the Scientific Research Starting Foundation of Ningbo University of Technology (Grant No. 2022KQ51).References
- Simon M. Sze [2012] M.-K. L. Simon M. Sze, Semiconductor devices: physics and technology (Wiley, New York, 2012).
- Ideue et al. [2017] T. Ideue, K. Hamamoto, S. Koshikawa, M. Ezawa, S. Shimizu, Y. Kaneko, Y. Tokura, N. Nagaosa, and Y. Iwasa, Bulk rectification effect in a polar semiconductor, Nat. Phys. 13, 578 (2017).
- Shukla et al. [2023] R. K. Shukla, L. Chotorlishvili, V. Vijayan, H. Verma, A. Ernst, S. S. Parkin, and S. K. Mishra, Quantum information diode based on a magnonic crystal, Mater. Quantum. Technol. 3, 035003 (2023).
- Chen et al. [2017] X. Chen, M. Roemer, L. Yuan, W. Du, D. Thompson, E. Del Barco, and C. A. Nijhuis, Molecular diodes with rectification ratios exceeding 105 driven by electrostatic interactions, Nat. Nanotech. 12, 797 (2017).
- Nadeem et al. [2023] M. Nadeem, M. S. Fuhrer, and X. Wang, The superconducting diode effect, Nat. Rev. Phys. 5, 558 (2023), arXiv:2301.13564 .
- Wakatsuki et al. [2017] R. Wakatsuki, Y. Saito, S. Hoshino, Y. M. Itahashi, T. Ideue, M. Ezawa, Y. Iwasa, and N. Nagaosa, Nonreciprocal charge transport in noncentrosymmetric superconductors, Science Advances 3, 10.1126/sciadv.1602390 (2017).
- Nagaosa and Yanase [2024] N. Nagaosa and Y. Yanase, Nonreciprocal transport and optical phenomena in quantum materials, Annual Review of Condensed Matter Physics 15, 63 (2024).
- Tokura and Nagaosa [2018] Y. Tokura and N. Nagaosa, Nonreciprocal responses from non-centrosymmetric quantum materials, Nature Communications 9, 3740 (2018).
- Mendoza-Arenas and Clark [2024] J. J. Mendoza-Arenas and S. R. Clark, Giant rectification in strongly interacting driven tilted systems, PRX Quantum 5, 010341 (2024).
- Lee et al. [2020] K. H. Lee, V. Balachandran, R. Tan, C. Guo, and D. Poletti, Giant spin current rectification due to the interplay of negative differential conductance and a non-uniform magnetic field, Entropy 22, 1311 (2020).
- Pereira [2019] E. Pereira, Perfect thermal rectification in a many-body quantum ising model, Physical Review E 99, 032116 (2019).
- Zhao et al. [2023] X. Zhao, Y. Xing, J. Cao, S. Liu, W.-X. Cui, and H.-F. Wang, Engineering quantum diode in one-dimensional time-varying superconducting circuits, npj Quantum Information 9, 59 (2023).
- Isobe et al. [2020] H. Isobe, S.-Y. Xu, and L. Fu, High-frequency rectification via chiral Bloch electrons, Science Advances 6, 1 (2020), arXiv:1812.08162 .
- Min et al. [2023] L. Min, Y. Zhang, Z. Xie, S. V. G. Ayyagari, L. Miao, Y. Onishi, S. H. Lee, Y. Wang, N. Alem, L. Fu, and Z. Mao, Colossal nonreciprocal Hall effect and broadband frequency mixing due to a room temperature nonlinear Hall effect, 27, 635 (2023), arXiv:2303.03738 .
- Onishi and Fu [2022] Y. Onishi and L. Fu, High-efficiency energy harvesting based on nonlinear Hall rectifier, , 1 (2022), arXiv:2211.17219 .
- Daido and Yanase [2023] A. Daido and Y. Yanase, Rectification and nonlinear Hall effect by fluctuating finite-momentum Cooper pairs, , 1 (2023), arXiv:2302.10677 .
- Qin et al. [2024] F. Qin, R. Chen, and C. H. Lee, Light-enhanced nonlinear hall effect, arXiv preprint arXiv:2401.18038 (2024).
- Strambini et al. [2022] E. Strambini, M. Spies, N. Ligato, S. Ilić, M. Rouco, C. González-Orellana, M. Ilyn, C. Rogero, F. S. Bergeret, J. S. Moodera, P. Virtanen, T. T. Heikkilä, and F. Giazotto, Superconducting spintronic tunnel diode, Nature Communications 13, 2431 (2022).
- de Araujo et al. [2024] C. I. L. de Araujo, P. Virtanen, M. Spies, C. González-Orellana, S. Kerschbaumer, M. Ilyn, C. Rogero, T. T. Heikkilä, F. Giazotto, and E. Strambini, Superconducting spintronic heat engine, Nature Communications 15, 4823 (2024), arXiv:2310.18132 .
- Geng et al. [2023] Z. Geng, A. Hijano, S. Ilić, M. Ilyn, I. J. Maasilta, A. Monfardini, M. Spies, E. Strambini, P. Virtanen, M. Calvo, C. González-Orellána, A. P. Helenius, S. Khorshidian, C. I. L. de Araujo, F. Levy-Bertrand, C. Rogero, F. Giazotto, F. S. Bergeret, T. T. Heikkilä, S. Ilic, M. Ilyn, I. J. Maasilta, A. Monfardini, M. Spies, E. Strambini, P. Virtanen, M. Calvo, C. Gonzalez-Orellana, A. P. Helenius, S. Khorshidian, C. I. L. de Araujo, F. Levy-Bertrand, C. Rogero, F. Giazotto, F. S. Bergeret, and T. T. Heikkilä, Superconductor-ferromagnet hybrids for non-reciprocal electronics and detectors, Superconductor Science and Technology 36, 123001 (2023), arXiv:2302.12732 .
- Braginski [2019] A. I. Braginski, Superconductor electronics: Status and outlook, Journal of superconductivity and novel magnetism 32, 23 (2019).
- Jacquod et al. [2012] P. Jacquod, R. S. Whitney, J. Meair, and M. Büttiker, Onsager relations in coupled electric, thermoelectric, and spin transport: The tenfold way, Phys. Rev. B 86, 155118 (2012).
- Hu et al. [2007] J. Hu, C. Wu, and X. Dai, Proposed Design of a Josephson Diode, Physical Review Letters 99, 067004 (2007).
- Misaki and Nagaosa [2021] K. Misaki and N. Nagaosa, Theory of the nonreciprocal Josephson effect, Physical Review B 103, 245302 (2021), arXiv:2002.06458 .
- Scharf et al. [2016] B. Scharf, A. Matos-Abiague, J. E. Han, E. M. Hankiewicz, and I. Žutić, Tunneling planar hall effect in topological insulators: Spin valves and amplifiers, Phys. Rev. Lett. 117, 166806 (2016).
- Ren and Zhu [2014] J. Ren and J.-X. Zhu, Asymmetric Andreev reflection induced electrical and thermal Hall-like effects in metal/anisotropic superconductor junctions, Physical Review B 89, 064512 (2014).
- Salehi [2023] M. Salehi, Anisotropic angle-dependent Andreev reflection at the ferromagnet/superconductor junction on the surface of topological insulators, Physica Scripta 98, 025822 (2023), arXiv:2301.06137 .
- Zhou and Spivak [1998] F. Zhou and B. Spivak, Hall Effect in SN and SNS Junctions, Physical Review Letters 80, 3847 (1998).
- Parafilo et al. [2023] A. V. Parafilo, V. M. Kovalev, and I. G. Savenko, Photoinduced anomalous supercurrent Hall effect, Physical Review B 108, L180509 (2023), arXiv:2307.03314 .
- Blonder et al. [1982] G. E. Blonder, M. Tinkham, and T. M. Klapwijk, Transition from metallic to tunneling regimes in superconducting microconstrictions: Excess current, charge imbalance, and supercurrent conversion, Physical Review B 25, 4515 (1982).
- [31] See Supplemental Material at URL-will-be-inserted-by-publisher for more details.
- Bagwell [1994] P. F. Bagwell, Critical current of a one-dimensional superconductor, Physical Review B 49, 6841 (1994).
- Sanchez Canizares and Sols [1995] J. Sanchez Canizares and F. Sols, Self-consistent current-voltage characteristics of normal-superconductor interfaces, Journal of Physics: Condensed Matter 7, L317 (1995).
- Sánchez-Cañizares and Sols [1997] J. Sánchez-Cañizares and F. Sols, Self-consistent scattering description of transport in normal-superconductor structures, Physical Review B 55, 531 (1997).
- Riedel and Bagwell [1999] R. Riedel and P. F. Bagwell, Excess currents larger than the point contact limit in normal-metal/superconducting junctions, Superlattices and Microstructures 25, 683 (1999).
- Lukic and Nicol [2007] V. Lukic and E. J. Nicol, Conductance characteristics between a normal metal and a two-band superconductor carrying a supercurrent, Physical Review B 76, 144508 (2007).
- Zinkl et al. [2022] B. Zinkl, K. Hamamoto, and M. Sigrist, Symmetry conditions for the superconducting diode effect in chiral superconductors, Physical Review Research 4, 033167 (2022), arXiv:2111.05340 .
- Wang et al. [2022] D. Wang, Q.-H. Wang, and C. Wu, Symmetry Constraints on Direct-Current Josephson Diodes, , 1 (2022), arXiv:2209.12646 .
- Zhang et al. [2020] E. Zhang, X. Xu, Y.-C. Zou, L. Ai, X. Dong, C. Huang, P. Leng, S. Liu, Y. Zhang, Z. Jia, X. Peng, M. Zhao, Y. Yang, Z. Li, H. Guo, S. J. Haigh, N. Nagaosa, J. Shen, and F. Xiu, Nonreciprocal superconducting NbSe2 antenna, Nature Communications 11, 5634 (2020).
- Ando et al. [2020] F. Ando, Y. Miyasaka, T. Li, J. Ishizuka, T. Arakawa, Y. Shiota, T. Moriyama, Y. Yanase, and T. Ono, Observation of superconducting diode effect, Nature 584, 373 (2020).
- Bauriedl et al. [2022] L. Bauriedl, C. Bäuml, L. Fuchs, C. Baumgartner, N. Paulik, J. M. Bauer, K.-Q. Lin, J. M. Lupton, T. Taniguchi, K. Watanabe, C. Strunk, and N. Paradiso, Supercurrent diode effect and magnetochiral anisotropy in few-layer NbSe2, Nature Communications 13, 4266 (2022), arXiv:2110.15752 .
- Itahashi et al. [2020] Y. M. Itahashi, T. Ideue, Y. Saito, S. Shimizu, T. Ouchi, T. Nojima, and Y. Iwasa, Nonreciprocal transport in gate-induced polar superconductor SrTiO3, Science Advances 6, 1 (2020).
- Yasuda et al. [2019] K. Yasuda, H. Yasuda, T. Liang, R. Yoshimi, A. Tsukazaki, K. S. Takahashi, N. Nagaosa, M. Kawasaki, and Y. Tokura, Nonreciprocal charge transport at topological insulator/superconductor interface, Nature Communications 10, 2734 (2019).
- Masuko et al. [2022] M. Masuko, M. Kawamura, R. Yoshimi, M. Hirayama, Y. Ikeda, R. Watanabe, J. J. He, D. Maryenko, A. Tsukazaki, K. S. Takahashi, M. Kawasaki, N. Nagaosa, and Y. Tokura, Nonreciprocal charge transport in topological superconductor candidate Bi2Te3/PdTe2 heterostructure, npj Quantum Materials 7, 104 (2022).
- Hou et al. [2023] Y. Hou, F. Nichele, H. Chi, A. Lodesani, Y. Wu, M. F. Ritter, D. Z. Haxell, M. Davydova, S. Ilić, O. Glezakou-Elbert, A. Varambally, F. S. Bergeret, A. Kamra, L. Fu, P. A. Lee, and J. S. Moodera, Ubiquitous Superconducting Diode Effect in Superconductor Thin Films, Physical Review Letters 131, 027001 (2023), arXiv:2205.09276 .
- Wakamura et al. [2024] T. Wakamura, M. Hashisaka, S. Hoshino, M. Bard, S. Okazaki, T. Sasagawa, T. Taniguchi, K. Watanabe, K. Muraki, and N. Kumada, Gate-tunable giant superconducting nonreciprocal transport in few-layer -MoTe2, Physical Review Research 6, 013132 (2024), arXiv:2303.09747 .
- Narita et al. [2022] H. Narita, J. Ishizuka, R. Kawarazaki, D. Kan, Y. Shiota, T. Moriyama, Y. Shimakawa, A. V. Ognev, A. S. Samardak, Y. Yanase, and T. Ono, Field-free superconducting diode effect in noncentrosymmetric superconductor/ferromagnet multilayers, Nature Nanotechnology 17, 823 (2022), arXiv:2206.00483 .
- Hoshino et al. [2018] S. Hoshino, R. Wakatsuki, K. Hamamoto, and N. Nagaosa, Nonreciprocal charge transport in two-dimensional noncentrosymmetric superconductors, Physical Review B 98, 054510 (2018), arXiv:1805.05735 .
- Wakatsuki and Nagaosa [2018] R. Wakatsuki and N. Nagaosa, Nonreciprocal Current in Noncentrosymmetric Rashba Superconductors, Physical Review Letters 121, 026601 (2018), arXiv:1712.02086 .
- Scammell et al. [2022] H. D. Scammell, J. I. A. Li, and M. S. Scheurer, Theory of zero-field superconducting diode effect in twisted trilayer graphene, 2D Materials 9, 025027 (2022), arXiv:2112.07841 .
- Ilić and Bergeret [2022] S. Ilić and F. S. Bergeret, Theory of the Supercurrent Diode Effect in Rashba Superconductors with Arbitrary Disorder, Physical Review Letters 128, 177001 (2022), arXiv:2108.00209 .
- Daido et al. [2022] A. Daido, Y. Ikeda, and Y. Yanase, Intrinsic Superconducting Diode Effect, Physical Review Letters 128, 037001 (2022), arXiv:2106.03326 .
- Legg et al. [2022] H. F. Legg, D. Loss, and J. Klinovaja, Superconducting diode effect due to magnetochiral anisotropy in topological insulators and Rashba nanowires, Physical Review B 106, 104501 (2022), arXiv:2205.12939 .
- Zaccone and Fomin [2024] A. Zaccone and V. M. Fomin, Theory of superconductivity in thin films under an external electric field, Phys. Rev. B 109, 144520 (2024).
- Davydova et al. [2022] M. Davydova, S. Prembabu, and L. Fu, Universal Josephson diode effect, Science Advances 8, 1 (2022), arXiv:2201.00831 .
- Valentini et al. [2024] M. Valentini, O. Sagi, L. Baghumyan, T. de Gijsel, J. Jung, S. Calcaterra, A. Ballabio, J. Aguilera Servin, K. Aggarwal, M. Janik, T. Adletzberger, R. Seoane Souto, M. Leijnse, J. Danon, C. Schrade, E. Bakkers, D. Chrastina, G. Isella, and G. Katsaros, Parity-conserving Cooper-pair transport and ideal superconducting diode in planar germanium, Nature Communications 15, 169 (2024).
- Fominov and Mikhailov [2022] Y. V. Fominov and D. S. Mikhailov, Asymmetric higher-harmonic SQUID as a Josephson diode, Physical Review B 106, 134514 (2022), arXiv:2208.10856 .
- Souto et al. [2022] R. S. Souto, M. Leijnse, and C. Schrade, Josephson Diode Effect in Supercurrent Interferometers, Physical Review Letters 129, 267702 (2022), arXiv:2205.04469 .
- Fukaya et al. [2024] Y. Fukaya, M. T. Mercaldo, D. Margineda, A. Crippa, E. Strambini, F. Giazotto, C. Ortix, and M. Cuoco, Design of supercurrent diode by vortex phase texture, (2024), arXiv:2403.04421 .
- Ciaccia et al. [2023] C. Ciaccia, R. Haller, A. C. C. Drachmann, T. Lindemann, M. J. Manfra, C. Schrade, and C. Schönenberger, Gate-tunable Josephson diode in proximitized InAs supercurrent interferometers, Physical Review Research 5, 033131 (2023), arXiv:2304.00484 .
- Costa et al. [2023a] A. Costa, C. Baumgartner, S. Reinhardt, J. Berger, S. Gronin, G. C. Gardner, T. Lindemann, M. J. Manfra, J. Fabian, D. Kochan, N. Paradiso, and C. Strunk, Sign reversal of the Josephson inductance magnetochiral anisotropy and 0–-like transitions in supercurrent diodes, Nature Nanotechnology 18, 1266 (2023a), arXiv:2212.13460 .
- Costa et al. [2023b] A. Costa, J. Fabian, and D. Kochan, Microscopic study of the Josephson supercurrent diode effect in Josephson junctions based on two-dimensional electron gas, Physical Review B 108, 054522 (2023b), arXiv:2303.14823 .
- Mazur et al. [2022] G. P. Mazur, N. van Loo, D. van Driel, J. Y. Wang, G. Badawy, S. Gazibegovic, E. P. A. M. Bakkers, and L. P. Kouwenhoven, The gate-tunable Josephson diode, , 1 (2022), arXiv:2211.14283 .
- Turini et al. [2022] B. Turini, S. Salimian, M. Carrega, A. Iorio, E. Strambini, F. Giazotto, V. Zannier, L. Sorba, and S. Heun, Josephson Diode Effect in High Mobility InSb Nanoflags, Nano Letters 22, 8502 (2022), arXiv:2207.08772 .
- Margineda et al. [2023a] D. Margineda, A. Crippa, E. Strambini, Y. Fukaya, M. T. Mercaldo, M. Cuoco, and F. Giazotto, Sign reversal diode effect in superconducting Dayem nanobridges, Communications Physics 6, 343 (2023a), arXiv:2306.00193 .
- Reinhardt et al. [2023] S. Reinhardt, T. Ascherl, A. Costa, J. Berger, S. Gronin, G. C. Gardner, T. Lindemann, M. J. Manfra, J. Fabian, D. Kochan, C. Strunk, and N. Paradiso, Link between supercurrent diode and anomalous Josephson effect revealed by gate-controlled interferometry, , 22 (2023), arXiv:2308.01061 .
- Jeon et al. [2022] K.-R. Jeon, J.-K. Kim, J. Yoon, J.-C. Jeon, H. Han, A. Cottet, T. Kontos, and S. S. P. Parkin, Zero-field polarity-reversible Josephson supercurrent diodes enabled by a proximity-magnetized Pt barrier, Nature Materials 21, 1008 (2022).
- Baumgartner et al. [2022a] C. Baumgartner, L. Fuchs, A. Costa, S. Reinhardt, S. Gronin, G. C. Gardner, T. Lindemann, M. J. Manfra, P. E. Faria Junior, D. Kochan, J. Fabian, N. Paradiso, and C. Strunk, Supercurrent rectification and magnetochiral effects in symmetric Josephson junctions, Nature Nanotechnology 17, 39 (2022a).
- Baumgartner et al. [2022b] C. Baumgartner, L. Fuchs, A. Costa, J. Picó-Cortés, S. Reinhardt, S. Gronin, G. C. Gardner, T. Lindemann, M. J. Manfra, P. E. Faria Junior, D. Kochan, J. Fabian, N. Paradiso, and C. Strunk, Effect of Rashba and Dresselhaus spin–orbit coupling on supercurrent rectification and magnetochiral anisotropy of ballistic Josephson junctions, Journal of Physics: Condensed Matter 34, 154005 (2022b), arXiv:2111.13983 .
- Lu et al. [2023] B. Lu, S. Ikegaya, P. Burset, Y. Tanaka, and N. Nagaosa, Tunable Josephson Diode Effect on the Surface of Topological Insulators, Physical Review Letters 131, 096001 (2023), arXiv:2211.10572 .
- Tanaka et al. [2022] Y. Tanaka, B. Lu, and N. Nagaosa, Theory of giant diode effect in -wave superconductor junctions on the surface of a topological insulator, Physical Review B 106, 214524 (2022), arXiv:2205.13177 .
- Cayao et al. [2023] J. Cayao, N. Nagaosa, and Y. Tanaka, Enhancing the Josephson diode effect with Majorana bound states, Physical Review B 109, L081405 (2023), arXiv:2309.15567 .
- Lotfizadeh et al. [2023] N. Lotfizadeh, B. Pekerten, P. Yu, W. Strickland, A. Matos-Abiague, and J. Shabani, Superconducting Diode Effect Sign Change in Epitaxial Al-InAs Josepshon Junctions, 1, 1 (2023), arXiv:2303.01902 .
- Alidoust et al. [2021] M. Alidoust, C. Shen, and I. Žutić, Cubic spin-orbit coupling and anomalous Josephson effect in planar junctions, Physical Review B 103, L060503 (2021), arXiv:2101.08272 .
- Amundsen et al. [2024] M. Amundsen, J. Linder, J. W. A. Robinson, I. Žutić, and N. Banerjee, Colloquium : Spin-orbit effects in superconducting hybrid structures, Reviews of Modern Physics 96, 021003 (2024), arXiv:2210.03549 .
- Fu et al. [2024] P.-H. Fu, Y. Xu, S. A. Yang, C. H. Lee, Y. S. Ang, and J.-F. Liu, Field-effect Josephson diode via asymmetric spin-momentum locking states, Physical Review Applied 21, 054057 (2024), arXiv:2212.01980 .
- Pal et al. [2022] B. Pal, A. Chakraborty, P. K. Sivakumar, M. Davydova, A. K. Gopi, A. K. Pandeya, J. A. Krieger, Y. Zhang, M. Date, S. Ju, N. Yuan, N. B. M. Schröter, L. Fu, and S. S. P. Parkin, Josephson diode effect from Cooper pair momentum in a topological semimetal, Nature Physics 18, 1228 (2022), arXiv:2112.11285 .
- Trahms et al. [2023] M. Trahms, L. Melischek, J. F. Steiner, B. Mahendru, I. Tamir, N. Bogdanoff, O. Peters, G. Reecht, C. B. Winkelmann, F. von Oppen, and K. J. Franke, Diode effect in Josephson junctions with a single magnetic atom, Nature 615, 628 (2023), arXiv:2212.04432 .
- Margineda et al. [2023b] D. Margineda, A. Crippa, E. Strambini, Y. Fukaya, M. T. Mercaldo, C. Ortix, M. Cuoco, and F. Giazotto, Back-action supercurrent diodes, , 1 (2023b), arXiv:2311.14503 .
- Wu et al. [2022] H. Wu, Y. Wang, Y. Xu, P. K. Sivakumar, C. Pasco, U. Filippozzi, S. S. P. Parkin, Y.-J. Zeng, T. McQueen, and M. N. Ali, The field-free Josephson diode in a van der Waals heterostructure, Nature 604, 653 (2022).
- Wei et al. [2022] Y.-j. Wei, H.-L. Liu, J. Wang, and J.-F. Liu, Supercurrent rectification effect in graphene-based Josephson junctions, Physical Review B 106, 165419 (2022).
- Xie et al. [2023] Y.-M. Xie, D. K. Efetov, and K. T. Law, -Josephson Junction in Twisted Bilayer Graphene Induced by a Valley-Polarized State, Physical Review Research 5, 023029 (2023), arXiv:2202.05663 .
- Zhang et al. [2022] Y. Zhang, Y. Gu, P. Li, J. Hu, and K. Jiang, General Theory of Josephson Diodes, Physical Review X 12, 041013 (2022), arXiv:2112.08901 .
- Hu et al. [2023] J.-X. Hu, Z.-T. Sun, Y.-M. Xie, and K. T. Law, Josephson Diode Effect Induced by Valley Polarization in Twisted Bilayer Graphene, Physical Review Letters 130, 266003 (2023), arXiv:2211.14846 .
- Legg et al. [2023] H. F. Legg, K. Laubscher, D. Loss, and J. Klinovaja, Parity-protected superconducting diode effect in topological Josephson junctions, Physical Review B 108, 214520 (2023), arXiv:2301.13740 .
- Wang et al. [2024] J. Wang, Y. Jiang, J. J. Wang, and J.-F. Liu, Efficient Josephson diode effect on a two-dimensional topological insulator with asymmetric magnetization, Physical Review B 109, 075412 (2024).
- Zazunov et al. [2023] A. Zazunov, J. Rech, T. Jonckheere, B. Grémaud, T. Martin, and R. Egger, Approaching ideal rectification in superconducting diodes through multiple Andreev reflections, , 1 (2023), arXiv:2307.14698 .
- Zazunov et al. [2024] A. Zazunov, J. Rech, T. Jonckheere, B. Grémaud, T. Martin, and R. Egger, Nonreciprocal charge transport and subharmonic structure in voltage-biased Josephson diodes, Physical Review B 109, 024504 (2024), arXiv:2307.15386 .
- Ding et al. [2022] P. Ding, C. H. Lee, X. Wu, and R. Thomale, Diagnosis of pairing symmetry by vortex and edge spectra in kagome superconductors, Phys. Rev. B 105, 174518 (2022).
- Ding et al. [2023] P. Ding, T. Schwemmer, C. H. Lee, X. Wu, and R. Thomale, Hyperbolic fringe signal for twin impurity quasiparticle interference, Phys. Rev. Lett. 130, 256001 (2023).
- Bozkurt et al. [2023] A. M. Bozkurt, J. Brookman, V. Fatemi, and A. R. Akhmerov, Double-Fourier engineering of Josephson energy-phase relationships applied to diodes, SciPost Phys. 15, 204 (2023).
- Yerin et al. [2024] Y. Yerin, S.-L. Drechsler, A. A. Varlamov, M. Cuoco, and F. Giazotto, Supercurrent rectification with time-reversal symmetry broken multiband superconductors, Phys. Rev. B 110, 054501 (2024).
- Banerjee and Scheurer [2024] S. Banerjee and M. S. Scheurer, Altermagnetic superconducting diode effect, Phys. Rev. B 110, 024503 (2024).
- Yu et al. [2024] W. Yu, J. J. Cuozzo, K. Sapkota, E. Rossi, D. X. Rademacher, T. M. Nenoff, and W. Pan, Time reversal symmetry breaking and zero magnetic field josephson diode effect in dirac semimetal mediated asymmetric squids, Phys. Rev. B 110, 104510 (2024).
- Yuan and Fu [2018] N. F. Q. Yuan and L. Fu, Zeeman-induced gapless superconductivity with a partial Fermi surface, Physical Review B 97, 115139 (2018), arXiv:1801.03522 .
- Yuan and Fu [2021] N. F. Q. Yuan and L. Fu, Topological metals and finite-momentum superconductors, Proceedings of the National Academy of Sciences 118, 1 (2021), arXiv:2009.03848 .
- Hart et al. [2017] S. Hart, H. Ren, M. Kosowsky, G. Ben-Shach, P. Leubner, C. Brüne, H. Buhmann, L. W. Molenkamp, B. I. Halperin, and A. Yacoby, Controlled finite momentum pairing and spatially varying order parameter in proximitized HgTe quantum wells, Nature Physics 13, 87 (2017), arXiv:1509.02940 .
- De Gennes [2018] P.-G. De Gennes, Superconductivity of metals and alloys (CRC press, 2018).
- Tkachov et al. [2015] G. Tkachov, P. Burset, B. Trauzettel, and E. M. Hankiewicz, Quantum interference of edge supercurrents in a two-dimensional topological insulator, Physical Review B 92, 045408 (2015), arXiv:1409.7301 .
- Scharf et al. [2021] B. Scharf, A. Braggio, E. Strambini, F. Giazotto, and E. M. Hankiewicz, Thermodynamics in topological Josephson junctions, Physical Review Research 3, 033062 (2021), arXiv:2103.10923 .
- Dolcini et al. [2015] F. Dolcini, M. Houzet, and J. S. Meyer, Topological Josephson junctions, Physical Review B 92, 035428 (2015).
- Fu et al. [2022] P.-H. Fu, Y. Xu, X.-L. Yu, J.-F. Liu, and J. Wu, Electrically modulated Josephson junction of light-dressed topological insulators, Physical Review B 105, 064503 (2022).
- Rohlfing et al. [2009] F. Rohlfing, G. Tkachov, F. Otto, K. Richter, D. Weiss, G. Borghs, and C. Strunk, Doppler shift in Andreev reflection from a moving superconducting condensate in Nb/InAs Josephson junctions, Physical Review B 80, 220507 (2009), arXiv:0903.0321 .
- Zhu et al. [2021] Z. Zhu, M. Papaj, X.-A. Nie, H.-K. Xu, Y.-S. Gu, X. Yang, D. Guan, S. Wang, Y. Li, C. Liu, J. Luo, Z.-A. Xu, H. Zheng, L. Fu, and J.-F. Jia, Discovery of segmented Fermi surface induced by Cooper pair momentum, Science 374, 1381 (2021), arXiv:2010.02216 .
- Andreev [1964] A. F. Andreev, The thermal conductivity of the intermediate state in superconductors, Soviet Physics JETP 19, 1228 (1964).
- Mortensen et al. [1999] N. A. Mortensen, K. Flensberg, and A.-P. Jauho, Angle dependence of Andreev scattering at semiconductor–superconductor interfaces, Physical Review B 59, 10176 (1999), arXiv:9807049 [cond-mat] .
- Fu et al. [2020] P.-H. Fu, J.-F. Liu, and J. Wu, Transport properties of Majorana drumhead surface states in topological nodal-ring superconductors, Physical Review B 102, 075430 (2020).
- Datta et al. [1996] S. Datta, P. F. Bagwell, and M. P. Anantram, Scattering theory of transport for mesoscopic superconductors, (1996).
- Kjaergaard et al. [2016] M. Kjaergaard, F. Nichele, H. J. Suominen, M. P. Nowak, M. Wimmer, A. R. Akhmerov, J. A. Folk, K. Flensberg, J. Shabani, C. J. Palmstrøm, and C. M. Marcus, Quantized conductance doubling and hard gap in a two-dimensional semiconductor–superconductor heterostructure, Nature Communications 7, 12841 (2016), arXiv:1603.01852 .
- Groth et al. [2013] C. Groth, M. Wimmer, A. Akhmerov, and X. Waintal, Kwant: a software package for quantum transport, New Journal of Physics 16 (2013).
- Anantram and Datta [1996] M. P. Anantram and S. Datta, Current fluctuations in mesoscopic systems with Andreev scattering, Physical Review B 53, 16390 (1996).
- Smolyaninova et al. [2016] V. N. Smolyaninova, C. X. J. Jensen, W. B. Zimmerman, J. C. Prestigiacomo, M. Osofsky, H. Kim, N. D. Bassim, Z. Xing, M. M. Qazilbash, and I. I. Smolyaninov, Enhanced superconductivity in aluminum-based hyperbolic metamaterials, Scientific Reports 6 (2016).
- López-Núñez et al. [2023] D. López-Núñez, Q. P. Montserrat, G. Rius, E. Bertoldo, A. Torras-Coloma, M. Martínez, and P. Forn-Díaz, Magnetic penetration depth of aluminum thin films, (2023), arXiv:2311.14119 [cond-mat.supr-con] .
- Beenakker [2006] C. W. J. Beenakker, Specular Andreev Reflection in Graphene, Physical Review Letters 97, 067007 (2006), arXiv:0604594 [cond-mat] .