Transmutation operators and a new representation for solutions of perturbed Bessel equations
Abstract
New representations for an integral kernel of the transmutation operator and for a regular solution of the perturbed Bessel equation of the form are obtained. The integral kernel is represented as a Fourier-Jacobi series. The solution is represented as a Neumann series of Bessel functions uniformly convergent with respect to . For the coefficients of the series convenient for numerical computation recurrent integration formulas are obtained. The new representation improves the ones from [24] and [23] for large values of and and for non-integer values of .
The results are based on application of several ideas from the classical transmutation (transformation) operator theory, asymptotic formulas for the solution, results connecting the decay rate of the Fourier transform with the smoothness of a function, the Paley-Wiener theorem and some results from constructive approximation theory.
We show that the analytical representation obtained among other possible applications offers a simple and efficient numerical method able to compute large sets of eigendata with a nondeteriorating accuracy.
1 Introduction
In the present work we consider a second order singular differential equation
| (1.1) |
where is a real number, , is a complex-valued function satisfying the condition
and is a (complex) spectral parameter. Equations of the form (1.1) appear naturally in many real-world applications after a separation of variables and therefore have received considerable attention (see, e.g., [4], [7], [8], [9], [14], [18], [29, Sect. 3.7], [32], [33], [39]).
In [21] a new representation for solutions of one-dimensional Schrödinger equation (the case in (1.1)) in the form of Neumann series of Bessel functions (NSFB) [3, 40] was obtained. The representation possesses such remarkable properties as exponentially fast convergence for smooth potentials and uniform error bound for partial sums for all . The idea behind this representation is the existence of the transmutation operator connecting a solution of the equation with the solution of the simpler equation having . A transmutation operator can be realized in the form of a Volterra integral operator. Expanding its integral kernel into a Fourier-Legendre series allowed us to obtain the NSBF representation for the solution.
In [24] we proposed an NSBF representation for the regular solution of (1.1) normalized by its asymptotics at zero. However, the above mentioned advantages of the regular case were lost for the representation from [24]. The reasons are the following. First, for any fixed the function decays as as . For that reason any error bound uniform with respect to is useful only in some neighborhood of , and for large values of the parameter this neighborhood becomes rather small. Second, the exponential convergence of the partial sums was lost for , the convergence was bounded by (here is the truncation parameter) independently of the smoothness of the potential. The reason was in the underlying Mehler’s integral representation for the solution :
here and is an even function, and denotes the spherical Bessel function of the first kind, see [1, Section 10.1]. The integral kernel admits the following representation
| (1.2) |
where and , extended by 0 onto the whole line, possesses at least derivatives as a function of . As a result, for non-integer values of the decay rate of the Fourier-Legendre coefficients of is polynomial and is determined by the first term in (1.2), independent on the smoothness of .
To overcome the first problem, one can use the transmutation operator for the perturbed Bessel equation. Recall that a transmutation operator intertwining (1.1) with the unperturbed Bessel equation
| (1.3) |
has the form [38, 34, 10, 37, 16]
| (1.4) |
In such case, if one takes as a regular solution of (1.3) (note that this solution remains bounded and does not decay as , see [1, (9.2.1)]), finds an approximation for satisfying and defines an approximate solution by using this in (1.4), one easily obtains (applying the Cauchy-Schwartz inequality) that
uniformly for . And since does not decay as , such approximation is useful for both small and large values of .
However, the problem of constructing an approximation for which at the same time the integrals in (1.4) can be easily evaluated and rapid decay of the error bound as can be proved, is not an easy task, see, e.g., [25] for an attempt. The integral kernel is a solution of a singular Goursat problem which can be transformed into one of the several equivalent integral equations, see [38], [10], [16]. We do not expect that any of these integral equations can provide an efficient approximation method for the integral kernel. The main reason is the following: we conjecture that the integral kernel has the form
where is a nice function (in the sense that it is at least in the second variable for sufficiently smooth potentials). The base for such conjecture is the formula (4.6) from [9]
proved there under the assumption that possesses a holomorphic extension onto the disk of radius . We believe that the factor plays a crucial role in the construction of a good approximation to , however it gets strongly obscured in the known integral equations for .
In [23] we proposed to use a series representation for the integral kernel and an Erdelyi-Kober operator to obtain a series representation for the integral kernel , and for integer values of the partial sums provided a good approximation for . For non-integer values of , the approximation obtained was not practical to substitute it into (1.4).
In the present paper we show that the Legendre polynomials are not the best choice for representing the kernel , and one needs to use the Jacobi polynomials instead. The motivation for this claim is the formula (1.2) and the following representation for
which follows from formula (4.4) from [9] and is proved there under the assumption that possesses a holomorphic extension onto the disk of radius .
We show that the factor should be used as a weight for the Fourier-Jacobi expansion, and can be represented as
| (1.5) |
where stands for the Jacobi polynomials, leading to the following representation for the integral kernel
| (1.6) |
where we denoted
| (1.7) |
As a result, the following representation for the regular solution of (1.1) is obtained
| (1.8) |
We show the uniform with respect to convergence rate estimates for (1.8), prove faster than polynomial convergence for potentials and present efficient for numerical implementation recurrent formulas to calculate the coefficients in which only integration is used, and no differentiation is required.
For the derivative of the regular solution we obtain the following representation
| (1.9) |
possessing all the remarkable properties of (1.8): uniform with respect to error bounds for truncated series, faster than polynomial convergence for potentials and efficient for numerical implementation formulas to calculate the coefficients .
The representation (1.6) for the integral kernel together with the decay rate estimates for the coefficients can be of the independent interest for studying the transmutation operator for perturbed Bessel equation and for solving the inverse spectral problem like it was done in the regular case in [19], [11], [20].
We would like to mention that despite of lots of technical details in proofs, application of the representations (1.8) and (1.9) for numerical solution of boundary value or spectral problems for equation (1.1) is very simple. All that one needs is a solution of the equation
and its derivative (both can be obtained numerically). Then one calculates the coefficients and using (7.7)–(7.9) and (7.11). To estimate optimal values of and one utilizes the equalities (8.1) and (8.3). Computation of both and for each fixed reduces to the computation of the values of several Bessel functions. As a result, for example, several hundreds eigenvalues of a Sturm-Liouville problem can be obtained in less than a second.
The paper is organized as follows. In Section 2 we present some preliminary information about transmutation operators and asymptotic estimates of the solutions. In Section 3 we study the smoothness of the integral kernel (Propositions 3.3 and 3.4) and convergence rate of its Fourier-Jacobi expansion (Theorem 3.5 and Proposition 3.6). In Section 4 we show that the integral kernel possesses Fourier-Jacobi representation (1.6) (Theorem 4.1), extend this representation to a wider class of potentials and prove its convergence rate (Theorem 4.3). In Section 5 we obtain the representation (1.8) (Theorem 5.2). In Section 6 we present necessary facts about the derivative of the regular solution, its relation with the transmutation operator and prove the representation (1.9) (Theorems 6.2 and 6.3). In Section 7 we obtain the recurrent formulas for the coefficients and . In Section 8 we present numerical results for solution of two spectral problems and study the decay of the coefficients . In Appendix A we prove that the transmutation integral kernel depends continuously on the potential (Corollary A.3). Finally, in Appendix B we prove that the regular solution of equation (1.1) is non-vanishing on the whole for any sufficiently large negative (Proposition B.1).
2 Transmutation operator, solution asymptotics and Mehler-type integral representation
Denote
| (2.1) |
This function is a regular solution of equation (1.3) satisfying the asymptotic condition
| (2.2) |
By we denote the regular solution of (1.1) satisfying the same asymptotic condition at 0.
Assume that . Then [38], [34], [10], [16] there exists a unique continuous kernel such that for all
| (2.3) |
The integral kernel satisfies
| (2.4) |
The operator is called the transmutation operator.
The existence of the transmutation operator (2.3) can be established for wider class of potentials. For the purposes of this work we need that the integral kernel as a function of belongs to for each fixed . Let us introduce the notation [17]
| (2.5) |
Then the following condition on is sufficient for the integral kernel to belong to :
| (2.6) |
For the proof we refer the reader to [34, §2], the case of non-integer values of is also covered taking [13] into account.
The difference between the solutions and satisfies the inequality [17, (2.18)]
from which it follows for the potential satisfying condition (2.6) that
| (2.7) |
More can be said about the asymptotic behavior of the solution as if the potential possesses several derivatives on the whole segment . Indeed, similarly to the proof of Proposition 4.5 from [24] (see also [15, Theorem 4]) one can see that if , , i.e., possesses derivatives, the last one belonging to , then
| (2.8) |
where
| (2.9) |
and as a function of is an even entire function of exponential type .
Application of the Paley-Wiener theorem leads to the following Mehler-type integral representation for the solution , see [24]
| (2.10) |
where
By , we denote the fractional-order Sobolev space, also called Bessel potential space [2, Chap. 7] consisting of functions satisfying and , where is the Fourier transform operator. Then, extending the integral kernel as a function of by 0 outside of and denoting the resulting function again by we have the following [24, Proposition 4.1]. is a continuous, even, compactly supported on function and such that for any sufficiently small .
Additionally, if , then [24, (4.24)]
| (2.11) |
where (extended by 0 outside of ) is a continuous, even function satisfying for any sufficiently small .
The integral kernels and are related by the following relations [23, (2.5) and (2.6)]
| (2.12) |
and
| (2.13) |
here is an arbitrary integer satisfying .
3 Fourier-Jacobi expansion of the integral kernel
In this section we show that the integral kernel can be expanded into a Fourier-Jacobi series (1.5), study error bounds for the remainder of the truncated series and the decay rate of the coefficients .
We recall some definitions from the approximation theory used in this section. By we denote the largest integer smaller than , and let . Then .
Following [31] we say that a function is Lipschitz of an order on (may be a segment or the whole line) if
-
1.
there exist the derivatives of of all orders up to the order ;
-
2.
for all ;
-
3.
satisfies the Lipschitz condition of order , i.e., there exists a positive constant such that
We will denote the class of such functions by .
Following [28] we say that a function belongs to the Zygmund class on some for some if
-
1.
for all ;
-
2.
satisfies the Zygmund condition for some constant , i.e.,
Note that .
The following proposition immediately follows from [28, Theorems 1 and 3] and shows the relationship between the decay rate of the Fourier transform and the smoothness of a function.
Proposition 3.1.
Suppose is such that and its Fourier transform satisfies for some
Then
and
Moreover, for any , ,
Following [26] we introduce the following notations and definitions. Let be the set of algebraic polynomials of degree not greater than . Let , , . We define as best weighted polynomial approximation of a function such that the quantity
Denote by the orthonormal expansion of with respect to the system of normalized Jacobi polynomials , that is
| (3.1) |
where
Then the best weighted polynomial approximation of the function coincides with the norm of the remainder of its Fourier-Jacobi expansion:
| (3.2) |
Let , be the set of functions satisfying
-
1.
is a -times iterated integral of in ;
-
2.
, .
By we define the set of functions satisfying .
Consider the following modulus of continuity:
| (3.3) |
where is defined by , .
Then the following result holds
Theorem 3.2 ([26]).
Let for some . Then
In the rest of this section we apply Proposition 3.1 and Theorem 3.2 to estimate the decay rate of the coefficients and of the remainder of the Fourier-Jacobi expansion of the integral kernel .
Proposition 3.3.
Let satisfy condition (2.6) and be fixed. Let the integral kernel from (2.10) as a function of be extended by outside of . For the sake of simplicity we denote this extended function by the same letter . Then
-
1.
; moreover, if , then ;
-
2.
there exist functions , bounded on and continuous on , such that
If additionally , then the above statements hold for the integral kernel from (2.11) with the change of by in all the formulas: , etc.
Proof.
Note that by (2.10) the function is the Fourier transform of the function , which is continuous on and decays as when due to (2.7) (see also the proof of Theorem 4.1 from [24]). Hence the first statement follows immediately from Proposition 3.1.
To prove the second part, consider Taylor’s formula for the function at the points and . Since the function is compactly supported on and continuous together with its derivatives up to the order on the whole , we have
hence (for )
| (3.4) |
for some .
Now, satisfies Zygmund’s condition on the whole . Hence choosing the points , and and taking into account that , we obtain
| (3.5) |
It follows from (3.4) and (3.5) that for
Now,
The proofs for as well as for are similar.
The proof for the case is completely similar if one uses (2.9). ∎
Let be fixed. Consider the functions
The expansion (1.5) reduces to the Fourier-Jacobi expansion of the function .
Proposition 3.4.
Proof.
Note that the derivative of order , , of the function can be written as
| (3.6) |
where are some polynomials in .
It is sufficient to prove that each term in (3.6), multiplied by , belongs to . We have
| (3.7) |
Due to Proposition 3.3
and (3.7) reduces to
integrable over since and .
For the proof in the case one applies a completely similar reasoning for the function
and notes that due to (2.11) the functions and differ by a polynomial in and hence belong to the same class . ∎
As it follows from Proposition 3.4, the function always belongs at least to . So we may expand it into a Fourier-Jacobi series (3.1). Returning to the integral kernel we have
| (3.8) |
where
| (3.9) |
The function is even, so all coefficients and we obtain the representation (1.5). The following theorem provides a convergence estimate.
Theorem 3.5.
If additionally , the right hand side of the inequality (3.10) can be improved to
| (3.11) |
Proof.
Note that
| (3.12) |
Let . Due to Proposition 3.4 and Theorem 3.2 we obtain that
| (3.13) |
Let us estimate the modulus of continuity (3.3). Due to the Minkowski inequality, it is sufficient to estimate (3.3) for each term in (3.6) separately. We only present the estimates for the first integral. We have for the integrand in (3.3)
| (3.14) |
Consider the first term. If , then by the Lipschitz property of the function (see Proposition 3.3) we have
Hence the first term can be bounded by
| (3.15) |
If , the function is differentiable, and by the mean value theorem
where . For the sake of simplicity we assume that , so and , the other case is similar. Then due to Proposition 3.3
(note that since ). Hence the first term can be bounded by
| (3.16) |
where we have used that and that for .
The proof for the second term in (3.14) can be done similarly with the help of the mean value theorem and Proposition 3.3, we left the details to the reader.
As a result, taking into account that , we obtain that
| (3.17) |
For the proof of the case when , one performs the proof for the function and notes that and differ by a polynomial of order , hence their best polynomial approximations coincide starting with . ∎
As for the pointwise convergence of the series in (1.5), we have the following result.
Proposition 3.6.
Let satisfy condition (2.6). The series in (1.5) converges absolutely and uniformly with respect to on any segment . If is absolutely continuous on , then the series converges absolutely and uniformly with respect to on the whole segment .
The following weighted estimate holds
| (3.18) |
Here the parameter is from the inclusion (and is taken equal to if ).
Comparing (3.8) with (1.5) we see that
| (3.19) |
where
is the square of the norm of the Jacobi polynomial , see [1, 22.2.1].
Corollary 3.7.
Proof.
By (3.12), (3.2) and Theorem 3.5
| (3.22) |
for all such that . Since , see [35, (IV.7.8)], (3.20) immediately follows from (3.19) and (3.22).
Proof of the second statement is similar. ∎
Corollary 3.8.
4 Fourier-Jacobi expansion of the integral kernel
In this section we apply formula (2.13) to the representation (1.5) and show all the necessary intermediate results like the possibility of termwise differentiation, convergence rate estimates etc.
Theorem 4.1.
Suppose that . Then the representation (1.6) is valid for the integral kernel . The series converges absolutely and uniformly with respect to for any small . If additionally , then the series converges absolutely and uniformly with respect to on .
Proof.
Let , , so .
Suppose initially that . Taking in the formula (2.13) we obtain
| (4.1) |
Here we interchanged the sum and the integral which is possible because the series (1.5) converges uniformly, see Proposition 3.6, and the factor is bounded.
To evaluate the integral in (4.1) we use the formula (2.21.1.4) from [30]. Recall that
where are the Gegenbauer polynomials and is the Pochhammer symbol, see [1]. Then
Here we used that in the formula (2.21.1.4) from [30] the sum in the first term is finite and the second term disappear due to the presence of the expression , in the denominator. Using the reflection formula we obtain
hence
| (4.2) |
Substituting (4.2) in (4.1) and noting that we obtain the expression
| (4.3) |
To justify the possibility for termwise differentiation of the series in (4.3) we show that the series and all termwise derivatives up to the order converge at the point and that the termwise derivative of order is uniformly convergent with respect to on any containing the point .
We recall that it is possible to introduce the generalized Jacobi polynomials for arbitrary real parameters and , we refer the reader to [36, Sect. 4.22] for details. Note that (see [1, 22.2.2 and 22.5.2]) for any
| (4.4) |
here are the shifted Jacobi polynomials.
Hence at we need to obtain the absolute convergence of the series
| (4.5) |
Values of the Jacobi polynomials at zero are uniformly bounded by , see [36, Theorem 7.32.2]. The fraction of Gamma functions behaves as as , see [35, (IV.7.18)], and since , we obtain that . Due to (3.24) for we have . As a result, the terms of the series (4.5) decay at least as and the series converges absolutely.
For the derivative of order we obtain from (4.4)
| (4.6) |
The Jacobi polynomials in (4.6) are uniformly bounded by for , see [35, Theorem 7.5]. Due to [35, (IV.7.18)] we have , . So the uniform convergence of the series
would follow from the absolute convergence of the series
| (4.7) |
Consider
| (4.8) |
where we have used the estimate (3.21) with . Hence
which proves the uniform convergence of the termwise derivative of order .
In the presented proof the factor was left outside the sum, this was required to show termwise differentiability of the series in (4.3). Including this factor we can show the uniform convergence of (1.6) for . Indeed, as it follows from [35, Theorem 7.5], there is a constant such that for all and
Hence for any there is a constant such that for all
and the same proof involving the absolute convergence of the series (4.7) shows uniform convergence of (1.6) for .
The uniform convergence on the whole segment can be obtained similarly taking into account that imposing additional requirements on the decay rate of the coefficients , and, hence, on the smoothness of the potential to be able to apply the estimate (3.21). We left the details to the reader.
Now suppose that , i.e., . Taking in the formula (2.13) we obtain
Using the formulas (22.5.20) and (22.5.21) from [1] we obtain
While formula (4.22.2) from [36] states
Hence
| (4.9) |
Using the Legendre duplication formula we obtain
Using these identities it follows from (4.9) that
| (4.10) |
Observe that if one takes (4.3) and applies 2 derivatives (and utilizes formula (4.6) for ), one obtains a series containing exactly expressions (4.10). That is, the proof for the case of integer can be finished exactly the same as it was done in the case on non-integer . ∎
Lemma 4.2.
Let be fixed. The system of functions
| (4.11) |
forms an orthonormal basis of .
Proof.
The orthonormality of the functions from (4.11) follows from the following equality
| (4.12) |
where is the Kronecker delta symbol and is the square of the norm of the Jacobi polynomial .
Theorem 4.3.
Let for some and be fixed. Then for the truncated series
| (4.13) |
the following estimate holds
| (4.14) |
for all satisfying .
Proof.
Suppose initially that , that is, Theorem 4.1 holds.
Note that by Lemma 4.2 the terms of the series (1.6) are orthogonal. Hence, up to a multiplicative constant (dependent on ), the norm of the series in (1.6) equals to
where we used that , . Now we proceed similarly to (4.8).
| (4.15) |
where we used (3.21) for . The last inequality proves convergence of the series in (1.6).
Since the series in (1.6) converges in and converges pointwise to for all , the limit of the series is equal to . Due to the orthogonality of the terms of the series
the proof of the last inequality is similar to (4.15) with the use of (3.21) with the parameter .
Let us suppose now that satisfies (2.6) only. Since the integral kernel as a function of belongs to , it can be expanded into Fourier series with respect to system (4.11). We can write this expansion in the following form
| (4.16) |
where
| (4.17) |
Note that the coefficients are defined by (3.9), (3.19) and (1.7). For absolutely continuous potentials coefficients and coincide as follows from the first part of this theorem. Considering a sequence of absolutely continuous potentials converging to the potential in (see notations of Appendix A) and using Corollary A.3 we can conclude that for all for any potential satisfying condition (2.6). ∎
5 Representation of the regular solution
In this section we substitute the representation (1.6) for the integral kernel into (2.3) and obtain the representation (1.8) for the regular solution.
First we need the following lemma.
Lemma 5.1.
| (5.1) |
Proof.
Applying the change of variable the integral converts to
We will calculate this integral using the formula 2.22.12.3 from [30]. We would like to point out that direct application of this formula results in an expression containing
that is, in the numerator and in the denominator due to the negative integer parameter in the hypergeometric function. To overcome this difficulty we apply the classical technique of passage to the limit. Consider for the integral
It is easy to see that as . On the other hand, the formula 2.22.12.3 from [30] gives
where was reduced to due to two equal parameters. Applying in the last expression the formula (see [36, (4.21.5)])
and noting also that the hypergeometric function reduces to due to two pairs of equal parameters we obtain that
where formula 9.1.69 from [1] was used. ∎
Theorem 5.2.
Let satisfy condition (2.6). Then the regular solution of (1.1) satisfying the asymptotic condition (2.2) as admits the following representation
| (5.2) |
where the coefficients are related to by (1.7). The series (5.2) converges absolutely and uniformly with respect to on any compact subset of the complex plane.
Suppose additionally that for some . Denote by
| (5.3) |
an approximate solution obtained by truncating the series in (5.2). Then the following estimate holds uniformly for
| (5.4) |
here is the parameter of smoothness of the potential .
6 Representation for the derivative of the regular solution
In this section we obtain a representation for the derivative of the regular solution. We are looking for a representation possessing the same remarkable properties of uniform with respect to error bounds and exponentially fast convergence for smooth potentials. For that, instead of differentiating the representation (5.2) with respect to , we differentiate (1.4) and proceed similarly to what were done in Sections 3–5. First we recall some facts about the derivative, the transmutation operator and Mehler’s representation from [24].
Let be the regular solution of (1.1) satisfying the asymptotics (2.2) as . Then
| (6.1) |
here denotes .
For the following Mehler’s type representation holds
where is an even, compactly supported on function satisfying .
The integral kernels and are related by the following formula
| (6.2) |
The following estimates hold. If , then
And if for some , then
where
By the Paley-Wiener theorem
where as a function of is even, compactly supported on and satisfies . Moreover,
where is a polynomial in of degree less or equal to .
Comparing the above formulas for the derivative with the corresponding ones for the solution, one can see that the same relations hold between the integral kernels and and between the integral kernels and . Similar estimates for the solution and its derivative hold, similar improvement exists depending on the smoothness of the potential . The only difference is that the requirement should be changed to . With this change, the scheme presented in Sections 3–5 can be applied without significant changes for the derivative. We left the details for the reader and only present the final results.
Proposition 6.1.
Let for some . Then the integral kernel has the following representation
| (6.3) |
Denote by
Let be fixed. Then the following estimates hold
| (6.4) |
and
| (6.5) |
Comparing (6.2) with (2.12) we may conclude from (2.13) that
| (6.6) |
here can be arbitrary integer satisfying . And similarly to Section 4 we obtain the following result.
Theorem 6.2.
Suppose for some . Then the following representation
| (6.7) |
is valid. Here we defined
| (6.8) |
The series converges absolutely and uniformly with respect to for any small and for any fixed converges in .
For the truncated series
| (6.9) |
the following estimate holds
| (6.10) |
for all satisfying .
Theorem 6.3.
Let . Then the derivative of the regular solution considered in Theorem 5.2 has the following representation
| (6.11) |
where the coefficients are related to the coefficients by (6.8). The series (6.11) converges absolutely and uniformly with respect to on any compact subset of the complex plane.
Denote by
| (6.12) |
an approximate solution obtained by truncating the series in (6.11). Then the following estimate holds uniformly for
| (6.13) |
Remark 6.4.
The validity of representations (6.7) and (6.11) can be established under a weaker condition on the potential , at least under the condition . The proof can be done similarly to Sections 4, 5 and Appendix A. See also proof of Theorem 7.1 from [24] for estimations of derivatives of regular solutions. We left the details for a separate work.
7 Recurrent formulas for the coefficients and
Note that the functions are twice differentiable and grow not faster than polynomially in (which can be seen from (3.9), (3.19) and (1.7), see also [24]). The same is true for and . Taking into account the inequality , , one may verify that the series (5.2) can be differentiated twice termwise.
So let us substitute (5.2) into equation (1.1). Similarly to [24, Section 6] we obtain that
| (7.1) |
After applying the formula
| (7.2) |
equality (7.1) can be rewritten in the form
where
| (7.3) |
and
Due to the orthogonality of the functions on we obtain from (7.3) that , , which can be written in the following form (c.f. [21] and [24])
Note that due to (3.9), (3.19) each of the coefficients is a linear combination of the Fourier-Legendre coefficients of the integral kernel studied in [24]. Hence, using (4.12) from [24] and (1.7) one can see that the functions satisfy the following initial conditions
Let denotes the regular solution of the equation normalized by the asymptotic condition
and suppose that for all . If the regular solution of the equation vanish in it is always possible to perform a spectral shift such that new equation possesses a non-vanishing solution, see Appendix B. Then a solution of an equation
| (7.4) |
can be easily obtained using the Pólya factorization of , . The function
| (7.5) |
is a solution of (7.4). Note also that the expression (7.5) gives the unique solution of (7.4) satisfying , . And since the function , , the expression (7.5) can be used to reconstruct the functions , .
It is easy to verify that the function is given by the expression
| (7.6) |
Hence one can start with (7.6) and define for
To eliminate the first and second derivatives of resulting from the term , one may apply the integration by parts and obtain (similarly to [21]) the following recurrent formulas.
| (7.7) | ||||
| (7.8) |
and finally
| (7.9) |
To obtain the formulas for the coefficients we proceed as follows. Differentiating (5.2) we have that
Comparing this expression with (6.11), utilizing (7.2) and rearranging terms, we arrive at the equality
where
Again, due to the orthogonality of the functions on we obtain that the coefficients are equal to 0, that is,
Using (7.6) and (7.9) these formulas can be written as
| (7.10) | ||||
| (7.11) |
8 Numerical examples
The general scheme of application of the proposed representation (5.2) and (6.11) for the solution of boundary value and spectral problems for equation (1.1) is basically the same as for the paper [24]. One starts with computing a particular solution of the equation , then computes the coefficients and and obtains approximations for the regular solution and its derivative. The particular solution together with its derivative can be calculated using the SPPS representation [7, Section 3]. The assumption for the solution to be non-vanishing automatically holds if , . For other cases one may need to apply the spectral shift as described in Appendix B. The coefficients and can be computed using (7.7)–(7.9) and (7.11). To perform an indefinite integration numerically one may use a piecewise polynomial interpolation or approximation and integrate the resultant polynomial. For machine precision arithmetics we use the fifth degree polynomial interpolation (resulting in the 6 point Newton-Cottes rule), in previous papers we also used spline interpolation (much slower) or Clenshaw-Curtis rule (mainly for higher precision arithmetics). We refer the reader to [21] and [24] for further details.
We would like to mention that the coefficients and decay as , see (3.24) and (1.7), and decay faster then polynomially for smooth potentials . However computation errors propagate through the recurrent formulas (7.9) and (7.11), meaning that after several dozens of coefficients the computation error will be comparable with the value of the coefficient itself. Equality (2.4) can be used to estimate an optimum number of the coefficients . One can write (2.4) using the representation (1.6) and (1.7) as
| (8.1) |
and take as an optimal value for the index minimizing the discrepancy between the left hand side and the truncated sum. In order to present similar equality allowing one to estimate an optimal number of the coefficients , we conjecture that the the following formula holds.
| (8.2) |
For the potentials possessing holomorphic extension onto the disk of radius one can easily verify that (8.2) holds using formulas (2.3) and (4.6) from [9]. For the general case approximation by smooth potentials (e.g., polynomials) should work, however we do not want to enter into details in this paper.
On the base of (8.2) and (6.7) we obtain the following equality
| (8.3) |
allowing one to estimate an optimal number of coefficients to use.
All the computations were performed in machine precision using Matlab 2017. All the functions involved were represented by their values on an uniform mesh of 5001 points. The analytic expression was used only to obtain the value of the potential at the mesh points, all other computations were done numerically. We would like to emphasize that our aim was to show that even straightforward implementation of the proposed representations can deliver in almost no time results which are comparable or even superior to those produced by the best existing software packages.
8.1 Example 1
Consider the following spectral problem
| (8.4) | |||
| (8.5) |
The regular solution of equation (8.4) can be written as
allowing one to compute with any precision arbitrary sets of eigenvalues using, e.g., Wolfram Mathematica.
The value was considered in [4, Example 2], [7, Example 7.3] and [24, Example 9.1]. We compared the results with those obtained using (5.3) with . Exact eigenvalues together with the absolute errors of the approximate eigenvalues obtained using different methods are presented in Table 1. The proposed method is abbreviated as New NSBF. NSBF corresponds to the original representation from [24] used with . As one can see from the results, the proposed method easily outperforms both the SPPS method and the previous NSBF method. The relative error of all found eigenvalues was less than , making it comparable with the best available software packages like Matslise [27]. It is worth to mention that the computation time for the proposed method was less than 0.25 sec on Intel i7-7600U equipped notebook.
| (Exact/Matslise) | (New NSBF) | (NSBF) | (SPPS) | ([4]) | |
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 5 | |||||
| 7 | |||||
| 10 | |||||
| 20 | |||||
| 50 | |||||
| 100 |
We also compared the results provided by the proposed method to those of [23] and [24] where other methods based on the transmutation operators and Neumann series of Bessel functions were implemented. The following values of were considered: , , , , and . We present the results on Figure 1. One can appreciate that the proposed method produces eigenvalues with non-deteriorating error and outperforms the other two methods. Also, for non-integer values of the parameter , only few coefficients are necessary in comparison with hundreds required for the method from [24].
 |
 |
 |
 |
 |
 |
8.2 Example 2
Consider the same equation as in Subsection 8.1 with a different boundary condition:
| (8.6) |
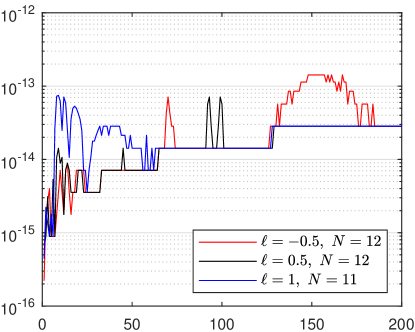
For this problem we compare the proposed method with the original NSBF representation [24, Example 7.2]. We considered three values of the parameter , , and and computed 200 approximate eigenvalues. Absolute errors of the obtained eigenvalues are presented on Figure 2, on the left – the proposed method, on the right – the original NSBF representation. One can see the advantage of the proposed method, especially for non-integer values of .

8.3 Decay of the coefficients
In this example we would like to illustrate numerically how far or close are the estimates of Theorem 3.5 and Corollary 3.7 from the computed decay of the coefficients . Taking into account (1.7), estimate (3.21) states that for one has
| (8.7) |
Assuming the coefficients are nicely behaved, one may suppose they should satisfy
| (8.8) |
Note that it is more like a guess and not a proven inequality. The proven inequality (3.24) is worse by a factor of .
We considered the following potentials
| (8.9) |
It is easy to see that , but . We took and for each of the potentials we computed the coefficients , . On the left in Figure 3 we present a log-log plot of the values against . Such type of plot allows one to reveal dependencies of the form . The exponent corresponds to the slope of the linear part of the curve. We obtained the following values for the exponent (the values are reported up to 2 decimal digits).
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 1.45 | 3.38 | 3.39 | 5.30 | 5.34 | 7.31 |
As one can see, the exponent indeed increases when the smoothness of the potential increases by 2, but the exponent also increases in the steps of 2 (approximately), not in the steps of 1 as predicted by (8.8). And even the decay rate for the discontinuous potential is better that those that the prediction (8.8) gives for absolutely continuous potential, suggesting Theorem 4.1 may hold under weaker assumptions on , (2.6) may be enough.


To verify the dependence of the decay of the coefficients on , we considered the potential and computed the coefficients , for different values of . On the right in Figure 3 we present a log-log plot of the values against . As one can see, the exponents in the dependencies are essentially the same and do not depend on .
Appendix A Continuous dependence of regular solutions and integral kernels on potentials
Many proofs related to transmutation operators are performed for smooth potentials and are followed by a phrase “considering an approximation by smooth potentials and passing to the limit” to show the validity for not so smooth potentials. However we are not aware of a rigorous result showing continuous dependence of the integral kernel on the potential for perturbed Bessel equations with potentials satisfying condition (2.6). For that reason we decided to include the proof in the present paper.
Consider two equations
| (A.1) |
where potentials and are complex valued functions satisfying condition (2.6). Without loss of generality we may assume that the parameter is equal for both potentials.
Let , denote regular solutions of (A.1) satisfying the asymptotics (2.2). We are going to estimate for each fixed . Following the notations from [17] and according to [17, Lemma 2.2], solutions satisfy the integral equations
where is Green’s function of the initial value problem. Hence their difference satisfies the equation
| (A.2) |
The following estimates hold [17, (A.1), (A.2) and (2.18)] for all
where is defined in (2.5) and the constant can be bounded by
Suppose initially that . We obtain from (A.2) that
| (A.3) |
Let us divide (A.3) by to obtain
| (A.4) |
The first term after “” sign is a non-decreasing function. The function is continuous on due to asymptotic condition (2.2). Hence applying Grönwall’s inequality we obtain that
or
The proof for the case is completely similar, the additional factor results in the change of and by and . Combining we obtain the following estimate
| (A.5) |
Let us introduce the notation
Theorem A.1.
Proof.
Corollary A.2.
Let the potentials and satisfy condition (2.6) with the same exponent and let be corresponding integral kernels of the transmutation operators. Then for each
Proof.
Corollary A.3.
Let the potential satisfy condition (2.6) with a parameter and let be a sequence of potentials such that
| (A.6) |
Let , and , be corresponding integral kernels. Then for any
Proof.
It follows from (A.6) that the quantities are uniformly bounded by for all . Hence the convergence follows immediately from Corollary A.2.
Recall that the integral kernel is the Fourier transform of the regular solution satisfying the asymptotics at 0. Dividing (A.5) by we obtain that
Using the last inequality one can prove that following the proof for the kernels and with minimal changes. ∎
Appendix B On existence of non-vanishing particular solution
Problem of existence of a non-vanishing particular solution of a differential equation naturally arises in the construction of coefficients for both SPPS [22, 7] and Neumann series of Bessel functions [21, 24] representations for solutions. While for a non-singular case it is always possible to choose such linear combination of linearly independent particular solutions that it will not vanish on the whole interval of interest (see [22, Remark 5], see also [5]), a perturbed Bessel equation possesses only one (up to a multiplicative constant) regular solution which either vanishes at some point or not. In this appendix we show that at least it is always possible to perform such spectral shift, i.e., consider an equation
| (B.1) |
that its regular solution will be non-vanishing on .
In some situations such value of is easy to choose. For example, if is real valued and bounded from below, any works, see, e.g., [7, Corollary 3.3]. For real valued potentials any having works since the equality would imply the existence of imaginary eigenvalue for selfadjoint problem (B.1) with Dirichlet boundary conditions formulated on , c.f., [8, Remark 4.1]. Lemma 3.1 from [6] shows that for real valued potentials satisfying any satisfying works.
The following proposition shows the existence of such for any potential satisfying
| (B.2) |
Proposition B.1.
Proof.
Let , . The regular solution of (B.1) can be written in the form
where is the modified Bessel function of the first kind. The function satisfies, see [17, Lemma 2.2]
where the constant does not depend on ; if and if .
Due to the asymptotics , [1, (9.7.1)], there exists such that for all . Let (the integral is finite due to the condition (B.2)) and let be such that .
If and , then
and hence .
Let . We may estimate the function by the first term of its Taylor series, i.e.,
Since , there exists such that
Take . Then it follows from the inequality that . Hence
and so .
Hence for all values of greater than the function does not vanish on . ∎
References
- [1] M. Abramovitz and I. A. Stegun, Handbook of mathematical functions, New York: Dover, 1972.
- [2] R. A. Adams, Sobolev Spaces. Pure and Applied Mathematics, Vol. 65, New York–London: Academic Press, 1975.
- [3] A. Baricz, D. Jankov and T. K. Pogány, Neumann series of Bessel functions, Integral Transforms Spec. Funct. 23 (2012), no. 7, 529–538.
- [4] A. Boumenir and B. Chanane, Computing eigenvalues of Sturm-Liouville systems of Bessel type, P. Edinburgh Math. Soc. 42 (1999), 257–265.
- [5] R. Camporesi and A. J. Di Scala, A generalization of a theorem of Mammana, Colloq. Math. 122 (2011), no. 2, 215–223.
- [6] R. Carlson, Inverse spectral theory for some singular Sturm-Liouville problems, J. Differ. Equations 106 (1993), 121–140.
- [7] R. Castillo-Pérez, V. V. Kravchenko and S. M. Torba, Spectral parameter power series for perturbed Bessel equations, Appl. Math. Comput. 220 (2013), 676–694.
- [8] R. Castillo-Pérez, V. V. Kravchenko and S. M. Torba, Analysis of graded-index optical fibers by the spectral parameter power series method, J. Optics 17 (2015), 025607 (9pp).
- [9] H. Chébli, A. Fitouhi and M. M. Hamza, Expansion in series of Bessel functions and transmutations for perturbed Bessel operators, J. Math. Anal. Appl. 181 (1994), no. 3, 789–802.
- [10] M. Coz and Ch. Coudray, The Riemann solution and the inverse quantum mechanical problem, J. Math. Phys. 17 (1976), no. 6, 888–893.
- [11] B. B. Delgado, K. V. Khmelnytskaya, V. V. Kravchenko, The transmutation operator method for efficient solution of the inverse Sturm-Liouville problem on a half-line, Math. Meth. Appl. Sci. 42 (2019) 7359–7366.
- [12] R. Devore and G. Lorentz, Constructive approximation, Berlin: Springer-Verlag, 1993.
- [13] J. L. Griffith, Hankel transforms of functions zero outside a finite interval, J. Proc. Roy. Soc. New South Wales 89 (1955), 109–115.
- [14] J.-C. Guillot and J. V. Ralston, Inverse spectral theory for a singular Sturm-Liouville operator on [0,1], J. Differ. Equations 76 (1988), no. 2, 353–373.
- [15] A. Fitouhi and M. M. Hamza, A uniform expansion for the eigenfunction of a singular second-order differential operator, SIAM J. Math. Anal. 21 (1990), 1619–1632.
- [16] M. Holzleitner, Transformation operators for spherical Schrödinger operators, J. Math. Anal. Appl. 481 (2020), no. 1, 123430, 27 pp.
- [17] A. Kostenko, A. Sakhnovich and G. Teschl, Inverse eigenvalue problems for perturbed spherical Schrödinger operators, Inverse Problems 26 (2010), 105013 (14pp).
- [18] A. Kostenko and G. Teschl, On the singular Weyl-Titchmarsh function of perturbed spherical Schrödinger operators, J. Differ. Equations 250 (2011), 3701–3739.
- [19] V. V. Kravchenko, On a method for solving the inverse Sturm–Liouville problem, J. Inverse Ill-pose P. 27 (2019), 401–407.
- [20] V. V. Kravchenko, Direct and inverse Sturm-Liouville problems: A method of solution, Birkhäuser, Basel, 2020.
- [21] V. V. Kravchenko, L. J. Navarro and S. M. Torba, Representation of solutions to the one-dimensional Schrödinger equation in terms of Neumann series of Bessel functions, Appl. Math. Comput. 314 (2017), 173–192.
- [22] V. V. Kravchenko and R. M. Porter, Spectral parameter power series for Sturm–Liouville problems, Math. Meth. Appl. Sci. 33 (2010), 459–468.
- [23] V. V. Kravchenko, E. L. Shishkina and S. M. Torba, On a series representation for integral kernels of transmutation operators for perturbed Bessel equations, Math. Notes 104 (2018), 552–570.
- [24] V. V. Kravchenko, S. M. Torba and R. Castillo-Pérez, A Neumann series of Bessel functions representation for solutions of perturbed Bessel equations, Appl. Anal. 97 (2018), 677–704.
- [25] V. V. Kravchenko, S. M. Torba and J. Yu. Santana-Bejarano, Generalized wave polynomials and transmutations related to perturbed Bessel equations, Math. Meth. Appl. Sci. 42 (2019), 5008–5028.
- [26] N. X. Ky, On weighted polynomial approximation with a weight in -space, Acta Math. Hung. 27 (1976), no. 1-2, 101–107.
- [27] V. Ledoux and M. Van Daele, Matslise 2.0: A Matlab toolbox for Sturm-Liouville computations, ACM Trans. Math. Softw. 42 (2016), 29:1–18.
- [28] F. Móricz, Absolutely convergent Fourier integrals and classical function spaces, Arch. Math. 91 (2008), 49–62.
- [29] K. Okamoto, Fundamentals of optical waveguides, San Diego: Academic Press, 2000.
- [30] A. P. Prudnikov, Yu. A. Brychkov and O. I. Marichev, Integrals and series. Vol. 2. Special functions, New York: Gordon & Breach Science Publishers, 1986, 750 pp.
- [31] G. Sampson and H. Tuy, Fourier transforms and their Lipschitz classes, Pac. J. Math. 75 (1978), no. 2, 519–537.
- [32] S. M. Sitnik and E. L. Shishkina, Method of transmutaitons for differential equations with Bessel operators, Moskow: Fizmatlit, 2019 (in Russian).
- [33] A. S. Sohin, The inverse scattering problem for an equation with a singularity (in Russian), Mat. Fiz. i Funkcional. Anal. 2 (1971), 182–235.
- [34] V. V. Stashevskaya, On the inverse problem of spectral analysis for a differential operator with a singularity at zero (in Russian), Zap. Mat. Otdel. Fiz.-Mat.Fak.KhGU i KhMO 25 (4) (1957) 49–86.
- [35] P. K. Suetin, Classical orthogonal polynomials, 3rd ed. (in Russian), Moscow: Fizmatlit, 2005, 480 pp.
- [36] G. Szegö, Orthogonal Polynomials, revised edition, New York: American Mathematical Society, 1959.
- [37] K. Trimeche, Transmutation operators and mean-periodic functions associated with differential operators, Harwood Academic Publishers, 1988.
- [38] V. Ya. Volk, On inversion formulas for a differential equation with a singularity at , Uspehi Matem. Nauk (N.S.) 8 (1953). no. 4(56), 141–151.
- [39] J. Weidmann, Spectral Theory of Ordinary Differential Operators, Lecture Notes in Math., Berlin: Springer, 1987.
- [40] J. E. Wilkins, Neumann series of Bessel functions, Trans. Amer. Math. Soc. 64 (1948), 359–385.