Translators of the Gauss curvature flow
Abstract.
A -translator is a surface in Euclidean space that moves by translations in a spatial direction and under the -flow, where is the Gauss curvature and is a constant. We classify all -translators that are rotationally symmetric. In particular, we prove that for each there is a -translator intersecting orthogonally the rotation axis. We also describe all -translators invariant by a uniparametric group of helicoidal motions and the translators obtained by separation of variables.
Key words and phrases:
-translator, Darboux surface, surface of revolution, separation of variables.1991 Mathematics Subject Classification:
53C44, 53A15, 35J961. Introduction and results
The flow by powers of the Gauss curvature was initiated by Chow [8] after the articles of Firey and Tso ([11, 15]). These works were the starting point of the theory of the flow by the Gaussian curvature ([1, 16]), a topic of high activity in geometric analysis that continues to the present. Given a smooth immersion of a strictly convex surface in Euclidean space , we consider the -flow as a one-parameter family of smooth immersions , such that and satisfying the flow
where is a constant, is the unit normal of and is the Gauss curvature at . An interesting problem is the evolution of a surface through the flow. As an example for the reader, if the surface becomes spherical ([3]).
If the surface moves under the -flow along a spatial direction , then satisfies for some positive constant . The vector is assumed to be unitary and it is called the speed of the flow. After a dilation, we can assume that . A surface is called a translator by the -flow with speed , or simply, a -translator in case that is understood, if
| (1) |
The notion of translator by positive powers of the Gauss curvature appeared in [17]. See also [9, 14].
In this paper we want to find examples of -translators under the geometric condition that the surface is defined kinematically as the movement of a curve by a uniparametric family of rigid motions of . Following Darboux [10, Livre I], we consider surfaces parametrized by , where and are two spatial curves and is an orthogonal matrix. The cases that we are interesting are: rotational surfaces ( is a uniparametric group of rotations and is constant), helicoidal surfaces ( is a uniparametric group of helicoidal motions), translation surfaces ( is the identity) and ruled surfaces ( is a straight-line). Since we have left to one side the study of the evolution of the surface, we do not require that to be positive but only that has sense. For example, may be negative if . This will be implicitly assumed in all the results.
In the flow by powers of the Gaussian curvature, it is known that the -flow is special because it has an interpretation in affine differential geometry as the affine normal flow of a convex surface ([2, 6]). However, in base of our proofs, this case will appear as natural because when we express the equation (1) for each one of the above three types of surfaces and when is exactly , this equation is greatly simplified due to a cancellation of terms. This makes the arguments easier than in the general case of .
Planes are examples of -translators for any provided the plane is parallel to the speed of the flow. Throughout this paper, we will discard planes as examples of -translators. Other examples that we will not consider in the class of -translators are the surfaces whose Gauss curvature is constant, where now the equation (1) says that the unit normal vector makes a constant angle with a fixed direction. Similarly, we discard the case .
It is important to point out that there is not a priori relation between the speed vector and the special parametrization of each of the above Darboux surfaces. So, if one considers the study of translators one can prescribed the speed , usually, the vector in the literature. However, if one considers one of the above types of Darboux surfaces, the parametrization has no relation with . This can be clearly seen for rotational surfaces (also helicoidal surfaces). The rotation axis of the surface is, initially, independent of the vector . However, as we will see, for rotational and helicoidal surfaces, the speed must be parallel to the axis (Propositions 2.1 and 3.1). Something similar occurs for translations surfaces where, if one prescribes that the surface is , the speed may be arbitrary.
The organization of this paper is as follows. In Section 2, we obtain all rotational -translators. Recall that in [17], Urbas obtains these surfaces for using the Legendre transform (see also [13] for a similar calculation). Our approach uses simple geometric arguments and it holds for any (Theorem 2.2). In particular, for each value of , we prove the existence of rotational examples intersecting orthogonally the rotation axis (Corollary 2.4). Section 3 is devoted to the study of -translators of helicoidal type. Although we are not able to obtain explicit parametrizations of these surfaces, we do a first integration of the generating curve (Theorem 3.2), also in terms of the Bour function (Theorem 3.3). In Section 4, we obtain the classification of all solutions of (1) obtained by separation of variables , where are the canonical coordinate system of . Although these solutions depend on a particular choice of coordinates of , our result holds for any speed vector . In particular, we prove that there are -translators only if (Theorems 4.1 and 4.3). Besides we provide new examples of -translators of type , we also give new examples of -translators obtained by separation of variables of type (Example 4.4). Finally, in Section 5, we investigate the existence of ruled -translators, proving that there are not ruled -translators, except trivial cases (Theorem 5.1).
The authors have extended the results of this paper for (spacelike and timelike) -translators in Lorentz-Minkowski space ([4]).
2. Rotational -translators
In this section, we classify the surfaces of revolution satisfying (1). A first question is if there is a relation between the rotation axis of the surface and the speed vector . As it is expectable, we prove that the vector must be parallel to the rotation axis.
Proposition 2.1.
Let be a -translator. If is a surface of revolution, then the rotation axis is parallel to the speed vector .
Proof.
After a rigid motion, we can assume that the rotation axis is the -axis. The generating curve of a rotational surface is a curve included in the coordinate -plane which can be assumed that it is a graph on the -axis, except in the case that this curve is a straight-line parallel to the -axis. In this particular situation, the surface is a circular cylinder where we know that . Thus a circular cylinder satisfies (1) if , that is, the vector is parallel to the -axis, proving the result for this particular case.
Suppose now the general case that the generating curve writes as where is a smooth function. Then a parametrization of is
| (2) |
where . The unit normal vector is
and the principal curvatures of are
If , then (1) writes as
or equivalently
where
Since the functions are linearly independent, we conclude . If is constantly , then is constant and the surface is a plane. This case was initially discarded. Therefore from , we find that , concluding that is parallel to . ∎
After a rigid motion, we will assume that the rotation axis is the -axis and consequently from this proposition, that after a symmetry about the -plane if necessary. Then (1) is
Set . Notice that and . In terms of , the above equation becomes
A first integration gives
| (3) |
In the case , the condition says that the domain of is when . Otherwise, we need to distinguish if is negative or positive, that is, belongs to or not. If , the parenthesis in (3) must be positive, yielding . On the other hand, using now that , we have , so this is the restriction on because . If , then . Since the parenthesis in (3) must be positive because , then we obtain and from the fact that , the restriction is . To summarize, we have
| (4) |
Hence we deduce
| (5) |
As conclusion, we have the classification of all -translators that also are surfaces of revolution.
Theorem 2.2.
Let be a -translator. If is a surface of revolution about the -axis, then is a circular cylinder of arbitrary radius or parametrizes as (2) where
| (6) |
Furthermore, the maximal domain of the function is
-
(1)
, if .
-
(2)
, if .
-
(3)
, if . In this case, we have
In all these cases, we understand that if in the radicand in the left-end of the interval is negative, then the value of this end is .
Proof.
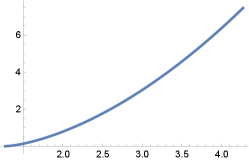
We point that it is expectable that in the case the domain cannot be because there are no entire graphs that are -translators if ([17, Sect. 4]) and if ([18, Th. 6.1]). It deserves to note the case because it is possible to integrate explicitly (6) (see also [14]). See Figure 1.
Corollary 2.3.
Rotational -translators form a uniparametric family of surfaces parametrized by (2), where
The maximal domain of is if and if . For the value , is the parabola , the graphic of intersects orthogonally the rotation axis and the surface is a paraboloid.
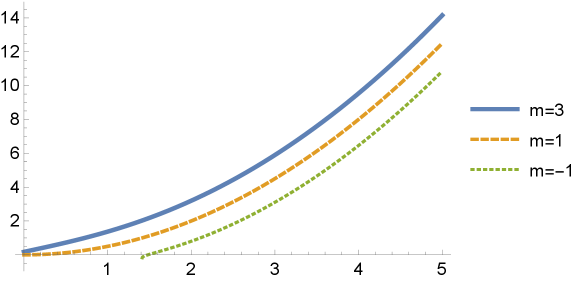
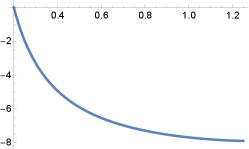
By (4), we point out that the maximal domain of is not in general. However, an interesting case to investigate is if there are generating curves that meet orthogonally the rotation axis. We prove that this occurs for all cases of . See Figure 2.
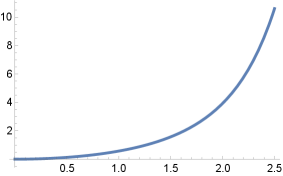
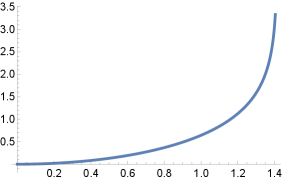
Corollary 2.4.
For each , there are rotational -translators whose generating curves intersect orthogonally the rotation axis. These surfaces are unique up to vertical translations. Furthermore,
-
(1)
If , the maximal domain of is , and
-
(2)
If , the maximal domain is , with
Proof.
The condition on the orthogonality with the rotation axis requires that is defined at and . From (5), it is immediate that must be and the same occurs in the particular case . This solution is at because from (5), we have . Hence is in its domain by regularity ([5, 12]). The uniqueness is consequence of the solvability of (6).
We point out that in some particular cases, the integrals in (6) can be explicitly solved. Here, we denote by to emphasize the parameter where we also assume .
-
(1)
Case . Then
and
defined on
-
(2)
Case . Now
and the solution is
defined on
-
(3)
For , we have
and
and defined on .
3. Helicoidal -translators
Consider a helicoidal surface in with axis whose generating curve is included in the -plane and pitch . Without loss of generality, we can assume that where is a smooth function. Then parametrizes by
| (7) |
If , then the unit normal vector is
and the Gauss curvature is
Then is a -translator if
| (8) |
As a first conclusion, we prove that must be parallel to the -axis. The proof is similar of Proposition 2.1.
Proposition 3.1.
Let be a -translator. If is a helicoidal surface, then the axis is parallel to the speed vector .
Proof.
Equation (8) can be written as . From , we obtain
Combining both equations, we have . Thus and hence, . ∎
From this proposition, we can assume that . Then (8) is
| (9) |
We will obtain a first integration of this equation. For this, let
Then and thus (9) is equivalent to
If , the solution is , with . If , the solution of this equation is
In terms of the function , we have
In particular, this gives a restriction on the domain of .
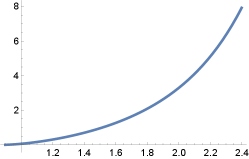
Theorem 3.2.
Let be a -translator. If is a helicoidal surface about the -axis and pitch , then parametrizes as (7), where
| (10) |
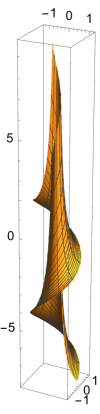
Following Lee [14] we may also use the approach of Bour ([7]). More explicitly, the Bour coordinates are defined by and , where
The first fundamental form is now where the so-called Bour function is introduced by the relation Using the Bour function , the terms , and can be determined by
| (11) |
With the above discussion, the Gauss curvature is now and Then (1) is now
or equivalently
Setting and , we have
A first integration is
| (12) |
where is a integration constant with if . Because can be viewed a function of , we may interchange their roles. Therefore, we obtain again a classification of helicoidal -translators in terms of the Bour function .
Theorem 3.3.
Let be a -translator. If is a helicoidal surface about the -axis and pitch , then parametrizes as
where is the Bour function, and is
| (13) |
with ( if ).
Proof.
Because we see as a function of in (12), can be considered as a new variable. Then we have the first equality in (11), where depends on this new variable and as do and Considering this, together in (7), we have the parametrization of the helicoidal -translator. Up to or not, from (12) we complete the proof. ∎
Again, for some particular values of , (12) can be explicitly integrated. We present the cases ([14]), and .
-
(1)
Case The solution is
-
(2)
Case . The solution is
where
-
(3)
Case Then,
In particular, we can express in terms of ,
4. -translators of translation type
By a translation surface of we mean a surface given by the sum of two curves contained in two coordinate planes. This is a particular case of a Darboux surface where is the identity. After a rigid motion, the surface is the sum of the curves and , where and are smooth functions in one variable. Thus the surface parametrizes by
| (14) |
If we see the surface as the graph of , then the problem of finding all translation surfaces that are -translator is equivalent to ask which are the solutions of (1) obtained by separation of variables . In this section we classify all -translators of translation type.
We calculate all terms of equation (1). Let us observe that once we have the parametrization (14), we cannot prescribed the speed because the parametrization (14) was previously fixed after a rigid motion. Thus in order to calculate all terms of (1), the vector is assumed in all its generality. The computation of (1) gives
| (15) |
where the prime denotes the derivatives with respect to the corresponding variables or in each case.
In order to clarify the arguments, we separate the case . This case appears because the denominators in (15) are cancelled.
Theorem 4.1.
Let be a -translator with speed of translation type parametrized by (14). Up to a change of the roles of and , the function is , , and is one of the following functions depending on the speed :
-
(1)
If the speed is , then , .
-
(2)
If the speed is , then
(16) where .
Proof.
Now (15) is
| (17) |
Let us observe the symmetry of the roles of and , so it is enough to distinguish cases according to the function . Notice that is not constantly because the case was initially discarded.
- (1)
-
(2)
Suppose that is not constant. Differentiating successively (17) with respect to and next with respect to , we obtain for all . If at some , , then is constant in some interval and we are in the previous case (1) interchanging the roles of and . Thus in its domain, which it is a contradiction because is not a constant function.
∎
Let us observe that the surfaces of the case (1) of Theorem 4.1 are affinities of the paraboloid and that the speed . Other consequence of this result is that we find -translators where the speed is parallel to the -plane by choosing . If we assume that the speed is , as usually is taken as a convention in the literature (e.g. [9, 17]), then changing the roles of and , we can provide examples of translation surfaces whose speed is .
Example 4.2.
Let and . Suppose that a -translator parametrizes as . In this case, (1) is
Hence and
for some constant . Integrating,
with , . For example, choose and . Then the surface is
If we see this surface as the graph on the -plane, and after a symmetry about the -plane, we have
We now consider the general case .
Theorem 4.3.
If , there are not -translators that are surfaces of translation.
Proof.
Again by the symmetry of the roles of and , we discuss according to the function . Recall that (and consequently, ) cannot be constantly because then would be . Then (15) is
| (18) |
We differentiate (18) with respect to , and after some manipulations, we arrive to
where . The above equation is a polynomial equation on of degree , which we write as
where all coefficients are functions on the variable . Therefore they must vanish because . We have
Since , we obtain . Now
Using into , we arrive to , obtaining a contradiction. This completes the proof. ∎
Translations surfaces appear as surfaces obtained by the translation of a curve along another curve. As we have seen, in case that the two curves are included in coordinate planes, then the surface can be written as . As we said, the problem to classify all translation surfaces that are -translators is equivalent to solve equation (1) by separation of variables. Other way of separation of variables is assuming that , for two smooth functions and . However, the equation (1) is difficult to solve in all its generality. We only show an example where we can obtain non-trivial examples if .
Example 4.4.
. Assume and the speed is . Instead to assume , we suppose . Then the parametrization of the surface is , , and (1) is
| (19) |
Because , then and so, . We divide (19) with obtaining
| (20) |
Differentiating successively (20) with respect to and , we have
Because , then , where Now (20) is
for some nonzero constant . Then and differentiating and using that , we deduce that . For the function , we have
in particular, . The solution of this equation is . We come back to (19), obtaining
We see as a function of , . Then , so
which is an ODE of Bernoulli type. The solution is
The solution of this equation together the above function provide an example of a -translator given by .
5. Ruled -translators
In this section we study the solutions of (1) when the surface is ruled. A parametrization of a ruled surface is
where is a smooth function with for all and is a curve parametrized by arc-length.
A case to discard is that is a cylindrical surface because . Thus, is a non-constant function. In such a case, we can choose to be the striction curve, that is, for all . Then
where the parenthesis denotes the determinant of the three vectors. In particular, we are assuming that is not constantly . On the other hand, the unit normal vector is
In particular, is negative, so we are assuming that is an integer. Then (1) writes as
or equivalently,
| (21) |
The Wronskian of the functions is
Since , the Wronskian if not , proving these three functions are linearly independent. This yields a contradiction with (21). As a conclusion, we have the following result.
Theorem 5.1.
There are not -translators that are ruled surfaces.
Let us notice that this result of non-existence has discarded the case that the surface is cylindrical (the rulings are parallel to ) or that , that is, the surface is developable. The condition together is equivalent to the case that the base curve is a planar curve parallel to , obtaining that the surface is part of a plane.
Acknowledgments
This publication is part of the Project I+D+i PID2020-117868GB-I00, supported by MCIN/ AEI/10.13039/501100011033/
References
- [1] B. Andrews, Contraction of convex hypersurfaces in Euclidean space. Calc. Var. Partial Differ. Eq. 2 (1994), 151–171.
- [2] B. Andrews, Contraction of convex hypersurfaces by their affine normal. J. Differential Geom. 43 (1996), 207–230.
- [3] B. Andrews, Gauss curvature flow: the fate of the rolling stones. Invent. Math. 138 (1999), 151–161.
- [4] M. E. Aydin, R. López, Rotational -Translators in Minkowski space. Preprint 2022.
- [5] L. Caffarelli, Interior estimates for solutions of the Monge-Ampère equation. Ann. of Math. 131 (1990), 135–150.
- [6] E. Calabi, Hypersurfaces with maximal affinely invariant area. Amer. J. Math. 104 (1982), 91–126.
- [7] M. P. do Carmo, M. Dajczer, Helicoidal surfaces with constant mean curvature. Tohoku Math. J. 34 (1982), 425–425.
- [8] B. Chow, Deforming convex hypersurfaces by the nth root of the Gaussian curvature. J. Differential Geom. 22 (1985). 117–138.
- [9] K. Choi, P. Daskalopoulos, K.-A. Lee, Translating solutions to the Gauss curvature flow with flat sides, Analysis PDE 14 (2021), 595–616.
- [10] G. Darboux, Leçons sur la Théorie Générale des Surfaces et ses Applications Géométriques du Calcul Infinitésimal, vol. 1–4. Chelsea Publ. Co, reprint, 1972.
- [11] W. J. Firey, Shapes of worn stones. Mathematika 21 (1974), 1–11.
- [12] D. Gilbarg, N. Trudinger, Second Order Elliptic Partial Differential Equations. Second edition, Springer-Verlag, 1983.
- [13] H. Ju, J. Bao, H. Jian, Existence for translating solutions of Gauss curvature flow on exterior domains. Nonlinear Anal. 75 (2012), 3629–3640.
- [14] H. Lee, Isometric deformations of the -flow translators in with helicoidal symmetry. C. R. Math. Acad. Sci. Paris 351 (2013), 477–482.
- [15] K. Tso, Deforming a hypersurface by its Gauss-Kronecker curvature. Comm. Pure Appl. Math. 38 (1985), 867–882.
- [16] J. Urbas, An expansion of convex hypersurfaces. J. Differential Geom. 33 (1991), 91–125.
- [17] J. Urbas, Complete noncompact self-similar solutions of Gauss curvature flows, I: Positive powers. Math. Ann. 311 (1998), 251–274.
- [18] J. Urbas, Complete noncompact self-similar solutions of Gauss curvature flows, II: Negative powers. Adv. Differ. Equ. 4(3) (1999), 323–346.