Tracking Dynamical Features via Continuation and Persistence

Dynamical systems enter the field of data science in two ways: either directly, as in the case of dynamic data, or indirectly, as in the case of images, where gradient dynamics are useful. Forman’s discrete Morse theory [10, 11, 16] combines topology with gradient dynamics via combinatorial vector fields. Discrete Morse theory has been used to simplify datasets and to extract topological features from them [1, 7, 15, 26]. When coupled with persistent homology [7, 8, 9], this theory can be useful for analyzing complex data [12, 17, 18].

Conley theory [4] is a generalization of classical Morse theory beyond gradient dynamics. Conley’s approach to dynamical systems is motivated by the observation that in many areas, perhaps most notably biology, the differential equations governing systems of interest are known only roughly. Generally, this is due to the presence of several parameters which cannot be measured or estimated precisely. A similar situation occurs in data science, where a time series dataset that is collected from a dynamical process only crudely approximates the underlying system. This observation has motivated recent studies [2, 6, 14, 20, 21, 23] on a variant of Conley theory for combinatorial vector fields.

The primary objects of interest in Conley theory are isolated invariant sets, each of which is a salient feature of a vector field, together with an associated homological invariant called the Conley index (see Section 2). Notably, isolated invariant sets with non-trivial Conley index persist under small perturbations. The geometry of the isolated invariant set may change, and even the topology may change, but the Conley index associated with the isolated invariant set remains the same. The isolated invariant set cannot suddenly vanish or change from an attractor to a repeller or vice versa. From this observation, we get the notion of the continuation of an isolated invariant set in a dynamical system to another one in a nearby system. This local idea becomes global by making the continuation relation transitive.

Given a path in the space of dynamical systems, one can track an invariant set along the path so long as the invariant set remains isolated. When the isolation is lost, continuation “breaks” and the Conley index is not well-defined. Typically, this may be observed when two isolated invariant sets merge. Isolation may eventually be regained, but there is no guarantee that the Conley index will be recovered. We propose to use persistence [7, 8, 9] in the discrete setting to connect continuations. First, we show how continuation can be detected and maintained algorithmically in a combinatorial multivector field, which is a discretized version of a continuous vector field. In fact, the continuation itself may be viewed as a special case of persistence where all bars persist for the duration of the continuation. When continuation “breaks,” we observe the birth and death of homology classes.

The combination of continuation and persistence allows us to algorithmically track an isolated invariant set and its associated Conley index in the setting of combinatorial dynamical systems. Recall that a combinatorial dynamical system is generated by a multivector field. A multivector field is a partition of a simplicial complex into sets that are convex with respect to the face poset. We track an isolated invariant set in a sequence of such fields where each field differs from its adjacent ones by an atomic rearrangement. Each atomic rearrangement is either an atomic coarsening or an atomic refinement. We show that an atomic refinement always permits continuation and thus the Conley index of the tracked invariant set persists. In the case of coarsening, we may not be able to continue. In such a case, we select an isolated invariant set that is a minimal perturbation of the previous one and compute the persistence of the Conley index between them. Hence, while there may come a point where we can no longer track an isolated invariant set, we can use persistence to track the lifetime of the homological features that are associated with the isolated invariant set.

The top row of Figure 1 presents flow lines from three flows on a simplicial complex with vertices marked from A to N. The same figure also shows three combinatorial multivector fields represented as three different partitions of the collection of cells into multivectors. Each multivector is depicted as a connected component, and it is easy to see that they are convex with respect to the face poset. The multivector fields are constructed as follows: if the flow transversely crosses an edge $e$ into a triangle $t$, then $e$ and $t$ are put in the same multivector. Else, $e$ is put into the same multivector as both of its incident triangles. If the flow line originating at a vertex $v$ immediately enters triangle $t$, then $v$ and $t$ are put into the same multivector. See [22, 23] for additional information on this construction.

There are two saddle stationary points in each flow, indicated by small black dots. For all three flows, the lower saddle is located in triangle $GHK$. However, the upper one moves from triangle $CDG$ in the left flow, through triangle $DGH$ in the middle flow and finally it shares triangle $GHK$ with the lower saddle in the right flow. On the combinatorial level, the upper saddle in the left flow is represented by an isolated invariant set $S_{1}$ consisting of one multivector $\{CFG,CDG,DGH,CF,CG,DG,DH\}$ marked in yellow. The Conley index of $S_{1}$ is non-trivial only in dimension one and has exactly one generator. Using methods from this paper, $S_{1}$ can be tracked to an isolated invariant set $S_{2}$ containing the upper saddle of the middle flow and consisting of one multivector $\{CDG,DGH,CG,DG,DH\}$, also marked in yellow. The isolated invariant set $S_{3}$ containing the upper saddle of the right flow consists of one multivector $\{CDG,DGH,FGJ,GJK,GHK,CG,DG,DH,FG,JK,GH,GJ,GK\}$, again marked in yellow. It is not a continuation of $S_{2}$, because in the right flow the two saddles are too close to one another to be distinguishable with the resolution of the triangulation. Furthermore, the Conley index has changed. It is only nontrivial in dimension one, but unlike $S_{1}$ and $S_{2}$, it has two generators. Hence, in the right multivector field, a new generator is born. We show how to capture the birth of this generator using persistence, and we depict the associated barcode beneath the top row of Figure 1. The familiar reader will note that the Conley index of $S_{3}$ is the same as that of a monkey saddle. However, because of the finite resolution, we cannot discriminate between two nearby saddles and a monkey saddle. One can view a multivector field as a combinatorial object that represents flows up to the resolution permitted by a triangulation. This purely combinatorial view of the top row of Figure 1 is presented in the bottom row. In subsequent examples, we use this style.

In this section, we review multivector fields, combinatorial dynamical systems, and isolated invariant sets. Throughout this paper, $K$ will always denote a finite simplicial complex. Furthermore, we will only consider simplicial homology [13, 25] with coefficients taken from a finite field. Much of the foundational work on combinatorial dynamical systems was first published in [21] and subsequently generalized in [20]. This work was heavily influenced by Forman’s discrete Morse theory [10, 11]. Combinatorial dynamical systems are constructed via multivector fields, which require a notion of convexity. Given a finite simplicial complex $K$, we let $\leq$ denote the face relation on $K$. Formally, if $\sigma,\tau\in K$, then $\sigma\leq\tau$ if and only if $\sigma$ is a face of $\tau$. The set $A$ is convex if for each pair $\sigma,\tau\in A$ where there exists a $\rho\in K$ satisfying $\sigma\leq\rho\leq\tau$, we have that $\rho\in A$.

A multivector is a convex subset of a simplicial complex. A partition of $K$ into multivectors is a multivector field on $K$. Multivectors are not required to have a unique maximal element under $\leq$, nor are they required to be connected. Disconnected multivectors do not appear in practice, and in the interest of legibility, all examples that we include in this paper only depict connected multivectors. However, all of our theoretical results do hold for disconnected multivectors. We draw a multivector $V$ by drawing an arrow from each nonmaximal element $\sigma\in V$ to each maximal element $\tau\in V$ where $\sigma\leq\tau$. If $\sigma$ is the only element of a multivector, or a singleton, then we mark $\sigma$ with a circle. Each $\sigma\in K$ is contained in a unique multivector $V\in\mathcal{V}$. We denote the unique multivector in $\mathcal{V}$ containing $\sigma$ as $[\sigma]_{\mathcal{V}}$.

A multivector field $\mathcal{V}$ induces dynamics on $K$. Given a simplex $\sigma\in K$, we denote the closure of $\sigma$ as $\operatorname{\sf cl}(\sigma):=\{\tau\in K\;|\;\tau\leq\sigma\}$. For a set $A\subseteq K$, the closure of $A$ is given by $\operatorname{\sf cl}(A):=\cup_{\sigma\in A}\operatorname{\sf cl}(\sigma)$. A set $A$ is closed if and only if $A=\operatorname{\sf cl}(A)$. The multivector field $\mathcal{V}$ induces a multivalued map $F_{\mathcal{V}}\;:\;K\multimap K$ where $F_{\mathcal{V}}(\sigma):=\operatorname{\sf cl}(\sigma)\cup[\sigma]_{\mathcal{V}}$. Informally, this will mean that if one is at a simplex $\sigma$, then one can move either to a face of $\sigma$ or to a simplex $\tau$ in the same multivector as $\sigma$. We allow moving within any single multivector because, on the level of flows, the behavior within the multivector is beyond the resolution of the given simplicial complex. Conversely, we do not allow moving from a cell to its coface, unless they are in the same multivector, because this does not respect the underlying flow.

The multivalued map $F$ gives a notion of paths and solutions to $\mathcal{V}$. We let $\mathbb{Z}_{[i,j]}:=\mathbb{Z}\cap[i,j]$. A path is a function $\rho\;:\;\mathbb{Z}_{[0,n]}\to K$ where $\rho(i+1)\in F_{\mathcal{V}}(\rho(i))$ for $i\in\mathbb{Z}_{[0,n-1]}$. Likewise, a solution is a function $\rho\;:\;\mathbb{Z}\to K$ where $\rho(i+1)\in F_{\mathcal{V}}(\rho(i))$. However, there are several trivial solutions in a multivector field. If $\sigma\in K$, then there is a solution $\rho$ where $\rho(i)=\sigma$ for all $i\in\mathbb{Z}$. That is, every simplex is a fixed point. This does not match the intuition from differential equations: only a very select set of simplices should be fixed points under $F_{\mathcal{V}}$. To enforce this, we use the notion of a critical multivector. But first, we define the mouth of a set $A$, denoted $\operatorname{\sf mo}(A)$, to be $\operatorname{\sf mo}(A):=\operatorname{\sf cl}(A)\setminus A$. The multivector $V$ is critical if $H(\operatorname{\sf cl}(A),\operatorname{\sf mo}(A))\neq 0$. Intuitively, critical multivectors with one maximal element correspond to stationary points in the flow setting. Thus, only simplices in critical multivectors should be fixed points under $F$. Essential solutions enforce this requirement [20].

The invariant part of a set $A\subseteq K$, denoted $\operatorname{\sf Inv}_{\mathcal{V}}(A)$, is given by the set of simplices $\sigma\in A$ for which there exists an essential solution $\rho\;:\;\mathbb{Z}\to A$ where $\rho(i)=\sigma$ for some $i\in\mathbb{Z}$. A set $S\subseteq K$ is an invariant set if and only if $S=\operatorname{\sf Inv}_{\mathcal{V}}(S)$. For examples of invariant sets, see Figure 2. We are interested in a special type of invariant set.

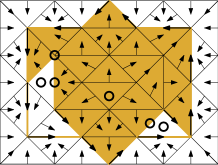
Figure 3 illustrates the concept of isolation. An invariant set $S$ is $\mathcal{V}$-compatible if $S$ is equal to the union of a set of multivectors in $\mathcal{V}$. For examples, see Figure 4. This gives an equivalent formulation of an isolated invariant set.

In this section, we introduce the protocol for tracking an isolated invariant set across multivector fields. Results in the continuous theory imply that under a sufficiently small perturbation, some homological features of an isolated invariant set do not change. Hence, we require a notion of a small perturbation of a multivector field. In particular, let $\mathcal{V}$ and $\mathcal{V}^{\prime}$ denote two multivector fields on $K$. If each multivector $V^{\prime}\in\mathcal{V}^{\prime}$ is contained in a multivector $V\in\mathcal{V}$, $|\mathcal{V}\setminus\mathcal{V}^{\prime}|=1$, and $|\mathcal{V}^{\prime}\setminus\mathcal{V}|=2$, then $\mathcal{V}^{\prime}$ is an atomic refinement of $\mathcal{V}$. It is so-called because $\mathcal{V}^{\prime}$ is obtained by “splitting” exactly one multivector in $\mathcal{V}$ into two multivectors, while all the other multivectors remain the same. Symmetrically, we say that $\mathcal{V}$ is an atomic coarsening of $\mathcal{V}^{\prime}$. More broadly, it is said that $\mathcal{V}$ and $\mathcal{V}^{\prime}$ are atomic rearrangements of each other. In Figures 5, 6, 7, 8, and 9, the two multivector fields are atomic rearrangements of each other. In these figures, we draw the multivectors that are splitting or merging in red.

Given an isolated invariant set $S$ under $\mathcal{V}$, and an atomic rearrangement of $\mathcal{V}$ denoted $\mathcal{V}^{\prime}$, we aim to find an isolated invariant set $S^{\prime}$ that is a minimal perturbation of $S$. We accomplish this through two mechanisms: continuation and persistence. When we use continuation, or when we attempt to continue, we check if there exists an $S^{\prime}$ under $\mathcal{V}^{\prime}$ that is in some sense the same as $S$. If there is at least one such $S^{\prime}$, then we choose a canonical one. This is explained in Section 4. If there is no $S^{\prime}$ to which we can continue, then we use persistence. In particular, we choose a canonical isolated invariant set $S^{\prime}$ under $\mathcal{V}^{\prime}$, and while $S$ does not continue to $S^{\prime}$, we can use zigzag persistence to observe which features of $S$ are absorbed by $S^{\prime}$. We elaborate on this scheme in Section 5. To choose $S^{\prime}$, we require the following result.

The set $S$ is an isolated invariant set by assumption, so Proposition 3 implies that $S$ is convex and $\mathcal{V}$-compatible. Thus, if $S$ is also $\mathcal{V}^{\prime}$-compatible, a natural choice is then to use Proposition 4 and take $S^{\prime}:=\operatorname{\sf Inv}_{\mathcal{V}^{\prime}}(S)$. However, if $S$ is not $\mathcal{V}^{\prime}$-compatible, then the situation is more complicated. The set $S$ is not $\mathcal{V}^{\prime}$-compatible precisely when $\mathcal{V}^{\prime}$ is an atomic coarsening of $\mathcal{V}$, and the unique multivector $V\in\mathcal{V}^{\prime}\setminus\mathcal{V}$, occasionally called the merged multivector, has the properties that $V\cap S\neq\emptyset$ and $V\not\subseteq S$. In such a case, we use the notation $\langle S\cup V\rangle_{\mathcal{V}^{\prime}}$ to denote the intersection of all $\mathcal{V}^{\prime}$-compatible and convex sets that contain $S\cup V$. The simplicial complex $K$ is $\mathcal{V}^{\prime}$-compatible and convex, so $\langle S\cup V\rangle_{\mathcal{V}^{\prime}}$ always exists and $S\subsetneq\langle S\cup V\rangle_{\mathcal{V}^{\prime}}$. We observe that $\langle S\cup V\rangle_{\mathcal{V}^{\prime}}$ is $\mathcal{V}^{\prime}$-compatible and convex, and thus it is the minimal convex and $\mathcal{V}^{\prime}$-compatible set that contains $S$. In such a case, we use Proposition 4 and take $S^{\prime}:=\operatorname{\sf Inv}_{\mathcal{V}^{\prime}}(\langle S\cup V\rangle_{\mathcal{V}^{\prime}}$ ). These principles are enumerated in the following Tracking Protocol.

We include an example of Step 1a in Figure 5, Step 1b in Figure 6, Step 1c in Figure 7, Step 1d in Figure 8, and Step 2f in Figure 9. Each figure depicts a multivector field and a seed isolated invariant set on the left, and an atomic rearrangement and the resulting isolated invariant set on the right. By iteratively applying this protocol (until $S^{\prime}=\emptyset$, in which case we are done), we can track how an isolated invariant set changes across several atomic rearrangements. See Figure 10 and the associated barcode in Figure 11. The following proposition shows that any two multivector fields $\mathcal{V}_{1}$ and $\mathcal{V}_{2}$ can be related by a sequence of atomic rearrangements, and hence the Tracking Protocol can be used to track how an isolated invariant set changes across an arbitrary sequence of multivector fields.

Now, we introduce continuation in the combinatorial setting, and we justify the canonicity of the choices made in Step 1 of the Tracking Protocol. In addition, we show that if Step 1 is used to obtain $S^{\prime}$ from $S$, then $S$ and $S^{\prime}$ are related by continuation. Continuation is closely related to the Conley index, so we begin with a brief review of the topic.

In the previous section, we explicated Step 1 of the protocol, which uses continuation to track an isolated invariant set across a changing multivector field. In this section, we first place continuation in the persistence framework by showing how to translate the idea of combinatorial continuation into a zigzag filtration [3, 7] that does not introduce spurious information. Then, we use the persistence view of continuation to justify Step 2f of the Tracking Protocol, which permits us to capture changes in an isolated invariant set when no continuation is possible. In particular, it permits us to track an isolated invariant set even in the presence of a bifurcation that changes the Conley index. If the isolated invariant set that we are tracking collides, or merges, with another isolated invariant set, then we follow the newly formed isolated invariant set, and persistence captures which aspects of our original isolated invariant set persist into the new one. Conversely, if an isolated invariant set splits, we track the smallest isolated invariant set that contains all of the child invariant sets. We begin by reviewing some results on computing the persistence of the Conley index from [5].