Trace Embeddings from Zero Surgery Homeomorphisms

The study of $4$-manifolds is distinguished by the remarkable difference between smooth and topological $4$-manifolds compared to other dimensions. This manifests in the failure of Smale’s h-cobordism theorem which Smale used to prove the high dimensional Poincaré conjecture [Sma60]. This left open the $4$-dimensional Poincaré conjecture which asserts that every smooth $4$-manifold homotopy equivalent to $S^{4}$, i.e. a homotopy $S^{4}$, is homeomorphic to $S^{4}$. Freedman resolved the $4$-dimensional Poincaré conjecture and showed that simply connected, smooth $4$-manifolds are determined up to homeomorphism by their intersection forms [Fre82]. Donaldson contrasted this topological simplicity with his Diagonalization Theorem and showed that $4$-manifolds do not smoothly admit such a straightforward classification [Don83]. The resulting study of $4$-manifolds have yielded an abundance of exotic pairs of $4$-manifolds: pairs of $4$-manifolds homeomorphic, but not diffeomorphic to each other. Unique to dimension $4$ are phenomena such as infinite families of exotic smooth structures on $\mathbb{R}^{4}$ and small closed $4$-manifolds such as $\mathbb{CP}^{2}\#2\overline{\mathbb{CP}}^{2}$ [Tau87, AP10]. Remarkably, this exotic behavior has not been shown to occur with the $4$-sphere: the most basic example of a closed $4$-manifold. This is the focus of the Smooth $4$-dimensional Poincaré conjecture (SPC4).

Historically, the consensus among experts is that SPC4 is false due to the aforementioned exotica and the many constructions of homotopy spheres that are not known to be standard. The difficulty with exhibiting an exotic $S^{4}$ is that the invariants used to distinguish smooth structures are typically known to vanish on homotopy $4$-spheres. This changed with Rasmussen’s invention of his eponymous $s$-invariant [Ras10], a slice obstruction coming from Khovanov Homology [Kho00]. A knot is smoothly slice if it is the boundary of a smooth properly embedded disk in $B^{4}$. Rasmussen defined the $s$-invariant $s(K)\in 2\mathbb{Z}$ for any knot $K$ and showed that if $s(K)\neq 0$, then $K$ is not slice. Unlike prior slice obstructions, it is not clear that the $s$-invariant vanishes on knots slice in a homotopy ball other than $B^{4}$. In theory, one could show that a homotopy sphere $\Sigma$ is exotic by finding a knot $K$ slice in the homotopy ball $\Sigma-\mathop{\rm int}(B^{4})$ and has $s(K)\neq 0$. Then $K$ would not be slice in the standard $B^{4}$ and sliceness of $K$ smoothly distinguishes $\Sigma$ from the standard $S^{4}$.

Freedman, Gompf, Morrison, and Walker (FGMW) attempted this strategy on the intensely studied family of Cappell-Shaneson spheres $\Sigma_{n}$. They found knots slice in $\Sigma_{n}-\mathop{\rm int}(B^{4})$, hoping that one of these knots would have non-vanishing $s$-invariant. They were only able to do the calculations for two of their knots and got zero for both [FGMW10]. Surprisingly, only six days after FGMW posted their results, Akbulut showed that all $\Sigma_{n}$ are standard [Akb10]. Indirectly, this shows that all of the knots FGMW considered had vanishing $s$-invariant.

Piccirillo’s acclaimed proof that the Conway knot is not slice has renewed interest in the $s$-invariant. Piccirillo’s proof takes advantage of and makes apparent the uniqueness of Rasmussen’s $s$-invariant among other slice obstructions [Pic20]. It now seems more likely that the $s$-invariant could be used to distinguish a homotopy sphere from $S^{4}$. However, the Cappell-Shaneson spheres $\Sigma_{n}$ were the most promising potentially exotic homotopy spheres. With $\Sigma_{n}$ now standardized, we are left with a dearth of homotopy spheres.

Recently, Piccirillo worked with Manolescu to revive this idea of FGMW to use the $s$-invariant to find an exotic $S^{4}$. Unlike FGMW, they don’t use knots slice in a known homotopy sphere and in some sense, they reverse the FGMW approach. They propose a way to build a new homotopy sphere $\Sigma$ which comes with such a knot already. To construct an exotic $S^{4}$, they propose to take a pair of knots $(K,K^{\prime})$ which satisfy three conditions:

This would allow one to construct a homotopy sphere $\Sigma$ where $K^{\prime}$ is slice in $\Sigma-\mathop{\rm int}(B^{4})$. Then $\Sigma$ would have the properties that FGMW wanted and would be an exotic $S^{4}$. Manolescu and Piccirillo initiated a search for such a pair of knots, but did not find any that satisfied all three conditions. They did find pairs $(K,K^{\prime})$ which have homeomorphic zero surgeries, $s(K^{\prime})<0$, and could not immediately determine the sliceness of $K$. They conclude the following:

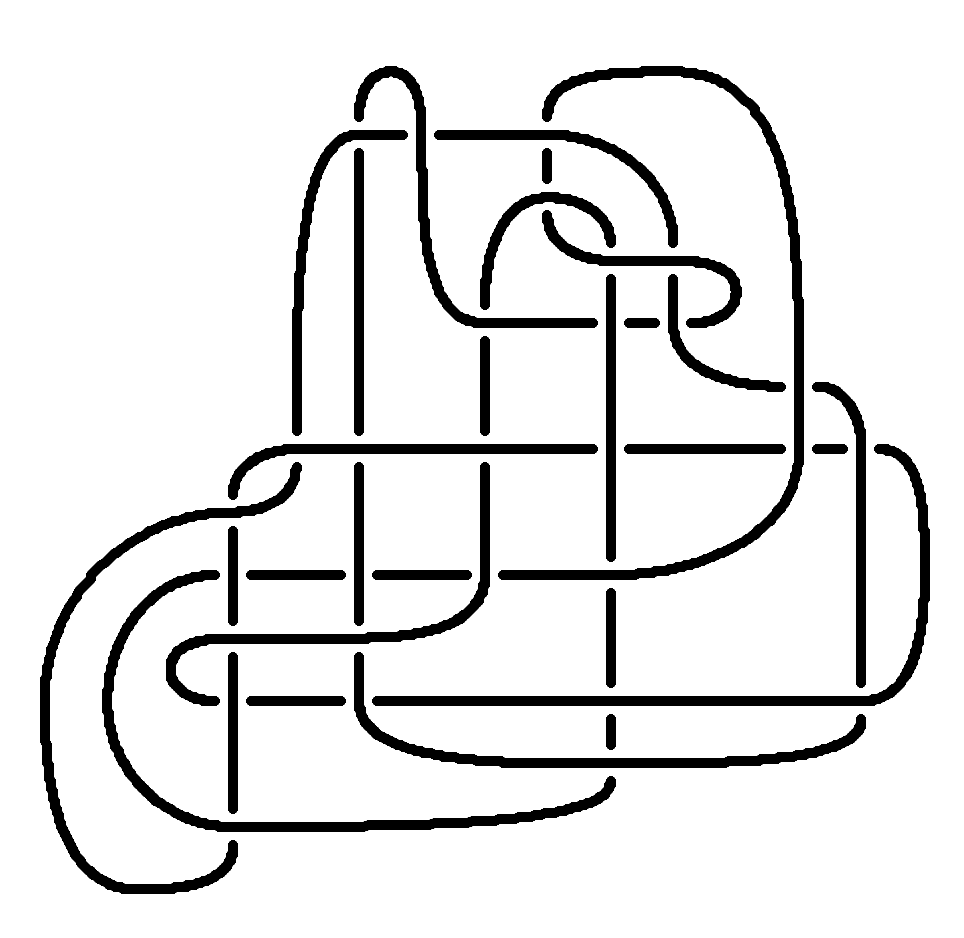
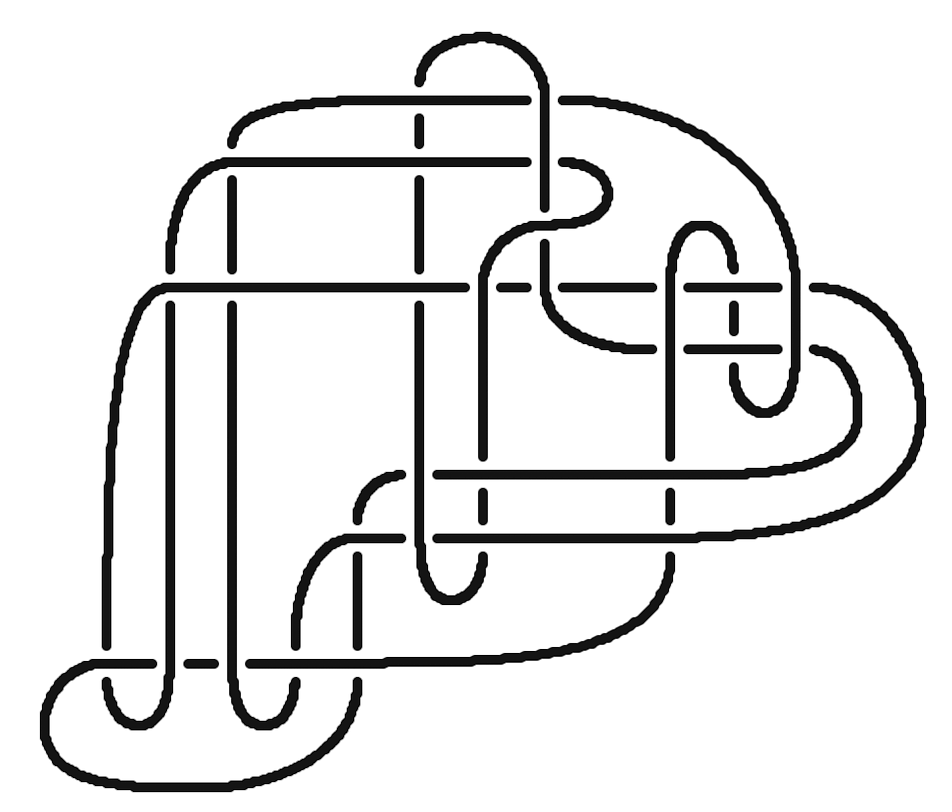
SPC4 is a difficult, long open problem and disproving it by constructing an exotic $S^{4}$ is an ambitious task. Another difficult, long open problem that might be more approachable is to construct an exotic positive definite $4$-manifold. Historically, we have had more and earlier success constructing exotic $4$-manifolds closer to positive definite with larger topology. In particular, it is easier to construct exotic $4$-manifolds with larger $b_{2}(X)=\mathop{\rm rank}(H_{2}(X))$. We can adapt the above strategy to $\#n\mathbb{CP}^{2}$ using an adjunction inequality for the $s$-invariant in $\#n\mathbb{CP}^{2}$ [MMSW19]. We now want $K$ to be $H$-slice in $\#n\mathbb{CP}^{2}$, that is $K$ should bound a null-homologous disk $D$ in $\#n\mathbb{CP}^{2}-\mathop{\rm int}(B^{4})$. To obstruct $H$-sliceness of $K^{\prime}$ in $\#n\mathbb{CP}^{2}$, we need $s(K^{\prime})<0$. Manolescu and Piccirillo again found pairs of knots in their search that satisfied all but one of the necessary conditions.

The knots $K_{1},\dots,K_{5}$ are good candidates to be slice. They have Alexander polynomial $1$ and are topologically slice by Freedman [Fre82], that is they bound topologically, locally flat disks in $B^{4}$. Therefore, all obstructions to topological sliceness automatically vanish on these knots. Many smooth concordance invariants such as Ozsváth-Szabó’s $\tau$-invariant and Rasmussen’s $s$-invariant also vanish on them. In addition, the knots $K_{1}^{\prime},\dots,K_{5}^{\prime}$ would be slice in a homotopy $B^{4}$ and many of the necessary invariants vanish on these knots. At first thought, one would need new slice obstructions that are stronger than those currently available. Despite all of this we are able to show the following:

The difficulty here is the vanishing of invariants that obstruct sliceness or $H$-sliceness of $K_{i}$. This is the same problem that arises when trying to determine sliceness of the Conway knot. For the Conway knot, Piccirillo finds a knot $K$ that shares a zero trace with the Conway knot. Since sliceness is determined by the zero trace, the Conway knot is slice if and only if $K$ is slice. Calculating $s(K)$ shows that $K$ is not slice and therefore the Conway knot is not slice [Pic20]. One might hope to extend the zero surgery homeomorphism $S^{3}_{0}(K_{i})\rightarrow S^{3}_{0}(K_{i}^{\prime})$ to a zero trace diffeomorphism. For many of these pairs, the zero surgery homeomorphisms do not extend and it appears they may never have homeomorphic traces. Without a trace diffeomorphism, we can’t access the trace embedding lemma to identify sliceness of $K$ and $K^{\prime}$. Instead, we extend $S^{3}_{0}(K_{i})\rightarrow S^{3}_{0}(K_{i}^{\prime})$ to a diffeomorphism of the traces after blowing up. This allows us to relate their slice properties stably and work with $H$-sliceness of $K_{i}^{\prime}$ instead of the difficult $K_{i}$.

Manolescu and Piccirillo considered an infinite six parameter family of zero surgery homeomorphisms. They found the knots $K_{1},\dots,K_{23}$ by checking $3375$ zero surgery homeomorphisms in this family. One might try to expand the search and consider more pairs from this family. We show that such an effort would be in vain and prove a stronger version of Theorem 1.1.

This is proved in a more general form in Theorem 3.9. This theorem rules out finding an exotic $S^{4}$ (or $\#n\mathbb{CP}^{2}$) using the $s$-invariant and zero surgery homeomorphisms from the Manolescu-Piccirillo family. This does not show the stronger statement that such $(K,K^{\prime})$ can not be used to construct an exotic $S^{4}$. In principal, a $(K,K^{\prime})$ from the Manolescu-Piccirillo family could still have $K$ slice and $K^{\prime}$ not slice. Such a pair would exhibit an exotic $S^{4}$, but this theorem shows that the $s$-invariant $s(K^{\prime})$ would not obstruct sliceness and detect exoticness.

In Theorem 3.13, we attempt to generalize the above theorem assuming a conjectural inequality for Rasmussen’s $s$-invariant. We establish conditions on when these methods apply and would rule out using the $s$-invariant with zero surgery homeomorphisms to construct an exotic $S^{4}$ or $\#n\mathbb{CP}^{2}$. These methods are not special to the $s$-invariant and might also apply to other obstructions to $H$-sliceness in $\#n\mathbb{CP}^{2}$ or other $4$-manifolds. As new and stronger concordance invariants are inevitably constructed, there will surely be new attempts to construct exotic $4$-manifolds using $H$-sliceness and zero surgery homeomorphisms. Such hypothetical future attempts will likely need to revisit this work.

Our methods do not apply to all zero surgery homeomorphisms and leaves hope that the $s$-invariant could be used to find an exotic $S^{4}$ or $\#n\mathbb{CP}^{2}$. We construct an infinite family of zero surgery homeomorphisms which are not susceptible to our methods. These zero surgery homeomorphisms are not a serious attempt at constructing an exotic $S^{4}$ or $\#n\mathbb{CP}^{2}$. Instead they are an illustration of the continued viability of Manolescu and Piccirillo’s approach and an invitation to the topological community to continue it.

Manolescu and Piccirillo also consider pairs of knots $(K,K^{\prime})$ which have have homeomorphic $0$-surgeries, $K$ is slice, and $K^{\prime}$ has indeterminate sliceness. They give a family of knots $\{J_{n}\ |\ n\in\mathbb{Z}\}$ related by annulus twist homeomorphisms $\phi_{n}:S^{3}_{0}(J_{0})\rightarrow S^{3}_{0}(J_{n})$. $J_{0}$ bounds a ribbon disk and this gives a family of homotopy spheres $Z_{n}=E(D)\cup_{\phi_{n}}-X_{0}(J_{n})$.

To prove this, we draw these manifolds upside down as $X_{0}(J_{n})\cup-E(D)$. Drawing the exterior upside down directly with the standard algorithm is difficult and results in a complicated diagram. Instead we will describe an algorithm for any ribbon knot $K$ bounding a ribbon disk $D$, how to draw a Kirby diagram of $S^{4}$ as $X_{0}(K)\cup-E(D)$. We can then use this to draw a Kirby diagram of $-Z_{n}$ showing the trace embedding $X_{0}(J_{n})\subset-Z_{n}$. Using this diagram of $-Z_{n}$, we then show that each $Z_{n}$ is standard.

All manifolds are smooth and oriented. Any embeddings or homeomorphism are orientation preserving. Boundaries are oriented with outward normal first. All homology groups have integral coefficients.

The author would like to thank Ciprian Manolescu and Lisa Piccirillo for helpful correspondences as well as for allowing the author to use the images in Figure 1. The author would also like to thank his advisors Bob Gompf and John Luecke for their help and support. As noted in [MP21], some cases of the above results were already established by others. Dunfield and Gong showed that $K_{6},\dots,K_{21}$ are not slice using their program to compute twisted Alexander polynomial [DG] and Kyle Hayden showed that $Z_{1}$ is standard

We will need to recall Manolescu and Piccirillo’s proposed construction of an exotic $S^{4}$ or $\#n\mathbb{CP}^{2}$. To simplify the discussion, we combine these cases into one and define $\#0\mathbb{CP}^{2}$ to be $S^{4}$ via the empty connected sum. Whenever $\#n\mathbb{CP}^{2}$ appears it will be implicit that $n\geq 0$ and likewise with $\#n\overline{\mathbb{CP}}^{2}$.

Let $X$ be a smooth, closed, oriented $4$-manifold and let $X^{\circ}=X-\mathop{\rm int}(B^{4})$.

$H$-sliceness is a generalization of sliceness: a knot is slice (in $B^{4}$) if and only if it is $H$-slice in $S^{4}$. Recall that the $k$-trace $X_{k}(K)$ of $K$ is obtained by attaching a $2$-handle to $B^{4}$ along $K$ with framing $k$. The classical trace embedding lemma asserts a knot $K$ is slice if and only if the zero trace $X_{0}(K)$ smoothly embeds in $S^{4}$. We have an analogous statement for a knot to be $H$-slice in $X$.

Suppose $K$ is $H$-slice in $X$ with $H$-slice disk $D\subset X^{\circ}$ and there is a zero surgery homeomorphism $\phi:S^{3}_{0}(K)\rightarrow S^{3}_{0}(K^{\prime})$. Let $\nu(D)$ be a tubular neighborhood of $D$ and let the exterior of $D$ be $E(D)=X^{\circ}-\nu(D)$. The exterior naturally has boundary $S^{3}_{0}(K)$ and we can define $X^{\prime}=E(D)\cup_{\phi}-X_{0}(K^{\prime})$. $K^{\prime}$ is $H$-slice in $X^{\prime}$ by Lemma 2.2 and if $X$ is simply connected, $X^{\prime}$ is homeomorphic to $X$ (Lemma $3.3$ of [MP21]). If $K^{\prime}$ is not $H$-slice in $X$, then $H$-sliceness of $K^{\prime}$ smoothly distinguishes $X^{\prime}$ from $X$.

Constructing an exotic $\#n\mathbb{CP}^{2}$ with zero surgery homeomorphisms sounds promising, but there are difficulties with this approach which have only recently been resolved. The first challenge was overcoming the Akbulut-Kirby conjecture which asserts that knots with homeomorphic zero surgeries are concordant. $H$-sliceness is preserved by concordance and therefore this construction would be more difficult than producing counterexamples to the Akbulut-Kirby conjecture. Fortunately, Yasui disproved the Akbulut-Kirby conjecture in $2015$. In doing so, he showed that concordance invariants, such as the Ozsváth-Szabó $\tau$-invariant or Rasmussen’s $s$-invariant, could distinguish knots in concordance that share a zero surgery [Yas15].

This brings us to the second difficulty with this strategy. We need to obstruct $H$-sliceness of $K^{\prime}$ in the standard $\#n\mathbb{CP}^{2}$ without obstructing $H$-sliceness of $K$ in a homotopy $\#n\mathbb{CP}^{2}$. Obstruction from gauge and Floer theoretic concordance invariants, like the $\tau$-invariant, tend to apply in any homotopy $\#n\mathbb{CP}^{2}$ [OS03]. In particular, such invariants always vanish on knots slice in a homotopy $S^{4}$. However, Rasmussen’s $s$-invariant does provide an obstruction to $H$-sliceness in $\#n\mathbb{CP}^{2}$ that may not hold in a homotopy $\#n\mathbb{CP}^{2}$.

Recall that a framed knot is a knot $K$ in $S^{3}$ together with a framing $k\in\mathbb{Z}$. We will denote a framed knot by $(K,k)$ and extend this naturally to framed links. To conduct their search, Manolescu and Piccirillo need a source of zero surgery homeomorphisms and so they define special RBG-links.

Given a special RBG-link we can define a pair of knots and a zero surgery homeomorphism between them. The following proposition and its proof is the first half of Theorem $1.2$ of [MP21] for a special RBG-link. We reproduce it here because understanding the special RBG-link construction will be fundamental to proving our key lemmas.

Given a diagram of $L$, we can perform this construction diagrammatically. We take $L$ to be a surgery diagram of $S^{3}_{r,b,g}(R,B,G)$ and slam dunk $(R,r)\cup(G,0)$. To do this, first isotope $(G,0)$ into meridianal position so $(G,0)$ bounds a disk $\Delta_{G}$. This disk intersects $(B,0)$ in some number of points as shown in Figure 2(a). Slide $(B,0)$ over $(R,r)$ so that it no longer intersects $\Delta_{G}$ as shown in Figure 2(b). To finish the slam dunk, delete $(R,r)$ and $(G,0)$ leaving $(K_{B},0)$.

Let $W$ be a smooth, closed, oriented $4$-manifold. If $D$ is a disk properly embedded in $W^{\circ}$, then $D$ has a well defined tubular neighborhood $\nu(D)=D\times\mathbb{R}^{2}$. Then $D=D\times\{0\}$ has a parallel pushoff $D^{*}=D\times\{p\}\subset\nu(D)$ for some nonzero $p$. $K^{*}=\partial D^{*}$ is a knot parallel to $K$ and defines a framing on $K$.

If we say $K$ is $k$-slice in $W$ with $k\in\mathbb{Z}$, then we mean $(K,k)$ is slice in $W$. This framing $k$ will be equal to the negative of the self intersection number of $D$, i.e. $k=-[D]\cdot[D]$. The exterior $E(D)=W^{\circ}-\nu(D)$ of $D$ has boundary $\partial E(D)$ naturally identified with $S^{3}_{k}(K)$. We can view the deleted $\nu(D)$ and $int(B^{4})$ as a trace and get a trace embedding lemma.

This will allow us later to construct framed slice disks by finding trace embeddings. We will be working with framed slice disks in $\#n\overline{\mathbb{CP}}^{2}$ and in this setting, it is often more practical to construct the disks directly. To construct knots $H$-slice in some $\#n\overline{\mathbb{CP}}^{2}$, one can use a full positive twist along algebraically zero strands as in Lemma $3.2$ of [MP21]. This generalizes to framed sliceness, but now we need to keep track of how the framing changes.

The above lemma can be used to show that an arbitrary knot $K$ will be slice in some $\#n\overline{\mathbb{CP}}^{2}$. First observe that a crossing change can be realized as a positive twist on two strands. Then a sequence of crossing changes that unknot $K$ can be used to construct a slice disk $D$ for $K$ with some framing in $\#n\overline{\mathbb{CP}}^{2}$. Our arguments require checking that certain framed knots associated to a zero surgery homeomorphism are slice in some $\#n\overline{\mathbb{CP}}^{2}$ or $\#n\mathbb{CP}^{2}$. To quantify this we define the projective slice framings.

Homological considerations imply that a strictly negative framed knot cannot be slice in a negative definite $4$-manifold and therefore $\mathbb{PF}_{+}(K)\geq 0$. Furthermore, in a negative definite $4$-manifold, the only homology class with self intersection number zero is the zero homology class.

Once we have one of these framings, Lemma 2.8 immediately realizes any framing larger than $\mathbb{PF}_{+}(K)$. Take $D$ a disk realizing $\mathbb{PF}_{+}(K)$ and $\Delta$ a meridianal disk of $K$.

We can construct framed slice disks in $\#n\overline{\mathbb{CP}}^{2}$, but we would also like to have lower bounds on these framings as well. To do so, we can use the adjunction inequality for the Ozsváth-Szabó $\tau$-invariant.

There is an analogous adjunction inequality conjectured for the $s$-invariant.

[MMSW19] proved this in the nullhomologous case and conjectured this in analogy to the adjunction inequality for $\tau(K)$. We replace $2\tau(K)$ with $s(K)$ like their slice genus bounds, but we limit this conjecture to $W=\#n\overline{\mathbb{CP}}^{2}-\mathop{\rm int}(B^{4})$. It’s not clear how to approach Conjecture 2.14 for arbitrary negative definite $W$ or even if it should hold in such $W$. However, if this conjecture holds, we can replace $x=2\tau(K)$ with $s(K)$ throughout the proof of Corollary 2.13. When $K$ is $(-1)$-slice in some $\#n\mathbb{CP}^{2}$, we conjecturally get the same restriction on $s(K)$ as we did when $K$ is $H$-slice is some $\#n\mathbb{CP}^{2}$.

In this subsection, we show that $K_{1},\dots,K_{23}$ are not slice, nor are they H-slice in any $\#n\mathbb{CP}^{2}$. To do this, we will relate H-sliceness of $K_{i}$ in $\#n\mathbb{CP}^{2}$ stably with $K_{i}^{\prime}$ after a connected sum with some $\#r\mathbb{CP}^{2}$. We see this first at the level of traces as a stable trace diffeomorphism.

This is a generalization of techniques [Akb77, Pic19, Pic20] used to construct trace diffeomorphisms. The $(R,r)=(U,0)$ slice in $B^{4}$ case of the lemma is the dualizable link construction and its proof is insightful here. Construct a Kirby diagram by placing a dot on $R$ and attaching $2$-handles to $B$ and $G$. Cancelling the dotted $R$ with $B$ or $G$ diagrammatically is a slam dunk resulting in $X_{0}(K_{G})$ and $X_{0}(K_{B})$ respectively. The framed sliceness of $(R,r)$ in $W$ allows us to “dot” $(R,r)$ and proceed in a similar manner.

When a zero surgery homeomorphism extends to a zero trace diffeomorphism, the $H$-slice trace embedding lemma identifies the $H$-sliceness of the two knots. If the zero surgery homeomorphism doesn’t extend, Lemma 3.1 sometimes allows us to extend to a diffeomorphism after a connected sum with $-W$. This makes the trace embedding lemma available and allows us to relate $H$-sliceness of the two knots.

Now we are ready to prove our first theorem.

We have dispensed of the main question relatively quickly and have shown that $K_{1},\dots,K_{23}$ are not slice or $H$-slice in any $\#n\mathbb{CP}^{2}$. However, to prove this we needed that the associated special RBG-links all had $r\geq 0$. If we had negative $r<0$ instead, then $(R,r)$ would be slice in $\#|r|\mathbb{CP}^{2}$. If $K$ was $H$-slice in $\#n\mathbb{CP}^{2}$, then $K^{\prime}$ would be $H$-slice in $\#n\mathbb{CP}^{2}\#|r|\overline{\mathbb{CP}}^{2}$ by Corollary 3.2. This would not contradict $s(K^{\prime})<0$ and our proof would not work. It seems quite mysterious that we had this necessary condition on $r$ for all $23$ pairs of knots. Fortunately, we can explain this and do so in the following subsection. Before we proceed, we take a short detour to provide a generalization of Corollary 3.2 from special RBG-links to arbitrary zero surgery homeomorphisms. One can safely skip to the next subsection, but this method may offer some useful benefits in practice.

For a special RBG-link homeomorphism, one can take $(m,k)$ to be $(R,r)$. This recovers the conclusion of Corollary 3.2 and gives another proof of Theorem 3.3. However, we do not get a stable diffeomorphism $X^{\prime}\#-W\cong X\#-W$ like in Corollary 3.2. The advantage of this is that it does not need a special RBG-link and has the further benefit that the input data is more malleable. It seems non-trivial to find special RBG-links representing a given zero surgery homeomorphism with a different $(R,r)$. However, $(m,k)$ was a choice of diagrammatic representative of $\phi^{-1}(\mu_{K^{\prime}},0)\subset S^{3}_{0}(K)$ and can be modified via slides over $K$.

This section is devoted to explaining why $r$ was positive for all of Manolescu and Piccirillo’s knot pairs. We observed after proving Theorem 3.3 that we needed the relevant special RBG-link to have $r\geq 0$ for our proof to work. Having positive $r\geq 0$ for all $23$ knot pairs seems unlikely and it would be quite unsatisfactory if a necessary hypothesis in our proof was left unexplained. We investigate this by widening our view and considering the infinite six parameter family of special RBG-links $L(a,b,c,d,e,f)$ that these knot pairs arose from. These $L(a,b,c,d,e,f)$ were constructed by Manolescu and Piccirillo as a source of candidates for their exotic $\#n\mathbb{CP}^{2}$ construction. We prove that this would always occurs for any member $L(a,b,c,d,e,f)$ of the Manolescu-Piccirillo family: if $r<0$, then $s(K),s(K^{\prime})\geq 0$. This allows us to prove a strong generalization of Theorem 3.3 from $K_{1},\dots,K_{23}$ to any $(K,K^{\prime})$ coming from some $L(a,b,c,d,e,f)$.

To show that $s(K),s(K^{\prime})$ are non-negative when $r<0$, we construct and analyze slice disks for $(K,-1)$ and $(K^{\prime},-1)$ in $\#|r|\mathbb{CP}^{2}$. We build these slice disks by exploiting two properties of the special RBG-links $L(a,b,c,d,e,f)$. The first was that they had $R=U$ and the second was that they were small.

Some small RBG-links with $R=U$ will not to be useful to construct an exotic $\#n\mathbb{CP}^{2}$. If either of the intersection numbers $\Delta_{B}\cap G$ or $\Delta_{G}\cap B$ is strictly less than $2$, then $K_{B}=K_{G}$ by Proposition $4.11$ of [MP21]. If $R=U$ and $r\geq 0$, then the proof of Theorem 3.3 can be applied. What remains can be dealt with via the following lemma.