Towards efficient representation identification in supervised learning

Before we describe the data generation process we use, we give an example of the data generation process that is compatible with the assumptions in (Khemakhem et al., 2020a).

where $\mathsf{Bernoulli}(\frac{1}{2})$ is the uniform Bernoulli distribution over $\{0,1\}$, $\mathcal{N}$ is normal distribution, $\mathbf{1}\in\mathbb{R}^{d}$ is the vector that together with the label $Y$ selects the mean of the latent $Z$, $\mathsf{I}$ is a $d$ dimensional identity matrix, $g$ is a bijection that generates the observations $X$. In Figure 1 (a), we show the causal directed acyclic graph (DAG) corresponding to the above data generation process, where the labels cause the latent variables (Schölkopf et al., 2012). Most of the current non-linear ICA models are only compatible with this view of the data generation process. This may be valid for some settings, but it is not perfectly suited for human labelled datasets where a label is assigned based on the underlying latent factors of variations. Hence, we focus on the opposite perspective (Arjovsky et al., 2019) when the latent variables generate the labels. The assumptions regarding the data generation process studied in our work are defined formally ahead.

We also contrast the DAGs of the two data generation processes in Figure 1. The nature of the auxiliary information (labels) in the data generation process we study (Assumption 1) is very different from the one in prior works (equation 1); conditioning on the auxiliary information (labels) in our data generation process does not make the latent variables independent. Our setting could be interpreted as multi-task supervised learning, where the downstream task labels serve as the auxiliary information generated from shared latent variables.
Remark. The classic non-identifiability results in Locatello et al. (2019) and Hyvärinen and Pajunen (1999) assumed that the latent factors of variation are all mutually independent. These results implied that without some knowledge, e.g., auxiliary information (labels), it is impossible to disentangle the latent variables. While (Khemakhem et al., 2020a) showed that it is possible to succeed in the presence of auxiliary information, their data generation process assumes that the latent variables are not mutually independent and thus is not consistent with assumptions in (Locatello et al., 2019) and (Hyvärinen and Pajunen, 1999). Whereas our work shows that the auxiliary information helps in the case considered in (Locatello et al., 2019) and (Hyvärinen and Pajunen, 1999), since the auxiliary information is introduced downstream of the latent variables.

Our objective is to learn the model $g^{-1}$ (or the generator $g$) from the observed data and labels pairs $(X,Y)$, such that for new observations $X$ we can recover the latent variables $Z$ that generated $X$. We can not always learn the exact latent variables $Z$ but may only identify them to some degree. Let us denote the model learned as $\tilde{g}^{-1}$ (with its inverse $\tilde{g}$). We now describe a general notion (commonly used in the literature) of identification for the learned map $\tilde{g}^{-1}$ with respect to the true map $g^{-1}$.

In the above definition, if $\mathcal{A}$ was the set of all the permutation maps $\mathcal{P}$, then $\tilde{g}^{-1}\sim_{\mathcal{P}}g^{-1}$ denotes identification up to permutations. Permutation identification guarantees that we learn the true latent vector but do not learn the indices of the true latent, which is not important for many downstream tasks. In other words, identification up to permutations of the latent variables is the gold standard for identification. Our aim is to identify the latent variables $Z$ by inverting the data generating process (learning $g^{-1}$) up to permutations.

We first study the setting when the number of tasks $k$ is equal to the dimension of the latent variables $d$. Before we describe the theorem, we state assumptions on the hypothesis class of the representations ($\mathcal{H}_{\Phi}$) and the classifier ($\mathcal{H}_{\Theta}$).

The above assumption ensures that the true solutions $g^{-1}$ and $\Gamma$ are in the respective hypothesis classes that the learner searches over. Also, the invertibility assumption on the hypothesis in $\mathcal{H}_{\Theta}$ is needed to ensure that we do not have redundant tasks for the identification of the latent variables. Under the above assumption and the assumptions of our data generation process (1), we state the following identification result for the case when k=d.

The proof for the same is available in Appendix Section A. This implies that for the DAGs in Figure 1 (b), it is possible to recover the true latents up to permutation and scaling. This result extends the current disentanglement guarantees (Khemakhem et al., 2020b) that exist for models where labels cause the latent variables (latent variables are conditionally independent) to the settings where latent variables cause the label (latent variables are not conditionally independent). In multi-task learning literature (Caruana, 1997; Zhang and Yang, 2017), it has been argued that learning across multiple tasks with shared layers leads to internal representations that transfer better. The above result states the conditions when the ideal data generating representation shared across tasks can be recovered.

Remark. Since we use a linear model for the label generation process, one can ask what happens if we apply noisy linear ICA techniques (Davies, 2004; Hyvarinen, 1999) on the label itself (when $k=d$) to recover $Z$ followed by a regression to predict $Z$ from $X$. Noisy linear ICA require the noise distribution to be Gaussian and would not work when $N_{Y}$ is not a Gaussian. Since we do not make such distributional assumptions on $N_{Y}$, we cannot rely on noisy linear ICA on labels.

In this section, we study the setting when the number of tasks $k$ is equal to one. Since this setting is extreme, we need to make stronger assumptions to show latent identification guarantees. Before we lay down the assumptions, we provide some notation. Since we only have a single task, instead of using the matrix $\Gamma\in\mathbb{R}^{k\times d}$, we use $\gamma\in\mathbb{R}^{d}$ to signify the coefficients that generate the label in the single task setting. We assume each component of $\gamma$ is non-zero. In the single task setting for regression problems, the label generation is written as $Y\leftarrow\gamma^{\mathsf{T}}Z+N_{Y}$, and the rest of the notation is the same as the data generation process in Assumption 1. We rewrite the data generation process in Assumption 1 for the single task case in terms of normalized variables $U=Z\odot\gamma$.

Note that $g^{{}^{\prime}}$ is invertible since $g$ is invertible and each element of $\gamma$ is also non-zero. Hence, for simplicity, we can deal with the identification of $U$. If we identify $U$ up to permutation and scaling, then $Z$ is automatically identified up to permutation and scaling. The predictor we learn is a composition of linear predictor $\theta$ and a representation $\Phi$, which is written as $\theta\circ\Phi(X)=\theta^{\mathsf{T}}\Phi(X)$. The learner searches for $\theta$ in the set $\mathcal{H}_{\theta}$, where $\mathcal{H}_{\theta}$ consists of linear predictors with all non-zero components, and $\Phi$ in the set $\mathcal{H}_{\Phi}$.

We can further simplify the predictor as follows: $\theta^{\mathsf{T}}\Phi(X)=\boldsymbol{1}^{\mathsf{T}}(\Phi(X)\odot\theta)$, where $\Phi(X)\odot\theta$ is component-wise multiplication expressed as $\Phi(X)\odot\theta=[\Phi_{1}(X)*\theta_{1},\cdots,\Phi_{d}(X)*\theta_{d}]$. Therefore, instead of searching over $\mathcal{H}_{\theta}$ such that all components of $\theta$ are non-zero, we can fix $\mathcal{H}_{\theta}=\{\boldsymbol{1}\}$ and carry out the search over representations $\mathcal{H}_{\Phi}$ only. For the rest of the section, without loss of generality, we assume the predictor is of the form $\boldsymbol{1}\circ\Phi(X)=\boldsymbol{1}^{\mathsf{T}}\Phi(X)$. We restate the IC-ERM (4) with this parametrization and an additional constraint that all components are now required to be independent and identically distributed (i.i.d.). We provide a formal definition for the convenience of the reader below, where $\stackrel{{\scriptstyle d}}{{=}}$ denotes identical in distribution.

The reparametrized IC-ERM (4) constraint is stated as follows.

Next, we state the assumptions on each component of $U$ (recall each component of $U$ is i.i.d. from Assumption 3) and $\mathcal{H}_{\Phi}$ under which we show that the reparametrized IC-ERM objective (equation (6)) recovers the true latent variables $U$ up to permutations. We assume each component of $U$ is a continuous random variable with probability density function (PDF) $r$. Define the support of each component of $U$ as $\mathcal{S}=\{u\;|\;r(u)>0,u\in\mathbb{R}\}$. Define a ball of radius $\sqrt{2}p$ as $\mathcal{B}_{p}=\{u\;|\;|u|^{2}\leq 2p^{2},u\in\mathbb{R}\}$.

Remark on the PDFs under the above assumption. The above assumption considers distributions in the exponential family, where the log-PDF can be expressed as a polynomial. Note that as long as the support of the distribution is bounded, every polynomial with bounded coefficients leads to a valid PDF (i.e., it integrates to one) and we only need to set the value of $a_{0}$ appropriately.

We now state our assumptions on the hypothesis class $\mathcal{H}_{\Phi}$ that the learner searches over. Observe that $\Phi(X)$ can be written as $h(U)=\Phi\Big{(}g^{{}^{\prime}}(U)\Big{)}$ (since $X=g^{{}^{\prime}}(U)$). We write the set of all the maps $h$ constructed from composition of $\Phi\in\mathcal{H}_{\Phi}$ and $g^{{}^{\prime}}$ as $\mathcal{H}_{\Phi}\circ g^{{}^{\prime}}$. Define $w(u_{1},\cdots,u_{d})=\log\Big{(}\big{|}\mathsf{det}\big{[}J(h(u_{1},\cdots,u_{d}))\big{]}\big{|}\Big{)}$, where $\mathsf{det}$ is the determinant, $J(h(u_{1},\cdots,u_{d}))$ is the Jacobian of $h$ computed at $(u_{1},\cdots,u_{d})$. The set of all the $w$’s obtained from all $h\in\mathcal{H}_{\Phi}\circ g^{{}^{\prime}}$ is denoted as $\mathcal{W}$

Define $p_{\mathsf{min}}=\max\Big{\{}\kappa\log(8(d-1)),\frac{4a_{\mathsf{max}}(d-1)}{a_{\mathsf{min}}},\frac{\log\Big{(}\frac{4b_{\mathsf{max}}*n_{\mathsf{poly}}}{a_{\mathsf{min}}}\Big{)}}{2}+q\Big{\}}$, where $n_{\mathsf{poly}}$ is the maximum number of non-zero coefficients in any polynomial $w\in\mathcal{W}$, $\kappa$ is small constant (see Appendix C).

Proof sketch. The complete proof is available in Appendix Section C and we provide an overview here. We use the optimality condition that the prediction made by the learned model, $\boldsymbol{1}^{\mathsf{T}}h(U)$, exactly matches the true mean, $\boldsymbol{1}^{\mathsf{T}}U$, along with the constraints that each component of $U$ are i.i.d. and each component of $h(U)$ are i.i.d., to derive that the distributions of $U$ and $h(U)$ are the same. We substitute this condition in the change of variables formula that relates the densities of $U$ and $h(U)$. Using the Assumption 5, we can show that if the highest absolute value of $U$ and the highest absolute value of $h(U)$ are not equal, then the term with the highest absolute value among $U$ and $h(U)$ will dominate, leading to contradiction in the identity obtained by change of variables formula. Based on this, we can conclude that the highest absolute value of $U$ and the highest absolute value of $h(U)$ must be equal. We iteratively apply this argument to show that all the absolute values of $U$ and $h(U)$ are related by permutation. We can extend this argument to the actual values instead of absolute values. Since $h$ is analytic we argue that the relationship of permutation holds in a neighborhood. Then we use properties of analytic functions (Mityagin, 2015) to conclude that the relationship holds on the entire space.
Why does the bound on $p$ grow linearly in $d$? We provide some geometric intuition into why the degree of the polynomial ($p$) of the log-PDF ($\log(r)$) needs to be large. If the dimension of the latent space $d$ is large, then the second term in $p_{\mathsf{min}}$ dominates, i.e., $p$ has to grow linearly in $d$. The simplification in the proof yields that the mapping $h$ must satisfy the following condition – $\|u\|_{k}=\|h(u)\|_{k}$ for all $k\in\{1,\cdots,p\}$, where $\|\cdot\|_{k}$ is the $k^{th}$ norm. Hence, $h$ is a bijection that preserves all norms up to the $p^{th}$ norm. If $U$ is $2$ dimensional, then the a bijection $h$ that preserves the $\ell_{1}$ norm and the $\ell_{2}$ norm is composed of permutations and sign-flips. In general, since $U$ is $d$ dimensional, we need at least $d$ constraints on $h$ in the form $\|u\|_{k}=\|h(u)\|_{k}$ and thus $p\geq d$, which ensure that the only map that satisfies these constraints is composed of permutations and sign-flips.
Significance and remarks on Theorem 2. Theorem 2 shows that if we use IC-ERM principle, i.e., constraint the representations to be independent, then we continue to recover the latents even if the number of tasks is small. We can show that the above theorem also extends to binary classification. We admit that strong assumptions were made to arrive at the above result, while other assumptions such as bound on $p$ growing linearly in $d$ seem necessary, but we would like to remind the reader that we are operating in the extreme single task regime. In the previous section, when the number of tasks was equal to the dimension of the latent (when we have sufficiently many tasks), we had shown the success of the IC-ERM (4) objective (Theorem 1) for identification of latent variables with much fewer assumptions. In contrast, in Theorem 2, we saw that with more assumptions on the distribution we can guarantee latent recovery with even one task. If we are in the middle, i.e., when the number of tasks is between one and the dimension of the latent, then the above Theorem 2 says we only require the assumptions (Assumptions 3, 4, 5) to hold for at least one task.
Note on the case k$>$d: We did not discuss the case when the number of tasks is greater than the dimension of the latent variables. This is because we can select a subset $S^{{}^{\prime}}$ of tasks, such that $|S^{{}^{\prime}}|=d$ and then proceed in a similar fashion as Theorem 1. This question arises commonly in linear ICA literature, and selecting a subset of tasks is the standard practice.

Regression. Figure 2 and 3 show a comparison of the performance of the three approaches across $d=16$ and $d=50$ for various tasks. The results for the case of $d=24$ are in the Appendix E.1 (due to space limits). In both cases, we find that the method ERM-ICA is significantly better than the other approaches in terms of guaranteeing permutation and scaling based identification. All three approaches have similar label prediction performance. We observe a similar trend for the case of $d=24$ shown in the Appendix  E.1.
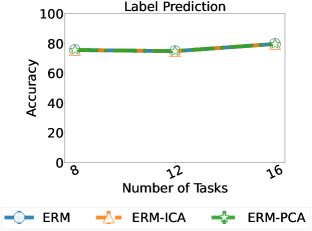
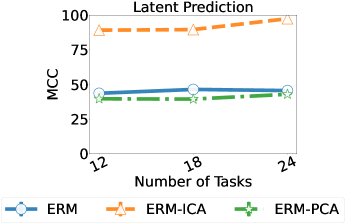
Classification. Figure 4 and 5 show a comparison of the performance of the three approaches across $d=16$ and $d=24$ for various tasks. In both cases, we find that the method ERM-ICA is better than the other approaches in terms of guaranteeing permutation and scaling based identification, except in the case of 24 data dimensions with a total of 12 tasks. All three approaches have similar label prediction performance. For classification, unlike regression, the improvements are smaller and we do not see improvement for $d=50$ (comparisons for the case of $d=50$ are in the Appendix E.2). We see a worse performance in the classification setting because the ERM model does not learn the Bayes optimal predictor unlike regression.
Discussion. We have shown that ERM-ICA achieves significant improvement in latent recovery with much fewer tasks (up to $\frac{d}{2}$). However, in our theory we proved that under certain assumptions solving the reparametrized IC-ERM objective (Eq (6)) can achieve identification even with a single task. Note that we only approximate equation (6) with ERM-ICA, and if we build better approximations of the ideal approach (IC-ERM), then we can witness gains with even fewer tasks. We believe that building such approximations is a fruitful future work.