Towards Deeper Graph Neural Networks
Abstract.
Graph neural networks have shown significant success in the field of graph representation learning. Graph convolutions perform neighborhood aggregation and represent one of the most important graph operations. Nevertheless, one layer of these neighborhood aggregation methods only consider immediate neighbors, and the performance decreases when going deeper to enable larger receptive fields. Several recent studies attribute this performance deterioration to the over-smoothing issue, which states that repeated propagation makes node representations of different classes indistinguishable. In this work, we study this observation systematically and develop new insights towards deeper graph neural networks. First, we provide a systematical analysis on this issue and argue that the key factor compromising the performance significantly is the entanglement of representation transformation and propagation in current graph convolution operations. After decoupling these two operations, deeper graph neural networks can be used to learn graph node representations from larger receptive fields. We further provide a theoretical analysis of the above observation when building very deep models, which can serve as a rigorous and gentle description of the over-smoothing issue. Based on our theoretical and empirical analysis, we propose Deep Adaptive Graph Neural Network (DAGNN) to adaptively incorporate information from large receptive fields. A set of experiments on citation, co-authorship, and co-purchase datasets have confirmed our analysis and insights and demonstrated the superiority of our proposed methods.
1. Introduction
Graphs, representing entities and their relationships, are ubiquitous in the real world, such as social networks, point clouds, traffic networks, knowledge graphs, and molecular structures. Recently, many studies focus on developing deep learning approaches for graph data, leading to rapid development in the field of graph neural networks. Great successes have been achieved for many applications, such as node classification (Kipf and Welling, 2017; Hamilton et al., 2017; Veličković et al., 2018; Monti et al., 2017; Gao et al., 2018; Xu et al., 2018; Klicpera et al., 2019; Wu et al., 2019), graph classification (Gilmer et al., 2017; Ying et al., 2018; Zhang et al., 2018; Xu et al., 2019; Gao and Ji, 2019; Lee et al., 2019; Ma et al., 2019; Yuan and Ji, 2020) and link prediction (Zhang and Chen, 2017, 2018; Cai and Ji, 2020). Graph convolutions adopt a neighborhood aggregation (or message passing) scheme to learn node representations by considering the node features and graph topology information together, among which the most representative method is Graph Convolutional Networks (GCNs) (Kipf and Welling, 2017). GCN learns representation for a node by aggregating representations of its neighbors iteratively. However, a common challenge faced by GCN and most other graph convolutions is that one layer of graph convolutions only consider immediate neighbors and the performance degrades greatly when we apply multiple layers to leverage large receptive fields. Several recent works attribute this performance degradation to the over-smoothing issue (Li et al., 2018; Xu et al., 2018; Chen et al., 2020), which states that representations from different classes become inseparable due to repeated propagation. In this work, we study this performance deterioration systematically and develop new insights towards deeper graph neural networks.
We first systematically analyze the performance degradation when stacking multiple GCN layers by using our quantitative metric for node representation smoothness measurement and a data visualization technique. We observe and argue that the main factor compromising the performance greatly is the entanglement of representation transformation and propagation. After decoupling these two operations, it is demonstrated that deeper graph neural networks can be deployed to learn graph node representations from larger receptive fields without suffering from performance deterioration. The over-smoothing issue is shown to affect performance only when extremely large receptive fields are utilized. We further give a theoretical analysis of the above observation when building very deep models, which shows that graph node representations will become indistinguishable when depth goes infinity. This aligns with the over-smoothing issue. The previous descriptions of the over-smoothing issue simplify the assumption of non-linear activation function (Li et al., 2018; Xu et al., 2018) or make approximations of different probabilities (Xu et al., 2018). Our theoretical analysis can serve as a more rigorous and gentle description of the over-smoothing issue. Based on our theoretical and empirical analysis, we propose an efficient and effective network, termed as Deep Adaptive Graph Neural Network, to learn node representations by adaptively incorporating information from large receptive fields. Extensive experiments on citation, co-authorship, and co-purchase datasets demonstrate the reasonability of our insights and the superiority of our proposed network.
2. Background and Related Works
First, we introduce our notations used throughout this paper. Generally, we let bold uppercase letters represent matrices and bold lowercase letters denote vectors. A graph is formally defined as , where is the set of nodes (vertices) that are indexed from to and is the set of edges between nodes in . and are the numbers of nodes and edges, respectively. In this paper, we consider unweighted and undirected graphs. The topology information of the whole graph is described by the adjacency matrix , where if an edge exists between node and node , otherwise 0. The diagonal matrix of node degrees are denoted as , where . denotes the neighboring nodes set of node . An attributed graph has a node feature matrix , where each row represents the feature vector of node and is the dimension of node features.
2.1. Graph Convolution Operations
Most popular graph convolution operations follow a neighborhood aggregation (or message passing) fashion to learn a node representation by propagating representations of its neighbors and applying transformation after that. The -th layer of a general graph convolution can be described as
| (1) | ||||
is the representation of node at -th layer and is initialized as node feature . Most graph convolutions, like GCN (Kipf and Welling, 2017), GraphSAGE (Hamilton et al., 2017), GAT (Veličković et al., 2018), and GIN (Xu et al., 2019), can be obtained under this framework by deploying different propagation and transformation mechanisms.
Without losing generalization, we focus on the Graph Convolutional Network (GCN) (Kipf and Welling, 2017), the most representative graph convolution operation, in the following analysis. The -th layer forward-propagation process is formulated as
| (2) |
where and are the output and input node representation matrices of layer . , where is the adjacency matrix with added self-connections. is the diagonal node degree matrix. is a layer-specific trainable weight matrix. is a non-linear activation function like ReLU (Nair and Hinton, 2010). Intuitively, GCN learns representation for each node by propagating neighbors’ representations and conducting non-linear transformation after that. GCN is originally applied for semi-supervised classification, where only partial nodes have training labels in a graph. Thanks to the propagation process, representation of a labeled node carries the information from its neighbors that are usually unlabeled, thus training signals can be propagated to the unlabeled nodes.
2.2. Related Works
From Eq.(2), one layer GCN only considers immediate neighbors, i.e. one-hop neighborhood. Multiple layers should be applied if multi-hop neighborhood is needed. In practice, however, the performance of GCN degrades greatly when multiple layers are stacked. Several works reveal that stacking many layers can bring the over-smoothing issue, which means that representations of nodes converge to indistinguishable limits. To our knowledge, (Li et al., 2018) is the first attempt to demystify the over-smoothing issue in the GCN model. The authors first demonstrate that the propagation process of the GCN model is a special symmetric form of Laplacian smoothing (Taubin, 1995), which makes the representations of nodes in the same class similar, thus significantly easing the classification task. Then they show that repeatedly stacking many layers may make representations of nodes from different classes indistinguishable. The same problem is studied in (Xu et al., 2018) by analyzing the connection of nodes’ influence distribution and random walk (Lovász et al., 1993). Recently, SGC (Wu et al., 2019) is proposed by reducing unnecessary complexity in GCN. The authors show that SGC corresponds to a low-pass-type filter on the spectral domain, thus deriving smoothing features across a graph. Another recent work (Chen et al., 2020) verify that smoothing is the nature of most typical graph convolutions. It is showed that reasonable smoothing makes graph convolutions work and over-smoothing results in poor performance.
Due to the potential concern of the over-smoothing issue, a limited neighborhood is usually used in practice and it is difficult to extend. However, long-range dependencies should be taken into consideration, especially for peripheral nodes. Also, small receptive fields are not enough to propagate training signals to the whole graph when the number of training nodes is limited under a semi-supervised learning setting. (Li et al., 2018) applies co-training and self-training to overcome the limitation of shallow architectures. A smoothness regularizer term and adaptive edge optimization are proposed in (Chen et al., 2020) to relieve the over-smoothing problem. Jumping Knowledge Network (Xu et al., 2018) deploys a layer-aggregation mechanism to adaptively select a node’s sub-graph features at different ranges rather than to capture equally smoothed representations for all nodes. (Klicpera et al., 2019) utilizes the relationship between GCN and PageRank (Page et al., 1999) to develop a propagation mechanism based on personalize PageRank, which can preserve the node’s local information while gather information from a large neighborhood. Recently, Geom-GCN (Pei et al., 2020) and non-local GNNs (Liu et al., 2020) are proposed to capture long-range dependencies for disassortative graph by designing non-local aggregators.









3. Empirical and Theoretical Analysis of Deep GNNs
In this section, we first propose a quantitative metric to measure the smoothness of graph node representations. Then we utilize this metric, along with a data visualization technique, to rethink the performance degradation when utilizing GCN layer to build deep graph neural networks. We observe and argue that the entanglement of representation transformation and propagation is a prominent factor that compromises the network performance. After decoupling these two operations, deeper graph neural networks can be built to learn graph node representations from large receptive fields without suffering from performance degradation. The over-smoothing issue is shown to influence the performance only when extremely large receptive fields are adopted. Further, we provide a theoretical analysis of the above observation when building very deep models, which aligns with the conclusion of over-smoothing issue and can serve as a rigorous description of the over-smoothing issue.
3.1. Quantitative Metric for Smoothness
Smoothness is a metric that reflects the similarity of node representations. Here, we first define a similarity metric between the representations of node and node with their Euclidean distance:
| (3) |
where is the feature representation of node and denotes the Euclidean norm. The Euclidean distance is a simple but effective way to measure the similarity of two representations, especially in high dimensional space. Smaller Euclidean distance value incidates higher similarity of two representations. To remove the influence of the magnitude of feature representations, we use normalized node representations to compute their Euclidean distance, thus constraining in the range of .
Based on the similarity metric in Eq.(3), we further propose a smoothness metric for node , which is computed as the average distance between node to other nodes:
| (4) |
Hence, measures the similarity of node ’s representations to the entire graph. For instance, a node in the periphery or a leaf node usually has a large smoothness metric value. Further, we can use to represent the smoothness metric value of the whole graph . Its mathematical expression is defined as:
| (5) |
Here, is negatively related to the overall smoothness of nodes’ representations in graph .











3.2. Why Deeper GNNs Fail?
In this section, we utilize our proposed smoothness metric to investigate the performance deterioration phenomenon in deep graph neural networks. Here, we mainly use the GCN layer for analysis, but the main results can be easily applied to other graph deep learning methods. Besides using our proposed metric from the quantitative perspective, we employ a data visualization technique t-SNE (Maaten and Hinton, 2008). t-SNE provides an interpretable visualization, especially on high-dimensional data. t-SNE is capable of capturing both the local structure and the global structure like clusters in high-dimensional data, which is consistent with the classification of nodes. Hence, we utilize t-SNE to demonstrate the discriminative power of node representations in the graph.
We develop a series of graph neural networks (GNNs) with different depths in terms of the number of GCN layers, and evaluate them on three citation datasets; those are Cora, CiteSeer and PubMed (Sen et al., 2008). In particular, we also include a graph neural network with depth of 0, which is approximated with a multi-layer perceptron network. A GNN with depth of 0 can be viewed as aggregating information from a 0-hop neighborhood, which only considers node features while with the graph structure ignored. We conduct 100 runs for each model on each dataset, using the same data split scheme as (Kipf and Welling, 2017).
The result on Cora is illustrated in Figure 2. We provide results on other datasets in Section A.1 in the appendix. We can observe that test accuracy increases as the rise of the number of layers in the beginning, but degrades dramatically from 3 layers. Besides, from the t-SNE visualization on Cora in Figure 1 (t-SNE visualization results of other datasets are provided in Appendix A.3.), the discriminative power of the node representations derived by different numbers of GCN layers has the similar trend. The node representations generated by multiple GCN layers, like 6 layers, are very difficult to be separated.
Several studies (Li et al., 2018; Chen et al., 2020) attribute this performance degradation phenomenon to the over-smoothing issue. However, we question this view for the following two reasons. First, we hold that the over-smoothing issue only happens when node representations propagate repeatedly for a large number of iterations, especially for a graph with sparsely connected edges. As shown in Table 1, all these three citation datasets have a small value of edge density, hence several propagation iterations are not enough to make over-smoothing happen, theoretically. Second, as shown in Figure 2, the smoothness metric value of graph node representations has a slight downward trend as the number of propagation iterations increases. According to (Li et al., 2018), the node representations suffering from the over-smoothing issue will converge to the same value or be proportional to the square root of the node degree, where the corresponding smoothness metric value should be close to , computed by our quantitative metric. However, the metric value in our experiments is relatively far from the ideal over-smoothing situation.
In this work, we argue that it is the entanglement of transformation and propagation that significantly compromise the performance of deep graph neural networks. Our argument is originated from the following two intuitions. First, the entanglement of representation transformation and propagation makes the number of parameters in transformation intertwined with the receptive fields in propagation. As illustrated in Eq.(1), one hop propagation requires a transformation function, thus leading to a large number of parameters when considering a large receptive field. Hence, it might be hard to train a deep GNN with a large number of parameters. This can possibly explain why the performance of multiple GCN layers in Figure 2 fluctuates greatly. Second, representation propagation and transformation should be viewed as two separate operations. Note that the class of a node can be totally predictable by its initial features, which explains why MLP, as shown in Figure 2 and 1, performs well without using any graph structure information. Propagation based on the graph structure can help to ease the classification task by making node representations in the same class to be similar, under the assumption that connected nodes usually belong to the same class. For instance, intuitively, the class of a document is completely determined by its content (i.e. its feature derived by word embedding), instead of the references relationships with other documents. Utilizing its neighbors’ features just eases the classification of documents. Hence, representation transformation and propagation play their distinct roles from feature and structure aspects, respectively.
To support and verify our argument, we decouple the propagation and transformation in Eq.(2), leading to the following model:
| (6) | ||||
denotes the new feature matrix transformed from the original feature matrix by an MLP network, where is the number of classes. After the transformation, we apply a -steps propagation to derive the output feature matrix . A softmax classifier is applied to compute the classification probabilities. Notably, the separation of transformation and propagation processes is also adopted in (Klicpera et al., 2019) and (Wu et al., 2019) but for the sake of reducing complexity. In this work, we analyze this scheme systematically and reveal that it can help to build deeper models without suffering from performance degradation, which has not been prioritized by the community.
The test accuracy and smoothness metric value of representations with different numbers of layers adopted in Eq.(6) on Cora are illustrated in Figure 4 (Results for other datasets are shown in Appendix A.2). After resolving the entanglement of feature transformation and propagation, deeper models is capable of leveraging larger receptive fields without suffering from performance degradation. We can observe that the over-smoothing issue starts compromising the performance at an extremely large receptive field, such as 75-hop on Cora. The smoothness metric value decreases greatly after that, which is demonstrated by the metric value of nearly 0. Besides, from the t-SNE visualization in Figure 3 (The t-SNE visualization results of other datasets are provided in Appendix A.4), deep models with large receptive fields, like 50-hop, still generating distinguishable node representations, which is impressive compared to the regular GCN model. In practice, we usually do not need an extremely large receptive field because the highest shortest path distance in a connected component usually is an acceptable small number. Thus training signals can be propagated to the entire graph with a small number of layers. This is demonstrated by the fact that graph neural networks with 2 or 3 GCN layers usually perform competitively. However, deep models with large receptive fields are necessary to incorporate more information, especially with limited training nodes under a semi-supervised learning setting.
3.3. Theoretical Analysis of Very Deep Models
The empirical analysis in the previous section shows that decoupling transformation and propagation can help to build much deeper models which can leverage larger receptive fields to incorporate more information. In this section, we provide a theoretical analysis of the above observation when building very deep graph neural networks, which aligns with the over-smoothing issue. (Li et al., 2018) and (Xu et al., 2018) study the over-smoothing issue from the perspective of Laplacian smoothing and nodes’ influence distribution, with several simplified assumptions like non-linear transformation and probability approximations. After decoupling transformation from propagation, our theoretical analysis can serve as a more rigorous and gentle description of the over-smoothing issue. In this section, we strictly describe the over-smoothing issue for 2 typical propagation mechanisms.
and , where , are two frequently utilized propagation mechanisms. The row-averaging normalization is adopted in GraphSAGE (Hamilton et al., 2017) and DGCNN (Zhang et al., 2018). The symmetrical normalization scheme is applied in GCN (Kipf and Welling, 2017). In the following, we describe the over-smoothing issue by proving the convergence of and , respectively, when goes to infinity.
Let be a row vector whose all entries are . Function normalizes a vector to sum to and function normalizes a vector such that its magnitude is .
Theorem 3.1.
Given a connected graph , , where is the matrix with all rows are and .
Theorem 3.2.
Given a connected graph , , where .
From the above two theorems, we can derive the exact convergence value of and , respectively, when goes to infinity in an infinite deep model. Hence, applying infinite layers to propagate information iteratively is equivalent to utilizing or to propagate features by one step. Rows of are the same and rows of are proportional to the square root value of the corresponding nodes’ degrees. Therefore, rows of or are linearly inseparable and utilizing them as propagation mechanism will generate indistinguishable representations, thereby leading to the over-smoothing issue.
To prove these two theorems, we first introduce the following two lemmas. The proofs of these two lemmas can be found in Appendix A.5 and A.6.
Lemma 3.3.
Given a graph , is an eigenvalue of with left eigenvector and right eigenvector if and only if is an eigenvalue of with left eigenvector and right eigenvector .
Lemma 3.4.
Given a connected graph , and always have an eigenvalue with unique associated eigenvectors and all other eigenvalues satisfy . The left and right eigenvectors of associated with eigenvalue are and , respectively. For , they are and .

Proof.
(of Theorem 3.1) can be viewed as a transition matrix because all entries are nonnegative and each row sums to . The graph can be further regarded as a Markov chain, whose transition matrix is . This Markov chain is irreducible and aperiodic because the graph is connected and self-loops are included in the connectivity. If a Markov chain is irreducible and aperiodic, then , where is the matrix with all rows equal to and can be computed by , s.t. (Kumar and Varaiya, 2015). It is obvious that is the unique left eigenvector of and is normalized such that all entries sum to . Hence, , where is the matrix with all rows are and from Lemma 3.4. ∎
Proof.
(of Theorem 3.2) Although cannot be processed as a transition matrix like , it is a symmetric matrix, which is diagonalizable. We have , where is an orthogonal matrix whose columns are normalized eigenvectors of and is the diagonal matrix whose diagonal entries are the eigenvalues. Then the -th power of can be computed by
| (7) |
where is the normalized right eigenvector associated with . From Lemma 3.4, always has an eigenvalue with unique associated eigenvectors and all other eigenvalues satisfy . Hence, . ∎
These two theorems hold for connected graphs that are frequently studied in graph neural networks. For a disconnected graph, these theorems can also be applied to each of its connected components, which means that applying these propagation mechanisms infinite times will generate indistinguishable node representations in each connected components.
The above theorems reveal that over-smoothing will make node representations inseparable and provide the exact convergence value of frequently used propagation mechanisms. Theoretically, we have proved that the over-smoothing issue is inevitable in very deep models. Further, the convergence speed is a more important factor that we should consider in practice. Mathematically, according to Eq.(7), the convergence speed depends on the other eigenvalues except of the propagation matrix, especially the second largest eigenvalue. Intuitively, the propagation matrix is determined by the topology information of the corresponding graph. This might be the reason for our observation in Section 3.2 that a sparsely connected graph suffers from the over-smoothing only when extremely deep models are applied.
4. Deep Adaptive Graph Neural Network
In this section, we propose Deep Adaptive Graph Neural Network (DAGNN) based on the above insights. Our DAGNN contributes two prominent advantages. First, it decouples the representation transformation from propagation so that large receptive fields can be applied without suffering from performance degradation, which has been verified in Section 3.2. Second, it utilizes an adaptive adjustment mechanism that can adaptively balance the information from local and global neighborhoods for each node, thus leading to more discriminative node representations. The mathematical expression of DAGNN is defined as
| (8) | ||||||
where is the number of node classes. is the feature matrix derived by applying an MLP network to the original feature matrix. We utilize the symmetrical normalization propagation mechanism , where . is a hyperparameter that indicates the depth of the model. is a trainable projection vector. is an activation function and we apply sigmoid. stack, reshape and squeeze are utilized to rearrange the data dimension so that dimension can be matched during computation.
An illustration of our proposed DAGNN is provided in Figure 5. There are three main steps in DAGNN: transformation, propagation and adaptive adjustment. We first utilize a shared MLP network for feature transformation. Theoretically, MLP can approximate any measurable function (Hornik et al., 1989). Obviously, only contains the information of individual nodes themselves with no structure information included. After transformation, a propagation mechanism is applied to gather neighborhood information. denotes the representations obtained by propagating information from nodes that are -hop away, hence captures the information from the subtree of height rooted at individual nodes. As the depth increase, more global information is included in because the corresponding subtree is deeper. However, it is difficult to determine a suitable . Small may fail to capture sufficient and essential neighborhood information, while large may bring too much global information and dilute the special local information. Furthermore, each node has a different subtree structure rooted at this node and the most suitable receptive field for each node should be different. To this end, we include an adaptive adjustment mechanism after the propagation. We utilize a trainable projection vector that is shared by all nodes to generate retainment scores. These scores are used for representations that carry information from various range of neighborhood. These retainment scores measure how much information of the corresponding representations derived by different propagation layers should be retained to generate the final representation for each node. Utilizing this adaptive adjustment mechanism, DAGNN can adaptively balance the information from local and global neighborhoods for each node. Obviously, the transformation process and the adaptive adjustment process have trainable parameters and there is no trainable parameter in the propagation process, leading to a parameter-efficient model. Note that DAGNN is trained end-to-end, which means that these three steps are considered together when optimizing the network.
| Dataset | #Classes | #Nodes | #Edges | Edge Density | #Features | #Training Nodes | #Validation Nodes | #Test Nodes |
|---|---|---|---|---|---|---|---|---|
| Cora | 7 | 2708 | 5278 | 0.0014 | 1433 | 20 per class | 500 | 1000 |
| CiteSeer | 6 | 3327 | 4552 | 0.0008 | 3703 | 20 per class | 500 | 1000 |
| PubMed | 3 | 19717 | 44324 | 0.0002 | 500 | 20 per class | 500 | 1000 |
| Coauthor CS | 15 | 18333 | 81894 | 0.0005 | 6805 | 20 per class | 30 per class | Rest nodes |
| Coauthor Physics | 5 | 34493 | 247962 | 0.0004 | 8415 | 20 per class | 30 per class | Rest nodes |
| Amazon Computers | 10 | 13381 | 245778 | 0.0027 | 767 | 20 per class | 30 per class | Rest nodes |
| Amazon Photo | 8 | 7487 | 119043 | 0.0042 | 745 | 20 per class | 30 per class | Rest nodes |
| Models | Cora | CiteSeer | PubMed | |||
|---|---|---|---|---|---|---|
| Fixed | Random | Fixed | Random | Fixed | Random | |
| MLP | ||||||
| ChebNet | ||||||
| GCN | ||||||
| GAT | ||||||
| APPNP | ||||||
| SGC | ||||||
| DAGNN (Ours) | ||||||
| Models |
|
|
|
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LogReg | ||||||||||||
| MLP | ||||||||||||
| LabelProp | ||||||||||||
| LabelProp NL | ||||||||||||
| GCN | ||||||||||||
| GAT | ||||||||||||
| MoNet | ||||||||||||
| GraphSAGE-mean | ||||||||||||
| GraphSAGE-maxpool | N/A | |||||||||||
| GraphSAGE-meanpool | ||||||||||||
| DAGNN (Ours) |
Decoupling representation transformation from propagation and utilizing the learnable retainment score to adaptively adjust the information from local and global neighborhoods make DAGNN have the ability to generate suitable representations for specific nodes from large and adaptive receptive fields. Besides, removing the entanglement of representation transformation and propagation, we can derive a large neighborhood without introducing more trainable parameters. Also, transforming representations to a low dimensional space at an early stage makes DAGNN computationally efficient and memory-saving. In order to compute efficiently, we choose to compute it sequentially from right to left with time complexity , which saves the computational cost compared to of calculating first.
Notably, there are no fully-connected layers utilized as a classifier at the end of this model. In our DAGNN, the final representations are used as the final prediction. Thus, the cross-entropy loss for all labeled examples can be calculated as
| (9) |
where is the set of labeled nodes and is the label indicator matrix. is the number of classes.
5. Experimental Studies
In this section, we conduct extensive experiments on node classification tasks to evaluate the superiority of our proposed DAGNN. We begin by introducing datasets and experimental setup we utilized. We then compare DAGNN with prior state-of-the-art baselines to demonstrate the effectiveness of DAGNN. Also, we deploy some performance studies to further verify the proposed model.
5.1. Datasets and Setup
We conduct experiments on datasets based on citation, co-authorship, or co-purchase graphs for semi-supervised node classification tasks; those are Cora (Sen et al., 2008), CiteSeer (Sen et al., 2008), PubMed (Sen et al., 2008), Coauthor CS (Shchur et al., 2018), Coauthor Physics (Shchur et al., 2018), Amazon Computers (Shchur et al., 2018), and Amazon Photo (Shchur et al., 2018). The statistics of these datasets are summarized in Table 1. The detailed description of these datasets are provided in Appendix A.7.
We implemented our proposed DAGNN and some necessary baselines using Pytorch (Paszke et al., 2017) and Pytorch Geometric (Fey and Lenssen, 2019), a library for deep learning on irregularly structured data built upon Pytorch. We consider the following baselines: Logistic Regression (LogReg), Multilayer Perceptron (MLP), Label Propagation (LabelProp) (Chapelle et al., 2009), Normalized Laplacian Label Propagation (LabelProp NL) (Chapelle et al., 2009), ChebNet (Defferrard et al., 2016), Graph Convolutional Network (GCN) (Kipf and Welling, 2017), Graph Attention Network(GAT) (Veličković et al., 2018), Mixture Model Network (MoNet) (Monti et al., 2017), GraphSAGE (Hamilton et al., 2017), APPNP (Klicpera et al., 2019), and SGC (Wu et al., 2019). We aim to provide a rigorous and fair comparison between different models on each dataset by using the same dataset splits and training procedure. We tune hyperparameters for all models individually and some baselines even achieve better results than their original reports. For our DAGNN, we tune the following hyperparameters: (1) k {5, 10, 20}, (2) weight decay {0, 2e-2, 5e-3, 5e-4, 5e-5}, and (3) dropout rate {0.5, 0.8}. Our code is publicly available 111https://github.com/divelab/DeeperGNN.
| #Training nodes per class | 1 | 2 | 3 | 4 | 5 | 10 | 20 | 30 | 40 | 50 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MLP | 30.3 | 35.0 | 38.3 | 40.8 | 44.7 | 53.0 | 59.8 | 63.0 | 64.8 | 65.4 | 64.0 |
| GCN | 34.7 | 48.9 | 56.8 | 62.5 | 65.3 | 74.3 | 79.1 | 80.8 | 82.2 | 82.9 | 84.7 |
| GAT | 45.3 | 58.8 | 66.6 | 68.4 | 70.7 | 77.0 | 80.8 | 82.6 | 83.4 | 84.0 | 86.1 |
| APPNP | 44.7 | 58.7 | 66.3 | 71.2 | 74.1 | 79.0 | 81.9 | 83.2 | 83.8 | 84.3 | 85.4 |
| SGC | 43.7 | 59.2 | 67.2 | 70.4 | 71.5 | 77.5 | 80.4 | 81.3 | 81.9 | 82.1 | 83.6 |
| DAGNN (Ours) | 58.4(23.7) | 67.7(18.8) | 72.4(15.6) | 75.5(13.0) | 76.7(11.4) | 80.8(6.5) | 83.7(4.6) | 84.5(3.7) | 85.6(3.4) | 86.0(3.1) | 87.1(2.4) |
5.2. Overall Results
The results on citation datasets are summarized in Table 2. To ensure a fair comparison, we use 20 labeled nodes per class as the training set, 500 nodes as the validation set, and 1000 nodes as the test set for all models. For each model, we conduct runs for the fixed training/validation/test split from (Kipf and Welling, 2017), which is commonly used to evaluate performance by the community. Also, we conduct runs for each model on randomly training/validation/test splits, where we additionally ensure uniform class distribution on the train split as (Fey and Lenssen, 2019). We compute the average test accuracy of runs. As shown in Table 2, our DAGNN model performs better than the representative baselines by significant margins. Also, the fact that DAGNN achieves state-of-the-art performance on random splits demonstrates the strong robustness of DAGNN. Quantitatively, for the randomly split data, the improvements of DAGNN over GCN are 4.6%, 3.0%, and 3.0% on Cora, CiteSeer, and PubMed, respectively.
The results on co-authorship and co-purchase datasets are summarized in Table 3. We utilize 20 labeled nodes per class as the training set, 30 nodes per class as the validation set, and the rest as the test set. The results of baselines are obtained from (Shchur et al., 2018). For DAGNN, we conduct runs for randomly training/validation/test splits as (Shchur et al., 2018) to ensure a fair comparison with baselines. Our DAGNN model achieves better performance over the current state-of-the-art models by significant margins of 1.5%, 1.0%, 1.0%, and 0.6% on the Coauthor CS, Coauthor Physics, Amazon Computers, and Amazon Photo, respectively. Note that DAGNN reduces the error rate by on average.
In summary, our DAGNN achieves superior performance on all these seven datasets, which significantly demonstrates the effectiveness of our proposed model. These results verify the superiority of learning node representations from large and adaptive receptive fields, which is achieved by decoupling transformation from propagation and utilizing an adaptive adjustment mechanism in DAGNN.
5.3. Training Set Sizes
The number of training samples is usually limited in the real world graph. Hence, it is necessary to explore how models perform with different training set sizes. To further demonstrate the advantage that our DAGNN is capable of capturing information from large and adaptive receptive fields, we conduct experiments with different training set sizes for several representative baselines. MLP only utilizes node features to learn representations. GCN and GAT include the structure information by propagation representations through edges, however, only limited receptive fields can be taken into consideration and it is shown in Section 3.2 that performance degrades when stacking multiple GCN layers to enable large receptive fields. APPNP, SGC, and our DAGNN all have the ability to deploy a large receptive field. Note that for a fair comparison, we set the depth in APPNP, SGC, and DAGNN as 10, where information in the 10-hop neighborhood can be included. For each model, we conduct runs on randomly training/validation/test splits for every training set size on Cora dataset. The results are present in Table 4 where our improvements over GCN are also highlighted. Our DAGNN achieves the best performance under different training set sizes. Notably, The superiority of our DAGNN can be demonstrated more obviously when fewer training nodes are used. The improvement of DAGNN over GCN increases greatly when the number of training nodes decreases. Extremely, only utilizing one training node per class, DAGNN achieves an overwhelming result over GCN by a significant margin of 23.7%. These considerable improvements are mainly attributed to the advantage that DAGNN can incorporate information from large receptive fields by removing the entanglement of representation transformation and propagation. Reachable large receptive fields are beneficial for propagating training signals to distant nodes, which is very essential when the number of training nodes is limited. APPNP and SGC also can gather information from a large neighborhood, but they perform not as good as DAGNN. This performance gap is mainly caused by the adaptive adjustment of DAGNN, which can adjust the information from different receptive fields for each node adaptively.

5.4. Model Depths
In order to investigate when over-smoothing happens in our DAGNN, we conduct experiments for DAGNN with different depths. For each dataset, we choose different hyperparameter in DAGNN, which means the -hop neighborhood is visible by each node, and conduct runs for each setting. The results are illustrated in Figure 6. For citation and co-authorship datasets, very deep models with large numbers of propagation iterations can be applied with keeping stable or slightly decreasing performance, which can be attributed to the design that we decouple the transformation from propagation and utilize adaptive receptive fields to learn node representations in DAGNN. Note that performances on co-purchase datasets decrease obviously with the increment of depth. This should be resulted by their larger value of edge density than other datasets, as shown in Table 1. Intuitively, when nodes are more densely connected, their representations will become indistinguishable by applying a smaller number of propagation iterations, which aligns with our assumption in Section 3.3 that further connection exists between the graph topology information and convergence speed.
6. Conclusion
In this paper, we consider the performance deterioration problem existed in current deep graph neural networks and develop new insights towards deeper graph neural networks. We first provide a systematical analysis on this issue and argue that the key factor that compromises the network performance is the entanglement of representation transformation and propagation. We propose to decouple these two operations and show that deep graph neural networks without this entanglement can leverage large receptive fields without suffering from performance deterioration. Further, we provide a theoretically analysis of the above strategy when building very deep models, which can serve as a rigorous and gentle description of the over-smoothing issue. Utilizing our insights, DAGNN is proposed to conduct node representation learning with the ability to capture information from large and adaptive receptive fields. According to our comprehensive experiments, our DAGNN achieves a better performance than current state-of-the-art models by significant margins, especially when training samples are limited, which demonstrates its superiority.
Acknowledgements.
This work was supported in part by National Science Foundation grants DBI-1922969, IIS-1908166, and IIS-1908198.References
- (1)
- Cai and Ji (2020) Lei Cai and Shuiwang Ji. 2020. A Multi-Scale Approach for Graph Link Prediction. In Thirty-Four AAAI Conference on Artificial Intelligence.
- Chapelle et al. (2009) Olivier Chapelle, Bernhard Scholkopf, and Alexander Zien. 2009. Semi-supervised learning (chapelle, o. et al., eds.; 2006)[book reviews]. IEEE Transactions on Neural Networks 20, 3 (2009), 542–542.
- Chen et al. (2020) Deli Chen, Yankai Lin, Wei Li, Peng Li, Jie Zhou, and Xu Sun. 2020. Measuring and Relieving the Over-smoothing Problem for Graph Neural Networks from the Topological View. In Thirty-Four AAAI Conference on Artificial Intelligence.
- Defferrard et al. (2016) Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. 2016. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in neural information processing systems. 3844–3852.
- Fey and Lenssen (2019) Matthias Fey and Jan E. Lenssen. 2019. Fast Graph Representation Learning with PyTorch Geometric. In ICLR Workshop on Representation Learning on Graphs and Manifolds.
- Gao and Ji (2019) Hongyang Gao and Shuiwang Ji. 2019. Graph U-Nets. In International Conference on Machine Learning. 2083–2092.
- Gao et al. (2018) Hongyang Gao, Zhengyang Wang, and Shuiwang Ji. 2018. Large-scale learnable graph convolutional networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1416–1424.
- Gilmer et al. (2017) Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. 2017. Neural message passing for quantum chemistry. In International Conference on Machine Learning. 1263–1272.
- Hamilton et al. (2017) Will Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive representation learning on large graphs. In Advances in Neural Information Processing Systems. 1024–1034.
- Hornik et al. (1989) Kurt Hornik, Maxwell Stinchcombe, Halbert White, et al. 1989. Multilayer feedforward networks are universal approximators. IEEE Transactions on Neural Networks 2, 5 (1989), 359–366.
- Kipf and Welling (2017) Thomas N Kipf and Max Welling. 2017. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations.
- Klicpera et al. (2019) Johannes Klicpera, Aleksandar Bojchevski, and Stephan Günnemann. 2019. Predict then propagate: Graph neural networks meet personalized pagerank. In International Conference on Learning Representations.
- Kumar and Varaiya (2015) Panqanamala Ramana Kumar and Pravin Varaiya. 2015. Stochastic systems: Estimation, identification, and adaptive control. Vol. 75. SIAM.
- Lee et al. (2019) Junhyun Lee, Inyeop Lee, and Jaewoo Kang. 2019. Self-Attention Graph Pooling. In International Conference on Machine Learning. 3734–3743.
- Li et al. (2018) Qimai Li, Zhichao Han, and Xiao-Ming Wu. 2018. Deeper insights into graph convolutional networks for semi-supervised learning. In Thirty-Second AAAI Conference on Artificial Intelligence.
- Liu et al. (2020) Meng Liu, Zhengyang Wang, and Shuiwang Ji. 2020. Non-Local Graph Neural Networks. arXiv preprint arXiv:2005.14612 (2020).
- Lovász et al. (1993) László Lovász et al. 1993. Random walks on graphs: A survey. Combinatorics, Paul erdos is eighty 2, 1 (1993), 1–46.
- Ma et al. (2019) Yao Ma, Suhang Wang, Charu C Aggarwal, and Jiliang Tang. 2019. Graph convolutional networks with eigenpooling. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 723–731.
- Maaten and Hinton (2008) Laurens van der Maaten and Geoffrey Hinton. 2008. Visualizing data using t-SNE. Journal of machine learning research 9, Nov (2008), 2579–2605.
- McAuley et al. (2015) Julian McAuley, Christopher Targett, Qinfeng Shi, and Anton Van Den Hengel. 2015. Image-based recommendations on styles and substitutes. In Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval. 43–52.
- Monti et al. (2017) Federico Monti, Davide Boscaini, Jonathan Masci, Emanuele Rodola, Jan Svoboda, and Michael M Bronstein. 2017. Geometric deep learning on graphs and manifolds using mixture model cnns. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 5115–5124.
- Nair and Hinton (2010) Vinod Nair and Geoffrey E Hinton. 2010. Rectified linear units improve restricted boltzmann machines. In International Conference on Machine Learning. 807–814.
- Page et al. (1999) Lawrence Page, Sergey Brin, Rajeev Motwani, and Terry Winograd. 1999. The PageRank citation ranking: Bringing order to the web. Technical Report. Stanford InfoLab.
- Paszke et al. (2017) Adam Paszke, Sam Gross, Soumith Chintala, Gregory Chanan, Edward Yang, Zachary DeVito, Zeming Lin, Alban Desmaison, Luca Antiga, and Adam Lerer. 2017. Automatic differentiation in pytorch. In Proceedings of Neural Information Processing Systems Autodiff Workshop.
- Pei et al. (2020) Hongbin Pei, Bingzhe Wei, Kevin Chen-Chuan Chang, Yu Lei, and Bo Yang. 2020. Geom-gcn: Geometric graph convolutional networks. In International Conference on Learning Representations.
- Sen et al. (2008) Prithviraj Sen, Galileo Namata, Mustafa Bilgic, Lise Getoor, Brian Galligher, and Tina Eliassi-Rad. 2008. Collective classification in network data. AI magazine 29, 3 (2008), 93–93.
- Seneta (2006) Eugene Seneta. 2006. Non-negative matrices and Markov chains. Springer Science & Business Media.
- Shchur et al. (2018) Oleksandr Shchur, Maximilian Mumme, Aleksandar Bojchevski, and Stephan Günnemann. 2018. Pitfalls of graph neural network evaluation. arXiv preprint arXiv:1811.05868 (2018).
- Taubin (1995) Gabriel Taubin. 1995. A signal processing approach to fair surface design. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques. ACM, 351–358.
- Veličković et al. (2018) Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. 2018. Graph attention networks. In International Conference on Learning Representation.
- Wu et al. (2019) Felix Wu, Amauri Souza, Tianyi Zhang, Christopher Fifty, Tao Yu, and Kilian Weinberger. 2019. Simplifying Graph Convolutional Networks. In International Conference on Machine Learning. 6861–6871.
- Xu et al. (2019) Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. 2019. How powerful are graph neural networks?. In International Conference on Learning Representations.
- Xu et al. (2018) Keyulu Xu, Chengtao Li, Yonglong Tian, Tomohiro Sonobe, Ken-ichi Kawarabayashi, and Stefanie Jegelka. 2018. Representation Learning on Graphs with Jumping Knowledge Networks. In International Conference on Machine Learning. 5449–5458.
- Ying et al. (2018) Zhitao Ying, Jiaxuan You, Christopher Morris, Xiang Ren, Will Hamilton, and Jure Leskovec. 2018. Hierarchical graph representation learning with differentiable pooling. In Advances in neural information processing systems. 4800–4810.
- Yuan and Ji (2020) Hao Yuan and Shuiwang Ji. 2020. StructPool: Structured Graph Pooling via Conditional Random Fields. In International Conference on Learning Representations.
- Zhang and Chen (2017) Muhan Zhang and Yixin Chen. 2017. Weisfeiler-lehman neural machine for link prediction. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 575–583.
- Zhang and Chen (2018) Muhan Zhang and Yixin Chen. 2018. Link prediction based on graph neural networks. In Advances in Neural Information Processing Systems. 5165–5175.
- Zhang et al. (2018) Muhan Zhang, Zhicheng Cui, Marion Neumann, and Yixin Chen. 2018. An end-to-end deep learning architecture for graph classification. In Thirty-Second AAAI Conference on Artificial Intelligence.
Appendix A Appendix
In this section, we provide necessary information for reproducing our insights and experimental results. These include the quantitative results and qualitative visualization on more datasets that can further support our insights, the proofs of lemmas, and the detailed description of datasets.
A.1. Test Accuracy and Smoothness Metric Value of GCNs
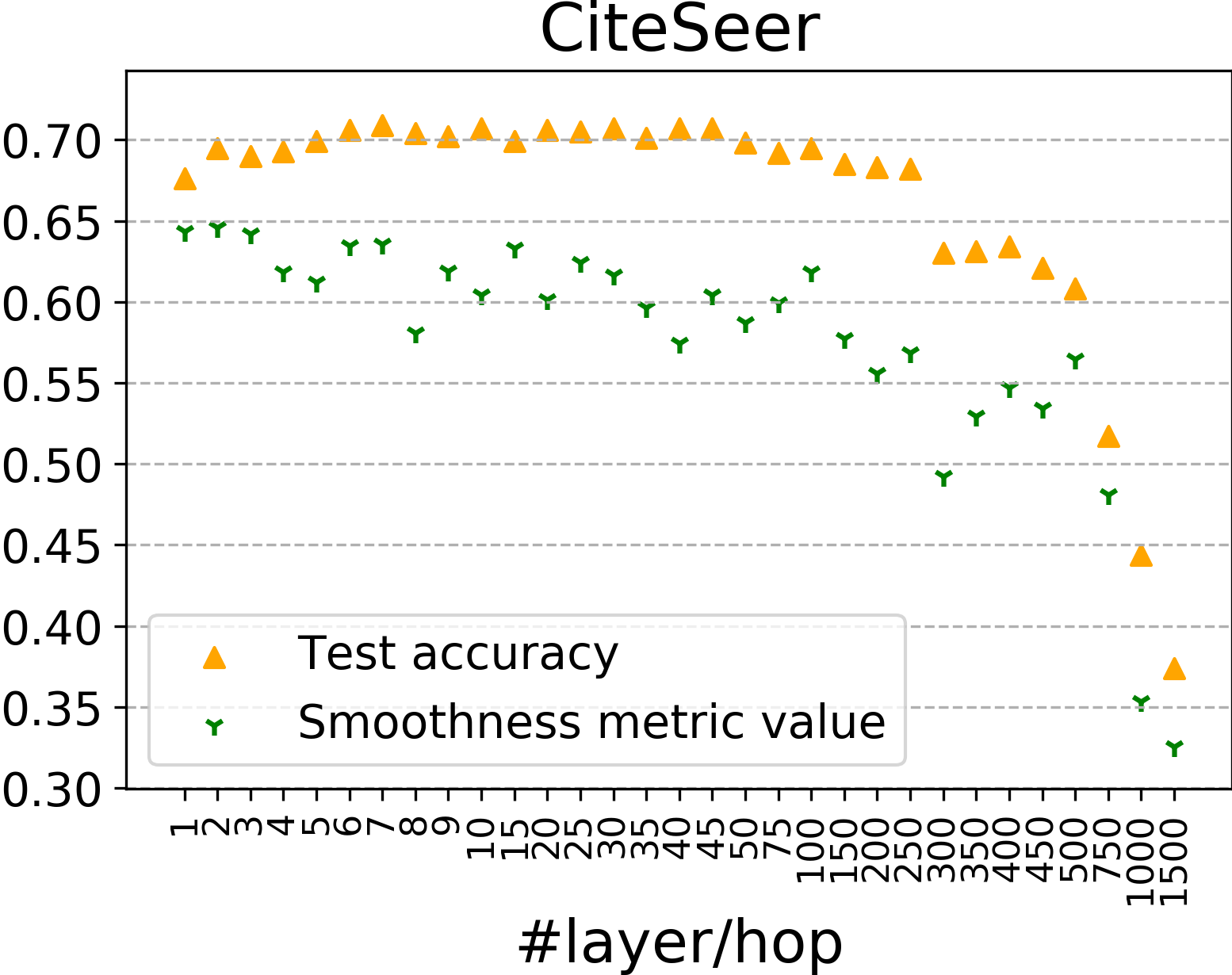
Test accuracy and smoothness metric value of node representations with different numbers of GCN layers are shown in Figure 7 for CiteSeer and PubMed. They have the same trends as we discussed in Section 3.2.


A.2. Test Accuracy and Smoothness Metric Value of Models as Eq.(6)
Test accuracy and smoothness metric value of node representations with different numbers of layers adopted in models as Eq.(6) are shown in Figure 8 for CiteSeer and PubMed. It is illustrated that after decoupling transformation from propagation, we can apply deeper models without suffering from performance degradation.

A.3. Visualization of Representations Derived by GCNs
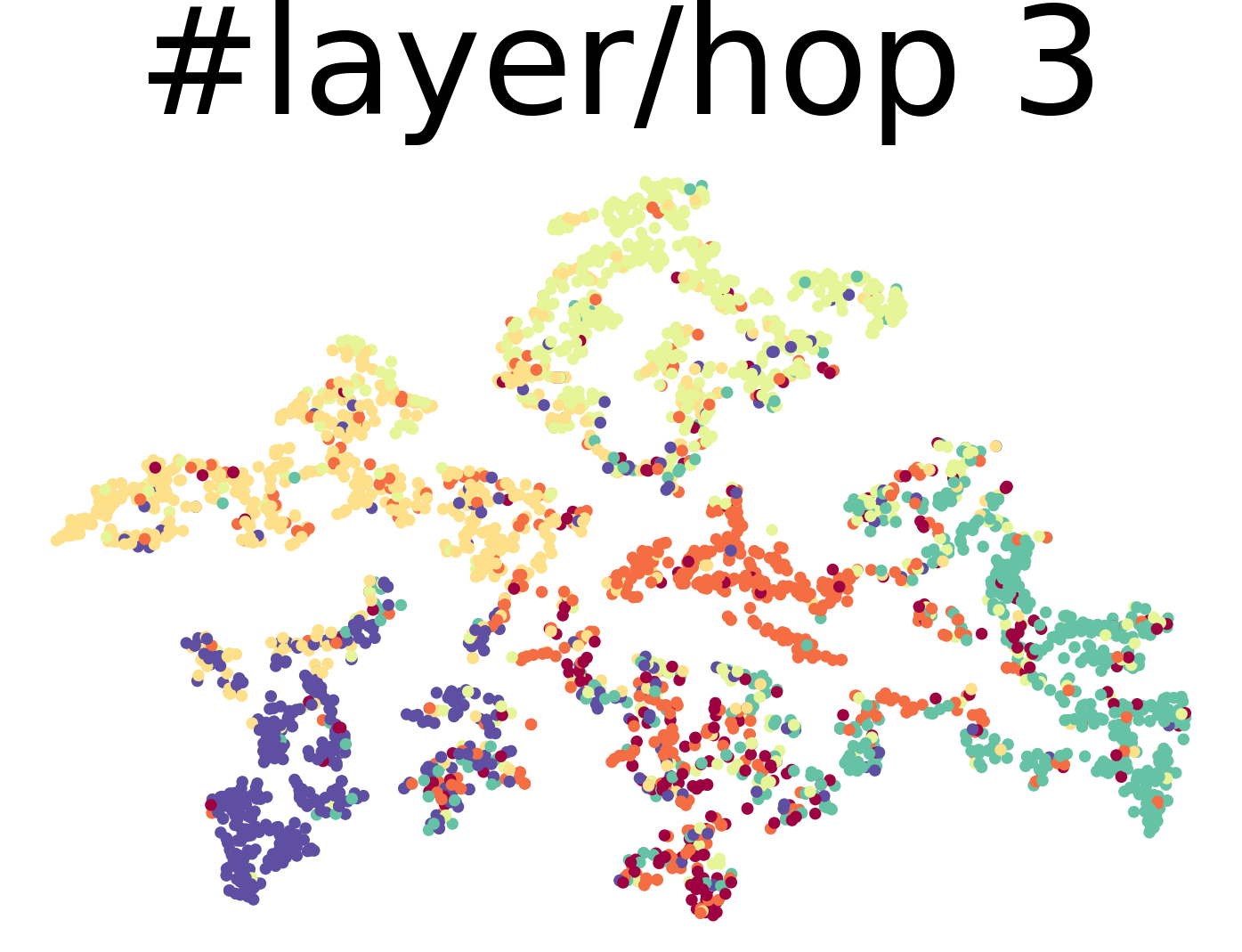
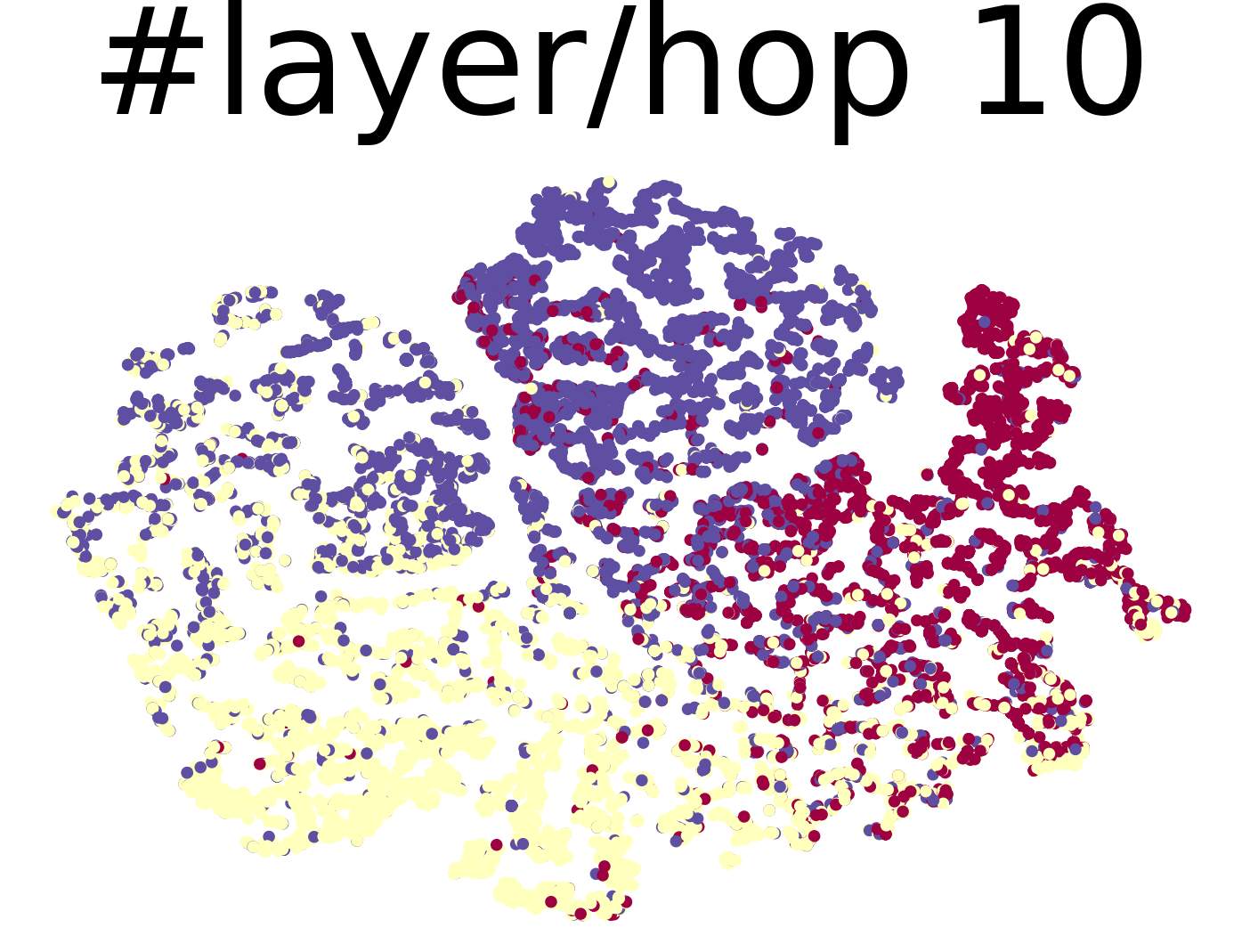
The t-SNE visualization of node representations derived by different numbers of GCN layers are shown in Figure 9 and 10 for CiteSeer and PubMed, respectively. The node representations become indistinguishable when several layers are deployed.

















A.4. Visualization of Representations Derived by Models as Eq.(6)
The t-SNE visualization of node representations derived by model as Eq.(6) with different numbers of layers are shown in Figure 11 and 12 for CiteSeer and PubMed, respectively. It is shown that after the entanglement of representation transformation and propagation is removed, the model with a large receptive field, such as 50-hop, still generating distinguishable node representations. The over-smoothing issue affects the distinguishability only when an extremely receptive field, like 200-hop, is adopted.

















A.5. Proof for Lemma 3.3
Proof.
If is an eigenvalue of with left eigenvector and right eigenvector , we have and , i.e. and . We right multiply the first eigenvalue equation with and left multiply the second eigenvalue equation with , respectively. Then we can derive and . Hence, is also an eigenvalue of with left eigenvector and right eigenvector . From to , we can prove it in the same way. ∎
A.6. Proof for Lemma 3.4
Proof.
We first prove that and always have an eigenvalue 1 and all eigenvalues satisfy . We have because each row of sums to . Therefore, is an eigenvalue of . Suppose that there exists an eigenvalue that with eigenvector , then the length of the right side in grows exponentially when goes to infinity. This indicates that some entries of shoulde be larger than . Nevertheless, all entries of are positive and each row of always sums to , hence no entry of can be larger than , which leads to contradiction. From Lemma 3.3, and have the same eigenvalues. Therefore, and always have an eigenvalue 1 and all eigenvalues satisfy .
According to the Perron-Frobenius Theorem for Primitive Matrices (Seneta, 2006), there exists an eigenvalue for an non-negative primitive matrix such that for any eigenvalue and the eigenvectors associated with are unique. The property that the given graph is connected can guarantee that for : s.t. . Furthermore, there must exsit some that can make all entries of to be simultaneously positive because self-loops are included in the graph. Formally, : for . Hence, is a non-negative primitive matrix. From the Perron-Frobenius Theorem for Primitive Matrices, always has an eigenvalue with unique associated eigenvectors and all other eigenvalues satisfy . Based on Lemma 3.3, this property can be extended to . We then compute the eigenvectors associated with eigenvalue . Obviously, is the right eigenvector of associated with eigenvalue . Next, assume is the left eigenvector of associated with eigenvalue and thus is the left eigenvector of associated with eigenvalue . We know is a symmetric matrix, whose left and right eigenvectors associated with the same eigenvalue are simply each other’s transpose. Hence, we utilize to obtain . After deriving the eigenvectors of associated with eigenvalue , corresponding eigenvectors of can be computed by Lemma 3.3. ∎
A.7. Datasets Description and Statistics
Citation datasets. Cora, CiteSeer and PubMed (Sen et al., 2008) are representative citation network datasets where nodes and edges denote documents and their citation relationships, respectively. Node features are formed by bay-of-words representations for documents. Each node has a label indicating what field the corresponding document belongs to.
Co-authorship datasets. Coauthor CS and Coauthor Physics (Shchur et al., 2018) are co-authorship graphs datasets. Nodes denote authors, which are connected by an edge if they co-authored a paper. Node features represent paper keywords for each author’s papers. Each node has a label denoting the most active fields of study for the corresponding author.
Co-purchase datasets. Amazon Computers and Amazon Photo (Shchur et al., 2018) are segments of the Amazon co-purchase graph (McAuley et al., 2015) where nodes are goods and edges denote that two goods are frequently bought together. Node features are derived from bag-of-words representations for product reviews and class labels are given by the product category.
The datasets statistics are summarized in Table 1.