Toward Practical Entity Alignment Method Design: Insights from New Highly Heterogeneous Knowledge Graph Datasets
Abstract.
The flourishing of knowledge graph (KG) applications has driven the need for entity alignment (EA) across KGs. However, the heterogeneity of practical KGs, characterized by differing scales, structures, and limited overlapping entities, greatly surpasses that of existing EA datasets. This discrepancy highlights an oversimplified heterogeneity in current EA datasets, which obstructs a full understanding of the advancements achieved by recent EA methods.
In this paper, we study the performance of EA methods in practical settings, specifically focusing on the alignment of highly heterogeneous KGs (HHKGs). Firstly, we address the oversimplified heterogeneity settings of current datasets and propose two new HHKG datasets that closely mimic practical EA scenarios. Then, based on these datasets, we conduct extensive experiments to evaluate previous representative EA methods. Our findings reveal that, in aligning HHKGs, valuable structure information can hardly be exploited through message-passing and aggregation mechanisms. This phenomenon leads to inferior performance of existing EA methods, especially those based on GNNs. These findings shed light on the potential problems associated with the conventional application of GNN-based methods as a panacea for all EA datasets. Consequently, in light of these observations and to elucidate what EA methodology is genuinely beneficial in practical scenarios, we undertake an in-depth analysis by implementing a simple but effective approach: Simple-HHEA. This method adaptly integrates entity name, structure, and temporal information to navigate the challenges posed by HHKGs. Our experiment results conclude that the key to the future EA model design in practice lies in their adaptability and efficiency to varying information quality conditions, as well as their capability to capture patterns across HHKGs. The datasets and source code are available at https://github.com/IDEA-FinAI/Simple-HHEA.
1. Introduction
Knowledge Graphs (KGs) are the most representative ways to store knowledge in the form of connections of entities. With the development of KG and relevant applications (e.g., Question Answering (Fu et al., 2020), Information Retrieval (Reinanda et al., 2020)) in recent years, the need for aligning KGs from different sources has become increasingly important in these fields. Entity Alignment (EA) in KGs, which aims to integrate KGs from different sources based on practical requirements, is a fundamental technique in the field of data integration.
Most KGs derived from different sources are heterogeneous, which brings difficulties when aligning entities. Existing EA studies mainly make efforts to identify and leverage the correlation between heterogeneous KGs from various perspectives (e.g., entity names, structure information, temporal information) through deep learning techniques. GNN is one of the most popular techniques for mining graph-structured information. Along with the development of GNN-related techniques, over 70 studies of EA since 2019, according to the statistics (Zhang et al., 2022), have incorporated GNNs into their approaches. Benefiting from the strong ability of GNNs to capture KGs’ structure correlations, related methods have achieved remarkable performance on benchmark EA datasets.
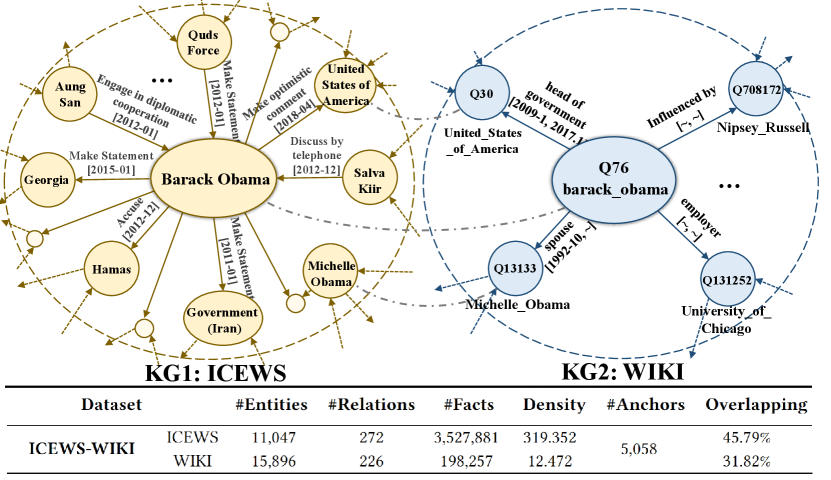
How to overcome the heterogeneity and mine the correlations between KGs is the main concern of EA. Existing EA methods evaluate the performance on several widely-used KG datasets, especially cross-lingual KGs (e.g., DBP15K(EN-FR)). However, the heterogeneity between KGs is not limited to linguistic differences. Different data sources, scales, structures, and other information (e.g., temporal information ) are more widespread heterogeneities among knowledge graphs, and need to be studied urgently in the EA area. The highly heterogeneous KGs (HHKGs) indicate that the source and target KG are far different from each other (e.g., General KG-Domain KG). Figure 1 vividly presents a toy example of HHKGs, in which KGs have different scales, structures, and densities, and the overlapping ratio is exceedingly low. For temporal knowledge graphs (TKGs), the difference in temporal information can also be considered as a kind of heterogeneity. The above characteristics lead to the challenges of EA on HHKGs.
The requirements of practical applications reveal the indispensability of studying HHKG alignment. For example, personal KGs (Balog and Kenter, 2019; Yang et al., 2022) intend to integrate domain knowledge about people with general KG for personalized social recommendations; Geospatial database, which is today at the core of an ever-increasing number of Geographic Information Systems, needs to align entities from multiple knowledge providers (Balsebre et al., 2022). These applications have urgent needs for EA on HHKGs. Unfortunately, most EA methods are evaluated on a few benchmarks, there is a lack of datasets for conducting research on HHKGs. This one-sided behavior hinders our understanding of the real progress achieved by EA methods, especially GNN-based methods, and results in the limitations of previous EA methods when applied in practical scenarios. In general, a rethinking of EA methods especially GNN-based methods is warranted. The goal of this work is to answer two essential research questions:
-
•
RQ1: From the dataset view, what are the existing EA datasets’ limitations, and the gaps between them and practical scenarios?
-
•
RQ2: From the method view, what is the EA method that we really need in practical applications?
To answer RQ1, we conduct a rethinking of the existing EA datasets, and discuss the gap between them and practical scenarios through statistical analysis. Based on the analysis, we sweep the unreasonable assumption (e.g., KGs always satisfy 1-to-1 assumption of entities) and eliminate oversimplified settings (e.g., the excessive similarity of KGs in scale, structure, and other information) of previous datasets and propose two new entity alignment datasets called ICEWS-WIKI and ICEWS-YAGO.
To answer RQ2, we perform empirical evaluations across a wide range of representative EA methods on HHKG datasets. It is noticed that the performances of GNN-based methods, which achieve competitive performances on previous EA datasets, decrease sharply under HHKG conditions. That is to say, GNN-based methods, which primarily rely on leveraging implicit patterns in structure information for EA, do not demonstrate significant advantages over other EA methods when the structure information of HHKGs becomes challenging to utilize. The above phenomena lead us to rethink the so-called progress of existing GNN-based EA methods.
To further investigate the components of GNN that lead to performance degradation, and understand how the characteristics of HHKGs influence these methods, we conduct statistical analysis, ablation studies, and sensitivity studies of GNN-based EA methods on HHKGs, and can summarize that:
(1) The structure information of HHKGs is complicated to utilize through message passing and aggregation mechanisms, resulting in the GNN-based methods’ poor performance. The entity name information is not effectively utilized because more noise is aggregated when facing highly heterogeneous graph structures.
(2) It cannot be ignored to leverage structure information, especially when the quality of other types of information cannot be guaranteed. Therefore, we need to design EA models that can mimic the self-loop mechanism of GNNs, and adaptively exploit different types of information between HHKGs.
In light of these observations, and with the intent to discover what makes an EA methodology genuinely beneficial in practical scenarios, we propose a simple but effective method: Simple-HHEA, which can jointly leverage the entity name, structure, and temporal information of HHKGs. We conduct extensive experiments on the proposed datasets and a previous benchmark dataset.
Our experimental insights emphasize three keys for EA models in real-world scenarios: (1) the methods should possess adaptability to various information quality conditions to meet the demands of diverse applications; (2) the methods need the capability to extract clues from highly heterogeneous data for EA; (3) efficiency is also vital, striving for a simple yet effective model that maintains high accuracy while conserving resources.
To summarize, our main contributions are as follows:
(1) We recognize the limitations of previous EA benchmark datasets, and propose a challenging but practical task, i.e., EA on HHKGs. To this end, we have constructed two new datasets to facilitate the examination of EA in practical applications.
(2) We rethink existing GNN-based EA methods. Through adequate analysis and experiments on new datasets, we shed light on the potential issues resulting from oversimplified settings of previous EA datasets to facilitate robust and open EA developments.
(3) We propose an in-depth analysis to provide direction for future EA method improvement through the implementation of a simple but effective approach: Simple-HHEA.
2. Rethinking Existing EA Researches
Dataset #Entities #Relations #Facts Density #Anchors Overlapping Struc. Sim. Temporal DBP15K(EN-FR) EN 15,000 193 96,318 6.421 15,000 100 63.4% No FR 15,000 166 80,112 5.341 100 No DBP-WIKI DBP 100,000 413 293,990 2.940 100,000 100 74.8% No WIKI 100,000 261 251,708 2.517 100 No ICEWS-WIKI ICEWS 11,047 272 3,527,881 319.352 5,058 45.79 15.4% Yes WIKI 15,896 226 198,257 12.472 31.82 Yes ICEWS-YAGO ICEWS 26,863 272 4,192,555 156.072 18,824 70.07 14.0% Yes YAGO 22,734 41 107,118 4.712 82.80 Yes
2.1. Limitations of Existing EA Datasets
Upon conducting an extensive review of the field, we noted that a substantial majority of Entity Alignment (EA) studies, specifically more than 90%, utilize a set of established benchmark datasets for evaluation. These include, but are not limited to, DBP15K datasets, DBP-WIKI, and WIKI-YAGO datasets. These datasets have undoubtedly made substantial contributions to the progression of EA research. However, when applied to the study of HHKGs, the intrinsic limitations of these datasets become increasingly prominent. These limitations largely stem from the inherent characteristics of these datasets. Regrettably, these widely used datasets exhibit a degree of simplification. While these feature may making them convenient for conventional EA studies, it significantly deviates from the high heterogeneity and complexity commonly found in real-world KGs. Consequently, these datasets fail to adequately represent the challenges posed by practical applications. This divergence between the characteristics of benchmark datasets and piratical scenarios poses substantial challenges to the alignment of entities within HHKGs.
In this paper, we delve into the prevalent issues inherent in existing EA datasets by conducting rigorous statistical analyses on widely-used datasets, DBP15K(EN-FR) and DBP-WIKI, proposed by OpenEA (Sun et al., 2020). Our choice to examine DBP15K(EN-FR) is driven by two factors: (1) its exemplary nature as it shares similar characteristics with other datasets, thereby enhancing the generalizability of our analysis; For example, through the statistical analysis (Zhao et al., 2020), we can observed that DBP15K(EN-FR), other DBP15K series dataset, DBP-WIKI, and SRPRS have the same feature that aligned KGs share the similar scale, density, structure distribution, and overlapping ratios. (2) the datasets are extensively employed within the EA research community, making them the representation of benchmark datasets, and its broad acceptance by the EA community ensures the applicability of our findings.
With DBP15K(EN-FR) and DBP-WIKI as our focal point, we assess these datasets from three critical dimensions: scale, structure, and overlapping ratios. Through this systematic exploration, we aim to provide valuable insights into the challenges inherent in existing EA datasets and inform future research directions A comprehensive overview of the dataset statistics is presented in Table 1.
Scale. The statistical analysis of DBP15K(EN-FR) and DBP-WIKI shows that the KGs exhibit similarities in the number of entities, relations, and facts, indicating that the scales of aligned KGs are same. However, in practical scenarios, KGs from different sources are not always same in scale, and even show significant differences. In recent years, there has been research (Sun et al., 2020) focused on aligning large-scale KGs. However, there is still a lack of research and datasets modeling KGs that are significantly different in scale, which widely exist. For example, the ICEWS(05-15) dataset contains more facts (461,329) compared to YAGO (138,056) and WIKIDATA (150,079) dataset (García-Durán et al., 2018). Thus, it is impossible to explore the impact of scale differences between KGs in real-world scenarios.

Structure. The KGs of DBP15K(EN-FR) and DBP-WIKI are similar in density, and also have similar degree distributions as shown in Figure 2, which reflect that the KGs are similar in structure.
To further evaluate the neighborhood similarity between KGs, we propose a new metric called structure similarity, which is the average similarity of aligned neighbors of aligned entity pairs, and details are illustrated in A.3. The structure similarity of KGs in DBP15K(EN-FR) and DBP-WIKI reaches 63.4% and 74.8%, indicating that the entity pairs share similar neighborhoods.
The analysis of the structure of DBP15K(EN-FR) and DBP-WIKI reveals that the structure information of the aligned KGs in previous datasets is similar and easy to leverage, particularly by GNN-based EA methods, such as (Wang et al., 2018; Chen et al., 2022; Mao et al., 2021). These methods exhibit abilities to capture and leverage the structure correlation between KGs, resulting in impressive performances on previous EA datasets. It is worth further investigation to determine if these EA methods, verified on previous datasets, are still effective in piratical scenarios where the structure information of two KGs is significantly different.
Overlapping ratio. We can also notice that the overlapping ratio of DBP15K(EN-FR) and DBP-WIKI is 100, which refers to another important characteristic of most EA datasets: 1-to-1 assumption (each entity in a KG must have a counterpart in the second KG). As discussed in the recent EA benchmark study (Leone et al., 2022), the 1-to-1 assumption deviates from practical KGs. Especially when the alignment is performed between KGs from different sources (e.g., the global event-related ICEWS and the general KG denoted as WIKI), the entities that can be aligned only make up a small fraction of the aligned KGs, which is manifested by a low overlapping ratio. For example, some non-political entities in YAGO (e.g., football clubs) do not appear in the ICEWS dataset.
In conclusion, through the statistical analysis of DBP15K(EN-FR), we find that the previous EA datasets are oversimplified under the unrealistic assumption (i.e., 1-to-1 assumption) and settings (i.e., the same scale, structure), which are easy to leverage but deviate from real-world scenarios. This one-sided behavior hinders our understanding of the real progress achieved by previous EA methods, especially GNN-based methods, and causes the potential limitations of these methods for applications. Moreover, the heterogeneities between real-world KGs are not only language but also the scales, structure, coverage of knowledge, and others, overcoming the heterogeneities and aligning KGs helps complete and enrich them. Therefore, new EA datasets, which can mimic KGs’ heterogeneities in more practical scenarios, are urgently needed for EA research.
2.2. Towards Practical Datasets
To address the limitations of previous EA datasets, in this paper, we present two new EA datasets called ICEWS-WIKI and ICEWS-YAGO, which integrate the event knowledge graph derived from the Integrated Crisis Early Warning System (ICEWS) and general KGs (i.e., WIKIDATA, YAGO). There is a considerable demand to align them in real-world scenarios. ICEWS is a representative domain-specific KG, which contains political events with time annotations that embody the temporal interactions between politically related entities. WIKIDATA and YAGO are two common KGs with extensive general knowledge that can provide background information. Aligning them can provide a more comprehensive view to understand events and serve temporal knowledge reasoning tasks. The detailed construction processes are illustrated in A.4
Dataset Analysis. An ideal comparison should include KGs as they are. From the EA research view, the proposed datasets sweep the oversimplified settings and assumptions (i.e., KGs always satisfy the 1-to-1 assumption, and KGs are similar in scale and structure) of previous datasets, and thus are closer to the real-world scenarios.
In scale, the original two KGs differ significantly in scale. Correspondingly, the datasets maintained the original distribution of the two KGs during sampling, which means that the constructed dataset maintained the scale difference of the KGs.
In structure, we preserved the feature of the original KGs that the density is significantly different. Figure 2 also shows that the two proposed datasets exhibit highly different degree distributions. The structure similarities are very low (15.4%, 14.0% of ICEWS-WIKI/ YAGO) compared with DBP15K(EN-FR) (66.4%), referring that the KGs of the new datasets are highly heterogeneous in structure.
In overlapping ratio, the datasets mimic a more common scenario that the KGs come from various sources (i.e., domain-specific KGs and general KGs). The differences in the sources are typically not language but the coverage of knowledge, which result in a small proportion of overlapping entities. The EA task on the new dataset is challenging but also reaps huge fruits once realized. As shown in Table 1, the overlapping ratio of the new dataset is exceedingly low compared with DBP15K(EN-FR), which means that the new datasets do not follow the 1-to-1 assumption.
Moreover, an increasing number of KGs like YAGO and WIKIDATA contain temporal knowledge, and two recent studies (Xu et al., 2021, 2022) shows that KGs’ temporal information is helpful.
Through the statistical analysis, we deem that the proposed datasets are highly heterogeneous, which can mimic the considerable practical EA scenarios, and help us better understand the demands and challenges of real-world EA applications. We expect the proposed datasets to help design better EA models that can deal with more challenging problem instances, and offer a better direction for the EA research community.
The proposed datasets are not only meaningful for EA research but also valuable in the field of KG applications. From the KG application view, ICEWS, WIKIDATA, and YAGO are widely adopted in various KG tasks such as temporal query (Xu et al., 2019, 2020a, 2020b; Lin et al., 2022), KG completion (Lacroix et al., 2018; Nayyeri et al., 2021) and question answering (Mavromatis et al., 2022; Saxena et al., 2021). Properly aligning and leveraging these KGs will provide more comprehensive insights for understanding temporal knowledge and benefit downstream tasks.
2.3. Rethinking Existing EA Methods
Translation-based EA Methods. Translation-based EA approaches (Chen et al., 2017; Sun et al., 2017, 2018; Zhu et al., 2017) are inspired by the TransE mechanism (Bordes et al., 2013), focusing on knowledge triplets . Their scoring functions assess the triplet’s validity to optimize knowledge representation. MTransE (Chen et al., 2017) uses a translation mechanism for entity and relation embedding, leveraging pre-aligned entities for vector space transformation. Both AlignE (Sun et al., 2018) and BootEA (Sun et al., 2018) adjust aligned entities within triples to harmonize KG embeddings, with BootEA incorporating bootstrapping to address limited training data.
GNN-based EA Methods. In recent years, GNNs have gained popularity in EA tasks for their notable capabilities in modeling both structure and semantic information in KGs (Wang et al., 2018; Cao et al., 2019; Zhu et al., 2021; Mao et al., 2020b, a). GCN-Align (Wang et al., 2018) exemplifies GNN-based EA methods, utilizing GCN for unified semantic space entity embedding. Enhancements like RDGCN (Chen et al., 2022) and Dual-AMN (Mao et al., 2021) introduced features to optimize neighbor similarity modeling. Recent methodologies, e.g., TEA-GNN (Xu et al., 2021), TREA (Xu et al., 2022), and STEA (Cai et al., 2022), have integrated temporal data, underscoring its significance in EA tasks.
Essentially, GNNs can be considered as a framework incorporating four key mechanisms: information messaging (or propagation), attention, aggregation, and self-loop. Each of these plays a fundamental role in GNNs’ effective performance in EA tasks. We first give a formulation to the general attention-based GNNs as follows:
| (1) |
where denotes the learned entity embedding, MSG, ATT, AGG, and SELF denote message passing, attention aggregation, and self-loop mechanism, respectively.
Specifically, Message passing (MSG) enables nodes to exchange information and assimilate features from neighbors, encapsulating local context crucial for EA tasks, as illustrated in Figure 3. Attention (ATT) assigns varied weights to nodes during messaging and aggregation, allowing GNNs to focus on more pertinent nodes, thereby enhancing the extraction of essential structural and semantic KG traits. Aggregation (AGG) offers a summarized view of a node’s local context by compiling neighbor information into a concise representation. Lastly, the Self-loop (SELF) mechanism ensures the preservation of intrinsic node features amidst the learning process, even in the face of intricate intra-graph interactions.

Other EA Methods. Certain EA approaches transcend the above bounds. PARIS (Suchanek et al., 2011) is a representative non-neural EA method, which aligns entities in KGs using iterative probabilistic techniques, considering entity names and relations. Fualign (Wang et al., 2023) unifies two KGs based on trained entity pairs, learning a collective representation. BERT-INT (Tang et al., 2020) addresses KG heterogeneity by solely leveraging side information, outperforming existing datasets. However, its exploration of KG heterogeneity remains limited to conventional datasets, not capturing the nuances of practical HHKGs.
In the context of EA in HHKGs, the efficacy of these methods and mechanisms may be influenced by various factors, such as the level of heterogeneity, the number of overlapping entities, and the quality and quantity of structure and semantic information. This highlights the need for an in-depth analysis in HHKG settings, which will be the focus of our subsequent experimental investigation. This investigation is expected to shed light on the real progress made by EA methods and guide future research toward more effective and robust solutions for real-world EA challenges.
3. Experimental Study
In this section, we delve into an experimental study to verify the effectiveness of representative EA methods, aiming to shed light on three main questions, which are detailed below:
-
•
Q1: What is the effect of existing EA methods on HHKGs?
-
•
Q2: Do GNNs really bring performance gain? Which components of GNNs play a key role in EA performance?
In our experiment, we utilized two classic datasets, DBP15K(EN-FR) and DBP-WIKI, and introduced our new datasets: ICEWS-WIKI and ICEWS-YAGO, detailed in Table 1. By reviewing EA methods, we categorized them based on input features, embedding modules, and training strategies, subsequently selecting 13 representative models. These include translation-based methods such as MTransE (Chen et al., 2017) AlignE (Sun et al., 2018), and BootEA (Sun et al., 2018), GNN-based methods like GCN-Align (Wang et al., 2018), RDGCN (Chen et al., 2022), TREA (Xu et al., 2022), TEA-GNN (Xu et al., 2021), STEA (Cai et al., 2022), and Dual-AMN (Mao et al., 2021), and several other methods like PARIS (Suchanek et al., 2011), BERT (Devlin et al., 2019) and FuAlign (Wang et al., 2023). We adopted two main evaluation metrics: Hits@k () and Mean Reciprocal Rank (MRR). More intricate settings can be found in A.5.
Models Settings DBP15K(EN-FR) DBP-WIKI ICEWS-WIKI ICEWS-YAGO Struc. Name. Temp. Semi. Hits@1 Hits@10 MRR Hits@1 Hits@10 MRR Hits@1 Hits@10 MRR Hits@1 Hits@10 MRR Trans. MTransE 0.247 0.577 0.360 0.281 0.520 0.363 0.021 0.158 0.068 0.012 0.084 0.040 AlignE ✓ 0.481 0.824 0.599 0.566 0.827 0.655 0.057 0.261 0.122 0.019 0.118 0.055 BootEA ✓ ✓ 0.653 0.874 0.731 0.748 0.898 0.801 0.072 0.275 0.139 0.020 0.120 0.056 GNN GCN-Align ✓ 0.411 0.772 0.530 0.494 0.756 0.590 0.046 0.184 0.093 0.017 0.085 0.038 RDGCN ✓ ✓ 0.873 0.950 0.901 0.974 0.994 0.980 0.064 0.202 0.096 0.029 0.097 0.042 Dual-AMN(basic) ✓ 0.756 0.948 0.827 0.786 0.952 0.848 0.077 0.285 0.143 0.032 0.147 0.069 Dual-AMN(semi) ✓ ✓ 0.840 0.965 0.888 0.869 0.969 0.908 0.037 0.188 0.087 0.020 0.093 0.045 Dual-AMN(name) ✓ ✓ 0.954 0.994 0.970 0.983 0.996 0.991 0.083 0.281 0.145 0.031 0.144 0.068 TEA-GNN ✓ ✓ - - - - - - 0.063 0.253 0.126 0.025 0.135 0.064 TREA ✓ ✓ - - - - - - 0.081 0.302 0.155 0.033 0.150 0.072 STEA ✓ ✓ ✓ - - - - - - 0.079 0.292 0.152 0.033 0.147 0.073 Other BERT ✓ 0.937 0.985 0.956 0.941 0.980 0.963 0.546 0.687 0.596 0.749 0.845 0.784 FuAlign ✓ ✓ 0.936 0.988 0.955 0.980 0.991 0.986 0.257 0.570 0.361 0.326 0.604 0.423 BERT-INT ✓ ✓ 0.990 0.997 0.993 0.996 0.997 0.996 0.561 0.700 0.607 0.756 0.859 0.793 PARIS ✓ ✓ 0.902 - - 0.963 - - 0.672 - - 0.687 - - Ours Simple-HHEA ✓ ✓ 0.948 0.991 0.960 0.967 0.988 0.979 0.720 0.872 0.754 0.847 0.915 0.870 Simple-HHEA ✓ ✓ ✓ 0.959 0.995 0.972 0.975 0.991 0.988 0.639 0.812 0.697 0.749 0.864 0.775
3.1. Results and Discussion
To answer Q1, we conducted a detailed analysis in four dimensions (datasets, training strategies, embedding modules, and input features). The main experiment results are shown in Table 2.
From the perspective of datasets, baselines that generally perform well on DBP15K(EN-FR) and DBP-WIKI decrease significantly on new datasets, especially GNN-based and translation-based methods. In practice, existing EA methods are difficult to reach the required accuracy performance for applications on HHKGs.
From the perspective of training strategies, we found that the semi-supervised methods (i.e., BootEA, Dual-AMN(semi), and STEA) did not improve performance compared to their basic models (i.e., AlignE and Dual-AMN(basic)), indicating that the existing semi-supervised strategies are not suitable for HHKGs.
From the perspective of embedding modules, neither translation-based methods nor GNN-based methods struggle to capture the correlation between HHKGs, thus the performance of these models is disappointing on new datasets. Especially, the performances of GNN-based methods, which demonstrate the superiority on the DBP15K(EN-FR) dataset, drop sharply on HHKGs. For example, the SOTA GNN-based model Dual-AMN(basic) (Mao et al., 2021), which performs well on the DBP15K datasets, but only achieved MRR of 0.143 and 0.069 on ICEWS-WIKI and ICEWS-YAGO respectively. The huge performance drops of GNN-based methods responses to Q2. In previous EA datasets, KGs have similar structure information and thus GNN-based EA methods can easily exploit the structure similarities between entity pairs for alignment purposes. By contrast, a pair of identical entities often have diverse neighborhoods in two HHKGs, resulting in poor performances. BERT and BERT-INT, which mainly leverages side information instead of aggregating neighbors, perform better among others (attains MRR of 0.607 and 0.793). FuAlign, which adopt the translation mechanism, performs poorly on HHKGs. Despite not utilizing neural mechanisms, PARIS performed competitively on HHKGs.
From the perspective of input features, the models are capable of utilizing entity name information except Dual-AMN(name) outperform the others, indicating to some extent the importance of entity name information in the context of EA models. Specifically, BERT achieves decent results (MRRs of 0.596 and 0.784) on ICEWS-WIKI and ICEWS-YAGO datasets by directly inputting name embeddings generated by BERT into CSLS similarity (Lample et al., 2018). However, RDGCN and Dual-AMN(name), which also utilize entity name information, perform badly on HHKG datasets. BERT-INT and FuAlign use entity name information without a GNN framework, notably, they perform much better than existing GNN-based EA models, proving that the aggregation mechanism limits their performance on our HHKG datasets. The utilization of structure information on HHKGs does not bring promising performance gains. Whether structure information is essential for EA on HHKGs still remains to be explored. In terms of temporal information, TREA outperforms Dual-AMN with temporal information utilization, proving that temporal information is also valuable in EA tasks when available.
Generally, the efficacy of existing methods is constrained, especially when applied to HHKGs. Specifically, entity name and temporal information play critical roles in alignment, offering a necessary foundation for entity matching across varied KGs. However, under high heterogeneity, the effectiveness of structure information decreases, presenting challenges for traditional EA methods.
3.2. GNN-based EA methods on HHKGs
To answer Q2 and delve deeper into the performance influence of key components of GNNs (i.e., MSG, ATT, AGG, SELF) mentioned in Section 2.3, we further take the SOTA GNN-based method: Dual-AMN as an example, and devised case studies and ablation studies.
Messaging passing (MSG). To explore the influence of MSG, we conduct case studies as shown in Figure 4.

The experiment reveal that as the structure similarity between entities decreases and their neighbors with alignment labels becomes different, the GNN-based Dual-AMN(name) model can hardly leverage structure information through message passing for EA. From the perspective of label propagation, the performance of GNNs deteriorates because they struggle to propagate the correct alignment labels from pre-aligned entity pairs to unobserved entities.
We also conduct ablation studies to verify the effectiveness of ATT, AGG, and SELF on HHKGs, as shown in Table 3.
| Settings | ICEWS-WIKI | ICEWS-YAGO | ||||
|---|---|---|---|---|---|---|
| Hits@1 | Hits@10 | MRR | Hits@1 | Hits@10 | MRR | |
| Dual-AMN(basic) | 0.077 | 0.285 | 0.143 | 0.032 | 0.147 | 0.069 |
| w/o ATT | 0.049 | 0.241 | 0.112 | 0.021 | 0.102 | 0.049 |
| w/o AGG | 0.000 | 0.001 | 0.001 | 0.000 | 0.001 | 0.001 |
| w/o SELF | 0.072 | 0.231 | 0.136 | 0.031 | 0.135 | 0.068 |
| w/o ATT, AGG, SELF | 0.000 | 0.001 | 0.001 | 0.000 | 0.001 | 0.001 |
| Dual-AMN(name) | 0.083 | 0.281 | 0.145 | 0.031 | 0.144 | 0.068 |
| w/o ATT | 0.053 | 0.246 | 0.113 | 0.020 | 0.108 | 0.050 |
| w/o AGG | 0.622 | 0.796 | 0.691 | 0.804 | 0.876 | 0.831 |
| w/o SELF | 0.082 | 0.288 | 0.151 | 0.031 | 0.140 | 0.066 |
| w/o ATT, AGG, SELF | 0.471 | 0.631 | 0.528 | 0.770 | 0.863 | 0.805 |
Attention (ATT). It plays a critical role in both scenarios, emphasizing the significance of certain nodes and edges in the graph, thus contributing to more accurate alignment decisions.
Aggregation (AGG). The experiment results underscore a dual role of the AGG, which manifests differently depending on the availability of entity name information for EA. In scenarios where entity name information is absent, the elimination of the aggregation mechanism causes a considerable decline in performance. Conversely, when name information is available, the removal of the aggregation mechanism surprisingly improves the model’s performance. This improvement could be attributed to the aggregation mechanism’s propensity to introduce noise within HHKGs, which can obscure the valuable cues embedded in the entity name.
Self-loop (SELF). The self-loop mechanism’s marginal influence suggests its role might be overshadowed by other components, especially in a highly heterogeneous context. However, after removing AGG, the self-loop mechanism serves a critical function by maintaining each node’s individual features, acting as a form of identity preservation and feature selection in the face of HHKGs.
Through this analysis, it becomes evident that major factor causing a drastic decrease in performance is the challenge faced by the message passing and aggregation mechanisms of GNNs on HHKGs. These mechanisms struggle to propagate and aggregate valuable information amidst the influx of unrelated data. This revelation highlights the need for more in-depth analysis and more nuanced, data-aware approaches in model design and applications, especially when dealing with highly heterogeneous settings.
4. Toward Practical EA Methods
Incorporating the above insights, our consideration in this section is to address two critical questions: What constitutes an effective EA model for applications, and which factor is impactful in practical scenarios? To answer it, we embark on a comprehensive examination by implementing a Simple but effective Highly Heterogeneous Entity Alignment method, namely Simple-HHEA.
4.1. Model Details for Simple-HHEA
Entity Name Encoder. We first adopted BERT (Devlin et al., 2019) to encode the entity names into initial embeddings. Then we introduced a feature whitening transformation proposed by (Su et al., 2021) to reduce the dimension of the initial embeddings. The integration of BERT and the whitening layer allows the model to effectively capture the semantic meaning of entities, without requiring additional supervision. Finally, we adopted a learnable linear transformation to get the transformed entity name embeddings .
Entity Time Encoder is designed to verify the power of temporal information, building upon evidence of its effectiveness as demonstrated in the comparative experiments of Dual-AMN and TREA. Simple-HHEA first annotates the time occurrence of each entity according to facts in KGs. Specifically, for our proposed HHKG datasets, the time set ranges from 1995 to 2021 (in months) of KGs. The encoder can obtain a binary temporal vector for entity denoted as , where if facts involving happen at the time point, otherwise . We adopted Time2Vec (Goel et al., 2020) to obtain the learnable time representation , expressed as:
| (2) |
where is the element of , here we adopt as the activation function to capture the continuity and periodicity of time, s and s are learnable parameters.
Then, the encoder sums the time representations obtained by Time2Vec of the entity occurrence time points, and gets entity time embeddings through a learnable linear transformation . Unlike other methods that strictly correspond to time, Time2Vec can model the cyclical patterns inherent in the temporal data.
Simple-HHEA+. To study the use of the structure information in EA between HHKGs, based on basic Simple-HHEA, we introduced an entity structure encoder, which is different from the aggregation mechanism for modeling structure information. To synchronously model the one-hop and multi-hop relations, the encoder employs a biased random walk with a balance between BFS and DFS (Wang et al., 2023). Denote as the selected node at th step of random walks, and as the generated path. The probability of an entity being selected is defined as:
| (3) |
where denotes entity ’s 1-hop neighbors except ; is the length of the shortest path between and ; is a hyper-parameter to make a trade-off between BFS and DFS (Wang et al., 2023). Once an entity is selected, the relation in the triple is selected simultaneously.
Then, the Skip-gram model together with a linear transformation are employed to learn entity embeddings based on the generated random walk paths to capture structure information of KGs. It eliminates the aggregation or message-passing mechanisms and doesn’t require supervision.
The linear transformations adopted in each encoder bear similarities to the self-loop mechanism in GNNs, a mechanism that has been validated for its effectiveness in previous experiments. By employing linear transformations, the Simple-HHEA model aims to be adapted to different data situations. Finally, the multi-view embeddings of entities are calculated by concatenating different kinds of embeddings, expressed as:
where denoted the concatenation operation.
We adopt Margin Ranking Loss as the loss function for training, and Cross-domain Similarity Local Scaling (CSLS) (Lample et al., 2018) as the distance metric to measure similarities between entity embeddings.
4.2. In-depth Analyses of EA on HHKGs
This section aims to uncover the essential EA model needed in practical scenarios through a comprehensive comparison of Simple-HHEA, Simple-HHEA+, and other baseline methods.
Simple-HHEA vs. baseline methods. As a critical tool for the in-depth analysis in this section, we will first examine the performance of Simple-HHEA. Table 2 shows the comparison results. Compared with the current SOTA methods: BERT-INT and PARIS, Simple-HHEA and Simple-HHEA+ achieve competitive performances on the previous datasets: DBP15K(EN-DE) and DBP-WIKI. For the two HHKG datasets, we can observe that Simple-HHEA and Simple-HHEA outperform baselines (including BERT-INT) by Hits@1 on ICEWS-WIKI, and Hits@1 on ICEWS-YAGO.
The introduction of Simple-HHEA aims to guide the design of future EA models. While it is straightforward in design, experimental comparisons affirm that a well-conceived simple model can also achieve commendable results. We also conduct an efficiency analysis as shown in Table 4. It corroborates the efficiency superiority of Simple-HHEA over baselines, which indicates that enhancing model efficiency through a simpler design is also essential in practical, rather than pursuing accuracy without considering complexity.
| Model | Number of Parameters |
|---|---|
| MTransE | |
| AlignE | |
| BootEA | |
| GCN-Align | |
| GCN-Align | |
| TEA-GNN | |
| TREA | |
| STEA | |
| Simple-HHEA |
Ablation Studies. We performed ablation studies by ablating Simple-HHEA to analyze how and when each component of it adds benefit to the EA task as shown in Table 5. It is worth noting that the whitening strategy contributes significantly (5.8% and 6.1% improvement on Hits@1) to the great performance of our model, and the temporal information also brings the performance improvement (1.9% and 1.8% on Hits@1). By contrast, the introduction of structure information of Simple-HHEA+ degrades the performance.
| Model | DBP15K(EN-FR) | DBP-WIKI | ICEWS-WIKI | ICEWS-YAGO | ||||
|---|---|---|---|---|---|---|---|---|
| Hits@1 | MRR | Hits@1 | MRR | Hits@1 | MRR | Hits@1 | MRR | |
| Simple-HHEA | 0.948 | 0.960 | 0.967 | 0.979 | 0.720 | 0.754 | 0.847 | 0.870 |
| Temp | - | - | - | - | 0.701 | 0.748 | 0.829 | 0.857 |
| Whitening | 0.923 | 0.942 | 0.930 | 0.956 | 0.632 | 0.683 | 0.786 | 0.820 |
| Simple-HHEA+ | 0.959 | 0.972 | 0.975 | 0.988 | 0.639 | 0.697 | 0.749 | 0.775 |
Questioning whether entity name information always holds value, and if structure information is indeed ineffective on HHKGs, we conducted sensitivity experiments.
The impact of structure information. To ponder how structure information affects EA on HHKGs, we selected several SOTA GNN-based methods (which mainly leverage structure information) and Simple-HHEA, and then randomly masked proportions (0% ~80%) of facts in KGs to mimic different graph structure conditions.
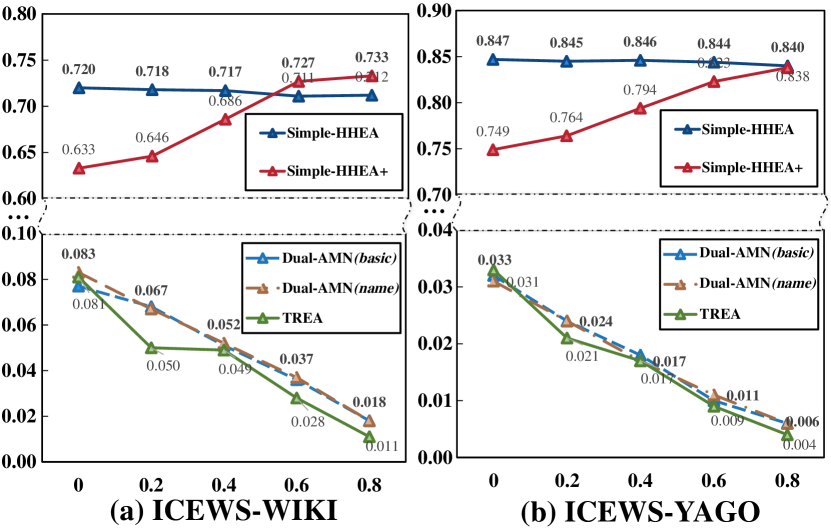
As shown in Figure 5, the mask of structure information affects the overall performance of GNN-based EA methods on both datasets with the mask ratio of facts increasing. This phenomenon proves that GNN-based EA methods’ performance mainly depends on the structure information, even on HHKGs. The structure information is difficult to exploit in HHKGs due to their structure dissimilarity, while they still learn a part of meaningful patterns of the HHKGs’ structural information for EA, which indicates that existing GNN-based EA methods still have much room for improvement by better leveraging structure information in HHKGs.
For Simple-HHEA, with the mask ratio of graph structure gradually increasing, the temporal information is lost, resulting in the performance decreases of Simple-HHEA. It is worth noting that as the mask ratio of structure information increases, the performance of Simple-HHEA+ improves. At a mask ratio of 60%, Simple-HHEA+ even outperforms the basic version. This reflects that in HHKGs, the overly complex and highly heterogeneous structure information will introduce additional noise, and distract the structure correlation mining of Simple-HHEA+ for EA.
In conclusion, the structure information should not be ignored, especially when the quality of other types of information cannot be guaranteed. Future EA methods should consider strategies for pruning and extracting valuable cues from highly heterogeneous structural data for effective EA.
The impact of entity name information. The phenomenon observed in Table 2 is that both GNN-based methods (e.g., Dual-AMN(name)) and other methods (e.g., BERT-INT, FuAlign, Simple-HHEA) can utilize same entity name information, but their performance varies widely. To explore the role of the entity name information for EA, we randomly mask a proportion (0% ~100%) of entity names, for mimicking different entity name conditions.

As shown in Figure 6, while the mask ratio of entity names gradually increases, the performances of the EA methods which highly rely on entity name information, drop sharply. For BERT-INT, although it uses neighbor information in its mechanism setting, it still needs to filter candidate entities through entity name similarities, so the performance decreases vividly. In addition to entity name information, FuAlign learns structure information through TransE (Bordes et al., 2013). Therefore, when entity name information is gradually masked, its drop is much smaller than BERT-INT, which indicates that the use of structure information plays a more prominent role in FuAlign, and slows down the performance degradation. Dual-AMN(name)’s performance does not change significantly when the entity name information is masked, which shows that Dual-AMN(name) can leverage structure information to achieve a stable performance when entity name information is absent.
As the mask ratio of entity name gradually increases, the basic Simple-HHEA also drops sharply like other baselines which highly rely on the quantity of entity name information. Notably, as the quality of entity name information declines, the role of the entity structure encoder in Simple-HHEA+ becomes prominent, even surpassing the basic version when the mask ratio is . It indicates that the structure information should not be ignored in EA, especially when the quality of other information can not be guaranteed.
We further designed experiments to explore the performance of Simple-HHEA+ when both name and structure information are changed. As shown in Figure 7, when the quality of entity name information is high (the name mask ratio is less than 80%), the performance of the model decreases when reducing the mask ratio of the structure information; Notably, when the quality of entity name information becomes very low (mask ratio reaches 80%), the above phenomenon is reversed, and the performance increases when introducing entity structure information. This phenomenon reflects that when the quality of different types of information changes, our proposed Simple-HHEA+ can also achieve self-adaptation through simple learnable linear transformations.
In summary, the design of effective EA methods requires the ability to exploit various types of information and adapt to different levels of information quality.

5. Insights
5.1. From the Perspective of Datasets
It’s crucial to develop more datasets that closely resemble real-world entity alignment scenarios. As analyzed in Section 2.1, designing datasets that model different practical conditions is essential for researching practical EA methods. The two datasets proposed in this paper focus on the highly heterogeneous nature of KGs in EA. The reflections on EA method design based on these datasets lead us to conclude that datasets are foundational to EA research before designing new methods.
5.2. From the Perspective of Method Design
Attention could be given to the design of message propagation and aggregation mechanisms in GNNs or to proposing new EA paradigms different from existing GNN approaches. Detailed analysis in Sections 3.2 and 4.2 reveals limitations in existing message propagation and aggregation mechanisms, especially in highly heterogeneous KG scenarios. Two directions can be considered: designing new GNN methods with a focus on MSG, ATT, AGG, and SELF mechanisms, or proposing entirely new paradigms different from existing GNN schemes.
(1) For new GNN method design, experiments in Sections 3.2 and 4.2 suggest insights for future GNN-based EA method design. Based on Figure 4, we find that existing GNNs struggle with accurate alignment in highly heterogeneous structural scenarios. Additionally, as shown in Figure 5, reducing structural information surprisingly improves the performance of Simple-HHEA, even surpassing versions that don’t utilize structural information. This counterintuitive phenomenon can guide us in designing new GNN methods’ message propagation and aggregation modules. For instance, models could automatically prune neighbors or combine relational and temporal information to design new attention mechanisms that identify valuable neighbors for EA, reducing the negative impact of aggregating noisy information. Furthermore, analysis of the Self-loop mechanism in Section 3.2 highlights its value in preserving node-specific information and feature selection. Optimizing this mechanism in new GNN designs could enhance its feature selection capabilities and improve EA effectiveness.
(2) For proposing new paradigms different from existing GNN schemes, our experiments reveal that various non-GNN models, even traditional probabilistic models like PARIS, achieve good results. Thus, EA method design need not be confined to GNN architectures. Notably, recent studies like BERT-INT and Fualign have also acknowledged this, though they still have limitations. This direction offers rich research potential, such as combining neural-symbolic methods (noting PARIS’s competitive performance in our experiments) and integrating knowledge graphs with large language models.
5.3. From the Perspective of Feature Utilization
Effective utilization of name information can mitigate the negative impacts of high heterogeneity in graphs, but the use of structural and temporal information, especially when the quality of name information is uncertain, could not be overlooked. EA methods need to adapt to varying feature quality conditions. In highly heterogeneous knowledge graphs, effective utilization of name information significantly improves EA performance. However, combining separate and comprehensive analyses of each feature type in Section 4.2 of EA on HHKGs reveals the importance of utilizing structural and temporal information. Simultaneously, designing adaptive feature fusion modules to face different feature conditions and maintain stable performance is essential.
6. Conclusion and Future Work
In this paper, we re-examine the existing benchmark EA datasets, and construct two new datasets, which aim to study EA on HHKGs. Then, we rethink the existing EA methods with extensive experimental studies, and shed light on the limitations resulting from the oversimplified settings of previous EA datasets. To explore what EA methodology is genuinely beneficial in applications, we undertake an in-depth analysis by implementing a simple but effective approach: Simple-HHEA. The extensive experiments show that the success of future EA models in practice hinges on adaptability and efficiency under diverse information quality scenarios, and their ability to discern patterns in HHKGs.
In the future, building upon the analysis of this paper, we summarize several exciting directions:
More high-quality EA datasets. There is a need for more datasets that closely mimic practical EA scenarios. As analyzed in Section 2.1, designing datasets that model various real-world conditions is crucial for researching practical EA methods. Future research could focus on proposing high-quality datasets around application needs to promote the field of EA.
More advanced methods. Attention could be paid to the design of message propagation and aggregation mechanisms in GNNs, or proposing new EA paradigms different from existing GNN methods. Our detailed analysis in Sections 3.2 and 4.2 reveals limitations in current message propagation and aggregation mechanisms, especially in highly heterogeneous graph scenarios. Future directions include: (1) Designing new GNN methods that optimize information propagation, attention mechanisms, and information aggregation, to enhance the ability to identify valuable external information for EA; (2) Proposing new paradigms, such as combining neural-symbolic methods or integrating knowledge graphs with large language models.
More sophisticated feature utilization. Design methods that can adapt to different information quality conditions in real-world scenarios and combine various types of information (e.g., temporal, multimodal) for EA. Future designs could focus on adaptive feature fusion modules to accommodate different feature conditions while maintaining stable performance.
More application scenarios. The datasets proposed in our paper are worth exploring further for both academic and practical application value. Beyond EA research, our datasets, such as ICEWS-WIKI/YAGO, have significant value for cross-graph inference and temporal knowledge graph completion and prediction. Additionally, as our research originated from practical application challenges, future work will also explore more application scenarios to promote practical implementation.
References
- (1)
- Balog and Kenter (2019) Krisztian Balog and Tom Kenter. 2019. Personal Knowledge Graphs. In Proceedings of the 2019 ACM SIGIR International Conference on Theory of Information Retrieval. ACM, 217–220. https://doi.org/10.1145/3341981.3344241
- Balsebre et al. (2022) Pasquale Balsebre, Dezhong Yao, Gao Cong, and Zhen Hai. 2022. Geospatial Entity Resolution. In Proceedings of the ACM Web Conference 2022. ACM, 3061–3070. https://doi.org/10.1145/3485447.3512026
- Bordes et al. (2013) Antoine Bordes, Nicolas Usunier, Alberto García-Durán, Jason Weston, and Oksana Yakhnenko. 2013. Translating Embeddings for Modeling Multi-relational Data. In Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013. Proceedings of a meeting held December 5-8, 2013, Lake Tahoe, Nevada, United States, Christopher J. C. Burges, Léon Bottou, Zoubin Ghahramani, and Kilian Q. Weinberger (Eds.). 2787–2795. https://proceedings.neurips.cc/paper/2013/hash/1cecc7a77928ca8133fa24680a88d2f9-Abstract.html
- Cai et al. (2022) Li Cai, Xin Mao, Meirong Ma, Hao Yuan, Jianchao Zhu, and Man Lan. 2022. A Simple Temporal Information Matching Mechanism for Entity Alignment between Temporal Knowledge Graphs. In Proceedings of the 29th International Conference on Computational Linguistics. International Committee on Computational Linguistics, Gyeongju, Republic of Korea, 2075–2086. https://aclanthology.org/2022.coling-1.181
- Cao et al. (2019) Yixin Cao, Zhiyuan Liu, Chengjiang Li, Zhiyuan Liu, Juanzi Li, and Tat-Seng Chua. 2019. Multi-Channel Graph Neural Network for Entity Alignment. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics. Association for Computational Linguistics, Florence, Italy, 1452–1461. https://doi.org/10.18653/v1/P19-1140
- Chen et al. (2017) Muhao Chen, Yingtao Tian, Mohan Yang, and Carlo Zaniolo. 2017. Multilingual Knowledge Graph Embeddings for Cross-lingual Knowledge Alignment. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI 2017, Melbourne, Australia, August 19-25, 2017, Carles Sierra (Ed.). ijcai.org, 1511–1517. https://doi.org/10.24963/ijcai.2017/209
- Chen et al. (2022) Zhibin Chen, Yuting Wu, Yansong Feng, and Dongyan Zhao. 2022. Integrating Manifold Knowledge for Global Entity Linking with Heterogeneous Graphs. Data Intelligence 4, 1 (2022), 20–40. https://doi.org/10.1162/dint_a_00116
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers). Association for Computational Linguistics, Minneapolis, Minnesota, 4171–4186. https://doi.org/10.18653/v1/N19-1423
- Fu et al. (2020) Bin Fu, Yunqi Qiu, Chengguang Tang, Yang Li, Haiyang Yu, and Jian Sun. 2020. A survey on complex question answering over knowledge base: Recent advances and challenges. ArXiv preprint abs/2007.13069 (2020). https://arxiv.org/abs/2007.13069
- García-Durán et al. (2018) Alberto García-Durán, Sebastijan Dumančić, and Mathias Niepert. 2018. Learning Sequence Encoders for Temporal Knowledge Graph Completion. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Brussels, Belgium, 4816–4821. https://doi.org/10.18653/v1/D18-1516
- Goel et al. (2020) Rishab Goel, Seyed Mehran Kazemi, Marcus Brubaker, and Pascal Poupart. 2020. Diachronic Embedding for Temporal Knowledge Graph Completion. In The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, February 7-12, 2020. AAAI Press, 3988–3995. https://aaai.org/ojs/index.php/AAAI/article/view/5815
- Kipf and Welling (2017) Thomas N. Kipf and Max Welling. 2017. Semi-Supervised Classification with Graph Convolutional Networks. In 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings. OpenReview.net. https://openreview.net/forum?id=SJU4ayYgl
- Lacroix et al. (2018) Timothée Lacroix, Nicolas Usunier, and Guillaume Obozinski. 2018. Canonical Tensor Decomposition for Knowledge Base Completion. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, July 10-15, 2018 (Proceedings of Machine Learning Research, Vol. 80), Jennifer G. Dy and Andreas Krause (Eds.). PMLR, 2869–2878. http://proceedings.mlr.press/v80/lacroix18a.html
- Lample et al. (2018) Guillaume Lample, Alexis Conneau, Marc’Aurelio Ranzato, Ludovic Denoyer, and Hervé Jégou. 2018. Word translation without parallel data. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net. https://openreview.net/forum?id=H196sainb
- Leone et al. (2022) Manuel Leone, Stefano Huber, Akhil Arora, Alberto García-Durán, and Robert West. 2022. A critical re-evaluation of neural methods for entity alignment. Proceedings of the VLDB Endowment 15, 8 (2022), 1712–1725. https://doi.org/10.14778/3529337.3529355
- Lin et al. (2022) Xueyuan Lin, Chengjin Xu, Fenglong Su, Gengxian Zhou, Tianyi Hu, Ningyuan Li, Mingzhi Sun, Haoran Luo, et al. 2022. TFLEX: Temporal Feature-Logic Embedding Framework for Complex Reasoning over Temporal Knowledge Graph. ArXiv preprint abs/2205.14307 (2022). https://arxiv.org/abs/2205.14307
- Mao et al. (2021) Xin Mao, Wenting Wang, Yuanbin Wu, and Man Lan. 2021. Boosting the Speed of Entity Alignment 10 ×: Dual Attention Matching Network with Normalized Hard Sample Mining. In Proceedings of the Web Conference 2021. ACM, 821–832. https://doi.org/10.1145/3442381.3449897
- Mao et al. (2020a) Xin Mao, Wenting Wang, Huimin Xu, Man Lan, and Yuanbin Wu. 2020a. Mraea. In Proceedings of the 13th International Conference on Web Search and Data Mining. ACM, 420–428. https://doi.org/10.1145/3336191.3371804
- Mao et al. (2020b) Xin Mao, Wenting Wang, Huimin Xu, Yuanbin Wu, and Man Lan. 2020b. Relational Reflection Entity Alignment. In CIKM ’20: The 29th ACM International Conference on Information and Knowledge Management, Virtual Event, Ireland, October 19-23, 2020, Mathieu d’Aquin, Stefan Dietze, Claudia Hauff, Edward Curry, and Philippe Cudré-Mauroux (Eds.). ACM, 1095–1104. https://doi.org/10.1145/3340531.3412001
- Mavromatis et al. (2022) Costas Mavromatis, Prasanna Lakkur Subramanyam, Vassilis N. Ioannidis, Adesoji Adeshina, Phillip R. Howard, Tetiana Grinberg, Nagib Hakim, and George Karypis. 2022. TempoQR: Temporal Question Reasoning over Knowledge Graphs. In Thirty-Sixth AAAI Conference on Artificial Intelligence, AAAI 2022, Thirty-Fourth Conference on Innovative Applications of Artificial Intelligence, IAAI 2022, The Twelveth Symposium on Educational Advances in Artificial Intelligence, EAAI 2022 Virtual Event, February 22 - March 1, 2022. AAAI Press, 5825–5833. https://ojs.aaai.org/index.php/AAAI/article/view/20526
- Nayyeri et al. (2021) Mojtaba Nayyeri, Chengjin Xu, Franca Hoffmann, Mirza Mohtashim Alam, Jens Lehmann, and Sahar Vahdati. 2021. Knowledge Graph Representation Learning using Ordinary Differential Equations. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Online and Punta Cana, Dominican Republic, 9529–9548. https://doi.org/10.18653/v1/2021.emnlp-main.750
- Reinanda et al. (2020) Ridho Reinanda, Edgar Meij, Maarten de Rijke, et al. 2020. Knowledge graphs: An information retrieval perspective. Foundations and Trends® in Information Retrieval 14, 4 (2020), 289–444.
- Saxena et al. (2021) Apoorv Saxena, Soumen Chakrabarti, and Partha Talukdar. 2021. Question Answering Over Temporal Knowledge Graphs. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers). Association for Computational Linguistics, Online, 6663–6676. https://doi.org/10.18653/v1/2021.acl-long.520
- Su et al. (2021) Jianlin Su, Jiarun Cao, Weijie Liu, and Yangyiwen Ou. 2021. Whitening sentence representations for better semantics and faster retrieval. ArXiv preprint abs/2103.15316 (2021). https://arxiv.org/abs/2103.15316
- Suchanek et al. (2011) Fabian M Suchanek, Serge Abiteboul, and Pierre Senellart. 2011. PARIS: Probabilistic Alignment of Relations, Instances, and Schema. Proceedings of the VLDB Endowment 5, 3 (2011).
- Sun et al. (2017) Zequn Sun, Wei Hu, and Chengkai Li. 2017. Cross-lingual entity alignment via joint attribute-preserving embedding. In International Semantic Web Conference. Springer, 628–644.
- Sun et al. (2018) Zequn Sun, Wei Hu, Qingheng Zhang, and Yuzhong Qu. 2018. Bootstrapping Entity Alignment with Knowledge Graph Embedding. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI 2018, July 13-19, 2018, Stockholm, Sweden, Jérôme Lang (Ed.). ijcai.org, 4396–4402. https://doi.org/10.24963/ijcai.2018/611
- Sun et al. (2020) Zequn Sun, Qingheng Zhang, Wei Hu, Chengming Wang, Muhao Chen, Farahnaz Akrami, and Chengkai Li. 2020. A benchmarking study of embedding-based entity alignment for knowledge graphs. Proceedings of the VLDB Endowment 13, 12 (2020), 2326–2340. https://doi.org/10.14778/3407790.3407828
- Tang et al. (2020) Xiaobin Tang, Jing Zhang, Bo Chen, Yang Yang, Hong Chen, and Cuiping Li. 2020. BERT-INT: A BERT-based Interaction Model For Knowledge Graph Alignment. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI 2020, Christian Bessiere (Ed.). ijcai.org, 3174–3180. https://doi.org/10.24963/ijcai.2020/439
- Velickovic et al. (2018) Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. 2018. Graph Attention Networks. In 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net. https://openreview.net/forum?id=rJXMpikCZ
- Wang et al. (2023) Chenxu Wang, Zhenhao Huang, Yue Wan, Junyu Wei, Junzhou Zhao, and Pinghui Wang. 2023. FuAlign: Cross-lingual entity alignment via multi-view representation learning of fused knowledge graphs. Inform. Fusion 89 (2023), 41–52. https://doi.org/10.1016/j.inffus.2022.08.002
- Wang et al. (2018) Zhichun Wang, Qingsong Lv, Xiaohan Lan, and Yu Zhang. 2018. Cross-lingual Knowledge Graph Alignment via Graph Convolutional Networks. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Brussels, Belgium, 349–357. https://doi.org/10.18653/v1/D18-1032
- Xu et al. (2020a) Chengjin Xu, Mojtaba Nayyeri, Fouad Alkhoury, Hamed Shariat Yazdi, and Jens Lehmann. 2020a. TeRo: A Time-aware Knowledge Graph Embedding via Temporal Rotation. In Proceedings of the 28th International Conference on Computational Linguistics. International Committee on Computational Linguistics, Barcelona, Spain (Online), 1583–1593. https://doi.org/10.18653/v1/2020.coling-main.139
- Xu et al. (2019) Chengjin Xu, Mojtaba Nayyeri, Fouad Alkhoury, Hamed Shariat Yazdi, and Jens Lehmann. 2019. Temporal knowledge graph embedding model based on additive time series decomposition. ArXiv preprint abs/1911.07893 (2019). https://arxiv.org/abs/1911.07893
- Xu et al. (2020b) Chengjin Xu, Mojtaba Nayyeri, Yung-Yu Chen, and Jens Lehmann. 2020b. Knowledge Graph Embeddings in Geometric Algebras. In Proceedings of the 28th International Conference on Computational Linguistics. International Committee on Computational Linguistics, Barcelona, Spain (Online), 530–544. https://doi.org/10.18653/v1/2020.coling-main.46
- Xu et al. (2021) Chengjin Xu, Fenglong Su, and Jens Lehmann. 2021. Time-aware Graph Neural Network for Entity Alignment between Temporal Knowledge Graphs. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Online and Punta Cana, Dominican Republic, 8999–9010. https://doi.org/10.18653/v1/2021.emnlp-main.709
- Xu et al. (2022) Chengjin Xu, Fenglong Su, Bo Xiong, and Jens Lehmann. 2022. Time-aware Entity Alignment using Temporal Relational Attention. In Proceedings of the ACM Web Conference 2022. ACM, 788–797. https://doi.org/10.1145/3485447.3511922
- Yang et al. (2022) Yu Yang, Jiangxu Lin, Xiaolian Zhang, and Meng Wang. 2022. Pkg. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 3334–3338. https://doi.org/10.1145/3477495.3531671
- Zhang et al. (2022) Rui Zhang, Bayu Distiawan Trisedya, Miao Li, Yong Jiang, and Jianzhong Qi. 2022. A benchmark and comprehensive survey on knowledge graph entity alignment via representation learning. The VLDB Journal 31, 5 (2022), 1143–1168. https://doi.org/10.1007/s00778-022-00747-z
- Zhao et al. (2020) X. Zhao, W. Zeng, J. Tang, W. Wang, and F. Suchanek. 2020. An Experimental Study of State-of-the-Art Entity Alignment Approaches. IEEE Transactions on Knowledge and Data Engineering PP, 99 (2020), 1–1.
- Zhu et al. (2017) Hao Zhu, Ruobing Xie, Zhiyuan Liu, and Maosong Sun. 2017. Iterative Entity Alignment via Joint Knowledge Embeddings. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI 2017, Melbourne, Australia, August 19-25, 2017, Carles Sierra (Ed.). ijcai.org, 4258–4264. https://doi.org/10.24963/ijcai.2017/595
- Zhu et al. (2021) Yao Zhu, Hongzhi Liu, Zhonghai Wu, and Yingpeng Du. 2021. Relation-Aware Neighborhood Matching Model for Entity Alignment. In Thirty-Fifth AAAI Conference on Artificial Intelligence, AAAI 2021, Thirty-Third Conference on Innovative Applications of Artificial Intelligence, IAAI 2021, The Eleventh Symposium on Educational Advances in Artificial Intelligence, EAAI 2021, Virtual Event, February 2-9, 2021. AAAI Press, 4749–4756. https://ojs.aaai.org/index.php/AAAI/article/view/16606
Appendix A Appendix
A.1. Preliminary
Knowledge Graph (KG) Knowledge graph (KG) stores the real-world knowledge in the form of facts , given a set of entities and relations , the denotes the set of facts , where respectively denote the head entity and tail entity, denotes the relation. Besides, we also model the temporal information in KGs, given timestamps , we denote as the temporal information of the facts, and each fact is represented in the form of .
Based on the basic concept of the KGs, we proposed a concept called highly heterogeneous knowledge graphs (HHKGs). Specifically, it is a relative concept, and indicates that the source KG and the target KG are far different from each other in scale, structure, and overlapping ratios.
Entity Alignment (EA) plays a crucial role in the field of knowledge graph research. Given two KGs, and , the goal of EA is to determine the identical entity set . In this set, each pair represents the same real-world entity but exists in different KGs.
A.2. Related Works
Translation-based Entity Alignment. Translation-based EA approaches (Chen et al., 2017; Sun et al., 2017, 2018; Zhu et al., 2017) are inspired by the TransE mechanism (Bordes et al., 2013), focusing on knowledge triplets . Their scoring functions assess the triplet’s validity to optimize knowledge representation. MTransE (Chen et al., 2017) uses a translation mechanism for entity and relation embedding, leveraging pre-aligned entities for vector space transformation. Both AlignE (Sun et al., 2018) and BootEA (Sun et al., 2018) adjust aligned entities within triples to harmonize KG embeddings, with BootEA incorporating bootstrapping to address limited training data.
GNN-based Entity Alignment. GNNs, designed to represent graph-structured data using deep learning, have become pivotal in EA tasks (Wang et al., 2018; Cao et al., 2019; Zhu et al., 2021; Mao et al., 2020b, a). Foundational models like GCN (Kipf and Welling, 2017) and GAT (Velickovic et al., 2018) create entity embeddings by aggregating neighboring entity data, with GAT emphasizing crucial neighbors through attention. GCN-Align (Wang et al., 2018) exemplifies GNN-based EA methods, utilizing GCN for unified semantic space entity embedding. Enhancements like RDGCN (Chen et al., 2022) and Dual-AMN (Mao et al., 2021) introduced features to optimize neighbor similarity modeling. Recent methodologies, e.g., TEA-GNN (Xu et al., 2021), TREA (Xu et al., 2022), and STEA (Cai et al., 2022), have integrated temporal data, underscoring its significance in EA tasks. A fundamental assumption of these methods is the similarity in neighborhood structures across entities, yet its universality remains unexplored.
Others. Certain EA approaches transcend the above bounds. PARIS (Suchanek et al., 2011) aligns entities in KGs using iterative probabilistic techniques, considering entity names and relations. Fualign (Wang et al., 2023) unifies two KGs based on trained entity pairs, learning a collective representation. BERT-INT (Tang et al., 2020) addresses KG heterogeneity by solely leveraging side information, outperforming existing datasets. However, its exploration of KG heterogeneity remains limited to conventional datasets, not capturing the nuances of practical HHKGs.
A.3. Structure Similarity
To further evaluate the neighborhood similarity between KGs, we propose a new metric called structure similarity, which is the average similarity of aligned neighbors of aligned entity pairs, its function is expressed as follows:
| (4) | ||||
where A denotes KGs’ adjacency matrix, is the vector of entity , which reflects 1-hop neighbors of , is aligned entity pairs.
A.4. Datasets Construction
We illustrate the detailed construction processes of the datasets. For ease of explanation, we will take ICEWS-WIKI as an example in the following discussion, while the process for ICEWS-YAGO is similar.
Firstly, we pre-processed the raw event data of ICEWS obtained from the official website 111 https://dataverse.harvard.edu/dataverse/icews in the period from 1995 to 2021, and transformed the raw data into the KG format including entities, relations, and facts. Concretely, we pre-processed the entity name in ICEWS, and retrieved corresponding entities in Wikidata through the official Wikidata API. Next, we reviewed the candidate entity pairs, and manually filtered unrealistic data, resulting in 20,826 high-quality entity pairs across ICEWS and WIKIDATA. Then, we sampled the neighbors of the above entity pairs from the original data without enforcing the 1-to-1 assumption. To keep the distribution of the dataset similar to the original KGs, we adopted the Iterative Degree-based Sampling (IDS) algorithm (Sun et al., 2020). It simultaneously deletes entities in two KGs, under the guidance of the original KGs’ degree distribution, until the demanded size is achieved. Finally, the ICEWS-WIKI dataset is obtained after sampling. Table 1 summarizes the statistics of the proposed datasets.
A.5. Detailed Experiment Settings
A.5.1. Datasets
We first adopted two representative EA datasets DBP15K(EN-FR) and DBP-WIKI (Sun et al., 2020), which were widely adopted previously. To measure the real effect of the existing EA methods on HHKGs, we also conducted extensive experiments on our proposed datasets: ICEWS-WIKI and ICEWS-YAGO. The statistics of these selected datasets are summarized in Table 1.
A.5.2. Baselines
After carefully reviewing existing EA studies, we found that most existing EA models can be summarized and classified from the following three perspectives: (1) input features, (2) embedding modules, and (3) training strategies. Specifically, for input features, EA methods mainly adopt entity name information, structure information, and other information (e.g., temporal information). For embedding modules, EA methods mainly adopt translation mechanisms, GNN mechanisms, and others. For training ways, EA methods mainly follow supervised and semi-supervised strategies.
Then, based on the above observations, we selected 11 state-of-the-art EA methods, which cover different input features, embedding modules, and training strategies. The characteristics of these models are annotated in Table 2. We outline the baselines based on the type of embedding module.
Translation-based methods: MTransE (Chen et al., 2017), AlignE (Sun et al., 2018), and BootEA (Sun et al., 2018). BootEA is one of the most competitive translation-based EA methods. Above translation-based methods adopt TransE (Bordes et al., 2013) to learn entity embeddings for EA.
GNN-based methods: GCN-Align (Wang et al., 2018), RDGCN (Chen et al., 2022), TREA (Xu et al., 2022), and Dual-AMN (Mao et al., 2021). GCN-Align and RDGCN are two GCN-based EA methods, where RDGCN uses entity name information. Dual-AMN is one of the most competitive GAT-based EA methods. We evaluate the performance of Dual-AMN under three conditional settings(basic/semi/name), where Dual-AMN(semi) adopts the semi-supervised strategy, and Dual-AMN(name) utilizes entity name information. TEA-GNN (Xu et al., 2021), TREA (Xu et al., 2022) and STEA (Cai et al., 2022) additionally leverage temporal information for EA.
Other methods: BERT (Devlin et al., 2019), FuAlign (Wang et al., 2023), and BERT-INT (Tang et al., 2020). BERT denotes the basic pre-trained language model we adopted for initial entity embedding by using entity name information. FuAlign and BERT-INT are two advanced methods that comprehensively leverage structure and entity name information without GNNs. PARIS (Suchanek et al., 2011) is a probabilistic algorithm that iteratively aligns entities in knowledge graphs, even without pre-existing alignments.
A.5.3. Evaluation Settings
In this section, we provide detailed explanations of the model settings, feature initialization, and evaluation metrics.
Model Settings. For all baselines of our experiments, we followed their hyper-parameter configurations reported in the original papers except that we keep the hidden dimensions for fair comparisons. We followed the 3:7 splitting ratio in training/ testing data. All baselines follow the same pre-process procedure to obtain the initial feature as input. In order to eliminate the influence of randomness, all experimental results are performed 10 times, and we take the average as the results. We use PyTorch for developing our work. Our experiments are performed on a CentOS Machine with sixteen 2.1GHz Intel cores and four 24GB TITAN RTX GPUs.
Feature Initialization. In our experiments, all EA models, which are capable of modeling entity name information, adopt the same entity name embeddings. Specifically, in DBP15K(EN-FR), we used machine translation systems to get entity names. In DBP-WIKI, we converted the QIDs from wikidata into entity names. In ICEWS-WIKI and ICEWS-YAGO, we used their entity names. After obtaining the textual feature of entities, we adopted the BERT with the whitening transformation (Su et al., 2021) to get the initial name embedding.
In addition, for the structure-based EA methods that do not leverage any entity name information, we followed the original settings of these methods to initialize embeddings randomly.
Evaluation Metrics. Following the previous work, we adopted two evaluation metrics: (1) Hits@k: the proportion of correctly aligned entities ranked in the top k () similar to source entities. (2) Mean Reciprocal Rank (MRR): the average of the reciprocal ranks of results. Higher Hits@k and MRR scores indicate better entity alignment performance.