\externaldocument

supplement

Toward Mixed Analog-Digital Quantum Signal Processing: Quantum AD/DA Conversion and the Fourier Transform

Yuan Liu*, , John M. Martyn*, Jasmine Sinanan-Singh, Kevin C. Smith, Steven M. Girvin, and Isaac L. Chuang Manuscript created December, 2023. *These authors contributed equally. (Corresponding author: Yuan Liu.)Y. Liu is with the Departments of Electrical and Computer Engineering, Computer Science, and Physics (affiliated), North Carolina State University, Raleigh, North Carolina 27606, USA. He was also with the Department of Physics, Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139 USA (e-mail: [email protected]).J.M. Martyn is with the Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA (e-mail: [email protected]).J. Sinanan-Singh is with the Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA (e-mail: [email protected]).K.C. Smith was with the Department of Physics and the Yale Quantum Institute, Yale University, New Haven, Connecticut 06511 USA and Brookhaven National Laboratory, Upton, New York 11973, USA (e-mail: [email protected]).S.M. Girvin is with the Department of Physics and the Yale Quantum Institute, Yale University, New Haven, Connecticut 06511, USA (e-mail: [email protected]).I.L. Chuang is with the the Department of Physics, and the Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA (e-mail: [email protected]). 0000-0003-1468-942X 0000-0002-4065-6974 0000-0002-2397-1518 0000-0002-6470-5494 0000-0001-7296-523X

Abstract

Signal processing stands as a pillar of classical computation and modern information technology, applicable to both analog and digital signals. Recently, advancements in quantum information science have suggested that quantum signal processing (QSP) can enable more powerful signal processing capabilities. However, the developments in QSP have primarily leveraged digital quantum resources, such as discrete-variable (DV) systems like qubits, rather than analog quantum resources, such as continuous-variable (CV) systems like quantum oscillators. Consequently, there remains a gap in understanding how signal processing can be performed on hybrid CV-DV quantum computers. Here we address this gap by developing a new paradigm of mixed analog-digital QSP. We demonstrate the utility of this paradigm by showcasing how it naturally enables analog-digital conversion of quantum signals— specifically, the transfer of states between DV and CV quantum systems. We then show that such quantum analog-digital conversion enables new implementations of quantum algorithms on CV-DV hardware. This is exemplified by realizing the quantum Fourier transform of a state encoded on qubits via the free-evolution of a quantum oscillator, albeit with a runtime exponential in the number of qubits due to information theoretic arguments. Collectively, this work marks a significant step forward in hybrid CV-DV quantum computation, providing a foundation for scalable analog-digital signal processing on quantum processors.

Index Terms:

Quantum Information and Signal Processing, Quantum Fourier Transform, Sampling and Interpolation, Hybrid Discrete-Continuous-Variable System, Quantum Computing

I Introduction

The ability to process signals in an efficient and robust manner is a cornerstone of engineering and technology, from audio and speech recognition, to computer design and communications [1, 2]. In the wake of modern computers, sophisticated frameworks and algorithms have been developed to process classical signals, including the fast Fourier transform [3], Shannon sampling [4], and filter design [5].

Classical signal processing has benefited from both digital and analog computing devices [6, 7, 8, 9]. While digital signal processing enables the processing of discretized signals, analog signal processing is particularly useful for processing continuous signals, such as audio and speech data [10, 11, 12]. Hybrid analog-digital computing [13, 14] has also shown great promise, with notable applications in improving energy efficiency and solving nonlinear partial differential equations [15, 16].

In contrast to the classical setting, quantum systems, governed by the laws of quantum mechanics, exhibit fundamentally different behavior than their classical counterparts and have been shown to facilitate more powerful models of computation than classical computers [17, 18, 19]. It is therefore natural to ask if quantum computation can process signals more efficiently and powerfully than classical methods.¹¹1In posing this question, we are interested in processing quantum signals (quantum amplitudes) using quantum resources, rather than processing classical signals on a quantum computer.

A pioneering work in this direction [20] introduced a quantum-inspired signal processing paradigm predicated on quantum-mechanical concepts, to design an array of novel classical signal processing methods. Extending this line of research, Refs. [21, 22, 23] proposed quantum signal processing (QSP) as a quantum algorithm that enables the design and implementation of a polynomial transformation of a quantum amplitude. QSP has since been generalized to transform a linear operator embedded in a larger Hilbert space, leading to the celebrated quantum singular value transformation (QSVT) [24, 25]. As an illustration of the power of QSP and QSVT, Ref. [26] shows how major quantum algorithms, including Grover search, Shor’s factoring algorithm, and Hamiltonian simulation, can all be realized through QSVT. Inspired by this remarkable progress, a number of recent works have further generalized QSP and QSVT [27, 28, 29, 30, 31, 32], studied the noise robustness of QSP [33, 34], presented algorithms for efficient computation of QSP/QSVT transformations [35, 36, 37, 38], and showcased applications of QSP/QSVT to relevant problems [39, 40, 41, 42, 43, 44].

These developments in QSP rely on the capabilities of digital quantum computers, in which quantum states are encoded in discrete-variable (DV) systems, i.e., qubits (or possibly qudits). Separate from these DV systems, continuous-variable (CV) quantum systems, such as the quantum harmonic oscillator, are ubiquitous in practice and also provide useful quantum resources [45, 46]. A prominent example of such CV systems is the electromagnetic (EM) wave used in wireless and communications [47, 48], which obey classical wave mechanics at high intensity, but exhibit quantum effects at low intensity. Recent experimental progress in the control and engineering of CV quantum systems has made them essential to quantum information science, prompting efforts to harness CV systems for computation [49, 50, 51, 52, 53, 54, 55, 46, 56, 57, 58, 59, 60, 61]. In this direction, recent works have developed hybrid CV-DV quantum processors [57, 61], which combine DV and CV quantum systems into a powerful new framework for quantum computation, with natural applications to problems such as simulating coupled fermion-boson systems [61, 62].

Because QSP algorithms have primarily leveraged DV quantum systems, we currently lack the ability to use CV systems and hybrid CV-DV processors in this context. This is in stark contrast to the situation in classical signal processing, which has profited from both analog and digital modes of computation. A major challenge in extending QSP to CV and CV-DV quantum systems is the drastic differences between DV and CV quantum states. For instance, while DV quantum states have finite dimensionality, CV quantum states have infinite dimensionality and are supported over the entire real axis in position space.

In this work, we address this challenge by establishing a framework of mixed analog-digital QSP, which enables processing of quantum signals on hybrid CV-DV quantum hardware. Our framework encompasses two signal processing primitives: (1) hybrid single-variable QSP for constructing polynomial transformations of either position $\hat{x}$ or momentum $\hat{p}$ , and (2) hybrid non-Abelian QSP for constructing polynomial transformations of both $\hat{x}$ and $\hat{p}$ . We use “non-Abelian” to refer to the fact that the quantum mechanical operators $\hat{x}$ and $\hat{p}$ do not commute, i.e., $[\hat{x},\hat{p}]=\hat{x}\hat{p}-\hat{p}\hat{x}\neq 0$ . The polynomials achievable with the hybrid single-variable QSP are characterized by the QSP theorems established in Refs. [44, 21, 22, 23], whereas the polynomials achievable with hybrid non-Abelian QSP are in principle more powerful [61] but a complete theory has yet to be established.

The ability to perform QSP on CV-DV hardware provides a cookbook for implementing quantum algorithms on hybrid quantum processors. To facilitate the development of these algorithms, one requires a mechanism to reliably convert between CV states and DV states. It is known that such analog-to-digital (AD) and digital-to-analog (DA) conversion can be accomplished in classical signal processing via sampling and interpolation, respectively. However, a quantum analogue of these concepts is not obvious [63], yet strides have been made in the context of the Gottesman-Kitaev-Preskill code [64, 65]. A key distinction between classical and quantum AD/DA conversion is that the quantum case must be unentangling: the input and output states must be unentagled across the DV and CV systems, as otherwise information in the initial state will remain in the quantum correlations between the systems, inaccessible to either party individually. As the concept of entanglement does not exist classically, this requirement must be treated with care. Here we show how such a quantum AD/DA conversion mechanism is naturally enabled by mixed analog-digital QSP. In particular, we illustrate two protocols that transfer a DV state into an equivalent CV state, and vice-versa, and provide analytical error bounds on their performance. The first protocol is constructed with hybrid single-variable QSP, while the second protocol, initially introduced in Ref. [66], can be recontextualized as an instance of non-Abelian hybrid QSP.

As an application of this paradigm, we use our quantum AD/DA conversion protocols to implement the quantum Fourier transform of a state on qubits by using the natural dynamics (free-evolution) of an oscillator. This is realized in three steps: 1) transferring the initial state on qubits to an oscillator; 2) performing free-evolution of the oscillator; 3) and transferring the oscillator state back to qubits. Importantly, our construction is fully coherent and does not require post-selection, in contrast to an alternative construction put forth in Ref. [67]. From a signal processing perspective due to the Nyquist criteria, the required CV oscillator phase space area (analog signals) must be proportional to the Hilbert space dimension of the DV system (number of data points for digital signals) to avoid significant loss of information for general quantum states. This renders the runtime of our protocol (or physical resources required) necessarily linear in the dimension of the DV Hilbert space (i.e. exponential in the number of qubits), despite the fact that the gate count can still scale polynomially.

The rest of the paper is organized as follows. We first review basics of signal processing and hybrid DV-CV quantum systems in Sec. II, and subsequently present mixed analog-digital QSP in Sec. III, including hybrid single-variable QSP and non-Abelian hybrid QSP. Then in Sec. IV, we present two protocols for quantum AD/DA conversion. Armed with hybrid QSP and quantum AD/DA conversion, in Sec. V we show how to realize the Fourier transform of a DV quantum state by the free evolution of a CV system. Finally, in Sec. VI we conclude and discuss the outlook of this work.

II Overview of Signal Processing and CV-DV Quantum Systems

In this section, we present the concepts that underlie classical signal processing and quantum signal processing, with the aim of familiarizing readers from either community with the necessary background to understand this work. Sec. II-A overviews classical signal processing, and highlights the continuous-discrete and periodic-aperiodic nature of classical signals. Thereafter, Sec. II-B introduces the basics of DV and CV quantum systems and operations.

II-A Overview of classical signal processing data types

Refer to caption — Figure 1: Schematic of time- and frequency-domain analog and digital signals. Conversions between them are accomplished via the Fourier transform and sampling/interpolation.

We begin by summarizing classical signal types in Fig. 1, including the relationships between them. In classical systems, a signal is a physical quantity that is a real-valued continuous function of time, such as electric current or voltage, although complex representations can be used to ease mathematical description. These analog signals can be converted to the frequency domain by the continuous Fourier transform (upper panel of Fig. 1), and processed with analog filters. To improve the robustness of signal processing, continuous signals are often “quantized”²²2Despite the name, this has no relation to quantum mechanics. into discrete signals via sampling, or equivalently analog-digital (A/D) conversion. In this context, a discrete signal may be transformed to frequency domain by the discrete Fourier transform (lower panel of Fig. 1). Inversely, discrete signals can also be converted into continuous signals via interpolation, or digital-analog (D/A) conversion. In addition to being continuous or discrete, signals can also be periodic or aperiodic, and often require correspondingly different treatments. To accommodate these differences, windowing and padding techniques are used to connect signal processing tasks between signals of different periodicity.

Depending on whether the time-domain signal is periodic or aperiodic, and continuous or discrete, there are four possible signal types. Similarly, the corresponding frequency domain signals also have four types. As a result, there are sixteen possible transformations that connect time-domain signals to their frequency domain counterparts. These transformations are often named according to the characteristics of the signals they transform between. For example, the continuous Fourier transform connects a continuous aperiodic signal in the time domain to a frequency-domain signal that is also continuous and aperiodic. Likewise, padding/windowing techniques and sampling/interpolation transform a continuous aperiodic signal in the time domain to its discrete periodic counterpart in the frequency domain. Similarly, a discrete Fourier series connects discrete periodic signals in time and frequency domain. Other transformations can be likewise defined to connect any pair of time- and frequency-domain signals. See Refs. [1, 2] for more details.

Beyond processing analog and digital signals on classical computers, recent developments in quantum computing and engineering raise the question: can mixed analog-digital signal processing be achieved on quantum systems? And if so, how can one define notions of quantum sampling and interpolation to bridge analog and digital quantum data, and how can we use these methods to implement algorithms like the Fourier transform? Addressing these questions is crucial but challenging due to the fundamental differences between quantum and classical systems. As we will see later in this paper, we obtain affirmative answers to these questions, yet their resolution requires a strong understanding of discrete and continuous variable quantum systems, to which we now turn.

II-B Review of DV and CV Quantum Systems and Operations

Here we review the basics of discrete-variable (Sec. II-B1) and continuous-variable (Sec. II-B2) quantum systems, including the quantum gates operations achievable on these systems.

II-B1 Quantum States and Operations on Qubits

A qubit is a two-level quantum system whose state can be represented as a linear combination of two orthonormal basis states, denoted by $\ket{0}$ and $\ket{1}$ . That is, an arbitrary state can be written as $\ket{\psi}=c_{0}\ket{0}+c_{1}\ket{1}$ , for $c_{0},c_{1}\in\mathbb{C}$ , where it is normalized as $|c_{0}|^{2}+|c_{1}|^{2}=1$ . Conventionally, we write $\ket{0}=[1,0]^{T}$ , $\ket{1}=[0,1]^{T}$ , and $\ket{\psi}=[c_{0},c_{1}]^{T}$ .

To transform a one qubit state $\ket{\psi}$ to another $\ket{\psi^{\prime}}$ , we require a single-qubit gate, denoted $R_{\bm{\hat{b}}}(\theta)$ , such that $\ket{\psi^{\prime}}=R_{\bm{\hat{b}}}(\theta)\ket{\psi}$ . In general, $R_{\bm{\hat{b}}}(\theta)$ can be an arbitrary $2\times 2$ special unitary matrix (SU(2)), which is generated by a set of $2\times 2$ Hermitian matrices known as the Pauli matrices:

\displaystyle\sigma_{x}=\begin{bmatrix}0&1\\ 1&0\end{bmatrix},~{}~{}\sigma_{y}=\begin{bmatrix}0&-i\\ i&0\end{bmatrix},~{}~{}\sigma_{z}=\begin{bmatrix}1&0\\ 0&-1\end{bmatrix}

(1)

\displaystyle R_{\bm{\hat{b}}}(\theta)=e^{-i\frac{\theta}{2}\bm{\hat{b}}\cdot\bm{\sigma}},

(2)

where $i=\sqrt{-1}$ , and $\bm{\sigma}=[\sigma_{x},\sigma_{y},\sigma_{z}]$ is a vector of the Pauli matrices, $\theta\in[0,4\pi)$ is a rotation angle, and $\bm{\hat{b}}=[b_{x},b_{y},b_{z}]\in\mathbb{R}^{3}$ is a vector of unit length, $|b_{x}|^{2}+|b_{y}|^{2}+|b_{z}|^{2}=1$ . In general, $\theta$ and $\bm{\hat{b}}$ can be chosen from a continuum of possibilities to realize an arbitrary single-qubit gate.

To apply quantum computation to multiple qubits, additional gates that entangle qubits are needed. One common such gate is the controlled-NOT (CNOT) operation, which acts on two qubits as ${\rm CNOT}=\frac{I+\sigma_{z}}{2}\otimes I+\frac{I-\sigma_{z}}{2}\otimes\sigma_{x}$ where $I$ is the $2\times 2$ identity matrix, and $\otimes$ is the tensor product. It can be shown [17] that the gate set $\mathcal{S}_{0}=\{R_{\bm{\hat{b}}}(\theta),{\rm CNOT}\}$ forms a universal gate set, such that an arbitrary gate on $n$ qubits (i.e., a $2^{n}\times 2^{n}$ unitary matrix) can be decomposed into a product of $R_{\bm{\hat{b}}}(\theta)$ and ${\rm CNOT}$ gates.

Despite its universality, the set $\mathcal{S}_{0}$ contains infinitely many gates due to the continuous parameterization of $R_{\bm{\hat{b}}}(\theta)$ . It turns out an arbitrary gate $R_{\bm{\hat{b}}}(\theta)$ can be decomposed into a finite sequence of gates from the discrete set $\{H,T\}$ , where

H=\frac{1}{\sqrt{2}}\begin{bmatrix}1&1\\ 1&-1\end{bmatrix},\quad T=\begin{bmatrix}1&0\\ 0&e^{i\frac{\pi}{4}}\end{bmatrix}

(3)

are the Hadamard gate and $T$ gate, respectively. This implies that the set $\mathcal{S}_{1}=\{H,T,{\rm CNOT}\}$ is a universal gate set for qubit-based quantum computation [68]. According to the Solovay-Kitaev theorem, constructing an $\epsilon$ -approximation to arbitrary gate $R_{\bm{\hat{b}}}(\theta)$ requires $O(\log^{c}(\frac{1}{\epsilon}))$ $H$ or $T$ gates, where $c$ is a constant close to $2$ [69, 70]. As a byproduct of this result, synthesizing an arbitrary $n$ -qubit unitary requires $O(4^{n}\log^{c}(\frac{1}{\epsilon}))$ gates from the set $\mathcal{S}_{1}$ [69].

II-B2 Quantum States and Operations on Oscillators

In contrast to qubits, the computational capabilities of continuous variable quantum systems are less well-studied (for an introduction see [61]). Here we will consider the paradigmatic continuous variable system — the quantum harmonic oscillator. The quantum harmonic oscillator arises in any quantum system that exhibits oscillations, such as molecular vibrations [71], microwave photons in cavities [72], and phonons in solids [73, 74]. Its Hamiltonian is given by the quantized version of the familiar classical harmonic oscillator

H_{0}=\frac{p^{2}}{2m}+\frac{1}{2}m\omega_{0}^{2}x^{2},

(4)

where $p$ and $x$ are the momentum and position, and $m$ and $\omega_{0}$ are the mass and frequency of the oscillator. Mathematically, the quantization of the harmonic oscillator is achieved by introducing momentum and position operators $\hat{p}$ and $\hat{x}$ that obey the canonical commutation relation $[\hat{x},\hat{p}]:=\hat{x}\hat{p}-\hat{p}\hat{x}=i$ . Setting $\hbar=1$ and $m\omega_{0}=1$ for simplicity, these operators can be conveniently expressed in terms of the annihilation and creation operators, $a,a^{\dagger}$ , respectively, defined as

\hat{p}=\frac{i(a^{\dagger}-a)}{\sqrt{2}}\,,~{}~{}~{}~{}~{}~{}~{}~{}~{}\hat{x}=\frac{a+a^{\dagger}}{\sqrt{2}},

(5)

and obeying $[a,a^{\dagger}]=1$ .

After quantization, the Hamiltonian of the quantum harmonic oscillator is given by $\hat{H}_{0}=\omega_{0}(\hat{n}+\frac{1}{2})$ where $\hat{n}:=a^{\dagger}a$ is known as the number operator. The number operator has non-negative integer eigenvalues $n\in\mathbb{Z}_{0}^{+}$ , which correspond to number of excitations in the oscillator. Incidentally, the corresponding eigenstates, which we denote by $|n\rangle$ , are also the eigenstates of the Hamiltonian

\displaystyle\hat{H}_{0}\ket{n}=E_{n}\ket{n},

(6)

with eigenvalues (i.e., energy) $E_{n}=\omega_{0}(n+\frac{1}{2})$ for $n=0,1,2,\ldots$ . Similar to the qubit case, an arbitrary oscillator state can be written as a linear combination of $\ket{n}$ as $\ket{\psi}=\sum_{n=0}^{\infty}c_{n}\ket{n}$ for $c_{n}\in\mathbb{C}$ and $\sum_{n=0}^{\infty}|c_{n}|^{2}=1$ . Adjacent eigenstates are related to each other by $a,a^{\dagger}$ as:

	$\displaystyle a^{\dagger}\ket{n}$	$\displaystyle=\sqrt{n+1}\ket{n+1},$		(7)
	$\displaystyle a\ket{n}$	$\displaystyle=\sqrt{n}\ket{n-1}.$		(8)

In the language of linear algebra, $|n\rangle$ can be represented by a (infinite-dimensional) column vector with its $n$ -th entry set to 1 and the rest to 0; for example, $\ket{0}=\begin{bmatrix}1&0&0&\cdots\end{bmatrix}^{T}$ , $\ket{1}=\begin{bmatrix}0&1&0&\cdots\end{bmatrix}^{T}$ , and $\ket{2}=\begin{bmatrix}0&0&1&0&\cdots\end{bmatrix}^{T}$ . In this basis, Eqs. (7) and (8) lend themselves to the following matrix representation for $\hat{p},\hat{x}$ :

\displaystyle\hat{p}

\displaystyle=\frac{i}{\sqrt{2}}\begin{bmatrix}0&-1&0&0&\cdots\\ 1&0&-\sqrt{2}&0&\cdots\\ 0&\sqrt{2}&0&-\sqrt{3}&\cdots\\ 0&0&\sqrt{3}&0&\cdots\\ \vdots&\vdots&\vdots&\vdots&\ddots\end{bmatrix},

(9)

\displaystyle\hat{x}

\displaystyle=\frac{1}{\sqrt{2}}\begin{bmatrix}0&1&0&0&\cdots\\ 1&0&\sqrt{2}&0&\cdots\\ 0&\sqrt{2}&0&\sqrt{3}&\cdots\\ 0&0&\sqrt{3}&0&\cdots\\ \vdots&\vdots&\vdots&\vdots&\ddots\end{bmatrix}.

(10)

Just as the Pauli matrices generate an arbitrary single-qubit operation as per Eq. (2), an arbitrary unitary operation on an oscillator can be represented as

\displaystyle U=e^{-ih(\hat{x},\hat{p})},

(11)

where $h(\hat{x},\hat{p})$ is a function of $\hat{x},\hat{p}$ , often expressed as a polynomial in $\hat{x}$ and $\hat{p}$ . Universal control of an oscillator requires the ability to implement the above unitary for any such $h(\hat{x},\hat{p})$ of finite degree. In a similar manner, an entangling gate between two oscillators can be defined to achieve universal quantum computation on multiple oscillators.

However, despite the parallel discussion of Eq. (2) and Eq. (11), qubit gates and oscillator gates differ significantly. For example, in the qubit case, any even power of a Pauli matrix is the identity (e.g., $\sigma_{x}^{2}=1$ ), whereas in the oscillator case powers of $\hat{x},\hat{p}$ are non-trivial. This distinction arises from the infinite dimensionality of the oscillator, and complicates the construction of unitary operations on CV systems.

Nonetheless, a simple example of such a unitary operator on a CV system is the free-evolution of an oscillator, given by

\displaystyle R(\theta)=e^{-i\theta a^{\dagger}a},

(12)

where $\theta=\omega_{0}t$ is a rotation angle. When $\theta=\frac{\pi}{2}$ , this becomes the “Fourier gate” $F=R(\frac{\pi}{2})$ , which acts as

\displaystyle F^{\dagger}\hat{x}F

\displaystyle=\hat{p},\qquad F^{\dagger}\hat{p}F=-\hat{x}.

(13)

Evidently, the Fourier gate swaps the position $\hat{x}$ with the momentum operator $\hat{p}$ , thus enacting a continuous Fourier transform on the underlying wave function.

Lastly, we note that in practical/numerical studies of CV systems, the infinite-dimensional Hilbert space can be truncated to a finite dimension by selecting a large integer $N_{\rm max}$ to represent the maximum excitation number. Truncating the states and operations past this cutoff renders the system finite dimensional, effectively mapping the oscillator into an $N_{\rm max}$ -dimensional qudit. In this setting, it has been established how to perform universal qudit-based quantum computation using oscillators [60, 59], yet an analogue of the Solovay-Kitaev theorem for oscillators has not been established [75].

III Mixed Analog-Digital Quantum Signal Processing

Leveraging the gates and operations defined in the previous section, here we present analog-digital quantum signal processing for hybrid CV-DV systems. We first discuss hybrid single-variable QSP in Sec. III-A, followed by a generalization to bi-variate non-Abelian QSP in Sec. III-B.

III-A Hybrid Single-variable QSP

After analyzing the states and gates of qubits and oscillators, a natural question is how to compose these gates into useful quantum computations. This has been well-studied in DV quantum computation, leading to a variety of qubit-based algorithms, such as Trotter formulas [76], linear combination of unitaries [77], variational algorithms [78], and quantum signal processing [26]. Many of these DV algorithms admit adaptations to hybrid CV-DV quantum processors, as explicated in Refs. [57, 61]. As the focus of our work is signal processing, let us present CV-DV QSP [44], as an adaptation of QSP to hybrid CV-DV processors.

As we review in Appendix A, QSP provides a systematic framework for implementing a polynomial transformation of a linear operator, that is encoded in a block of a matrix (e.g., as one of its matrix elements). This is achieved by designing an alternating sequence of a fixed $z$ -rotation that encodes the operator (i.e. the “signal”), and parameterizable $x$ -rotations. Such a QSP sequence of length $d$ generates a degree $d$ polynomial, parameterized by the angles of the $x$ -rotations. Importantly, for any polynomial bounded as $|P(x)|\leq 1$ over $-1\leq x\leq 1$ , we can efficiently compute the corresponding angles with a classical algorithm [79, 35, 80, 38]. In fact, an early such method for determining these angles relied on Remez-type exchange algorithms [81], ubiquitous in filter design in classical signal processing, thus inspiring the name “quantum signal processing” [22].

In generalizing QSP to hybrid CV-DV systems, let us define an important oscillator gate, the displacement gate $D(\alpha)$ :

\displaystyle D(\alpha)=e^{\alpha a^{\dagger}-\alpha^{*}a}=e^{i\sqrt{2}\Im{\alpha}\hat{x}-i\sqrt{2}\Re{\alpha}\hat{p}}

(14)

where $\alpha\in\mathbb{C}$ is a complex number. As its name suggests, $D(\alpha)$ displaces the oscillator quadrature operators— $\hat{x}$ by the real component of $\alpha$ , and $\hat{p}$ by the imaginary component:

	$\displaystyle D^{\dagger}(\alpha)\,\hat{x}\,D(\alpha)=\hat{x}+\sqrt{2}\Re{\alpha},$		(15)
	$\displaystyle D^{\dagger}(\alpha)\,\hat{p}\,D(\alpha)=\hat{p}+\sqrt{2}\Im{\alpha}.$		(16)

The displacement gate itself is considered a “Gaussian” operation, meaning that it only manipulates the oscillator wave function classically and cannot generate non-classical states. However, by coupling an oscillator to a qubit, the following entangling gate, known as the conditional displacement operation, can be generated:

\displaystyle W_{z}^{(\kappa)}=e^{-i\frac{\kappa}{2}\hat{x}\sigma_{z}}=\begin{bmatrix}\hat{w}&0\\ 0&\hat{w}^{-1}\end{bmatrix},~{}~{}~{}~{}~{}~{}\hat{w}=e^{-i\frac{\kappa}{2}\hat{x}}.

(17)

where $\kappa\in\mathbb{R}$ is a real-valued displacement parameter. This is a powerful operation that imparts a qubit-dependent momentum boost on the oscillator and can indeed generate quantum entanglement between qubits and oscillators [55]. The gate in Eq.(17) is also a standard gate on trapped ion quantum computers [82]. Importantly, we can equivalently interpret this as a $z$ -rotation of the qubit through an angle $\kappa\hat{x}$ proportional to the position of the oscillator. Likewise, Eq. (17) indicates that $W_{z}^{(\kappa)}$ encodes the variable $\hat{w}$ in its upper left block (of the $2\times 2$ qubit subspace). This identification suggests that $W_{z}^{(\kappa)}$ could be combined with parameterizable $\hat{x}$ -rotations to develop a QSP sequence that generates a polynomial transformation of $\hat{w}$ .

Following this intuition, we propose the following hybrid single-variable QSP sequence of $d$ operations to produce a polynomial transformation in $\hat{w}$ :

\displaystyle e^{i\phi_{0}\sigma_{x}}\prod_{j=1}^{d}W_{z}^{(\kappa)}e^{i\phi_{j}\sigma_{x}}=\begin{bmatrix}F(\hat{w})&iG(\hat{w})\\ iG(\hat{w}^{-1})&F(\hat{w}^{-1})\end{bmatrix}.

(18)

As we show in Appendix A, $F(\hat{w})$ and $G(\hat{w})$ are degree $d$ Laurent polynomials in $\hat{w},\hat{w}^{-1}$ with real coefficients and parity $d\mod 2$ (i.e., consisting of only even or odd coefficients):

	$\displaystyle F(\hat{w})$	$\displaystyle=\sum_{n=-d}^{d}f_{n}\hat{w}^{n}=\sum_{n=-d}^{d}f_{n}e^{-i\frac{n\kappa}{2}\hat{x}}:=f(\hat{x}),$		(19)
	$\displaystyle G(\hat{w})$	$\displaystyle=\sum_{n=-d}^{d}g_{n}\hat{w}^{n}=\sum_{n=-d}^{d}g_{n}e^{-i\frac{n\kappa}{2}\hat{x}}:=g(\hat{x})$		(20)

where $f_{n},g_{n}\in\mathbb{R}$ . Evidently, $F(\hat{w})$ and $G(\hat{w})$ equate to periodic functions $f(\hat{x})$ and $g(\hat{x})$ , both with periods of $\frac{4\pi}{\kappa}$ in position space. The coefficients $f_{n},g_{n}$ can be computed by evaluating the Fourier series coefficients of $f(x)$ and $g(x)$ for $-d\leq n\leq d$ :

\displaystyle f_{n}=\sum_{n=-d}^{d}f(x)e^{i\frac{n\kappa}{2}x},~{}~{}g_{n}=\sum_{n=-d}^{d}g(x)e^{i\frac{n\kappa}{2}x}.

(21)

In addition, the unitarity of Eq. (18) requires $F(\hat{w})F(\hat{w}^{-1})+G(\hat{w})G(\hat{w}^{-1})=I$ .

Note that even though $\kappa\hat{x}$ is a quantum operator rather than a classical rotation angle, this construction is identical to ordinary QSP as we discuss in Appendix A, and thus the associated results carry over. Crucially, for any real Laurent polynomial $F(\hat{w})$ of degree $d$ written in the form of Eq. (20), there exists a set of phases $\{\phi_{0},\phi_{1},...,\phi_{d}\}$ such that the gate sequence of Eq. (18) produces $F(w)$ , and we can determine these phases.

Moreover, the construction in Eq. (18) can be changed to be a function of momentum $\hat{p}$ by instead using the following qubit-dependent position kick in place of $W_{z}^{(\kappa)}(\hat{\theta})$ :

\displaystyle W_{z}^{(\lambda)}=e^{-i\frac{\lambda}{2}\hat{p}\sigma_{z}}

\displaystyle=\begin{bmatrix}\hat{v}&0\\ 0&\hat{v}^{-1}\end{bmatrix},~{}~{}~{}\hat{v}=e^{-i\frac{\lambda}{2}\hat{p}}.

(22)

More generally, to construct an operator that is a function of a linear combination of $\hat{x}$ and $\hat{p}$ , such as $\frac{\kappa}{2}\hat{x}+\frac{\lambda}{2}\hat{p}$ , one can apply QSP to the operator $e^{-i(\frac{\kappa}{2}\hat{x}+\frac{\lambda}{2}\hat{p})\sigma_{z}}$ . By varying the parameters $\kappa$ and $\lambda$ , it is therefore possible to cover the entire phase space. As such, this simple generalization of QSP to hybrid CV-DV systems allows us to implement a large class of operations on oscillators, with precision that improves with increasing polynomial degree $d$ . This is useful in variety of applications; for example, Ref. [44] uses this construction to design an interferometer for quantum sensing applications in the few-shot limit, and Ref. [61] demonstrates how to use this technique to create a cat state in the oscillator by applying a conditional displacement followed by a QSP sequence.

III-B Hybrid Non-Abelian QSP

The hybrid single-variable QSP of the previous section is limited in application to functions of either $\hat{x}$ , $\hat{p}$ , or a linear combination thereof. Here we extend this constructing to multivariate functions in $\hat{x}$ and $\hat{p}$ by presenting hybrid non-Abelian QSP[83]. In a system comprised of one qubit and one oscillator, we define non-Abelian QSP by the following sequence of the two conditional displacements Eqs. (17) and (22), interspersed with $X$ rotations parameterized by a set of phases $\{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}\}$ for $j=1,2,\cdots,d$ :

	$\displaystyle U_{d}$	$\displaystyle=e^{i\phi_{0}\sigma_{x}}\prod_{j=1}^{d}W_{z}^{(k)}e^{i\phi_{j}^{(k)}\sigma_{x}}W_{z}^{(\lambda)}e^{i\phi_{j}^{(\lambda)}\sigma_{x}}$
		$\displaystyle=\begin{bmatrix}F_{d}(w,v)&iG_{d}(w,v)\\ iG_{d}(v^{-1},w^{-1})&F_{d}(v^{-1},w^{-1})\end{bmatrix}.$		(23)

As we show in Appendix B, this sequence implements a bivariate Laurent polynomial transformation in the non-commuting variables $\hat{w}$ and $\hat{v}$ , which takes the following form:

\displaystyle F_{d}(\hat{w},\hat{v})=\sum_{r,s=-d}^{d}f_{rs}\hat{w}^{r}\hat{v}^{s},~{}~{}G_{d}(\hat{w},\hat{v})=\sum_{r,s=-d}^{d}g_{rs}\hat{w}^{r}\hat{v}^{s},

(24)

where $f_{rs}$ and $g_{rs}$ are complex coefficients parameterized by the phase angles $\{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}\}$ . Note that because $\hat{w}$ and $\hat{v}$ do not commute, their order in Eq. (24) matters. Here we will express these polynomials with the factors of $\hat{w}$ always written to the left of $\hat{v}$ , and refer to this convention as canonical.

In using this construction, it would be desirable to show that for an arbitrary Laurent polynomial $F_{d}(\hat{w},\hat{v})$ , there always exist corresponding QSP phases $\{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}\}$ . However, the bi-variate nature of non-Abelian QSP renders the (single-variable) QSP theorem of Ref. [84] inapplicable. Similarly, the non-commutativity of $\hat{w}$ and $\hat{v}$ inhibits application of the recent developments in multivariate QSP of commuting variables [27, 28, 85]. Accordingly, a characterization of the transformations achievable by non-Abelian QSP requires a more complete theory of polynomial transformations of two non-commuting variables, which has yet to be developed [30].

IV Quantum AD/DA Conversion: Sampling and Interpolation of Quantum Data

In this section, we present two methods for AD/DA conversion of quantum signals on hybrid CV-DV systems. Analogous to classical signal processing, this procedure effectively realizes sampling and interpolation of quantum data. Physically, sampling transfers a CV state to a DV state, whereas interpolation transfers a DV state to a CV state. We will refer to these procedures as quantum A/D (analog-to-digital) and D/A (digital-to-analog) conversion, respectively. In the following, we will use subscripts $Q$ and $O$ to distinguish DV states (qubits) and CV states (oscillator), respectively.

Formally, in quantum D/A conversion, we begin with an $n$ -qubit state $|\psi\rangle_{Q}=\sum_{\mathbf{x}}c_{\mathbf{x}}|\mathbf{x}\rangle_{Q}$ , where $\mathbf{x}=(x_{1},x_{2},...,x_{n})$ is a Boolean-valued vector and $|\mathbf{x}\rangle_{Q}=|x_{1}\rangle|x_{2}\rangle...|x_{n}\rangle$ is the corresponding qubit state. We will also use the binary representation of integers, in which $\mathbf{x}$ corresponds to the integer $x=\sum_{j=1}^{n}x_{j}\cdot 2^{n-j}=x_{1}\cdot 2^{n-1}+x_{2}\cdot 2^{n-2}...+x_{n}\cdot 2^{0}$ . Our goal is to transfer $|\psi\rangle_{Q}$ to an analogous oscillator state $|\psi\rangle_{O}=\sum_{\mathbf{x}}c_{\mathbf{x}}|x,\Delta\rangle_{O}$ , where $|x,\Delta\rangle_{O}$ is a basis state in continuous space parameterized by the integer $x$ and a spacing parameter $\Delta$ . Intuitively, $|x,\Delta\rangle_{O}$ can be viewed as a state localized around the position $q=x\Delta$ , such that adjacent basis states (i.e., $|x\pm 1,\Delta\rangle_{O}$ ) are separated by $\Delta$ ; the exact form of the basis states depends on the AD/DA conversion implementation, as discussed below.

Ultimately, we wish to construct an $n$ -qubit quantum D/A conversion unitary $U_{\text{D/A}}(\Delta,n)$ , that obeys

\displaystyle U_{\text{D/A}}(\Delta,n)|\psi\rangle_{Q}|0,\Delta\rangle_{O}=|\mathbf{0}\rangle_{Q}|\psi\rangle_{O},

(25)

where $|0,\Delta\rangle_{O}$ is the initial oscillator state, and $\mathbf{0}$ is a vector of all $0$ ’s. Crucially, the initial and final states must be unentangled to ensure that the information content of the qubits state is fully transferred to the oscillator. Any residual entanglement would indicate that information remains in the quantum correlations between the systems, inaccessible to either party individually. As this conversion operation is unitary, its inverse furnishes an $n$ -qubit quantum A/D conversion unitary:

\displaystyle U_{\text{D/A}}(\Delta,n)^{\dagger}|\mathbf{0}\rangle_{Q}|\psi\rangle_{O}=|\psi\rangle_{Q}|0,\Delta\rangle_{O}.

(26)

Below, we will present two methods to realize quantum AD/DA conversion. The first protocol uses hybrid single-variable QSP; the second protocol is an adaptation of the state transfer protocol of Ref. [66], which we show is an instance of non-Abelian QSP. For both protocols, we prove analytical bounds on their performance and resource requirements.

IV-A Quantum AD/DA Conversion: Hybrid Single-Variable QSP

Our first quantum AD/DA conversion protocol employs hybrid single-variable QSP. For this protocol, it would be ideal for the oscillator basis states $|x,\Delta\rangle_{O}$ to be position eigenstates $|q\rangle_{O}$ , with eigenvalues $q=x\Delta$ at integer multiples of the spacing parameter. Realistically however, an exact position eigenstate is un-normaliazable and cannot be prepared, so we instead take our basis states to be Gaussians of width $\sigma\ll\Delta$ centered around $x\Delta$ :

|x,\Delta\rangle_{O}^{\text{Gaus}}:=\frac{1}{\sqrt{\sigma}(2\pi)^{1/4}}\int dqe^{-(q-x\Delta)^{2}/4\sigma^{2}}|q\rangle_{O},

(27)

which reduces to a position eigenstate as $\sigma\rightarrow 0$ . These states are nearly orthonormal for small $\sigma/\Delta$ :

^{\text{Gaus}}_{\ \ O}\langle y,\Delta|x,\Delta\rangle_{O}^{\text{Gaus}}=e^{-\frac{\Delta^{2}}{\sigma^{2}}\frac{(x-y)^{2}}{8}},

(28)

which approaches the Kronecker delta $\delta_{x,y}$ as $\sigma/\Delta\rightarrow 0$ .

D/A Conversion Protocol: We first focus on the D/A conversion protocol, as the corresponding A/D protocol is simply its inverse. The D/A protocol consists of two stages: first, a series of conditional displacements are applied between the qubits and oscillator, and then the intermediate state is disentangled by a series of hybrid single-variable QSP operations. We will denote the resulting D/A conversion unitary by $U_{\text{D/A}}^{\text{S-V}}(\Delta,n)$ , using “S-V” for single-variable QSP.

Stage 1 – Displacement: First, we apply a series of controlled displacements to the oscillator: $\prod_{j=1}^{n}D_{j}(\Delta 2^{n-j})$ , where $D_{j}(\Delta 2^{n-j})$ is a displacement (as in Eq. (14)), controlled by the $j^{\text{th}}$ qubit. This transforms the initial state as

	$\displaystyle\|\psi\rangle_{Q}\|0,\Delta\rangle_{O}^{\text{Gaus}}$	$\displaystyle=\sum_{\mathbf{x}}c_{\mathbf{x}}\|\mathbf{x}\rangle_{Q}\|0,\Delta\rangle_{O}^{\text{Gaus}}$		(29)
		$\displaystyle\qquad\qquad\mapsto\sum_{\mathbf{x}}c_{\mathbf{x}}\|\mathbf{x}\rangle_{Q}\|x,\Delta\rangle_{O}^{\text{Gaus}}.$		(29)

We could imagine disentangling this state as

\sum_{\mathbf{x}}c_{\mathbf{x}}|\mathbf{x}\rangle_{Q}|x,\Delta\rangle_{O}^{\text{Gaus}}\mapsto\sum_{\mathbf{x}}c_{\mathbf{x}}|\mathbf{0}\rangle_{Q}|x,\Delta\rangle_{O}^{\text{Gaus}}=|\mathbf{0}\rangle_{Q}|\psi\rangle_{O}^{\text{Gaus}},

(30)

to achieve the desired D/A conversion, where $|\psi\rangle_{O}^{\text{Gaus}}$ is the transferred wave function encoded in the basis of Gaussian states. We realize this disentangling procedure with hybrid single-variable QSP as follows.

Stage 2 – QSP: In the QSP stage, we disentangle the qubits and oscillator by enacting an operation that sets each qubit to $|0\rangle$ as in Eq. (30). This operation would act as $|x_{j}\rangle|x,\Delta\rangle_{O}^{\text{Gaus}}\mapsto|0\rangle|x,\Delta\rangle_{O}^{\text{Gaus}}$ for each qubit $j$ , or equivalently flip qubit $j$ conditioned on the bit $x_{j}$ . Here we implement this operation as a series of hybrid single-variable QSP sequences, one for each qubit.

This desired behavior requires that we determine the bits $\{x_{j}\}$ from the oscillator’s binary representation $|x,\Delta\rangle_{O}^{\text{Gaus}}$ . Observe that the bit $x_{j}$ of the position $x\Delta=\Delta\sum_{j=1}^{n}2^{n-j}x_{j}$ can be read out by a “square wave” function:

S_{j}(\hat{x}):=\Theta\left(\cos\left[\tfrac{\pi}{2^{n-j}}\left(\tfrac{\hat{x}}{\Delta}-2^{n-j-1}+\tfrac{1}{2}\right)\right]\right)=1-x_{j},

(31)

where $\Theta(\cdot)$ is the Heaviside step function. For visual intuition, we depict this function in Fig. 2, illustrating how such a square wave function outputs the bits $x_{j}$ .

We may then use this observation to construct the unitary

	$\displaystyle R_{j}(\hat{x}):$	$\displaystyle=\begin{pmatrix}S_{j}(\hat{x})&\sqrt{1-S_{j}(\hat{x})^{2}}\\ -\sqrt{1-S_{j}(\hat{x})^{2}}&S_{j}(\hat{x})\end{pmatrix}$
		$\displaystyle=\begin{cases}I&x_{j}=0\\ i\sigma_{y}&x_{j}=1,\end{cases}$		(32)

where $\hat{x}$ denotes the position operator. This operation correctly flips the $j^{\text{th}}$ qubit conditioned on $x_{j}$ : $R_{j}(\hat{x})|x_{j}\rangle|x,\Delta\rangle_{O}^{\text{Gaus}}=|0\rangle|x,\Delta\rangle_{O}^{\text{Gaus}}$ .³³3Here we take $|x,\Delta\rangle_{O}^{\text{Gaus}}$ to be an exact position eigenstate; we will remedy this assumption and evaluate performance on $|x,\Delta\rangle_{O}^{\text{Gaus}}$ shortly. Therefore, the sequence $\prod_{j=1}^{n}R_{j}(\hat{x})$ correctly disentangles all $n$ qubits.

Our strategy is to approximate each $R_{j}(\hat{x})$ as a hybrid single-variable QSP sequence. In particular, for the $j$ th sequence, we will choose our variable to be $\hat{w}_{j}=e^{\frac{\pi}{2^{n-j}}(\hat{x}/\Delta-2^{n-j-1}+1/2)}$ . We can then employ hybrid single-variable QSP to implement a real-valued Laurent polynomial that approximates the step function as $F(\hat{w}_{j})\approx S_{j}(\hat{x})$ , corresponding to the operation (see Eq. (18)):

\begin{pmatrix}F(\hat{w}_{j})&i\sqrt{1-F(\hat{w}_{j})^{2}}\\ i\sqrt{1-F(\hat{w}_{j})^{2}}&F(\hat{w}_{j})\end{pmatrix}.

(33)

This follows from choosing $F(\hat{w}_{j})$ to be real, as $F(\hat{w}_{j})=F(\hat{w}_{j}^{-1})\in\mathbb{R}$ . Upon conjugation by a phase gate $S$ , this operation becomes

\displaystyle\begin{pmatrix}F(\hat{w}_{j})&\sqrt{1-F(\hat{w}_{j})^{2}}\\ -\sqrt{1-F(\hat{w}_{j})^{2}}&F(\hat{w}_{j})\end{pmatrix}=:\tilde{R}_{j}(\hat{x}),

(34)

which approximates $\tilde{R}_{j}(\hat{x})\approx R_{j}(\hat{x})$ because $F(\hat{w}_{j})\approx S_{j}(\hat{x})$ , where the accuracy in this approximation is dictated by the polynomial approximation. The accuracy and cost of such an approximation is established in the literature: a QSP polynomial can approximate the step function to within some error $\epsilon$ , except within a region of width $\delta$ centered around the discontinuity, and the degree of this polynomial is $\mathcal{O}\left(\frac{1}{\delta}\log(\frac{1}{\epsilon})\right)$ [39, 41]. In aggregate then, by applying the series of QSP sequences $\prod_{j=1}^{n}\tilde{R}_{j}(\hat{x})$ to intermediate state of Eq. (29), we disentangle the qubits and oscillator, and (approximately) produce the desired final state $|\mathbf{0}\rangle_{Q}|\psi\rangle_{O}$ .

A/D Conversion Protocol: Because the D/A conversion protocol is unitary, its inverse furnishes an analogous quantum A/D conversion protocol. In this direction, take the initial state to be $|\mathbf{0}\rangle_{Q}|\psi\rangle_{O}^{\text{Gaus}}=|\mathbf{0}\rangle_{Q}\sum_{x}c_{x}|x,\Delta\rangle_{O}^{\text{Gaus}}$ . Then, by applying the inverted sequence $\prod_{j=n}^{1}\tilde{W}_{j}(\hat{x})^{\dagger}$ , and subsequently the inverted controlled displacements $\prod_{j=n}^{1}D_{j}(-\Delta 2^{n-j})$ , one obtains the transferred state $|\psi\rangle_{Q}|0,\Delta\rangle_{O}^{\text{Gaus}}$ .

Performance: We illustrate the circuit of the D/A conversion protocol in Fig. 3, showcasing its decomposition into controlled displacements and QSP operations. For intuition, we also depict in Fig. 4a the Wigner function (e.g. a phase space quasiprobability distribution; see Ref. [61] for a detailed definition) of the oscillator upon D/A conversion for various initial 3-qubit states. Let us now analyze the gate complexity and error of this protocol.

The first stage requires $n$ displacement gates of sizes $\Delta 2^{n-j}$ for $j=1,...,n$ . This translates to a total displacement amount

\sum_{j=1}^{n}\Delta 2^{n-j}=\mathcal{O}(\Delta 2^{n}),

(35)

and thus a time complexity $\mathcal{O}(\Delta 2^{n})$ . This scales as $2^{n}$ when the controlled displacements are implemented with a fixed coupling between the qubits and oscillator, yet can be reduced if sufficient squeezing is available on the quantum device (e.g. by selecting $\Delta=\mathcal{O}(2^{-n})$ ).

In the second stage, we take the polynomial implemented by the $j^{\text{th}}$ QSP sequence to be an approximation to the step function that suffers error at most $\epsilon$ outside of a region of width $\delta_{j}$ centered about the discontinuity. Each such QSP sequence requires $\mathcal{O}(\frac{1}{\delta_{j}}\log(1/\epsilon))$ gates [40, 26]. To ensure that the $j^{\text{th}}$ QSP sequence can discern the correct bit $x_{j}$ when acting on a state located at position $q=x\Delta$ , we require that the width of the approximate step function be $\delta_{j}\leq\mathcal{O}(\tfrac{1}{2^{n-j}})$ . Therefore, the total gate complexity of all the QSP sequences is

\displaystyle\mathcal{O}\big{(}\textstyle\sum_{j}\tfrac{1}{\delta_{j}}\log(1/\epsilon)\big{)}=\mathcal{O}(2^{n}\log(1/\epsilon)).

(36)

As the gates comprising the QSP sequences (i.e. rotations) take time $\mathcal{O}(1)$ , this corresponds to a time complexity $\mathcal{O}(2^{n}\log(1/\epsilon))$ .

The total time complexity of this D/A conversion is thus

\displaystyle T_{\rm D/A}=\mathcal{O}\left(2^{n}\left(\Delta+\log(1/\epsilon)\right)\right).

(37)

Again, for constant $\Delta$ , this scales linearly in the dimension of the DV Hilbert space; this is expected as we are directly encoding the initial state in $2^{n}$ basis states equally spaced in position space. In principle, one could more efficiently encode this information via a binary encoding on multiple oscillators.

Lastly, to analyze the fidelity of this D/A conversion, note its two sources of error: first, the basis states are not exact position eigenstates but rather Gaussians of finite width $\sigma$ ; and second, the QSP polynomial is only an accurate approximation to within error $\epsilon$ , and fails near the discontinuity of the step function. A careful analysis of these errors, presented in Appendix C, indicates that the fidelity between the output state of this protocol and the desired state $\ket{\mathbf{0}}_{Q}\ket{\psi}_{O}^{\text{Gaus}}$ is

1-\mathcal{O}(n\epsilon)-e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})}.

(38)

Note that this depends on the ratio $\sigma/\Delta$ , and consequently, the degree to which the basis states are orthogonal. Therefore, one can improve fidelity by either squeezing the initial state to decrease $\sigma$ , or selecting a larger spacing $\Delta$ . In particular, to achieve a fidelity at least $1-\varepsilon$ , it suffices to select $\epsilon=\mathcal{O}(\varepsilon/n)$ and $(\Delta/\sigma)^{2}=\mathcal{O}(\log(1/\varepsilon))$ , which translates to an overall time complexity

T_{\rm D/A}=\mathcal{O}\left(2^{n}\left(\sigma\sqrt{\log(1/\varepsilon)}+\log(n/\varepsilon)\right)\right).

(39)

Lastly, recall that the inverse of this protocol provides a quantum A/D conversion protocol. Because the inverse is just the time-reversed operation, its gate and time complexities are the same as that of D/A conversion, as is the asymptotic expression for the fidelity.

Collectively, the results of these AD/DA conversion protocols can be summarized as follows:

Theorem 1 (Quantum AD/DA Conversion with Hybrid Single Variable QSP).

The quantum D/A conversion protocol based on hybrid single-variable QSP achieves a fidelity $1-\mathcal{O}(n\epsilon)-e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})}\big{)}$ , at a gate complexity of $\mathcal{O}(2^{n}\log(1/\epsilon))$ and time complexity $\mathcal{O}(2^{n}(\Delta+\log(1/\epsilon)))$ , where $n$ is the number of qubits of the DV state, $\epsilon$ is the error on the the polynomial realized by QSP, $\sigma$ is the width of the initial Gaussian wave function of the oscillator, and $\Delta$ is a spacing parameter.

Analogously, in reverse this furnishes a quantum A/D conversion protocol that achieves a fidelity $1-\mathcal{O}(n\epsilon)-e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})}$ and identical gate and time complexities.

IV-B Quantum AD/DA Conversion: Hybrid Non-Abelian QSP

Recently, Ref. [89] proposed a method to transfer a CV state to an $n$ -qubit state by enacting a series of controlled displacements between the oscillator and each qubit. This naturally defines an A/D conversion protocol, which in reverse furnishes a D/A conversion protocol. Below, we review these protocols and provide bounds on their performance. We also show how these protocols can be viewed as instances of hybrid non-Abelian QSP, and thus we will refer to them accordingly.

A/D Conversion Protocol: To begin, let us denote the A/D conversion unitary of Ref. [89] by $U_{\text{D/A}}^{\text{N-A}}(\Delta,n)^{\dagger}$ , using “N-A” for non-Abelian. We define this by its Hermitian conjugate such that its inverse $U_{\text{D/A}}^{\text{N-A}}(\Delta,n)$ performs D/A conversion, in line with our notation of Eq. (25). This operation uses a spacing parameter $\Delta$ and transfers a CV state to $n$ qubits.

The initial state of this protocol is $|\mathbf{0}\rangle_{Q}|\psi\rangle_{O}$ , where $|\psi\rangle_{O}=\int dq\ \psi(q)dq|q\rangle_{O}$ is a state on the oscillator to be transferred to the $n$ qubits. Explicitly, $U_{\text{D/A}}^{\text{N-A}}(\Delta,n)^{\dagger}$ is the unitary operation

U_{\text{D/A}}^{\text{N-A}}(\Delta,n)^{\dagger}=\prod_{j=n}^{1}W_{j}V_{j}=W_{n}V_{n}\cdots W_{1}V_{1},

(40)

where

V_{j}=e^{i\frac{\pi}{2^{j}\Delta}\hat{x}\hat{\sigma}_{y}^{(j)}},\quad W_{j}=\begin{cases}e^{i\frac{\Delta}{2}2^{j-1}\hat{p}\hat{\sigma}_{x}^{(j)}}&j<n,\\ e^{-i\frac{\Delta}{2}2^{j-1}\hat{p}\hat{\sigma}_{x}^{(j)}}&j=n,\end{cases}

(41)

are momentum boosts and displacements of the oscillator, and the superscript ${(j)}$ denotes action on the $j^{\text{th}}$ qubit (e.g. $\sigma_{x}^{(j)}$ acts on qubit $j$ ). As shown in Ref. [89], application of $U_{\text{D/A}}^{\text{N-A}}(\Delta,n)^{\dagger}$ to the initial state outputs the state

\displaystyle\sum_{\mathbf{s}\in\{-1,+1\}^{n}}\int dq\ \psi(q+q_{\mathbf{s}})\prod_{j=1}^{n}\cos(\tfrac{\pi q}{\Delta 2^{j}})|\phi_{\mathbf{s}}\rangle_{Q}|q\rangle_{O},

(42)

where the sum runs over all $\mathbf{s}\in\{-1,+1\}^{n}$ , and the basis states are

|\phi_{\textbf{s}}\rangle=(-1)^{\gamma_{\textbf{s}}}\cdot\bigotimes_{j=1}^{n}\left[\frac{1}{\sqrt{2}}\big{(}|0\rangle+s_{j}|1\rangle\big{)}\right],

(43)

for a scalar $\gamma_{s}$ defined as

\gamma_{\mathbf{s}}=\sum_{j=1}^{n-2}\frac{1}{2}(s_{j}+s_{j+1})+\frac{1}{2}(s_{n-1}-s_{n}).

(44)

For instance, if $\mathbf{s}=(1,-1,1,-1)$ , then $\gamma_{\mathbf{s}}=1$ , and $|\phi_{\mathbf{s}}\rangle=(-1)\cdot|+\rangle|-\rangle|+\rangle|-\rangle$ . In addition, the value $q_{\textbf{s}}$ in Eq. (42) is

q_{\textbf{s}}=\frac{\Delta}{2}\Bigg{(}\sum_{j=1}^{n-1}s_{j}2^{j-1}-s_{n}2^{n-1}\Bigg{)}.

(45)

This quantity takes $2^{n}$ discrete values in the range $[-\tfrac{\Delta}{2}(2^{n}-1),\tfrac{\Delta}{2}(2^{n}-1)]$ , with each possible value equally spaced by $\Delta$ .

Two approximations are used in Ref. [89] to simplify the state of Eq. (42). First, it is assumed that the support of $\psi(q)$ is limited to $|q|\leq\tfrac{\Delta}{2}(2^{n}-1)$ , such that one can make the replacement $\prod_{j=1}^{n}\cos(\tfrac{\pi q}{\Delta 2^{j}})\approx\text{sinc}(\tfrac{\pi q}{\Delta})$ over the support of the wave function. Second, it is also assumed that $\int dq\ \psi(q+q_{\mathbf{s}})\text{sinc}(\tfrac{\pi q}{\Delta})\approx\psi(q_{\mathbf{s}})\int dq\ \text{sinc}(\tfrac{\pi q}{\Delta})$ , which dictates that $\psi(q)$ be slowly varying relative to $\text{sinc}(\tfrac{\pi q}{\Delta})$ , i.e., $|\tfrac{d\psi}{dq}|\ll 1/\Delta$ . With both of these approximations made, Eq. (42) simplifies to

\sum_{\mathbf{s}}\sqrt{\Delta}\psi(q_{\mathbf{s}})|\phi_{\mathbf{s}}\rangle_{Q}\otimes\frac{1}{\sqrt{\Delta}}\int dq\ \text{sinc}(\tfrac{\pi q}{\Delta})|q\rangle_{O}.

(46)

Notably, the oscillator is now decoupled from the qubits, and therefore the initial CV state $\psi(q)$ has been transferred to a corresponding qubits state $\sum_{\mathbf{s}}\sqrt{\Delta}\psi(q_{\mathbf{s}})|\phi_{\mathbf{s}}\rangle_{Q}$ , encoded in the $\{|\phi_{\mathbf{s}}\rangle_{Q}\}$ basis.

D/A Conversion Protocol: This A/D conversion protocol can be run in reverse to achieve D/A conversion. In this direction, one first prepares the qubits in the state $\sum_{\mathbf{s}}c_{\mathbf{s}}|\phi_{\mathbf{s}}\rangle$ , and the oscillator in the sinc state $|0,\Delta\rangle_{O}^{\text{sinc}}=\frac{1}{\sqrt{\Delta}}\int dq\ \text{sinc}(\tfrac{\pi q}{\Delta})|q\rangle_{O}$ .⁴⁴4As explained in Ref. [89], this exact state is unphysical because it has infinite energy, but it can be well approximated by a squeezed vacuum. Then, enacting $U_{\text{D/A}}^{\text{N-A}}(\Delta,n)=\prod_{j=1}^{n}V_{j}^{\dagger}W_{j}^{\dagger}$ (approximately) outputs the state

\displaystyle|\mathbf{0}\rangle_{Q}\otimes\sum_{\mathbf{s}}c_{\mathbf{s}}\frac{1}{\sqrt{\Delta}}\int dq\ \text{sinc}\left(\tfrac{\pi(q-q_{\mathbf{s}})}{\Delta}\right)|q\rangle_{O}=|\mathbf{0}\rangle_{Q}|\psi\rangle_{O}^{\text{sinc}}.

(47)

This has transferred the initial DV state to a CV state encoded in the basis of displaced “sinc states”:

|q_{\mathbf{s}},\Delta\rangle_{O}^{\text{sinc}}:=\frac{1}{\sqrt{\Delta}}\int dq\ \text{sinc}\left(\tfrac{\pi(q-q_{\mathbf{s}})}{\Delta}\right)|q\rangle_{O}.

(48)

A sinc state is a state in continuous space peaked around $q=q_{s}$ , with adjacent sinc state peaks separated by $\Delta$ , such they are orthonormal: ${}^{\text{sinc}}_{O}\langle q_{\mathbf{s}},\Delta|q_{\mathbf{s}^{\prime}},\Delta\rangle_{O}^{\text{sinc}}=\delta_{\mathbf{s}\mathbf{s}^{\prime}}$ . Satisfyingly, this representation of $|\psi\rangle_{O}^{\text{sinc}}$ as a sum of displaced sinc functions is analogous to the construction of Shannon’s sampling theorem [90]. By this connection, this protocol can be viewed as a quantum realization of Shannon’s sampling theorem.

Recontextualization as Non-Abelian QSP: This AD/DA conversion protocol can be reinterpreted as an instance of non-Abelian QSP. In the D/A direction, we rewrite the term $V_{j}^{\dagger}W_{j}^{\dagger}$ in the language of non-Abelian QSP as

		$\displaystyle e^{-i\frac{\pi}{4}\sigma_{y}^{(j)}}(V_{j}^{\dagger}W_{j}^{\dagger})e^{i\frac{\pi}{4}\sigma_{y}^{(j)}}=e^{-i\frac{\pi}{\Delta 2^{j}}\hat{x}\hat{\sigma}_{y}^{(j)}}e^{\mp i\frac{\Delta}{2}2^{j-1}\hat{p}\hat{\sigma}_{z}^{(j)}}$		(49)
	$\displaystyle=$	$\displaystyle e^{i\frac{\pi}{4}\sigma_{x}^{(j)}}e^{-i\frac{\pi}{\Delta 2^{j}}\hat{x}\hat{\sigma}_{z}^{(j)}}e^{-i\frac{\pi}{4}\sigma_{x}^{(j)}}e^{\mp i\frac{\Delta}{2}2^{j-1}\hat{p}\hat{\sigma}_{z}^{(j)}},$		(49)

where the $-$ sign is taken for $j<n$ , and the $+$ sign for $j=n$ . By comparing this expression to the non-Abelian QSP sequence of Eq. (23), it is readily identified that $V_{j}^{\dagger}W_{j}^{\dagger}$ , upon conjugation by $e^{-i\frac{\pi}{4}\sigma_{y}^{(j)}}$ , corresponds to a degree-1 non-Abelian QSP sequence with the displacement amounts

\displaystyle k=\frac{2\pi}{\Delta 2^{j}},~{}~{}~{}~{}\lambda=\mp\frac{\Delta 2^{j}}{2},

(50)

for the $j^{\text{th}}$ qubit, and with QSP phases

\displaystyle\phi_{0}=\frac{\pi}{4},~{}~{}~{}\phi_{1}^{(k)}=-\frac{\pi}{4},~{}~{}~{}\phi_{1}^{(\lambda)}=0

(51)

for all $j$ qubits. In this incarnation, this AD/DA conversion protocol may be interpreted as a product of $n$ degree- $1$ non-Abelian QSP sequences, where each sequence acts between the oscillator and the $j^{\text{th}}$ qubit. This identification suggests that this protocol could admit a generalization by using a higher degree non-Abelian QSP sequences.

Performance: We illustrate the circuit of the D/A conversion protocol in Fig. 5, showing the series of $V_{j}^{\dagger}W_{j}^{\dagger}$ operations acting between the oscillator and qubits. We also illustrate in Fig. 4b the Wigner function of the final oscillator state after D/A conversion for various initial 3-qubit states. Let us next analyze the gate complexity and performance of this protocol.

As per Eq. (40), this protocol requires $n$ gates, which collectively require a total displacement $\sum_{j=1}^{n}\mathcal{O}(\Delta 2^{j})=\mathcal{O}(\Delta 2^{n})$ . As in the previous AD/DA conversion protocol, this implies an overall time complexity $\mathcal{O}(\Delta 2^{n})$ when the displacements are implemented with a fixed coupling between the qubits and oscillator, although this can be reduced with a sufficiently tunable and strong coupling.

Next, consider the fidelity of this protocol. Ref. [89] presents numerical results on the fidelity achieved in the A/D direction. For example, in transferring the harmonic oscillator eigenstate $|3\rangle$ onto $n$ qubits, the protocol achieves infidelity $\approx 0.2$ for $n=4$ , and $\approx 9\cdot 10^{-4}$ for $n=10$ , indicating that the performance improves drastically with increasing $n$ . Achieving this performance however requires that $\Delta$ be carefully tuned for each value of $n$ to maximize the fidelity, yet no analytical bounds on fidelity are provided in Ref. [89] to guide this tuning. Here, we fill this gap by providing fidelity bounds in both the D/A and A/D directions.

In the A/D direction, the exact output state of Eq. (42) is approximately equal to the desired output state of Eq. (46). The approximations used in reaching this desired state require that $\psi(q)$ have support limited to $|q|\leq\tfrac{\Delta}{2}(2^{n}-1)$ , and be slowly varying as $|\frac{d\psi}{dq}|\ll 1/\Delta$ . A careful analysis of this protocol, presented in Appendix C, indicates that the fidelity between these two states, and thus the fidelity of the A/D direction, is

	$\displaystyle 1$	$\displaystyle-\mathcal{O}\Bigg{(}\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq\|\psi(q)\|^{2}+\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq\|\psi(q)\|^{2}\Bigg{)}$		(52)
		$\displaystyle-\mathcal{O}\Bigg{(}\Delta\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}dq\big{\|}\tfrac{d}{dq}\|\psi(q)\|^{2}\big{\|}\Bigg{)}.$		(52)

Notably, these two contributions to the infidelity arise precisely from the approximations used in simplifying the exact state to the approximate state. The first contribution depends on the support of $\psi(q)$ outside of $|q|\leq\tfrac{\Delta}{2}(2^{n}-1)$ , and the second on the derivative of $\psi(q)$ .

Moreover, D/A conversion is defined by Eq. (47). By an analysis similar to the A/D direction, also presented in Appendix C, we find that the fidelity of D/A conversion is

1-\mathcal{O}\Bigg{(}\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq|\psi(q)|^{2}+\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq|\psi(q)|^{2}\Bigg{)},

(53)

where now $\psi(q)=\frac{1}{\sqrt{\Delta}}\sum_{\mathbf{s}}c_{\mathbf{s}}\text{sinc}\left(\tfrac{\pi(q-q_{\mathbf{s}})}{\Delta}\right)$ is the CV wave function upon ideal D/A conversion. Evidently, in this direction, the fidelity is impeded only by the support of $\psi(q)$ outside $|q|<\tfrac{\Delta}{2}(2^{n}-1)$ . A term analogous to the second contribution in Eq. (52) is absent, because the approximation that produces this contribution is naturally satisfied in the D/A direction; see Appendix C for details.

In summary, the performance of AD/DA conversion via non-Abelian QSP is encapsulated in the following theorem:

Theorem 2 (Quantum AD/DA Conversion with Non-Abelian QSP).

The quantum D/A conversion protocol based on hybrid non-Abelian QSP achieves a fidelity

1-\mathcal{O}\left(\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq|\psi(q)|^{2}+\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq|\psi(q)|^{2}\right),

(54)

at a gate complexity $\mathcal{O}(n)$ and time complexity $\mathcal{O}(\Delta 2^{n})$ , where $n$ is the number of qubits, $\psi(q)=\frac{1}{\sqrt{\Delta}}\sum_{\mathbf{s}}c_{\mathbf{s}}\mathrm{sinc}\left(\tfrac{\pi(q-q_{\mathbf{s}})}{\Delta}\right)$ is the resulting CV wave function, $\{c_{\mathbf{s}}\}$ are the coefficients of the initial qubit state $\ket{\psi}_{Q}=\sum_{x}c_{\mathbf{s}}|\phi_{\mathbf{s}}\rangle_{Q}$ being transferred, and $\Delta$ is a spacing parameter.

Analogously, in reverse this furnishes a quantum A/D conversion protocol with identical gate and time complexity, and a fidelity given by Eq. (52).

V Quantum Fourier Transform from Oscillator Evolution

The above quantum AD/DA conversion protocols can be used to implement quantum algorithms on hybrid CV-DV processors. We demonstrate this by using these protocols to implement the quantum Fourier transform (QFT) on CV-DV hardware. The QFT is an important quantum subroutine, ubiquitous in many quantum algorithms, such as Shor’s algorithm [91], phase estimation [17], and quantum gradient estimation [92]. It is defined on an $n$ -qubit state $|\psi\rangle_{Q}=\sum_{\mathbf{x}}c_{\mathbf{x}}|\mathbf{x}\rangle_{Q}$ as the unitary transformation

U_{\text{QFT}}|\psi\rangle_{Q}=\sum_{\mathbf{x}}\Bigg{[}\sum_{\mathbf{y}}\frac{1}{\sqrt{2^{n}}}c_{\mathbf{y}}e^{2\pi ixy/2^{n}}\Bigg{]}|\mathbf{x}\rangle_{Q},

(55)

which effectively implements a discrete Fourier transform of the coefficients $c_{\mathbf{x}}$ . While the traditional construction of the QFT as a DV quantum circuit is well-known [17, 93], the construction on CV-DV hardware will differ significantly due to the fundamental differences between oscillators and qubits.

To motivate our construction of the QFT on a CV-DV system, recall that the free evolution of an oscillator swaps position and momentum (see Eq. (13)), thus applying a continuous Fourier transform to the underlying wave function. Using this intuition, we show that by transferring an initial DV state to an oscillator state, enacting a free evolution for an appropriately chosen time, and finally transferring the state back to qubits, the QFT of the initial DV state can be extracted. Importantly however, modifications are required to connect this continuous Fourier transform to the discrete Fourier transform implemented by the QFT.

Prior work in this direction includes Ref. [67], which describes a way of using Kerr nonlinearities between two oscillators to perform the QFT. However, they encode the qubit states into Fock states on the oscillators, which requires a time an order of magnitude greater than a single photon coherence time, and hence limits their utility. Their algorithm also requires that one perform a photon-number resolved measurement and post-select to disentangle the two oscillators, which requires significant runtime and control. On the other hand, the QFT algorithms we put forth here are not inhibited by these challenges.

In this section, we first describe a correspondence between the continuous Fourier transform and the discrete Fourier transform, which will allow us to bridge the gap between oscillator evolution and the QFT. Thereafter, we develop two algorithms for realizing the QFT on CV-DV hardware by incorporating the above AD/DA conversion protocols, first using single-variable QSP, and then non-Abelian QSP.

V-A Continuous-Discrete Fourier Transform Correspondence

Crucial to our construction of the QFT is a correspondence between the continuous Fourier transform and the discrete Fourier transform. Specifically, consider a discrete signal $c_{x}$ for $x\in[0,...,N-1]$ , that is made periodic over $x\in\mathbb{Z}$ and encoded in a continuous function $f(q)$ as

f(q)=\sum_{x\in\mathbb{Z}}c_{x}g(q-x\Delta),

(56)

where $g(q)$ is a basis function localized about $q=0$ and $\Delta$ is the spacing between basis functions. The continuous Fourier transform of this function evaluates to

\tilde{f}(p)=\sum_{x\in\mathbb{Z}}c_{x}\tilde{g}(p)e^{ipx\Delta},

(57)

where $\tilde{g}(p)$ is the Fourier transform of $g(q)$ . Splitting the index $x$ into $x=Nk+y$ for $k\in\mathbb{Z}$ and $y\in[0,1,...,N-1]$ , this can be rewritten as

		$\displaystyle\sum_{k\in\mathbb{Z}}e^{ipNk\Delta}\sum_{y=0}^{N-1}c_{y}e^{ipy\Delta}\tilde{g}(p)$		(58)
		$\displaystyle=\sum_{l\in\mathbb{Z}}\tilde{g}(\tfrac{2\pi}{\Delta}\tfrac{l}{N})\frac{2\pi}{N\Delta}\delta(p-\tfrac{2\pi}{\Delta}\tfrac{l}{N})\cdot\sum_{y=0}^{N-1}c_{y}e^{i2\pi yl/N}$
		$\displaystyle=\sum_{l\in\mathbb{Z}}\frac{2\pi}{\Delta}\tilde{g}(\tfrac{2\pi}{\Delta}\tfrac{l}{N})\delta(p-\tfrac{2\pi}{\Delta}\tfrac{l}{N})\cdot\tilde{c}_{l}$

where we have noted that $\sum_{k\in\mathbb{Z}}e^{ipNk\Delta}=\frac{2\pi}{N\Delta}\sum_{l\in\mathbb{Z}}\delta(p-\tfrac{2\pi}{\Delta}\tfrac{l}{N})$ is a Dirac comb, and we have denoted by $\tilde{c}_{l}$ the discrete Fourier transform of $c_{y}$ . Evidently then, the continuous Fourier transform of a discrete signal that is encoded periodically in continuous basis functions results in a sum over the discrete Fourier transform of the signal, with coefficients proportional to the Fourier transform of the basis function.

This correspondence can be used to perform the quantum Fourier transform by letting $c_{x}$ be the coefficients of an initial state on qubits. Then, $f(q)$ represents the wave function of an oscillator after transferring the qubits state with basis function $g(q)$ . By enacting a continuous Fourier transform on the oscillator (i.e. free evolution), the new wave function given by Eq. (58) will pluck out the states $|q=\tfrac{2\pi l}{N\Delta}\rangle$ with coefficients proportional to the discrete Fourier transform of $c_{x}$ . As this discrete Fourier transform equates to the coefficients of QFT, we find that appropriately transferring this state back to qubits produces the QFT of the initial state. This is of course requires a suitable choice of basis function $g(q)$ whose Fourier transform behaves favorably.

We use this correspondence to perform the QFT in both protocols presented below. We also show that by prepending the initial state with $a$ ancilla qubits $|+\rangle^{\otimes a}$ , we are able to make the corresponding discrete signal approximately periodic, and exploit the correspondence successfully, with a fidelity that improves with increasing $a$ .

V-B Quantum Fourier Transform Protocols

We now combine the quantum AD/DA conversion protocols of Sec. IV with the above correspondence to realize the QFT on a CV-DV system, and provide analytical bounds on its performance. It is first important to recall that AD/DA conversion with single-variable QSP uses a basis of Gaussian states $g^{\text{Gaus}}(q)=\frac{1}{\sqrt{\sigma}\sqrt[4]{2\pi}}e^{-q^{2}/4\sigma^{2}}$ (see Eq. (27)), and AD/DA conversion with non-Abelian QSP uses a basis of sinc states $g^{\text{sinc}}(q)=\frac{1}{\sqrt{\Delta}}\text{sinc}(\tfrac{\pi q}{\Delta})$ (see Eq. (48)). Both of these basis functions transform favorably under continuous Fourier transform, which allows us to successfully exploit the above correspondence. The Gaussian function maps to another Gaussian function $\tilde{g}^{\text{Gaus}}(p)=\sqrt{\sigma}(2/\pi)^{1/4}e^{-\sigma^{2}p^{2}}$ , and the sinc function maps to a box function $\tilde{g}^{\text{sinc}}(p)=(\Delta/2\pi)^{1/2}1_{|q|\leq\pi/\Delta}$ where $1_{|q|\leq\pi/\Delta}$ is an indicator function.

V-B1 QFT Protocol 1: Hybrid Single Variable QSP

Using the single-variable QSP D/A conversion protocol, the high level construction of the QFT is as follows. We first transfer the qubits state to an equivalent oscillator state with spacing $\Delta$ , and then apply a displacement operation to make the state symmetric about $q=0$ in position space. Subsequently, we apply the Fourier gate to the oscillator, and finally transfer the oscillator state back to qubits with a reciprocal spacing $\frac{\pi}{2^{n}\Delta}=:\Delta^{\prime}$ by using a modified D/A conversion unitary $\tilde{U}_{\text{D/A}}^{\text{S-V}}(\Delta^{\prime},n)^{\dagger}$ , where the controlled displacements that comprise this unitary are each doubled. This modification implements the correct phases of the QFT; intuitively, it ensures that the product of the displacements equate to the proper phase $(x\Delta)\cdot(y\cdot 2\cdot\Delta^{\prime})=2\pi xy/2^{n}$ . Throughout this construction, ancilla qubits are appended to the initial state to make the underlying state periodic and increase the fidelity with the exact QFT.

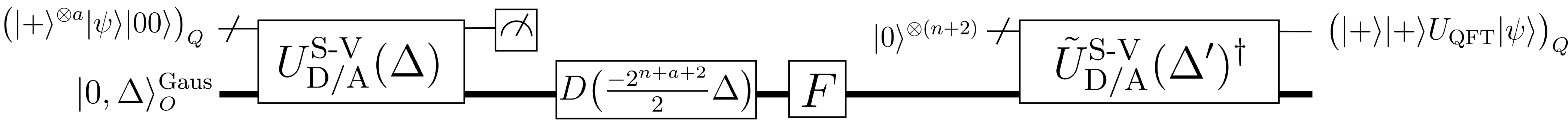
Let us verify this QFT construction on the input state $|\psi\rangle_{Q}=\sum_{\mathbf{x}}c_{\mathbf{x}}|{\mathbf{x}}\rangle_{Q}$ by going through it step-by-step. For illustrative purposes, we present the corresponding QFT circuit in Fig. 6. Note that in this figure, the initial state is appended by $|00\rangle$ , which as we will see later, will improve the fidelity with the exact QFT. To simplify the current presentation, we exclude these qubits for now, and include them at the end of the algorithm when they are necessary.

Step 1: First prepend $|\psi\rangle_{Q}$ by $a$ ancilla qubits $|+\rangle_{Q}^{\otimes a}$ :

\displaystyle\left(|+\rangle^{\otimes a}|\psi\rangle\right)_{Q}

\displaystyle=\frac{1}{\sqrt{2^{a}}}\sum_{k=0}^{2^{a}-1}\sum_{x=0}^{2^{n}-1}c_{\mathbf{x}}|2^{n}\cdot k+x\rangle_{Q}.

(59)

The coefficients of this state are $c_{\mathbf{x}}/\sqrt{2^{a}}$ and repeat over $2^{a}$ periods of size $2^{n}$ . This renders the coefficients approximately periodic and will enable us to exploit the aforementioned continuous-discrete Fourier transform correspondence.

Step 2: Next, use the D/A conversion unitary $U^{\text{S-V}}_{\rm D/A}(\Delta,n+a)$ to transfer this state to the oscillator, producing the state

|\mathbf{0}\rangle_{Q}\frac{1}{\sqrt{2^{a}}}\sum_{k=0}^{2^{a}-1}\sum_{x=0}^{2^{n}-1}c_{\mathbf{x}}|2^{n}\cdot k+x,\Delta\rangle_{O}.

(60)

This step suffers infidelity $\mathcal{O}((n+a)\epsilon)+e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})}$ , where $\epsilon$ is the error in the QSP polynomial approximation to the square wave function.

Step 3: At this stage, the initial state has been mapped to an oscillator state, encoded in a basis of states with peaks from $q=0\cdot\Delta$ to $q=(2^{n+a}-1)\cdot\Delta$ . The next step is to symmetrize these basis states about $q=0$ by applying a displacement $D(\tfrac{-2^{n+a}}{2}\Delta)$ to the oscillator, producing the state

\displaystyle\frac{1}{\sqrt{2^{a}}}\sum_{k=-2^{a}/2}^{2^{a}/2-1}\sum_{x=0}^{2^{n}-1}c_{\mathbf{x}}|x+2^{n}k,\Delta\rangle_{O},

(61)

where we have symmetrized the sum over $k$ .

Step 4: Written in the position basis, the current state is

\displaystyle\sum_{k=-2^{a}/2}^{2^{a}/2-1}\sum_{x=0}^{2^{n}-1}\frac{c_{\mathbf{x}}}{\sqrt{2^{a}\sigma\sqrt{2\pi}}}\int dqe^{-(q-(2^{n}k+x)\Delta)^{2}/4\sigma^{2}}|q\rangle_{O}.

(62)

The next step is to apply the Fourier gate (Eq. (12)) to this state, which enacts a continuous Fourier transform on the underlying wave function and produces

\displaystyle\sqrt{\frac{\sigma}{2^{a}}\sqrt{\frac{2}{\pi}}}\int dq\sum_{\mathbf{x}}c_{\mathbf{x}}e^{iq\Delta x}\left[\sum_{k=-2^{a}/2}^{2^{a}/2-1}e^{iq2^{n}k\Delta}\right]e^{-\sigma^{2}q^{2}}|q\rangle_{O}.

(63)

The factor $\sum_{k=-2^{a}/2}^{2^{a}/2-1}e^{iq\Delta 2^{n}k}$ in brackets is known as a Dirichlet kernel. In the limit of large $a$ , it behaves under an integral as a Dirac comb $\sum_{l\in\mathbb{Z}}\delta(\frac{q\Delta 2^{n}}{2\pi}-l)$ , suffering an error $\mathcal{O}(1/2^{a})$ . Taking the large $a$ limit in Eq. (63), this factor will select out values $q_{l}:=l\frac{2\pi}{\Delta 2^{n}}$ from the integral, such that we can re-express the state as

\displaystyle\sqrt{\frac{2\pi\sigma}{\Delta 2^{n}}\sqrt{\frac{2}{\pi}}}\sum_{l\in\mathbb{Z}}\sum_{\mathbf{x}}c_{\mathbf{x}}e^{i2\pi lx/2^{n}}e^{-\sigma^{2}q_{l}^{2}}\widetilde{|q_{l}\rangle}_{O},

(64)

where

\displaystyle\widetilde{|q_{l}\rangle}_{O}:=\sqrt{\frac{\Delta 2^{n}}{2\pi 2^{a}}}\int_{q_{l}-\frac{\pi}{\Delta 2^{n}}}^{q_{l}+\frac{\pi}{\Delta 2^{n}}}dq\left[\sum_{k=-2^{a}/2}^{2^{a}/2-1}e^{iq2^{n}k\Delta}\right]|q\rangle_{O}

(65)

is a normalized state that becomes increasingly concentrated around $q=q_{l}$ with increasing $a$ . The infidelity suffered in taking the large $a$ limit and simplifying the state to Eq. (64) is $\mathcal{O}(1/2^{a})$ . Observe that taking this limit has given rise to a phase $e^{i2\pi lx/2^{n}}$ , which will ultimately reproduce the QFT.

Step 5: Lastly, we introduce $n$ qubits in the state $|\mathbf{0}\rangle_{Q}$ , and transfer the oscillator state to the $n$ qubits using the modified inverse D/A conversion unitary $\tilde{U}_{\text{D/A}}^{\text{S-V}}(\Delta^{\prime},n)^{\dagger}$ , where $\Delta^{\prime}=\frac{\pi}{2^{n}\Delta}$ is the reciprocal spacing. As we mentioned earlier, this operation is modified such that the controlled displacements comprising it are doubled. The application of this operation is rather involved, and is fully presented in Appendix D. The result is that the output of this stage is approximately a product state $|\alpha\rangle_{Q}|\beta\rangle_{O}$ , with infidelity $\mathcal{O}(\sigma/\Delta)$ . The qubits state is

\displaystyle|\alpha\rangle_{Q}=\sum_{\mathbf{x}}c_{\mathbf{x}}e^{-i\pi x/2}U_{\text{QFT}}|\mathbf{x}\rangle_{Q},

(66)

which is nearly the QFT of $|\psi\rangle_{Q}$ , and the oscillator state is

\displaystyle|\beta\rangle_{O}=\sqrt{\frac{2\pi\sigma}{\Delta}\sqrt{\frac{2}{\pi}}}\sum_{m\in\mathbb{Z}}e^{-\sigma^{2}(\frac{2\pi}{\Delta}m)^{2}}\widetilde{|\tfrac{2\pi}{\Delta}(m-\tfrac{1}{4})\rangle}_{O},

(67)

which is a discretized Gaussian state in the basis $\widetilde{|q_{l}\rangle}$ .

Evidently, the qubits state deviates from the QFT by a phase $e^{-i\pi x/2}$ . This phase arises because the action of free evolution on a state symmetrized about position $q=0$ (as we have here) really implements a symmetric QFT, with coefficients given by a sum symmetrized about $y=0$ : $\sum_{y=-2^{n}/2}^{2^{n}/2-1}c_{y}e^{2\pi ixy/2^{n}}$ . This can be mapped to the usual QFT by shifting $y\mapsto y+2^{n}/2$ , as the expense of incurring a phase $e^{-i\pi x/2}$ .

Fortunately, this phase is inconsequential and can be removed by appending $|00\rangle$ to the initial state as $(|\psi\rangle|00\rangle)_{Q}$ . This guarantees that $x\ \text{mod}\ 4=0$ for any nonzero $c_{\mathbf{x}}$ , such that each phase is $e^{-i\pi x/2}=1$ . Then, A/D conversion onto $n+2$ qubits yields the state [17]

U_{\text{QFT}}(|\psi\rangle|00\rangle)=|+\rangle|+\rangle U_{\text{QFT}}(|\psi\rangle),

(68)

from which the QFT of $|\psi\rangle$ may be extracted. This addresses the additional ancilla qubits $|00\rangle$ depicted in Fig. 6.

Performance: The bulk of the gate count of this protocol comes from the D/A conversion via single-variable QSP. Copying over the complexities from Sec. IV-A, we find a gate count $\mathcal{O}(2^{n+a}\log(1/\epsilon))$ and time complexity $\mathcal{O}(2^{n+a}(\Delta+\log(1/\epsilon)))$ . Likewise, by aggregating together the infidelities suffered at each step above, we find a total fidelity

1-\mathcal{O}((n+a)\epsilon)-\mathcal{O}(\sigma/\Delta)-\mathcal{O}(1/2^{a}),

(69)

where $\epsilon$ is the error in the QSP polynomial approximation to a square wave function. As expected, the fidelity is maximized in the limit of small QSP error, large relative spacing between the oscillator basis states, and a large number of ancilla qubits.

Overall, this analysis has proven the following theorem:

Theorem 3 (QFT from Oscillator Evolution and AD/DA Conversion (Single-Variable QSP)).

Using the single-variable QSP AD/DA conversion protocol, oscillator evolution, and additional bosonic gates one can realize the quantum Fourier transform of an $n$ qubit state with fidelity $1-\mathcal{O}((n+a)\epsilon)-\mathcal{O}(e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})})-\mathcal{O}(1/2^{a})$ , gate complexity of $\mathcal{O}(2^{n+a}\log(1/\epsilon))$ , and time complexity $\mathcal{O}(2^{n+a}(\Delta+\log(1/\epsilon)))$ , where $a$ is the number of ancilla qubits, $\epsilon$ is the error of the QSP polynomial, and $\Delta$ is a spacing parameter.

V-B2 QFT Protocol 2: Hybrid Non-Abelian QSP

Analogous to the presentation above, we can also implement the QFT using AD/DA conversion via non-Abelian QSP. Our approach is to first change the basis of the qubits state from the computational basis to the basis $\{|\phi_{\mathbf{s}}\rangle\}$ used in the non-Abelian QSP D/A conversion protocol (see Eq. (43)). Subsequently, we transfer the qubits state to the oscillator, symmetrize the state about $q=0$ in position space, and then apply the Fourier gate. Finally, we transfer the oscillator state back to the qubits with an appropriately-chosen reciprocal spacing, and then transform back to the computational basis to yield the QFT of the initial state. We will again use ancilla qubits throughout the protocol to improve the fidelity with the exact QFT.

We depict the circuit that implements this algorithm in Fig. 7. Let’s again verify its performance by studying its action on an initial $n$ -qubit state $|\psi\rangle_{Q}=\sum_{\mathbf{x}}c_{\mathbf{x}}|\mathbf{x}\rangle_{Q}$ .

Step 1: As before, first prepend $|\psi\rangle$ by $a$ ancilla qubits $|+\rangle^{\otimes a}$ to make the coefficients approximately periodic:

\displaystyle\left(|+\rangle^{\otimes a}|\psi\rangle\right)_{Q}=\frac{1}{\sqrt{2^{a}}}\sum_{k=0}^{2^{a}-1}\sum_{x=0}^{2^{n}-1}c_{\mathbf{x}}|2^{n}\cdot k+x\rangle_{Q}.

(70)

Step 2: The next step is to map this state from the computational basis to the basis $\{|\phi_{\mathbf{s}}\rangle\}$ , which will enable us to use D/A conversion via non-Abelian QSP. To specify an appropriate correspondence between these bases, recall that in this context the string $\mathbf{s}\in\{+1,-1\}^{n+a}$ is associated with a position $q_{\mathbf{s}}=\tfrac{\Delta}{2}(\sum_{j=1}^{n+a-1}s_{j}2^{j-1}-s_{n+a}2^{n+a-1})$ that takes discrete values in the range $[-\tfrac{\Delta}{2}(2^{n+a}-1),\tfrac{\Delta}{2}(2^{n+a}-1)]$ with spacing $\Delta$ (see Eq. (45)). We will therefore index each such possible value by an integer $s$ , defined as

	$\displaystyle s:$	$\displaystyle=\tfrac{1}{\Delta}\left(q_{\mathbf{s}}+\tfrac{\Delta}{2}(2^{n+a}-1)\right)$		(71)
		$\displaystyle=\sum_{j=1}^{n+a-1}\frac{1+s_{j}}{2}2^{j-1}+\frac{1-s_{n+a}}{2}2^{n+a-1},$		(71)

which takes values $s\in\{0,1,...,2^{n+a}-1\}$ .

We then assume access to a unitary operator $\mathcal{T}$ that maps between these bases as $\mathcal{T}|s\rangle=|\phi_{\mathbf{s}}\rangle$ . As shown in Appendix D, $\mathcal{T}$ can be easily implemented as a product of local operations:

\mathcal{T}=(H\sigma_{x})^{\otimes(n+a-1)}\cdot H_{n+a}\cdot\sigma_{z}^{(1)}\sigma_{z}^{(n+a)}\cdot\mathcal{P}_{\leftrightarrow},

(72)

where $\mathcal{P}_{\leftrightarrow}$ is a permutation operation which reverses the order of qubits (i.e., $\mathcal{P}_{\leftrightarrow}|0011\rangle=|1100\rangle$ ). $\mathcal{P}_{\leftrightarrow}$ can be realized as a product of swap gates, or alternatively accommodated for at no cost by simply adopting a convention to reverse order the qubits of the input state. Applying $\mathcal{T}$ to Eq. (70) generates

\displaystyle\frac{1}{\sqrt{2^{a}}}\sum_{k=0}^{2^{a}-1}\sum_{x=0}^{2^{n}-1}c_{\mathbf{x}}|\phi_{2^{n}\cdot k+x}\rangle_{Q}.

(73)

where we are now indexing $|\phi_{s}\rangle$ by the associated integer $s=2^{n}\cdot k+x$ to simplify analysis.

Step 3: Next, prepare the oscillator in the sinc state $|0,\Delta\rangle_{O}^{\text{sinc}}=\tfrac{1}{\sqrt{\Delta}}\int dq\ \text{sinc}\left(\tfrac{\pi q}{\Delta}\right)|q\rangle_{O}$ , and transfer the qubits state to the oscillator by applying the D/A conversion unitary $U_{\text{D/A}}^{\text{N-A}}(\Delta,n+a)$ as per Eq. (47), producing the state

\displaystyle|\mathbf{0}\rangle_{Q}\otimes\frac{1}{\sqrt{2^{a}}}\sum_{k=0}^{2^{a}-1}\sum_{x=0}^{2^{n}-1}\frac{c_{\mathbf{x}}}{\sqrt{\Delta}}\int dq\ \text{sinc}\left(\tfrac{\pi(q-q_{2^{n}\cdot k+x})}{\Delta}\right)|q\rangle_{O}.

(74)

The infidelity suffered in this step is quantified by the expression in Eq. (52); a careful analysis of this scenario, presented in Appendix D, indicates that the infidelity scales as $\mathcal{O}(1/2^{a})$ . By inserting the expression for $q_{s}$ and symmetrizing the sum over $k$ , the expression for the oscillator state simplifies to

\displaystyle\sum_{x=0}^{2^{n}-1}\sum_{k=-2^{a}/2}^{2^{a}/2-1}\frac{c_{\mathbf{x}}}{\sqrt{2^{a}\cdot\Delta}}\text{sinc}\left(\tfrac{\pi(q-\Delta(2^{n}\cdot k+x-1/2))}{\Delta}\right).

(75)

Step 4: Next, symmetrize the oscillator state about $q=0$ by applying a displacement $D\big{(}\tfrac{\Delta}{2}\big{)}$ , outputting the wave function

\displaystyle\sum_{x=0}^{2^{n}-1}\sum_{k=-2^{a}/2}^{2^{a}/2-1}\frac{c_{\mathbf{x}}}{2^{a}\sqrt{\Delta}}\text{sinc}\left(\tfrac{\pi(q-\Delta(2^{n}\cdot k+x))}{\Delta}\right).

(76)

Step 5: Subsequently, we apply the Fourier gate to the oscillator, which transforms the above wave function to its continuous Fourier transform:

\displaystyle\sqrt{\frac{\Delta}{2\pi}}1_{|q|\leq\pi/\Delta}\sum_{x=0}^{2^{n}-1}\sum_{k=-2^{a}/2}^{2^{a}/2-1}\frac{c_{\mathbf{x}}}{\sqrt{2^{a}}}e^{iq\Delta x}e^{iq\Delta 2^{n}k}=:\tilde{\psi}(q).

(77)

Step 6: After the Fourier gate, we will perform the inverse of Steps 4 and 5, but now with the reciprocal spacing $\Delta^{\prime}=\tfrac{2\pi}{2^{n+a}\Delta}$ chosen to produce the QFT. We first enact the inverse of Step 5; that is, we apply the displacement $D(-{\Delta^{\prime}}/{2})$ , which transforms the wave function to $\tilde{\psi}(q+{\Delta^{\prime}}/{2})$ .

Step 7: Next, we perform the inverse of Step 4 by transferring the oscillator state back to a state on $n+a$ qubits by applying $U_{\text{D/A}}^{\text{N-A}}(\Delta^{\prime})^{\dagger}$ . As per Eq. (42), this produces the state

		$\displaystyle\sum_{s=0}^{2^{n+a}-1}\int dq\ \tilde{\psi}(q_{s}^{\prime\prime})\text{sinc}(\tfrac{\pi q}{\Delta^{\prime}})\|\phi_{\mathbf{s}}\rangle_{Q}\|q\rangle_{O},$		(78)
		$\displaystyle\tilde{\psi}(q_{s}^{\prime\prime})=\sum_{x}\sqrt{\tfrac{\Delta}{2\pi 2^{a}}}\int_{\frac{-\pi}{\Delta}}^{\frac{\pi}{\Delta}}dq\ c_{\mathbf{x}}e^{iq_{s}^{\prime\prime}\Delta x}\left[\sum_{k}e^{iq_{s}^{\prime\prime}\Delta 2^{n}k}\right]\text{sinc}(\tfrac{\pi q}{\Delta^{\prime}})$		(78)

where $q_{s}^{\prime\prime}:=q+q_{s}^{\prime}+\frac{\Delta}{2}$ , and $q_{s}^{\prime}=\Delta^{\prime}s-\tfrac{\Delta^{\prime}}{2}(2^{n+a}-1)$ . Note that we have not used any approximations to simplify this expression, as was done in Sec. IV-B. Doing so is unnecessary here, and does not inhibit implementation of the QFT.

As in the previous QFT protocol, the factor $\sum_{k=-2^{a}/2}^{2^{a}/2-1}e^{i(q+q_{s}^{\prime}+\frac{\Delta}{2})\Delta 2^{n}k}$ in brackets is the Dirichlet kernel, which in the limit of large $a$ behaves as the Dirac comb $\sum_{l\in\mathbb{Z}}\delta(\frac{(q+q_{s})\Delta 2^{n}}{2\pi}-l)$ , suffering error $\mathcal{O}(1/2^{a})$ at finite $a$ . One can take this limit to drastically simplify this state; the full technical analysis is presented in Appendix D. The final result is that the state simplifies to the product state

\displaystyle\Bigg{[}\sum_{l=0}^{2^{n}-1}\left(\frac{1}{\sqrt{2^{n}}}\sum_{x=0}^{2^{n}-1}c_{\mathbf{x}}e^{i2\pi lx/2^{n}}e^{-i\pi x/2}\right)|\phi_{s=2^{a}l}\rangle_{Q}\Bigg{]}\widetilde{|0\rangle}_{O},

(79)

where here

\widetilde{|0\rangle}_{O}:=\sqrt{\frac{\Delta 2^{n}}{2\pi}}\int_{\tfrac{-\pi}{\Delta 2^{n}}}^{\tfrac{\pi}{\Delta 2^{n}}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k=-2^{a}/2}^{2^{a}/2-1}e^{iq\Delta 2^{n}k}|q\rangle_{O},

(80)

is a state that becomes increasingly concentrated around $q=0$ with increasing $a$ , and the infidelity in reaching Eq. (79) is $\mathcal{O}(1/2^{a})$ . Evidently, the oscillator and qubits are now decoupled, and the qubits state resembles the QFT evaluated in the basis $|\phi_{s=2^{a}l}\rangle$ . Again, the presence of the QFT coefficients arises from the continuous-discrete correspondence of the Fourier transform discussed earlier.

Step 8: To extract the QFT from this state, the last step is to transform from the $\{|\phi_{s}\rangle\}$ basis back to the computational basis using $\mathcal{T}^{\dagger}$ . This acts as $\mathcal{T}^{\dagger}|\phi_{s=2^{a}l}\rangle=|2^{a}l\rangle=|l\rangle|0\rangle^{\otimes a}$ , such that its application to the previous state produces

		$\displaystyle\left[\sum_{l,x=0}^{2^{n}-1}\frac{1}{\sqrt{2^{n}}}c_{\mathbf{x}}e^{i2\pi lx/2^{n}}e^{-i\pi x/2}\|l\rangle\otimes\|0\rangle^{\otimes a}\right]_{Q}\otimes\widetilde{\|0\rangle}_{O}$		(81)
	$\displaystyle=$	$\displaystyle\left[\sum_{x=0}^{2^{n}-1}e^{-i\pi x/2}c_{\mathbf{x}}U_{\text{QFT}}\left(\|x\rangle\right)\otimes\|0\rangle^{\otimes a}\right]_{Q}\otimes\widetilde{\|0\rangle}_{O}$		(81)

Evidently, the remaining state on the first $n$ qubits is nearly the QFT of the initial state, up to a phase $e^{-i\pi x/2}$ , just as in the previous QFT protocol. Again, this phase arises because this protocol really implements a symmetric QFT, and can be removed by appending $|00\rangle$ to the initial state, outputting the state $U_{\text{QFT}}(|\psi\rangle|00\rangle)=|+\rangle|+\rangle U_{\text{QFT}}(|\psi\rangle)$ .

Performance: Consider first the complexity of this QFT protocol, the bulk of which is due to the use of non-Abelian AD/DA conversion. As per the performance bounds in Sec. IV-B, the gate count scales as $\mathcal{O}(n+a)$ , and the time complexity as $\mathcal{O}(\Delta 2^{n+a})$ . Next, by summing the infidelities suffered at Step 3 and Step 7, we find the overall fidelity of this QFT protocol is simply $1-\mathcal{O}(1/2^{a})$ , which is maximized in the limit of a large number of ancilla qubits.

In summary, this has proven the following theorem:

Theorem 4 (QFT from Oscillator Evolution and AD/DA Conversion Via Non-Abelian QSP)).

Using AD/DA conversion via hybrid non-Abelian QSP , oscillator evolution, and additional bosonic gates one can realize the quantum Fourier transform of an $n$ qubit state with fidelity $1-\mathcal{O}(1/2^{a})$ , gate complexity $\mathcal{O}(n+a)$ , and time complexity $\mathcal{O}(\Delta 2^{n+a})$ , where $a$ is the number of ancilla qubits and $\Delta$ is a spacing parameter.

VI Conclusion and Outlook

In this paper, we have established a framework of mixed analog-digital QSP for execution on hybrid CV-DV quantum hardware. These algorithms generate polynomial transformations of position and momentum, and open the door to a wide variety of algorithms on CV-DV quantum processors. We used this framework to present two unitary protocols that convert a DV quantum state to a CV quantum state and vice-versa (Theorems 1 and 2), thus furnishing a quantum counterpart to AD/DA conversion in classical signal processing. We established the gate and time complexity of both AD/DA conversion protocols; notably, the protocol based on hybrid non-Abelian QSP achieves an efficient gate count of $O(n)$ for converting between an $n$ -qubit state and a CV state.

As a further contribution, we demonstrated how this framework can realize the quantum Fourier transform of an $n$ -qubit state by simply transferring the qubits state to an oscillator, letting the oscillator undergo free-evolution, and then transferring the state back to the qubits (Theorems 3 and 4). Importantly, the protocol incorporating non-Abelian QSP requires only $O(n)$ hybrid CV-DV gates to implement the QFT, as opposed to the $O(n^{2})$ gates of the conventional construction of the QFT [17].

Despite these results, ample open questions remain to be addressed. First, while we have shown that non-Abelian QSP offers more efficient protocols for AD/DA conversion and the QFT compared to its single-variable counterpart, a complete theory of non-Abelian QSP remains to be established, fundamentally hinging upon an extension of QSP to the multivariate setting [27, 94, 30, 85]. Second, while classical digital signal processing benefits from its robustness, it is not clear how to use analog-digital QSP can be made robust against the noise afflicting quantum oscillators and qubits. One idea is to generalize the connection between classical signal processing, frames [95], and wavelet theory [96] to the quantum setting. Conversely, frames and wavelets could also guide the design of novel QSP algorithms.

In addition, while our implementation of the QFT with non-Abelian QSP achieves a gate count linear in the number of qubits, there exist more gate-efficient constructions of the QFT on qubits, which leverage parallelization [97]. Accordingly, it remains an open question how to parallelize our QFT construction over multiple oscillators, which could perhaps prove advantageous. In addition, it would be interesting to investigate what other algorithms and operations could be realized through analog-digital QSP. For instance, analogous to our QFT constructions, the fractional quantum Fourier transform [98, 99] could be realized by letting the oscillator evolve for only a fraction of its period. Likewise, given the unification of quantum algorithms afforded by QSP, it appears promising that analog-digital QSP could act as a Rosetta Stone for translating quantum algorithms from DV hardware to hybrid CV-DV hardware.

Just as the fundamental roles that analog and digital signal processing play in classical computing, our framework provides a concrete way to process mixed analog-digital quantum signals. One example of such analog quantum data is electromagnetic waves that may arise in radar and wireless communications. Despite the fact that current antennas are mostly classical, advancements in quantum hardware have opened opportunities to explore quantum effects of these EM waves with quantum antennas [47, 48]. There are also opportunities to design quantum matched filters and filter banks to enhance detection and estimation sensitivity [100, 101, 102]. More broadly, it would be exciting to synthesize our QSP framework with classical mixed signal processing [14, 2] to develop a theory of quantum-classical signal processing. Beyond theoretical work, co-designing these novel signal processing frameworks with hardware and chips could harness quantum information to make real-world impacts in the forthcoming quantum era of electrical and computer engineering [103, 104].

Acknowledgment

The authors thank Nathan Wiebe and Shraddha Singh for helpful discussions. YL, ILC, and SMG acknowledge the support by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Co-design Center for Quantum Advantage (C²QA) under contract number DE-SC0012704. JMM was supported from the National Science Foundation Graduate Research Fellowship under Grant No. 2141064. SMG acknowledges support by the Army Research Office (ARO) under Grant Number W911NF-23-1-0051. JS was supported in part by the Army Research Office under the CVQC project W911NF-17-1-0481. JS and YL were supported in part by NTT Research.

External interest disclosure: SMG is a consultant for, and an equity holder in, Quantum Circuits, Inc.

References

[1] A. V. Oppenheim, Discrete-time signal processing. Pearson Education India, 1999.
[2] J. G. Proakis, Digital signal processing: principles, algorithms, and applications, 4/E. Pearson Education India, 2007.
[3] C. Van Loan, Computational frameworks for the fast Fourier transform. SIAM, 1992.
[4] R. J. I. Marks, Introduction to Shannon sampling and interpolation theory. Springer Science & Business Media, 2012.
[5] S. Winder, Analog and digital filter design. Elsevier, 2002.
[6] B. J. MacLennan, “A review of analog computing,” Department of Electrical Engineering & Computer Science, University of Tennessee, Technical Report UT-CS-07-601 (September), 2007. [Online]. Available: https://web.eecs.utk.edu/~bmaclenn/papers/RAC-TR.pdf
[7] G. E. Cowan, R. C. Melville, and Y. P. Tsividis, “A VLSI analog computer/digital computer accelerator,” IEEE Journal of Solid-State Circuits, vol. 41, no. 1, pp. 42–53, 2005. [Online]. Available: https://doi.org/10.1109/JSSC.2005.858618
[8] W. Haensch, T. Gokmen, and R. Puri, “The next generation of deep learning hardware: Analog computing,” Proceedings of the IEEE, vol. 107, no. 1, pp. 108–122, 2018. [Online]. Available: https://doi.org/10.1109/JPROC.2018.2871057
[9] A. Vergis, K. Steiglitz, and B. Dickinson, “The complexity of analog computation,” Mathematics and computers in simulation, vol. 28, no. 2, pp. 91–113, 1986.
[10] S. Shuvo, A. A. Akib, M. M. Rahman, T. Islam, R. U. Rashid, S. Mahnaz, M. S. Anwar, S. A. Fattah, and C. Shahnaz, “Analog signal processing based hardware implementation of real-time audio visualizer,” in 2020 IEEE Region 10 Symposium (TENSYMP). IEEE, 2020, pp. 1852–1856. [Online]. Available: https://doi.org/10.1109/TENSYMP50017.2020.9230976
[11] B. Gold, N. Morgan, and D. Ellis, Speech and audio signal processing: processing and perception of speech and music. John Wiley & Sons, 2011.
[12] A. Ambardar et al., Analog and digital signal processing. PWS Boston, MA, 1995.
[13] R. Sharpeshkar, Ultra low power bioelectronics: Fundamentals, biomedical applications, and bio-inspired system. Cambridge University Press, 2010.
[14] W. Kester, Mixed-signal and DSP design techniques. Newnes, 2003.
[15] N. Guo, Y. Huang, T. Mai, S. Patil, C. Cao, M. Seok, S. Sethumadhavan, and Y. Tsividis, “Energy-efficient hybrid analog/digital approximate computation in continuous time,” IEEE Journal of Solid-State Circuits, vol. 51, no. 7, pp. 1514–1524, 2016. [Online]. Available: https://doi.org/10.1109/JSSC.2016.2543729
[16] Y. Huang, N. Guo, M. Seok, Y. Tsividis, K. Mandli, and S. Sethumadhavan, “Hybrid analog-digital solution of nonlinear partial differential equations,” in Proceedings of the 50th Annual IEEE/ACM International Symposium on Microarchitecture, 2017, pp. 665–678. [Online]. Available: https://doi.org/10.1145/3123939.312455
[17] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information. Cambridge University Press, 2010.
[18] J. Preskill, “Lecture notes for physics 229: Quantum information and computation,” California Institute of Technology, 1998.
[19] A. Y. Kitaev, A. Shen, and M. N. Vyalyi, Classical and quantum computation. American Mathematical Soc., 2002, no. 47.
[20] Y. C. Eldar and A. V. Oppenheim, “Quantum signal processing,” IEEE Signal Processing Magazine, vol. 19, no. 6, pp. 12–32, 2002. [Online]. Available: https://doi.org/10.1109/MSP.2002.1043298
[21] K. R. Brown, A. W. Harrow, and I. L. Chuang, “Arbitrarily accurate composite pulse sequences,” Phys. Rev. A, vol. 70, p. 052318, Nov 2004. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevA.70.052318
[22] G. H. Low, T. J. Yoder, and I. L. Chuang, “Methodology of resonant equiangular composite quantum gates,” Phys. Rev. X, vol. 6, p. 041067, Dec 2016. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevX.6.041067
[23] G. H. Low, “Quantum signal processing by single-qubit dynamics,” Ph.D. dissertation, Massachusetts Institute of Technology, 2017.
[24] A. Gilyén, “Quantum singular value transformation & its algorithmic applications,” (PhD Thesis), 2019. [Online]. Available: https://hdl.handle.net/11245.1/20e9733e-6014-402d-afa9-20f3cc4a0568
[25] A. Gilyén, Y. Su, G. H. Low, and N. Wiebe, “Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics,” in Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, 2019, pp. 193–204. [Online]. Available: https://doi.org/10.1145/3313276.3316366
[26] J. M. Martyn, Z. M. Rossi, A. K. Tan, and I. L. Chuang, “Grand unification of quantum algorithms,” PRX Quantum, vol. 2, p. 040203, Dec 2021. [Online]. Available: https://link.aps.org/doi/10.1103/PRXQuantum.2.040203
[27] Z. M. Rossi and I. L. Chuang, “Multivariable quantum signal processing (m-qsp): prophecies of the two-headed oracle,” Quantum, vol. 6, p. 811, 2022. [Online]. Available: https://quantum-journal.org/papers/q-2022-09-20-811/
[28] Z. M. Rossi, J. L. Ceroni, and I. L. Chuang, “Modular quantum signal processing in many variables,” 2023. [Online]. Available: https://arxiv.org/abs/2309.16665
[29] D. Motlagh and N. Wiebe, “Generalized quantum signal processing,” arXiv preprint arXiv:2308.01501, 2023.
[30] B. Németh, B. Kövér, B. Kulcsár, R. B. Miklósi, and A. Gilyén, “On variants of multivariate quantum signal processing and their characterizations,” 2023. [Online]. Available: https://arxiv.org/abs/2312.09072
[31] Z. M. Rossi, V. M. Bastidas, W. J. Munro, and I. L. Chuang, “Quantum signal processing with continuous variables,” 2023. [Online]. Available: https://arxiv.org/abs/2304.14383
[32] L. Laneve, “Quantum signal processing over su(n),” 2024. [Online]. Available: https://arxiv.org/abs/2311.03949
[33] A. K. Tan, Y. Liu, M. C. Tran, and I. L. Chuang, “Perturbative model of noisy quantum signal processing,” Physical Review A, vol. 107, no. 4, p. 042429, 2023. [Online]. Available: https://doi.org/10.1103/PhysRevA.107.042429
[34] Y. Kikuchi, C. Mc Keever, L. Coopmans, M. Lubasch, and M. Benedetti, “Realization of quantum signal processing on a noisy quantum computer,” npj Quantum Information, vol. 9, no. 1, p. 93, 2023. [Online]. Available: https://doi.org/10.1038/s41534-023-00762-0
[35] R. Chao, D. Ding, A. Gilyen, C. Huang, and M. Szegedy, “Finding angles for quantum signal processing with machine precision,” 2020. [Online]. Available: https://arxiv.org/abs/2003.02831
[36] Y. Dong, X. Meng, K. B. Whaley, and L. Lin, “Efficient phase-factor evaluation in quantum signal processing,” Phys. Rev. A, vol. 103, p. 042419, Apr 2021. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevA.103.042419
[37] Y. Dong, L. Lin, H. Ni, and J. Wang, “Infinite quantum signal processing,” 2022. [Online]. Available: https://arxiv.org/abs/2209.10162
[38] L. Ying, “Stable factorization for phase factors of quantum signal processing,” Quantum, vol. 6, p. 842, 2022. [Online]. Available: https://doi.org/10.22331/q-2022-10-20-842
[39] G. H. Low and I. L. Chuang, “Hamiltonian simulation by uniform spectral amplification,” 2017. [Online]. Available: https://arxiv.org/abs/1707.05391
[40] G. H. Low and I. Chuang, “Optimal hamiltonian simulation by quantum signal processing,” Phys. Rev. Lett., vol. 118, p. 010501, 2017. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevLett.118.010501
[41] J. M. Martyn, Y. Liu, Z. E. Chin, and I. L. Chuang, “Efficient fully-coherent quantum signal processing algorithms for real-time dynamics simulation,” The Journal of Chemical Physics, vol. 158, no. 2, p. 024106, 01 2023. [Online]. Available: https://doi.org/10.1063/5.0124385
[42] Y. Dong, J. Gross, and M. Y. Niu, “Beyond heisenberg limit quantum metrology through quantum signal processing,” arXiv preprint arXiv:2209.11207, 2022. [Online]. Available: https://arxiv.org/abs/2209.11207
[43] I. Novikau, E. A. Startsev, and I. Y. Dodin, “Quantum signal processing for simulating cold plasma waves,” Physical Review A, vol. 105, no. 6, Jun. 2022. [Online]. Available: http://dx.doi.org/10.1103/PhysRevA.105.062444
[44] J. Sinanan-Singh, G. L. Mintzer, I. L. Chuang, and Y. Liu, “Single-shot quantum signal processing interferometry,” arXiv preprint arXiv:2311.13703, 2023. [Online]. Available: https://arxiv.org/abs/2311.13703
[45] N. Liu, J. Thompson, C. Weedbrook, S. Lloyd, V. Vedral, M. Gu, and K. Modi, “Power of one qumode for quantum computation,” Phys. Rev. A, vol. 93, p. 052304, May 2016. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevA.93.052304
[46] S. L. Braunstein and P. van Loock, “Quantum information with continuous variables,” Rev. Mod. Phys., vol. 77, pp. 513–577, Jun 2005. [Online]. Available: https://link.aps.org/doi/10.1103/RevModPhys.77.513
[47] G. Y. Slepyan, S. Vlasenko, and D. Mogilevtsev, “Quantum antennas,” Advanced Quantum Technologies, vol. 3, no. 4, p. 1900120, 2020. [Online]. Available: https://doi.org/10.1002/qute.201900120
[48] S. Mikki, “Quantum antenna theory for secure wireless communications,” in 2020 14th European Conference on Antennas and Propagation (EuCAP). IEEE, 2020, pp. 1–4. [Online]. Available: https://doi.org/10.23919/EuCAP48036.2020.9135570
[49] N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, “Extending the lifetime of a quantum bit with error correction in superconducting circuits,” Nature, vol. 536, pp. 441–445, Jul. 2016. [Online]. Available: http://dx.doi.org/10.1038/nature18949
[50] P. Campagne-Ibarcq, A. Eickbusch, S. Touzard, E. Zalys-Geller, N. E. Frattini, V. V. Sivak, P. Reinhold, S. Puri, S. Shankar, R. J. Schoelkopf, L. Frunzio, M. Mirrahimi, and M. H. Devoret, “Quantum error correction of a qubit encoded in grid states of an oscillator,” Nature, vol. 584, no. 7821, pp. 368–372, 2020. [Online]. Available: https://doi.org/10.1038/s41586-020-2603-3
[51] V. V. Sivak, A. Eickbusch, B. Royer, S. Singh, I. Tsioutsios, S. Ganjam, A. Miano, B. L. Brock, A. Z. Ding, L. Frunzio, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, “Real-time quantum error correction beyond break-even,” 2023. [Online]. Available: https://doi.org/10.1038/s41586-023-05782-6
[52] Y. Ma, Y. Xu, X. Mu, W. Cai, L. Hu, W. Wang, X. Pan, H. Wang, Y. P. Song, C. L. Zou, and L. Sun, “Error-transparent operations on a logical qubit protected by quantum error correction,” Nature Physics, 2020. [Online]. Available: https://doi.org/10.1038/s41567-020-0893-x
[53] Z. Ni, S. Li, X. Deng, Y. Cai, L. Zhang, W. Wang, Z.-B. Yang, H. Yu, F. Yan, S. Liu, C.-L. Zou, L. Sun, S.-B. Zheng, Y. Xu, and D. Yu, “Beating the break-even point with a discrete-variable-encoded logical qubit,” Nature, 2023. [Online]. Available: https://doi.org/10.1038/s41586-023-05784-4
[54] J. M. Gertler, B. Baker, J. Li, S. Shirol, J. Koch, and C. Wang, “Protecting a bosonic qubit with autonomous quantum error correction,” Nature, vol. 590, no. 7845, pp. 243–248, 2021. [Online]. Available: https://doi.org/10.1038/s41586-021-03257-0
[55] A. Eickbusch, V. Sivak, A. Z. Ding, S. S. Elder, S. R. Jha, J. Venkatraman, B. Royer, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, “Fast universal control of an oscillator with weak dispersive coupling to a qubit,” Nature Physics, vol. 18, no. 12, pp. 1464–1469, 2022. [Online]. Available: https://doi.org/10.1038/s41567-022-01776-9
[56] C. Weedbrook, S. Pirandola, R. García-Patrón, N. J. Cerf, T. C. Ralph, J. H. Shapiro, and S. Lloyd, “Gaussian quantum information,” Rev. Mod. Phys., vol. 84, pp. 621–669, May 2012. [Online]. Available: http://link.aps.org/doi/10.1103/RevModPhys.84.621
[57] U. L. Andersen, J. S. Neergaard-Nielsen, P. Van Loock, and A. Furusawa, “Hybrid discrete-and continuous-variable quantum information,” Nature Physics, vol. 11, no. 9, pp. 713–719, 2015. [Online]. Available: http://dx.doi.org/10.1038/nphys3410
[58] S. Krastanov, V. V. Albert, C. Shen, C.-L. Zou, R. W. Heeres, B. Vlastakis, R. J. Schoelkopf, and L. Jiang, “Universal control of an oscillator with dispersive coupling to a qubit,” Phys. Rev. A, vol. 92, p. 040303, Oct 2015. [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevA.92.040303
[59] B. Mischuck and K. Mølmer, “Qudit quantum computation in the jaynes-cummings model,” Phys. Rev. A, vol. 87, p. 022341, Feb 2013. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevA.87.022341
[60] Y. Liu, J. Sinanan-Singh, M. T. Kearney, G. Mintzer, and I. L. Chuang, “Constructing qudits from infinite-dimensional oscillators by coupling to qubits,” Phys. Rev. A, vol. 104, p. 032605, Sep 2021. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevA.104.032605
[61] Y. Liu, S. Singh, K. C. Smith, E. Crane, J. M. Martyn, A. Eickbusch, A. Schuckert, R. D. Li, J. Sinanan-Singh, M. B. Soley, T. Tsunoda, I. L. Chuang, N. Wiebe, and S. M. Girvin, “Hybrid oscillator-qubit quantum processors: Instruction set architectures, abstract machine models, and applications,” arXiv:2407.10381, 2024. [Online]. Available: https://arxiv.org/abs/2407.10381
[62] E. Crane, K. C. Smith, A. Schuckert, T. Tomesh, A. Eickbusch, J. M. Martyn, S. Kühn, L. Funcke, N. Wiebe, M. A. DeMarco, I. L. Chuang, and S. Girvin, “Hybrid oscillator-qubit quantum processors: Simulating fermions, bosons & gauge fields,” In preparation, 2024.
[63] A. Kitaev and W. A. Webb, “Wavefunction preparation and resampling using a quantum computer,” 2009. [Online]. Available: https://arxiv.org/abs/0801.0342
[64] D. Gottesman, A. Kitaev, and J. Preskill, “Encoding a qubit in an oscillator,” Phys. Rev. A, vol. 64, p. 012310, Jun 2001. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevA.64.012310
[65] B. M. Terhal and D. Weigand, “Encoding a qubit into a cavity mode in circuit qed using phase estimation,” Physical Review A, vol. 93, no. 1, Jan. 2016. [Online]. Available: http://dx.doi.org/10.1103/PhysRevA.93.012315
[66] J. Hastrup and U. L. Andersen, “Improved readout of qubit-coupled gottesman–kitaev–preskill states,” Quantum Science and Technology, vol. 6, no. 3, p. 035016, Jun. 2021. [Online]. Available: http://dx.doi.org/10.1088/2058-9565/ac070d
[67] Q.-M. Chen, F. Deppe, R.-B. Wu, L. Sun, Y.-x. Liu, Y. Nojiri, S. Pogorzalek, M. Renger, M. Partanen, K. G. Fedorov et al., “Quantum fourier transform in oscillating modes,” arXiv preprint arXiv:1912.09861, 2019. [Online]. Available: https://arxiv.org/abs/1912.09861
[68] P. Boykin, T. Mor, M. Pulver, V. Roychowdhury, and F. Vatan, “A new universal and fault-tolerant quantum basis,” Information Processing Letters, vol. 75, no. 3, pp. 101–107, 2000. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S0020019000000843
[69] C. M. Dawson and M. A. Nielsen, “The solovay-kitaev algorithm,” 2005. [Online]. Available: https://arxiv.org/abs/quant-ph/0505030
[70] A. Harrow, “Quantum compiling,” Ph.D. dissertation, Massachusetts Institute of Technology, Department of Physics, 2001.
[71] E. A. Arsenault, A. J. Schile, D. T. Limmer, and G. R. Fleming, “Vibronic coupling in energy transfer dynamics and two-dimensional electronic–vibrational spectra,” The Journal of chemical physics, vol. 155, no. 5, p. 054201, 2021.
[72] H. J. Kimble, “Strong interactions of single atoms and photons in cavity qed,” Physica Scripta, vol. 1998, no. T76, p. 127, jan 1998. [Online]. Available: https://dx.doi.org/10.1238/Physica.Topical.076a00127
[73] N. W. Ashcroft and N. D. Mermin, Solid State Physics. Holt-Saunders, 1976.
[74] S. M. Girvin and K. Yang, Modern condensed matter physics. Cambridge University Press, 2019.
[75] S. Becker, N. Datta, L. Lami, and C. Rouzé, “Energy-constrained discrimination of unitaries, quantum speed limits, and a gaussian solovay-kitaev theorem,” Phys. Rev. Lett., vol. 126, p. 190504, May 2021. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevLett.126.190504
[76] A. M. Childs, Y. Su, M. C. Tran, N. Wiebe, and S. Zhu, “Theory of trotter error with commutator scaling,” Phys. Rev. X, vol. 11, p. 011020, Feb 2021. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevX.11.011020
[77] A. M. Childs and N. Wiebe, “Hamiltonian simulation using linear combinations of unitary operations,” Quantum Information and Computation, vol. 12, no. 11 & 12, Nov. 2012. [Online]. Available: http://dx.doi.org/10.26421/QIC12.11-12
[78] J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia, Y. Li, E. Grant, L. Wossnig, I. Rungger, G. H. Booth et al., “The variational quantum eigensolver: a review of methods and best practices,” Physics Reports, vol. 986, pp. 1–128, 2022. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S0370157322003118
[79] J. Haah, “Product decomposition of periodic functions in quantum signal processing,” Quantum, vol. 3, p. 190, 2019. [Online]. Available: https://quantum-journal.org/papers/q-2019-10-07-190/
[80] Y. Dong, X. Meng, K. B. Whaley, and L. Lin, “Efficient phase-factor evaluation in quantum signal processing,” Physical Review A, vol. 103, no. 4, Apr. 2021. [Online]. Available: http://dx.doi.org/10.1103/PhysRevA.103.042419
[81] W. Fraser, “A survey of methods of computing minimax and near-minimax polynomial approximations for functions of a single independent variable,” J. ACM, vol. 12, no. 3, p. 295–314, jul 1965. [Online]. Available: https://doi.org/10.1145/321281.321282
[82] C. Flühmann and J. P. Home, “Direct characteristic-function tomography of quantum states of the trapped-ion motional oscillator,” Phys. Rev. Lett., vol. 125, p. 043602, Jul 2020. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevLett.125.043602
[83] S. Singh, B. Royer, and S. Girvin, “Towards non-abelian quantum signal processing: Error-corrected universal gate teleportation for GKP codes,” In Preparation, 2024.
[84] G. H. Low, T. J. Yoder, and I. L. Chuang, “Optimal arbitrarily accurate composite pulse sequences,” Phys. Rev. A, vol. 89, p. 022341, Feb 2014. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevA.89.022341
[85] N. Gomes, H. Lim, and N. Wiebe, “Multivariable qsp and bosonic quantum simulation using iterated quantum signal processing,” 2024. [Online]. Available: https://arxiv.org/abs/2408.03254
[86] T. J. Stavenger, E. Crane, K. C. Smith, C. T. Kang, S. M. Girvin, and N. Wiebe, “C2QA - Bosonic Qiskit,” in 2022 IEEE High Performance Extreme Computing Conference (HPEC), 2022, pp. 1–8. [Online]. Available: https://ieeexplore.ieee.org/document/9926318
[87] “Bosonic Qiskit Github Repository,” https://github.com/C2QA/bosonic-qiskit.
[88] J. Johansson, P. Nation, and F. Nori, “QuTiP: An open-source python framework for the dynamics of open quantum systems,” Computer Physics Communications, vol. 183, no. 8, p. 1760–1772, Aug. 2012. [Online]. Available: http://dx.doi.org/10.1016/j.cpc.2012.02.021
[89] J. Hastrup, K. Park, J. B. Brask, R. Filip, and U. L. Andersen, “Universal unitary transfer of continuous-variable quantum states into a few qubits,” Phys. Rev. Lett., vol. 128, p. 110503, Mar 2022. [Online]. Available: https://link.aps.org/doi/10.1103/PhysRevLett.128.110503
[90] C. E. Shannon, “Communication in the presence of noise,” Proceedings of the IRE, vol. 37, no. 1, pp. 10–21, 1949. [Online]. Available: https://doi.org/10.1109/JRPROC.1949.232969
[91] P. W. Shor, “Algorithms for quantum computation: discrete logarithms and factoring,” in Proceedings 35th annual symposium on foundations of computer science. IEEE, 1994, pp. 124–134. [Online]. Available: https://doi.org/10.1109/SFCS.1994.365700
[92] A. Gilyén, S. Arunachalam, and N. Wiebe, “Optimizing quantum optimization algorithms via faster quantum gradient computation,” in Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics, Jan. 2019, p. 1425–1444. [Online]. Available: http://dx.doi.org/10.1137/1.9781611975482.87
[93] J. Chen, E. Stoudenmire, and S. R. White, “Quantum fourier transform has small entanglement,” PRX Quantum, vol. 4, no. 4, Oct. 2023. [Online]. Available: http://dx.doi.org/10.1103/PRXQuantum.4.040318
[94] H. Mori, K. Fujii, and K. Mizuta, “Comment on ”multivariable quantum signal processing (m-qsp): prophecies of the two-headed oracle”,” 2023. [Online]. Available: https://arxiv.org/abs/2310.00918
[95] O. Christensen et al., An introduction to frames and Riesz bases. Springer, 2003, vol. 7.
[96] I. Daubechies, Ten lectures on wavelets. SIAM, 1992.
[97] R. Cleve and J. Watrous, “Fast parallel circuits for the quantum fourier transform,” in Proceedings 41st Annual Symposium on Foundations of Computer Science. IEEE, 2000, pp. 526–536. [Online]. Available: https://doi.org/10.1109/SFCS.2000.892140
[98] S. Weimann, A. Perez-Leija, M. Lebugle, R. Keil, M. Tichy, M. Gräfe, R. Heilmann, S. Nolte, H. Moya-Cessa, G. Weihs et al., “Implementation of quantum and classical discrete fractional fourier transforms,” Nature Communications, vol. 7, no. 1, p. 11027, 2016. [Online]. Available: http://dx.doi.org/10.1038/ncomms11027
[99] H. M. Ozaktas and M. A. Kutay, “The fractional fourier transform,” in 2001 European Control Conference (ECC). IEEE, 2001, pp. 1477–1483. [Online]. Available: https://doi.org/10.23919/ECC.2001.7076127
[100] R. Calderbank, S. D. Howard, and B. Moran, “Waveform diversity in radar signal processing,” IEEE Signal Processing Magazine, vol. 26, no. 1, pp. 32–41, 2009. [Online]. Available: https://doi.org/10.1109/MSP.2008.930414
[101] C. W. Helstrom, “Quantum detection and estimation theory,” Journal of Statistical Physics, vol. 1, pp. 231–252, 1969. [Online]. Available: https://doi.org/10.1007/BF01007479
[102] C. Helstrom and R. Kennedy, “Noncommuting observables in quantum detection and estimation theory,” IEEE Transactions on Information Theory, vol. 20, no. 1, pp. 16–24, 1974. [Online]. Available: https://doi.org/10.1109/TIT.1974.1055173
[103] X. Zhou, A. Shen, S. Hu, W. Ni, X. Wang, E. Hossain, and L. Hanzo, “Towards quantum-native communication systems: New developments, trends, and challenges,” 2023. [Online]. Available: https://arxiv.org/abs/2311.05239
[104] F. Zhang, B. Jin, Z. Lan, Z. Chang, D. Zhang, Y. Jiao, M. Shi, and J. Xiong, “Quantum wireless sensing: Principle, design and implementation,” in Proceedings of the 29th Annual International Conference on Mobile Computing and Networking, 2023, pp. 1–15. [Online]. Available: https://doi.org/10.1145/3570361.3613258
[105] J. Wang, Y. Dong, and L. Lin, “On the energy landscape of symmetric quantum signal processing,” Quantum, vol. 6, p. 850, 2022. [Online]. Available: https://quantum-journal.org/papers/q-2022-11-03-850/

Appendix A A Brief Review of Quantum Signal Processing

The idea behind quantum signal processing (QSP) is to use qubit operations to implement a polynomial transformation of a linear operator[40, 26]. In its simplest incarnation, QSP considers a fixed $z$ -rotation

U(y):=e^{iy\sigma_{z}}=\begin{bmatrix}e^{iy}&0\\ 0&e^{-iy}\end{bmatrix}.

(82)

Then, the QSP sequence is constructed as an interspersed product of this $z$ -rotation and parameterizable $x$ -rotations:

e^{i\phi_{0}X}\prod_{j=1}^{d}U(y)e^{i\phi_{j}X}=\begin{bmatrix}F(e^{iy})&iG(e^{iy})\\ iG(e^{-iy})&F(e^{-iy})\end{bmatrix}.

(83)

where $\{\phi_{0},\ldots,\phi_{d}\}$ are the parametric phases of the $x$ -rotations. As expressed in this equation, the matrix elements of this sequence are degree $d$ Laurent polynomials:

\displaystyle F(e^{iy})

\displaystyle=\sum_{n=-d}^{d}f_{n}e^{iny},\qquad G(e^{iy})

\displaystyle=\sum_{n=-d}^{d}g_{n}e^{iny}

(84)

where $F(\cdot)$ and $G(\cdot)$ are Laurent polynomials with real coefficients $f_{n},g_{n}\in\mathbb{R}$ and parity $d\mod 2$ (i.e., only even or odd coefficients are non-zero, depending on $d$ ). By unitarity, these polynomials obey $F(e^{iy})F(e^{-iy})+G(e^{iy})G(e^{-iy})=1$ . Importantly, for any such polynomials, there exist corresponding phases $\phi_{j}$ . In addition, these phases can be computed efficiently with classical algorithms [38, 35, 36, 79, 105].

Moreover, QSP can be generalized beyond single qubit dynamics. Important such generalizations are the quantum eigenvalue transformation and the quantum singular value transformation [24]. These work by replacing $U(y)$ with a unitary block encoding of a linear operator $A$ :

\begin{bmatrix}A&\cdot\\ \cdot&\cdot\end{bmatrix}

(85)

(this requires $\|A\|$ by unitarity). By analogy with $U(y)$ , which itself block-encodes $e^{iy}$ in its upper left block as per Eq. (82), one can construct an analogous QSP sequence that outputs a polynomial in $A$ :

\begin{bmatrix}F(A)&\cdot\\ \cdot&\cdot\end{bmatrix},

(86)

where $F(A)$ obeys conditions analogous to $F(e^{iy})$ . This polynomial can be chosen to act on either the eigenvalues of $A$ or its singular values (e.g. if $A$ is rectangular), corresponding to the eigenvalue transformation and singular value transformation, respectively. See Ref. [26] for a tutorial and more details.

In the main text, we extended this construction of QSP to hybrid CV-DV systems. Our hybrid single-variable QSP was constructed directly as an extension of Eqs. (83) and (84) to bosonic operators $\hat{x}$ and $\hat{p}$ . On the other hand, our hybrid non-Abelian QSP was designed as a natural generalization of this interspersed sequence to multiple variables.

Appendix B Forward Direction of the Hybrid CV-DV Non-Abelian QSP Theorem

In this section, we focus on showing an inductive proof that the above claim in Eqs. (23) and (24) is correct: starting from $U_{d}$ given by Eq. (23), we will show that $U_{d+1}$ takes an analogous form with Laurent polynomials given by Eq. (24).

Consider a single iteration of the non-Abelian hybrid QSP sequence:

{strip}

\displaystyle W_{z}^{(k)}e^{i\phi_{j}^{(k)}\sigma_{x}}W_{z}^{(\lambda)}e^{i\phi_{j}^{(\lambda)}\sigma_{x}}=\begin{bmatrix}w(vA_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}}-v^{-1}D_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}})&iw(vB_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}}+v^{-1}C_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}})\\ iw^{-1}(vC_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}}+v^{-1}B_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}})&w^{-1}(-vD_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}}+v^{-1}A_{\phi_{j}^{(k)},\phi_{j}^{(\lambda)}})\end{bmatrix}

(87)

where we use the shorthand notation $A_{\phi_{1},\phi_{2}}\equiv\cos\phi_{1}\cos\phi_{2},~{}B_{\phi_{1},\phi_{2}}\equiv\cos\phi_{1}\sin\phi_{2},~{}C_{\phi_{1},\phi_{2}}\equiv\sin\phi_{1}\cos\phi_{2},~{}D_{\phi_{1},\phi_{2}}\equiv\sin\phi_{1}\sin\phi_{2}$ . Then we have

	$\displaystyle U_{d+1}$	$\displaystyle=U_{d}\left(W_{z}^{(k)}e^{i\phi_{d+1}^{(k)}\sigma_{x}}W_{z}^{(\lambda)}e^{i\phi_{d+1}^{(\lambda)}\sigma_{x}}\right)$
		$\displaystyle=\begin{bmatrix}F_{d+1}(w,v)&iG_{d+1}(w,v)\\ iG_{d+1}(w^{-1},v^{-1})&F_{d+1}(w^{-1},v^{-1})\end{bmatrix}.$		(88)

Let’s compute $F_{d+1}(w,v)$ and $G_{d+1}(w,v)$ explicitly. First calculating $F_{d+1}(w,v)$ , we have

	$\displaystyle F_{d+1}(w,v)$
$\displaystyle=$	$\displaystyle F_{d}(w,v)\left[wvA_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}-wv^{-1}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\right]$
	$\displaystyle+iG_{d}(w,v)\left[iw^{-1}vC_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}+iw^{-1}v^{-1}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\right]$
$\displaystyle=$	$\displaystyle\sum_{rs=-d}^{d}\bigg{(}f_{rs}w^{r}v^{s}wvA_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}-f_{rs}w^{r}v^{s}wv^{-1}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}$
	$\displaystyle-g_{rs}w^{r}v^{s}w^{-1}vC_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}-g_{rs}w^{r}v^{s}w^{-1}v^{-1}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\bigg{)}.$	(89)

We would like to express this in the canonical form defined by Eq. (24).

From the Baker–Campbell–Hausdorff formula, we have the following elementary relationship between $w$ and $v$ :

\displaystyle v^{s}w=wv^{s}e^{is\frac{\lambda k}{4}},~{}~{}~{}~{}v^{s}w^{-1}=w^{-1}v^{s}e^{-is\frac{\lambda k}{4}}.

(90)

Substituting this into Eq. (89), $F_{d+1}(w,v)$ can be recast into the canonical form

	$\displaystyle F_{d+1}(w,v)$
$\displaystyle=$	$\displaystyle\sum_{r,s=-d}^{d}\bigg{(}f_{rs}w^{r+1}v^{s+1}e^{is\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}$
	$\displaystyle\qquad\qquad-f_{rs}w^{r+1}v^{s-1}e^{is\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}$
	$\displaystyle\qquad\qquad-g_{rs}w^{r-1}v^{s+1}e^{-is\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}$
	$\displaystyle\qquad\qquad-g_{rs}w^{r-1}v^{s-1}e^{-is\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\bigg{)}.$	(91)

Several observations are immediately in order:

1.

The power of $w$ and $v$ at most change by 1, and therefore $F_{d+1}$ is a degree $d+1$ bivariate Laurent polynomial.
2.

The non-commutative nature of $\hat{x}$ and $\hat{p}$ gives rise to an additional complex phase $e^{\pm is\frac{\lambda k}{4}}$ in the polynomial coefficients.

Denoting the Laurent polynomial coefficients of $F_{d+1}$ and $G_{d+1}$ are $f^{\prime}_{rs}$ and $g^{\prime}_{rs}$ , then using the above expression, we can explicitly write these coefficients in terms of $f_{rs}$ and $g_{rs}$ :

$\bullet$ Case 1: $r=d,d+1$ :

\displaystyle f^{\prime}_{rs}=\begin{cases}f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}~{}~{}~{}s=d,d+1\\ f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}|s|\leq d-1,\\ -f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}~{}s=-d,-(d+1).\end{cases}

$\bullet$ Case 2: $r=-d,-d-1$ :

\displaystyle f^{\prime}_{rs}=\begin{cases}-g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}s=-d,-d-1\\ -g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}|s|\leq d-1,\\ g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}~{}~{}s=d,d+1.\end{cases}

$\bullet$ Case 3: $|r|\leq d-1$ :

\displaystyle f^{\prime}_{rs}=\begin{cases}f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}|s|\leq d-1\\ f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}s=d,d+1\\ -f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}s=-d,-d-1.\end{cases}

The above three cases can be understood in Fig. 8.

Similarly to Eq. (89), the new polynomial $G_{d+1}(w,v)$ is

	$\displaystyle G_{d+1}(w,v)$
$\displaystyle=$	$\displaystyle F_{d}(w,v)\left[wvB_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}+wv^{-1}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\right]$
	$\displaystyle-G_{d}(w,v)\left[w^{-1}vD_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}-w^{-1}v^{-1}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\right]$
$\displaystyle=$	$\displaystyle\sum_{r,s=-d}^{d}\bigg{(}f_{rs}w^{r+1}v^{s+1}e^{is\frac{k\lambda}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}$
	$\displaystyle\qquad\qquad+f_{rs}w^{r+1}v^{s-1}e^{is\frac{k\lambda}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}$
	$\displaystyle\qquad\qquad-g_{rs}w^{r-1}v^{s+1}e^{-is\frac{k\lambda}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}$
	$\displaystyle\qquad\qquad+g_{rs}w^{r-1}v^{s-1}e^{-is\frac{k\lambda}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\bigg{)},$	(92)

where we have used Eq. (90) to arrive at the last line. From this iterative relation, we can similarly express the coefficients $g^{\prime}_{r,s}$ in terms of $f_{rs}$ and $g_{rs}$ :

1) $r=d,d+1$ :

\displaystyle g^{\prime}_{rs}=\begin{cases}f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}~{}~{}s=d,d+1\\ f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}+f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}|s|\leq d-1,\\ f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}~{}~{}s=-d,-(d+1).\end{cases}

2) $r=-d,-d-1$ :

\displaystyle g^{\prime}_{rs}=\begin{cases}g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}~{}~{}~{}~{}s=-d,-d-1\\ -g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}+g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}|s|\leq d-1,\\ g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}~{}~{}~{}~{}~{}~{}s=d,d+1.\end{cases}

3) $|r|\leq d-1$ :

\displaystyle g^{\prime}_{rs}=\begin{cases}f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}+f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ -g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}+g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}|s|\leq d-1\\ f_{r-1,s-1}e^{i(s-1)\frac{\lambda k}{4}}B_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}~{}-g_{r+1,s-1}e^{-i(s-1)\frac{\lambda k}{4}}D_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}s=d,d+1\\ f_{r-1,s+1}e^{i(s+1)\frac{\lambda k}{4}}C_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}}\\ ~{}+g_{r+1,s+1}e^{-i(s+1)\frac{\lambda k}{4}}A_{\phi_{d+1}^{(k)},\phi_{d+1}^{(\lambda)}},~{}~{}s=-d,-d-1.\end{cases}

These relationships suggest that if $d$ is even, then $f_{rs}$ is only non-zero when $r,s$ are both even. Likewise, if $d$ is odd, then $f_{r,s}$ is non-zero when $r,s$ are both odd.

Appendix C Details on Quantum AD/DA Conversion Protocols

Here we include additional information on the AD/DA conversion protocols of Sec. IV, including additional caveats and proofs of performance bounds.

C-A Quantum AD/DA Conversion: Hybrid Single-Variable QSP

C-A1 Fidelity Bound

In the context of quantum AD/DA conversion via hybrid single-variable QSP, let us study how the fidelity of the second stage (the QSP stage) scales with $w$ and $\epsilon$ . This stage suffers from two possible error modes. First, the QSP polynomial approximation is only accurate to within $\epsilon$ , and fails within the region $\big{|}\cos[\frac{\pi}{2^{n-j}}(x-2^{n-j-1}+\frac{1}{2})]\big{|}\leq 2\delta_{j}$ . Second, the state of the bosonic mode is not an exact position eigenstate but is instead a Gaussian of finite width $\sigma$ . Let us consider the impact of these effects on the basis states $|\mathbf{x}\rangle_{Q}|x,\Delta\rangle_{O}^{\text{Gaus}}$ which span the intermediate state. Accounting for both error modes, we find that the overlap between the state output by this stage and the desired output state $|\mathbf{0}\rangle_{Q}|x,\Delta\rangle_{O}^{\text{Gaus}}$ can be expressed as

		$\displaystyle{}_{Q}\langle\mathbf{0}\|_{O}^{\text{Gaus}}\langle x,\Delta\|\prod_{j=1}^{n}R_{j}(\hat{x})\|\mathbf{x}\rangle_{Q}\|x,\Delta\rangle_{O}^{\text{Gaus}}=$		(93)
		$\displaystyle\int_{-\infty}^{\infty}dq\prod_{j=1}^{n}A_{j}(q/\Delta)\frac{1}{\sqrt{2\pi}\sigma}e^{-(q-x\Delta)^{2}/2\sigma^{2}}=$
		$\displaystyle\int_{-\infty}^{\infty}dq^{\prime}\prod_{j=1}^{n}A_{j}(x+q^{\prime}/\Delta)\frac{1}{\sqrt{2\pi}\sigma}e^{-q^{\prime 2}/2\sigma^{2}},$

where $A_{j}(x+\tfrac{q^{\prime}}{\Delta})$ is the function

A_{j}(x+q^{\prime}/\Delta)=\begin{cases}P_{j}(x+q^{\prime}/\Delta)&x_{j}=0\\ \sqrt{1-P_{j}(x+q^{\prime}/\Delta)^{2}}&x_{j}=1,\end{cases}

(94)

and we have used the substitution $q^{\prime}=q-x\Delta$ to reach the second line. Note that at $q^{\prime}=0$ , $P_{j}(x)$ suffers error at most $\epsilon$ from the desired step function, such that $\prod_{j}A_{j}(x)\geq(1-\epsilon)^{n}\geq 1-n\epsilon$ . This condition remains true if $\big{|}\cos[\frac{\pi}{2^{n-j}}(x+\tfrac{q^{\prime}}{\Delta}-2^{n-j-1}+\frac{1}{2})]\big{|}\geq 2\delta_{j}$ , which we can satisfy for all $j$ and any $x$ if $|\delta|\leq\frac{\Delta}{\pi}\cos^{-1}(2\delta_{1})$ , and $\delta_{1},\Delta$ are chosen such that $\frac{\Delta}{\pi}\cos^{-1}(2\delta_{1})\geq 1/2$ , i.e., a sufficiently large $\Delta$ and sufficiently small $\delta_{1}=\mathcal{O}(\tfrac{1}{2^{n}})$ . Assuming such a choice is made, we can therefore lower bound the overlap as

		$\displaystyle(1-n\epsilon)\cdot\int_{\frac{-\Delta}{\pi}\cos^{-1}(2w)}^{\frac{\Delta}{\pi}\cos^{-1}(2w)}dq^{\prime}\frac{1}{\sqrt{2\pi}\sigma}e^{-q^{\prime 2}/2\sigma^{2}}$		(95)
		$\displaystyle=(1-n\epsilon)\left(1-2\int_{\frac{\Delta}{\pi}\cos^{-1}(2w)}^{\infty}dq^{\prime}\frac{1}{\sqrt{2\pi}\sigma}e^{-q^{\prime 2}/2\sigma^{2}}\right),$		(95)

where we have used the normalization of the Gaussian distribution in obtaining the second line. Using the inequality $\int_{a}^{\infty}dte^{-t^{2}}\leq\frac{1}{2a}\int_{a}^{\infty}2t\cdot e^{-t^{2}}=e^{-a^{2}}/2a$ , we find that this quantity is lower bounded by

(1-n\epsilon)\left(1-\frac{e^{-u^{2}}}{u\sqrt{\pi}}\right)

(96)

where $u=\frac{\Delta}{\sqrt{2}\sigma\pi}\cos^{-1}(2\delta_{1})$ . This scales asymptotically as $1-\mathcal{O}(n\epsilon)+\mathcal{O}(e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})}\cdot\sigma/\Delta)$ .

By an analogous argument, the overlap between the state output by this protocol and an incorrect basis state $|\mathbf{0}\rangle|y\Delta\rangle_{O}$ (for $y\neq x$ ) is upper bounded by $e^{-\tfrac{-\Delta^{2}}{8\sigma^{2}}(x-y)^{2}}$ . Accordingly, for an arbitrary input state, its overlap with the incorrect basis states scales as $\mathcal{O}(e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})})$ . Accounting for both of these contributions, the total fidelity of this protocol scales asymptotically as $1-\mathcal{O}(n\epsilon)-\mathcal{O}(e^{-\mathcal{O}(\Delta^{2}/\sigma^{2})})$ .

C-B Quantum AD/DA Conversion: Hybrid Non-Abelian QSP

C-B1 Fidelity Bound

Next, let us consider the fidelity of quantum AD/DA conversion with hybrid Non-Abelian QSP. The exact state output by this protocol is the state in Eq. (42), which is approximately equal to the desired state of Eq. (46), in which the qubits and oscillator are decoupled. The infidelity between these two states can be attributed to the two approximations used in moving from Eq. (42) to Eq. (46). Let us investigate this by first considering the inner product between these two states, which equates to

\sum_{s}\int_{-\infty}^{\infty}dq\ \psi(q_{s})^{*}\psi(q+q_{s})\text{sinc}\left(\tfrac{\pi q}{\Delta}\right)\prod_{k=1}^{n}\cos(\tfrac{\pi q}{\Delta 2^{k}}).

(97)

First consider the contribution to this integral from the region $q\in[-\tfrac{\Delta}{2}2^{n},\tfrac{\Delta}{2}2^{n}]$ . To knead this into a cleaner expression, we will first note the infinite product identity

\prod_{k=1}^{\infty}\cos(\tfrac{\pi q}{\Delta 2^{k}})=\text{sinc}\left(\tfrac{\pi q}{\Delta}\right).

(98)

This allows us to write the contribution to the overlap as

\sum_{s}\int_{-\frac{\Delta}{2}2^{n}}^{\frac{\Delta}{2}2^{n}}dq\ \psi(q_{s})^{*}\psi(q+q_{s})\frac{1}{\prod_{k=n+1}^{\infty}\cos(\tfrac{\pi q}{\Delta 2^{k}})}\text{sinc}^{2}\left(\tfrac{\pi q}{\Delta}\right).

(99)

Next we make use of the fact that $\text{sinc}^{2}\left(\tfrac{\pi q}{\Delta}\right)$ behaves as a delta function for small $\tfrac{\Delta}{2}$ :

		$\displaystyle\text{sinc}^{2}(\tfrac{\pi q}{\Delta})\approx\Delta\delta(q),$		(100)
		$\displaystyle\int dq\ f(q)\text{sinc}^{2}(\tfrac{\pi q}{\Delta})=\Delta f(0)+\mathcal{O}(\Delta^{2}f^{\prime}(0)),$		(100)

for small $\Delta$ and an analytical function $f(q)$ . Over the integration region, the function $\frac{1}{\prod_{k=n+1}^{\infty}\cos(\tfrac{\pi q}{\Delta 2^{k}})}$ is well behaved with bounded value and derivative. Therefore we can invoke this limit and find that the prior integral becomes

\displaystyle\Delta\sum_{s}|\psi(q_{s})|^{2}+\mathcal{O}\left(\Delta^{2}\sum_{s}\psi(q_{s})^{*}\psi^{\prime}(q_{s})\right).

(101)

As $q_{s}\in[-\tfrac{\Delta}{2}(2^{n}-1),\tfrac{\Delta}{2}(2^{n}-1)]$ in steps size $\Delta$ , the first term is a Riemann sum from $q=-\tfrac{\Delta}{2}(2^{n}-1)$ to $q=\tfrac{\Delta}{2}(2^{n}-1)$ with $2^{n}$ steps of size $\Delta$ . By invoking the standard error bound on Riemann sums, we find that this equates to

		$\displaystyle\Delta\sum_{s}\|\psi(q_{s})\|^{2}=$		(102)
		$\displaystyle\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}dq\|\psi(q)\|^{2}+\mathcal{O}\left(\frac{\Delta}{2}\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}\big{\|}\tfrac{d}{dq}\|\psi(q)\|^{2}\big{\|}\right)=$
		$\displaystyle 1-\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq\|\psi(q)\|^{2}-\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq\|\psi(q)\|^{2}$
		$\displaystyle\qquad+\mathcal{O}\left(\Delta\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}dq\big{\|}\tfrac{d}{dq}\|\psi(q)\|^{2}\big{\|}\right),$

where we have used the normalization of $\psi(q)$ in obtaining the last line. Next, by a similar analysis, the error term in Eq. (101) scales as

		$\displaystyle\Delta^{2}\sum_{s}\psi(q_{s})*\psi^{\prime}(q_{s})\sim\Delta\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}dq\tfrac{d}{dq}\|\psi(q)\|^{2}=$		(103)
		$\displaystyle\qquad\Delta\left[\|\psi(\tfrac{\Delta}{2}(2^{n}-1))\|^{2}-\|\psi(-\tfrac{\Delta}{2}(2^{n}-1))\|^{2}\right].$		(103)

Next, let us consider the contribution to the overlap from the rest of the integration range, starting first with the region $q\in[\tfrac{\Delta}{2}2^{n},\infty]$ . To bound this contribution, note that

\prod_{k=1}^{n}\cos(\tfrac{\pi q}{\Delta 2^{k}})=(-1)^{m}\prod_{k=1}^{n}\cos(\tfrac{\pi(q-m\Delta 2^{n})}{\Delta 2^{k}})

(104)

for integer $m$ . So this product is periodic and peaked at each $m\Delta 2^{n}$ , with alternating sign. Accordingly, we may write the integral over $q\in[\tfrac{\Delta}{2}2^{n},\infty]$ as

		$\displaystyle\sum_{m=1}^{\infty}(-1)^{m}\int_{(m-\tfrac{1}{2})\Delta 2^{n}}^{(m+\tfrac{1}{2})\Delta 2^{n}}dq\Bigg{[}\prod_{k=1}^{n}\cos(\tfrac{\pi(q-m\Delta 2^{n})}{\Delta 2^{k}})\Bigg{]}$		(105)
		$\displaystyle\qquad\qquad\qquad\times\sum_{s}\psi(q_{s})^{*}\psi(q+q_{s})\text{sinc}\left(\tfrac{\pi q}{\Delta}\right).$		(105)

As before, we may write $\prod_{k=1}^{n}\cos(\tfrac{\pi(q-m\Delta 2^{n})}{\Delta 2^{k}})=\text{sinc}(\tfrac{\pi(q-m\Delta 2^{n})}{\Delta})/\prod_{k=n+1}^{\infty}\cos(\tfrac{\pi(q-m\Delta 2^{n})}{\Delta 2^{k}})$ , and make use of the fact that $\text{sinc}\left(\tfrac{\pi q}{\Delta}\right)$ also behaves as a delta function for small $\Delta$ :

		$\displaystyle\text{sinc}(\tfrac{\pi q}{\Delta})\approx\Delta\delta(q),$		(106)
		$\displaystyle\int dq\ f(q)\text{sinc}(\tfrac{\pi q}{\Delta})=\Delta f(0)+\mathcal{O}(\Delta^{2}f^{\prime}(0)),$		(106)

for small $\Delta$ and an analytical function $f(q)$ . Using this small $\Delta$ limit under the integral plucks out the value

\displaystyle\frac{\text{sinc}\left(\tfrac{\pi q}{\Delta}\right)\sum_{s}\psi(q_{s})^{*}\psi(q+q_{s})}{\prod_{k=n+1}^{\infty}\cos(\tfrac{\pi(q-n\Delta 2^{n})}{\Delta 2^{k}})}\Bigg{|}_{q=n\Delta 2^{n}}\propto\text{sinc}\left(\pi n2^{n}\right)=0,

(107)

and the error in this result scales as

	$\displaystyle\sim$	$\displaystyle\Delta^{2}\frac{\tfrac{d}{dq}\text{sinc}\left(\tfrac{\pi q}{\Delta}\right)\sum_{s}\psi(q_{s})^{*}\psi(q+q_{s})}{\prod_{k=n+1}^{\infty}\cos(\tfrac{\pi(q-m\Delta 2^{n})}{\Delta 2^{k}})}\Bigg{\|}_{q=m\Delta 2^{n}}=$		(108)
		$\displaystyle\Delta^{2}\frac{(-1)^{m}}{m\Delta 2^{n}}\sum_{s}\psi(q_{s})^{*}\psi(m\Delta 2^{n}+q_{s})$		(108)

For a wave function whose magnitude decays for $|q|\geq\tfrac{\Delta}{2}(2^{n}-1)$ (which is our case here, as we assume the bulk of the wave function is contained in $|q|\geq\tfrac{\Delta}{2}(2^{n}-1)$ ), this scales as

		$\displaystyle\lesssim\frac{(-1)^{m}}{4\cdot m2^{n}}\sum_{s}\Delta\|\psi(n\Delta 2^{n}+q_{s})\|^{2}$		(109)
		$\displaystyle\approx\frac{(-1)^{m}}{4\cdot m2^{n}}\int_{(m-\tfrac{1}{2})\Delta 2^{n}}^{(m+\tfrac{1}{2})\Delta 2^{n}}dq\|\psi(q)\|^{2}$		(109)

Inserting this expression into Eq. (105), we find that the sum over all $m$ is sufficiently bounded by $O\big{(}\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq|\psi(q)|^{2}\big{)}$ . Moreover, an analogous strategy bounds the contribution to the overlap from the integration range $q\in[-\infty,-\tfrac{\Delta}{2}2^{n},]$ as $\mathcal{O}\left(\int_{-\infty}^{-\tfrac{\Delta}{2}(2^{n}-1)}dq|\psi(q)|^{2}\right)$ .

Finally, piecing together each of the above contributions to the overlap of Eq. (97), we find that the fidelity of this A/D conversion protocol, scales as

	$\displaystyle 1$	$\displaystyle-\mathcal{O}\Bigg{(}\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq\|\psi(q)\|^{2}+\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq\|\psi(q)\|^{2}\Bigg{)}$		(110)
		$\displaystyle-\mathcal{O}\Bigg{(}\Delta\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}dq\big{\|}\tfrac{d}{dq}\|\psi(q)\|^{2}\big{\|}\Bigg{)}.$		(110)

This expression justifies the two approximations used above in simplifying Eq. (42) to Eq. (46). Recall that these approximates demanded that (1) the support of $\psi(q)$ be primarily limited to $|q|\leq\tfrac{\Delta}{2}(2^{n}-1)$ , which corresponds to the first infidelity contribution above; and (2) that $\psi(q)$ be slowly varying relative to the sinc function, i.e., $|\tfrac{d\psi}{dq}|\ll 1/\Delta$ , which corresponds to the infidelity contribution from the last term above.

Moreover, because this A/D protocol is unitary, its inverse (D/A conversion) achieves an analogous expression for fidelity, upon re-interpreting $\psi(q)$ as the wave function of qubits state transferred to the basis of sinc states: $\psi(q)=\frac{1}{\sqrt{\Delta}}\sum_{s}c_{s}\text{sinc}\left(\tfrac{\pi(q-q_{\mathbf{s}})}{\Delta}\right)$ . Inserting this expression into Eq. (101) and the following analysis, we find that the overlap between the exact and approximate state is roughly

\Delta\sum_{s}|\psi(q_{s})|^{2}=\sum_{s}|c_{s}|^{2}=1,

(111)

with an error term that scales as $\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq|\psi(q)|^{2}+\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq|\psi(q)|^{2}$ . Hence, the fidelity of the D/A conversion protocol furnished by $U_{\text{D/A}}^{\text{S-V}}(\Delta,n)$ is

1-\Bigg{(}\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq|\psi(q)|^{2}+\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq|\psi(q)|^{2}\Bigg{)}.

(112)

Appendix D Details on Steps of QFT Protocols

D-A QFT Protocol 1: Hybrid Single-Variable QSP

Here we provide additional details on the QFT protocol using hybrid single-variable QSP.

D-A1 Analysis of Step 5

Let us work through the details of Step 5 of the QFT protocol. As shown in Sec. V, at the beginning of this stage the state of the oscillator is

\displaystyle\sqrt{\frac{2\pi\sigma}{\Delta 2^{n}}\sqrt{\frac{2}{\pi}}}\sum_{l\in\mathbb{Z}}\sum_{\mathbf{x}}c_{\mathbf{x}}e^{i2\pi lx/2^{n}}e^{-\sigma^{2}q_{l}^{2}}\widetilde{|q_{l}\rangle}_{O},

(113)

where

\widetilde{|q_{l}\rangle}_{O}:=\sqrt{\frac{\Delta 2^{n}}{2\pi}}\int_{q_{l}-\frac{\pi}{\Delta 2^{n}}}^{q_{l}+\frac{\pi}{\Delta 2^{n}}}dq\left[\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{iq2^{n}k\Delta}\right]|q\rangle_{O}

(114)

is a normalized state concentrated around $q=q_{l}$ . We then introduce $n$ qubits in the state $|0\rangle^{\otimes n}$ , and apply the A/D conversion protocol to transfer the oscillator state to the qubits. Specifically, we use the operation $\tilde{U}_{\text{D/A}}^{\text{S-V}}(\frac{\pi}{2^{n}\Delta},n)^{\dagger}$ , which is modified such that the controlled displacements that comprise it are each doubled (relative to the usual construction of Fig. 3). Let’s work through the application of this operation piece-by-piece.

The first stage of $\tilde{U}_{\text{D/A}}^{\text{S-V}}(\frac{\pi}{2^{n}\Delta},n)^{\dagger}$ is the series of QSP operations (see Fig. 3), which implement square waves with periods $\frac{2\pi}{2^{j}\Delta}$ that flip the $j^{\text{th}}$ qubit dependent on the $j^{\text{th}}$ bit of the oscillator position. In aggregate, these operations partition position space into periods of size $2\pi/\Delta$ . As per the construction of the square wave function in Eq. (31), these periods are $((m-\tfrac{1}{4})\cdot\tfrac{2\pi}{\Delta},\ (m+\tfrac{3}{4})\cdot\tfrac{2\pi}{\Delta})$ for $m\in\mathbb{Z}$ . The square waves of the QSP sequences divide each such period into $2^{n}$ sub-regions, each labeled by an $n$ -bit string $\mathbf{y}$ corresponding to the integer $y=\frac{\Delta 2^{n}}{2\pi}(q+\frac{\pi}{2\Delta})\text{ mod }2^{n}$ . That is, each sub-region is $(\tfrac{2\pi}{\Delta 2^{n}}([m-\tfrac{1}{4}]2^{n}+y),\tfrac{2\pi}{\Delta 2^{n}}([m-\tfrac{1}{4}]2^{n}+y+1))$ and is labeled by $y\in\{0,...,2^{n}-1\}$ . The overall action of the (inverse) QSP sequences is to re-entangle the qubits with the oscillator by flipping the qubits to the state $|\mathbf{0}\rangle_{Q}|q\rangle_{O}\mapsto|\mathbf{y}\rangle_{Q}|q\rangle_{O}$ for the string $\mathbf{y}$ corresponding to position $q$ .

Consider the action of these QSP operations on the state in Eq. (113). If each QSP polynomial in the series is chosen to approximate the square wave to within the accuracy spelled out in Sec. IV-A, then these operations correctly discern the $j^{\text{th}}$ bit of the position $q_{l}$ from the oscillator state $\widetilde{|q_{l}\rangle}_{O}$ . Because $q_{l}=l\frac{2\pi}{\Delta 2^{n}}$ , the above analysis indicates that this position corresponds to $l=2^{n}([m-\tfrac{1}{4}]+y)$ . Using this insight, the overall action of the QSP operations therefore produces the following state

		$\displaystyle\sqrt{\frac{2\pi\sigma}{\Delta 2^{n}}\sqrt{\frac{2}{\pi}}}\sum_{m}\sum_{\mathbf{x},\mathbf{y}}c_{\mathbf{x}}e^{i2\pi([m-\tfrac{1}{4}]2^{n}+y)x/2^{n}}$		(115)
		$\displaystyle\qquad\qquad\qquad\qquad\qquad\times e^{-\sigma^{2}q_{l}^{2}}\|\mathbf{y}\rangle_{Q}\widetilde{\|q_{l}\rangle}_{O}=$
		$\displaystyle\sqrt{\frac{2\pi\sigma}{\Delta 2^{n}}\sqrt{\frac{2}{\pi}}}\sum_{m}\sum_{\mathbf{x},\mathbf{y}}c_{\mathbf{x}}e^{i2\pi yx/2^{n}}e^{-i\pi x/2}$
		$\displaystyle\qquad\qquad\qquad\qquad\qquad\times e^{-\sigma^{2}q_{l}^{2}}\|\mathbf{y}\rangle_{Q}\widetilde{\|q_{l}\rangle}_{O}.$

As per the use of $n$ QSP sequences, the infidelity suffered at this step is $\mathcal{O}(n\epsilon)$ where $\epsilon$ is the error of the polynomial approximation to the step function.

In the next stage of $\tilde{U}_{\text{st}}^{\text{S-V}}(\frac{\pi}{2^{n}\Delta},n)^{\dagger}$ , a sequence of controlled displacements $\prod_{j=1}^{n}D_{c_{j}}(\frac{2\pi}{\Delta 2^{j}})$ is applied (which are doubled relative to the usual construction). Collectively, these operations act on the oscillator as $|q\rangle_{O}\mapsto|q-\sum_{j}y_{j}\frac{2\pi}{2^{j}\Delta}\rangle_{O}=|q-\frac{2\pi}{\Delta}\cdot\frac{y}{2^{n}}\rangle_{O}$ , which equivalently maps $\widetilde{|q_{l}\rangle}_{O}\mapsto\widetilde{|\tfrac{2\pi}{\Delta}(m-\tfrac{1}{4})\rangle}_{O}$ . The effect is to displace each sub-region of the CV wave function by different amount so that all the $2^{n}$ sub-regions interfere with each other to produce the QFT coefficients. Changing variables to $q^{\prime}=q-\frac{2\pi}{\Delta}\frac{y}{2^{n}}$ in the integral, the resulting state is

		$\displaystyle\sqrt{\frac{2\pi\sigma}{\Delta 2^{n}}\sqrt{\frac{2}{\pi}}}\sum_{m}\sum_{\mathbf{y}}\sum_{\mathbf{x}}c_{\mathbf{x}}e^{i2\pi yx/2^{n}}e^{-i\pi x/2}$		(116)
		$\displaystyle\qquad\qquad\qquad\qquad\qquad\times e^{-\sigma^{2}q_{l}^{2}}\|\mathbf{y}\rangle_{Q}\widetilde{\|=\tfrac{2\pi}{\Delta}(m-\tfrac{1}{4})\rangle}_{O}.$		(116)

To simplify this, note that in the limit of small $\sigma/\Delta$ , $e^{-\sigma^{2}q_{l}^{2}}=e^{-\sigma^{2}(\frac{2\pi}{\Delta 2^{n}}[2^{n}(m-\tfrac{1}{4})+y])^{2}}\approx e^{-\sigma^{2}(\frac{2\pi}{\Delta}m)^{2}}$ . Making this approximation in the above state incurs an infidelity $\mathcal{O}(\sigma/\Delta)$ , and allows us to re-express the state as

		$\displaystyle\frac{1}{\sqrt{2^{n}}}\sum_{\mathbf{y}}\sum_{\mathbf{x}}c_{\mathbf{x}}e^{i2\pi lx/2^{n}}e^{-i\pi x/2}\|\mathbf{y}\rangle_{Q}$		(117)
		$\displaystyle\qquad\qquad\times\sqrt{\frac{2\pi\sigma}{\Delta}\sqrt{\frac{2}{\pi}}}\sum_{m}e^{-\sigma^{2}(\frac{2\pi}{\Delta}m)^{2}}\widetilde{\|\tfrac{2\pi}{\Delta}(m-\tfrac{1}{4})\rangle}_{O}.$		(117)

where now the qubits and oscillator are decoupled. Notably, this is the product state $|\alpha\rangle_{Q}|\beta\rangle_{O}$ quoted in Eqs. (66) and (67).

D-B QFT Method 2: Non-Abelian QSP

Here we provide additional details on the QFT protocol using non-Abelian QSP.

D-B1 Implementing the Change of Basis Operation $\mathcal{T}$

In the QFT protocol of Sec. V-B, we used the change of basis operation $\mathcal{T}$ . On $n$ qubits, this operation is defined by a vector $\mathbf{s}\in\{-1,+1\}^{n}$ and its associated integer $s$ :

\displaystyle s=\sum_{j=1}^{n-1}\frac{1+s_{j}}{2}2^{j-1}+\frac{1-s_{n}}{2}2^{n-1}.

(118)

$\mathcal{T}$ maps that maps between a computational basis state $|s\rangle$ and a corresponding state $|\phi_{\mathbf{s}}\rangle$ defined in Eq. (43) as

|\phi_{\textbf{s}}\rangle=(-1)^{\gamma_{\textbf{s}}}\cdot\bigotimes_{j=1}^{n}\left[\frac{1}{\sqrt{2}}\big{(}|0\rangle+s_{j}|1\rangle\big{)}\right]

(119)

where the phase $\gamma_{\mathbf{s}}$ is

\gamma_{\mathbf{s}}=\sum_{j=1}^{n-2}\frac{1}{2}(s_{j}+s_{j+1})+\frac{1}{2}(s_{n-1}-s_{n}).

(120)

For instance, if $\mathbf{s}=(1,-1,1,-1)$ , then the computational basis state is $|1010\rangle$ ; on the other hand $\gamma_{\mathbf{s}}=1$ such that $|\phi_{\mathbf{s}}\rangle=(-1)\cdot|+\rangle|-\rangle|+\rangle|-\rangle$ .

$\mathcal{T}$ can be implemented as a simple product of local operations:

\mathcal{T}=(H\sigma_{x})^{\otimes(n-1)}\cdot H_{n}\cdot\prod_{j=1}^{n-1}(\sigma_{z}^{(j)}\sigma_{z}^{(j+1)})\cdot\mathcal{P}_{\leftrightarrow},

(121)

where $\mathcal{P}_{\leftrightarrow}$ is a permutation operator that reverses the order of qubits (i.e., $\mathcal{P}_{\leftrightarrow}|0011\rangle=|1100\rangle$ ). To verify this, note that the state $|s\rangle$ can be written in the computational basis as

|s\rangle=|\tfrac{1-s_{n}}{2}\rangle\otimes\bigotimes_{j=n-1}^{1}|\tfrac{1+s_{j}}{2}\rangle.

(122)

where we have noted that $s_{n}$ is the most significant bit as per Eq. (118), and hence this tensor product is from $j=n$ down to $j=1$ . The action of $\mathcal{P}_{\leftrightarrow}$ reverses the order of this tensor product, mapping this state to

\mathcal{P}_{\leftrightarrow}|s\rangle=|\tfrac{1-s_{n}}{2}\rangle\otimes\bigotimes_{j=0}^{n-1}|\tfrac{1+s_{j}}{2}\rangle=:|\overleftrightarrow{s}\rangle.

(123)

$\mathcal{P}_{\leftrightarrow}$ can be implemented as a product of $O(n^{2})$ swap gates acting locally between adjacent qubits; each such swap gate be constructed as a product of 3 CNOT gates. Alternatively, $\mathcal{P}_{\leftrightarrow}$ can be accommodated for at no cost by simply changing one’s convention to reverse the order of the qubits comprising the input state.

Next, the action of the product of $Z$ ’s on $|\overleftrightarrow{s}\rangle$ generates the following phase:

		$\displaystyle\prod_{j=1}^{n-1}(\sigma_{z}^{(j)}\sigma_{z}^{(j+1)})\bigotimes_{j=1}^{n-1}\|\tfrac{1+s_{j}}{2}\rangle\otimes\|\tfrac{1-s_{j}}{2}\rangle=$		(124)
		$\displaystyle\prod_{j=1}^{n-2}(-1)^{(1+s_{j})/2}\cdot(-1)^{(1+s_{j+1})/2}$
		$\displaystyle\ \ \times(-1)^{(1+s_{n-1})/2}(-1)^{(1-s_{n})/2}\tilde{\|s\rangle}=$
		$\displaystyle(-1)^{n-1}(-1)^{\sum_{j=0}^{n-2}(s_{j}+s_{j+1})/2+(s_{n-1}-s_{n})/2}\|\overleftrightarrow{s}\rangle=$
		$\displaystyle(-1)^{n-1}(-1)^{\gamma_{s}}\|\overleftrightarrow{s}\rangle.$

This implements the desired phase $(-1)^{\gamma_{s}}$ , up to a global phase $(-1)^{n-1}$ . Moreover, note that we can simplify the product $\prod_{j=1}^{n-1}(\sigma_{z}^{(j)}\sigma_{z}^{(j+1)})$ as

\prod_{j=1}^{n-1}(\sigma_{z}^{(j)}\sigma_{z}^{(j+1)})=\sigma_{z}^{(1)}\sigma_{z}^{(n)}.

(125)

Lastly, the product of Hadamards and bit flips, $(H\sigma_{x})^{\otimes(n-1)}$ , maps from the computational basis to the $|\pm\rangle$ basis as $H\sigma_{x}|\tfrac{1+s_{j}}{2}\rangle=|s_{j}\rangle$ (i.e., $|0\rangle\mapsto|-\rangle$ and $|1\rangle\mapsto|+\rangle$ ); and $H_{n}$ as $H_{n}|\tfrac{1-s_{n}}{2}\rangle=|s_{n}\rangle$ (i.e., $|0\rangle\mapsto|+\rangle$ and $|1\rangle\mapsto|-\rangle$ ). Because the states $|\phi_{s}\rangle$ are defined in the $|\pm\rangle$ basis, this appropriately prepares the state $|\phi_{s}\rangle$ . In aggregate, the change of basis transformation $\mathcal{T}$ can be implemented (up to a global phase) as a simple product of local operations:

\mathcal{T}=(H\sigma_{x})^{\otimes(n-1)}\cdot H_{n}\cdot\sigma_{z}^{(1)}\sigma_{z}^{(n)}\cdot\mathcal{P}_{\leftrightarrow}.

(126)

D-B2 Step 7 Analysis

In Step 7, we obtained the state (see Eq. (78))

		$\displaystyle\sum_{s,j}\sqrt{\frac{\Delta}{2\pi}}\int_{-\pi/\Delta}^{\pi/\Delta}dq\ c_{j}e^{i(q+\frac{\Delta^{\prime}}{2}+q_{s}^{\prime})\Delta j}$		(127)
		$\displaystyle\qquad\quad\times\left[\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{i(q+\frac{\Delta^{\prime}}{2}^{\prime}+q_{s}^{\prime})\Delta 2^{n}k}\right]\text{sinc}(\tfrac{\pi q}{\Delta^{\prime}})\|\phi_{\mathbf{s}}\rangle_{Q}\|q\rangle_{O},$		(127)

where $q_{s}^{\prime}=\Delta^{\prime}s-\tfrac{\Delta^{\prime}}{2}^{\prime}(2^{n+a}-1)$ . To simplify this expression, note the factor $\sum_{k=-2^{a}/2}^{2^{a}/2-1}e^{i(q+\frac{\Delta^{\prime}}{2}+q_{s}^{\prime})\Delta 2^{n}k}$ in brackets is a Dirichlet kernel. In the limit of large $a$ , it behaves as the sum of delta functions $\sum_{l\in\mathbb{Z}}\delta((q+\tfrac{\Delta^{\prime}}{2}^{\prime}+q_{s}^{\prime})\Delta 2^{n}-2\pi l)$ , with an overall error $\mathcal{O}(1/2^{a})$ at finite $a$ . Because the integral of Eq. (127) extends from $q=-\pi/\Delta$ to $\pi/\Delta$ , the delta functions select out the values $q+q_{s}^{\prime}+\frac{\Delta^{\prime}}{2}=\tfrac{2\pi l}{\Delta 2^{n}}$ for integers $l=-2^{n}/2$ to $l=2^{n}/2$ . Taking the large $a$ limit, we can factor out the more slowly varying components of the integrand evaluated at the values $q=\tfrac{2\pi l}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}=\tfrac{2\pi l}{\Delta 2^{n}}-\Delta^{\prime}(s-\tfrac{2^{n+a}}{2})$ , while leaving the fast varying term $\sum_{k}e^{i(q+q_{s}^{\prime}+\frac{\Delta^{\prime}}{2})\Delta 2^{n}k}$ in the integrand. Splitting up the integral into a sum over $l$ of integrals from $q=\tfrac{2\pi(l-1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}$ to $q=\tfrac{2\pi(l+1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}$ , we can rewrite the above state as

		$\displaystyle\sqrt{\frac{\Delta}{2\pi}}\sum_{s,j,l}c_{j}e^{i2\pi lj/2^{n}}\text{sinc}\left(\tfrac{\pi}{\Delta^{\prime}}(\tfrac{2\pi l}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2})\right)\|\phi_{s}\rangle_{Q}$		(128)
		$\displaystyle\ \times\Bigg{[}\int_{\tfrac{2\pi(l-1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}}^{\tfrac{2\pi(l+1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{i(q+q_{s}^{\prime}+\frac{\Delta^{\prime}}{2})\Delta 2^{n}k}\|q\rangle_{O}\Bigg{]}=$
		$\displaystyle\sqrt{\frac{\Delta}{2\pi}}\sum_{s,j,l}c_{j}e^{i2\pi lj/2^{n}}\text{sinc}\left(\pi\left(2^{a}l-(s-\tfrac{2^{n+a}}{2})\right)\right)\|\phi_{s}\rangle_{Q}$
		$\displaystyle\ \times\Bigg{[}\int_{\tfrac{2\pi(l-1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}}^{\tfrac{2\pi(l+1/2)}{\Delta 2^{n}}-q_{s}-\frac{\Delta^{\prime}}{2}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{i(q+q_{s}^{\prime}+\frac{\Delta^{\prime}}{2})\Delta 2^{n}k}\|q\rangle_{O}\Bigg{]},$

where the infidelity suffered at finite $a$ is $\mathcal{O}(1/2^{a})$ .

To knead this into the QFT, first let $\tilde{s}=s-\tfrac{2^{n+a}}{2}\in[-2^{n+a}/2,-2^{n+a}/2+1,...,2^{n+a}/2]$ . Then note that $\text{sinc}(\pi(2^{a}l-\tilde{s}))=\delta_{2^{a}l,\tilde{s}}$ , which extracts out the values $\tilde{s}=2^{a}l\ \Rightarrow\ s=2^{a}(l+\tfrac{2^{n}}{2})$ from the summation over $s$ , and enforces $q_{s}^{\prime}+\frac{\Delta^{\prime}}{2}=\frac{2\pi l}{\Delta 2^{n}}$ . This forces the state in the brackets to become

		$\displaystyle\int_{\tfrac{-\pi}{\Delta 2^{n}}}^{\tfrac{\pi}{\Delta 2^{n}}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{i(q+\tfrac{2\pi l}{2^{n}\Delta})\Delta 2^{n}k}\|q\rangle=$		(129)
		$\displaystyle\int_{\tfrac{-\pi}{\Delta 2^{n}}}^{\tfrac{\pi}{\Delta 2^{n}}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{iq\Delta 2^{n}k}\|q\rangle,$		(129)

where we’ve noted $e^{i2\pi lk}=1$ . This state is concentrated around $q=0$ (because the sum converges to the delta function $\delta(\tfrac{q\Delta 2^{n}}{2\pi})$ for large $a$ ), and has norm

		$\displaystyle\Bigg{\|}\int_{\tfrac{-\pi}{\Delta 2^{n}}}^{\tfrac{\pi}{\Delta 2^{n}}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{iq\Delta 2^{n}k}\|q\rangle\Bigg{\|}^{2}=$		(130)
		$\displaystyle\int_{\tfrac{-\pi}{\Delta 2^{n}}}^{\tfrac{\pi}{\Delta 2^{n}}}dq\frac{1}{2^{a}}\sum_{k,m}e^{iq\Delta 2^{n}(k-m)}=$
		$\displaystyle\frac{1}{2^{a}}\sum_{k,m}\frac{2\pi}{\Delta 2^{n}}\delta_{km}=\frac{2\pi}{\Delta 2^{n}}.$

Let us therefore denote the corresponding normalized state by

\widetilde{|0\rangle}:=\sqrt{\frac{\Delta 2^{n}}{2\pi}}\int_{\tfrac{-\pi}{\Delta 2^{n}}}^{\tfrac{\pi}{\Delta 2^{n}}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{iq\Delta 2^{n}k}|q\rangle.

(131)

We can therefore rewrite the total state of the system as

		$\displaystyle\sqrt{\frac{\Delta}{2\pi}}\sum_{j,l}c_{j}e^{i2\pi lj/2^{n}}\sqrt{\frac{2\pi}{\Delta 2^{n}}}\|\phi_{s=2^{a}(l+2^{n}/2)}\rangle_{Q}\widetilde{0\rangle}_{O}$		(132)
		$\displaystyle=\Bigg{[}\sum_{l=-2^{n}/2}^{2^{n}/2}\left(\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}c_{j}e^{i2\pi lj/2^{n}}\right)\|\phi_{s=2^{a}(l+2^{n}/2)}\rangle\Bigg{]}\widetilde{\|0\rangle}.$		(132)

Evidently, the oscillator and qubits are decoupled, and the state of the qubits is the quantum Fourier transform of the initial state, evaluated in the basis $|\phi_{s=2^{a}(l+2^{n}/2)}\rangle$ . Moreover, if we shift the index of summation to $l\mapsto l+2^{n}/2$ , we can rewrite this state expression as

\displaystyle\Bigg{[}\sum_{l=0}^{2^{n}-1}\left(\frac{1}{\sqrt{2^{n}}}\sum_{j=0}^{2^{n}-1}c_{j}e^{i2\pi lj/2^{n}}e^{-i\pi j/2}\right)|\phi_{s=2^{a}l}\rangle\Bigg{]}\widetilde{|0\rangle}.

(133)

This is the state quoted in the main text in Eq. (79)

D-B3 Fidelity Analysis

Consider the fidelity of this QFT protocol. As we mentioned in Sec. V, the first source of infidelity occurs in Step 3 due to the usage of the D/A conversion protocol. The fidelity of this is quantified in Eq. (110), and scales as

\displaystyle 1-\mathcal{O}\Bigg{(}\int_{-\infty}^{-\frac{\Delta}{2}(2^{n+a}-1)}dq|\psi(q)|^{2}+\int_{\frac{\Delta}{2}(2^{n+a}-1)}^{\infty}dq|\psi(q)|^{2}\Bigg{)}

(134)

where $\psi(q)$ is the wave function after being transferred to the oscillator, which at this stage is

\displaystyle\sum_{j=0}^{2^{n}-1}\sum_{k=-2^{a}/2}^{2^{a}/2-1}\frac{1}{\sqrt{2^{a}\cdot\Delta}}c_{j}\text{sinc}\left(\tfrac{\pi(q-\Delta(2^{n}\cdot k+j-\tfrac{1}{2}))}{\Delta}\right).

(135)

Let us consider the integral from $q=\tfrac{\Delta}{2}(2^{n+a}-1)$ to $\infty$ . In this regime, the wave function scales at worst as

|\psi(q)|^{2}\sim\frac{1}{2^{a}\cdot\Delta}\text{sinc}^{2}\left[\tfrac{\pi(q-\frac{\Delta}{2}(2^{n+a-1})))}{\Delta}\right]

(136)

such that the integral is (using the substitution $q^{\prime}=q-\tfrac{\Delta}{2}(2^{n+a}-1)$ ):

\mathcal{O}\Bigg{(}\frac{1}{2^{a}\cdot\Delta}\int_{0}^{\infty}dq^{\prime}\text{sinc}^{2}\left[\tfrac{\pi q^{\prime})}{\Delta}\right]\Bigg{)}=\mathcal{O}(1/2^{a}).

(137)

Moreover, the other source of infidelity arises from taking the large $a$ limit in Step 7 when approximating the factor $\sum_{k=-2^{a}/2}^{2^{a}/2-1}e^{iq\Delta 2^{n}k}$ as a sum of delta functions. The infidelity suffered in making this approximation is $\mathcal{O}(1/2^{a})$ . Summing these contributions to the infidelity, we find the overall fidelity of this QFT protocol is

1-\mathcal{O}(1/2^{a}).

(138)

	$\displaystyle\|\psi\rangle_{Q}\|0,\Delta\rangle_{O}^{\text{Gaus}}$	$\displaystyle=\sum_{\mathbf{x}}c_{\mathbf{x}}\|\mathbf{x}\rangle_{Q}\|0,\Delta\rangle_{O}^{\text{Gaus}}$		(29)
		$\displaystyle\qquad\qquad\mapsto\sum_{\mathbf{x}}c_{\mathbf{x}}\|\mathbf{x}\rangle_{Q}\|x,\Delta\rangle_{O}^{\text{Gaus}}.$		(29)

		$\displaystyle\Delta\sum_{s}\|\psi(q_{s})\|^{2}=$		(102)
		$\displaystyle\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}dq\|\psi(q)\|^{2}+\mathcal{O}\left(\frac{\Delta}{2}\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}\big{\|}\tfrac{d}{dq}\|\psi(q)\|^{2}\big{\|}\right)=$
		$\displaystyle 1-\int_{-\infty}^{-\frac{\Delta}{2}(2^{n}-1)}dq\|\psi(q)\|^{2}-\int_{\frac{\Delta}{2}(2^{n}-1)}^{\infty}dq\|\psi(q)\|^{2}$
		$\displaystyle\qquad+\mathcal{O}\left(\Delta\int_{-\frac{\Delta}{2}(2^{n}-1)}^{\frac{\Delta}{2}(2^{n}-1)}dq\big{\|}\tfrac{d}{dq}\|\psi(q)\|^{2}\big{\|}\right),$

		$\displaystyle\prod_{j=1}^{n-1}(\sigma_{z}^{(j)}\sigma_{z}^{(j+1)})\bigotimes_{j=1}^{n-1}\|\tfrac{1+s_{j}}{2}\rangle\otimes\|\tfrac{1-s_{j}}{2}\rangle=$		(124)
		$\displaystyle\prod_{j=1}^{n-2}(-1)^{(1+s_{j})/2}\cdot(-1)^{(1+s_{j+1})/2}$
		$\displaystyle\ \ \times(-1)^{(1+s_{n-1})/2}(-1)^{(1-s_{n})/2}\tilde{\|s\rangle}=$
		$\displaystyle(-1)^{n-1}(-1)^{\sum_{j=0}^{n-2}(s_{j}+s_{j+1})/2+(s_{n-1}-s_{n})/2}\|\overleftrightarrow{s}\rangle=$
		$\displaystyle(-1)^{n-1}(-1)^{\gamma_{s}}\|\overleftrightarrow{s}\rangle.$

		$\displaystyle\sqrt{\frac{\Delta}{2\pi}}\sum_{s,j,l}c_{j}e^{i2\pi lj/2^{n}}\text{sinc}\left(\tfrac{\pi}{\Delta^{\prime}}(\tfrac{2\pi l}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2})\right)\|\phi_{s}\rangle_{Q}$		(128)
		$\displaystyle\ \times\Bigg{[}\int_{\tfrac{2\pi(l-1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}}^{\tfrac{2\pi(l+1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{i(q+q_{s}^{\prime}+\frac{\Delta^{\prime}}{2})\Delta 2^{n}k}\|q\rangle_{O}\Bigg{]}=$
		$\displaystyle\sqrt{\frac{\Delta}{2\pi}}\sum_{s,j,l}c_{j}e^{i2\pi lj/2^{n}}\text{sinc}\left(\pi\left(2^{a}l-(s-\tfrac{2^{n+a}}{2})\right)\right)\|\phi_{s}\rangle_{Q}$
		$\displaystyle\ \times\Bigg{[}\int_{\tfrac{2\pi(l-1/2)}{\Delta 2^{n}}-q_{s}^{\prime}-\frac{\Delta^{\prime}}{2}}^{\tfrac{2\pi(l+1/2)}{\Delta 2^{n}}-q_{s}-\frac{\Delta^{\prime}}{2}}dq\frac{1}{\sqrt{2^{a}}}\sum_{k}e^{i(q+q_{s}^{\prime}+\frac{\Delta^{\prime}}{2})\Delta 2^{n}k}\|q\rangle_{O}\Bigg{]},$

Toward Mixed Analog-Digital Quantum Signal Processing: Quantum AD/DA Conversion and the Fourier Transform

Abstract

Index Terms:

I Introduction

II Overview of Signal Processing and CV-DV Quantum Systems

II-A Overview of classical signal processing data types

II-B Review of DV and CV Quantum Systems and Operations

II-B1 Quantum States and Operations on Qubits

II-B2 Quantum States and Operations on Oscillators

III Mixed Analog-Digital Quantum Signal Processing

III-A Hybrid Single-variable QSP

III-B Hybrid Non-Abelian QSP

IV Quantum AD/DA Conversion: Sampling and Interpolation of Quantum Data

IV-A Quantum AD/DA Conversion: Hybrid Single-Variable QSP

Theorem 1 (Quantum AD/DA Conversion with Hybrid Single Variable QSP).

IV-B Quantum AD/DA Conversion: Hybrid Non-Abelian QSP

Theorem 2 (Quantum AD/DA Conversion with Non-Abelian QSP).

V Quantum Fourier Transform from Oscillator Evolution

V-A Continuous-Discrete Fourier Transform Correspondence

V-B Quantum Fourier Transform Protocols

V-B1 QFT Protocol 1: Hybrid Single Variable QSP

Theorem 3 (QFT from Oscillator Evolution and AD/DA Conversion (Single-Variable QSP)).

V-B2 QFT Protocol 2: Hybrid Non-Abelian QSP

Theorem 4 (QFT from Oscillator Evolution and AD/DA Conversion Via Non-Abelian QSP)).

VI Conclusion and Outlook

Acknowledgment

References

Appendix A A Brief Review of Quantum Signal Processing

Appendix B Forward Direction of the Hybrid CV-DV Non-Abelian QSP Theorem

Appendix C Details on Quantum AD/DA Conversion Protocols

C-A Quantum AD/DA Conversion: Hybrid Single-Variable QSP

C-A1 Fidelity Bound

C-B Quantum AD/DA Conversion: Hybrid Non-Abelian QSP

C-B1 Fidelity Bound

Appendix D Details on Steps of QFT Protocols

D-A QFT Protocol 1: Hybrid Single-Variable QSP

D-A1 Analysis of Step 5

D-B QFT Method 2: Non-Abelian QSP

D-B1 Implementing the Change of Basis Operation 𝒯\mathcal{T}

D-B2 Step 7 Analysis

D-B3 Fidelity Analysis

D-B1 Implementing the Change of Basis Operation $\mathcal{T}$