Toward discovering the excited baryons through nonleptonic weak decays of
Abstract
The nonleptonic weak decay processes are studied using the constituent quark model. The branching fraction of is predicted to be . Considering the newly observed resonance as a conventional -wave excite state with spin-parity , the newly measured ratio at Belle can be well understood. Besides, the production rates for the missing wave state , two spin quartet wave states and , and two -wave states and are also investigated. It is expected that these missing excited baryons should have large potentials to be discovered through the nonleptonic weak decays of in forthcoming experiments by Belle II and/or LHCb.
I Introduction
Establishing a relatively complete hadron spectrum and understanding the properties of hadrons are important topics in hadron physics. The knowledge about the baryon spectrum is very scarce. So far, the ground state and its four possible excited states , , , and , have been observed in experiments ParticleDataGroup:2020ssz . The unambiguous discovery of in both production and decay was by Barnes et al. in 1964 using the -meson beam at the Brookhaven National Laboratory Abrams:1964tu ; Barnes:1964pd . In 1985, the and resonances decaying into were observed in an experiment at the CERN SPS charged hyperon beam using incident Biagi:1985rn . In 1987, the resonance was produced in interactions at SLAC Aston:1987bb . In 1988, the resonance was observed in the invariant mass spectrum with a signal significance claimed to be at least 5.5 standard deviations by using the scattering at SLAC Aston:1988yn . Since then, there was no progress toward searching for resonances for as long as 30 years due to no effective production mechanisms. In order to promote the experiment, people proposed to produce states on a proton target in CLAS12 through the photoproduction processes Afanasev:2012fh , or produce them by using a secondary kaon beam from the photoproduction processes at JLab etc. Amaryan:2015swp ; Briscoe:2015qia .
In 2018, the first low-lying resonance was observed by the Belle Collaboration in the and invariant mass distributions by using a data sample of annihilations Belle:2018mqs . The resonance may favor the low-lying -wave excited state with Xiao:2018pwe ; Liu:2019wdr ; Aliev:2018yjo ; Aliev:2018syi ; Polyakov:2018mow , although it may be a candidate of hadronic molecule state as discussed in the literatures Wang:2007bf ; Wang:2008zzz ; Valderrama:2018bmv ; Lin:2018nqd ; Huang:2018wth ; Pavao:2018xub ; Lu:2020ste ; Ikeno:2020vqv . Recently, the Belle Collaboration also discovered the resonance by using the weak decay process Belle:2021gtf . The measured branching fraction ratio is Belle:2021gtf . Such a large relative ratio indicates that the weak decay processes may provide a new and ideal platform to investigate the low-lying excited states both theoretically and experimentally. 111Here and after, we donote excited state as with mass in the unit of MeV.
| Ref. Oh:2007cr | Ref. Capstick:1985xss | Ref. Faustov:2015eba | Ref. Chao:1980em | Ref. Chen:2009de | Ref. Pervin:2007wa | Ref. Engel:2013ig | Ref. Liu:2019wdr | Observed mass | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1694 | 1635 | 1678 | 1675 | 1673 | 1656 | 1642(17) | 1672 | 1672.45 | ||
| 1837 | 1950 | 1941 | 2020 | 2015 | 1923 | 1944(56) | 1957 | |||
| 1978 | 2000 | 2038 | 2020 | 2015 | 1953 | 2049(32) | 2012 | 2012.5 | ||
| 2140 | 2220 | 2301 | 2190 | 2182 | 2191 | 2350(63) | 2232 | |||
| 2165 | 2173 | 2065 | 2078 | 2170 | 2159 | |||||
| 2282 | 2345 | 2304 | 2265 | 2263 | 2194 | 2470(49) | 2245 | |||
| 2345 | 2401 | 2265 | 2260 | 2210 | 2303 | |||||
| 2140 | 2255 | 2301 | 2210 | 2202 | 2175 | 2481(51) | 2141 | |||
| 2282 | 2280 | 2304 | 2215 | 2208 | 2182 | 2470(49) | 2188 | |||
| 2280 | 2401 | 2225 | 2224 | 2178 | 2252 | |||||
| 2295 | 2332 | 2210 | 2205 | 2183 | 2321 |
Theoretical studies on the resonances mainly focus on the mass spectrum within various approaches, such as nonrelativistic quark models Kalman:1982ut ; Menapara:2021vug ; Pervin:2007wa ; Liu:2019wdr ; Chao:1980em ; Chen:2009de , relativistic quark models Capstick:1985xss ; Faustov:2015eba ; Loring:2001kx ; Santopinto:2014opa , Lattice QCD Engel:2013ig ; CLQCD:2015bgi , and the Skyrme model Oh:2007cr . The predicted mass spectrum for the conventional baryons are collected in Table 1 as a reference. It can be seen that most of the predicted masses for the -, - and -wave states lies in the mass ranges , , and MeV, respectively. Additionally, in Refs. An:2013zoa ; An:2014lga ; Yuan:2012zs , the authors investigated the low-lying five-quark configurations with negative parity and further considered their mixing combined the corresponding low-lying three-quark configurations. Recently, stimulated by the newly observed resonance at Belle, the strong decay behaviors of some low-lying -, - and -wave resonances were also systematically investigated using the chiral quark model Xiao:2018pwe ; Liu:2019wdr and model Wang:2018hmi . The results suggest that the -, - and -wave baryons have relatively narrow decay widths of less than 50 MeV, and they may be discovered in the and/or final states. Some previous studies of the decays can be found in the Refs. Bijker:2000gq ; Bijker:2015gyk .
On the other hand, there are only a few studies on the productions of and its excited states through the weak decays of in theory. For example, the productions of the ground state have been studied via semileptonic decays of using a constituent quark model Pervin:2006ie and the nonleptonic two-body decays of by the covariant confined quark model Gutsche:2018utw ; Korner:1992wi and the light-front quark model Hsiao:2020gtc . In Ref. Pervin:2006ie , the author also studied the productions of the -wave excited states , which are considered via the semileptonic weak decay processes using a quark model. On the other hand, the newly observed resonance as a dynamically generated state was theoretically studied in the nonleptonic weak decays of and in Ref. Zeng:2020och . So far, the productions of the -, - and -wave excited states via the nonleptonic weak decay processes are not systematically studied in theory.
In this work, we systematically study the production of the low-lying -, - and -wave resonances via the hadronic weak decays of using the constituent quark model. Recently, this model has been developed to study the hadronic weak decays of , the heavy quark conserving weak decays of , and hyperon weak radiative decay by Niu et al. Niu:2020gjw ; Niu:2021qcc ; Niu:2020aoz . This model is similar to that developed to deal with the semileptonic decays of heavy and baryons in Refs. Pervin:2006ie ; Pervin:2005ve .
II framework
II.1 The model
A unique feature of is that this decay proceeds only via external -emission diagram Cheng:2021qpd , which is displayed in Fig. 1. We consider the simple quark-level transition , which is relevant for the Cabibbo-favored decay process of . The effective Hamiltonian for can be given by Buchalla:1995vs
| (1) |
where GeV-2 is the Fermi constant ParticleDataGroup:2020ssz , and and are the Wilson coefficients taken at the scale Buchalla:1995vs . The Cabibbo-Kobayashi-Maskawa matrix elements and are taken from the Review of Particle Physics (RPP) ParticleDataGroup:2020ssz , and the current-current operators are
| (2) | |||||
| (3) |
with (, ) representing the th quark field in a meson or baryon, and and being color indices.
According to its parity behavior, can be separated into a parity-conserving part () and a parity-violating part () Niu:2020gjw ,
| (4) |
With a non-relativistic expansion, the two operators can be approximately expressed as Niu:2020gjw
| (5) | |||||
| (6) | |||||
In the above equations, and stand for the momentum and mass of the th quark, respectively, as shown in Fig. 1. The ( and , ) are color factors, is the dimension-two unit matrix, and is the flavor operator which transforms quark to quark. The and stand for the spin of the th quark and the fourth antiquark, respectively. is a symmetry factor and equals to one for a direct pion emission process considering in present work.
In order to evaluate the spin matrix element and including an antiquark, the particle-hole conjugation Racah:1942gsc should be employed. Within the particle-hole conjugation relation:
| (7) |
the antiquark spin transforms as follows: and . For instance:
| (8) |
For a given decay process , the transition amplitude is calculated by
| (9) | |||||
where , and stands for the wave functions of the initial baryon , final meson and final baryon , respectively. , , and are the momentum, the total angular momentum and the third component of the total angular momentum of the initial baryon and the final baryon , respectively. q is the three-momentum of the final state meson in the initial state rest frame.
Then, the partial decay width for a given decay process can be expressed as
| (10) |
where is the phase-space factor for the decay.
The choice of phase space is not clear. For the phase space factor , there are three typical options adopted in the literature Kokoski:1985is ; Kumano:1988ga ; Geiger:1994kr ; Capstick:2000qj . The usual option is the relativistic phase-space factor (RPF)
| (11) |
where is the mass of the initial hadron , while and stand for the energies of final hadrons and , respectively.
To match the transition matrix element calculated non-relativistically, a fully nonrelativistic phase-space factor (NRPF) is used, that is
| (12) |
where and is the mass of the final hadron and , respectively.
However, in many cases the momenta of the final hadrons are quite large so that the relativistic phase space is significantly different from the nonrelativistic limit. In Ref. Kokoski:1985is , Kokoski and Isgur suggested a “mock-hadron” phase-space factor (MHPF),
| (13) |
in their calculation of meson decay widths. The , and are effective hadron masses of hadron , and , respectively. They are evaluated with a spin-independent inter-quark interaction. In the weak-binding limit, the mass of meson is degenerate with that of meson.
II.2 Wave functions
To work out the decay amplitude , we need the wave functions of the initial and final states. Here, the initial state is the ground baryon, the final states are the meson and the states. These wave functions are constructed within the non-relativistic constituent quark model. For simplicity, the spatial wave functions of the baryons and mesons are adopted the harmonic oscillator form in our calculations.
The spatial wave function for a baryon with principal quantum number , total orbital angular momentum quantum numbers , and is a product of the -oscillator part and the -oscillator part. In momentum space, the baryon spatial wave function is given by Liu:2019wdr
| (14) |
with , , and
| (15) |
Here, is th solid harmonic polynomial. and are the internal momenta of the - and -oscillator wave functions, respectively. They can be expressed as functions of the quark momenta ():
| (16) | |||||
| (17) |
The and are the principal quantum numbers of the - and -mode oscillators, respectively. and are the orbital angular momentum quantum numbers of the - and -mode oscillators, respectively. stand for different excitation modes with different permutation symmetries. and are two oscillator parameters. For the baryons, we have , while for the charmed baryons, we have
| (18) |
where and stand for the masses of the strange and charmed quarks, respectively. The flavor and spin wave functions of the and baryons have been given in our previous works Xiao:2013xi ; Wang:2017kfr . The product of spin, flavor, and spatial wave functions of the heavy baryons must be symmetric since the color wave function is antisymmetric. The details about the quark model classifications for the spectrum can be found in the works of Wang:2017kfr ; Yao:2018jmc ; Zhong:2007gp , while for the baryon spectrum can be found in Refs. Xiao:2013xi ; Liu:2019wdr .
Finally, the wave function of the meson is constructed by
| (19) |
where the spin wave function is
| (20) |
and the flavor wave function is
| (21) |
The spatial wave function in the momentum space is adopted the simple harmonic oscillator form
| (22) |
where is a size parameter of the meson wave function. The and stand for the quark momenta of the meson as shown in Fig. 1.
II.3 Parameters
For self consistency, the quark model parameters are taken the same as those adopted in our previous work Wang:2017kfr . The constituent masses for the , and quarks are taken to be MeV, MeV and MeV, respectively. For the initial state , the harmonic oscillator parameter is taken to be MeV, the other harmonic oscillator parameter is related to by . For the final state , a unified harmonic oscillator parameter is adopted, i.e., MeV. For the meson, the size parameter is taken to be MeV as that adopted in Ref. Niu:2020gjw . The masses for the , and are taken the RPP average values 140 MeV, 1672 MeV and 2695 MeV, respectively ParticleDataGroup:2020ssz . In the MHPF defined in Eq. (13), we need determine the effective masses of the mock hadrons. For the process , we adopt GeV, consistent with Kokoski and Isgur Kokoski:1985is , and and .
III Numerical results and discussion
In this work, considering the uncertainties from the relativistic effect, we perform our calculations with the three typical phase space options, RPF, NRPF and MHPF. Our results are listed in Table 3. It is seen that the nonleptonic weak decay properties of have a significance dependence on the options of the phase space factor. The results from RPF and MHPF are comparable with each other. However, the predicted partial widths with NRPF are a factor of smaller those calculated with RPF and MHPF.
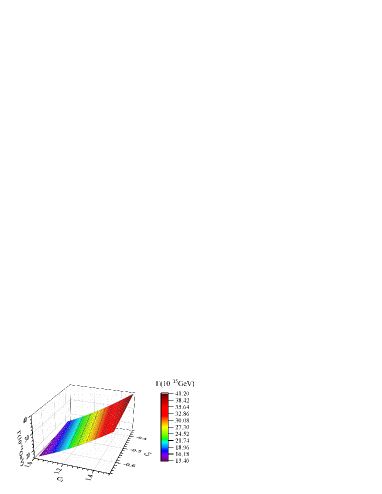
The Wilson coefficients and are usually taken to be and at the scale Buchalla:1995vs . These coefficients have some uncertainties due to their scale dependencies. To see the effects of the uncertainties of and on our results, as an example in Fig. 2 we plot the partial width of as a function of the and in the range of and . From the figure, one can see that considering a uncertainty for the Wilson coefficients and at the scale, the partial decay width of lies in the range of GeV, which shows a sizeable decadency on the Wilson coefficients.
III.1
First, we study the weak decay process . This weak decay process, as an important process, has been widely studied by the Belle, BaBar, CLEO, SELEX, FOCUS collaborations Belle:2017szm ; BaBar:2007jdg ; CLEO:2000dhf ; FOCUS:2003ylx ; Solovieva:2008fw ; SELEX:2007bim ; BaBar:2005yiy . With the RPF, the partial decay width of is predicted to be
| (23) |
By using the measured lifetime of ParticleDataGroup:2020ssz , we further predict the branching fraction
| (24) |
If adopting the MHPF, there is a correction to the results of RMF. However, when adopting the NRPF the results are about a factor of smaller than that predicted with RMF. From Table 2, it is found that our predicted branching fraction with both RPF and MHPF is close to the predictions in Refs. Cheng:1996cs ; Hsiao:2020gtc . While, if adopting the NRPF, our predicted branching fraction is consistent with that from the covariant confined quark model Gutsche:2018utw .
| RPF/MHPF/NRPF | Ref. Gutsche:2018utw | Ref. Cheng:1996cs | Ref. Hsiao:2020gtc | Ref. Korner:1992wi | |
| 1.05%/0.82%/0.16% | 0.2% | 1.0% | 0.5% | 2.3% |
Furthermore, combined the predicted branching fraction of with the measured relative branching ratios and , the branching fractions for the three-body weak decay processes can be obtained easily. With the RPF, we have
| (25) | |||||
| (26) |
While when adopting the NRPF, we have small branching fractions
| (27) | |||||
| (28) |
due to the small nonrelativistic phase space factor.
III.2
In the family, there are two -wave states and with spin-parity and , respectively. The newly observed resonance may favor the assignment of state, since both the measured mass and width are consistent with the quark model predictions Xiao:2018pwe ; Liu:2019wdr ; Aliev:2018yjo ; Aliev:2018syi ; Polyakov:2018mow . The masses of the unestablished states are taken the predictions in Ref. Liu:2019wdr , which have been collected in Table 1. However, the classified in the quark model is still missing.
| RPF | NRPF | MHPF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| final state | (MeV) | |||||||||
| 1672 | 26 | 10.5 | 1.0 | 3.8 | 1.6 | 1.0 | 21 | 8.2 | 1 | |
| 1957 | 9.5 | 3.8 | 0.38 | 2.0 | 0.80 | 0.50 | 8.7 | 3.6 | 0.44 | |
| 2012 | 5.4 | 2.2 | 0.22 | 1.2 | 0.49 | 0.31 | 5.2 | 2.1 | 0.26 | |
| 2232 | 1.2 | 5.0 | 0.05 | 3.9 | 0.16 | 0.01 | 1.5 | 6.3 | 0.08 | |
| 2159 | 3.0 | 1.2 | 0.12 | 0.8 | 0.34 | 0.21 | 3.3 | 1.4 | 0.17 | |
| 2245 | 2.1 | 8.4 | 0.008 | 6.7 | 2.7 | 0.002 | 2.6 | 1.1 | 0.01 | |
| 2303 | 1.3 | 5.0 | 5.0 | 5.4 | 2.0 | 1 | 1.9 | 7.7 | 9.4 | |
| 2141 | 3.3 | 1.3 | 0.13 | 8.8 | 0.36 | 0.23 | 3.6 | 1.5 | 0.18 | |
| 2188 | 2.3 | 0.95 | 0.09 | 6.8 | 0.28 | 0.18 | 2.7 | 1.1 | 0.13 | |
| 2252 | 3.3 | 1.3 | 1.3 | 1.2 | 4.5 | 2.8 | 4.2 | 1.7 | 2.1 | |
| 2321 | 3.2 | 1.3 | 1.3 | 1.3 | 5.1 | 3.2 | 4.7 | 1.9 | 2.3 | |
Considering as the assignment, we have studied the process, the results are listed in Table 3. It is found that the baryon has a fairly large decay rate into , with the RPF or MHPF the branching fraction is predicted to be
| (29) |
Combining it with the branching fraction of obtained in Eq.(24), we predict the relative ratio
| (30) |
which is in good agreement with experimental value that was recently measured by the Belle Collaboration Belle:2021gtf . According to the strong decay properties of predicted using the constituent quark model in Refs. Liu:2019wdr ; Xiao:2018pwe , branching fractions of decaying into and are predicted to be and , respectively. Combining these strong branching fractions of with our predicted branching fractions for the weak decay processes ] in Eqs. (27)-(29), one can obtain
| (31) | |||||
| (32) | |||||
which are also consistent with the experimental values and recently measured by the Belle Collaboration Belle:2021gtf , respectively. It should be mentioned that these predicted relative ratios () are nearly independent on the options of phase space factor in the calculations.
Then we consider the weak decay rate of into the other -wave state by emitting a meson. The mass of is predicted to be MeV within the Lattice QCD Engel:2013ig and the relativized quark models Capstick:1985xss ; Faustov:2015eba . Experimentally, there seems to be a weak enhancement around 1950 MeV in the invariant mass distributions from the Belle observations Belle:2021gtf ; Belle:2018mqs , which may be a hint of . Hence, in the calculations the mass of is taken to be 1957 MeV. If adopting the RPF or MHPF, the branching fraction is predicted to be
| (33) |
which is about a factor of larger than that predicted with NRPF. The predicted branching fraction should be slightly larger than that of the final states. The branching fraction ratio between and is predicted to be
| (34) |
which is insensitive to options of the phase space factor. Such a large relative branching ratio indicates that the other missing -wave state has a good potential to be observed in the weak decay process .
According to the strong decay analysis in Refs. Liu:2019wdr ; Xiao:2018pwe ; Wang:2018hmi , the decays of should be nearly saturated by the and channels. Combined the strong decay properties predicted within the chiral quark model in Refs. Liu:2019wdr ; Xiao:2018pwe , we can estimate the ratios
| (35) | |||
| (36) |
which may provide useful references for future experiments.
To further explain the results of the and states, we fit the invariant mass spectrum of the process measured by Belle Collaboration Belle:2021gtf . In our analysis, we adopt a relativistic Breit-Wigner function to describe the event distribution ParticleDataGroup:2020ssz ; Xie:2015lta ; Xie:2018gbi ; Zhang:2017eui
| (37) |
where and stands for the invariant mass of and the resonance mass of , respectively. and are the partial decay widths of and , respectively. The total decay width are adopted as the predictions obtained in Ref. Liu:2019wdr , while stands for the background contributions. In this work a linear background (MeV is adopted, which is determined by fitting the backgrounds taken in Ref. Belle:2021gtf . Finally is a global parameter related to the resonance production rates.
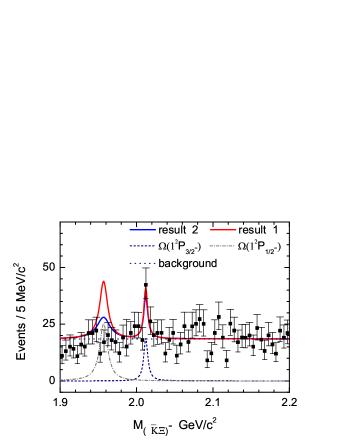
In Fig. 3, we shown our theoretical results for the invariant mass distributions of the decay . The red curve has been adjusted to the strength of the experimental data of Belle Collaboration Belle:2021gtf at the peak around 2012 MeV by taking . Furthermore, the dashed curve stands for the resonance contribution of with MeV and MeV, while the dash-dotted curve stands for the contribution with MeV and MeV. From Fig. 3 one can easily find that the state has a significant contribution around 2012 MeV and the experimental data around that energy can be well reproduced. However, the contribution of the state is overestimated comparing with the experimental data around 1957 MeV. Yet, the quark model predicted widths for the and states have uncertainties, we perform a new calculation with a slightly large width MeV for state, while we take the experimental value of MeV for . The new theoretical results are also shown in Fig. 3 with blue curve, where we see that the signal of the is much suppressed. It is expected that more precise experimental data can be used to pin down the contribution of the state in future.
On the other hand, the decay was investigated within the picture that the is a molecular state in Ref. Ikeno:2022jpe , where the numerical results are also consistent with the experimental data. Indeed, we need further efforts to understand the nature of state Belle:2022mrg ; Hu:2022pae .
III.3
There are six -wave states, and according to the quark quark model classification. Most of the predicted masses for the -wave states lies in the mass range MeV in various quark models. Taking the mass recently predicted in Ref. Liu:2019wdr , we calculate the weak decay properties for the processes. Our results are listed in Table 3. It is seen that has significant branching fractions decaying into the spin quartet states and . The predicted branching fractions can reach up to the order of . With the RPF, their relative ratios to are predicted to be
| (38) | |||
| (39) |
which are close to the results predicted with RPF and MHPF. The predicted branching fractions and ratios are comparable with those of decaying into the and channels. However, the decay rates of into the other four -wave states and are orders of magnitude smaller. The relatively large decay rates indicate that both and has good potentials to be established by using the weak decay processes .
We further analyze the reasons of the small decay rates of compared with that of as follows. We note that the helicity transition amplitudes
| (40) |
where () and () are the spacial and spin wave functions of the initial (final) baryons, respectively. For the decay processes involving the spin quartet states , the decay amplitude is the sum of and . These two terms have strong constructive and destructive interference for the and , respectively. Thus, the decay rates of are strongly suppressed by the destructive interference between the two terms of the helicity transition amplitude. While for the decay processes involving the spin doublet , the decay amplitudes are proportional to . In this term, the contribution from the part of the spin wave functions is about a factor of smaller than that for the spin quartet states. Thus, the decay rates of is suppressed by the relative small overlapping of the spin wave functions of the initial and final states.
According to the analysis of the strong decay properties Liu:2019wdr ; Xiao:2018pwe , the state has a width of MeV, and dominantly decays into the channel with a branching fraction . While the has a width of MeV, and dominantly decays into with a branching fraction . Thus, the and final states can be used to look for the and states if they are produced by the weak decays. For the state, by combining the results of RPF we can estimate the following ratios
| (41) | |||
| (42) |
while for the state, we can estimate the following ratios
| (43) | |||
| (44) |
The above predicted ratios are less dependent on the options of the phase space factor.
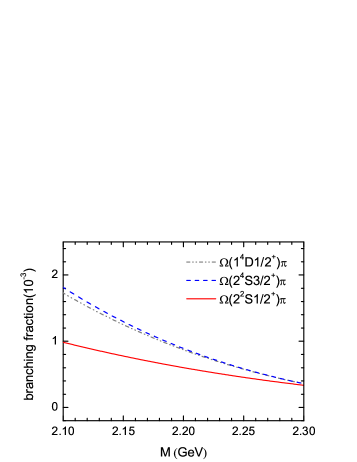
Finally, it should be pointed out that the predicted masses of the -wave states have some model dependencies. To see the effects from the mass uncertainties of the -wave states on our predicted weak decay properties, we plot the weak branching fractions of as functions of the masses of the -wave excited state in their possible range GeV in Fig. 4. It is seen that in the most possible mass range MeV, the upper limit of our predicted partial widths is about a factor of larger than that of the lower limit.
III.4
In the constituent quark model, there are two -wave states and . There are large uncertainties in the predictions of their masses in various quark models. The predicted masses scatter in the range of GeV. In Fig. 4, by using the RPF we plot the weak decay widths of the processes as functions of the masses of the -wave states. It is seen that in the mass range MeV, for the weak decay process , the partial decay width is predicted to be GeV, the branching fraction can reach up to
| (45) |
Combined with the predicted branching fraction , we obtain the relative branching ratio
| (46) |
The production rate of via the weak decay is about a factor of smaller than that of . Due to the large decay rate into the channel Liu:2019wdr ; Xiao:2018pwe , the state is suggested to be searched in the decay chain in future experiments.
For the other weak decay process , by using the RPF the partial decay width is predicted to be GeV, the branching fraction can reach up to
| (47) |
Similarly, the relative branching ratio is predicted to be
| (48) |
The production rate of via the weak decay is comparable with that of . The dominant decay mode of is the channel, and one can look for it in the decay chain .
IV Summary
In this work, we calculate the Cabbibo-favored weak decay processes within a constituent quark model. Our predicted branching fraction which is in agreement with the early predictions in orders in Refs. Cheng:1996cs ; Korner:1992wi . Considering the newly observed resonance as the conventional state, it is found that the measured ratio at Belle can be well understood within our model calculations here. The production potentials of the missing low-lying -, -, and -wave resonances via the hadronic weak decays of are discussed as well. Our main conclusions are summarized as follows.
i) The missing -wave state has a large potential to be observed in the decay chain . The production rate of via the hadronic weak decays of is even slightly larger than that of .
ii) For the -wave states, we find that both and have fairly large production rates via the and processes, respectively. Their production rates via the hadronic weak decays of are comparable with those of the -wave states. Both and are most likely to be observed in the process .
iii) The states and also have fairly large production rates via the hadronic weak decays of . Their production rates are about a factor of smaller than that of . Both and dominantly decay into the channel, thus, they can be looked for in the decay chains .
Finally, it should be mentioned that our predicted partial widths for the weak decay processes may have a large uncertainties due to relativistic effects. To roughly see the uncertainties from the relativistic corrections, we perform our calculations with the three typical phase space options, the relativistic phase space, the nonrelativistic phase space and the “mock-hadron” phase space. The predicted partial widths with the nonrelativistic phase space are a factor of smaller those calculated with the usual relativistic phase space and the “mock-hadron” phase space.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grants Nos.12205026, 12175065, 12075288, U1832173, 11775078, 11705056, 11735003, and 11961141012), and Applied Basic Research Program of Shanxi Province, China under Grant No.202103021223376. Qi-Fang Lü is partly supported by the State Scholarship Fund of China Scholarship Council under Grant No. 202006725011. Ju-Jun Xie is also supported by the Youth Innovation Promotion Association CAS.
References
- (1) P. A. Zyla et al. (Particle Data Group), Review of Particle Physics, PTEP 2020, 083C01 (2020).
- (2) G. S. Abrams, R. A. Burnstein, G. R. Charlton, T. B. Day, B. Kehoe, B. Sechi-Zorn, G. A. Show, M. C. Whatley, G. Wolsky and G. B. Yodh, et al. Example of decay , Phys. Rev. Lett. 13, 670 (1964).
- (3) V. E. Barnes, P. L. Connolly, D. J. Crennell, B. B. Culwick, W. C. Delaney, W. B. Fowler, P. E. Hagerty, E. L. Hart, N. Horwitz and P. V. C. Hough, et al. Observation of a Hyperon with Strangeness Minus Three, Phys. Rev. Lett. 12, 204 (1964).
- (4) S. F. Biagi, M. Bourquin, R. M. Brown, H. J. Burckhart, C. Doré, P. Extermann, M. Gailloud, C. N. P. Gee, W. M. Gibson and R. J. Gray, et al. First Observation of Resonances, Z. Phys. C 31, 33 (1986).
- (5) D. Aston, N. Awaji, T. Bienz, F. Bird, J. D’Amore, W. Dunwoodie, R. Endorf, K. Fujii, H. Hayashii and S. Iwata, et al. Observation of - Production in Interactions at 11-GeV/, Phys. Lett. B 194, 579-585 (1987).
- (6) D. Aston, N. Awaji, T. Bienz, F. Bird, J. D’Amore, W. Dunwoodie, R. Endorf, K. Fujii, H. Hayashii and S. Iwata, et al. Observation of a New at 2.47-GeV/ in Interactions at 11-GeV/, Phys. Lett. B 215, 799 (1988).
- (7) A. Afanasev, W. J. Briscoe, H. Haberzettl, I. I. Strakovskya, R. L. Workman, M. J. Amaryan, G. Gavalian, M. C. Kunkel, Y. I. Azimov and N. Baltzell, et al. Photoproduction of the Very Strangest Baryons on a Proton Target in CLAS12, JLAB-PR-12-008.
- (8) M. Amaryan, Physics opportunities with a secondary beam at JLab, AIP Conf. Proc. 1735, 040006 (2016).
- (9) W. J. Briscoe, M. Döring, H. Haberzettl, D. M. Manley, M. Naruki, I. I. Strakovsky and E. S. Swanson, Physics opportunities with meson beams, Eur. Phys. J. A 51, 129 (2015).
- (10) J. Yelton et al. (Belle), Observation of an Excited Baryon, Phys. Rev. Lett. 121, 052003 (2018).
- (11) M. S. Liu, K. L. Wang, Q. F. Lü and X. H. Zhong, baryon spectrum and their decays in a constituent quark model, Phys. Rev. D 101, 016002 (2020).
- (12) L. Y. Xiao and X. H. Zhong, Possible interpretation of the newly observed state, Phys. Rev. D 98, 034004 (2018).
- (13) T. M. Aliev, K. Azizi, Y. Sarac and H. Sundu, Nature of the through its strong decays, Eur. Phys. J. C 78, 894 (2018).
- (14) T. M. Aliev, K. Azizi, Y. Sarac and H. Sundu, Interpretation of the newly discovered , Phys. Rev. D 98, 014031 (2018).
- (15) M. V. Polyakov, H. D. Son, B. D. Sun and A. Tandogan, through the looking glass of flavour SU(3), Phys. Lett. B 792, 315 (2019).
- (16) M. P. Valderrama, as a hadronic molecule, Phys. Rev. D 98, 054009(2018).
- (17) Y. H. Lin and B. S. Zou, Hadronic molecular assignment for the newly observed state, Phys. Rev. D 98, 056013 (2018).
- (18) R. Pavao and E. Oset, Coupled channels dynamics in the generation of the resonance, Eur. Phys. J. C 78, 857 (2018).
- (19) Y. Huang, M. Z. Liu, J. X. Lu, J. J. Xie and L. S. Geng, Strong decay modes and of the in the and molecular scenario, Phys. Rev. D 98, 076012 (2018).
- (20) W. L. Wang, F. Huang, Z. Y. Zhang, Y. W. Yu and F. Liu, states in a chiral quark model, Commun. Theor. Phys. 48, 695 (2007).
- (21) W. L. Wang, F. Huang, Z. Y. Zhang and F. Liu, Xi anti-K interaction in a chiral model, J. Phys. G 35, 085003 (2008).
- (22) J. X. Lu, C. H. Zeng, E. Wang, J. J. Xie and L. S. Geng, Revisiting the as a hadronic molecule and its strong decays, Eur. Phys. J. C 80, 361 (2020).
- (23) N. Ikeno, G. Toledo and E. Oset, Molecular picture for the revisited, Phys. Rev. D 101, 094016 (2020).
- (24) Y. Li et al. (Belle), Evidence for the decay , Phys. Rev. D 104, 052005 (2021).
- (25) M. Pervin and W. Roberts, Strangeness -2 and -3 baryons in a constituent quark model, Phys. Rev. C 77, 025202 (2008).
- (26) K. T. Chao, N. Isgur and G. Karl, Strangeness -2 and -3 Baryons in a Quark Model With Chromodynamics, Phys. Rev. D 23, 155 (1981).
- (27) Y. Chen and B. Q. Ma, Light flavor baryon spectrum with higher order hyperfine interactions, Nucl. Phys. A 831, 1 (2009).
- (28) C. Menapara and A. K. Rai, Spectroscopic Study of Strangeness=-3 Baryon, [arXiv:2108.05071 [hep-ph]].
- (29) C. S. Kalman, Wave Baryons in a Consistent Quark Model With Hyperfine Interactions, Phys. Rev. D 26, 2326 (1982).
- (30) S. Capstick and N. Isgur, Baryons in a Relativized Quark Model with Chromodynamics, AIP Conf. Proc. 132, 267-271 (1985).
- (31) R. N. Faustov and V. O. Galkin, Strange baryon spectroscopy in the relativistic quark model, Phys. Rev. D 92, 054005 (2015).
- (32) U. Loring, B. C. Metsch and H. R. Petry, The Light baryon spectrum in a relativistic quark model with instanton induced quark forces: The Nonstrange baryon spectrum and ground states, Eur. Phys. J. A 10, 395 (2001).
- (33) E. Santopinto and J. Ferretti, Strange and nonstrange baryon spectra in the relativistic interacting quark-diquark model with a Gürsey and Radicati-inspired exchange interaction, Phys. Rev. C 92, 025202 (2015).
- (34) G. P. Engel et al., QCD with Two Light Dynamical Chirally Improved Quarks: Baryons, Phys. Rev. D 87, 074504 (2013).
- (35) J. Liang et al. (CLQCD), Spectrum and Bethe-Salpeter amplitudes of baryons from lattice QCD, Chin. Phys. C 40, 041001 (2016).
- (36) Y. Oh, and baryons in the Skyrme model, Phys. Rev. D 75, 074002 (2007).
- (37) C. S. An, B. C. Metsch and B. S. Zou, Mixing of the low-lying three- and five-quark states with negative parity, Phys. Rev. C 87, 065207 (2013).
- (38) C. S. An and B. S. Zou, Low-lying states with negative parity in an extended quark model with Nambu-Jona-Lasinio interaction, Phys. Rev. C 89, 055209 (2014).
- (39) S. G. Yuan, C. S. An, K. W. Wei, B. S. Zou and H. S. Xu, Spectrum of low-lying configurations with negative parity, Phys. Rev. C 87, 025205 (2013).
- (40) Z. Y. Wang, L. C. Gui, Q. F. Lü, L. Y. Xiao and X. H. Zhong, Newly observed state and strong decays of the low-lying excitations, Phys. Rev. D 98, 114023 (2018).
- (41) R. Bijker, J. Ferretti, G. Galata, H. Garca-Tecocoatzi and E. Santopinto, Strong decays of baryons and missing resonances, Phys. Rev. D 94, 074040 (2016).
- (42) R. Bijker, F. Iachello and A. Leviatan, Algebraic models of hadron structure. 2. Strange baryons, Annals Phys. 284, 89 (2000).
- (43) M. Pervin, W. Roberts and S. Capstick, Semileptonic decays of heavy omega baryons in a quark model, Phys. Rev. C 74, 025205 (2006).
- (44) J. G. Korner and M. Kramer, Exclusive nonleptonic charm baryon decays, Z. Phys. C 55, 659 (1992).
- (45) T. Gutsche, M. A. Ivanov, J. G. Körner and V. E. Lyubovitskij, Nonleptonic two-body decays of single heavy baryons , , and induced by emission in the covariant confined quark model, Phys. Rev. D 98, 074011 (2018).
- (46) Y. K. Hsiao, L. Yang, C. C. Lih and S. Y. Tsai, Charmed weak decays into in the light-front quark model, Eur. Phys. J. C 80, 1066(2020).
- (47) C. H. Zeng, J. X. Lu, E. Wang, J. J. Xie and L. S. Geng, Theoretical study of the state in the and decays, Phys. Rev. D 102, 076009 (2020).
- (48) P. Y. Niu, J. M. Richard, Q. Wang and Q. Zhao, Hadronic weak decays of in the quark model, Phys. Rev. D 102, 073005 (2020).
- (49) P. Y. Niu, J. M. Richard, Q. Wang and Q. Zhao, Hyperon Weak Radiative Decay, Chin. Phys. C 45, 013101 (2021).
- (50) P. Y. Niu, Q. Wang and Q. Zhao, Study of heavy quark conserving weak decays in the quark model, Phys. Lett. B 826, 136916 (2022).
- (51) M. Pervin, W. Roberts and S. Capstick, Semileptonic decays of heavy lambda baryons in a quark model, Phys. Rev. C 72, 035201 (2005).
- (52) H. Y. Cheng, Charmed Baryon Physics Circa 2021, Chin. J. Phys. 78, 324 (2022).
- (53) G. Buchalla, A. J. Buras and M. E. Lautenbacher, Weak decays beyond leading logarithms, Rev. Mod. Phys. 68, 1125 (1996).
- (54) G. Racah, Theory of Complex Spectra. II, Phys. Rev. 62, 438 (1942).
- (55) R. Kokoski and N. Isgur, Meson Decays by Flux Tube Breaking, Phys. Rev. D 35, 907 (1987).
- (56) P. Geiger and E. S. Swanson, Distinguishing among strong decay models, Phys. Rev. D 50, 6855-6862 (1994).
- (57) S. Kumano and V. R. Pandharipande, Decay of Mesons in Flux Tube Quark Model, Phys. Rev. D 38, 146-151 (1988).
- (58) S. Capstick and W. Roberts, Quark models of baryon masses and decays, Prog. Part. Nucl. Phys. 45, S241-S331 (2000).
- (59) K. L. Wang, Y. X. Yao, X. H. Zhong and Q. Zhao, Strong and radiative decays of the low-lying - and -wave singly heavy baryons, Phys. Rev. D 96, 116016 (2017).
- (60) L. Y. Xiao and X. H. Zhong, baryon strong decays in a chiral quark model, Phys. Rev. D 87, 094002 (2013).
- (61) X. H. Zhong and Q. Zhao, Charmed baryon strong decays in a chiral quark model, Phys. Rev. D 77, 074008 (2008).
- (62) Y. X. Yao, K. L. Wang and X. H. Zhong, Strong and radiative decays of the low-lying -wave singly heavy baryons, Phys. Rev. D 98, 076015 (2018).
- (63) J. Yelton et al. [Belle], Measurement of branching fractions of hadronic decays of the baryon, Phys. Rev. D 97, 032001 (2018).
- (64) B. Aubert et al. [BaBar], Production and decay of , Phys. Rev. Lett. 99, 062001 (2007).
- (65) D. Cronin-Hennessy et al. [CLEO], Observation of the charmed baryon at CLEO, Phys. Rev. Lett. 86, 3730 (2001).
- (66) J. M. Link et al. [FOCUS], Measurement of the lifetime, Phys. Lett. B 561, 41 (2003).
- (67) M. Iori et al. [SELEX], Measurement of the Lifetime, [arXiv:hep-ex/0701021 [hep-ex]].
- (68) B. Aubert et al. [BaBar], A Study of production and decays of baryons at BaBar, [arXiv:hep-ex/0507011 [hep-ex]].
- (69) E. Solovieva, R. Chistov, I. Adachi, H. Aihara, K. Arinstein, T. Aushev, A. M. Bakich, V. Balagura, U. Bitenc and A. Bondar, et al. Study of and Baryons at Belle, Phys. Lett. B 672, 1 (2009).
- (70) H. Y. Cheng, Nonleptonic weak decays of bottom baryons, Phys. Rev. D 56, 2799 (1997) [erratum: Phys. Rev. D 99, 079901 (2019)].
- (71) J. J. Xie and E. Oset, Role of the state in the and decays, Phys. Lett. B 753, 591 (2016).
- (72) J. J. Xie and E. Oset, Search for the state in decay by triangle singularity, Phys. Lett. B 792, 450 (2019).
- (73) X. Zhang and J. J. Xie, The three-pion decays of the , Commun. Theor. Phys. 70, 060 (2018).
- (74) N. Ikeno, W. H. Liang, G. Toledo and E. Oset, “Interpretation of the relative to from the molecular perspective, [arXiv:2204.13396 [hep-ph]].
- (75) [Belle], Observation of and measurement of the effective couplings of to and , [arXiv:2207.03090 [hep-ex]].
- (76) X. Hu and J. Ping, Analysis of as a molecule in the chiral quark model, [arXiv:2207.05598 [hep-ph]].