Topologically protected two-fluid edge states

Topology in matter permits the existence of edge states, which have a strong immunity to distortions of the underlying architecture. Although they are believed to be inherited from the topology of the bulk, these edge states present some properties only around the boundary and are forbidden in the bulk. Topological insulator in condensed matter physics is a well-known example of this phenomenon. Although such a system is an insulator in the bulk, it permits electron conductance along the edges, resulting in quantized Hall conductance [1, 2, 3, 4]. In general, the strong interaction between fermions can affect the topology of a fermion system and break the bulk-boundary correspondence (BBC) [5]. Nevertheless, recent work [6] shows that quantum spin system also exhibits BBC even in a thermal state. This indicates that although the BBC reveals a nontrivial topology of the energy band, it has a particular feature in the presence of interaction.

Beyond the realm of the well-known topological insulator, recent studies on the twisted bilayer graphene (TBG) show that at a series of magic twist angles, the moiré pattern yields the flat low-energy bands that promise strong electronic correlations [7, 8, 9]. The interplay of lattice geometry and many-body interactions induces exotic quantum states including superconducting [10, 11] and correlated insulating [12] behaviors, which have been achieved in experiments [13, 14]. An interesting question is whether such exotic quantum states exist in a topological system, where the energy band of edge states plays the same role as the moiré flat band, in the presence of strong electronic correlations. The $\eta$ pairing proposed by Yang [15] is a promising mechanism to address this problem. In the absence of Hubbard interaction $U$, an $\eta$ pair has zero energy in a bipartite lattice, thus the flat band appears when considering multiple $\eta$ pairs formed by electrons with momentums $\mathbf{k}$ and $\boldsymbol{\pi}-\mathbf{k}$ [15]. There are two common grounds between the flat bands of TBG and that of many-body edge states: They are formed by breaking the translational symmetry and have the potential to enhance electronic correlations. Importantly, such paired states become long lived in the presence of strong Hubbard repulsion [16, 17, 18, 19]. In addition, recent theoretical works [20, 21] suggest that the $\eta$-pairing states can be induced by pulse irradiation or heating. On the other hand, as a phenomenological theory, the two-fluid model was proposed several decades ago to explain the behavior of superfluid helium [22, 23] and a conventional superconductor [24]. It postulates that a superconductor possesses two parallel channels, one superconducting and one normal. Although it is a useful tool, so far two-fluid states have yet to be investigated in the framework of quantum mechanics, appearing as a many-body Hamiltonian eigenstate. For instance, even the usual BCS wave function [25] is not an eigenstate of a Hamiltonian system with a local potential energy.

In this paper, we consider an extended two-dimensional (2D) Su-Schrieffer-Heeger (SSH) [26] model with on-site Hubbard interaction $U$. Specifically, we examine the appearance of $\eta$-pairing edge states [see Fig. 1(a)]. In the absence of Hubbard interaction, the energy band is characterized by topologically invariant polarization in association with edge states. When $U$ switches on, the bulk states do not support the formation of $\eta$ pairs, which appear only at the edge and possess an off-diagonal long-range order (ODLRO) [27] in the topologically nontrivial phase. We further propose a concept of topologically protected two-fluid edge states. As many-body eigenstates of a 2D SSH Hubbard model, the two-fluid edge states contain two components: $\eta$-pairing fermions and unpaired fermions, which do not affect each other. The signature of the two-fluid edge states is observable in the dynamic behavior of resonant transmission. Based on the non-Hermitian quantum mechanics [28, 29, 30, 31, 32], we also develop a method to resolve the scattering problem involving multiple interacting fermions.

The remainder of this paper is organized as follows. In Sec. II, we introduce the concept of two-fluid states by a Hubbard model. In Sec. III, we demonstrate the existence of topological $\eta$-paring edge states in an extended 2D SSH Hubbard model, which also supports two-fluid edge states and the properties are studied in Sec. IV through dynamics of resonant transmission. In Sec. V, we summarize our results.

We begin with the Hamiltonian model of a general form and a brief summary of related results. The Hamiltonian is in the following form

on two sublattices $\mathrm{A}$ and $\mathrm{B}$. Here $H_{0}$ is the Hamiltonian of a simple Hubbard model with bipartite lattice symmetry

where the operator $c_{\mathbf{r},\sigma}$ ($c_{\mathbf{r},\sigma}^{\dagger}$) is the usual annihilation (creation) operator of a fermion with spin $\sigma\in\left\{\uparrow,\downarrow\right\}$ at site $\mathbf{r}$, and $n_{\mathbf{r},\sigma}=c_{\mathbf{r},\sigma}^{\dagger}c_{\mathbf{r},\sigma}$ is the number operator for a particle of spin $\sigma$ on site $\mathbf{r}$. As many previous studies [16, 17, 18, 19, 20, 21], here the interaction is purely on-site. Nevertheless, the weak nearest-neighbor interaction does not break the paired states [33] considered below. Unlike almost all studies on the $\eta$-pairing states, we consider an extra term $H_{\mathrm{intra}}$, representing the intrasublattice hopping. This term breaks the bipartite symmetry of $H_{0}$.

We first review well-established model properties of $H_{0}$ that are crucial to our conclusion (see Appendix A for more details). First, $H_{0}$ possesses SU(2) symmetry characterized by the generators $s^{+}=\left(s^{-}\right)^{\dagger}=\sum_{\mathbf{r}}s_{\mathbf{r}}^{+}$ and $s^{z}=\sum_{\mathbf{r}}s_{\mathbf{r}}^{z}$, where $s_{\mathbf{r}}^{+}=c_{\mathbf{r},\uparrow}^{\dagger}c_{\mathbf{r},\downarrow}$ and $s_{\mathbf{r}}^{z}=\left(n_{\mathbf{r},\uparrow}-n_{\mathbf{r},\downarrow}\right)/2$. Second, one can define the following operators

with $\eta_{\mathbf{r}}^{+}=c_{\mathbf{r},\uparrow}^{\dagger}c_{\mathbf{r},\downarrow}^{{\dagger}}$ ($-c_{\mathbf{r},\uparrow}^{\dagger}c_{\mathbf{r},\downarrow}^{{\dagger}}$) for $\mathbf{r}\in A$ ($\mathbf{r}\in B$), and $\eta_{\mathbf{r}}^{z}=\left(n_{\mathbf{r},\uparrow}+n_{\mathbf{r},\downarrow}-1\right)/2$, satisfying commutation relation $[\eta_{\mathbf{r}}^{+},$ $\eta_{\mathbf{r}}^{-}]=2\eta_{\mathbf{r}}^{z}$ and $[\eta_{\mathbf{r}}^{z},$ $\eta_{\mathbf{r}}^{\pm}]=\pm\eta_{\mathbf{r}}^{\pm}$. Straightforward algebra shows that

which is guaranteed by the bipartite lattice symmetry. These two properties allow the construction of two types of eigenstates of $H_{0}$: ferromagnetic (FM) and antiferromagnetic (AFM).

An $m$-fermion FM eigenstate with energy $\sum_{\left\{\mathbf{k}\right\}}^{m}\varepsilon_{\mathbf{k}}$ can be expressed as follows:

where $\left|\mathrm{Vac}\right\rangle$ is the vacuum state of the fermion $c_{\mathbf{r},\sigma}$, and $c_{\mathbf{k},\uparrow}^{\dagger}$ is the eigenmode of $H_{0}$ with $U=0$ —that is, $[c_{\mathbf{k},\sigma}^{\dagger},H_{0}(U=0)]=-\varepsilon_{\mathbf{k}}c_{\mathbf{k},\sigma}^{\dagger}$. Eigenstate $\left|\psi_{\mathrm{FM}}(m,l)\right\rangle$ is a saturated FM state, given that it is also an eigenstate of $s^{2}$ and $s^{z}$, with eigenvalues $m\left(m/2+1\right)/2$ and $l/2,$ respectively.

An $n$-pair AFM eigenstate can be expressed as

which obeys $H_{0}\left|\psi_{\mathrm{AFM}}(n)\right\rangle=nU\left|\psi_{\mathrm{AFM}}(n)\right\rangle$ and $s^{2}\left|\psi_{\mathrm{AFM}}(n)\right\rangle=0$. Obviously, an $\eta$-pairing state is spin singlet. Unlike all other spin singlet states, an AFM $\eta$-pairing eigenstate is independent of the detailed structure of the bipartite lattice, regardless of whether it contains short-, long-, or even infinite-range hopping terms. This feature is characterized by a correlator related to the off-diagonal element of the reduced density matrix of the system [27, 15].

Importantly, there is a mixture of two types of states, referred to as two-fluid state

which is a common eigenstate of $H_{0}$, $s^{2}$ and $s^{z}$ with eigenvalues $\sum_{\left\{\mathbf{k}\right\}}^{m}\varepsilon_{\mathbf{k}}+nU$, $m\left(m/2+1\right)/2$ and $l/2,$ respectively. States $\left|\psi_{\mathrm{2F}}(n,m,l)\right\rangle$ are demonstrated to be related to ODLRO and superconductivity for finite $n/N$ in a large-$N$ limit [27, 34, 35], where $N$ is the total number of lattice sites. In a comparison of states $\left|\psi_{\mathrm{AFM}}(n)\right\rangle$ and $\left|\psi_{\mathrm{FM}}(m,l)\right\rangle$, the first is a condensation of pairs, acting as a Bose-Einstein condensate, whereas the second is a free electron gas, acting as a normal conductor. Notably, eigenstate $\left|\psi_{\mathrm{2F}}(n,m,l)\right\rangle$ contains two components, paired and single electrons, and no scattering occurs between single electrons and $\eta$ pairs. This mechanism suggests the presence of resonant transmission channels for a Hubbard cluster in the state $\left|\psi_{\mathrm{AFM}}(n)\right\rangle$ as a scattering center. This can be verified by examining the scattering dynamics of an input Gaussian wave packet with resonant energy. Here we emphasize that the bipartite symmetry plays an important role in the formation of the AFM $\eta$-pairing states and the two-fluid states.

We wish to determine what happens in the presence of $H_{\mathrm{intra}}$. Obviously, the paired states are suppressed in general. However, the foregoing analysis remains true if there exists an invariant subspace spanned by a set of many-body states $\left\{\left|\psi_{\mathrm{p}}\right\rangle\right\}$, satisfying

We refer to these types of states as conditional $\eta$-pairing states. Furthermore, it would be interesting when states $\left\{\left|\psi_{\mathrm{p}}\right\rangle\right\}$ have special physical significant because an $\eta$-pairing state has ODLRO or superconductivity. We will consider a concrete example in which states $\left\{\left|\psi_{\mathrm{p}}\right\rangle\right\}$ are topologically protected edge states. These conditional $\eta$-pairing states permit the existence of two-fluid edge states, which support not only the superconductivity but also a single-fermion transmission channel at the system boundary.

We consider an extended 2D SSH Hubbard model on an $N_{x}\times N_{y}$ square lattice, as presented in the schematic in Fig. 1(b). The Hamiltonian consists of two parts

with $H_{\text{{0}}}=3\sum_{\mathbf{r},\sigma}(t_{x}c_{x,y,\sigma}^{{\dagger}}c_{x+1,y,\sigma}$ $+c_{x,y,\sigma}^{{\dagger}}c_{x,y+1,\sigma}+\mathrm{H.c.})+U\sum_{\mathbf{r}}n_{\mathbf{r},\uparrow}n_{\mathbf{r},\downarrow}$ and $H_{\mathrm{intra}}=\sum_{\mathbf{r},\sigma}t_{x}(c_{x,y,\sigma}^{{\dagger}}c_{x+1,y+1,\sigma}$ $+c_{x,y,\sigma}^{{\dagger}}c_{x+1,y-1,\sigma})+\mathrm{H.c.}$. Here, $x$ and $y$ [$\mathbf{r}=\left(x,y\right)$] are the lattice indexes in the $\hat{x}$ and $\hat{y}$ directions, respectively, and the parameter $t_{x}=\lambda^{\left(x\text{ }\mathrm{mod}\text{ }2\right)}$. The hopping term $H_{\mathrm{intra}}$ breaks the bipartite lattice symmetry, as indicated by the dashed lines in Fig. 1(b).

We first focus on the interaction-free case with $U=0$, where a single parameter $\lambda$ controls the topological quantum phase. The system is in the topologically nontrivial phase within $\left|\lambda\right|<1$ (see Appendix B). With the open boundary condition in $\hat{x}$ direction [see Fig. 1(a)] and in the large-$N_{x}$ limit, the system supports two degenerate edge modes

with the eigenenergy $E^{\mathrm{L}/\mathrm{R}}=6\cos k_{y}$ and the normalization constant $\Omega=\sqrt{1-\lambda^{2}}$. Here, $\left(a_{x,k_{y},\sigma},b_{x,k_{y},\sigma}\right)$ $=N_{y}^{-1/2}\sum_{y}\left(c_{2x-1,y,\sigma},c_{2x,y,\sigma}\right)e^{-ik_{y}y}$, and this transformation does not break the bipartite lattice symmetry. We note that

which indicates that edge states $\{|\psi_{k_{y},\sigma}^{\mathrm{L/R}}\rangle\}$ span an invariant subspace with bipartite lattice symmetry and make possible the formation of $\eta$-pairing eigenstates when $U$ is switched on. Notably, Eq. (11) still holds when disordered perturbation is introduced. This indicates that the $\eta$-pairing edge states are topologically protected. In the trivial phase $\left|\lambda\right|>1$, or when periodic boundary condition in both directions are taken, these paired eigenstates are absent. This is another important characterization of topological system.

To verify the existence of the $\eta$-pairing edge states $|\psi_{\text{{edge}}}\rangle$, we study the system $H_{2\text{{D}}}$ in two- and four-fermion subspaces with Hubbard interaction $U$ through exact diagonalization. To characterize the $\eta$-pairing edge states, we introduce the following correlator [27, 15]

where $\eta_{x,y}=\left(-1\right)^{y}c_{x,y,\downarrow}c_{x,y,\uparrow}$. The lattice index $x$ is fixed at the left end in Eq. (12), because the lattice possesses inversion symmetry, and for an edge state, the correlator should vanish in the bulk. For the eigenstate $|\psi_{\text{{edge}}}\rangle$ possessing ODLRO, the correlator $C\left(y^{\prime},y\right)$ is a constant when $\left|y^{\prime}-y\right|$ increases. This is a characteristic of superconductivity. When $\lambda\approx 0$, the presence of $\eta$-pairing edge states is clear; the two chains at the boundaries, which support the edge states, are isolated from the bulk of the cylinder, and the boundary chains can be regarded as approximate bipartite lattices. For the $\eta$-pairing state $\left|\psi(n)\right\rangle=(\eta^{{\dagger}})^{n}|\mathrm{vac}\rangle$ in a bipartite lattice, the correlator is [15]

This bipartite lattice corresponds to the isolated chain with $N_{y}$ sites at the boundary.

The $\eta$-pairing edge states are bound pairs localized at the boundary, which have substantial pairing energy and near-zero kinetic energy; thus, the pair density at the boundary $\mathcal{N}_{\text{{edge}}}=\sum_{y}\langle\psi_{\text{{edge}}}|n_{1,y,\uparrow}n_{1,y,\downarrow}|\psi_{\text{{edge}}}\rangle$ is useful in the search for the $\eta$-pairing edge states. One can search for $\eta$-pairing edge states in eigenstates with large $\mathcal{N}_{\text{{edge}}}$. We perform the numerical calculation for systems with different numbers of particles and parameters $\lambda$.

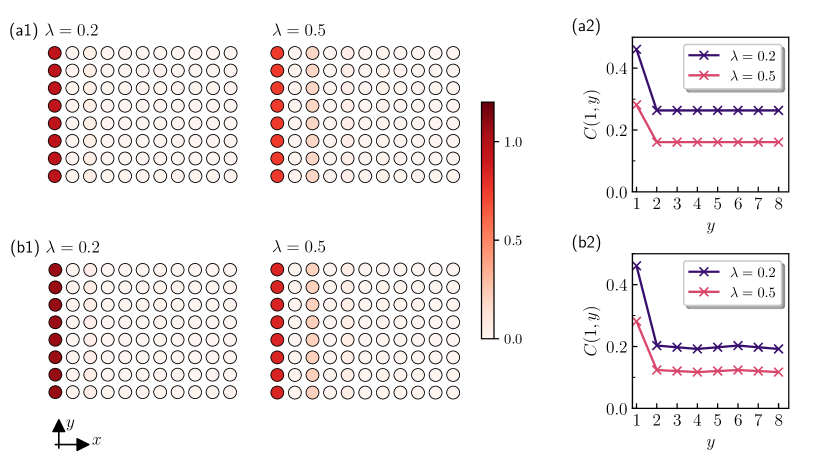
The numerical results of the correlator $C\left(y^{\prime},y\right)$ for the $\eta$-pairing edge states are shown in Fig. 2. The corresponding local particle density is presented in Appendix C. The lattice size of the system is set as $(N_{x},N_{y})=(5,4)$, where $N_{x}$ is truncated to an odd number such that the edge states appear in only one boundary. The interaction strength is $U=1.5$, and the number of particles are two (one spin up and one spin down, marked as $\uparrow\downarrow$), and four ($\uparrow\uparrow\downarrow\downarrow$) for Figs. 2(a) and (b), respectively. In the invariant subspaces of two and four fermions, there exist only one $\eta$-pairing state with one-pairing and two-pairing, respectively. A higher filling ratio will involve the bulk fermions, which have no contribution to the ODLRO. The correlators of a uniform chain in Eq. (13) are plotted as a comparison. One can see that until $\lambda=0.4$, these two states have the long-range correlation of $C\left(1,y\right)$. The comparison between the energies of two and four fermions indicates that there is no interaction between the paired fermions in small $\lambda$ limit, which is equivalent to finite $\left|\lambda\right|<1$ with large $N_{x}$. In Appendix C, we also give the numerical results of three fermions, and the approximate results of even- and odd-number fermions in a larger system. In these cases, the previous conclusions are still valid.

In the preceding section, we demonstrate the existence of the $\eta$-pairing edge states from the correlator. A natural question is that whether system $H_{\mathrm{2D}}$ supports a two-fluid state containing single fermions and $\eta$ pairs localized at the boundary of the system. We attempt to answer this question and demonstrate the properties of the two-fluid edge states.

Particle beam scattering is a conventional technique for detecting the nature of matter [36]. Because no scattering occurs between the single fermions and $\eta$ pairs, resonant transmission provides a means to present the features of two-fluid edge states. The detection of resonant transmission for a many-body state is somewhat challenging, both theoretically and experimentally. Nevertheless, exceptional point (EP) [30, 31, 32] dynamics in non-Hermitian quantum mechanics can reduce the difficulty of the calculation. For a system with parameters at EP, two or more eigenvalues along with their associated eigenstates become identical, leading to unidirectional dynamics. This allows us to employ EP dynamics to simulate the perfect resonant transmission of particles. It can shorten the lengths of the input and output leads, and the scattering process in a Hermitian system can be effectively treated as the dynamics of a non-Hermitian system (see Appendix D). In the following, we present the resonant transmission dynamics of the two-fluid edge states. For comparison, the scattering dynamics between a single fermion and an FM edge state are also examined.

We consider the dynamics in a non-Hermitian system, which consists of the 2D SSH Hubbard model $H_{2\text{{D}}}$ and two extra sites (with indexes $j=-1$ and $1$), connected by the unidirectional hopping

where $c_{\alpha,\sigma}^{\dagger}$ and $c_{\beta,\sigma}$ are fermion operators at the edge of the cylinder $H_{2\text{{D}}}$. A schematic of the system configuration is presented in Appendix D. When $\mu=E^{\mathrm{L/R}}=6\cos k_{y}$ is considered, a Jordan block with order of three should appear in single-particle subspace (see Appendix D). For the many-body case, if the two-fluid states remain eigenstates of $H_{2\text{{D}}}$, it still supports the Jordan block with order of three. This can be verified by examining the dynamic process. We take the initial state as $\left|\psi(0)\right\rangle=c_{-1,\uparrow}^{\dagger}|\psi_{\text{{edge}}}^{\mathrm{a}}\rangle$, with the AFM $\eta$-pairing edge state $|\psi_{\text{{edge}}}^{\mathrm{a}}\rangle$ satisfying $s^{2}|\psi_{\text{{edge}}}^{\mathrm{a}}\rangle=0$, and calculate the time evolution $\left|\psi(t)\right\rangle=e^{-iH_{\text{{NH}}}t}\left|\psi(0)\right\rangle/|e^{-iH_{\text{{NH}}}t}\left|\psi(0)\right\rangle|$. The expected final state is $\left|\psi_{\mathrm{final}}\right\rangle=c_{1,\uparrow}^{\dagger}|\psi_{\text{{edge}}}^{\mathrm{a}}\rangle$ when resonant transmission occurs. Here, the numerical computations are performed by using a uniform mesh in conducting time discretization.

To characterize the procedure, we introduce three quantities: the fidelity between the expected state and the evolved state

the particle density of the evolved state at different spatial regions

where $\mathbf{R}=\mathbf{R}_{-1}$ and $\mathbf{R}_{1}$ respectively represent the extra sites with indexes $j=-1$ and $1$, and $\mathbf{R}=\mathbf{R}_{\mathrm{C}}$ represents the sites of the scattering center $H_{2\text{{D}}}$; and the pair density

Figure. 3(a) presents the numerical results of the fidelity after a sufficiently long time as a function of $\mu$, and the two other quantities as functions of time $t$. As expected, the peaks appear at $\mu=-6$, $0$ and $6$, where the single fermion is resonantly transmitted from site $\mathbf{R}_{-1}$ to site $\mathbf{R}_{1}$. This can also be seen in the particle density $\rho_{\mathbf{R}}(t)$ and the pair density $\mathcal{N}_{\mathbf{R}}(t)$ for $\mu=0$ and $U=1.5$.

For comparison, in Fig. 3(b), we consider the time evolution of another initial state $\left|\psi(0)\right\rangle=c_{-1,\uparrow}^{\dagger}|\psi_{\text{{edge}}}^{\mathrm{b}}\rangle$, with the FM edge state $|\psi_{\text{{edge}}}^{\mathrm{b}}\rangle$ satisfying$\ s^{2}|\psi_{\text{{edge}}}^{\mathrm{b}}\rangle=2$, $s_{z}|\psi_{\text{{edge}}}^{\mathrm{b}}\rangle=0$, and the state $\left|\psi_{\mathrm{final}}\right\rangle=c_{1,\uparrow}^{\dagger}|\psi_{\text{{edge}}}^{\mathrm{b}}\rangle$. The numerical results indicate that the single fermion is scattered by the $\mathrm{FM}$ state $|\psi_{\text{{edge}}}^{\mathrm{b}}\rangle$ at any $\mu$ value due to the Hubbard interaction. When $\mu=0$ and $U=1.5$, two fermions are transmitted to site $\mathbf{R}_{1}$ after a sufficiently long time.

We present a concept of topologically protected two-fluid edge states and a means for their detection. We demonstrate the existence of such states in the 2D SSH Hubbard model, which provides an analog to the topological insulator. Such a material behaves as a conductor in its interior but possesses a surface containing superconducting states. In other words, the condensation of $\eta$ pairs can exist only on the surface of the material. We also determine that a two-fluid state can be formed as a many-body eigenstate of a realistic Hubbard model. By employing EP dynamics, a technique of the numerical simulation is developed to overcome the computational difficulty in the scattering problem of many-body system, which involve numerous basis vectors. It is expected to measure the resonant transmission in experiment via peaks in transmission coefficient [37, 38]. At present, the possible experimental implementation to explore the two-fluid edge states is ultracold fermions in an optical lattice [39].

In this Appendix, we present A. Symmetries, FM and AFM eigenstates for $H_{0}$; B. Solution of the extended 2D SSH model; C. More exact numerical results and approximate numerical results; and D. Non-Hermitian description of resonant transmission.