Topological Josephson Bifurcation Amplifier: Semiclassical theory
Abstract
Amplifiers based on Josephson junctions allow for a fast and noninvasive readout of superconducting qubits. Motivated by the ongoing progress toward the realization of fault-tolerant qubits based on Majorana bound states, we investigate the topological counterpart of the Josephson bifurcation amplifier. We predict that the bifurcation dynamics of a topological Josephson junction driven in the appropriate parameter regime may be used as an additional tool to detect the emergence of Majorana bound states.
I Introduction
In the past decade, the discovery and characterization of Majorana bound states (MBS) in solid-state devices has become a landmark of the field of topological materials and devices reviews . One promising implementation of MBS relies on semiconducting nanowires with strong spin-orbit coupling and proximity-induced superconductivityaguado2017 . In this setup, a magnetic field can induce a topological phase transition, where MBS emerge as localized states at the ends of the nanowire. Because of their spatial localization and the non-Abelian exchange statistics, these MBS are regarded as potential building blocks for fault-tolerant qubits karzig2017 .
In anticipation of the realization of MBS-based qubits, there has been a strong interest on the theoretical front to integrate MBS in circuit quantum electrodynamics (cQED) architectureshassler2011 ; muller2013 ; pekker2013 ; virtanen2013 ; ginossar2014 ; yavilberg2015 ; dmytruk2015 ; vayrynen2015 ; peng2016 ; dartiailh2017 ; cottet2017 ; trif2018 ; keselman2019 ; lopes2019 ; avila2020 ; arne2019 , the latter of which are widely employed in the readout and control of solid-state qubitsblais2020 . This theoretical effort has been accompanied by experimental progress towards the realization of superconducting circuits that are compatible with sizeable magnetic fieldslarsen2015 ; delange2015 ; woerkom2017 ; luthi2018 ; vidal2019 ; tosi2019 .
Motivated by the aforementioned developments, in the present work we introduce a topological version of the Josephson bifurcation amplifier (JBA), which is simply a JBA made from a topological Josephson junction. The original JBA is an amplifier designed to read out the state of superconducting qubits in topologically trivial Josephson junctionssiddiqi2005 ; vijay . It is based on the transition of an RF-driven Josephson junction between two distinct oscillation states near a dynamical bifurcation point. The main advantages of the JBA are high speed, high sensitivity and noninvasiveness. These advantages have led to some of the first single-shot qubit readouts of superconducting qubits mallet2009 ; bertet2011 ; schmitt2014 . Yet, the difficulty of calibration for different devices has resulted in JBAs giving way to simpler designs for qubit measurement, such as the Josephson parametric amplifier castellanos2007 ; hatridge2011 ; lin2013 . In our theoretical study, we show that the sensitive binary features and the high signal-to-noise ratio of the bifurcation dynamics offer new ways to detect the emergence of MBS in topological Josephson junctions.
The remainder of this paper is organized as follows. Section II provides a short review of the main concepts of the JBA and introduces its topological version. Section III highlights the signatures of the topological phase transition in key parameters governing the topological Josephson bifurcation amplifier (TJBA). In Sec. IV, we propose to use the TJBA in order to detect the coexisting and periodicities in a topological Josephson junction. Conclusions and final remarks are presented in Sec. V.
II Semiclassical theory of the TJBA
II.1 Josephson Bifurcation Amplifier: A review
We describe the topological Josephson bifurcation amplifier using the resistively and capacitively shunted (RCSJ) model of a Josephson junctionlikharev1986 ; blackburn2016 . In this model (Fig. 1), the Kirchhoff law for the electric current traversing the junction reads
| (1) |
where is the gauge-invariant superconducting phase difference between the two superconducting electrodes, and are the effective capacitance of the junction and the characteristic impedance of the microwave source generator, is the reduced flux quantum, is the bias current and is the grand potential of the junction at temperature . The first, second and third terms in the left hand side of Eq. (1) correspond to the displacement current, the dissipative ohmic current and the dissipationless (Josephson and Majorana) current, respectively. The critical current of the junction is given by .


In the RCSJ model, is treated as a classical variable, whereas is computed by diagonalizing a quantum mechanical Hamiltonian for each value of . Charging energy is not included in the Hamiltonian; instead, the phase fluctuations produced by the charging energy are incorporated via the displacement current in Eq. (1). This semiclassical approach is justified in the "transmon regime" that is relevant to the operation of the JBAvijay . In such regime, the Josephson energy of the junction (approximately given by ) greatly exceeds the charging energy .
In thermodynamic equilibrium, fermion parity constraints are absent for timescales that are long compared to quasiparticle poisoning times. Then, the grand potentialbeenakker2013 takes the form
| (2) |
where are the single-particle energies of the system, with and due to particle-hole symmetry (by convention, we take for ). For , Eq. (2) reduces to the ground state energy
| (3) |
The eigenvalues can be obtained by diagonalizing a tight-binding Hamiltonian describing a single-channel, one-dimensional superconducting/normal/superconducting heterostructure of finite length, where two long superconducting electrodes are separated by a weak link in the normal state. More details of the model are presented in Sec. II.3.
Equation (1) describes the dynamics of a fictitious particle of mass and position moving in a potential under the action of an external force . We consider a noisy sinusoidal AC-bias current,
| (4) |
where and are, respectively, the drive frequency and amplitude, and is a white-noise current produced by thermal fluctuations. We will focus in the case in which is small compared to the critical current of the junction. Then, the dynamics of the particle is akin to that of a nonlinear harmonic oscillator centered in one of the minima of , which are located at (). Because in the absence of parity constraints, we can concentrate on oscillations near without loss of generality.
Following the small oscillation approximation, Eq. (1) can be rewritten as
| (5) |
where the damping rate , the plasma frequency in the harmonic approximation and the leading anharmonicity parameter play a central role in the functioning of the JBA. They can be extracted from via
| (6) | ||||
where .
Figure 2 illustrates its solution in the absence of current noise. The various curves in this figure are well-known in the literaturevijay ; here, we highlight the most important points for completeness and later reference. In a frame rotating at the drive frequency, i.e. taking , we solve for the steady-state solution of Eq. (5). Ignoring rapidly oscillating terms (rotating-wave approximation), Fig. 2a displays the modulus of as a function of , for different values of . For small , the response of the oscillator is a Lorentzian peaked at . As the driving amplitude increases, the response of the oscillator becomes peaked at frequencies lower than (this is due to the fact that the anharmonicity parameter in Eq. (6) is negative). Beyond a critical value of (but still well below the critical current of the junction), there emerges a finite interval of for which the response of the oscillator is multi-valued, with three values of for each . In such an interval, the intermediate value of is not stable and the oscillator is thus said to be in a bistable regime, with a low- and a large-amplitude oscillation steady state.
Figure 2b shows the dependence of the bistable regime on the drive frequency. Bistability takes place when and , where and are the lower and upper bifurcation currents, respectively. These currents obey the relations
| (7) | ||||
where , and . At the bifurcation currents, the response of the oscillator switches between single-valued and two-valued. Thus, for (), the oscillation amplitude is single-valued and low (high). The fact that bifurcation currents depend on and will be important below.
Figure 2c presents the dependence of the steady-state solution on the drive amplitude, for a fixed value of the drive frequency (, red dashed vertical line in Fig. 2b). In the bistable regime (blue shaded central region), which of the two stable steady-states is reached depends on the initial state of the system and how the drive is turned on. In the case where the drive is turned on sufficiently slowly (compared to the timescale ) and in the absence of current noise, the steady state follows an hysteresis curve. For an initial state where , the low-amplitude steady-state is realized for any , and the system suddenly jumps to the high-amplitude solution at . Driving the the Josephson junction close to thus allows to detect small changes in the upper bifurcation current, independently from the width of the bistable region .

Thus far we have reviewed the phenomena of bifurcation and bistability in the absence of current noise (). In the presence of noise, due to either thermal or quantum fluctuations, the steady-state reached by the system is not deterministic. We define the bifurcation probability as the probability of the system reaching the high-amplitude state after evolution of the system for a time vijay ; bertet2011 . To estimate , we integrate Eq. (5) for a time and realizations of the noise . We consider uncorrelated white noise by taking from a zero-mean Gaussian distribution of variance . We then estimate the bifurcation probability by , where is the number of high amplitude steady-state solutions. This probability is experimentally measurable.
Figure 3 illustrates the dependence of on the drive amplitude in the presence of current noise. When and , the oscillator is with certainty in the low and high amplitude states, respectively. Due to the hysteretic nature of the bifurcation dynamics, is a sharp step function at in the absence of noise (blue curve). Current noise increases the width of the step function in the region . As we consider a low amplitude initial state and a smooth turn on of the drive, does not depend on the lower bifurcation current ( nA in Fig. 3). Because the bifurcation currents are sensitive to the intrinsic parameters of the junction (such as and ), small variations of the latter lead to significant changes in when lies in the vicinity of . As we explain below, this high sensitivity may allow for new ways to measure MBS properties in topological Josephson junctions.

II.2 Limiting forms of
Before turning to a more microscopic description of a Josephson junction by calculating the grand potential from a tight-binding model, it is helpful to consider two approximate limiting forms of in ideal tunnel junctions. These limiting cases will be useful to interpret some of the numerical results of the following sections.
In the case of conventional tunnel junction at low temperature, the ground state energy is , where is the Josephson energy associated to the tunneling of Cooper pairs and "const" is a independent number. From Eq. (6), the plasmon frequency and anharmonicity parameter are then and . In this case, is a constant because has a single harmonic ().
In the case of a topological tunnel junction, one instead finds (disregarding parity constraints) , where is the Majorana energy associated to the tunneling of single electrons. In particular, if the junction transparency is very low, and . In this tunnel regime where Cooper pair tunneling across the junction is negligible compared to single-particle tunneling, we have and . Once again, is a negative constant, but of smaller amplitude.
In general, when the dependence of has more than one harmonic (e.g. in topological junctions with comparable and , or even in trivial junctions that are neither in the tunneling nor in the perfectly transparent regimegolubov2004 ), will not be a constant.
Finally, for later reference, we note that in the literature of superconducting qubitsblais2020 , anharmonicity in the transmon regime is often defined as , where are the energy levels for the quantum anharmonic oscillator evaluated to first order in the strength of the quartic potential. The relation between and our anharmonicity parameter is . Thus, in a conventional tunnel junction.
II.3 Microscopic model of a topological junction
In order to account for topological effects, we calculate the grand potential defined in Eq. (2) by diagonalizing a tight-binding model of a 1D nanowire junction (see Fig. 4 for a sketch of the model). As this model has been extensively reviewed in the literature, see e.g. Ref. [cayao2018, ], we limit ourselves to providing a brief description.
We consider spinful fermions with annihilation (creation) operator (). Introducing the spinor , the Hamiltonian reads
| (8) |
where and are (respectively) the onsite and hopping matrices, with site-dependent parameters in order to create a junction. We define these matrices in terms of two sets of Pauli matrices, and (, acting respectively on the spin and the particle-hole sector of the spinor. Electrons can hop between lattice sites with a spin-independent nearest-neighbor tunneling amplitude and, due to spin-orbit coupling, a spin-flip tunneling amplitude . Then, the hopping matrix is
| (9) |
where away from the junction interface (see Fig. 4 and below). The onsite matrix reads
| (10) |
where the local mean-field superconducting gap is in the left superconducting lead, 0 in the weak link and in the right superconducting lead. The Zeeman energy associated to the applied magnetic field is assumed to be spatially homogeneous. Likewise, the chemical potential is assumed to be uniform and identical in the two superconducting electrodes, though we allow for a mismatch in the chemical potentials of the electrodes and the weak link. The value corresponds to the chemical potential being in the middle of the Zeeman gap of the normal state electronic bands.
Using parameters relevant to InAs nanowires aguado2017 , we take meV and meV (corresponding to a lattice constant nm and an electronic effective mass , with the bare electron mass). We take throughout the proximity-induced -wave superconducting gap to be meV. We also neglect the dependence of on and on . In reality, this dependence is smooth across a topological phase transition, and thus clearly distinguishable from the sharp features we will be discussing below. It is well-known that variations of and can drive the superconducting electrodes across a topological phase transitionreviews2 . The superconducting electrodes are in the topological phase (with a MBS in each extremity of the superconductors) for , and in the trivial phase otherwise.
To model the effect of a potential barrier at the superconductor/normal interface, we use a phenomenological transparency parameter . Both the hopping amplitude and the spin-orbit coupling parameter are scaled by at the interface. Throughout the text, we consider the cases and to study respectively the effect of a large potential barrier at the junction interface and the case of a clean junction with no potential barrier. We denote the former as the "tunnel" regime and the latter as the "transparent" regime. However, we note that the junction transparency also depends on the normal state Fermi velocity BTK ; heck2018 and is hence a function of , and most importantly . For example, even when , the junction’s characteristics (e.g. ) can resemble those of a true tunnel junction if is sufficiently negative.
In the numerical simulations, unless mentioned otherwise, the weak link is two sites long ("short junction" regime), whereas each superconducting electrode contains sites. The main qualitative points are relatively insensitive to the strength of spin-orbit coupling, though larger values of make it easier to observe the relevant features. Likewise, longer junction lengths do not change the main features discussed below, though they host additional properties that complicate the JBA-based detection of the topological phase transition; we elaborate on this issue below.

III Detection of the topological phase transition
In the preceding section, we have demonstrated that the JBA can be highly sensitive to changes in the current-phase characteristics of a Josephson junction. It is therefore natural to wonder whether a JBA could detect the emergence of Majorana bound states. Here, we investigate the signatures of the topological phase transition in key JBA observables. We begin by discussing the plasmon frequency and the anharmonicity parameter at zero (Sec. III.1) and finite (Sec. III.2) temperature. This analysis sets the stage for the subsequent computation (Sec. III.3) of bifurcation currents across the topological phase transition. In this section, we will focus on thermodynamic equilibrium, where Eq. (2) applies. In Sec. IV, we will depart from thermodynamic equilibrium in order to calculate and for different many-body states.
III.1 Plasmon frequency and anharmonicity parameter at zero temperature
Figure 5 shows the dependence of the Josephson plasmon frequency and the anharmonicity parameter on the magnetic field, for small oscillations of the superconducting phase difference in the vicinity of , in the many-body ground state. We show the results both in the "tunneling" regime (, Fig. 5a-d) and in the "transparent" regime (, Fig. 5e-h). In all cases, the most salient feature is the pronounced peak in and at the topological phase transition. As we explain next, these peaks can be attributed to the emergence of MBS.
In the tunneling regimetunnel1 , Fig. 5a evidences an abrupt growth of the plasmon frequency at the onset of the topological phase ( grows by more than GHz as changes by less than ). This behavior can be understood by analyzing as a function of . In our model for a topologically trivial tunnel junction, all single-particle "bands" are rather flat in (they would be completely independent of if ). Accordingly, depends weakly on and hence is relatively small. In the topological phase, the single-particle bands remain flat, except for those that result from the hybridization of MBS. The latter disperse parametrically more strongly with , because their "bandwidth" scales with the square root of the transparency, rather than with the transparency itself (as is the case for the non-Majorana bands). Hence, this explains why increases strongly at the onset of the topological phase, thus producing a strong peak in (Fig. 5b).
The aforementioned argument, derived in the context of a single-channel nanowire model, applies also to a less idealized tunnel junction that may host multiple subbands in the normal state. The simplest way to see this is by adding a term of the form to the ground state energy, where models the contribution from the multiple subbands to the conventional Josephson energy of the junction. As a result of the additional term in the energy, is shifted upwards in both the trivial and the topological regimes, but the ramp up of and the peak of at the onset of the topological phase remain unchangedEJ0 .
A related behavior has been identified for the DC critical current in earlier works, with a marked increase at the onset of the topological phase sanjose2014 ; cayao2017 ; huang2017 . At first glance, a similarity in the behavior of and the critical current is not surprising, the latter being proportional to in conventional Josephson junctions. Yet, for the unconventional junctions we are interested in, this relation of proportionality does not apply. Instead, all one can assert is that depends on the characteristics of the single-particle bands near , while the critical current depends on the slope of the single-particle bands near large () values of . Moreover, from an experimental point of view, the measurement of is qualitatively different from the measurement of the critical current; it can therefore offer an alternative way to probe the interpretation of a recent experiment reporting an enhanced critical current at the onset of the topological phasetiira2017 .
Let us now discuss the anharmonicity parameter. Still in the tunneling regime, Fig. 5c reflects a peculiar evolution of across the topological transition, which can be understood analytically. Deep in the trivial regime, we find , as expected for a conventional Josephson junction with . Deep in the topological regime, tends asymptotically to , as expected for (cf. Sec. II.2). In other words, in a tunnel junction, the evolution of across the topological phase transition reveals the emergence of MBS.
Figure 5 also displays the results for several values of . Even though we consider to be homogeneous throughout the system (i.e., in Fig. 1b), we have verified that the results do not change significantly when we vary in the superconducting electrodes while keeping pinned to zero in the weak link. We note that increases with in Fig. 5. This effect can be understood by observing that, for fixed , the junction transparency is a monotonically decreasing function of the ratio of the barrier amplitude and the normal-state Fermi velocity BTK . As for all the cases considered (Fermi level near the bottom of the band), increasing means a higher and hence an increase of the junction transparency. Although Fig. 5 shows only positive values of , we have checked that, for , the junction transparency effectively decreases. For , the behavior expected for a tunnel junction is found irrespective of the value of as the Fermi level in the normal state then lies below the bottom of the band (insulating regime).
Another effect of increasing is the appearance of oscillations in and as a function of ; their amplitude grows with . These oscillations are the microwave counterpart of the ones predicted in the DC critical current by Cayao et al.cayao2017 The oscillations take place only in the topological phase and arise from the hybridization between MBS localized at opposite extremities of each superconducting electrode, as well as from the hybridization between the MBS localized at the two opposite extremities of the entire system. Accordingly, the oscillations are washed out when the length of the superconducting electrodes becomes long enough (we find no evidence of them when doubling the electrodes size to sites).
Let us now discuss the transparent junction regime (see Fig. 5e-h). In this regime, the behavior of at the topological phase transition is also reminiscent of that predicted in earlier works for the DC critical current.sanjose2013 ; cayao2017 In those works, a kink of the critical current at the topological phase transition was identified and attributed to a band inversion taking place at the topological phase transition. A similar mechanism is at play in our case, as we explain next.
The underlying explanation begins by recognizing that a long superconducting electrode in the trivial phase hosts two different and quasi-independent -wave superconducting gaps in the energy spectrumsanjose2013 ; cayao2017 ; murthy2020 : one at the inner Fermi points (the " gap") and the other at the outer Fermi points (the " gap"). When , . As increases, decreases gradually and gets significantly suppressed when . The gap is far more sensitive to , vanishing when . This gap-closing point marks the topological phase transition. Near the transition, we have .
The next part of the explanation is to recall that in a short, transparent and topologically trivial junction, there is a single Andreev bound (or quasi-bound) state associated to each of the two -wave gaps of the electrodestunnel . In this regime, the rest of the single-particle states (the so-called scattering states) are largely dispersionless in , and therefore the main contribution to and originates from the two Andreev states bound by and . Although there is no simple analytical expression for the Andreev bound state dispersions in the presence of a generic magnetic fieldheck2018 , qualitative insight can be gained by neglecting the coupling between the two -wave gaps, adopting the Andreev approximation, and assuming perfect transparency. Then, we posit for the two ABS in the trivial phase, and we get
| (11) |
Across a topological phase transition from the trivial to the topological phase, crosses zero and inverts its sign, thereby changing its character from a superconducting gap to a magnetic gap. Accordingly, in the topological phase, no longer binds an Andreev state. Therefore, the contribution from to and in Eq. (III.1) is turned off for . This results in a kink for and as a function of at (and corresponding discontinuities in and ). Of course, such reasoning of "suddenly turning off" the contribution from at makes sense only at zero temperature; finite-temperature effects will be discussed in Sec. III.2.
Some of the features in Fig. 5 match qualitatively with the behavior expected from Eq. (III.1). First, is decreasing as we approach the topological phase transition. Second, a kink is visible at the transition, especially for larger values of , and continues to decrease as we get deeper in the topological phase (because keeps decreasing as is made larger). On the other hand, the results from Fig. 5g do not match qualitatively with Eq. (III.1). For one thing, is not a constant. Also, a clear kink in at the topological phase transition is present only if is sufficiently large. There are various possible reasons for these discrepancies.
First, the analytical expressions for are approximately valid at , but may fail qualitatively at larger . Even at , does not guarantee a perfect transparency of the junction; the actual transparency depends on the value of as well. If the transparency is not unity, one expects various competing harmonics in near (rather than just ), which in turn leads to not being constant. Second, the Andreev approximation upon which Eq. (III.1) is based is not satisfied in the low electron density regime required to have a topological Josephson junction; this is evidenced by the single-particle energy spectra we have calculated (not shown), wherein the ABS in the trivial phase have significant gaps at . Third, near , the Andreev state bound by is buried in the continuum of scattering statessanjose2013 ; murthy2020 ; this is due to the fact that in the vicinity of the phase transition. In other words, the ABS bound by undergoes multiple avoided crossings with scattering states near . Consequently, it is not accurate to neglect the -dependence of those scattering states, nor is it to ignore their contribution to and .
Next, we compare our results to relevant works in the literature. Our finding that and display prominent peaks at is seemingly more optimistic than that of a recent numerical study by Keselman et al.keselman2019 , who conclude that there are "no strong signatures of the topological transition itself on the simulated frequency spectra of the junction." This discrepancy in viewpoint might be explained by the different parameter regimes considered. In particular, the exact numerical treatment of charging energy in Ref. [keselman2019, ] comes at the expense of studying smaller systems ( sites), where finite-size effects smoothen the phase transition into a crossover. Below, we show that finite-temperature effects can likewise broaden and eventually erase the sharp signatures in . In another recent workavila2020 , Avila et al. have, to the contrary, reported an abrupt dip in the anharmonicity parameter at , stating it to be a "precise smoking gun" for the topological phase transition. We recall (see discussion at the end of Sec. II.2) that .
The theoretical treatments of Avila et al. and Keselman et al. differ from ours in that they treat the charging energy quantum mechanically, while we do so semiclassically. Yet, both approaches ought to yield similar results in the transmon regime. In Fig. 5g, we do find that can have a dip at in the transparent regime, though it is nowhere as pronounced as in Fig. 9b of Ref. [avila2020, ]. Moreover, the dip is not a generic feature when we vary parameters such as and (e.g., it is absent in Fig. 5c). What appears more generic in our case is the peak in at , whose origin we have explained above.
On a related note, while Avila et al. investigate the behavior of the nonlinear Josephson inductance in the topological and trivial phases, they do not point out specific signatures at the phase transition (at least Fig. 8 of Ref. [avila2020, ] does not show enough values of to ascertain any signatures). Yet, the inverse of this nonlinear inductance, close to , is proportional to . It would be interesting to find out whether the theory of Ref. [avila2020, ] agrees with our prediction for near .


Thus far, we have concentrated on short junctions either in the tunneling or in the transparent regimes. In junctions of intermediate transparency, does not display a kink or a sharp upturn at the topological phase transition; the peak of at can then be less pronounced. Even in those cases, we still observe a clear feature in at .
Longer junctions show the same phenomenology as the short junctions when it comes to the behavior of and at the topological phase transition (we have simulated weak links with up to sites). However, one additional aspect of the longer junctions is that they may host accidental (imposed neither by electronic topology nor by symmetry), parameter-sensitive, zero-energy touchings at in the topologically trivial phasevuik2019 . Because of particle-hole symmetry inherent to the single-particle spectrum, the positive-energy and negative-energy Andreev states that cross at zero energy have opposite curvatures and anharmonicities. As a result, the curvature of the occupied (negative-energy) single-particle states changes abruptly as a function of at the accidental zero-energy touchings. A corresponding discontinuity takes place in and (see Fig. 6 for an example). The magnitude of the discontinuities is diminished when the -dependence of the ABS at the zero-energy touching is smaller; hence, the effect is generally less pronounced in tunnel junctions. We note that no such discontinuities occur at the true topological phase transition, where positive- and negative-energy Andreev bound states coalesce at zero energy (as opposed to crossing it) as a function of . Hence, measuring and as a function of may allow to distinguish an accidental gap closing in the trivial phase (with a discontinuity in ) from a gap closing associated to a topological phase transition (with no discontinuity in but a peak in ).
Unfortunately, the aforementioned distinction is blurred at finite temperatures, where the discontinuities are transformed into rapid but continuous variations. Hence, at nonzero temperature, the behavior of and at accidental zero-energy touchings in the trivial phase can mimic the signatures of the topological phase transition. In this case, one way to disentangle the true MBS signatures is to analyze the dependence of the peaks in ; experiments of this type are feasiblefrolov2017 . The MBS-related peak at the phase transition will be displaced in as , while the peaks of trivial origin will not generically show such dependence, and can even disappear completely as is varied (see Fig. 6).
To conclude this subsection, we remark that our main results do not rely on the fact that a magnetic field has been used to induce a topological phase transition. Similar conclusions are reached when is held fixed and the topological phase transition is driven by variations in . In that case, we find that and show strong peaks at the topological phase transition, for the same reasons as the ones alluded to above.
III.2 Plasmon frequency and anharmonicity parameter at finite temperature
In the preceding subsection, we have investigated and at zero temperature, and have identified signatures of the topological phase transition therein. In this subsection, we study the effect of finite temperature on those features. We concentrate on temperatures that are low compared to the proximity-induced -wave superconducting gap . We find that the peaks of and at the topological phase transition are thermally broadened, though they remain noticeable at experimentally attainable temperatures. We also find a nontrivial temperature dependence of in the topological phase of tunnel junctions, which can be ascribed to the MBS localized on the opposite extremities of the weak link.
Our results are summarized in Fig. 7. The main aspects of this figure can be understood from the finite temperature expressions (derived from Eqs. (2) and (6)) for the plasmon frequency and the anharmonicity parameter near ,
| (12) |
where is the energy of the -th single particle state at (recall that for ), and denotes the -th derivative of with respect to (evaluated at ).
It follows from Eq. (III.2) that, whenever the energy of the lowest-lying state at largely exceeds , and will have a negligible temperature-dependence. In other words, the condition for a significant temperature-dependence of and is that (with the smallest single-particle eigenenergy) Another useful piece of information in Eq. (III.2) is that, for a fixed , the contribution of the given single-particle level to is suppressed when .
Let us now analyze in detail the content of Fig. 7. We divide the discussion in three parts, according to three regimes: (i) the trivial phase, (ii) the onset of the topological phase, and (iii) deep in the topological phase.
In the trivial phase of short junctions, there are no subgap states in our model at (regardless of the transparency) vuik2019 . Therefore, and the temperature-dependence of and is strong only if . At low temperatures, such condition is satisfied only close to the topological phase transition (because when ). This explains why, in Figs. 7a, c, e and g, the curves for different temperatures are superimposed deep in the trivial phase, but begin to diverge closer to the topological phase transition. The fact that is easily attained at the topological phase transition also explains why the zero-temperature kinks in and , which take place at the topological phase transition in highly transparent junctions (Fig. 5e-h), are washed out by thermal effects. Still, remnants of the kinks survive at low () but finite temperatures, in the form of broadened peaks for and . These peaks are evident in Figs. 7b, d, f and h.
At the onset of the topological phase (), four MBS emerge. Two of them, localized on the outer extremities of the superconducting electrodes, have near-zero energies that are essentially independent of in the vicinity of ; these dispersionless states do not contribute to and . For this reason, we will hereafter omit the two "outer" MBS from the discussion. In contrast, the two "inner" MBS localized on the opposite extremities of the weak link have a non-negligible bandwidth in , given by the hybridization energy ; these dispersive states can contribute appreciably to and . In a junction of high transparency, . Hence, in such junction, the leading temperature-dependence of and at originates mainly from the non-Majorana states. In contrast, in a junction of low transparency, and the leading temperature-dependence at originates from the inner MBS.

As the system is driven deeper into the topological phase, Fig. 7 reflects two possible scenarios. In the scenario of Fig. 7e-h, the junction is highly transparent and there are no dispersive subgap states at . In this case, , where we once again ignore the outer MBS. If (which is common not far from the topological phase transition), grows linearly with the magnetic field. Therefore, the temperature-dependence of and weakens gradually as grows, and becomes once again negligible when . This is why, in Fig. 7e and g, the curves for different temperatures tend to converge deep in the topological phase.
Contrastingly, in the scenario of Fig. 7a-d, the junction has low transparency. In this case, there are dispersive subgap MBS of energy at , so that . Moreover, the low junction transparency implies . Then, as temperature is raised well above , the contribution of MBS to is suppressed via the factor in Eq. (III.2). At the same time, the energies of the higher-energy (non-Majorana) scattering states are relatively dispersionless in and therefore make a relatively modest contribution to , much like in the trivial phase. As a result, is strongly reduced in the topological phase when . This explains the traits of Fig. 7a in the topological phase.
One intriguing outcome from the foregoing discussion is that it appears to be possible to thermally switch on and off the contribution from MBS to in short tunnel junctions, by going from to . This statement applies to longer junctions of low transparency as well. Although such junctions host low-energy Andreev-bound states in the trivial phase, their -dependence in the tunneling regime is relatively small; therefore, changing their thermal occupancy does not make a substantial difference to . We have verified this point for junctions with 20 and 50 sites in the weak link, and .
III.3 Bifurcation currents
Thus far, we have been concerned with the prediction and understanding of peaks in the derivatives of and across a topological phase transition. The connection between and with the operation of a JBA is made by Eq. (7). From this equation, it is clear that the bifurcation currents of the TJBA will display signatures of a topological phase transition.
The results are summarized in Fig. 8, which shows the lower and upper bifurcation currents as a function of the magnetic field, for short junctions of low (Fig. 8a-d) and high (Fig. 8e-h) transparency. The drive frequency is chosen to be below , as otherwise there is no bifurcation (cf. Sec. II).
The bifurcation currents are much smaller in the tunneling regime than in the transparent regime, because the critical current of the junction is much lower in the former. At the topological phase transition, the behaviour of bifurcation currents as function of magnetic field parallels that of , and thus their derivatives display peaks at . These peaks are broadened at finite temperature.
IV Detection of the Josephson effect
One of the characteristic signatures of the presence of MBS in a Josephson junction is the -periodic Josephson effectkitaev2001 ; fu2008 . The detection of this effect has been an active research topic in recent years. The leading experimental reports include missing Shapiro stepsrokhinson2012 ; bocquillon2016 and the halving of the Josephson radiation frequencylaroche2019 . In this section, we describe an alternative (albeit indirect) microwave signature of the Josephson effect in short tunnel junctions, which is amenable to detection by a TJBA.

We begin by showing and in a short tunnel junction, as a function of the magnetic field, for several of the lowest-energy many-body states (Fig. 9). In order to obtain these results, in Eq. (6) has been replaced by the energy of individual many-body states. This is unlike in Sec. III, where we concentrated on and in thermodynamic equilibrium. In the lowest-energy many-body state, all single-particle energy levels with are occupied; its corresponding energy is given by Eq. (3). The excited many-body states are constructed by creating particle-hole excitations on top of the lowest-energy state (one such excitation involves emptying a single-particle state and populating a single-particle state , for ); their corresponding energies are given by adding to Eq. (3) the excitation energies of the particle-hole pairs.
According to Fig. 9a and b, in the trivial phase of a tunnel junction, and are very similar for all the low-lying many-body states. Then, at the onset of the topological phase, both and split into two branches, which diverge gradually from one another as the magnetic field increases. Deeper in the topological phase, the lower branch of can reach zero at a critical value of the magnetic field and subsequently disappear. The magnitude of this upper critical field depends on microscopic details, and can be partly controlled by shunting the topological Josephson junction with an ordinary Josephson junction of Josephson energy (with ). As mentioned in Sec. III.1, may also model the contribution of multiple subbands to the Josephson energy in a quasi one-dimensional nanowire. The larger the value of , the higher the critical field at which the lower plasmon branch disappears in the topological phase. For large enough , the frequency of the lower plasmon branch saturates before reaching zero and the branch never disappears.

The preceding observations from Fig. 9a and b are closely related to the emergence of the -periodic Josephson effect in the topological phase. Next, we explain this connection by analyzing the energy spectrum of the junction (Fig. 10).
In the trivial regime of the tunnel junction, the dispersion of the single-particle states as a function of is approximately flat (Fig. 10a). Hence, when is sizeable, the energies of the many-body states (Fig. 10c) are of the form , where and "const" is a term independent of (though it takes different values for different many-body states). Note that is approximately the same for all the many-body states. This explains why and are very similar for different many-body states in the topologically trivial regime.
The situation is different in the topologically nontrivial regime of the tunnel junction, where the subgap single-particle states associated to the inner MBS display increased dispersion (Fig. 10b); this dispersion is qualitatively of the form , where is the hybridization energy of the inner MBS.
The occupation of these dispersive Majorana bands determines the parity of the inner MBS. Many-body states have a well-defined value of , with () if the localized single-particle level due to the hybridized MBS is empty (filled). Then, the energies of the many-body states take the approximate form , where . Once again, the magnitude of and does not change from one many-body state to another. The term in the energy is responsible for the -periodic Josephson effect; indeed, if is conserved, the many-body energies (and thus the supercurrent) are -periodic in .
We now come to the key observation. In the topological phase, the many-body states with have an absolute minimum at (mod ) (see Fig. 10d). In contrast, the many-body states with show a local (metastable) minimum at (mod ), if and only if . This local minimum exists because of the coexistence of and terms in the energy. When it exists, the local minimum of states at differs in curvature and anharmonicity from the absolute minima of the states at . As a result, from Eq. (6), the plasmon frequencies and anharmonicities associated to small oscillations around are -dependent:
| (13) |
When , and are identical for all many-body states. As the system enters the topological phase, grows together with and two distinct values of and emerge for . This explains the main trends observed in Fig. 9a and b.
If , the curvature of the local minimum for states at vanishes, and thus . For , the many-body states with have a maximum (rather than a local mimimum) at ; small oscillations can only take place in the vicinity of . But, because the minimum for states is identical to the minimum for states, it follows that there is only one branch of and when .
When , a magnetic field slightly higher than the one required to attain the topological phase is sufficient to lead to . The reason for this is that , being inversely proportional to , can be large in the tunneling regime (at least for the single-channel nanowire we consider). The interval of the magnetic field in which the metastable minimum is present is enhanced by increasing . For a sufficiently large , never exceeds , no matter how high is; an example of this situation is illustrated in Fig. 9, where the lower branch of saturates at a finite value at high . This saturation has to do with the fact that , decreasing with , eventually becomes smaller than deep in the topological phase, thereby stunting and reversing the growth of as the magnetic field increases.
The aforementioned features are echoed in the bifurcation currents of the TJBA. Figure 11a shows and for the lowest many-body states, in a short tunnel junction. In the trivial phase, the bifurcation currents for the low-lying many-body states are all similar. Beyond the topological phase transition, and split into two branches corresponding to and states. Accordingly, the switching probabilities between low- and high-amplitude oscillating states near become -dependent (see Fig. 11b-c). Roughly, can be regarded as two quantum states with distinct JBA switching probabilities.
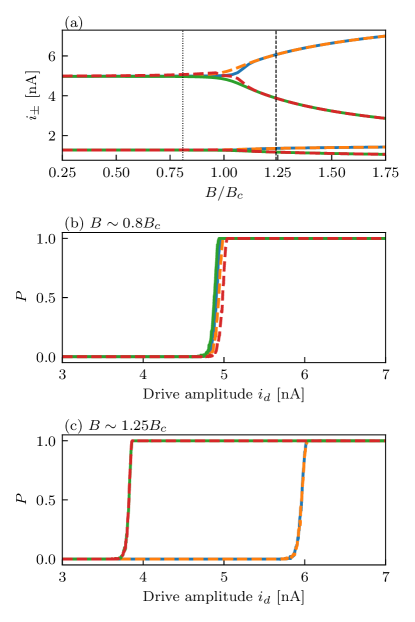
Let us now discuss the experimental observability of the 4-periodic Josephson effect in a TJBA. The underlying idea is to induce transitions between the absolute and local minima of the energy spectrum, and to measure the frequency of small oscillations of around those minima quickly enough (before energy relaxation to the absolute minimum takes place). We begin by noting that the vertical-in- transition between the and minima cannot be induced by microwave pulses, because electron-photon interactions preserve the MBS paritylopes2019 . This is unlike the case of the two quantum states in a superconducting qubit, the transition between which is routinely induced by microwave pulses.
Nonetheless, there are still two ways one can probe the presence of the metastable minimum with a JBA scheme. One is by letting the system spontaneously switch between the stable and metastable minima. This will occur due to quasiparticle poisoning or other vertical-in- processes that violate the conservation of . By repeating a JBA measurement many times for a fixed and , one will find two very different switching probabilities on the topological phase (provided that ), but not on the trivial phase. In addition, this type of measurement may allow to extract the lifetime of the inner MBS parity experimentally (provided that the escape time of away from the local minimum through thermal and quantum fluctuations is longer than ).
A more deterministic way of switching between stable and metastable minima is by applying current pulseslikharev1986 . A current pulse of short duration and amplitude comparable to the critical current of the junction can be applied to vary away from one minimum of the energy. For fixed , changes in that are odd multiples of will connect a local minimum with an absolute minimum (see Fig. 10d). The precise control of with the current pulse is not required, however; what is important is that, after the current pulse stops, will begin to oscillate around the nearest minimum. If , sometimes this minimum will be a local minimum, and other times it will be an absolute minimum. By measuring the state of the oscillator (low-amplitude vs high-amplitude) immediately after the current pulse is switched off, and repeating the whole process multiple times, two distinct switching probabilities will be apparent in the topological phase, but not in the trivial phase. This measurement protocol is analogous to the JBA-based measurement of Rabi oscillations and relaxation times in conventional superconducting qubitsvijay .
For the preceding measurement protocol to function, it is necessary that the lifetime of the metastable minimum be long compared to the JBA measurement time, the latter being of the order of microsecondsvijay . As mentioned above, the metastable minimum has a lifetime that is in part determined by the quantum/thermal fluctuations over the local potential barrier, as well as vertical-in- inelastic processes that flip . When , thermal fluctuations over the barrier are exponentially suppressed. Large quantum fluctuations of the phase (tunneling across the energy barrier around the metastable minimum) are likewise exponentially suppressed if the charging energy of the junction is small compared to the Josephson energy. Under these conditions, the lifetime of the metastable minimum is limited by quasiparticle poisoning processes, which are indeed slow compared to the timescale in which a JBA experiment can be realizedhays2018 .
So far, we have restricted our discussion to short tunnel junctions. The reason for this is that, in more transparent junctions of any length, the situation is less favorable for the TJBA-based detection of the -periodic Josephson effect. This is so for two main reasons. First, the scattering states display significant dispersion in more transparent junctions. Therefore, there is a wide spread of and for different many-body states, even in the trivial regime; this behavior is already incipient in Fig. 9c and d, for junctions with . Second, for , the Majorana bands near are buried within the scattering states (because in a transparent junction). As a result, the many-body states with are part of a continuum of states, which drastically decreases their lifetime and observability.
Concerning longer tunnel junctions (up to 50 sites in the weak link were studied), they do show the desired effect, but it is masked by the fact that there abound non-Majorana subgap states that disperse significantly. This leads to an array of different and for the low-lying many-body states, in the topological phase. Yet, the fact that one of the plasmon frequencies drops appreciably in the vicinity of the topological phase transition (even vanishing at a critical magnetic field if is sufficiently small) still holds and is related to the emergence of MBS.
We conclude this section by comparing our results to earlier works in the literature. First, the TJBA-based detection scheme for the -periodic Josephson effect relies on the dynamics of the superconducting phase difference near a minimum of the energy (e.g. ). As such, it is robust under energy gaps that can occur at due to parity violating processes. It also differs from existing proposals and experiments to measure the Josephson effect. The latter rely on swiping over multiple full periods along a single many-body state of fixed ; the swipe must be fast enough to overcome any putative energy gap at (through Landau-Zener tunneling).
Second, the splitting of and that we have reported is related to features previously predicted for microwave spectroscopy ginossar2014 ; keselman2019 ; avila2020 . In Ref. [ginossar2014, ], it was found that energy levels of a usual transmon qubit are split into doublets when . From Fig. 2 in that paper, it is evident that the plasmon frequencies would also be split in two for different sectors of the inner MBS parity. Yet, the authors restricted themselves to the regime , in which the splitting in and is very small, and also no systematic study of and was carried out as a function of the microscopic parameters of the system. Similarly, in Refs. [keselman2019, ] and [avila2020, ], a splitting of a spectral line in the microwave spectrum was noted at the topological phase transition in a way that is reminiscent of Fig. 9c. These studies focused on the charge qubit parameter regime where the observed splitting was dominated by the charging energy, while our work focus on the complementary transmon parameter regime where the splitting is dominated by . The possibility that the lower branch of and may disappear in the topological phase of tunnel junctions (for ) was not recognized in earlier works.
V Conclusions
In summary, we have proposed that a bifurcation amplifier built from a topological Josephson junction (a topological Josephson bifurcation amplifier, or TJBA) can be an interesting device to study various aspects related to Majorana bound states and their emergence in semiconductor nanowires with proximity-induced superconductivity.
Much of our effort has been devoted towards understanding the behavior of the Josephson plasmon frequency and the anharmonicity parameter as a function of the externally applied Zeeman field , in the transmon regime, at zero and finite temperature, as well as for different many-body states. The reason for this focus is that and are key variables that govern the operation of the bifurcation amplifier; small changes in those quantities can be sensed when the TJBA is driven in the vicinity of the bifurcation point. Though our analysis is based on a minimal model of a nanowire (single-channel, free from disorder), we have attempted to extract physical statements and results whose relevance should transcend the model’s simplicity.
Our work contains two main results. First, in the regimes of low and high transparency, and display pronounced peaks at the topological phase transition, which are reflected in the bifurcation currents of the TJBA. These peaks are associated to the emergence of MBS. Finite temperature broadens the peaks, which nonetheless remain significant provided that the thermal energy is well below () the proximity-induced -wave superconducting gap. Remarkably, in tunnel junctions, the contribution from MBS to can be turned on and off by varying the temperature. Another remarkable aspect is the evolution of the ratio across a topological phase transition in a junction of low transparency, at zero temperature. In the trivial phase, tends to a plateau of , which corresponds to the value found in a conventional Josephson junction. In contrast, in the topological phase, tends to a plateau of . The factor between the two plateaux originates from a fundamental change in the dependence of the ground state energy on the superconducting phase difference : it is in the trivial regime and in the topological regime (the absolute value applies in the absence of fermion parity constraints). The change is again due to the appearance of MBS.
Second, the TJBA can spot the emergence of unconventional periodicities in the current-phase characteristics of the junction, such as the -periodic Josephson effect that is induced by when the junction undergoes a topological phase transition. The TJBA-based approach for measuring the -periodic Josephson effect is centered on the dynamics of near an energy minimum; it therefore differs from proposals and experiments that rely on swiping over multiple full periods. The underlying concept relies on monitoring and for different many-body states near . Because of the coexistence between and terms in the ground state energy, and split into two branches each in the topological phase; the same behavior is present in the bifurcation currents of the TJBA. This splitting originates from MBS.
The above predictions and results are easier to validate in junctions that contain no subgap states other than the MBS. In our model, such is the case when the junction is short. In longer junctions, zero-energy Andreev bound states arise even in the trivial phase, thereby mimicking the signatures of MBS. In their presence, additional analysis is necessary in order to discern topological signatures from trivial ones. Similar issues complicate most detection schemes of MBS in semiconductor nanowires.
Although a TJBA has not yet been built, the ongoing progress in combining nanowire-based superconducting qubit technology with the magnetic fields required to realize MBS suggests that its fabrication is within reach. Ideally, the present work may provide an incentive for the experimental development of a TJBA, which will in turn encourage further theoretical studies on the device. Obvious tasks on the theory side include the adoption of more realistic models of nanowires, as well as a fully quantum mechanical treatment of the TJBA dynamics.
Note added: In the final stages of this work, a preprint appeared kurilovich2021 in which an analytical theory for the dynamics of a topological Josephson junction coupled to a cavity is presented. The findings of Ref. [kurilovich2021, ], which include a fork-like feature of the cavity frequency pull at the topological phase transition, are consistent with our results.
Acknowledgements.
This research was financed in part by the Canada First Research Excellence Fund and the Natural Science and Engineering Council of Canada. Numerical calculations were partly done with computer resources from Calcul Québec and Compute Canada. U.C.M. acknowledges the support from CNPq-Brazil (Project No. 309171/2019-9).Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- (1) For current perspectives of the field, see e.g. S. M. Frolov, M. J. Manfra and J. D. Sau, Nature Physics 16, 718 (2020); E. Prada, P. San-Jose, M. W. A. de Moor, A. Geresdi, E. J. H. Lee, J. Klinovaja, D. Loss, J. Nygard, R. Aguado and L. P. Kouwenhoven, Nat. Rev. Phys. 2, 575 (2020).
- (2) For a review of the theory and the experiments, see e.g. R. Aguado, La Rivista del Nuovo Cimento 40, 523 (2017); R. M. Lutchyn, E. P. A. M. Bakkers, L. P. Kouwenhoven, P. Krogstrup, C. M. Marcus, and Y. Oreg, Nature Reviews Materials 3, 52 (2018).
- (3) T. Karzig, C. Knapp, R. M. Lutchyn, P. Bonderson, M. B. Hastings, C. Nayak, J. Alicea, K. Flensberg, S. Plugge, Y. Oreg, C. M. Marcus and M. H. Freedman, Phys. Rev. B 95, 235305 (2017).
- (4) F. Hassler, A. R. Akhmerov, and C. W. J. Beenakker, New Journal of Physics 13, 095004 (2011).
- (5) C. Müller, J. Bourassa, and A. Blais, Phys. Rev. B 88, 235401 (2013).
- (6) D. Pekker, C.-Y. Hou, V. E. Manucharyan, and E. Demler, Phys. Rev. Lett. 111, 107007 (2013).
- (7) P. Virtanen and P. Recher, Phys. Rev. B 88, 144507 (2013).
- (8) E. Ginossar and E. Grosfeld, Nature Communications 5, 4772 (2014).
- (9) K. Yavilberg, E. Ginossar, and E. Grosfeld, Phys. Rev. B 92, 075143 (2015).
- (10) O. Dmytruk, M. Trif, and P. Simon, Phys. Rev. B 92, 245432 (2015).
- (11) J. Väyrynen, G. Rastelli, W. Belzig, and L. I. Glazman, Phys. Rev. B 92, 134508 (2015).
- (12) Y. Peng, F. Pientka, E. Berg, Y. Oreg, and F. von Oppen, Phys. Rev. B 94, 085409 (2016).
- (13) M.C. Dartiailh, T.Kontos, B. Douçot and A. Cottet, Phys. Rev. Lett. 118, 126803 (2017).
- (14) A. Cottet, M. C. Dartiailh, M. M. Desjardins, T. Cubanyes, L. C. Contamin, M. Delbecq, J. J. Viennot, L. E. Briuhat, B. Douçot and T. Kontos, J. Phys.: Condens. Matter 29, 433002 (2017).
- (15) M. Trif, O. Dmytruk, H. Bouchiat, R. Aguado, and P. Si- mon, Phys. Rev. B 97, 041415 (2018).
- (16) A. Keselman, C. Murthy, B. van Heck, and B. Bauer, SciPost Phys. 7, 50 (2019).
- (17) P. L. S. Lopes, S. Boutin, P. Karan, U. C. Mendes and I. Garate, Phys. Rev. B 99, 045103 (2019).
- (18) J. Avila, E. Prada, P. San-Jose and R. Aguado, Phys. Rev. B 102, 094518 (2020).
- (19) A. L. Grimsmo and T. B. Smith, Phys. Rev. B 99, 235420 (2019); T. B. Smith, M. C. Cassidy, D. J. Reilly, S. D. Bartlett and A. L. Grimsmo, Phys. Rev. X Quantum 1, 020313 (2020).
- (20) For a recent review, see e.g. A. Blais, A. L. Grimsmo, S. M. Girvin amd A. Wallraff, arXiv:2005.12667 (2020).
- (21) T. W. Larsen, K. D. Peterson, F. Kuenmeth, T. S. Jespersen, P. Krogstrup, J. Nygård and C. M. Marcus, Phys. Rev. Lett. 115, 127001 (2015).
- (22) G. de Lange, B. van Heck, A. Bruno, D. J. Woerkom, A. Geresdi, S. R. Plissard, E. P. A. M. Bakers, A. R. Akhmerov and L. DiCarlo, Phys. Rev. Lett. 115, 127002 (2015).
- (23) D. van Woerkom, A. Proutski, B. van Heck, D. Bouman, J. I. Väyrynen, L. I. Glazman, P. Krogstrup, J. Nygård, L. P. Kouwenhoven and A. Geresdi, Nature Physics 13, 876 (2017).
- (24) F. Luthi, T. Stavenga, O. W. Enzing, A. Bruno, C. Dickel, N. K. Langford, M. A. Rol, T. S. Jespersen, J. Nygård, P. Krogstrup and L. DiCarlo, Phys. Rev. Lett. 120, 100502 (2018).
- (25) L. Tosi, C. Metzger, M. F. Goffman, C. Urbina, H. Pothier, S. Park, A. Levy yeyati, J. Nygård and P. Krogstrup, Phys. Rev. X 9, 011010 (2019).
- (26) M. Pita-Vidal, A. Bargerbos, C.-K. Yang, D. J. van Woerkom, W. Pfaff, N. Haider, P. Krogstrup, L. P. Kouwenhoven, G. de Lange and A. Kou, Phys. Rev. Applied 14, 064038 (2020).
- (27) I. Siddiqi, R. Vijay, F. Pierre, C. M. Wilson, M. Metcalfe, C. Rigetti, L. Frunzio and M. H. Devoret, Phys. Rev. Lett. 93, 207002 (2005).
- (28) For reviews, see e.g. R. Vijay, M. H. Devoret and I. Siddiqi, Review of Scientific Instruments 80, 111101 (2009); R. Vijay, PhD dissertation (Yale University, 2008).
- (29) F. Mallet, F. R. Ong, A. Palacios-Laloy, F. Nguyen, P. Bertet, D. Vion and D. Esteve, Nat. Phys. 5, 791 (2009).
- (30) P. Bertet, F. R. Ong, M. Boissonneault, A. Bolduc, F. Mallet, A. Doherty, A. Blais, D. Vion and D. Esteve, in chapter 1 of Fluctuating Nonlinear Oscillators, edited by M. Dykman (Oxford University Press, 2011).
- (31) V. Schmitt, X. Zhou, K. Juliusson, B. Royer, A. Blais, P. Bertet, D. Vion and D. Esteve, Phys. Rev. A 90, 062333 (2014).
- (32) M. A. Castellanos-Beltran and K. W. Lehnert Applied Physics Letters 91, 083509 (2007).
- (33) M. Hatridge, R. Vijay, D. H. Slichter, J. Clarke and I. Siddiqi, Phys. Rev. B 83, 134501 (2011).
- (34) Z. R. Lin, K. Inomata, W. D. Oliver, K. Koshino, Y. Nakamura, J. S. Tsai and T. Yamamoto, Applied Physics Letters 103, 132602 (2013).
- (35) K. Likharev, Dynamics of Josephson junctions and circuits (Gordon and Breach, Amsterdam, 1986).
- (36) For a recent survey, see e.g. J. A. Blackburn, M. Cirillo and N. Gronbech-Jensen, Phys. Rep. 611, 1 (2016).
- (37) C. W. J. Beenakker, D. I. Pikulin, T. Hyart, H. Schomerus and J. P. Dahlhaus, Phys. Rev. Lett. 110, 017003 (2013).
- (38) For a review of current-phase relationships in topologically trivial Josephson junctions, see e.g. A. A. Golubov, M. Yu. Kupriyanov and E. Il’ichev, Rev. Mod. Phys. 76, 411 (2004).
- (39) J. Cayao, A. M. Black-Schaffer, E. Prada and R. Aguado, Beilstein J. Nanotechnol. 9, 1339 (2018).
- (40) For a review of the topological phase diagram, see e.g. J. Alicea, Reports on Progress in Physics 75, 076501 (2012).
- (41) G. E. Blonder, M. Tinkham, and T. M. Klapwijk Phys. Rev. B 25, 4515 (1982).
- (42) B. van Heck, J. I. Väyrynen and L. I. Glazman, Phys. Rev. B 96, 075404 (2017).
- (43) While the Josephson energy of the junction is reduced in the tunneling regime, we still assume that it is large compared to the charging energy of the junction.
- (44) The implicit assumption here is that will have a relatively featureless (or at least smooth) dependence in , for the values of that are required to induce a topological phase transition.
- (45) J. Cayao, P. San-Jose, A. Black-Schaffer, R. Aguado and E. Prada, Phys. Rev. B 96, 205425 (2017).
- (46) P. San-Jose, E. Prada and R. Aguado, Phys. Rev. Lett. 112, 137001 (2014).
- (47) H. Huang, Q.-F. Liang, D.-X. Yao and Z. Wang, Phys. Lett. A 381, 2033 (2017).
- (48) J. Tiira, E. Strambini, M. Amado, S. Roddaro, P. San-Jose, R. Aguado, F. S. Bergeret, D. Ercolani, L. Sorba and F. Giazotto, Nature Communications 8, 14984 (2017).
- (49) P. San-Jose, J. Cayao, E. Prada and R. Aguado, New J. Phys. 15, 075019 (2013).
- (50) C. Murthy, V. D. Kurilovich, P. D. Kurilovich, B. van Heck, L. I. Glazman and C. Nayak, Phys. Rev. B 101, 224501 (2020).
- (51) This discussion does not apply to junctions of low transparency, because scattering at the interface between the electrodes and the weak link invalidates the picture of two quasi-independent wave gaps.
- (52) Andreev bound states with near-zero energy (dubbed "quasi-Majorana states") have been predicted to be ubiquitous in the trivial phase of Josephson junctions with smooth potential barriers, and to mimic the behavior of Majorana bound states; see e.g. A. Vuik, B. Nijholt, A. R. Akhmerov and M. Wimmer, SciPost Phys. 7, 061 (2019). The quasi-Majorana bound states are absent if the barrier potential is steep. Even though our tight-binding model does not explicitly incorporate potential barriers, the single-particle energy spectra we obtain for short (long) junctions map roughly onto those corresponding to steep (smooth) potential barriers.
- (53) J. Chen, P. Yu, J. Stenger, M. Hocevar, D. Car, S. P. Plissard, E. P. A. M. Bakkers, T. D. Stanescu and S. M. Frolov, Science Advances 9, e1701476 (2017).
- (54) A. Y. Kitaev, Phys.-Usp. 44, 131 (2001).
- (55) L. Fu and C. L. Kane, Phys. Rev. B 79, 161408 (2009).
- (56) L. P. Rokhinson, X. Liu and J. K. Furdyna, Nature Physics 8, 795 (2012).
- (57) J. Wiedenmann et al., Nature Communications 7, 10303 (2016); E. Bocquillon, R. S. Deacon, J. Wiedenmann, P. Leubner, T. M. Klapwijk, C. Brüne, K. Ishibashi, H. Buhmann and L. W. Molenkamp, Nature Nanotechnology 12, 137 (2017).
- (58) D. Laroche, D. Bouman, D. J. van Woerkom, A. Proutski, C. Murthy, D. I. Pikulin, C. Nayak, R. J. J. van Gulik, P. Krogstrup, L. P. Kouwenhoven and A. Geresdi, Nature Communications 10, 245 (2019).
- (59) M. Hays, G. de Lange, K. Serniak, D. J. van Woerkom, D. Bouman, P. Krogstrup, J. Nygård, A. Geresdi, M. H. Devoret, Phys. Rev. Lett. 121, 047001 (2018).
- (60) V. D. Kurilovich, C. Murthy, P. D. Kurilovich, B. van Heck, L. I. Glazman and C. Nayak, arXiv:2102.05686 (2021).