Topological dissipative Kerr soliton combs in a valley photonic crystal resonator
Topological phases have become an enabling role in exploiting new applications of nonlinear optics in recent years. Here we theoretically propose a valley photonic crystal resonator emulating topologically protected dissipative Kerr soliton combs. It is shown that topological resonator modes can be observed in the resonator. Moreover, we also simulate the dynamic evolution of the topological resonator with the injection of a continuous-wave pump laser. We find that the topological optical frequency combs evolve from Turing rolls to chaotic states, and eventually into single soliton states. More importantly, such dissipative Kerr soliton combs generated in the resonator are inborn topologically protected, showing robustness against sharp bends and structural disorders. Our design supporting topologically protected dissipative Kerr soliton combs could be implemented experimentally in on-chip nanofabricated photonic devices.
I Introduction
Optical frequency combs have been undergoing revolutionized development in integrated photonic resonators. For coherent optical frequency combs in nonlinear micro-resonators, there exist stationary temporal solutions so-called dissipative Kerr solitons (DKSs). Such DKSs are attributed to the double balance between the micro-resonators Kerr effect and dispersion management, as well as losses and parametric gain [1]. This specific phenomenon of optical frequency combs has exploited numerous concepts, such as the Stokes soliton [2], breathing solitons [3], and soliton crystals [4]. Primitively, bulk crystalline and microdisks [5, 6, 7] are proved to be an appropriate breeding ground for DKS combs. Furthermore, the soliton combs are expanded to on-chip photonic devices including [8, 9, 10], [11, 12], and AlGaAs [13].
At the same time, topological phases of matter bring robustness to photonic devices. In parallel, advances in topological phases also excite sparks in nonlinear photonic systems. It has been experimentally proposed that the topological transport of second or third-harmonic waves can be conducted in chip-scale devices [14, 15]. Furthermore, such systems exhibit the topological protection of four-wave mixing processes [16]. Lately, theoretical research demonstrates topological optical frequency combs and temporal DKSs can be manipulated in coupled micro-resonators [17]. Topological nonlinear optics also gives inspiration for implementing topological protection of complex nonlinear processes, including topological exciton-polaritons [18, 19] and gap solitons [20, 21]. The topological platforms are also applied to build topological protection of quantum states, such as topological quantum sources [22], entangled states [23, 24, 25], and quantum interference [26]. Recent research has proposed a topological phase, namely the quantum valley Hall (QVH) effect [27, 28, 29, 30, 31], to implement valley kink states along the topological interface.
Here we theoretically investigate the generation and topological transport of DKS combs in a valley photonic crystal (VPC) slab. We confirm the existence of topologically protected kink states at the resonator modes in a whisper-gallery resonator. The nonlinear dynamic evolution of the topological resonator with an excited continuous-wave (CW) pump laser is numerically simulated. The result reveals that with the detuning of the pump laser, the optical frequency combs generated in the resonator can evolve into single soliton combs eventually. More importantly, these DKSs generated in the VPC resonator are topologically protected and show robustness against sharp bends and structural imperfections. Our design may give a new spark to the chip-scale operation of topological optical frequency combs.
II Topological resonators
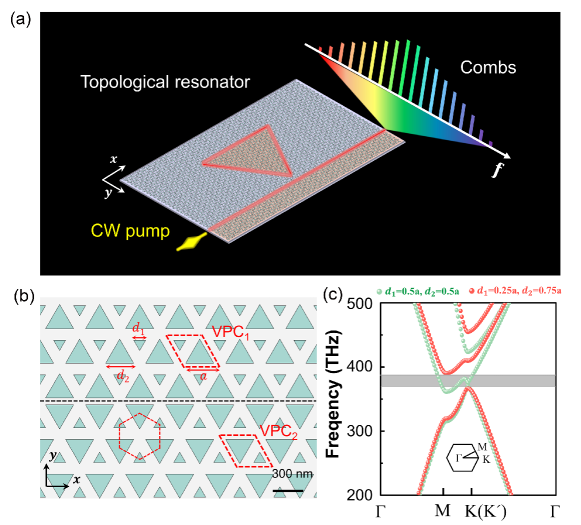
Topological resonator is a burgeoning platform integrating topological phases and cavity dynamics. Here we demonstrate a triangle topological resonator enforcing the DKS combs in a silicon nitride () VPC slab. As depicted in Fig. 1(a), a scheme of the VPC topological resonator is designed to produce topological frequency combs, where a bus waveguide is used to couple the pump into the resonator. When a CW laser is pumped at a resonator frequency, the third-order nonlinearity of material with appropriate dispersion leads to a frequency comb with the spacing of free spectral range (FSR). When it meets a balance between intrinsic dispersion and nonlinearity-induced parametric gain, the comb shows a fully coherent formation, so-called DKSs. Since the DKS comb is produced in the triangle topological resonator, it is inborn topological. Such topological protection brings the DKS combs robustness against sharp corners.
The two-dimensional (2D) close-up image of VPCs is shown in Fig. 1(b), which is composed of and [28, 29]. The nanohole sizes are determined by and , where the lattice constant is nm. As shown in Fig. 1(c), the calculated band structures of different VPCs reveal that there is a Dirac cone at the and valleys as illustrated by green dots. The equilateral triangular nanoholes with lattice symmetry preserve a graphene-like lattice model [29]. This lattice symmetry leads to degenerate Dirac points at the and valleys in the Brillouin zone. With the distortion of the unit cell (, and ), it opens a photonic bandgap at the Dirac cone due to the breaking of lattice symmetry, as displayed by red dots in Fig. 1(c). Theoretically, the valley Chern numbers of and are described by , respectively (Supplemental Material). This model exhibits valley kink states propagating along the interface between and , which shows robustness against certain disorders.
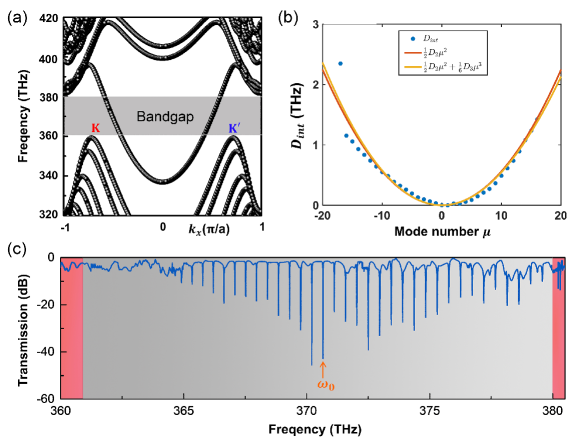
To study the underlying properties of topological VPCs, we perform the band calculation of VPCs. As shown in Fig. 2(a), the band opens a large gap from 361 THz to 380 THz. There exist a pair of valley-polarized topological kink states (corresponding to and respectively) in the complete bandgap. Due to the QVH effect, these kink states are locked to different valleys respectively, which refers to “valley-locked” chirality. Accordingly, this allows opposite propagating modes for kink states. These valley kink states are proven to be robust against defects and sharp corners (Supplemental Material). In addition, the light confinement of propagating modes along the interface results in the high-efficiency generation of frequency combs. For the resonators producing the optical frequency combs, the developed dispersion engineering, so-called integrated dispersion, plays an important role in comb formation [1]. A mode number is used to index the relative resonator mode counted concerning the pump mode . The Taylor expansion for indexed resonance modes around is given by
| (1) |
where the expansion term is described as at . The first-order term is related to the FSR of the resonator, which can be calculated as . And the second-order dispersion term corresponds to the group velocity dispersion (GVD): . Furthermore, it is convenient to define the integrated dispersion as
| (2) |
Integrated dispersion contains high-order dispersion terms of the resonator and can be calculated from the transmission spectrum. Fig. 2(b) shows dispersions of the topological resonator extracted from the simulated transmission (Fig. 2(c)), which indicates an anomalous GVD case with . Anomalous GVD is crucial for the generation of parametric oscillations and Kerr solitons.
Topological resonators based on VPCs have been proposed to conduct the lasing [32, 33], optical routing [34], filters [35], and quantum emitter [36]. Here we proposed a triangle topological resonator to produce DKS combs. A straight topological bus waveguide is used to couple the pump mode into the topological resonator, and then, guide the generated combs from the resonator to the bus waveguide. The gap width between the bus waveguide and the topological resonator is 3 cells. We numerically simulate the transmission spectrum of kink states for the topological resonator. As shown in Fig. 2(c), the resonator modes are observed in the whisper-gallery topological resonator. These modes have identical frequency separation, so-called the FSR. It is clear evidence that the topological resonator leads to an FSR of 450 GHz. A complete distinction is observed between topological bandgap and bulk states. For the region of bulk states, there is no resonator mode existing. Due to the excitations of valley kink states, topological optical frequency combs only appear at frequencies inside the topological bandgap.
The Lorentzian fitting of the simulated resonant dip at the pump frequency of 370.67 THz reveals a total Q factor of (Supplemental Material). The external loss and intrinsic loss are calculated as . Correspondingly, the intrinsic quality factor and external quality factor are calculated as . Therefore, the topological resonator satisfies , leading to the critical coupling. The threshold for parametric oscillation in the resonator is proportionable to , where is the effective volume of the pump. Hence, the generation of signal and idler sidebands from FWM is easy to manipulate in such high-Q VPC resonators.
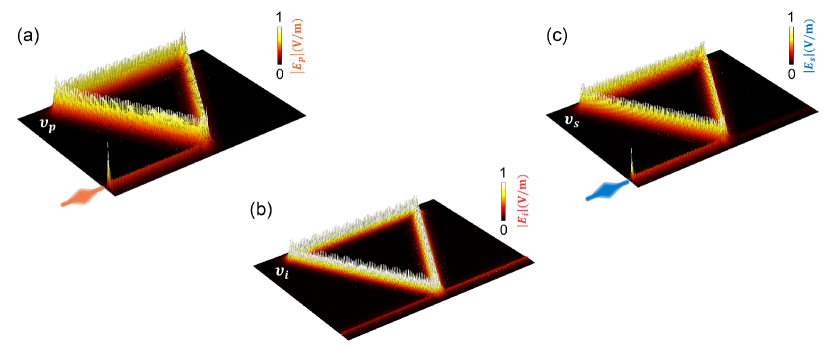
Thanks to the intrinsic nonlinearity of the resonator, numerous sidebands with equidistant gaps are produced in the resonator with the injection of a CW pump laser at the angular frequency of (indexed by the number ). To visualize the stimulated FWM process of the topological resonator, we simulate the electric field profiles of the FWM process with the selected signal and idler frequencies (). Such numerical model of the FWM process in VPCs is performed in the software COMSOL Multiphysics (for details, see Supplemental Material). As depicted in Fig. 3, the kink states of the pump, signal, and idler are excited in the coupled waveguide-resonator device. A circularly polarized excitation is used to emulate kink states along the bus waveguide. Since the pump frequency is consistent with the resonator mode , the injected pump is coupled to the topological resonator and excites the FWM process simultaneously. This chirality is also preserved for the cavity due to the same topology between the bus waveguide and the triangle cavity. There is no input for the kink state of the idler, thus, the generation of field profiles at the idler frequency gives clear evidence of the FWM processes [24]. The field profiles of topological resonator modes are concentrated at the interface, resulting in the high-efficiency generation of the FWM process. Remarkably, the resonator modes show robustness against sharp bends, confirming the topological nature of the QVH effect. Note that the direction of rotation in the topological ring is related to the injected pump mode (Supplemental Material).
III Topological Kerr soliton combs
DKS combs can be readily implemented in topological micro-resonators due to the intrinsic Kerr nonlinearity of nonlinear materials [17]. DKSs are temporal solutions to the balance between intrinsic dissipation and nonlinearity-induced parametric gain [1]. When the parametric gain of the cavity exceeds the decay rate, symmetrically spaced sidebands appear around the incident pump. Optical frequency combs can grow to DKSs with the tuning of the frequency of the pump laser. In general, the dynamics of optical frequency combs in the micro-resonator are described by Lugiato–Lefever equation (LLE)[37, 38]:
| (3) | ||||
where describes the evolution of the intracavity field, is related to the linewidth of resonator modes, is the detuning of the resonance frequency. is the coupling efficiency, where and are the intrinsic loss and external loss respectively. With proper approximations of the LLE, the dynamics of DKSs can be numerically simulated (Supplemental Material). To access the reproducible soliton state, the pump is detuned from the blue () to the red region (). In general, the evolution of optical frequency combs is recognized by several trajectories, including Turing rolls, chaotic states, breathing solitons, and eventually into the soliton states [1]. In the case of single soliton states, the comb spectrum is almost smooth and phase-locked [39]. Such single soliton states have been experimentally observed in a great deal of platforms [5, 8, 9, 10], therefore, we can conclude several tricks to excite single soliton states. First, solitons are always generated at the red tunning of resonance frequency due to the thermal effects of the cavity. Secondly, the combs of single soliton formation take parallel shapes of functions. Thirdly, in the time domain, multiple or single soliton state behaves with several spaced pulses or one ultrashort pulse upon a period of the round-trip time.
To numerically simulate the dynamic evolution of the topological resonator, we consider a whisper-gallery resonator as depicted in Fig. 2. The input pump frequency corresponds to the resonance frequency indexed by , leading to the generation of the spaced sidebands in other resonator modes () via FWM processes. Since the pattern of the topological resonator is constructed by interfaces between and , the optical frequency combs are generated at the interfaces, and they transport along a certain triangular path. However, when the incident pump is coincident with bulk bands, the output comb is barely visible. In the case of bulk modes, the incident pump is dissipated into the photonic crystals. Due to the topological protection of valley kink states, the backscattering around the sharp corners is negligible [40]. Therefore, the reflection of resonator modes at the sharp corners is not included in our theoretical model.
In our simulation, the actual pump power is 2.2 W, and the refractive index of is 2.0, with the nonlinear index . The FSR and dispersion are extracted from the simulated transmission (Fig. 2(c)), with calculated values of GHz and GHz. The simulated total Q factor indicates a value of . The external loss and the total energy loss rate of the resonator are calculated as rad/s and rad/s. In this case, the coupling efficiency of critical coupling is given by . The length of the topological resonator is , where is the side length of the triangular configuration. We assume the effective field cross-section area , and the nonlinear coefficient of the topological resonator is given by . We believe our topological DKSs can be experimentally accessed by present nanofabrication technology [39, 41].
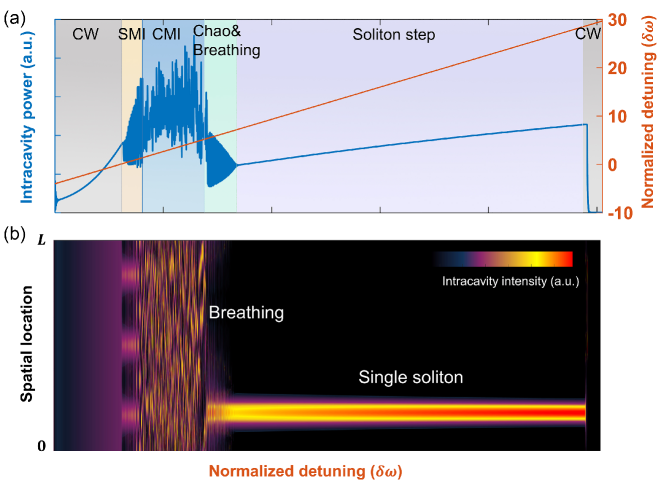
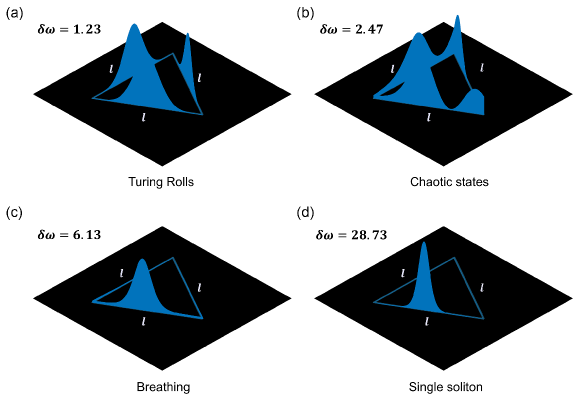
The simulated dynamic evolution of topological DKSs as a function of detuning is illustrated in Fig. 4(a). And the corresponding spatiotemporal evolution of the DKS excitation process is shown in Fig. 4(b). Three conspicuous forms are identified during the evolution process, that is, Turing rolls, chaotic states (breathing solitons), and single soliton states, respectively. Fig. 5 shows the spatial intensity distribution of the generated pulses with different detuning of the pump in the topological resonator, which can also be accessed from the spatiotemporal evolution (Supplemental Material). The pulses are circulated along the edge of the triangle topological resonator in a clockwise direction as time evolves.
In the early stages of evolution, the intensity build-up process leads to the increasing of intracavity power with the detuning from the blue side. The temporal pattern shows 3 equally spaced pulses within the triangular resonator, which is referred to as Turing rolls. Those stable pulses are attributed to the self-stabilization of the nonlinear evolution in the blue-detuned side of the resonance frequency. Thus, such a stage of modulation instability is referred to as stable modulation instability (SMI). We can observe that the cavity energy varies smoothly in the case of Turing rolls.
Those chaotic states are followed by the non-stationary behavior—breathing soliton states. Fig. 5(c) shows that there is only one pulse inside the topological resonator with the detuning , the amplitude and duration of the intracavity waveform are oscillated periodically, where the oscillation period is regarded as the breathing period. Correspondingly, the combs show periodical compression and stretching. Such instability occurs at the furcation of chaos and a stable DKS, which is referred to as Hopf bifurcation.
When the pump is further detuned to the red side (), actual soliton formation can be accessed because the intracavity field is bistable. The intracavity power shows the formation of a “step” characteristic, this “step” is the identification of solitons. The “length” of the soliton step corresponds to the pump power. For the intracavity energy, the oscillation quickly evolves to a relatively stable situation. This bistable state is an elaborate consequence of the off-resonance pump detuning and Kerr nonlinear shift of the resonator.
As shown in Fig. 4(b), the corresponding spatiotemporal formation of single soliton states also exhibits intriguing results. A quick comparison with the spatiotemporal intensity distribution of Turing rolls and chaotic states reveals that there exists only one ultrashort pulse upon a period of the round-trip time for a single soliton state. Once a single soliton state is accessed, the thermal nonlinearity of solitons makes the laser-cavity detuning self-stabilized. In this scenario, single soliton states can be stable for several hours. Note that multiple solitons may exist in the cavity with a stochastic separation number. Proceeding further, the comb degenerates to a continuous component due to the separation of the pump and resonance frequency.
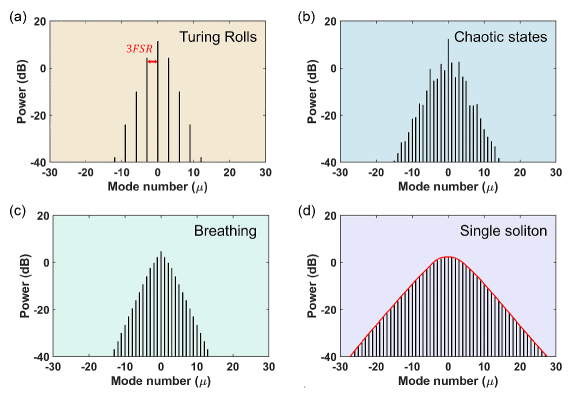
The formations of corresponding optical frequency combs are shown in Fig. 6. It is noted that generated Kerr frequency combs are composed of a CW pump component and relatively weak bilateral combs [6]. When the nonlinear gain overcomes the cavity losses, the developed primary comb so-called Turing rolls is generated. As seen in Fig. 6(a), the comb amplitudes of Turing rolls have distinctly contrast.
When the pump is further detuned to the red side, the increasing intracavity power initiates FWM processes, which leads to secondary sidebands and subcombs. The output comb of chaotic states is depicted in Fig. 6(b), Random variations of combs indicate that there is no stationary solution existing, leading to the incoherence of the waveform.
Following chaotic states, the generation of breathing solitons means the arrival of a low-detuning boundary of the soliton. As depicted in Fig. 6(c), the comb of breathing solitons takes the form of a triangular feature. Note that the amplitudes of the comb oscillate with the breathing period, and the comb returns to its initial state after one period.
The self-sustaining wavepackets of the single soliton state indicate that comb lines are phase-locked with each other (Fig. 6(d)). More importantly, the shape of the spectral output takes the form of functions. This behavior of a single soliton state in the topological resonator is analogous to that observed in single-ring resonators where exist single solitons.
We have shown many resemblances between topological resonators and single-ring resonators, however, for the DKS and single soliton combs produced in our design, thanks to the topological nature of VPCs, they are inherited to be robust against sharp bends and certain disorders. In the experimental realization, the strong thermal effect becomes an intractable element to produce stable solitons in the red-detuned region. To overcome this, heaters can be used to control the temperature of VPC chips [39, 41]. Based on the state-of-the-art nanofabrication technology, our topological DKS combs design could be implemented experimentally.
IV Conclusion
In this work, we have demonstrated a theoretical scheme exhibiting topological optical frequency combs and DKSs combs. The triangle resonator is composed of VPCs with different topologies and can excite topological valley kink resonator modes propagating along the interface. We numerically simulate the nonlinear dynamic evolution of the topological resonator with the injection of the pump laser. The result reveals that the single soliton states can be produced in the resonator, and they are born to be topological. This topological nature endows the DKS combs’ robustness against sharp bends and disorders. Our topological frequency combs could be readily accessed in on-chip nanofabricated photonics.
Acknowledgements.
This work is supported by the Key-Area Research and Development Program of Guangdong Province (2018B030325002), the National Natural Science Foundation of China (62075129, 61975119), the SJTU Pinghu Institute of Intelligent Optoelectronics (2022SPIOE204), and the Science and Technology on Metrology and Calibration Laboratory (JLJK2022001B002).References
- Kippenberg et al. [2018] T. J. Kippenberg, A. L. Gaeta, M. Lipson, and M. L. Gorodetsky, Dissipative kerr solitons in optical microresonators, Science 361, eaan8083 (2018).
- Yang et al. [2017] Q.-F. Yang, X. Yi, K. Y. Yang, and K. Vahala, Stokes solitons in optical microcavities, Nature Physics 13, 53 (2017).
- Bao et al. [2016] C. Bao, J. A. Jaramillo-Villegas, Y. Xuan, D. E. Leaird, M. Qi, and A. M. Weiner, Observation of fermi-pasta-ulam recurrence induced by breather solitons in an optical microresonator, Physical Review Letters 117, 163901 (2016).
- Cole et al. [2017] D. C. Cole, E. S. Lamb, P. Del’Haye, S. A. Diddams, and S. B. Papp, Soliton crystals in kerr resonators, Nature Photonics 11, 671 (2017).
- Liang et al. [2015] W. Liang, D. Eliyahu, V. S. Ilchenko, A. A. Savchenkov, A. B. Matsko, D. Seidel, and L. Maleki, High spectral purity kerr frequency comb radio frequency photonic oscillator, Nature Communications 6, 7957 (2015).
- Herr et al. [2014] T. Herr, V. Brasch, J. D. Jost, C. Y. Wang, N. M. Kondratiev, M. L. Gorodetsky, and T. J. Kippenberg, Temporal solitons in optical microresonators, Nature Photonics 8, 145 (2014).
- Yi et al. [2015] X. Yi, Q.-F. Yang, K. Y. Yang, M.-G. Suh, and K. Vahala, Soliton frequency comb at microwave rates in a high-q silica microresonator, Optica 2, 1078 (2015).
- Brasch et al. [2016] V. Brasch, M. Geiselmann, T. Herr, G. Lihachev, M. H. Pfeiffer, M. L. Gorodetsky, and T. J. Kippenberg, Photonic chip–based optical frequency comb using soliton cherenkov radiation, Science 351, 357 (2016).
- Zhou et al. [2022] L. Zhou, Y. Shen, C. Xi, X. Huang, and G. He, Computer-controlled microresonator soliton comb system automating soliton generation and expanding excursion bandwidth, Optics Continuum 1, 161 (2022).
- Joshi et al. [2016] C. Joshi, J. K. Jang, K. Luke, X. Ji, S. A. Miller, A. Klenner, Y. Okawachi, M. Lipson, and A. L. Gaeta, Thermally controlled comb generation and soliton modelocking in microresonators, Optics Letters 41, 2565 (2016).
- He et al. [2019a] Y. He, Q.-F. Yang, J. Ling, R. Luo, H. Liang, M. Li, B. Shen, H. Wang, K. Vahala, and Q. Lin, Self-starting bi-chromatic linbo 3 soliton microcomb, Optica 6, 1138 (2019a).
- Gong et al. [2019] Z. Gong, X. Liu, Y. Xu, M. Xu, J. B. Surya, J. Lu, A. Bruch, C. Zou, and H. X. Tang, Soliton microcomb generation at 2 m in z-cut lithium niobate microring resonators, Optics Letters 44, 3182 (2019).
- Pu et al. [2016] M. Pu, L. Ottaviano, E. Semenova, and K. Yvind, Efficient frequency comb generation in algaas-on-insulator, Optica 3, 823 (2016).
- Smirnova et al. [2019a] D. Smirnova, S. Kruk, D. Leykam, E. Melik-Gaykazyan, D.-Y. Choi, and Y. Kivshar, Third-harmonic generation in photonic topological metasurfaces, Physical Review Letters 123, 103901 (2019a).
- Kruk et al. [2021] S. S. Kruk, W. Gao, D.-Y. Choi, T. Zentgraf, S. Zhang, and Y. Kivshar, Nonlinear imaging of nanoscale topological corner states, Nano Letters 21, 4592 (2021).
- You et al. [2020] J. W. You, Z. Lan, and N. C. Panoiu, Four-wave mixing of topological edge plasmons in graphene metasurfaces, Science Advances 6, eaaz3910 (2020).
- Mittal et al. [2021a] S. Mittal, G. Moille, K. Srinivasan, Y. K. Chembo, and M. Hafezi, Topological frequency combs and nested temporal solitons, Nature Physics 17, 1169 (2021a).
- Kartashov and Skryabin [2017] Y. V. Kartashov and D. V. Skryabin, Bistable topological insulator with exciton-polaritons, Physical Review Letters 119, 253904 (2017).
- Banerjee et al. [2020] R. Banerjee, S. Mandal, and T. Liew, Coupling between exciton-polariton corner modes through edge states, Physical Review Letters 124, 063901 (2020).
- Smirnova et al. [2019b] D. A. Smirnova, L. A. Smirnov, D. Leykam, and Y. S. Kivshar, Topological edge states and gap solitons in the nonlinear dirac model, Laser & Photonics Reviews 13, 1900223 (2019b).
- Pernet et al. [2022] N. Pernet, P. St-Jean, D. D. Solnyshkov, G. Malpuech, N. Carlon Zambon, Q. Fontaine, B. Real, O. Jamadi, A. Lemaitre, M. Morassi, et al., Gap solitons in a one-dimensional driven-dissipative topological lattice, Nature Physics 18, 678 (2022).
- Mittal et al. [2018] S. Mittal, E. A. Goldschmidt, and M. Hafezi, A topological source of quantum light, Nature 561, 502 (2018).
- Chen et al. [2021] Y. Chen, X.-T. He, Y.-J. Cheng, H.-Y. Qiu, L.-T. Feng, M. Zhang, D.-X. Dai, G.-C. Guo, J.-W. Dong, and X.-F. Ren, Topologically protected valley-dependent quantum photonic circuits, Physical Review Letters 126, 230503 (2021).
- Jiang et al. [2021] Z. Jiang, Y. Ding, C. Xi, G. He, and C. Jiang, Topological protection of continuous frequency entangled biphoton states, Nanophotonics 10, 4019 (2021).
- Jiang et al. [2022] Z. Jiang, C. Xi, G. He, and C. Jiang, Topologically protected energy-time entangled biphoton states in photonic crystals, Journal of Physics D: Applied Physics 55, 315104 (2022).
- Mittal et al. [2021b] S. Mittal, V. V. Orre, E. A. Goldschmidt, and M. Hafezi, Tunable quantum interference using a topological source of indistinguishable photon pairs, Nature Photonics 15, 542 (2021b).
- Gao et al. [2018] F. Gao, H. Xue, Z. Yang, K. Lai, Y. Yu, X. Lin, Y. Chong, G. Shvets, and B. Zhang, Topologically protected refraction of robust kink states in valley photonic crystals, Nature Physics 14, 140 (2018).
- Yang et al. [2020] Y. Yang, Y. Yamagami, X. Yu, P. Pitchappa, J. Webber, B. Zhang, M. Fujita, T. Nagatsuma, and R. Singh, Terahertz topological photonics for on-chip communication, Nature Photonics 14, 446 (2020).
- Shalaev et al. [2019] M. I. Shalaev, W. Walasik, A. Tsukernik, Y. Xu, and N. M. Litchinitser, Robust topologically protected transport in photonic crystals at telecommunication wavelengths, Nature Nanotechnology 14, 31 (2019).
- Wang et al. [2022a] H. Wang, L. Sun, Y. He, G. Tang, S. An, Z. Wang, Y. Du, Y. Zhang, L. Yuan, X. He, et al., Asymmetric topological valley edge states on silicon-on-insulator platform, Laser & Photonics Reviews 16, 2100631 (2022a).
- He et al. [2019b] X.-T. He, E.-T. Liang, J.-J. Yuan, H.-Y. Qiu, X.-D. Chen, F.-L. Zhao, and J.-W. Dong, A silicon-on-insulator slab for topological valley transport, Nature Communications 10, 872 (2019b).
- Zeng et al. [2020] Y. Zeng, U. Chattopadhyay, B. Zhu, B. Qiang, J. Li, Y. Jin, L. Li, A. G. Davies, E. H. Linfield, B. Zhang, et al., Electrically pumped topological laser with valley edge modes, Nature 578, 246 (2020).
- Zhong et al. [2020] H. Zhong, Y. Li, D. Song, Y. V. Kartashov, Y. Zhang, Y. Zhang, and Z. Chen, Topological valley hall edge state lasing, Laser & Photonics Reviews 14, 2000001 (2020).
- Ma et al. [2019] J. Ma, X. Xi, and X. Sun, Topological photonic integrated circuits based on valley kink states, Laser & Photonics Reviews 13, 1900087 (2019).
- Gu et al. [2021] L. Gu, Q. Yuan, Q. Zhao, Y. Ji, Z. Liu, L. Fang, X. Gan, and J. Zhao, A topological photonic ring-resonator for on-chip channel filters, Journal of Lightwave Technology 39, 5069 (2021).
- Barik et al. [2020] S. Barik, A. Karasahin, S. Mittal, E. Waks, and M. Hafezi, Chiral quantum optics using a topological resonator, Physical Review B 101, 205303 (2020).
- Lugiato and Lefever [1987] L. A. Lugiato and R. Lefever, Spatial dissipative structures in passive optical systems, Physical Review Letters 58, 2209 (1987).
- Chembo and Menyuk [2013] Y. K. Chembo and C. R. Menyuk, Spatiotemporal lugiato-lefever formalism for kerr-comb generation in whispering-gallery-mode resonators, Physical Review A 87, 053852 (2013).
- Gaeta et al. [2019] A. L. Gaeta, M. Lipson, and T. J. Kippenberg, Photonic-chip-based frequency combs, Nature Photonics 13, 158 (2019).
- Wang et al. [2022b] H. Wang, G. Tang, Y. He, Z. Wang, X. Li, L. Sun, Y. Zhang, L. Yuan, J. Dong, and Y. Su, Ultracompact topological photonic switch based on valley-vortex-enhanced high-efficiency phase shift, Light: Science & Applications 11, 292 (2022b).
- Wang et al. [2020] W. Wang, L. Wang, and W. Zhang, Advances in soliton microcomb generation, Advanced Photonics 2, 034001 (2020).