Topological dipole Floquet solitons

PhySH Subject Headings: Solitons; Topological insulators, Floquet insulators.

Topological insulators represent a new phase of matter characterized by qualitatively different behavior of excitations in the bulk and at the edge of these topologically nontrivial materials. The phenomenology of topological insulators, originally developed in solid state physics R1 ; R2 , was extended to diverse areas of physics, where it stimulated numerous experimental realizations, e.g. in mechanics R3 ; R4 , acoustics R5 ; R6 , in atomic R7 ; R8 , optoelectronic R9 ; R10 ; R11 , and various photonic R12 ; R13 ; R14 ; R15 ; R16 ; R17 ; R18 ; R19 systems. The significant progress made in linear topological photonics is described in reviews R20 ; R21 ; R22 , while the investigation of topological effects in nonlinear systems is still in its infancy. In such systems evolution of the topological edge states may be considerably affected by nonlinearity and a whole set of novel phenomena, ranging from topologically-protected lasing to the formation of so-called topological edge solitons, becomes possible R23 ; R24 ; R25 . Nonlinearity has been shown to impact the modulational stability of topological edge states R26 ; R27 ; R28 , the direction of topological currents R29 , the appearance of topologically nontrivial phases R30 ; R31 ; R32 , and to lead to bistability R33 . Furthermore, nonlinearity can give rise to topological closed currents in the bulk of the photonic insulator R34 ; R35 and induce a topological current at its edges R36 . Nonlinear hybridization of topological and bulk states was observed in R37 , and the valley Hall effect for vortices in nonlinear system was predicted in R38 .

Nonlinearity allows the formation of edge solitons — unique states that exhibit topological protection and simultaneously feature a rich variety of shapes and interactions. Edge solitons were predicted in photonic Floquet insulators in continuous R26 ; R34 ; R39 ; R40 and discrete R41 ; R42 ; R43 ; R44 models, and in polariton microcavities R28 ; R45 ; R46 . Their counterparts in nontopological photonic graphene were observed in R47 . Floquet Bragg solitons were reported in R48 . Topological (non-Floquet) systems also allow the formation of Dirac R49 , Bragg R50 , and valley Hall R51 edge solitons. Even though such states may in principle be encountered in many physical systems, potentially including Bose-Einstein condensates in time-modulated potentials R52 ; R53 , only fundamental edge solitons with bell-shaped amplitude profiles have been reported to date. The only exception is Floquet dark-bright states introduced in R40 , where opposite signs of the dispersion in two components dictate the dark structure of one of them — nevertheless still representing a fundamental state.

Unlike regular solitons that are rigorously defined, the corresponding concept in nonlinear Floquet insulators refers generically to the observation of localized states in nonlinear topological insulators. Here, by a Floquet soliton (FS) we denote a beam localized in the $(x,y)$-plane near the interface between topologically different materials, which bears the following two properties: it belongs to a nonlinear family bifurcating from the respective linear Floquet-Bloch edge state, and in the weakly-nonlinear limit its envelope represents a conventional soliton solution of the averaged nonlinear equation with constant coefficients. Due to the broken transversal (in the $(x,y)$-plane) and longitudinal (along the $z$-direction) translational symmetries, such states are intrinsically nonstationary, undergoing small-scale oscillations that, as our numerical simulations reported below reveal, render them effectively metastable, thus they decay during evolution albeit remarkably slowly. Thus, the envelopes of FSs analyzed here for a kagome Floquet insulator are described by soliton-bearing coupled nonlinear Schrödinger (NLS) equations with constant coefficients and they remain localized during distances that dramatically exceed longitudinal lattice helical period R26 ; R35 .

The dipole FSs introduced here are comprised of contributions from different topological gaps with envelopes of different symmetries. For the existence of such solitons, the linear edge states they bifurcate from must have equal group velocities and at the same time experience equal signs of the dispersions (understood here in terms of the Floquet-Bloch spectrum). Then the system sustains FSs where both components are bright. The dipole envelope of the weaker component in such two-dimensional (2D) states is held in shape only by the nonlinear coupling to the stronger fundamental component, as in nontopological vector dipole solitons in uniform media R54 ; R55 ; R56 ; R57 . Dipole FSs are hybrid objects that are confined to the edge due to their topological nature, while the nonlinear self-phase modulation enables their localization along the edge. This is in contrast to conventional scalar 2D dipole solitons characterized by identical localization mechanism in two transverse dimensions R58 ; R59 ; R60 ; R61 .

The propagation of light along the $z$-axis of a helical kagome array with focusing cubic nonlinearity is governed by the nonlinear Schrödinger (NLS) equation for the dimensionless field amplitude $\psi$:

Here $\mathbf{r}=\mathbf{i}x+\mathbf{j}y$ is the radius-vector in the transverse plane, $x,y$ are the normalized transverse coordinates, ${{\Delta}_{\bot}}={{\partial}^{2}}/\partial{{x}^{2}}+{{\partial}^{2}}/\partial{{y}^{2}}$; $z$ is the normalized propagation distance and the refractive index profile is described by the function $\mathcal{R}(\mathbf{r},z)=\mathcal{R}(\mathbf{r},z+T)=\mathcal{R}(\mathbf{r}+L\mathbf{j},z)$. The array is comprised of identical waveguides of width $\sigma$ placed in the nodes ${{\mathbf{r}}_{nm}}$ of the kagome grid $\mathcal{R}(\mathbf{r},z)=p\sum\nolimits_{nm}{{{e}^{-{{[\mathbf{r}-{{\mathbf{r}}_{nm}}-\mathbf{s}(z)]}^{2}}/{{\sigma}^{2}}}}}$, where $p$ is the array depth, and $\mathbf{s}(z)={{r}_{0}}(\sin(\omega z),\cos(\omega z)-1)$ describes helical trajectory of each waveguide with the Floquet period $T=2\pi/\omega$ and radius ${{r}_{0}}$ [Fig. 1(a)]. The $y$-period of such array is $L=2d$, where $d$ is the separation between waveguides. To obtain edge states, we truncate the array in the $x$-plane to form zigzag boundaries [Fig. 1(d)]. Typical parameters of such structures are $d\sim 1.9$ ($19\;\mu\text{m}$ spacing), ${{r}_{0}}\sim 0.0-1.0$ (helix radius up to $10\;\mu\text{m}$), $p\sim 12$ (refractive index $\delta n\sim 9\times{{10}^{-4}}$), $\sigma\sim 0.4$ ($4\;\mu\text{m}$ wide waveguides), $T\sim 0-10$ (helix periods up to $12\;\text{mm}$). We assume excitation at $\lambda=800\;\text{nm}$. Arrays with such parameters can be readily created by femtosecond laser inscription R17 . Notice that topological protection of linear and nonlinear scalar modes in Floquet insulators with helical channels and similar array parameters have been shown in Refs. R26 ; R40 , therefore we expect the same degree of protection also for the dipole vector states analyzed below.

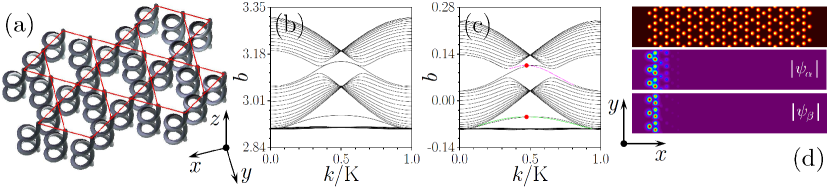
Linear eigenmodes of the helical array are Floquet-Bloch waves $\psi(\mathbf{r},z)={{\phi}_{\nu k}}(\mathbf{r},z){{e}^{i{{b}_{\nu k}}z}}$, where ${{\phi}_{\nu k}}(\mathbf{r},z)={{u}_{\nu k}}(\mathbf{r},z){{e}^{iky}}$ and the function ${{u}_{\nu k}}(\mathbf{r},z)={{u}_{\nu k}}(\mathbf{r},z+T)={{u}_{\nu k}}(\mathbf{r}+L\mathbf{j},z)$ is periodic along both $z$ and $y$ axes. Here $k$ denotes the Bloch momentum in the first Brillouin zone $k\in[-\operatorname{K}/2,+K/2)$, where $\operatorname{K}=2\pi/L$, $\nu$ is the mode index, while ${{b}_{\nu k}}\in[-\omega/2,+\omega/2)$ is a quasi-propagation-constant defined modulo $\omega$ and describing the phase ${{b}_{\nu k}}T$ accumulated by the Floquet-Bloch wave over one $z$-period. A representative spectrum of a truncated kagome array with straight waveguides (in this case, at ${{r}_{0}}=0$, $b$ is a standard propagation constant) is presented in Fig. 1(b) (for brevity, we omit subscripts in ${{b}_{\nu k}}$ in the figures). We show three upper bands, the lowest of which is nearly flat. Two pairs of degenerate edge states are clearly visible in the spectrum. For any non-zero helix radius ${{r}_{0}}\neq 0$, the system becomes topologically nontrivial as time-reversal symmetry is broken R62 ; R63 ; R64 . As a result, topological states occur on the left edge (we assign indices $\nu=\alpha,\beta$ to the “top” and “bottom” states) as marked by magenta and green lines in Fig. 1(c). Representative profiles of Floquet-Bloch waves from different gaps are shown in Fig. 1(d) (at $z=0$).

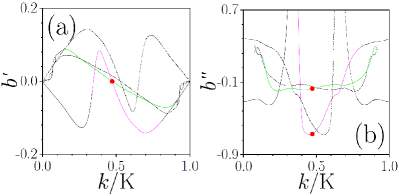
A remarkable property of the kagome topological insulator is that the derivatives ${{{b}^{\prime}}_{\nu}}=\partial{{b}_{\nu k}}/\partial k$, defining the group velocities ${{v}_{\nu}}=-{{{b}^{\prime}}_{\nu}}$ of two topological states coexisting at a given edge (see Appendix A for details) may coincide for certain values of the Bloch momentum $k$ [see, e.g. the red dots in Fig. 2(a)]. Importantly, the sign of the dispersion coefficients ${{{b}^{\prime\prime}}_{\nu}}={{\partial}^{2}}{{b}_{\nu k}}/\partial{{k}^{2}}$ for the momentum corresponding to the red dots is likewise identical [Fig. 2(b)]. Coexistence of topological edge states with coinciding group velocities ${{v}_{\alpha}}={{v}_{\beta}}$ and equal signs of the effective diffraction in the underlying linear system is necessary for the formation of multipole FSs as it allows for persistent nonlinearity- mediated coupling. For our parameters, the group velocities coincide at $k=0.472{K}$ (see Fig. 2).

To construct multipole FSs we focus on their bifurcation from the linear Floquet-Bloch states ${{\psi}_{\alpha k}}$ and ${{\psi}_{\beta k}}$. To this end we look for the solution in the form $\psi\approx{{A}_{\alpha}}(Y,z){{\phi}_{\alpha k}}{{e}^{i{{b}_{{}^{\alpha k}}}z}}+{{A}_{\beta}}(Y,z){{\phi}_{\beta k}}{{e}^{i{{b}_{\beta k}}z}}$, where ${{A}_{\alpha,\beta}}$ are the slowly-varying envelopes and $Y=y-{{v}_{\alpha,\beta}}z$ is the coordinate in the frame moving with velocity ${{v}_{\alpha,\beta}}=-{{{b}^{\prime}}_{\alpha,\beta}}$, identical for both components. We adopt a multiscale expansion that shows that the envelopes ${{A}_{\alpha,\beta}}$ are governed by the coupled focusing NLS equations (see Appendix A):

where ${{\chi}_{\nu}}={{\langle({{\left|{{\phi}_{\nu k}}\right|}^{2}},{{\left|{{\phi}_{\nu k}}\right|}^{2}})\rangle}_{T}}$ and ${{\chi}_{\operatorname{x}}}={{\langle({{\left|{{\phi}_{\alpha k}}\right|}^{2}},{{\left|{{\phi}_{\beta k}}\right|}^{2}})\rangle}_{T}}$ are the effective self- and cross-modulation coefficients, averaging over one $z$-period is defined as ${{\langle g\rangle}_{T}}={{T}^{-1}}\int_{0}^{T}{g(\mathbf{r},z)dz}$, and calculation of the inner product $(f,g)=\int_{S}{{{f}^{*}}(\mathbf{r},z)g(\mathbf{r},z)d\mathbf{r}}$ is performed over the entire transverse array area $S$. Floquet-Bloch states ${{\phi}_{\nu k}}$ are orthogonal and normalized at the same instant $z$ (see Appendix A): $({{\phi}_{\nu k}},{{\phi}_{{\nu}^{\prime}k}})={{\delta}_{\nu{\nu}^{\prime}}}$. Note that the considerable difference between quasi- propagation-constant mismatch $\delta{{b}_{k}}={{b}_{\alpha k}}-{{b}_{\beta k}}\approx 0.15$ and frequency of periodic modulation $(\omega\approx 0.78)$ ensures that coupling between the modes is entirely non-resonant and therefore exclusively mediated by nonlinearity. Efficient nonlinear coupling between waves with different momenta $k$ can only occur for a special ratio of propagation constants of the involved topological states, which is not met in our system.

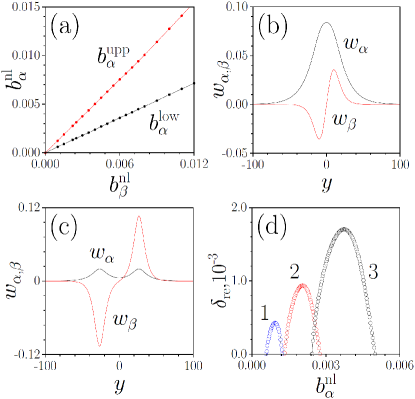
We are interested in bright dipole soliton solutions of Eqs. (2) that exist at ${{b}^{\prime\prime}_{\alpha}},{{b}^{\prime\prime}_{\beta}}<0$ [see Fig. 2(b)]. In such states the bell-shaped $\alpha$ component prevents (by creating an effective potential well via cross-phase modulation) out-of-phase poles of the dipole $\beta$ component from splitting, leading to the formation of stationary states. They can be found by the Newton method in the form ${{A}_{\alpha,\beta}}={{w}_{\alpha,\beta}}{{e}^{ib_{\alpha,\beta}^{\operatorname{nl}}z}}$, where the nonlinearity-induced phase shifts $b_{\alpha,\beta}^{\operatorname{nl}}$ should be sufficiently small (much smaller than the quasi-propagation constants, the topological-gap width, and longitudinal Brillouin zone $\omega$) to ensure that the profiles ${{w}_{\alpha,\beta}}$ are broad and satisfy the assumption of slow variation of the soliton profile. The properties of dipole solitons for nonlinear and dispersion coefficients corresponding to the edge states at $k=0.472\operatorname{K}$ are described in Fig. 3. For a fixed $b_{\beta}^{\operatorname{nl}}$ dipole solitons exist for $b_{\alpha}^{\operatorname{low}}\leq b_{\alpha}^{\operatorname{nl}}\leq b_{\alpha}^{\operatorname{upp}}$. The existence domain expands with $b_{\beta}^{\operatorname{nl}}$ [Fig. 3(a)]. Close to its lower border $b_{\alpha}^{\operatorname{low}}$ the dipole $\beta$ component vanishes and only fundamental $\alpha$ component remains, while at the upper border $b_{\alpha}^{\operatorname{upp}}$ the soliton splits into two states gradually separating as the amplitude of the $\alpha$ component vanishes. Representative profiles are shown in Fig. 3(b) and 3(c). By substituting the perturbed envelope solitons ${{A}_{\nu}}=({{w}_{\nu}}+{{\mu}_{\nu}}{{e}^{\delta z}}+\eta_{\nu}^{*}{{e}^{{{\delta}^{*}}z}}){{e}^{ib_{\nu}^{\operatorname{nl}}z}}$, where ${{\mu}_{\nu}},{{\eta}_{\nu}}\ll{{w}_{\nu}}$, into Eq. (2) one arrives at a linear eigenvalue problem (see Appendix B), whose solution yields the growth rate ${{\delta}_{\operatorname{re}}}=\operatorname{Re}\delta$ for the most unstable perturbation depicted in Fig. 3(d) as a function of $b_{\alpha}^{\operatorname{nl}}$. The growth rate ${{\delta}_{\operatorname{re}}}$ vanishes when $b_{\alpha}^{\operatorname{nl}}\to b_{\alpha}^{\operatorname{low}},b_{\alpha}^{\operatorname{upp}}$ and for the broad states considered here it remains well below ${{10}^{-3}}$ implying that the characteristic scale $1/{{\delta}_{\operatorname{re}}}$ of the instability development exceeds hundreds of helix periods $T$.

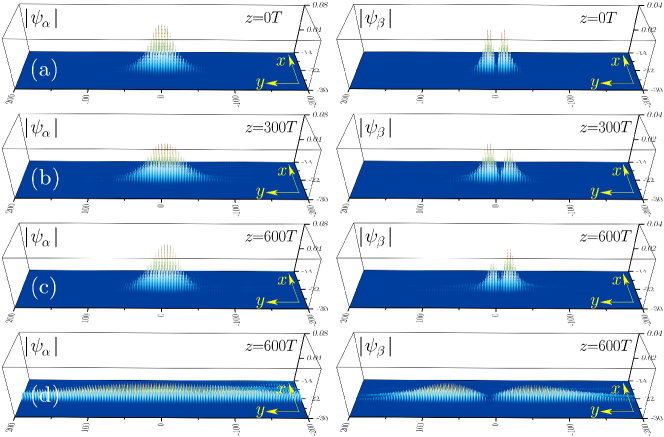
To confirm the accuracy of the model (2) and to confirm that topological dipole solitons are observable experimentally, we propagated Floquet-Bloch modes with exact dipole soliton envelopes, obtained from Eq. (2) for various $b_{\alpha,\beta}^{\operatorname{nl}}$ values, in the helical kagome array. Such evolution is governed by the full 2D model (1), which we solved with a split-step FFT method. The input for Eq. (1) was constructed as $\psi={{w}_{\alpha}}(Y){{\phi}_{\alpha k}}+{{w}_{\beta}}(Y){{\phi}_{\beta k}}$. In the right column of Fig. 4(a)-(c) we show (with dots) the modulus of the projections of the field $\psi$ on the linear Floquet-Bloch modes: ${{c}_{\nu}}=\int_{mL-d}^{mL+d}{\phi_{\nu k}^{*}(\mathbf{r},z)\psi(\mathbf{r},z)d\mathbf{r}}$ ($m\in\mathbb{Z}$ defines the $y$-period on which projection is calculated), and the input envelopes ${{w}_{\alpha,\beta}}$ (solid lines). The projections ${{c}_{\nu}}$ explicitly show that dipole soliton at all distances shown contains contributions from two Floquet-Bloch states, whose amplitudes remain practically unchanged and whose envelopes remain mutually localized.

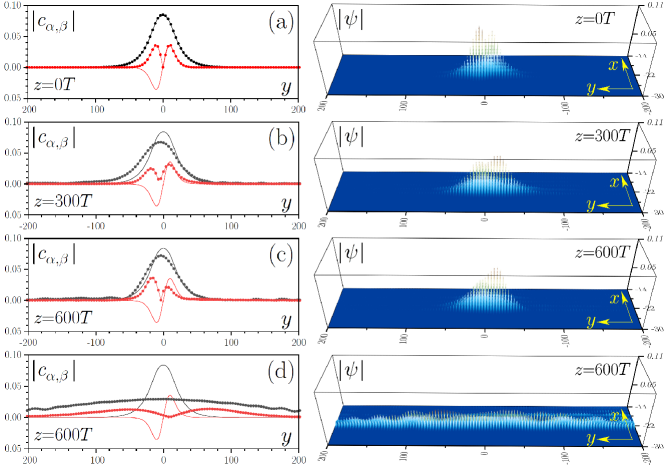
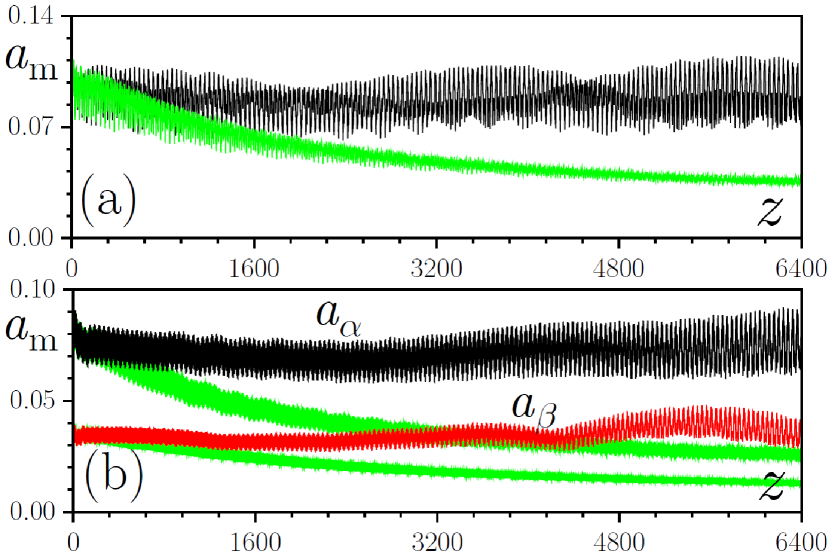
Propagation governed by (1) confirms the metastability of the dipole solitons, which survive over hundreds of helix periods even when small-scale noise (up to 5% in amplitude) is added into the input field distributions. The rotation of the waveguides induces fast $z$-oscillations of the soliton peak amplitude (a signature of its Floquet nature) and causes very weak radiation, which nevertheless does not destroy the dipole solitons at the considered distances. The weak radiation becomes noticeable only at propagation distances exceeding the ones shown here at least by one order of magnitude. Metastability [associated with very small, but nonzero growth rates ${{\delta}_{\operatorname{re}}}$ for perturbations of the envelope in Eq. (2)] results also in an extremely-slowly growth of the oscillations of the two poles (peaks) of the dipole component (small input noise only slightly affects phase of these oscillations), which nevertheless do not cause splitting of the dipole state at least up to $z<{{10}^{3}}T$. Splitting may occur, but at larger distances. The right column of Fig. 4(a)-(c) illustrates the corresponding evolution of the total field $\psi$. Since the group velocities of the two components are close to zero, the soliton remains virtually locked in place for the parameters chosen above, although for other helix parameters we obtained slowly moving states. If nonlinearity is switched off, wavepackets experience strong diffraction along the array edge at similar propagation distances [Fig. 4(d)], an observation that further confirms that the state from Fig. 4(a)-(c) is sustained by nonlinearity.

When the combination of two modes ${{\psi}_{\alpha}}$ and ${{\psi}_{\beta}}$ with different propagation constants (i.e., a total field of the form $\psi\sim{{\psi}_{\alpha}}+{{\psi}_{\beta}}$) is substituted into (1), one can formally reduce it to two purely nonlinearly coupled 2D NLS equations by collecting terms $\sim{{e}^{i{{b}_{\alpha k}}z}},{{e}^{i{{b}_{\beta k}}z}}$ and dropping the oscillating terms $\sim{{e}^{i({{b}_{\alpha k}}-{{b}_{\beta k}})z}}$ (thus, accounting only for self- and cross-phase modulation interactions and skipping four-wave mixing terms), without averaging over helix period $T$:

The advantage of such a reduction is that (3) allows to follow the evolution of each component. This reduction is partially justified due to rapid variation of phase difference $({{b}_{\alpha k}}-{{b}_{\beta k}})z$ between modes, but it has to be tested numerically because the scale ${{({{b}_{\alpha k}}-{{b}_{\beta k}})}^{-1}}>T$ is not the smallest one in the Floquet system. The model (3) can be also directly derived for two waves with different polarizations/wavelengths. The propagation of the dipole FS in the vector model (3) with a helical kagome array is illustrated in Fig. 5(a)-(c). Indeed, it shows metastable propagation of the dipole soliton, qualitatively similar to the dynamics encountered in the scalar model (Fig. 4). Also, the aforementioned oscillations of the dipole component at the equivalent distances closely match the oscillations of the corresponding projections in Fig. 4 (notice the different direction of the $y$-axis in panels with projections). As in the scalar model, switching-off nonlinearity causes strong diffraction (see Appendix C for the evolution of the peak amplitudes in the linear and nonlinear cases). The remarkable similarity between the dynamics in the scalar model (1) and in the vector model (3) shows that the periodic modulation of the array does not introduce any linear coupling of the involved modes.

In conclusion, we uncovered a new type of topological dipole FS, which is constructed using envelopes featuring the different symmetries imposed on two edge states from different topological gaps exhibiting equal group velocities. The solitonic nature of the wavepackets is consistent with their bifurcation from the linear Floquet-Bloch eigenstates at small amplitudes and by the preservation of their shape over extremely long propagation distances. Our prediction has broad implications, as dipole solitons can be observed for other types of Floquet insulators featuring at least two topological gaps, such as, e.g., Floquet Lieb insulators. It is plausible that more complex multicomponent solitons of non- fundamental nature may be also found. Finally, we anticipate that the reported results may be relevant for polaritonic and atomic nonlinear systems, where topological edge solitons can be sustained by different physical mechanisms.