Time-Resolved Focused Ion Beam Microscopy: Modeling, Estimation Methods, and Analyses

• •

  A new continuous-time probabilistic model for FIB microscopy wherein the data at any one pixel are related to a marked Poisson process. Conventional and continuous- and discrete-time time-resolved observation models are different functions of the marked Poisson process.

• •

  Fisher information analyses. We show that, at any ion dose level, continuous-time time-resolved measurements have Fisher information matching an upper bound that conventional measurements meet only in a low-dose limit. For conventional measurements, asymptotic expressions presented without proof in [19] are proven here.

• •

  Estimator analyses. Biases and variances of quotient-mode estimators in both the continuous- and discrete-time settings are derived. Convergence of the discrete-time estimator’s performance to the performance of the continuous-time estimator is proven.

We introduce our mathematical abstraction for the operation of a FIB microscope in Section II. This leads to four measurement models: an unimplementable oracle model, conventional measurement, and continuous- and discrete-time time-resolved measurement. The oracle and conventional cases are analyzed within Section II. Section III develops the novel continuous-time case in detail. Measurement distributions are derived, three estimators are introduced and simulated, and the performance of a quotient-mode estimator is rigorously analyzed. Section IV develops the discrete-time case first introduced in [19] in detail. Three estimators are simulated, and the performance of the discrete-time quotient-mode estimator is rigorously analyzed. Convergences of Fisher information and quotient-mode estimator performance to their continuous-time counterparts are shown. Section V compares all the estimators in a simulated HIM experiment, demonstrating substantial improvement of the time-resolved methods over the conventional interpretation of the collected data. Section VI provides concluding comments on how mean SE yield influences the advantages of TR methods, the time resolution necessary to capitalize on these advantages, the roles of the various estimators, and generalizations to indirect SE detection.

Table I summarizes the variables, symbols, and acronyms used in the manuscript.

Throughout this paper, we model the incident ions at the sample to be imaged as a Poisson process with known rate $\Lambda$ per unit time. Imaging proceeds by raster scanning with known dwell time $t$ at each pixel. Hence, the number of ions $M$ incident on a pixel is a Poisson random variable with known parameter $\lambda=\Lambda t$. Since pixel area is not relevant in our abstraction, we refer to $\lambda$ as the dose. The interaction of the $i$th incident ion with the sample causes a number $X_{i}$ of SEs to be detected. All of these SE counts are mutually independent Poisson random variables with parameter $\eta$, independent of the incident-ion Poisson process, and estimation of the mean SE yield $\eta$ is the objective of the imaging experiment. Our analysis is for each pixel separately, so no pixel indexing is necessary.

Note that a somewhat high 1 pA beam current corresponds to a rate of $6.2\times 10^{6}$ ions per second, or a mean ion interarrival time of 160 ns. The interaction between an incident ion and the sample and the subsequent detection of SEs occurs within a few femtoseconds [23]. With the SE detections happening so quickly, we abstract the SE detections caused by an incident ion to be simultaneous with the ion incidence. Thus, the model can be described as a marked Poisson process $\{(T_{1},X_{1}),\,(T_{2},X_{2}),\,\ldots\}$, where $(T_{1},\,T_{2},\,\ldots)$ is the arrival time sequence of the ions. The ion count $M$ is the largest $i$ such that $T_{i}\leq t$ (with $M=0$ when $T_{1}>t$). One realization on an interval $[0,t]$ is illustrated in Fig. 1(a). Note that the arrival times (horizontal) are arbitrary positive real numbers and the marks (vertical) are nonnegative integers.

Since cases of $X_{i}=0$ produce no detected SEs, the corresponding ion arrival time is not observable in practice. Thus consider also the thinned process $\{(\widetilde{T}_{1},\widetilde{X}_{1}),\,(\widetilde{T}_{2},\widetilde{X}_{2}),\,\ldots\}$, where $\widetilde{T}_{i}$ is the arrival time of the $i$th ion that produces a positive number of detected SEs and $\widetilde{X}_{i}$ is the corresponding number of detected SEs. Define $\widetilde{M}$ to be the largest $i$ such that $\widetilde{T}_{i}\leq t$ (with $\widetilde{M}=0$ when $\widetilde{T}_{1}>t$). Note that the thinned process is also a marked Poisson process because the events of the form $\{X_{i}=0\}$, which determine whether an arrival in the original Poisson process is retained, are independent of the arrival time process. Fig. 1(b) illustrates the thinned process for the realization of the underlying process in Fig. 1(a).

Now suppose the observation time interval $[0,t]$ is evenly divided into $n$ subintervals of length $t/n$. Counting the total number of SEs detected in each subinterval produces a discrete-time, discrete-valued random process:

$$Y_{k}=\sum_{\{i\ :\ T_{i}\in[(k-1)t/n,\,kt/n)\}}X_{i},\qquad k=1,\,2,\,\ldots,\,n.$$

(1)

We call an observation over a subinterval a subacquisition. Fig. 1(c) illustrates the partition of $[0,t]$ into subintervals and Fig. 1(d) illustrates the resulting discrete-time process for the realization of the underlying process in Fig. 1(a). Because of the independence of a Poisson process over disjoint intervals, $\{Y_{k}\}_{k=1}^{n}$ is an independent and identically distributed (i.i.d.) process. We can also view $\{Y_{k}\}_{k=1}^{n}$ as a marked Bernoulli process, where $\{Y_{k}>0\}$ indicates an arrival in discrete time slot $k$ and the “mark” is then the (nonzero) value $Y_{k}$.

The abstraction described here applies similarly to SEM and FIB microscopy. The main difference is the typical values of the mean SE yield $\eta$. In SEM, neglecting topographical effects (which tend to increase yield), for a sample with atomic number up to 83, the SE yield at the maximizing electron energy is typically 0.6 to 2 [24]. In FIB microscopy, SE yield is typically between 1 and 8 [25]. The advantages of TR measurements that are established in this paper diminish at smaller $\eta$ values. Furthermore, in FIB microscopy, sample damage is more of an impediment to improving image quality by increasing dose [12, 13, 14]. Thus, we concentrate on FIB microscopy.

We consider four measurement models for the probabilistic experiment described in Section II-A:

• •

  Oracle: Observe

  $$\{M,\,(T_{1},X_{1}),\,(T_{2},X_{2}),\,\ldots,\,(T_{M},X_{M})\}.$$

  (2)

  Though no current instrument provides this information, this measurement model provides a useful benchmark.

• •

  Conventional: Observe only

  $$Y=\sum_{i=i}^{M}X_{i}.$$

  (3)

  This would be the standard operation of a FIB microscope that has direct detection of SEs. Note that

  $$Y=\sum_{i=1}^{\widetilde{M}}\widetilde{X}_{i}$$

  (4)

  and

  $$Y=\sum_{k=1}^{n}Y_{k}$$

  (5)

  are equivalent to the definition of $Y$. As the sum of a $\operatorname{Poisson}(\lambda)$ number of mutually independent $\operatorname{Poisson}(\eta)$ random variables, (3) is the simplest of the expressions.

• •

  Continuous-time time-resolved (CTTR): Observe

  $$\{\widetilde{M},\,(\widetilde{T}_{1},\widetilde{X}_{1}),\,(\widetilde{T}_{2},\widetilde{X}_{2}),\,\ldots\,\,(\widetilde{T}_{\widetilde{M}},\widetilde{X}_{\widetilde{M}})\}.$$

  (6)

  This is an idealization of a FIB microscope with direct detection of SEs with perfect temporal precision.

• •

  Discrete-time time-resolved (DTTR): Observe

  $$\{Y_{1},\,Y_{2},\,\ldots,\,Y_{n}\}.$$

  (7)

  This is a model for the use of a FIB microscope to collect a set of low-dose subacquisitions.

Having established these abstractions, we can reiterate that our principal goal is to demonstrate substantial improvements from time-resolved measurements. In our previous work [19], we introduced the concept of DTTR measurement along with estimators to apply with these measurements, and we showed empirical improvements over the trivial estimator that is routinely applied with conventional measurements. The analysis of estimators in that work is limited, and certain theoretical assertions are made without proofs. The CTTR model introduced here is easier to analyze and represents a bound for what can be done with DTTR measurements. We also provide new analyses of estimators for the DTTR model. Through these results and Monte Carlo simulations, the convergence of DTTR estimators to CTTR estimators as $n\rightarrow\infty$ can be understood precisely (see Sections IV-B and IV-D).

We initially assume $M=m>0$. Then the oracle measurement (2) includes nonempty sets of ion arrival times $\{T_{1},\,T_{2},\,\ldots,\,T_{m}\}$ and of SE counts $\{X_{1},\,X_{2},\,\ldots,\,X_{m}\}$. The arrival times have beta distributions, with no dependence on parameter of interest $\eta$. Thus, arrival times are immaterial to estimation of $\eta$ (i.e., redundant with knowing $M$). The SE counts are i.i.d. observations with the $\operatorname{Poisson}(\eta)$ distribution, and it is elementary to show that $Y=X_{1}+X_{2}+\cdots+X_{m}$ is a sufficient statistic and that $Y/m$ is an efficient estimator of $\eta$ from the available data. In the case of $M=0$, there is no basis for any estimate of $\eta$, so we must assign some arbitrarily chosen number $\eta_{0}$.

From the arguments above, we define the oracle estimator

$$\widehat{\eta}_{\rm oracle}(M,X_{1},X_{2},\ldots,X_{M})=\left\{\begin{array}[]{@{\,}rl}\eta_{0},&M=0;\\ {{Y}/{M}},&M>0.\end{array}\right.$$

(8)

Conditioned on $M=m>0$, the mean-squared error (MSE) of this estimator is $\eta/m$ because $Y$ has mean $m\eta$ and variance $m\eta$. Using the Poisson distribution for $M$ and the total expectation theorem,

$$\mathrm{MSE}(\widehat{\eta}_{\rm oracle})=e^{-\lambda}(\eta-\eta_{0})^{2}+\sum_{m=1}^{\infty}\frac{\eta}{m}\frac{\lambda^{m}}{m!}e^{-\lambda}.$$

(9)

For large enough $\lambda$, the arbitrary guess of $\eta_{0}$ when $M=0$ has little impact on the MSE. Approximating the second term using (60) from Appendix A gives

$$\mathrm{MSE}(\widehat{\eta}_{\rm oracle})\approx\frac{\eta}{\lambda}\qquad\mbox{for large $\lambda$}.$$

(10)

It is straightforward to show that the conventional measurement $Y$ has Neyman Type A probability mass function (PMF)

$$\mathrm{P}_{Y}(y\,;\,\eta,\lambda)=\frac{e^{-\lambda}\eta^{y}}{y!}\sum_{m=0}^{\infty}\frac{(\lambda e^{-\eta})^{m}m^{y}}{m!},\quad y=0,\,1,\,\ldots,$$

(11)

mean

$$\mathrm{E}\!\left[\,{Y}\,\right]=\lambda\eta,$$

(12)

and variance

$$\mathrm{var}\!\left({Y}\right)=\lambda\eta+\lambda\eta^{2}.$$

(13)

Starting from (3), (11) follows from the law of total probability, (12) from iterated expectation with conditioning on $M$, and (13) from the law of total variance with conditioning on $M$ [19]. Reaching the same conclusions starting from (4) or (5) involves more complicated computations.

From (12), the baseline estimator

$$\widehat{\eta}_{\rm baseline}(Y)=\frac{Y}{\lambda}$$

(14)

is unbiased, and from (13) its MSE is

$$\mathrm{MSE}(\widehat{\eta}_{\rm baseline})=\frac{\eta(1+\eta)}{\lambda}.$$

(15)

If $\lambda$ ions were deterministically incident upon the sample, $Y$ would be a $\operatorname{Poisson}(\lambda\eta)$ random variable, with variance $\lambda\eta$, and the MSE of the baseline estimator would be $\eta/\lambda$. The excess variance in (13), consistent with experimental observations [26], and excess MSE in (15) are due to the random variation in the number of incident ions or the source shot noise. Our line of work mitigates this noise.

Since estimation under a Neyman Type A observation model is not well known, the potential efficiency of the baseline estimator is not evident. To this end, it is natural to evaluate the Fisher information (FI) about $\eta$ in $Y$ with $\lambda$ as a known parameter, which we denote by $\mathcal{I}_{Y}(\eta\,;\,\lambda)$.

The FI is defined as

$$\mathcal{I}_{Y}(\eta\,;\,\lambda)=\mathrm{E}\!\left[\,{\left(\frac{\partial\log\mathrm{P}_{Y}(y\,;\,\eta,\lambda)}{\partial\eta}\right)^{2}\,;\,\eta}\,\right],$$

(16)

where a known non-random parameter in the expectation is emphasized by putting it after a semicolon. From (11),

	$\displaystyle\log$	$\displaystyle\mathrm{P}_{Y}(y\,;\,\eta,\lambda)$
		$\displaystyle=-\lambda+y\log\eta-\log y!+\log\Bigg{(}\sum_{m=0}^{\infty}\frac{(\lambda e^{-\eta})^{m}m^{y}}{m!}\Bigg{)}.$

Then taking the derivative with respect to $\eta$, we find that

	$\displaystyle\frac{\partial\log\mathrm{P}_{Y}(y\,;\,\eta,\lambda)}{\partial\eta}$	$\displaystyle\!=\!$	$\displaystyle\frac{y}{\eta}-\frac{\sum_{m=0}^{\infty}\dfrac{m(\lambda e^{-\eta})^{m}m^{y}}{m!}}{\sum_{m=0}^{\infty}\dfrac{(\lambda e^{-\eta})^{m}m^{y}}{m!}}$
		$\displaystyle\!\stackrel{{\scriptstyle(a)}}{{=}}\!$	$\displaystyle\frac{y}{\eta}-\frac{{\mathrm{P}_{Y}(y+1\,;\,\eta,\lambda)}\bigg{/}{\dfrac{e^{-\lambda}\eta^{y+1}}{(y+1)!}}}{{\mathrm{P}_{Y}(y\,;\,\eta,\lambda)}\bigg{/}{\dfrac{e^{-\lambda}\eta^{y}}{y!}}}$
		$\displaystyle\!=\!$	$\displaystyle\frac{y}{\eta}-\frac{\mathrm{P}_{Y}(y+1\,;\,\eta,\lambda)}{\mathrm{P}_{Y}(y\,;\,\eta,\lambda)}\frac{y+1}{\eta},$

where (a) follows from (11). The FI is the second moment of the above expression:

$$\mathcal{I}_{Y}(\eta\,;\,\lambda)=\sum_{y=0}^{\infty}\left(\frac{y}{\eta}{-}\frac{\mathrm{P}_{Y}(y+1\,;\,\eta,\lambda)}{\mathrm{P}_{Y}(y\,;\,\eta,\lambda)}\frac{y+1}{\eta}\right)^{\!2}\mathrm{P}_{Y}(y\,;\,\eta,\lambda).$$

(17)

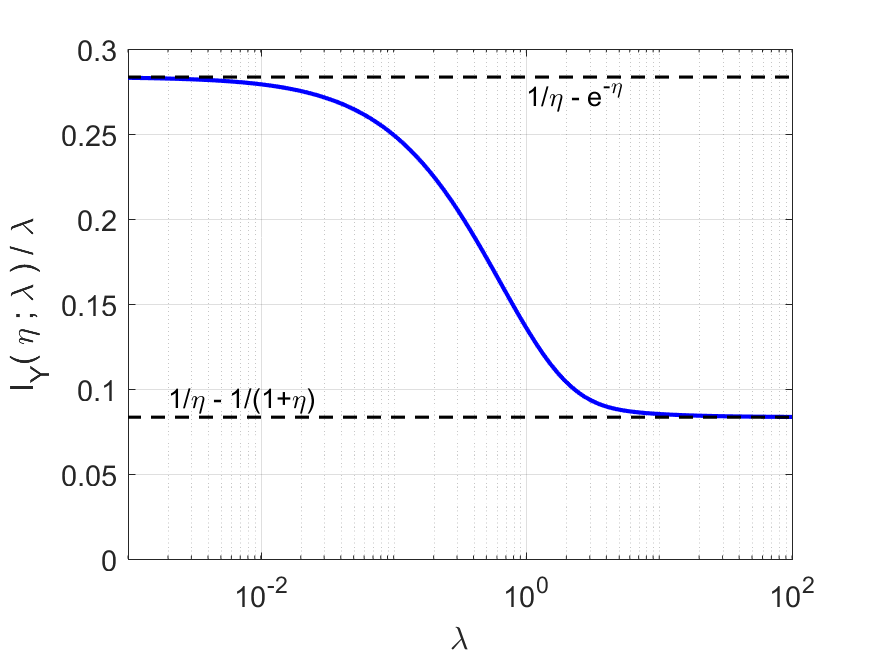
While (17) is not readily comprehensible, it can be used to numerically evaluate $\mathcal{I}_{Y}(\eta\,;\,\lambda)$ and to derive certain useful asymptotic approximations and limits. One can interpret the ratio $\mathcal{I}_{Y}(\eta\,;\,\lambda)/\lambda$ as the information gain per incident ion. As illustrated in Fig. 2, this normalized Fisher information is a decreasing function of $\lambda$, with

$$\lim_{\lambda\rightarrow 0}\frac{\mathcal{I}_{Y}(\eta\,;\,\lambda)}{\lambda}=\frac{1}{\eta}-e^{-\eta}$$

(18)

and

$$\lim_{\lambda\rightarrow\infty}\frac{\mathcal{I}_{Y}(\eta\,;\,\lambda)}{\lambda}=\frac{1}{\eta(1+\eta)}=\frac{1}{\eta}-\frac{1}{1+\eta}.$$

(19)

Detailed derivations are provided in Appendix B.

Using (19) to write

$$\mathcal{I}_{Y}(\eta\,;\,\lambda)\approx\frac{\lambda}{\eta(1+\eta)}\qquad\mbox{for large $\lambda$},$$

(20)

we have a match to the reciprocal of the MSE in (15). Thus, the baseline estimator achieves the Cramér–Rao bound (CRB) asympotically as $\lambda\rightarrow\infty$, but not otherwise (since the normalized FI is a decreasing function of $\lambda$).

One could seek improved estimators for low $\lambda$ or improved lower bounds to demonstrate that substantially better estimators do not exist. We do not pursue those goals here. In practice, improved estimators for low $\lambda$ may be of limited interest—even if they improve significantly upon the baseline estimator. For example, with reference to Fig. 2, FI suggests that one may be able to improve upon the baseline estimator by a factor of 3 at dose $\lambda=10^{-2}$. However, even the lowest possible MSE would be quite high at such a low dose.

The key observation from Fig. 2 and the limits in (18) and (19) is that low-dose measurements are more informative per incident ion than high-dose measurements. The remainder of the paper studies methods to realize improvements related to this gap while operating at any dose level—not only low dose. Furthermore, notice that the MSE in (15) has a simple inversely proportional relationship with $\lambda$. Most performance bounds and empirical performances in this paper share this simple $1/\lambda$ behavior, so we place little emphasis on the performance as $\lambda$ is varied. Instead, we concentrate on comparisons among different methods and the performance dependence on $\eta$.

The CTTR measurement (6) contains the number of incident ions that result in positive detected SEs $\widetilde{M}$, the arrival times of these ions $\{\widetilde{T}_{1},\,\widetilde{T}_{2},\,\ldots,\,\widetilde{T}_{\widetilde{M}}\}$, and the corresponding SE counts $\{\widetilde{X}_{1},\,\widetilde{X}_{2},\,\ldots,\,\widetilde{X}_{\widetilde{M}}\}$. As noted in Section II-A, the mutual independence of the arrival times in the underlying process $\{T_{1},\,T_{2},\,\ldots\}$ and all events of the form $\{X_{i}=0\}$ cause the Poisson process property to be preserved.

Since $\mathrm{P}({X_{i}=0})=e^{-\eta}$, the rate $\Lambda$ of the underlying process is reduced to $\Lambda(1-e^{-\eta})$ for the thinned process. For the thinned ion count over dwell time $t$, we have $\widetilde{M}\sim\operatorname{Poisson}(\lambda(1-e^{-\eta}))$, or more explicitly the PMF

$$\mathrm{P}_{\widetilde{M}}(\widetilde{m}\,;\,\eta,\lambda)=\exp(-\lambda(1-e^{-\eta}))\frac{(\lambda(1-e^{-\eta}))^{\widetilde{m}}}{{\widetilde{m}}!},$$

(21)

for $\widetilde{m}=0,\,1,\,\ldots$.

The distribution of the $\widetilde{X}_{i}$ variables is simply the zero-truncation of the $\operatorname{Poisson}(\eta)$ distribution:

$$\mathrm{P}_{\widetilde{X}_{i}}(j\,;\,\eta)=\frac{e^{-\eta}}{1-e^{-\eta}}\cdot\frac{\eta^{j}}{j!},\qquad j=1,\,2,\,\ldots.$$

(22)

While the interarrival times of the thinned process have a simple exponential distribution, this is not relevant to our estimation tasks: Under the CTTR measurement model, we have $\widetilde{M}$ available, and conditioned on $\widetilde{M}$, the thinned arrival times have beta distributions with no dependence on the parameter of interest $\eta$.

We would like to evaluate the FI about $\eta$ in the CTTR measurement (6) with $\lambda$ as a known parameter:

	$\displaystyle\mathcal{I}_{\rm CTTR}(\eta\,;\,\lambda)$	$\displaystyle\stackrel{{\scriptstyle(a)}}{{=}}\mathcal{I}_{(\widetilde{T}_{1},\widetilde{X}_{1}),\ldots,(\widetilde{T}_{\widetilde{M}},\widetilde{X}_{\widetilde{M}})|\widetilde{M}}(\eta\,;\,\lambda)+\mathcal{I}_{\widetilde{M}}(\eta\,;\,\lambda)$
		$\displaystyle\stackrel{{\scriptstyle(b)}}{{=}}\mathcal{I}_{\widetilde{X}_{1},\ldots,\widetilde{X}_{\widetilde{M}}|\widetilde{M}}(\eta\,;\,\lambda)+\mathcal{I}_{\widetilde{M}}(\eta\,;\,\lambda)$
		$\displaystyle\stackrel{{\scriptstyle(c)}}{{=}}\mathrm{E}\!\left[\,{\widetilde{M}}\,\right]\mathcal{I}_{\widetilde{X}_{i}}(\eta\,;\,\lambda)+\mathcal{I}_{\widetilde{M}}(\eta\,;\,\lambda)$
		$\displaystyle\stackrel{{\scriptstyle(d)}}{{=}}\lambda(1-e^{-\eta})\mathcal{I}_{\widetilde{X}_{i}}(\eta\,;\,\lambda)+\mathcal{I}_{\widetilde{M}}(\eta\,;\,\lambda),$		(23)

where (a) follows from the chain rule for FI [27]; (b) from the conditional distribution of each $\widetilde{T}_{i}$ given $\widetilde{M}$ having no dependence on $\eta$; (c) from additivity of FI and the independence of $\{\widetilde{M},\,\widetilde{X}_{1},\,\widetilde{X}_{2},\,\ldots,\,\widetilde{X}_{\widetilde{M}}\}$; and (d) from substitution of the mean of $\widetilde{M}$. Thus, we need to evaluate $\mathcal{I}_{\widetilde{X}_{i}}(\eta\,;\,\lambda)$ and $\mathcal{I}_{\widetilde{M}}(\eta\,;\,\lambda)$. The former, which represents the FI for estimating $\eta$ from $\widetilde{X}_{i}$ is

	$\displaystyle\mathcal{I}_{\widetilde{X}_{i}}(\eta\,;\,\lambda)$	$\displaystyle=\mathrm{E}\!\left[\,{\left(\frac{\partial\log\mathrm{P}_{\widetilde{X}_{i}}(\widetilde{X}_{i}\,;\,\eta,\lambda)}{\partial\eta}\right)^{\!2}\,;\,\eta}\,\right]$
		$\displaystyle\stackrel{{\scriptstyle(a)}}{{=}}\sum_{j=1}^{\infty}\left(\frac{j}{\eta}-\frac{1}{1-e^{-\eta}}\right)^{\!2}\frac{e^{-\eta}}{1-e^{-\eta}}\frac{\eta^{j}}{j!}$
		$\displaystyle=\frac{1}{1-e^{-\eta}}\frac{\eta+1}{\eta}-\frac{1}{(1-e^{-\eta})^{2}},$		(24)

where (a) uses the PMF in (22). Similarly, $\mathcal{I}_{\widetilde{M}}(\eta\,;\,\lambda)$, which represents the FI for estimating $\eta$ from $\widetilde{M}$, is

	$\displaystyle\mathcal{I}_{\widetilde{M}}(\eta\,;\,\lambda)=\mathrm{E}\!\left[\,{\left(\frac{\partial\log P_{\widetilde{M}}(\widetilde{M}\,;\,\eta,\lambda)}{\partial\eta}\right)^{\!2}\,;\,\eta}\,\right]$
	$\displaystyle\stackrel{{\scriptstyle(a)}}{{=}}\sum_{j=0}^{\infty}\left(\frac{e^{-\eta}}{1-e^{-\eta}}j-\lambda e^{-\eta}\right)^{\!2}\frac{e^{-\lambda(1-e^{-\eta})}[\lambda(1-e^{-\eta})]^{j}}{j!}$
	$\displaystyle=\frac{\lambda e^{-\eta}}{e^{\eta}-1},$		(25)

where (a) uses the PMF in (21). Finally, substituting (24) and (25) into (III-B) gives

$\displaystyle\mathcal{I}_{\rm CTTR}(\eta\,;\,\lambda)$

$\displaystyle=\lambda\left(\frac{1}{\eta}-{e^{-\eta}}\right).$

(26)

Notice that the FI for CTTR measurement matches the low-dose asymptote given in (18). It is exact and holds for all values of $\lambda$. The greater FI for CTTR measurement than for conventional measurement is suggestive of being able to improve upon the baseline estimator (14). In the following sections, we define new estimators and demonstrate their improvements.

In this section, we introduce estimators applicable to CTTR measurement (6). From (4), it is clear that the total number of detected SEs $Y$ is available. As we have explained in the derivation of $\mathcal{I}_{\rm CTTR}(\eta\,;\,\lambda)$ in Section III-B, with $\widetilde{M}$ available, there is no additional information about $\eta$ in the thinned ion incidence times $\{\widetilde{T}_{1},\,\widetilde{T}_{2},\,\ldots,\,\widetilde{T}_{\widetilde{M}}\}$. Furthermore, with $Y$ and $\widetilde{M}$ available, there is no additional information about $\eta$ in the positive SE counts $\{\widetilde{X}_{1},\,\widetilde{X}_{2},\,\ldots,\,\widetilde{X}_{\widetilde{M}}\}$. To see this, consider any observation vector $(\widetilde{X}_{1},\,\widetilde{X}_{2},\,\ldots,\,\widetilde{X}_{\widetilde{M}})=(j_{1},\,j_{2},\,\ldots,\,j_{m})$ conditioned on $\widetilde{M}=\widetilde{m}$. Using independence and (22), the likelihood of the observation (conditioned on $\widetilde{M}=\widetilde{m}$) is

$$\prod_{i=1}^{\widetilde{m}}\mathrm{P}_{\widetilde{X}_{i}}(j_{i}\,;\,\eta)=\left(\frac{e^{-\eta}}{1-e^{-\eta}}\right)^{\!\widetilde{m}}\frac{\eta^{j_{1}+j_{2}+\cdots+j_{\widetilde{m}}}}{j_{1}!\,j_{2}!\,\cdots\,j_{\widetilde{m}}!}.$$

(27)

As a function of $\eta$, the dependence on SE counts is only through their sum. Hence, all the estimators in the section depend only on $Y$ and $\widetilde{M}$.

By computing the MSE of $\widehat{\eta}_{\rm CTQM}$, we can evaluate the efficacy of the quotient mode estimator. We begin by noting that

$\displaystyle\mathrm{MSE}(\widehat{\eta}_{\rm CTQM})=\operatorname{bias}(\widehat{\eta}_{\rm CTQM})^{2}+\mathrm{var}\!\left({\widehat{\eta}_{\rm CTQM}}\right).$

(31)

As detailed in Appendix C, the bias is given by

	$\displaystyle\operatorname{bias}(\widehat{\eta}_{\rm CTQM})$	$\displaystyle=\mathrm{E}\!\left[\,{\widehat{\eta}_{\rm CTQM}}\,\right]-\eta$
		$\displaystyle=\left(\frac{e^{-\eta}-e^{-\lambda(1-e^{-\eta})}}{1-e^{-\eta}}\right)\eta.$		(32)

For fixed $\eta$, this is a nonzero bias even as dose $\lambda\rightarrow\infty$, consistent with the motivation for defining the CTLQM estimator to improve upon the CTQM estimator. If $\eta\rightarrow\infty$ as well, the bias vanishes, which is consistent with the convergence in distribution of $\widetilde{M}$ to $M$.

As also detailed in Appendix C, the variance is given by

	$\displaystyle\mathrm{var}\!\left({\widehat{\eta}_{\rm CTQM}}\right)$	$\displaystyle=\frac{\eta^{2}}{\rho^{2}}e^{-\lambda\rho}(1-e^{-\lambda\rho})$
		$\displaystyle\quad+\frac{\eta(\rho-\eta e^{-\eta})}{\rho^{2}}\sum_{j=1}^{\infty}\frac{1}{j}\frac{e^{-\lambda\rho}(\lambda\rho)^{j}}{j!},$		(33)

where we introduce

$$\rho=\mathrm{P}({X_{i}>0})={1-e^{-\eta}}$$

as a shorthand to make certain expressions more compact. Expression (33) can be combined with (60) from Appendix A to show that the variance vanishes as $\lambda\rightarrow\infty$, decaying asymptotically as $\sim 1/\lambda$. However, because of nonzero bias, the MSE is not inversely proportion to $\lambda$, and the MSE of $\widehat{\eta}_{\rm CTQM}$ relative to other estimates depends on $\lambda$. Substituting (III-D) and (33) into (31) gives an expression for the MSE of the CTQM estimator:

	$\displaystyle\mathrm{MSE}(\widehat{\eta}_{\rm CTQM})=$	$\displaystyle\ \frac{\eta^{2}}{\rho^{2}}\left(e^{-\eta}-e^{-\lambda\rho}\right)^{\!2}+\frac{\eta^{2}}{\rho^{2}}e^{-\lambda\rho}(1-e^{-\lambda\rho})$
		$\displaystyle+\frac{\eta(\rho-\eta e^{-\eta})}{\rho^{2}}\sum_{j=1}^{\infty}\frac{1}{j}\frac{e^{-\lambda\rho}(\lambda\rho)^{j}}{j!}.$		(34)

Substituting the upper bound (61) from Appendix A for the series in (34) gives

	$\displaystyle\mathrm{MSE}(\widehat{\eta}_{\rm CTQM})<$	$\displaystyle\ \frac{\eta^{2}}{\rho^{2}}\left(e^{-\eta}-e^{-\lambda\rho}\right)^{\!2}+\frac{\eta^{2}}{\rho^{2}}e^{-\lambda\rho}(1-e^{-\lambda\rho})$
		$\displaystyle+0.518\frac{\eta(\rho-\eta e^{-\eta})}{\rho^{2}}.$		(35)

To demonstrate the benefits afforded by CTTR measurement, in Fig. 3 we compare the conventional, oracle, CTQM, CTLQM and CTML estimators across ground truth $\eta\in[0,10]$. The MSE values in Fig. 3(a) are computed from $150\,000$ independent Monte Carlo trials, using a dose rate $\Lambda=1/1600$ ions per ns and dwell time $t=32\,000$ ns, for a total dose $\lambda=20$ ions per pixel. The curve for $\widehat{\eta}_{\rm baseline}$ matches the theoretical MSE expression (15). Although unimplementable, the curve for $\widehat{\eta}_{\rm oracle}$ also matches the theoretical MSE in (9).¹¹1We did not need to choose a value for $\eta_{0}$ because the event $\{M=0\}$, which has probability $e^{-20}\approx 2\cdot 10^{-9}$, did not occur in any of the trials. We can observe that $\widehat{\eta}_{\rm CTQM}$ has a large MSE for small $\eta$, caused largely by $\widetilde{M}$ severely underestimating $M$ in these cases. Predictably, $\widehat{\eta}_{\rm CTLQM}$ reduces MSE tremendously for small values of $\eta$ because the role of $\widetilde{M}$ is modified the most in these cases. For low $\eta$ (about 0 to 2.5), $\widehat{\eta}_{\rm CTML}$ achieves lowest MSE amongst all implementable estimators; for moderate $\eta$ (about 2.5 to 5.5), $\widehat{\eta}_{\rm CTQM}$ is slightly better than the others; and for large $\eta$ (about 5.5 and above), $\widehat{\eta}_{\rm CTQM}$, $\widehat{\eta}_{\rm CTLQM}$ and $\widehat{\eta}_{\rm CTML}$ all give nearly identical performance. It is noteworthy that CTQM converges with the oracle at $\eta$ above about 3.0, though the oracle is unimplementable in practice.

The MSE trends and comparisons can be better understood through the biases in Fig. 3(b) and variances in Fig. 3(c). Curves for $\widehat{\eta}_{\rm CTQM}$ coincide with the bias and variance expressions derived in (III-D) and (33). As previously noted, the large bias of $\widehat{\eta}_{\rm CTQM}$ for small values of $\eta$ is caused by the number of incident ions $M$ being severely underestimated by $\widetilde{M}$. The bias of $\widehat{\eta}_{\rm CTQM}$ can be corrected by the use of $\widehat{\eta}_{\rm CTLQM}$. The dashed cyan-colored curve in Fig. 3(c) is the CRB for any unbiased estimator, which is the reciprocal of (26). The variances of the implementable and approximately unbiased $\widehat{\eta}_{\rm CTLQM}$ and $\widehat{\eta}_{\rm CTML}$ estimators approximately coincide with the CRB.

The DTTR measurement (7) is a length-$n$ vector of SE counts collected over subacquisition dwell times of $t/n$. Thus, some modeling and analysis for DTTR measurement follows from scaling of $\lambda$ in expressions from Section II-D. Since $\{Y_{1},\,Y_{2},\,\ldots,\,Y_{n}\}$ are independent, their joint PMF is simply

$$\mathrm{P}_{Y_{1},Y_{2},\ldots,Y_{n}}(y_{1},y_{2},\ldots,y_{n}\,;\,\eta,\lambda)=\prod_{k=1}^{n}\mathrm{P}_{Y}(y_{k}\,;\,\eta,\lambda/n),$$

(36)

written in terms of the PMF in (11).

To evaluate the FI about $\eta$ in the DTTR measurement (7) with $\lambda$ as a known parameter is also quite simple. Because FI is additive over independent observations,

$\displaystyle\mathcal{I}_{\rm DTTR}(\eta\,;\,\lambda,n)$

$\displaystyle=n\,\mathcal{I}_{Y}(\eta\,;\,\lambda/n),$

(37)

expressed in terms of the FI in (17). While this FI inherits the complexity and lack of interpretability of (17), the distinction is that the relevant dose parameter in $\mathcal{I}_{Y}$ has been reduced from $\lambda$ to $\lambda/n$, so it is more reasonable to approximate with the low-dose asymptote (18). Specifically, we can write

	$\displaystyle\mathcal{I}_{\rm DTTR}(\eta\,;\,\lambda,n)$	$\displaystyle=\lambda\,\frac{\mathcal{I}_{Y}(\eta\,;\,\lambda/n)}{\lambda/n}$
		$\displaystyle\approx\lambda\left(\frac{1}{\eta}-e^{-\eta}\right),$		(38)

where the approximation holds for large enough $n$ because of (18). Note that (38) has the same expression as (26), so as $n\rightarrow\infty$, the FI of DTTR measurement converges from below to the FI of CTTR measurement.

In this section, we present estimators applicable to DTTR measurement (7) that were first introduced in [19]. The subsequent analyses are new.

Like in Section III-D, we analyze the MSE of $\widehat{\eta}_{\rm DTQM}$ by finding expressions for its bias and variance. In both calculations, we make use of a zero-truncated modification of the Neyman Type A distribution at ion incidence parameter $\lambda/n$. Let $p=\mathrm{P}({Y_{k}>0})$. Then using (11), we find

$$p=1-\mathrm{P}_{Y}(0\,;\,\eta,\lambda/n)=1-\exp\!\left(-\frac{\lambda}{n}(1-e^{-\eta})\right)\!.$$

(43)

If $\widetilde{Y}_{k}$ is the zero-truncated version of $Y_{k}$, then its PMF is

$$\mathrm{P}_{\widetilde{Y}_{k}}(y_{k})=\frac{1}{p}\frac{e^{-{{\lambda}/{n}}}\eta^{y_{k}}}{y_{k}!}\sum_{m=0}^{\infty}\frac{(\frac{\lambda}{n}e^{-\eta})^{m}m^{y_{k}}}{m!},\quad y_{k}=1,2,\ldots,$$

(44)

its mean is

$$\mathrm{E}[\,{\widetilde{Y}_{k}}\,]=\frac{1}{p}\frac{\lambda\eta}{n},$$

(45)

and its variance is

$$\mathrm{var}({\widetilde{Y}_{k}})=\frac{1}{p}\left(\frac{\lambda}{n}\eta+\frac{\lambda}{n}\eta^{2}+\left(\frac{\lambda}{n}\eta\right)^{2}\right)-\frac{1}{p^{2}}\left(\frac{\lambda}{n}\eta\right)^{2}.$$

(46)

Furthermore, as a sum of independent indicator random variables, $L$ is a binomial random variable with $n$ trials and success probability $p$ for each trial.

For $\ell>0$,

	$\displaystyle\mathrm{E}\!\left[\,{\widehat{\eta}_{\rm DTQM}\,|\,L=\ell}\,\right]$	$\displaystyle=\mathrm{E}\!\left[\,{\frac{Y}{L}\,|\,L=\ell}\,\right]=\frac{1}{\ell}\mathrm{E}\!\left[\,{Y\,|\,L=\ell}\,\right]$
		$\displaystyle\stackrel{{\scriptstyle(a)}}{{=}}\frac{1}{\ell}\mathrm{E}\!\left[\,{\sum_{j=1}^{\ell}\widetilde{Y}_{j}}\,\right]=\mathrm{E}\!\left[\,{\widetilde{Y}_{k}}\,\right],$		(47)

where (a) follows from using $\widetilde{Y}_{j}$ to denote the $j$th positive subacquistion $Y_{k}$. Trivially,

$$\mathrm{E}\!\left[\,{\widehat{\eta}_{\rm DTQM}\,|\,L=0}\,\right]=0.$$

(48)

Using $\mathrm{P}({L>0})=1-(1-p)^{n}$ and the total expectation theorem to combine (47) and (48) gives

$$\mathrm{E}\!\left[\,{\widehat{\eta}_{\rm DTQM}}\,\right]=\mathrm{E}[\,{\widetilde{Y}_{k}}\,](1-(1-p)^{n})).$$

The bias of $\widehat{\eta}_{\rm DTQM}$ is thus given by

	$\displaystyle\operatorname{bias}(\widehat{\eta}_{\rm DTQM})$	$\displaystyle=\mathrm{E}\!\left[\,{\widehat{\eta}_{\rm DTQM}}\,\right]-\eta$
		$\displaystyle=\frac{\lambda\eta}{np}\left[1-(1-p)^{n}\right]-\eta,$		(49)

where (45) has been substituted.

Similar arguments, detailed in Appendix D, yield

	$\displaystyle\mathrm{var}\!\left({\widehat{\eta}_{\rm DTQM}}\right)$	$\displaystyle=\left(\mathrm{E}[\,{\widetilde{Y}_{k}}\,]\right)^{2}\left[1-(1-p)^{n}\right](1-p)^{n}$
		$\displaystyle\quad+\mathrm{var}({\widetilde{Y}_{k}})\sum_{\ell=1}^{n}\frac{1}{\ell}\binom{n}{\ell}p^{\ell}(1-p)^{n-\ell},$		(50)

where $\mathrm{E}[\,{\widetilde{Y}_{k}}\,]$ is given in (45) and $\mathrm{var}({\widetilde{Y}_{k}})$ is given in (46). Since the behavior of the series in (IV-D) for large $n$ is not evident, we also derive in Appendix D the lower bound

	$\displaystyle\mathrm{var}\!\left({\widehat{\eta}_{\rm DTQM}}\right)$	$\displaystyle\geq\left(\mathrm{E}[\,{\widetilde{Y}_{k}}\,]\right)^{2}\left[1-(1-p)^{n}\right](1-p)^{n}$
		$\displaystyle\quad+\mathrm{var}({\widetilde{Y}_{k}})\frac{[1-(1-p)^{n}]^{2}}{np}.$		(51)

The expressions in (IV-D) and (IV-D) can be added to the square of the bias from (IV-D) to obtain the MSE of $\widehat{\eta}_{\rm DTQM}$ and a lower bound for this MSE.