Tilings of Benzels via the Abacus Bijection

In [1], Conway and Lagarias studied some tiling problems in which the regions that are to be tiled are, like the tiles themselves, composed of regular hexagons in a hexagonal grid; such regions are sometimes called polyhexes. Using combinatorial group theory in a clever and novel fashion, they were able to prove necessary and sufficient conditions for tileability. Later, Thurston [11] provided alternative perspectives and further results, and (more relevantly to our work here) Lagarias and Romano [4] determined the exact number of tilings for a particular one-parameter family of polyhex tiling problems. Meanwhile, physicists had worked in an essentially equivalent (more precisely, dual) setting, studying trimer covers [12] of the regular 6-valent planar graph, but the physicists’ interests were in asymptotic enumeration, not exact formulas for finite subgraphs of the 6-valent grid; furthermore, their proofs relied on the controversial Bethe ansatz, which tends to give correct answers but has not been rigorously established in all the contexts in which it has been applied.

In [8], inspired by the large and still-growing literature on exact enumeration of tilings (see [6] for an overview), Propp proposed using the tiles studied by Conway and Lagarias to tile different sorts of regions in the hexagonal grid not considered in earlier literature, and he made numerous conjectures regarding the exact number of tilings of those regions. We prove some of Propp’s conjectures here.

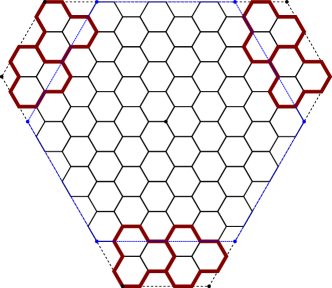
It is convenient to view the hexagonal grid as a tiling of the complex plane with regular hexagons of side length $1$. We can uniquely specify the exact positions of the unit hexagons, which we call the cells of the grid, by declaring that one of the hexagons has vertices $1\pm 1,1\pm\omega,1\pm\omega^{2}$, where $\omega=e^{2\pi i/3}$. Suppose $a$ and $b$ are positive integers satisfying $2\leq a\leq 2b$ and $2\leq b\leq 2a$. Following [8], we define the $(a,b)$-benzel to be the union of the cells lying entirely within the hexagon with vertices $a\omega+b,-a\omega^{2}-b,a\omega^{2}+b\omega,-a-b\omega,a+b\omega^{2},-a\omega-b\omega^{2}$. (This is the polyhex that we will attempt to tile using polyhexes consisting of three hexagonal cells, aka trihexes.) Note that this hexagon is centered at $0$, is invariant under rotation by $120^{\circ}$, and has sides whose lengths alternate between $2a-b$ and $2b-a$. Figure 1 shows the $(7,8)$-benzel. It can be shown (see [7]) that the number of cells in the $(a,b)$-benzel is

The prototiles in [1] and [8] consist of three cells and are of two forms: a stone consists of three hexagonal cells arranged in a triangle while a bone consists of three hexagonal cells arranged in a line. (Conway and Lagarias called them $T_{2}$’s and $L_{3}$’s and Thurston [11] called them $T_{2}$’s and tribones.) We will consider the various translationally-inequivalent rotations of these shapes to be distinct prototiles. Thus, there are really five different prototiles, which are shown in Figure 2. We call them the right stone, left stone, vertical bone, rising bone, and falling bone. Tilings of regions in the hexagonal grid using these prototiles will be referred to as stones-and-bones tilings.

Conway and Lagarias showed that for any simply-connected region in the hexagonal grid that admits a stones-and-bones tiling, the number of right stones minus the number of left stones in such a tiling is invariant (i.e., depends only on the region and not the specific tiling). This is the Conway–Lagarias invariant of the region. Propp [7] showed that the Conway–Lagarias invariant of the $(a,b)$-benzel is

Note that when $a+b\equiv 1\pmod{3}$, the number of cells in the $(a,b)$-benzel is three times its Conway–Lagarias invariant, which implies (because each tile uses $3$ cells) that a stones-and-bones tiling must consist entirely of right stones. We will prove that such a tiling exists and is unique.

Frequently, tiling problems will restrict the set of possible prototiles. There are $2^{5}-1=31$ nonempty subsets of our set of 5 prototiles. However, as benzels have threefold rotational symmetry—which preserves the two stones—the types of bones allowed does not affect the answer to enumerative questions; all that matters is the number of different bones that are allowed. Hence, there are really only $2\cdot 2\cdot 4-1=15$ inequivalent tiling problems to consider. Moreover, the $(a,b)$-benzel and $(b,a)$-benzel are reflections of each other across the real axis; as this reflection preserves the two stones as well as the number of types of allowed bones, each tiling problem is the same for the $(a,b)$-benzel as the $(b,a)$-benzel. We will often make use of this symmetry in order to assume without loss of generality that $a\leq b$.

Much of our work centers around the enumeration of tilings of benzels in which we allow just two types of bones and one type of stone. Since we only care about the number of allowed bones, we may assume that we are using rising bones and falling bones. Propp conjectured (see [8, Problems 2 and 3]) that if $(a,b)$ is of the form $(3n,3n)$ or $(3n+1,3n+2)$, then the number of tilings of the $(a,b)$-benzel using left stones, rising bones, and falling bones is $(2n)!!=2^{n}n!$. One of our main results resolves this conjecture; in fact, we will determine the number of such tilings of the $(a,b)$-benzel for all choices of $a$ and $b$.

On the other hand, we have the following theorem regarding tilings with right stones, rising bones, and falling bones.

Theorem 1.3 says nothing about what happens when $a+b\equiv 2\pmod{3}$.; Propp [8] gave the following conjecture in this case.

Our approach to proving Theorems 1.2 and 1.3 is to first transfer benzels from the hexagonal grid into the square grid. This allows us to use tools from the theory of ribbon tilings of Young diagrams. In particular, if $\lambda$ is a partition with $k$-core $\kappa$ and $k$-quotient $(\lambda^{(0)},\ldots,\lambda^{(k-1)})$, then there is a bijection (dubbed the “abacus bijection” by Gordon James [3] and rediscovered by Dennis Stanton and Dennis White (see [10] and [2]) that maps $k$-ribbon tableaux of shape $\lambda/\kappa$ to $k$-tuple Young tableaux of shape $(\lambda^{(0)},\ldots,\lambda^{(k-1)})$. For other authors’ descriptions of the bijection, see [3] or [5]. We felt the need to provide our own discussion and proof; we hope that our treatment of this bijection will be useful to researchers. More relevant to our purpose is a related bijection that we call $\operatorname{\mathsf{Compress}}$, which is apparently new. This bijection is between $k$-ribbon tilings of a Young diagram of a particular type and $(k-1)$-tilings of a related Young diagram; it is essentially a version of the abacus bijection that “forgets” the ordering of the tiles in a ribbon tableau. Our proofs of Theorems 1.2 and 1.3 employ these bijections as tools and combine them with several new ideas. Although we have made no attempt toward proving 1.4, we expect that it could be fruitful to transfer the problem into the square grid and employ techniques similar to those that we use.

We mention in passing that, like us, Conway and Lagarias transferred their tiling problem to the square grid. However, there are two key differences between their use of the tactic and ours. The first difference is that, as Thurston later demonstrated, the use of the square grid is not an essential feature of the translation of tiling problems into combinatorial group theory problems; in contrast, our adaptation of the theory of cores and quotients requires working in the square grid (where Ferrers graphs and Young diagrams live). The second difference is that in [1], all three bones are transferred to the square grid, at the cost of making one of them disconnected; in contrast, such disconnected tiles are forbidden in the theory of ribbon tilings.

The outline for the rest of the paper is as follows. Section 2 is brief; its purpose is to explain how to translate certain tiling problems in the hexagonal grid into tiling problems in the square grid. In Section 3, we provide a thorough discussion of $k$-cores, $k$-quotients, and the abacus bijection. Section 4 defines and develops the $\operatorname{\mathsf{Compress}}$ bijection. Section 5 is devoted to proving Theorem 1.1. We use the properties of $\operatorname{\mathsf{Compress}}$ discussed in Section 4 to prove Theorem 1.2 in Section 6 and to prove Theorem 1.3 in Section 7.

In this article, we draw the square grid in the complex plane so that the unit square cells are oriented like diamonds. More precisely, each square grid cell has vertices of the form $(a\pm 1)+bi$ and $a+(b\pm 1)i$, where $a$ and $b$ are integers such that $a+b$ is odd. We call each such square cell a box. A great deal of theory has already been developed for tilings of regions in the square grid; in order to make use of it, we will need a way of converting tilings in the hexagonal grid into tilings in the square grid. Notice that there are unit-width vertical strips of the complex plane that are traversed only by horizontal edges of the hexagonal grid, not by edges of the other two orientations. Removing these vertical strips and compressing the plane appropriately yields a bijective mapping from the hexagons in the hexagonal grid to rhombuses in the resulting rhombic grid. Rescaling the axes suitably transforms these rhombuses into squares of side length $\sqrt{2}$. Let us then rotate the resulting grid by $90^{\circ}$ counterclockwise.

The prototiles of Figure 2, transferred to this square grid, are shown in Figure 4. Notice that the vertical bone becomes a union of three disconnected boxes. When at most two types of bones are allowed, we can assume without loss of generality that the vertical bone is forbidden, which allows the resulting square grid tiling problem to exclusively use prototiles of connected boxes. In fact, when the vertical bone is forbidden, we can specifically leverage the theory of ribbon tilings. A ribbon is a connected union of boxes in the square grid in which no two boxes have the same $x$-coordinate; a $k$-ribbon is a ribbon that contains exactly $k$ unit squares. Our four prototiles (excluding the vertical bone) in the square grid are precisely the four $3$-ribbons. With these conventions, we will rename the right stone, left stone, rising bone, and falling bone the mountain stone, valley stone, negative bone, and positive bone.

The version of the bijection that we use is due to Gordon James (see [3]) but different forms of it seem to have been discovered independently by various people working in the field of modular representation theory around 1950; this community includes H. Farahat, J. S. Frame, D. E. Littlewood, T. Nakayama, M. Osima, G. de B. Robinson, R. A. Staal, and R. M. Thrall. The interested reader may find more details in the book [9] and the references it contains.

We identify integer partitions with their Young diagrams. We will draw the Young diagram of a partition $\lambda$ in Russian notation so that it lives within the square grid as we have chosen to draw it. Let us position the Young diagram so that its bottom-most point is $0$ and so that the boxes representing the first part of the partition have their lower-left edges lying along the ray $\mathbb{R}_{\geq 0}\,e^{3\pi i/4}$, as in Figure 5.

A coordinatized abacus word is a function $w$ from the set $\mathbb{Z}+1/2=\{n+1/2:n\in\mathbb{Z}\}$ to the alphabet $\{\circ,\bullet\}$ with the property that $w(-n-1/2)=\bullet$ and $w(n+1/2)=\circ$ for all sufficiently large $n$. Such words also arise in the study of the exclusion process; in that literature, $\bullet$ is called a particle and $\circ$ is called a vacancy. We can represent such a word as a bi-infinite sequence of the symbols $\circ$ and $\bullet$, where we place a period between the symbols $w(-1/2)$ and $w(1/2)$ to indicated the position $0$. For example, $\cdots\bullet\bullet\bullet\circ\bullet\!\!\hskip 1.084pt.\hskip 1.084pt\!\!\bullet\circ\circ\circ\cdots$ represents the coordinatized abacus word $w$ given by $w(-3/2)=w(n+1/2)=\circ$ for all integers $n\geq 1$ and $w(1/2)=w(-1/2)=w(m-1/2)$ for all integers $m\leq-2$. An abacus word is an orbit of a coordinatized abacus word under the natural $\mathbb{Z}$-action given by the shift map. As with coordinatized abacus words, we can represent abacus words as bi-infinite sequences using the symbols $\circ$ and $\bullet$; however, we no longer include the period in this representation.

Given a partition $\lambda$, we obtain an abacus word $\overline{w}_{\lambda}$ by traveling along its northern border from left to right and recording whether we go up or down at each step by writing the symbol $\circ$ to record an up step and the symbol $\bullet$ to record a down step. From this abacus word $\overline{w}_{\lambda}$, we obtain a coordinatized abacus word $w_{\lambda}$ by insisting that $w_{\lambda}(\ell)$ records whether the step whose midpoint has real part $\ell$ is up or down. For example, if $\lambda=(5,5,3,3,2)$ is the partition shown in Figure 5, then $w_{\lambda}=\cdots\bullet\bullet\bullet\circ\circ\bullet\bullet\circ.\!{}{}\circ\bullet\circ\bullet\bullet\circ\circ\circ\cdots$.

Each abacus word $\overline{w}$ (which is, by definition, an orbit under the shift map) has a unique representative of the form $w_{\lambda}$ for some partition $\lambda$. Indeed, in the partition $\lambda$, there must be the same number of up steps to the left of position $0$ as down steps to the right of position $0$, so

this value is also the number of boxes of $\lambda$ that are directly above the origin. We call $w_{\lambda}$ the canonical coordinatization of $w$.

Let us fix a positive integer $k$ and split the word $w_{\lambda}$ into $k$ words $w^{(0)}_{\lambda},\ldots,w^{(k-1)}_{\lambda}$ so that each $w^{(j)}_{\lambda}$ is obtained by reading every $k$-th symbol in $w_{\lambda}$. In other words, $w_{\lambda}^{(j)}$ is the word obtained by reading $w_{\lambda}(k\ell+j+1/2)$ for all $\ell\in\mathbb{Z}$. As above, we can coordinatize each of the words $w_{\lambda}^{(j)}$ so that it corresponds to an integer partition $\lambda^{(j)}$. For each $0\leq j\leq k-1$, there is a unique integer $c_{j}$ such that if we set $w^{(j)}_{\lambda}(\ell-c_{j}+1/2)=w_{\lambda}(k\ell+j+1/2)$ for all $\ell$, then $w_{\lambda}^{(j)}=w_{\lambda^{(j)}}$, the abacus word associated with the partition $\lambda^{(j)}$. The integers $c_{0},\ldots,c_{k-1}$ are called the $k$-charges of $\lambda$; they satisfy $c_{0}+\cdots+c_{k-1}=0$. The tuple $(\lambda^{(0)},\ldots,\lambda^{(k-1)})$ is called the $k$-quotient of $\lambda$. For an example of this construction, let $k=3$, and let $\lambda=(5,5,3,3,2)$ as shown in Figure 5. We have $w_{\lambda}^{(0)}=\cdots\bullet\bullet\bullet\circ\bullet\circ\circ\circ\cdots$, $w_{\lambda}^{(1)}=\cdots\bullet\bullet\bullet\circ\bullet\bullet\bullet\circ\circ\circ\cdots$, and $w_{\lambda}^{(2)}=\cdots\bullet\bullet\bullet\circ\circ\circ\cdots$. Then $\lambda^{(0)}=(1)$, $\lambda^{(1)}=(3)$, and $\lambda^{(2)}=\emptyset$ are shown in Figure 6. The $3$-charges are $c_{0}=c_{1}=1$ and $c_{2}=-2$.

Suppose there is a $k$-ribbon tile $T$ at the top of the Young diagram of $\lambda$ such that removing $T$ results in the Young diagram of a smaller partition. Let us remove it. Iterating this process, we can continue removing $k$-ribbon tiles until it is no longer possible to do so. The resulting partition $\kappa$ is called the $k$-core of $\lambda$; it is known that $\kappa$ does not depend on the order in which the $k$-ribbons were removed. We will consider the skew shape $\lambda/\kappa$. It will be convenient to think of $\kappa$ as a tile inside of $\lambda$.

A $k$-ribbon tableau of shape $\lambda/\kappa$ is a tuple $(T_{1},\ldots,T_{m})$ of $k$-ribbon tiles such that the set $\{\kappa,T_{1},\ldots,T_{m}\}$ forms a tiling of $\lambda$ and such that for every $1\leq i\leq m$, the set $\{\kappa,T_{1},\ldots,T_{i}\}$ forms a tiling of some Young diagram. One can imagine adding the tiles $\kappa,T_{1},\ldots,T_{m}$ one by one to build $\lambda$ from the bottom up. Let $\operatorname{RTab}_{k}(\lambda/\kappa)$ denote the set of $k$-ribbon tableaux of shape $\lambda/\kappa$.

A strict Young tableau of shape $\lambda$ is a filling of the square boxes of $\lambda$ (which is again drawn in Russian notation) with distinct positive integers so that numbers strictly increase as we move up (northeast or northwest). We write $\operatorname{cont}(\mathcal{T})$ for the content of a strict Young tableau $\mathcal{T}$, which is just the set of integers appearing in $\mathcal{T}$.

Suppose $(\alpha_{0},\ldots,\alpha_{k-1})$ is a $k$-tuple of partitions. We define a $k$-tuple Young tableau of shape $(\alpha_{0},\ldots,\alpha_{k-1})$ to be a $k$-tuple $(\mathcal{T}_{0},\ldots,\mathcal{T}_{k-1})$ of strict Young tableaux such that each $\mathcal{T}_{j}$ has shape $\alpha_{j}$ and $\operatorname{cont}(\mathcal{T}_{0})\cup\cdots\cup\operatorname{cont}(\mathcal{T}_{k-1})=[|\alpha_{0}|+\cdots+|\alpha_{k-1}|]$. (Here we use $[n]$ to denote $\{1,2,\dots,n\}$.) Note that these conditions force the sets $\operatorname{cont}(\mathcal{T}_{0}),\ldots,\operatorname{cont}(\mathcal{T}_{k-1})$ to be pairwise disjoint. Let $\operatorname{YT}_{k}(\alpha_{0},\ldots,\alpha_{k-1})$ be the set of $k$-tuple Young tableaux of shape $(\alpha_{0},\ldots,\alpha_{k-1})$.

As above, let $\lambda$ be a partition with $k$-quotient $(\lambda^{(0)},\ldots,\lambda^{(k-1)})$ and $k$-core $\kappa$. The abacus bijection is a bijection $\operatorname{\mathsf{Ab}}\colon\operatorname{RTab}_{k}(\lambda/\kappa)\to\operatorname{YT}_{k}(\lambda^{(0)},\ldots,\lambda^{(k-1)})$. To describe it, let us start with a $k$-ribbon tableau $(T_{1},\ldots,T_{m})\in\operatorname{RTab}_{k}(\lambda/\kappa)$. The intuitive idea is to remove the tiles $T_{m},\ldots,T_{1}$ in this order and insert the number $r$ into one of the boxes of one of $\lambda^{(0)},\ldots,\lambda^{(k-1)}$ at the point in time when we remove $T_{r}$. In order to be rigorous, it is convenient to define the bijection recursively. Thus, let us assume that we have already defined the abacus bijection on $\operatorname{RTab}_{k}(\mu/\kappa)$ whenever $|\mu/\kappa|<|\lambda/\kappa|$.

Let $\ell\in\mathbb{Z}$ and $j\in\{0,\ldots,k-1\}$ be such that $k\ell+j$ is the real part of the leftmost point in the $k$-ribbon tile $T_{m}$; the real part of the rightmost point in $T_{m}$ must be $k(\ell+1)+j+1$. There are $k+1$ steps in the northern boundary of the Young diagram of $\lambda$ that are part of the $k$-ribbon tile $T_{m}$; they are encoded by the symbols $w_{\lambda}(k\ell+j+1/2),\ldots,w_{\lambda}(k(\ell+1)+j+1/2)$. It is straightforward to see that $w_{\lambda}(k\ell+j+1/2)=\circ$ and $w_{\lambda}(k(\ell+1)+j+1/2)=\bullet$. Let $\mu$ be the partition whose Young diagram is obtained from that of $\lambda$ by removing $T_{m}$. Then $w_{\mu}$ agrees with $w_{\lambda}$ except that $w_{\mu}(k\ell+j+1/2)=\bullet$ and $w_{\mu}(k(\ell+1)+j+1/2)=\circ$. The $k$-charges of $\mu$ are the same as the $k$-charges $c_{0},\ldots,c_{k-1}$ of $\lambda$. Indeed, if we replace $\lambda$ by $\mu$, the quantities $|\{\ell<0:w_{\lambda}^{(j)}(\ell-c_{j}+1/2)=\circ\}|$ and $|\{\ell\geq 0:w_{\lambda}^{(j)}(\ell-c_{j}+1/2)=\bullet\}|$ will not change if $\ell\neq-1$ and will both decrease by $1$ if $\ell=-1$; more generally, adding or removing $k$-ribbons from the Young diagram of a partition $\nu$ to yield a new Young diagram of a partition $\nu^{\prime}$ does not change the $k$-charges. This implies $\lambda$, $\mu$, and $\kappa$ have the same $k$-charges. It follows that $\lambda^{(r)}=\mu^{(r)}$ for all $r\neq j$ and that the Young diagram of $\mu^{(j)}$ is obtained from that of $\lambda^{(j)}$ by removing a single box $B$. Note that the real parts of the leftmost and rightmost points in $B$ are $\ell-c_{j}$ and $\ell-c_{j}+2$, respectively. Since $(T_{1},\ldots,T_{m-1})\in\operatorname{RTab}_{k}(\mu/\kappa)$ and $|\mu/\kappa|<|\lambda/\kappa|$, we can apply the abacus bijection inductively to obtain a $k$-tuple Young tableau $\operatorname{\mathsf{Ab}}(T_{1},\ldots,T_{m-1})\in\operatorname{YT}_{k}(\mu^{(0)},\ldots,\mu^{(k-1)})$. The $k$-tuple Young tableau $\operatorname{\mathsf{Ab}}(T_{1},\ldots,T_{m})\in\operatorname{YT}_{k}(\lambda^{(0)},\ldots,\lambda^{(k-1)})$ is now obtained from $\operatorname{\mathsf{Ab}}(T_{1},\ldots,T_{m-1})$ by adding the box $B$ and filling it with the number $m$.

To prove that the map $\operatorname{\mathsf{Ab}}\colon\operatorname{RTab}_{k}(\lambda/\kappa)\to\operatorname{YT}_{k}(\lambda^{(0)},\ldots,\lambda^{(k-1)})$ is bijective, we construct its inverse by reversing the above procedure. Suppose we start with a $k$-tuple Young tableau $(\mathcal{T}^{(0)},\ldots,\mathcal{T}^{(k-1)})$ of shape $(\lambda^{(0)},\ldots,\lambda^{(k-1)})$. Let $m=|\lambda^{(0)}|+\cdots+|\lambda^{(k-1)}|$, and let $j\in\{0,\ldots,k-1\}$ be such that $m\in\operatorname{cont}(\mathcal{T}^{(j)})$. Let $B$ be the box of $\lambda^{(j)}$ containing $m$ in $\mathcal{T}^{(j)}$. Let $c_{0},\ldots,c_{k-1}$ be the $k$-charges of $\lambda$, and define $\ell$ so that $\ell-c_{j}$ is the real part of the leftmost point in $B$. We can reconstruct the partition $\mu^{(j)}$ by removing $B$ from $\lambda^{(j)}$. We can then reconstruct $\mu$, which is determined by its $k$-quotient $(\mu^{(0)},\ldots,\mu^{(k-1)})$ and $k$-charges $c_{0},\ldots,c_{k-1}$ (it has the same $k$-charges as $\lambda$), by letting $\mu^{(r)}=\lambda^{(r)}$ for all $r\neq j$. Let $\widetilde{\mathcal{T}}^{(j)}$ be the strict Young tableau of shape $\mu^{(j)}$ obtained by deleting $B$ from $\mathcal{T}^{(j)}$, and let $\widetilde{\mathcal{T}}^{(r)}=\mathcal{T}^{(r)}$ for all $r\neq j$. Then $(\widetilde{\mathcal{T}}^{(0)},\ldots,\widetilde{\mathcal{T}}^{(k-1)})$ is a $k$-tuple Young tableau of shape $(\mu^{(0)},\ldots,\mu^{(k-1)})$. As before, the words $w_{\lambda}$ and $w_{\mu}$ agree except that $(w_{\lambda}(k\ell+j+1/2),w_{\mu}(k\ell+j+1/2))=(\circ,\bullet)$ and $(w_{\lambda}(k(\ell+1)+j+1/2),w_{\mu}(k(\ell+1)+j+1/2))=(\bullet,\circ)$. This implies that $\lambda$ is obtained from $\mu$ by adding a $k$-ribbon tile $T_{m}$. Hence, $\mu$ and $\lambda$ have the same $k$-core $\kappa$. We may assume inductively that $\operatorname{\mathsf{Ab}}\colon\operatorname{RTab}_{k}(\mu/\kappa)\to\operatorname{YT}_{k}(\mu^{(0)},\ldots,\mu^{(k-1)})$ is a bijection, so we can re-obtain the $k$-ribbon tableau $(T_{1},\ldots,T_{m-1})\in\operatorname{RTab}_{k}(\mu/\kappa)$ as $\operatorname{\mathsf{Ab}}^{-1}(\widetilde{\mathcal{T}}^{(0)},\ldots,\widetilde{\mathcal{T}}^{(k-1)})$. Then $\operatorname{\mathsf{Ab}}^{-1}(\mathcal{T}^{(0)},\ldots,\mathcal{T}^{(k-1)})$ is the $k$-ribbon tableau $(T_{1},\ldots,T_{m})$.

Finally, we address the base case $|\lambda/\kappa|=0$, i.e., $\lambda=\kappa$. This implies $\operatorname{RTab}_{k}(\lambda/\kappa)=\{\emptyset\}$. If any of $\kappa^{(0)},\ldots,\kappa^{(k-1)}$ are nonempty, then applying our inverse map to remove a box implies that a $k$-ribbon can be removed from $\kappa$ to yield a smaller partition $\kappa^{\prime}$, contradicting the definition of the $k$-core. Thus $\kappa^{(0)}=\cdots=\kappa^{(k-1)}=\emptyset$, and $\operatorname{YT}_{k}(\lambda^{(0)},\ldots,\lambda^{(k-1)})=\{(\emptyset,\ldots,\emptyset)\}$. We obtain a trivial bijection $\operatorname{\mathsf{Ab}}\colon\operatorname{RTab}_{k}(\lambda/\kappa)\to\operatorname{YT}_{k}(\lambda^{(0)},\ldots,\lambda^{(k-1)})$.

This proves the following theorem.

A $k$-ribbon tableau of shape $\lambda/\mu$ is a $k$-ribbon tiling of $\lambda/\mu$ together with a certain ordering of the tiles. If we are given a $k$-ribbon tiling, then there is at least one way to order the tiles to obtain a $k$-ribbon tableau. Indeed, we can define a partial order $\prec$ on the set of tiles by declaring that $T\prec T^{\prime}$ whenever $T$ has a box that lies below one of the boxes in $T^{\prime}$. Then the orderings of the tiles that yield $k$-ribbon tableaux are precisely the linear extensions of this partially ordered set. Our interest in this article is in unordered tilings, so our main motivation for discussing the abacus bijection comes from the following corollary.

Suppose $\lambda$ is a partition with empty $k$-core whose $k$-quotient $(\lambda^{(0)},\dots,\lambda^{(k-1)})$ satisfies $\lambda^{(j)}=\emptyset$. Let $\rho$ be the partition with empty $(k-1)$-core whose $(k-1)$-quotient is

We will define a bijection $\operatorname{\mathsf{Compress}}$ from the set of $k$-ribbon tilings of $\lambda$ to the set of $(k-1)$-ribbon tilings of $\rho$. This bijection is essentially the unordered tiling equivalent of using the abacus bijection to map a $k$-ribbon tableau to a $k$-tuple Young tableau, removing the empty $\lambda^{(j)}$ to obtain a $(k-1)$-tuple Young tableau, and then lifting via the inverse abacus bijection on $(k-1)$-ribbons back to a $(k-1)$-ribbon tableau. However, without an ordering on our ribbons, a one-step description of our bijection exists, and it is simpler than this two-step process involving the abacus bijection.

Similar to how we removed vertical strips of the hexagonal grid that were traversed by horizontal edges and then compressed the plane to obtain the square grid in Section 2, our bijection is obtained by removing the vertical strips of the square grid that correspond to $\lambda^{(k-1)}=\emptyset$ and then compressing the plane to remove the empty space.

Identifying $\lambda$ with its Young diagram, let us write $P_{r}=\lambda\cap\{z\in\mathbb{C}:r\leq\operatorname{Re}(z)<r+1\}$, where $\operatorname{Re}(z)$ denotes the real part of $z$. The assumptions that $\lambda^{(j)}=\emptyset$ and that the $k$-charges of $\lambda$ are all zero (since its $k$-core is empty) guarantee that $P_{r}$ is a parallelogram whenever $r\equiv j\pmod{k}$; let us color these parallelograms green. Imagine deleting these green parallelograms, dividing what remains into vertical bands, sliding the remaining pieces of $\lambda$ lying left of the imaginary axis to the southeast, and sliding the remaining pieces of $\lambda$ lying right of the imaginary axis to the southwest. (Specifically, tile-pieces in the $i$-th band to the left of the imaginary axis slide $i$ steps southeast, while tile-pieces in the $i$-th band to the right of the imaginary axis slide $i$ steps southeast.) See Figure 8 for an example when $k=3$ and $j=1$. It is straightforward to check that the resulting shape will be the Young diagram of $\rho$. The bijection $\operatorname{\mathsf{Compress}}$ simply transfers the tiles in a $k$-ribbon tiling of $\lambda$ through this process so that they become $(k-1)$-ribbons that tile $\rho$. It is not difficult to check that if we start with a $(k-1)$-ribbon tiling $\mathcal{D}$ of $\rho$, then there is a unique way to lift it to a $k$-ribbon tiling $\mathcal{T}$ of $\lambda$ such that $\operatorname{\mathsf{Compress}}(\mathcal{T})=\mathcal{D}$; every $(k-1)$-ribbon has a unique square that will be extended into two squares, where the direction of extension depends on which side of the imaginary axis the square is on, yielding a $k$-ribbon. Hence, we only need to check that $\operatorname{\mathsf{Compress}}$ is well-defined; more precisely, we need to show that the remove-green compression process actually sends all of the tiles in a $k$-ribbon tiling of $\lambda$ to $(k-1)$-ribbons in $\rho$ (instead of disconnected shapes).

Let us fix a $k$-ribbon tiling $\mathcal{T}$ of $\lambda$. Suppose we order the tiles in $\mathcal{T}$ to form a $k$-ribbon tableau. When we apply the abacus bijection to this tableau, each tile will correspond to one of the boxes in the resulting $k$-tuple Young tableau. More precisely, a tile $T$ will correspond to one of the boxes in the Young tableau of shape $\lambda^{(r)}$, where $r\in\{0,1,\dots,k-1\}$ is congruent modulo $k$ to the real part of the leftmost point in $T$. Since $\lambda^{(j)}=\emptyset$, we cannot have $r=j$. Equivalently, $T$ cannot intersect two of the green parallelograms. It must intersect at least one of the green parallelograms because the real parts of the leftmost and rightmost points of $T$ are $k$ apart and because the horizontal distance between two consecutive green parallelograms is only $k-1$. This proves the following lemma.

Now choose a fixed green parallelogram $P=P_{r}$ in $\lambda$. The side lengths of $P$ are $\sqrt{2}$ and $2\alpha$ for some nonnegative integer $\alpha$. We can break $P$ into $\alpha$ smaller parallelograms whose side lengths are $\sqrt{2}$ and $2$; say these smaller parallelograms are $P^{1},\ldots,P^{\alpha}$, listed from bottom to top. Let $L^{s}$ and $R^{s}$ be the left and right vertical sides of $P^{s}$, respectively. Each tile in $\mathcal{T}$ that intersects $P$ must contain exactly one of $L^{1},\ldots,L^{\alpha}$ and exactly one of $R^{1},\ldots,R^{\alpha}$. It follows that for each $1\leq s\leq\alpha$, there is a tile $T^{s}$ that contains both $L^{s}$ and $R^{s}$. When we apply the compression process removing the green parallelograms, the piece of $T^{s}$ to the left of $P$ will connect with the piece of $T^{s}$ to the right of $P$ to form a $(k-1)$-ribbon, as desired. See Figure 9 for an illustration when $k=3$.

The relationship between the abacus bijection and the compress bijection is summarized in the following commutative diagram:

The map from $\operatorname{RTab}_{k}(\lambda)$ (respectively, $\operatorname{RTab}_{k-1}(\rho)$) to the set of $k$-ribbon tilings of $\lambda$ (respectively, $(k-1)$-ribbon tilings of $\rho$) simply forgets the ordering of the tiles. The map $\widetilde{\mathsf{Compress}}$ acts in the same way as the map $\operatorname{\mathsf{Compress}}$, except it preserves the ordering of the tiles as it compresses $k$-ribbon tiles into $(k-1)$-ribbon tiles.

When $a+b\equiv 1\pmod{3}$, we can use the Conway–Lagarias invariant to see that in any stones-and-bones tiling of the $(a,b)$-benzel (allowing all five types of stones and bones), the benzel must be tiled entirely by right stones. In this section, we prove Theorem 1.1, which states that such a tiling exists and is unique.

This immediately implies that for any tiling problem where only certain specified prototiles are allowed, there is a unique tiling of the $(a,b)$-benzel for $a+b\equiv 1\pmod{3}$ if and only if the right stone is an allowed prototile, and no tilings otherwise.

The goal of this section is to enumerate tilings of the $(a,b)$-benzel using two types of bones along with the left stone. Without loss of generality, we may assume the vertical bone is forbidden. Thus, our goal is to prove Theorem 1.2, which provides the enumeration of tilings using rising bones, falling bones, and left stones. It follows immediately from Theorem 1.1 that there are no such tilings when $a+b\equiv 1\pmod{3}$ (since the only stones-and-bones tiling of the $(a,b)$-benzel uses only right stones). If $a+b\equiv 2\pmod{3}$, the Conway–Lagarias invariant of the $(a,b)$-benzel is

Therefore, in this case, a stones-and-bones tiling of the $(a,b)$-benzel requires a strictly positive number of right stones, so again no such tiling exists. This completes the proof of Theorem 1.2 when $a+b\not\equiv 0\pmod{3}$, so we may assume throughout the rest of this section that $a+b\equiv 0\pmod{3}$.

After transferring the problem to the square grid as in Section 2, we are left to consider tilings using valley stones, negative bones, and positive bones, i.e., the three prototiles other than the mountain stone. Henceforth, we will refer to such tilings with these three allowed prototiles as mountainless tilings.

We will use the $\operatorname{\mathsf{Compress}}$ bijection from Section 4 with $k=3$, i.e., between certain 3-ribbon tilings and 2-ribbon tilings (also called domino tilings) of smaller shapes. Note that there are two 2-ribbons, the 2-ribbon analogs of the positive and negative bones. We will set $j=1$, so our bijection will be from 3-ribbon tilings of an integer partition $\lambda$ with 3-quotient $(\lambda^{(0)},\emptyset,\lambda^{(2)})$ and vanishing $3$-charges. As we will see later, the integer partition that ends up being relevant for our purposes is the partition $\lambda_{n}$ with 3-quotient $(\square_{n},\emptyset,\square_{n})$ and vanishing $3$-charges, where $\square_{n}=(n,n,\dots,n)$ is the integer partition consisting of $n$ parts of size $n$. The Young diagram of $\lambda_{n}$ consists of $n$ nested V-shapes $V_{1},\ldots,V_{n}$, listed from top to bottom. For each $1\leq i\leq n-1$, we will assign the color red to the boundary between $V_{i}$ and $V_{i+1}$; we call this boundary a red border. See Figure 11 for an example with $n=3$. Let us label the boxes in $\lambda_{n}$ with the letters A, B, C so that the label of a box is determined by reading the real part of its leftmost point modulo $3$, with A, B, C corresponding to $0$, $1$, $2$, respectively.

Recall that we are assuming $2\leq a\leq b\leq 2a$ and $a+b\equiv 0\pmod{3}$; say $a+b=3(N+1)$ with $N\geq 1$. Let $B_{a,b}$ be the region obtained by transferring the $(a,b)$-benzel into the square grid as in Section 2. We can embed $B_{a,b}$ inside of the Young diagram of $\lambda_{N}$. More precisely, it is not hard to see that there are exactly three boxes of maximal height in $B_{a,b}$, corresponding to the three rightmost cells of the $(a,b)$-benzel, and there are exactly three boxes of maximal height in $\lambda_{N}$. There is a unique way to embed $B_{a,b}$ into $\lambda_{N}$ so that the three maximal-height boxes in $B_{a,b}$ coincide with those of $\lambda_{N}$. Figures 13 and 14 illustrate this for $(a,b)=(7,8)$ and $(a,b)=(8,10)$, respectively; in each of these figures, the embedded image of $B_{a,b}$ is colored in blue in the diagram on the right.