Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels

There are also many ways to describe uncertainty relations, such as entropy [3, 4, 5, 6, 7], variance [8, 9, 10, 11] and majorization techniques [13, 12, 14, 15]. In particular, the quantum uncertainty can also be characterized by skew information. The skew information has been initially proposed by Wigner and Yanase [16], termed as Wigner-Yanase (WY) skew information. Then a more general quantity has been suggested by Dyson, called the Wigner-Yanase-Dyson (WYD) skew information [16]. This quantity has been further generalized in [17] and termed as generalized Wigner-Yanase-Dyson (GWYD) skew information. The uncertainty relations based on WY skew information, WYD skew information and GWYD skew information have been studied extensively [18, 20, 21, 19, 22, 23].

For a quantum state $\rho$ and an observable $A$, Furuichi, Yanagi and Kuriyama [24] defined another generalized Wigner-Yanase skew information,

$\displaystyle\mathrm{K}_{\rho}^{\alpha}(A)=-\frac{1}{2}\mathrm{Tr}\left(\left[\frac{\rho^{\alpha}+\rho^{1-\alpha}}{2},A\right]^{2}\right)=\frac{1}{2}\left\|\left[\frac{\rho^{\alpha}+\rho^{1-\alpha}}{2},A\right]\right\|^{2}~{},\,\,0\leq\alpha\leq 1,$

(2)

which, called as the weighted Wigner-Yanase-Dyson (WWYD) skew information in [23], is different from WYD skew information. Chen, Liang, Li and Wang [25] proposed then a generalized Wigner-Yanase skew information for arbitrary operator $E$ (not necessarily Hermitian),

$\displaystyle\mathrm{K}_{\rho}^{\alpha}(E)=-\frac{1}{2}\mathrm{Tr}\left(\left[\frac{\rho^{\alpha}+\rho^{1-\alpha}}{2},E^{{\dagger}}\right]\left[\frac{\rho^{\alpha}+\rho^{1-\alpha}}{2},E\right]\right)=\frac{1}{2}\left\|\left[\frac{\rho^{\alpha}+\rho^{1-\alpha}}{2},E\right]\right\|^{2}~{},\,\,0\leq\alpha\leq 1,$

(3)

which is termed as the modified weighted Wigner-Yanase-Dyson (MWWYD) skew information in [23]. By replacing the arithmetic mean of $\rho^{\alpha}$ and $\rho^{1-\alpha}$ with their convex combination, the two-parameter extension of the Wigner-Yanase skew information is introduced in [26],

	$\displaystyle\mathrm{K}_{\rho,\gamma}^{\alpha}(A)=$	$\displaystyle-\frac{1}{2}\mathrm{Tr}\left([(1-\gamma)\rho^{\alpha}+\gamma\rho^{1-\alpha},A]^{2}\right)$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\left\|\left[(1-\gamma)\rho^{\alpha}+\gamma\rho^{1-\alpha},A\right]\right\|^{2}~{},~{}\,\,0\leq\alpha\leq 1~{},\,\,0\leq\gamma\leq 1,$		(4)

which is called the $(\alpha,\gamma)$ weighted Wigner-Yanase-Dyson ($(\alpha,\gamma)$ WWYD) skew information in [27]. Note that Eq. (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) reduces to Eq. (2) when $\gamma=\frac{1}{2}$.

We defined the $(\alpha,\beta,\gamma)$ weighted Wigner-Yanase-Dyson ($(\alpha,\beta,\gamma)$ WWYD) skew information as [27],

	$\displaystyle\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(A)=$	$\displaystyle-\frac{1}{2}\mathrm{Tr}([(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta},A]^{2}\rho^{1-\alpha-\beta})$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\left\|\left[(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta},A\right]\rho^{\frac{1-\alpha-\beta}{2}}\right\|^{2},~{}~{}\alpha,\beta\geq 0,~{}\alpha+\beta\leq 1,0\leq\gamma\leq 1,$		(5)

which reduces to Eq. (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) when $\beta=1-\alpha$. We also defined the $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson ($(\alpha,\beta,\gamma)$ MWWYD) skew information with respect to a quantum state $\rho$ and an arbitrary operator $E$ (not necessarily Hermitian) in [27] as

	$\displaystyle\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E)=$	$\displaystyle-\frac{1}{2}\mathrm{Tr}([(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta},E^{{\dagger}}][(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta},E]\rho^{1-\alpha-\beta})$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\left\|\left[(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta},E\right]\rho^{\frac{1-\alpha-\beta}{2}}\right\|^{2},~{}~{}~{}\alpha,\beta\geq 0,~{}\alpha+\beta\leq 1,0\leq\gamma\leq 1,$		(6)

which is the non-Hermitian extension of the $(\alpha,\beta,\gamma)$ WWYD skew information. Eq. (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) reduces to Eq. (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) in [23] when $\gamma=\frac{1}{2}$. When $\beta=1-\alpha$, we obtain the $(\alpha,\gamma)$ modified weighted Wigner-Yanase-Dyson ($(\alpha,\gamma)$ MWWYD) skew information,

	$\displaystyle\mathrm{K}_{\rho,\gamma}^{\alpha}(E)=$	$\displaystyle-\frac{1}{2}\mathrm{Tr}([(1-\gamma)\rho^{\alpha}+\gamma\rho^{1-\alpha},E^{{\dagger}}][(1-\gamma)\rho^{\alpha}+\gamma\rho^{1-\alpha},E])$
	$\displaystyle=$	$\displaystyle\frac{1}{2}\left\|\left[(1-\gamma)\rho^{\alpha}+\gamma\rho^{1-\alpha},E\right]\right\|^{2},~{}~{}\,\,0\leq\alpha\leq 1~{},\,\,0\leq\gamma\leq 1,$		(7)

which is the non-Hermitian extension of the $(\alpha,\gamma)$ WWYD skew information. It reduces to Eq. (3) when $\gamma=\frac{1}{2}$.

Quantum channels characterize the general evolutions of quantum systems [29, 28], which play an essential role in quantum information processing. The uncertainty relations for quantum channels have been investigated from both the variance-based and entropic-based uncertainty measure [30, 31]. Specifically, the unitary channels are useful and commonly encountered in both quantum information theory and quantum computation [28]. Uncertainty relations for general unitary channels have been investigated both theoretically and experimentally [32, 33, 34]. Recently, the sum uncertainty relations for quantum channels have attracted considerable attention [35, 36, 37, 38, 27]. Fu, Sun and Luo [35] investigated the uncertainty relations for two quantum channels based on WY skew information for arbitrary operators. Afterwards, Zhang, Gao and Yan [36] generalized the uncertainty relations for two quantum channels to arbitrary $N$ quantum channels and proposed tighter lower bounds than the ones in [35] for two quantum channels. Zhang, Wu and Fei [37] proposed new bounds which are tighter than the results in [36]. Cai [38] confirmed that the results in [35] also hold for all metric-adjusted skew information. By employing the norm inequalities proposed in [37], we have established sum uncertainty relations for arbitrary $N$ quantum channels based on ($\alpha,\beta,\gamma$) MWWYD skew information [27] .

Following the idea in [39], the $(\alpha,\beta,\gamma)$ MWWYD skew information of a state $\rho$ with respect to a channel $\Phi$ has been defined as [27],

$$\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(\Phi)=\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{i}),$$

(8)

where $\alpha,\beta\geq 0,~{}\alpha+\beta\leq 1,0\leq\gamma\leq 1$, and $E_{i}(i=1,2,\cdots,n)$ are Kraus operators of the channel $\Phi$, i.e., $\Phi(\rho)=\sum_{i=1}^{n}E_{i}\rho E_{i}^{{\dagger}}$. Very recently, we provided the following uncertainty relations for arbitrary $N$ quantum channels $\{\Phi_{t}\}_{t=1}^{N}$ with $\Phi_{t}(\rho)=\sum_{i=1}^{n}E_{i}^{t}\rho(E_{i}^{t})^{\dagger},~{}t=1,2,\cdots,N$ ($N>2$) [27],

	$\displaystyle\sum_{t=1}^{N}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(\Phi_{t})\geq$	$\displaystyle\mathop{\mathrm{max}}\limits_{\pi_{t},\pi_{s}\in S_{n}}\frac{1}{N-2}\left\{\sum_{1\leq t<s\leq N}\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}+E_{\pi_{s}(i)}^{s})\right.$
		$\displaystyle\left.-\frac{1}{(N-1)^{2}}\left[\sum_{i=1}^{n}\left(\sum_{1\leq t<s\leq N}\sqrt{\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}+E_{\pi_{s}(i)}^{s})}\right)^{2}\right]\right\},$		(9)

	$\displaystyle\sum_{t=1}^{N}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(\Phi_{t})\geq$	$\displaystyle\mathop{\mathrm{max}}\limits_{\pi_{t},\pi_{s}\in S_{n}}\left\{\frac{1}{N}\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}\left(\sum_{t=1}^{N}E_{\pi_{t}(i)}^{t}\right)\right.$
		$\displaystyle\left.+\frac{2}{N^{2}(N-1)}\left[\sum_{i=1}^{n}\left(\sum_{1\leq t<s\leq N}\sqrt{\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}-E_{\pi_{s}(i)}^{s})}\right)^{2}\right]\right\},$		(10)

	$\displaystyle\sum_{t=1}^{N}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(\Phi_{t})\geq$	$\displaystyle\mathop{\mathrm{max}}\limits_{\pi_{t},\pi_{s}\in S_{n}}\frac{1}{2(N-1)}\left\{\frac{2}{N(N-1)}\left[\sum_{i=1}^{n}\left(\sum_{1\leq t<s\leq N}\sqrt{\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}\pm E_{\pi_{s}(i)}^{s})}\right)^{2}\right]\right.$
		$\displaystyle\left.+\sum_{1\leq t<s\leq N}\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}\mp E_{\pi_{s}(i)}^{s})\right\},$		(11)

where $\alpha,\beta\geq 0,~{}\alpha+\beta\leq 1,~{}0\leq\gamma\leq 1$, $S_{n}$ is the $n$-element permutation group and $\pi_{t},\pi_{s}\in S_{n}$ are arbitrary $n$-element permutations.

The remainder of this paper is structured as follows. In Section 2, we explore the $(\alpha,\beta,\gamma)$ MWWYD skew information-based sum uncertainty relations for arbitrary $N$ quantum channels. Especially, we show that when $\beta=1-\alpha$, i.e., when the $(\alpha,\beta,\gamma)$ MWWYD skew information becomes the $(\alpha,\gamma)$ MWWYD skew information, our new bounds are tighter than the existing ones by a detailed example. The uncertainty relations based on the $(\alpha,\beta,\gamma)$ MWWYD skew information for unitary channels are discussed in Section 3. We conclude with a summary in Section 4.

Let $\Phi$ be a quantum channel with Kraus representation, $\Phi(\rho)=\sum_{i=1}^{n}E_{i}\rho E_{i}^{{\dagger}}$. Following the idea in [37], we define the ($\alpha,\beta,\gamma$) MWWYD skew information of the channel as,

$\displaystyle\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(\Phi)=\frac{1}{2}\mathrm{Tr}(u^{\dagger}u)=\frac{1}{2}\|u\|^{2},$

(12)

where $\alpha,\beta\geq 0$, $\alpha+\beta\leq 1$, $0\leq\gamma\leq 1$, $u=(\left[(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta},E_{1}\right]\rho^{\frac{1-\alpha-\beta}{2}},\left[(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta}\right.$
$\left.,E_{2}\right]\rho^{\frac{1-\alpha-\beta}{2}},\cdots,\left[(1-\gamma)\rho^{\alpha}+\gamma\rho^{\beta},E_{n}\right]\rho^{\frac{1-\alpha-\beta}{2}})$ characterizes some intrinsic features of both the quantum state and the quantum channel. By employing operator norm inequalities and Eq. (12), we have the following theorem for arbitrary $N$ quantum channels.

Theorem 1 Let $\Phi_{1},\cdots,\Phi_{N}$ be $N$ quantum channels with Kraus representations $\Phi_{t}(\rho)=\sum_{i=1}^{n}E_{i}^{t}\rho(E_{i}^{t})^{\dagger},~{}t=1,2,\cdots,N$ ($N>2$). We have

$\displaystyle\sum_{t=1}^{N}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(\Phi_{t})\geq\mathop{\mathrm{max}}\{LB1,LB2,LB3\},$

(13)

where

	$\displaystyle LB1$	$\displaystyle=\mathop{\mathrm{max}}\limits_{\pi_{t},\pi_{s}\in S_{n}}\frac{1}{N-2}\left\{\sum_{1\leq t<s\leq N}\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}+E_{\pi_{s}(i)}^{s})\right.$
		$\displaystyle\left.-\frac{1}{(N-1)^{2}}\left[\sum_{1\leq t<s\leq N}\sqrt{\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}+E_{\pi_{s}(i)}^{s})}\right]^{2}\right\},$		(14)

	$\displaystyle LB2$	$\displaystyle=\mathop{\mathrm{max}}\limits_{\pi_{t},\pi_{s}\in S_{n}}\left\{\frac{1}{N}\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}\left(\sum_{t=1}^{N}E_{\pi_{t}(i)}^{t}\right)\right.$
		$\displaystyle\left.+\frac{2}{N^{2}(N-1)}\left[\sum_{1\leq t<s\leq N}\sqrt{\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}-E_{\pi_{s}(i)}^{s})}\right]^{2}\right\},$		(15)

	$\displaystyle LB3$	$\displaystyle=\mathop{\mathrm{max}}\limits_{\pi_{t},\pi_{s}\in S_{n}}\frac{1}{2(N-1)}\left\{\sum_{1\leq t<s\leq N}\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}\pm E_{\pi_{s}(i)}^{s})\right.$
		$\displaystyle\left.+\frac{2}{N(N-1)}\left[\sum_{1\leq t<s\leq N}\sqrt{\sum_{i=1}^{n}\mathrm{K}_{\rho,\gamma}^{\alpha,\beta}(E_{\pi_{t}(i)}^{t}\mp E_{\pi_{s}(i)}^{s})}\right]^{2}\right\},$		(16)

$\alpha,\beta\geq 0$, $\alpha+\beta\leq 1$, $0\leq\gamma\leq 1$, $S_{n}$ is the n-element permutation group and $\pi_{t},\pi_{s}\in S_{n}$ are arbitrary $n$-element permutations.

Note that when $\alpha=\beta=\frac{1}{2}$, Theorem 1 reduce to Theorem 1 in [37]. As a special case, we use the $(\alpha,\gamma)$ MWWYD skew information to compare our lower bounds with the existing ones. For convenience, we denote by $\overline{LB}1$, $\overline{LB}2$, $\overline{LB}3$ the right hand sides of (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels), (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) and (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels), respectively. The following example shows that our results give tighter lower bounds than $\overline{LB}1$, $\overline{LB}2$ and $\overline{LB}3$, see Figure 1.

Example 1 Given a qubit state $\rho=\frac{1}{2}(\mathbf{1}+\mathbf{r}\cdot\bm{\sigma})$, where $\mathbf{1}$ is the $2\times 2$ identity matrix, $\mathbf{r}=(\frac{\sqrt{3}}{2}\cos\theta,\frac{\sqrt{3}}{2}\sin\theta,0)$, $\bm{\sigma}=(\sigma_{1},\sigma_{2},\sigma_{3})$ with $\sigma_{j}$ $(j=1,2,3)$ the Pauli matrices, and $\mathbf{r}\cdot\bm{\sigma}=\sum^{3}_{j=1}r_{j}\sigma_{j}$. We consider the following three quantum channels:
(i) the amplitude damping channel $\Phi_{AD}$,

$\displaystyle\Phi_{AD}(\rho)=\sum_{i=1}^{2}A_{i}\rho A_{i}^{\dagger},\quad A_{1}=|0\rangle\langle 0|+\sqrt{1-q}|1\rangle\langle 1|,\quad A_{2}=\sqrt{q}|1\rangle\langle 1|;$

(ii) the phase damping channel $\Phi_{PD}$,

$\displaystyle\Phi_{PD}(\rho)=\sum_{i=1}^{2}B_{i}\rho B_{i}^{\dagger},\quad B_{1}=|0\rangle\langle 0|+\sqrt{1-q}|1\rangle\langle 1|,\quad B_{2}=\sqrt{q}|0\rangle\langle 1|;$

(iii) the bit flip channel $\Phi_{BF}$,

$\displaystyle\Phi_{BF}(\rho)=\sum_{i=1}^{2}C_{i}\rho C_{i}^{\dagger},\quad C_{1}=\sqrt{q}|0\rangle\langle 0|+\sqrt{q}|1\rangle\langle 1|,\quad C_{2}=\sqrt{1-q}(|0\rangle\langle 1|+|1\rangle\langle 0|)$

with $0\leq q<1$, respectively.

For the case $\alpha=\gamma=\frac{1}{4}$, $q=0.2$ and $\theta=\frac{\pi}{2}$, we have $\mathrm{K}_{\rho,\frac{1}{4}}^{\frac{1}{4}}(\Phi_{AD})+\mathrm{K}_{\rho,\frac{1}{4}}^{\frac{1}{4}}(\Phi_{PD})+\mathrm{K}_{\rho,\frac{1}{4}}^{\frac{1}{4}}(\Phi_{BF})=0.283955$. The lower bounds $\overline{LB}1$, $\overline{LB}2$ and $\overline{LB}3$ are 0.275596, 0.2644 and 0.256419, respectively, and the lower bounds $LB1$, $LB2$ and $LB3$ are 0.260707, 0.26726 and 0.265758, respectively. Obviously, $LB2$ is tightest among $LB1$, $LB2$ and $LB3$, which is also greater than $\overline{LB}2$ and $\overline{LB}3$ given in [27].

We also consider the case $\alpha=\gamma=\frac{1}{4}$. For $q=0.4$ and $q=0.9$, the sum and the lower bounds $\overline{LB}1$, $\overline{LB}2$, $\overline{LB}3$, $LB1$, $LB2$ and $LB3$ are shown in Figure 1, respectively. Especially, for $q=0.4$, the sum and the lower bounds are calculated for some special $\theta$, as listed in Table 1. It can be seen that for $q=0.4$, our lower bounds $LB2$ and $LB3$ are tighter than $\overline{LB}1$, $\overline{LB}2$ and $\overline{LB}3$. While for $q=0.9$, our lower bounds $LB2$ and $LB3$ are tighter than $\overline{LB}1$, $\overline{LB}2$ and $\overline{LB}3$.

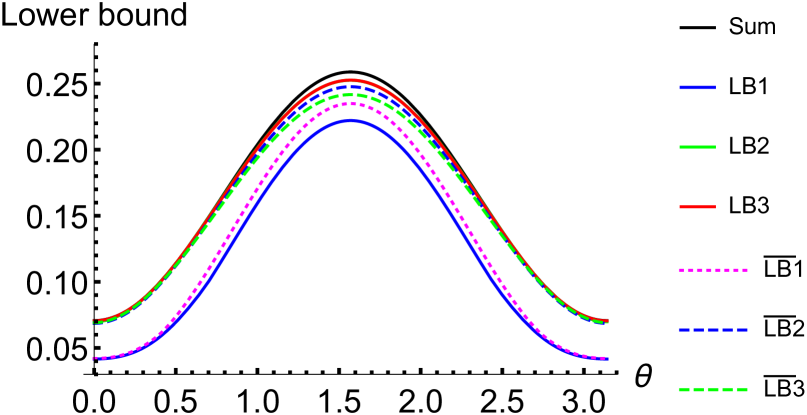
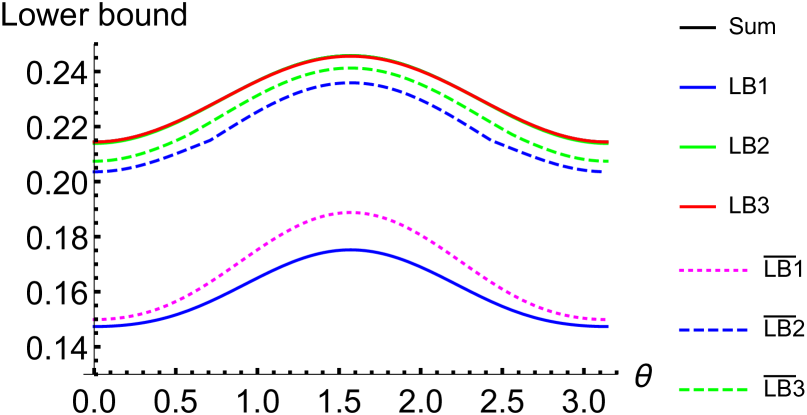
Table 1. Comparison among the uncertainty lower bounds q=0.4 $\overline{LB}1$ $\overline{LB}2$ $\overline{LB}3$ $LB1$ $LB2$ $LB3$ sum $\theta=\pi/2$ 0.234918 0.247658 0.241686 0.222065 0.252565 0.252654 0.258817 $\theta=\pi/3$ 0.17968 0.204421 0.20082 0.168362 0.208841 0.208534 0.211782 $\theta=\pi/5$ 0.0954994 0.13303 0.132687 0.0879256 0.135648 0.135459 0.135679 $\theta=\pi/7$ 0.066361 0.104405 0.104922 0.0632504 0.106043 0.106062 0.106096

The above results show that Theorem 1 in this paper improve the existing results ones given in [27].

Note that (19), (20) and (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) of Theorem 2 reduce to (13), (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) and (Tighter uncertainty relations based on $(\alpha,\beta,\gamma)$ modified weighted Wigner-Yanase-Dyson skew information of quantum channels) in [37] when $\alpha=\gamma=\frac{1}{2}$, respectively.

Example 2 Given a qubit state $\rho=\frac{1}{2}(\mathbf{1}+\mathbf{r}\cdot\bm{\sigma})$ with $\mathbf{r}=(\frac{\sqrt{2}}{2}\cos\theta,\frac{\sqrt{2}}{2}\sin\theta,0)$. Consider the following three unitary operators,

$$U_{1}=e^{\frac{i\pi\sigma_{1}}{8}}=\left(\begin{matrix}\cos\frac{\pi}{8}\ i\sin\frac{\pi}{8}\\ i\sin\frac{\pi}{8}\ \cos\frac{\pi}{8}\end{matrix}\right),U_{2}=e^{\frac{i\pi\sigma_{2}}{8}}=\left(\begin{matrix}\cos\frac{\pi}{8}\ \sin\frac{\pi}{8}\\ -\sin\frac{\pi}{8}\ \cos\frac{\pi}{8}\end{matrix}\right),U_{3}=e^{\frac{i\pi\sigma_{3}}{8}}=\left(\begin{matrix}e^{i\frac{\pi}{8}}\quad 0\\ \ 0\ -e^{i\frac{\pi}{8}}\end{matrix}\right),$$

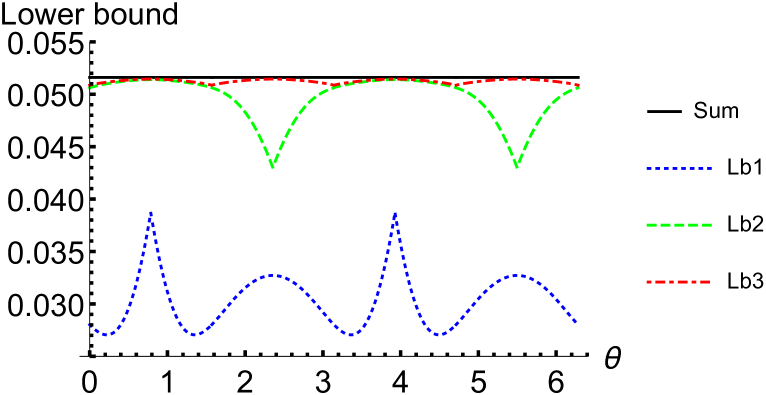
which correspond to the rotations around the $z$ axis of the Bloch sphere. When $\beta=1-\alpha$, i.e., when the $(\alpha,\beta,\gamma)$ MWWYD skew information reduces to the $(\alpha,\gamma)$ MWWYD skew information, the comparison among the lower bounds of Theorem 2 is presented in Figure 2, from which one sees that the lower bound $Lb3$ is tighter than $Lb2$ and $Lb1$ in this case.