Tight-binding model of Pt-based jacutingaites as combination of the honeycomb and kagome lattices

The crystal structure of jacutingaite ($M_{2}NX_{3}$, $\textrm{Z}=2$) has space group $P\bar{3}m1$ [25, 26]. The Pt-based jacutingaite monolayer and Wyckoff position of their elements are illustrated in Figure 1, where $M=\mathrm{Pt}$. The electronic characteristics of jacutingaite-family materials can be understood by taking into account their structure, which, with respect to the low-lying bands can be described as two interpenetrating honeycomb and kagome sub-lattices.

Jacutingaite-type systems have structural and electronic characteristics of both types of lattices. Thus, we propose a TB model that combines these two sub-lattices, i.e., a honeycomb-kagome (HK) structure, in order to obtain a better agreement with the DFT energy bands near the SOC energy gap, in comparison with the pure Kane-Mele model.

As shown in the next section the orbitals that contribute most significantly to the conduction and valence bands around the topological energy gap are S_1/2 orbitals from $N$ metal e 5D_5/2 orbitals from Pt $3e$. By taking into account only these elements, one can visualize (see Figure 2) the jacutingaite-like structure as a honeycomb buckled lattice, resembling the silicene or germanene structure, composed of $N$ metals and a planar kagome lattice formed by the Pt $3e$ elements.

In Figure 3 (a) the dotted lines connecting $N$ metals form the hexagons of a honeycomb lattice. The region highlighted by the black solid contour depicts a unit cell, showing that two $N$ metals per cell occupy non-equivalent sites, which are labeled as $A$ and $B$. We considered the on-site energy, nearest-neighbor (NN) and NNN hopping parameters as indicated by the arrows, as well as the SOC for the construction of the corresponding Hamiltonian term based on the buckled sub-lattice formed by $N$ metals.

In Figure 3 (b) the dotted lines connecting the Pt elements form a triangular geometry with an arrangement of interconnected hexagons. There are three Pt elements per cell occupying non-equivalent sites, which are labeled as $C$, $D$ and $E$. As in the previous case, we included an on-site energy, NN and NNN hopping parameters and SOC, as indicated by the arrows, for the construction of the Hamiltonian term for the planar sub-lattice formed by Pt elements.

Figure 3 (c) depicts the system as two interpenetrating honeycomb buckled and kagome planar sub-lattices. Thus, we considered the NN and NNN hopping parameters as indicated by the arrows, connecting a Pt to a $N$ metal, and two SOC terms, namely Pt–$N$–Pt and Pt–$N$–Pt–$N$–Pt. Figure 4 displays all cases of SOC mentioned. All possible hoppings for the distances smaller than that between NNN $N$ metal are used in this model.

We define the Hamiltonian for jacutingaite-like systems as:

$$\hat{H}_{HK}=\hat{H}_{\mathrm{h}}+\hat{H}_{\mathrm{k}}+\hat{H}_{\mathrm{hk}}$$

(1)

where the honeycomb and kagome sub-lattices terms are:

$$\hat{H}_{\mathrm{h}},\hat{H}_{\mathrm{k}}=\hat{H}_{\mathrm{on-site}}+\hat{H}_{\mathrm{NN}}+\hat{H}_{\mathrm{NNN}}+\hat{H}_{\mathrm{SOC}},$$

(2)

with

$$\hat{H}_{\mathrm{on-site}}=\sum_{p,\alpha}\epsilon_{p,\alpha}c^{\dagger}_{p;\alpha}c_{p,\alpha},$$

(3)

$$\hat{H}_{\mathrm{NN}}=-\sum_{\langle pq\rangle;\alpha}t^{{}^{\prime}}_{pq}c^{\dagger}_{p,\alpha}c_{q,\alpha},$$

(4)

$$\hat{H}_{\mathrm{NNN}}=-\sum_{\langle\langle pq\rangle\rangle;\alpha}t^{{}^{\prime\prime}}_{pq}c^{\dagger}_{p,\alpha}c_{q,\alpha},$$

(5)

$$\hat{H}_{\mathrm{SOC}}=i\sum_{\langle\langle pq\rangle\rangle;\alpha\beta}\lambda^{{}^{\prime\prime}}_{pq}c^{\dagger}_{p,\alpha}\big{(}\nu_{pq}\cdot\bm{\sigma}\big{)}c_{q,\beta}.$$

(6)

The first term contains the on-site energies given by $\epsilon_{p,\alpha}$, where $p$ and $\alpha$ represent an orbital and spin, respectively; the $\hat{H}_{\mathrm{NN}}$ and $\hat{H}_{\mathrm{NNN}}$ terms describe NN and NNN hopping between $p$ and $q$ orbitals, being $t^{\prime}_{pq}$ and $t^{\prime\prime}_{pq}$ the respective parameters and $\hat{H}_{\mathrm{SOC}}$ the SOC terms, with $\lambda^{{}^{\prime\prime}}_{pq}$ as SOC parameter between $p$ and $q$ orbitals and also between $\alpha$ and $\beta$ spin, where $c^{\dagger}_{p,\alpha}$($c_{p,\alpha}$) is the fermion creation (annihilation) operator at site $p$ and with spin $\alpha$ and $\nu_{pq}$ is a unit vector that connects the sites of localized $p$ and $q$ orbitals by a single intermediate site. Finally, $\bm{\sigma}=(\sigma_{x},\sigma_{y},\sigma_{z})$ is the vector of Pauli matrices. Figure 3 (c) illustrates the terms above.

For the honeycomb sub-lattice we have $\nu_{pq}$ as:

$$\nu_{im}=\Bigg{[}\frac{\big{(}\bm{d}_{ij}+\bm{d}_{jk}\big{)}\times\big{(}\bm{d}_{kl}+\bm{d}_{lm}\big{)}}{|\big{(}\bm{d}_{ij}+\bm{d}_{jk}\big{)}\times\big{(}\bm{d}_{kl}+\bm{d}_{lm}\big{)}|}\Bigg{]},$$

(7)

whereas for the kagome sub-lattice it is given by:

$$\nu_{jn}=\Bigg{[}\frac{\bm{d}_{jk}\times\bm{d}_{kl}+\bm{d}_{lm}\times\bm{d}_{mn}}{|\bm{d}_{jk}\times\bm{d}_{kl}+\bm{d}_{lm}\times\bm{d}_{mn}|}\Bigg{]},$$

(8)

with the $\{i,k,m\}$ indices refer to $h$S_1/2 orbitals from different sites belonging to the honeycomb sublattice, where $h=4,5\textrm{ and }6$ for $N=$ Zn, Cd and Hg, respectively, whereas the $\{j,l,n\}$ indices representing 5D_5/2 orbitals from different sites belonging to the kagome sublattice. Figures 4 (a) and (b) illustrates the definitions of Eqs. 7 and 8, respectively.

Next, $\hat{H}_{\mathrm{hk}}$ is the term that couples elements from different sub-lattices:

$$\hat{H}_{\mathrm{hk}}=\hat{H}_{\mathrm{NN}}^{ij}+\hat{H}_{\mathrm{NNN}}^{ij}+\hat{H}_{\mathrm{SOC}}^{jl}+\hat{H}_{\mathrm{SOC}}^{il}.$$

(9)

The $\hat{H}_{\mathrm{NN}}^{ij}$ and $\hat{H}_{\mathrm{NNN}}^{ij}$ are Hamiltonian describe NN and NNN hopping between $i$ and $j$ orbitals, being $t^{\prime}_{ij}$ and $t^{\prime\prime}_{ij}$ the respective parameters:

$$\hat{H}_{\mathrm{NN}}^{ij}=-\sum_{\langle ij\rangle;\alpha}t^{{}^{\prime}}_{ij}c^{\dagger}_{i,\alpha}c_{j,\alpha}$$

(10)

$$\hat{H}_{\mathrm{NNN}}^{ij}=-\sum_{\langle\langle ij\rangle\rangle;\alpha}t^{{}^{\prime\prime}}_{ij}c^{\dagger}_{i,\alpha}c_{j,\alpha}$$

(11)

and $\hat{H}_{\mathrm{SOC}}^{jl}$ as SOC Hamiltonian, with $\lambda^{{}^{\prime\prime}}_{jl}$ as SOC parameter between $j$ and $l$ orbitals of Pt–$N$–Pt:

$$\hat{H}_{\mathrm{SOC}}^{jl}=i\sum_{\langle jl\rangle}\lambda^{{}^{\prime}}_{jl}c^{\dagger}_{j,\alpha}\big{(}\nu_{jl}\cdot\bm{\sigma}\big{)}c_{l,\beta}$$

(12)

being:

$$\nu_{jl}=\Bigg{[}\frac{\bm{d}_{jk}\times\bm{d}_{kl}}{|\bm{d}_{jk}\times\bm{d}_{kl}|}\Bigg{]}$$

(13)

and $\hat{H}_{\mathrm{SOC}}^{il}$ as SOC Hamiltonian, with $\lambda^{{}^{\prime\prime}}_{il}$ as SOC parameter between $i$ and $l$ orbitals of Pt–N–Pt–N–Pt:

$$\hat{H}_{\mathrm{SOC}}^{il}=i\sum_{\langle\langle il\rangle\rangle}\lambda^{{}^{\prime\prime}}_{il}c^{\dagger}_{i,\alpha}\big{(}\nu_{il}\cdot\bm{\sigma}\big{)}c_{l,\beta}$$

(14)

being:

$$\nu_{il}=\Bigg{[}\frac{(\bm{d}_{ij}+\bm{d}_{jk})\times\bm{d}_{kl}}{|(\bm{d}_{ij}+\bm{d}_{jk})\times\bm{d}_{kl}|}\Bigg{]}$$

(15)

Figures 4 (d) and (c) illustrates the definitions of Eqs. 13 and 15, respectively.

Thus, the present TB model has twelve independent parameters, which can be adjusted using as reference the results from ab initio calculations, as shown below.

In order to investigate the structural and electronic properties of the Pt-based jacutingaite monolayers, first-principles DFT-based calculations [32, 33] were performed using the plane waves method as implemented on the Quantum ESPRESSO software package [34, 35]. A vacuum distance of 20 Å and dipole correction were inserted to decouple the periodic images [36].

The generalized gradient approximation of the Perdew–Burke–Ernzerhof (GGA-PBE) functional [37] was used to describe the exchange-correlation interaction. In order to solve Kohn-Sham equations, the valence electrons were treated explicitly while central electrons have been replaced by the optimized norm-conserving Vanderbilt pseudopotential [38, 39].

The structural optimization was performed by using Broyden–Fletcher–Goldfarb– Shanno interactive (BFGS) to minimize the total energy calculated by DFT [40, 41, 42], with energy threshold of $4.0\times 10^{-5}$ Ry and Hellmann-Feynman forces on each atom smaller than $4.0\times 10^{-5}$ Ry/Å. The self-consistent energy threshold was of $1.0\times 10^{-8}$ Ry, the plane-wave energy cutoff was set as 120 Ry and the Brillouin zone (BZ) is sampled by a $\Gamma$-centered $12\times 12\times 1$ Monkhrost-Pack grid.

Calculations were performed both with and without SOC. The calculation without the consideration of SOC were used as an intermediate step for the optimization of atomic structure and TB hopping parameters. The definite results are determined from the DFT calculations with the inclusion SOC considering the previously described results as starting points.

The PythTB package [43] was used for the TB calculations. The parameters of on-site energies and hopping amplitudes were adjusted to fit the DFT band structure in part of the BZ, for case without and with SOC, for applying the minimization process using the BFGS algorithm [40], for each $\vec{k}$ along the line between K($\textrm{K}^{\prime}$) and M points, where the cost function to be minimized

$$\mathrm{J}=\sum_{n,k}\Delta\epsilon_{n,\textbf{k}}=\sum_{n,k}\Big{(}\epsilon^{DFT}_{n,\textbf{k}}-\epsilon_{n,\textbf{k}}^{TB}\Big{)}^{2},$$

(16)

with $\epsilon^{DFT}_{n,\textbf{k}}$ and $\epsilon^{TB}_{n,\textbf{k}}$ being the energy of the $n$ band in momentum space as given by DFT and TB approaches, respectively. The index $n$ may assume four values, including the top of the valance band and the bottom of conduction band. The window of momentum space is such that $\textbf{k}\in$ $g$–M–K–$g^{\prime}$, where $g$ and $g^{\prime}$ are points in $\Gamma$–M and $\Gamma$–K paths, respectively. These points are adjusted to achieve a good description of the top of the valence band and bottom of the conduction band by the TB model. The convergence tolerance used was $10^{-11}$ eV. The bands considered were the valence and conduction bands around the Fermi level.

The first minimization consisted of finding the parameters corresponding to the SOC independent terms. Those were kept constant and a new minimization was performed to obtain the parameters corresponding to the SOC dependent terms. To improve the fit quality, a third minimization was carried out: parameters corresponding to the SOC dependent terms were kept fixed and those corresponding to the SOC independent terms were minimized. Lastly, the SOC independent terms were tested to verify whether they return band structures with Dirac points in the K and K^′ points. The code for our TB model of Pt-based jacutingaites presented in this work is available at [44].

The jacutingaite crystal presents hexagonal lattice and it also has a buckled honeycomb structure formed by $N$ elements, around a plane formed by the $M$ elements [25, 26, 31], as shown in Figure 1. For Pt-based jacutingaite, the lattice parameters and vertical buckling $N$–Pt–$N$ are presented in Table 1. The obtained structural parameters are in good agreement with other theoretical predictions found in literature [31].

For Pt-based jacutingaite, in the absence of SOC, the hexagonal $N$–Pt–$N$ buckled structure gives rise to Dirac points at the K (and K^′) points in momentum space. The projection of the energy bands near the Fermi level shows that the cone states are mostly composed by $N$ $2d$ transition metal (S_1/2 orbitals) hybridized with Pt $3e$ (5D_5/2 orbitals), which agrees with Reference [31].

Some features of the Dirac cones in jacutingaite differ from those of graphene. In the latter, the Dirac cones exhibit linear dispersion around the Fermi level at each K and K^′ points within the BZ. The introduction of SOC creates a gap of approximately 7 meV [45]. For Pt${}_{2}NX_{3}$, the SOC opens a gap between 50 meV – 154 meV at DFT-GGA-PBE level (Table 1). Already in this energy range is enable dissipationless charge transport at room temperature. Moreover, there are regions of the energy bands along K(K^′)–M, where the electron energy does not change significantly with respect to the momentum.

The honeycomb lattice and the sub-lattice symmetry of graphene is responsible for some of its unique electronic properties [1, 2, 3]. On the other hand, the presence of quasi-flat behavior of electronic bands in M-K region may be exhibited by other structures, such as the kagome lattice. Both can present topological electronic states and robustness against perturbations. However, in the absence of a magnetic field, the topological phase transition occurs only when SOC is null and gaps closes at K (or K^′) in the honeycomb lattice in the Kane-Mele model. The phase transitions in kagome lattice can be driven by the real NNN coupling and energy gap transitions with bands touching at other points in BZ different from K (and K^′) [46]. As the Pt $3e$ elements contribute significantly to the energy gap, the introduction of these two sublattices allows for the development of a more accurate TB model, which in turn may be used to study the properties of jacutingaite-based nanostructures. Some of those having been explored in the literature [47, 48, 49, 50, 51, 52] but not extended to larger systems.

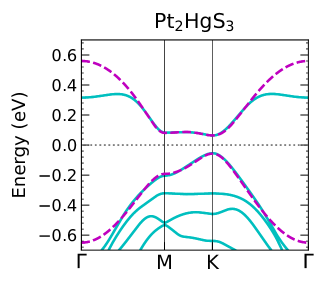
Figure 5 shows band structures for several Pt-based jacutingaite monolayers calculated by DFT-GGA (blue solid lines), as well as the results from the TB model (pink dashed lines). The TB results show very good agreement with the DFT bands within an energy interval of 0.6 eV to 1.0 eV and around the M–K path, which exhibits a quasi-flat dispersion in the conduction bands.

A reasonably accurate description of the electronic structure of the jacutingaite can be realized using an approach based on Maximally Localized Wannier Functions (MLWFs) [29]. The TB Hamiltonian obtained from the construction of MLWFs naturally involves a very large number of hopping parameters. For a structure such as that of jacutingaite, within the MLWFs formalism the number of hoppings terms is of the order of thousands. Thus, in order to study finite nanostructures and electronic transport properties, where a large real-space lattice is often required, the computational cost becomes very high. The model proposed in the present work is a TB Hamiltonian with an interaction radius reaching up to the $N$-NNN distance, and provides an accurate low-energy description with only twelve hopping parameters.

From the proposed model, and based on the band structures obtained via DFT, the twelve hopping parameters were defined for each monolayer structure and arranged in the Table 2, 3 and 4, as shown in the Figure 3 (a), (b) and (c), respectively, and for each term of the Equation 1.

The hopping terms in Table 2 are relatively similar for the different Pt-based jacutingaites, except for the $t^{{}^{\prime\prime}}_{\textrm{Zn}-\textrm{Zn}}$, which is a consequence of the more dispersive valence band of Pt₂ZnTe₃ as a way of compensating the SOC contribution from Te. The real NNN hopping terms are comparable to the SOC terms, which highlights its importance. In fact, if these terms are neglected, the results become qualitatively different from those obtained from first principles calculations. The negative value of $\lambda^{{}^{\prime\prime}}_{\textrm{Pt-Zn}}$ in Table 4 is due to a greater energy difference between M and K(K^′) points, being $E_{\textrm{M}}<E_{\textrm{K(K}^{\prime}\textrm{)}}$ in the conduction band compared to Pt₂ZnSe₃.

For Pt₂CdSe₃, Pt₂CdTe₃, Pt₂HgS₃ and Pt₂HgSe₃ the $\lambda^{{}^{\prime}}_{\textrm{Pt-Pt}}$ and $\lambda^{{}^{\prime\prime}}_{\textrm{Pt-Pt}}$ is about an order of magnitude larger than $\lambda^{{}^{\prime\prime}}_{N-N}$, due to a stronger hydridization between the orbitals 5D_5/2 and $h$S_1/2 for these monolayers.

In systems with strong SOC such as jacutingaite-like materials, the quantum numbers $|ljm_{j}m_{s}\rangle$ are strongly entangled and accurately describe the complexity of the electronic states of these materials. In this work, we are not considering time reversal symmetry breaking, therefore, we do not evidence the $m_{j}$.

In Figure 5 we show a comparison between the band structures for each Pt-based jacutingaite monolayer calculated by DFT-GGA and that obtained from the TB model described in the previous section. The TB model for interpenetrating honeycomb and kagome lattices shows good agreement with the DFT-GGA results and is quite accurate along the K(K^′)–M direction. We emphasize that this level of accuracy is missing in previous studies, where simpler TB Hamiltonians based on the Kane-Mele model were employed.

It is worth pointing out that quasi-flat bands are not seen in the Kane-Mele model and the states along K(K^′)–M present prominent features of the kagome lattice band, as illustrated in Figure 6 for the Pt₂HgSe₃. The same qualitative behavior is observed for the other considered materials.

The $\hat{H}_{\mathrm{hk}}$ term, which couples the honeycomb and kagome sub-lattices, as given by Equation 9, is responsible for the characteristic shape of the conduction band of jacutingaite, specifically the band flattening along M–K(K^′) direction. In Figure 7 one can visualize, for the case of Pt₂HgSe₃, the energy dispersion both with and without the inclusion of such term in Equation 1. The relevance of considering this coupling when dealing with Pt-based jacutingaite using tight-binding models thus becomes evident.

For Pt-based jacutingaites monolayers, in the absence of SOC, a calculation of the hybrid Wannier center (HWC) from the present TB model, one can observe that they are non-topological systems (see SM, Figure 2 [53]). The SOC thus opens the topological energy gap and that information is also captured by this model (see SM, Figure 3 [53]).

The calculation of topological invariants allows determining the topological character of a material based on its bulk structure [54], which is very useful for DFT simulation of crystalline systems. Another approach is to explore topological properties in materials is to consider finite size systems and investigate their edge or surface states. The combination of DFT simulations with the second strategy often implies high computational cost, which can be avoided by the use of a DFT derived TB model.

Edge states in topological 2D systems are topologically protected and robust against local perturbations [13, 15]. In case of Pt-based jacutingaite monolayers, which are QSH semiconductors, the edge states are protected by time-reversal symmetry and against backscattering processes, presenting robustness against non-magnetic perturbations [24, 29]. Understanding and manipulating these edge states not only defines the stability of materials, but also diversifies the possibilities for technological applications [20, 22, 45, 46, 47, 55].

We consider Pt-based jacutingaites nanoribbons with symmetric and asymmetric opposite edges. Figure 8 (a) and (b) shows nanoribbons with symmetric armchair and zigzag opposite edges. There is a pair of topological states of opposite spin at each edge connecting the valence and conduction bulk states, as we can visualize in their respective band structure in Figure 8. There are no significant differences in the edge states considering a symmetric or asymmetric configuration of the edge for all cases of Pt-based jacutingaites. The edges have the same geometry, with just a difference in translation in relation to each other and there are no overlap significant between edge states to change its energy dispersion. Since a nanoribbon is wide enough for the interaction between the edges not to destroy the topological character, the topological edge states are characterized predominantly by SOC.

The inclusion of NNN hopping terms can lead to the emergence of edge states, which has been a focus of recent studies [56]. The presence of these states, however, depends on the edge geometry, presence of defects, vacancies and external perturbations. In Figure 8 (a) it is possible to observe the existence of edge states within the energy spectrum of the conduction bands. These states emerge as a consequence of the mapping of asymmetric interactions (Figure 3 (b) and (c)).

Two Pt₂HgSe₃ nanoribbons with non-symmetric edges are represented in Figure 9 (a) and (b). For the case Pt₂HgSe₃ nanoribbon represents in Figure 9 (a) there is a small energy shift and a large momentum shift between the topological states of opposite edges, as shown in Figure 9 (c). For the case of the nanoribbon represents in Figure 9 (b) there is only a small energy shift between the topological states of opposite edges (see Figure 9 (d)). For other Pt-based jacutingaite nanoribbons see SM, Figure 4 and 5.

Depending on the geometric configuration of the edges, the topological edge states can be highly localized at the edges or be more delocalized. In Figure 10, there is a representation of the proportional penetration length of the edge states for Pt₂HgSe₃ nanoribbons with some possible terminations. For the configurations represented in Figure 10 (a) and (b), the states tend to be often localized, confined to a distance of up to $a$, for both cases, with the value of $a$ given in Table 1. For the configurations illustrated in Figure 10 (c) and (d), the edge states tend to be significantly more delocalized, with a penetration length of up to 7$a$ and 11$a$, respectively. A nanoribbon of width 85$a$ was considered for these terminations.

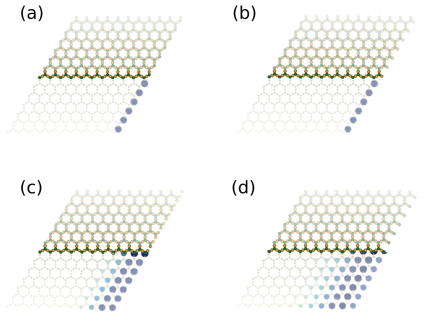
These results show that the corresponding dispersion bands and penetration length of the edge states to the topological edge states of Pt-based jacutingaite finite nanostructures are sensitive to the geometry of the edge. Additionally, these results demonstrate that the TB model can go beyond the computational limitations associated with DFT computational costs. The presented approach opens an avenue to explore large-scale structures in a computationally resource-efficient approach.