Threshold KNN-Shapley: A Linear-Time and Privacy-Friendly Approach to Data Valuation

The Shapley value (SV) [Sha53] is a classic concept from game theory to attribute the total gains generated by the coalition of all players. At a high level, it appraises each point based on the (weighted) average utility change caused by adding the point into different subsets of the training set. Formally, given a utility function $v(\cdot)$ and a training set $D$, the Shapley value of a data point $z\in D$ is defined as

For notation simplicity, when the context is clear, we omit the utility function and/or leave-one-out dataset, and write $\phi_{z}(D_{-z})$, $\phi_{z}(v)$ or $\phi_{z}$ depending on the specific dependency we want to stress.

The popularity of the Shapley value is attributable to the fact that it is the unique data value notion satisfying four axioms: Dummy player, Symmetry, Linearity, and Efficiency. We refer the readers to [GZ19], [JDW⁺19b] and the references therein for a detailed discussion about the interpretation and necessity of the four axioms in the ML context. Here, we introduce the linearity axiom which will be used later.

Formula (1) suggests that the exact Shapley value can be computationally prohibitive in general, as it requires evaluating $v(S)$ for all possible subsets $S\subseteq D$. Surprisingly, [JDW⁺19a, WJ23b] showed that for $K$-Nearest Neighbor (KNN), the computation of the exact Data Shapley score is highly efficient. Following its introduction, KNN-Shapley has rapidly gained attention and follow-up works across diverse areas of machine learning [GZE22, LZY20, LLY21, CS21]. In particular, it has been recognized by recent studies as “the most practical data valuation technique capable of handling large-scale data effectively” [PFTS21, KDI⁺22].

Specifically, the performance of an unweighted KNN classifier is typically evaluated by its validation accuracy. For a given validation set $D^{(\mathrm{val})}=\{z_{i}^{(\mathrm{val})}\}_{i=1}^{N_{\mathrm{val}}}$, we can define KNN’s utility function $v^{\texttt{KNN}}_{D^{(\mathrm{val})}}$ on a non-empty training set $S$ as $v^{\texttt{KNN}}_{D^{(\mathrm{val})}}(S):=\sum_{z^{(\mathrm{val})}\in D^{(\mathrm{val})}}v^{\texttt{KNN}}_{z^{(\mathrm{val})}}(S)$, where

is the probability of a (soft-label) KNN classifier in predicting the correct label for a validation point $z^{(\mathrm{val})}=(x^{(\mathrm{val})},y^{(\mathrm{val})})\in D^{(\mathrm{val})}$. In (2), $\pi^{(S)}(i;x^{(\mathrm{val})})$ is the index of the $i$th closest data point in $S$ to $x^{(\mathrm{val})}$. When $|S|=0$, $v^{\texttt{KNN}}_{z^{(\mathrm{val})}}(S)$ is set to the accuracy by random guessing. The distance is measured through suitable metrics such as $\ell_{2}$ distance. Here is the main result in [JDW⁺19a, WJ23b]:

Theorem 2 tells that for any validation data point $z^{(\mathrm{val})}$, we can compute the exact Shapley value $\phi^{\texttt{KNN}}_{z_{i}}\left(D_{-z_{i}};v^{\texttt{KNN}}_{z^{(\mathrm{val})}}\right)$ for all $z_{i}\in D$ by using a recursive formula within a total runtime of $O(N\log N)$. After computing the Shapley value $\phi^{\texttt{KNN}}_{z_{i}}\left(v^{\texttt{KNN}}_{z^{(\mathrm{val})}}\right)$ for each $z^{(\mathrm{val})}\in D^{(\mathrm{val})}$, one can compute the Shapley value corresponding to the full validation set by simply taking the sum of each $\phi^{\texttt{KNN}}_{z_{i}}\left(v^{\texttt{KNN}}_{z^{(\mathrm{val})}}\right)$, due to the linearity property (Theorem 1) of the Shapley value.

The growing popularity of data valuation techniques, particularly KNN-Shapley, underscores the critical need to mitigate the inherent privacy risks. In the quest for privacy protection, differential privacy (DP) [DMNS06] has emerged as the leading framework. DP has gained considerable recognition for providing robust, quantifiable privacy guarantees, thereby becoming the de-facto choice in privacy protection. However, while DP may seem like the ideal solution, its integration with KNN-Shapley is riddled with challenges. In this section, we introduce the background of DP and highlight the technical difficulties in constructing a differentially private variant for the current version of KNN-Shapley.

Background of Differential Privacy. We use $D,D^{\prime}\in\mathbb{N}^{\mathcal{X}}$ to denote two datasets with an unspecified size over space $\mathcal{X}$. We call two datasets $D$ and $D^{\prime}$ adjacent (denoted as $D\sim D^{\prime}$) if we can construct one by adding/removing one data point from the other, e.g., $D=D^{\prime}\cup\{z\}$ for some $z\in\mathcal{X}$.

That is, $(\varepsilon,\delta)$-DP requires that for all adjacent datasets $D,D^{\prime}$, the output distribution $\mathcal{M}(D)$ and $\mathcal{M}(D^{\prime})$ are close, where the closeness is measured by the parameters $\varepsilon$ and $\delta$. In our scenario, we would like to modify data valuation function $\phi_{z_{i}}(D_{-z_{i}})$ to satisfy $(\varepsilon,\delta)$-DP in order to protect the privacy of the rest of the dataset $D_{-z_{i}}$. Gaussian mechanism [DKM⁺06] is a common way for privatizing a function; it introduces Gaussian noise aligned with the function’s global sensitivity, which is the maximum output change when a single data point is added/removed from any given dataset.

Challenges in making KNN-Shapley being differentially private (overview). Here, we give an overview of the inherent difficulties in making the KNN-Shapley $\phi^{\texttt{KNN}}_{z_{i}}(D_{-z_{i}})$ (Theorem 2) to be differentially private, and we provide a more detailed discussion in Appendix B.3. (1) Large global sensitivity: In Appendix B.3, we show that the global sensitivity of $\phi^{\texttt{KNN}}_{z_{i}}(D_{-z_{i}})$ can significantly exceed the magnitude of $\phi^{\texttt{KNN}}_{z_{i}}$. Moreover, we prove that the global sensitivity bound cannot be further improved by constructing a specific pair of neighboring datasets that matches the bound. Hence, if we introduce random noise proportional to the global sensitivity bound, the resulting privatized data value score could substantially deviate from its non-private counterpart, thereby compromising the utility of the privatized data value scores. (2) Computational challenges in incorporating privacy amplification by subsampling: “Privacy amplification by subsampling” [BBG18] is a technique where the subsampling of a dataset amplifies the privacy guarantees due to the reduced probability of an individual’s data being included. Being able to incorporate such a technique is often important for achieving a decent privacy-utility tradeoff. However, in Appendix B.3 we show that the recursive nature of KNN-Shapley computation causes a significant increase in computational demand compared to non-private KNN-Shapley.

These challenges underscore the pressing need for new data valuation techniques that retain the efficacy and computational efficiency of KNN-Shapley, while being amenable to privatization.

Threshold-KNN (TKNN) [Ben75, ZZGW23] is a variant of KNN classifier that considers neighbors within a pre-specified threshold of the query example, rather than exclusively focusing on the exact $K$ nearest neighbors. Formally, for a training set $S$ and a validation data point $z^{(\mathrm{val})}=(x^{(\mathrm{val})},y^{(\mathrm{val})})$, we denote $\texttt{NB}_{x^{(\mathrm{val})},\tau}(S):=\{(x,y)|(x,y)\in S,d(x,x^{(\mathrm{val})})\leq\tau\}$ the set of neighbors of $x^{(\mathrm{val})}$ in $S$ within a pre-specified threshold $\tau$. Similar to the utility function for KNN, we define the utility function for TKNN classifier when using a validation set $D^{(\mathrm{val})}$ as the aggregated prediction accuracy $v^{\texttt{TKNN}}_{D^{(\mathrm{val})}}(S):=\sum_{z^{(\mathrm{val})}\in D^{(\mathrm{val})}}v^{\texttt{TKNN}}_{z^{(\mathrm{val})}}(S)$ where

where Constant can be the trivial accuracy of random guess.

Comparison with standard KNN. (1) Robustness to outliers. Compared with KNN, TKNN is better equipped to deal with prediction phase outliers [Ben75]. When predicting an outlier that is far from the entire training set, TKNN prevents the influence of distant, potentially irrelevant neighbors, leading to a more reliable prediction score for outliers. (2) Inference Efficiency. TKNN has slightly better computational efficiency compared to KNN, as it has $O(N)$ instead of $O(N\log N)$ inference time. This improvement is achieved because TKNN only requires the computation of neighbors within the threshold $\tau$, rather than searching for the exact $K$ nearest neighbors. (3) TKNN is also a consistent estimator. The consistency of standard KNN is a well-known theoretical result [GKKW02]. That is, for any target function that satisfies certain regularity conditions, KNN binary classifier/regressor is guaranteed to converge to the target function as the size of the training set grows to infinite. In Appendix C.1, we derived a similar consistency result for TKNN binary classifier/regressor.

With the introduction of TKNN classifier and its utility function, we now present our main result, the closed-form, efficiently computable Data Shapley formula for the TKNN classifier.

The main technical challenges of proving Theorem 5 lies in showing $\textbf{C}_{z^{(\mathrm{val})}}=(\mathbf{c},\mathbf{c}_{x^{(\mathrm{val})},\tau},\mathbf{c}_{z^{(\mathrm{val})},\tau}^{(+)})$, three simple counting queries on $D_{-z_{i}}$, are the key quantities for computing $\phi^{\texttt{TKNN}}_{z_{i}}$. In later part of the paper, we will often view $\phi^{\texttt{TKNN}}_{z_{i}}$ as a function of $\textbf{C}_{z^{(\mathrm{val})}}$ and denote $\phi^{\texttt{TKNN}}_{z_{i}}\left[\textbf{C}_{z^{(\mathrm{val})}}\right]:=f(\textbf{C}_{z^{(\mathrm{val})}})$ when we want to stress this dependency. The full version and the proof for TKNN-Shapley can be found in Appendix C.2.1. Here, we briefly discuss why TKNN-Shapley can achieve $O(N)$ runtime in total.

Efficient Computation of TKNN-Shapley. As we can see, all of the quantities in $\textbf{C}_{z^{(\mathrm{val})}}$ are simply counting queries on $D_{-z_{i}}$, and hence $\textbf{C}_{z^{(\mathrm{val})}}(D_{-z_{i}})$ can be computed in $O(N)$ runtime for any $z_{i}\in D$. A more efficient way to compute $\textbf{C}_{z^{(\mathrm{val})}}(D_{-z_{i}})$ for all $z_{i}\in D$, however, is to first compute $\textbf{C}_{z^{(\mathrm{val})}}(D)$ on the full dataset $D$, and we can easily show that each of $\textbf{C}_{z^{(\mathrm{val})}}(D_{-z_{i}})$ can be computed from that in $O(1)$ runtime (see Appendix C.2.2 for details). Hence, we can compute TKNN-Shapley $\phi^{\texttt{TKNN}}_{z_{i}}(v^{\texttt{TKNN}}_{z^{(\mathrm{val})}})$ for all $z_{i}\in D$ within an overall computational cost of $O(N)$.

Comparison with KNN-Shapley. TKNN-Shapley offers several advantages over the original KNN-Shapley. (1) Non-recursive: In contrast to the KNN-Shapley formula (Theorem 2), which is recursive, TKNN-Shapley has an explicit formula for computing the Shapley value of every point $z_{i}$. This non-recursive nature not only simplifies the implementation, but also makes it straightforward to incorporate techniques like subsampling. (2) Computational efficiency: TKNN-Shapley has $O(N)$ runtime in total, which is better than the $O(N\log N)$ runtime for KNN-Shapley.

As $\textbf{C}_{z^{(\mathrm{val})}}=(\mathbf{c},\mathbf{c}_{x^{(\mathrm{val})},\tau},\mathbf{c}_{z^{(\mathrm{val})},\tau}^{(+)})$ are the only quantities that depend on the dataset $D_{-z_{i}}$ in (4), privatizing these quantities is sufficient for overall privacy preservation, as DP guarantee is preserved under any post-processing [DR⁺14]. Since all of $\mathbf{c},\mathbf{c}_{x^{(\mathrm{val})},\tau}$ and $\mathbf{c}_{z^{(\mathrm{val})},\tau}^{(+)}$ are just counting queries, the function of $\textbf{C}_{z^{(\mathrm{val})}}(\cdot)$ has global sensitivity $\sqrt{3}$ in $\ell_{2}$-norm. This allows us to apply the commonly used Gaussian mechanism (Theorem 4) to release $\textbf{C}_{z^{(\mathrm{val})}}$ in a differentially private way, i.e., $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}(D_{-z_{i}}):=\texttt{round}\left(\textbf{C}_{z^{(\mathrm{val})}}(D_{-z_{i}})+\mathcal{N}\left(0,\sigma^{2}\mathbbm{1}_{3}\right)\right)$ where $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}$ is the privatized version of $\textbf{C}_{z^{(\mathrm{val})}}$, and the function round rounds each entry of noisy value to the nearest integer. The differentially private version of TKNN-Shapley value $\widehat{\phi}^{\texttt{TKNN}}_{z_{i}}(D_{-z_{i}})$ is simply the value score computed by (4) but use the privatized quantities $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}$. The privacy guarantee of releasing DP-TKNN-Shapley $\widehat{\phi}^{\texttt{TKNN}}_{z_{i}}(D_{-z_{i}})$ follows from the guarantee of Gaussian mechanism (see Appendix D.1 for proof).

While our approach may seem simple, we stress that simplicity is appreciated in DP as complex mechanisms pose challenges for correct implementation and auditing [LSL17, GHV20].

We give an overview (detailed in Appendix D.2) of several advantages of DP-KNN-Shapley here, including the efficiency, collusion resistance, and simplicity in incorporating subsampling.

By reusing privatized statistics, $\widehat{\phi}^{\texttt{TKNN}}_{z_{i}}$ can be efficiently computed for all $z_{i}\in D$. Recall that in practical data valuation scenarios, it is often desirable to compute the data value scores for all of $z_{i}\in D$. As we detailed in Section 4.2, for TKNN-Shapley, such a computation only requires $O(N)$ runtime in total if we first compute $\textbf{C}_{z^{(\mathrm{val})}}(D)$ and subsequently $\textbf{C}_{z^{(\mathrm{val})}}(D_{-z_{i}})$ for each $z_{i}\in D$. In a similar vein, we can efficiently compute the DP variant $\widehat{\phi}^{\texttt{TKNN}}_{z_{i}}$ for all $z_{i}\in D$. To do so, we first calculate $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}(D)$ and then, for each $z_{i}\in D$, we compute $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}(D_{-z_{i}})$. It is important to note that when releasing $\widehat{\phi}^{\texttt{TKNN}}_{z_{i}}$ to individual $i$, the data point they hold, $z_{i}$, is not private to the individual themselves. Therefore, as long as $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}(D)$ is privatized, $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}(D_{-z_{i}})$ and hence $\widehat{\phi}^{\texttt{TKNN}}_{z_{i}}$ also satisfy the same privacy guarantee due to DP’s post-processing property.

By reusing privatized statistics, DP-TKNN-Shapley is collusion resistance. In Section 5.1, we consider the single Shapley value $\phi^{\texttt{TKNN}}_{z_{i}}(D_{-z_{i}})$ as the function to privatize. However, when we consider the release of all Shapley values $(\widehat{\phi}^{\texttt{TKNN}}_{z_{1}},\ldots,\widehat{\phi}^{\texttt{TKNN}}_{z_{N}})$ as a unified mechanism, one can show that such a mechanism satisfies joint differential privacy (JDP) [KPRU14] if we reuse the privatized statistic $\widehat{\textbf{C}}_{z^{(\mathrm{val})}}(D)$ for the release of all $\widehat{\phi}^{\texttt{TKNN}}_{z_{i}}$. The consequence of satisfying JDP is that our mechanism is resilient against collusion among groups of individuals without any privacy degradation. That is, even if an arbitrary group of individuals in $[N]\setminus i$ colludes (i.e., shares their respective $\widehat{\phi}^{\texttt{TKNN}}_{z_{j}}$ values within the group), the privacy of individual $i$ remains uncompromised. Our method also stands resilient in scenarios where a powerful adversary sends multiple data points and receives multiple value scores.

Incorporating Privacy Amplification by Subsampling. In contrast to KNN-Shapley, the non-recursive nature of DP-TKNN-Shapley allows for the straightforward incorporation of subsampling. Besides the privacy guarantee, subsampling also significantly boosts the computational efficiency of DP-TKNN-Shapley.

Recall that the TKNN-Shapley corresponding to the full validation set $D^{(\mathrm{val})}$ is $\phi^{\texttt{TKNN}}_{z_{i}}\left(v^{\texttt{TKNN}}_{D^{(\mathrm{val})}}\right)=\sum_{z^{(\mathrm{val})}\in D^{(\mathrm{val})}}\phi^{\texttt{TKNN}}_{z_{i}}(D_{-z_{i}};z^{(\mathrm{val})})$. We can compute privatized $\phi^{\texttt{TKNN}}_{z_{i}}\left(v^{\texttt{TKNN}}_{D^{(\mathrm{val})}}\right)$ by simply releasing $\phi^{\texttt{TKNN}}_{z_{i}}(D_{-z_{i}};z^{(\mathrm{val})})$ for all $z^{(\mathrm{val})}\in D^{(\mathrm{val})}$. To better keep track of the privacy cost, we use the current state-of-the-art privacy accounting technique based on the notion of the Privacy Loss Random Variable (PRV) [DR16]. We provide more details about the background of privacy accounting in Appendix D.3. We note that PRV-based privacy accountant computes the privacy loss numerically, and hence the final privacy loss has no closed-form expressions.

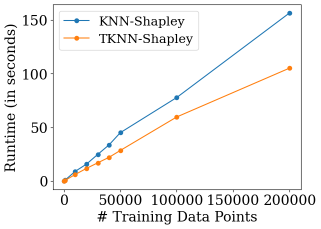
We evaluate the runtime efficiency of TKNN-Shapley in comparison to KNN-Shapley (see Appendix E.2 for details as well as more experiments). We choose a range of training data sizes $N$, and compare the runtime of both methods at each $N$. As demonstrated in Figure 2, TKNN-Shapley achieves better computational efficiency than KNN-Shapley across all training data sizes. In particular, TKNN-Shapley is around 30% faster than KNN-Shapley for large $N$. This shows the computational advantage of TKNN-Shapley mentioned in Section 4.2.

In this section, we evaluate the performance of both DP and non-DP version of TKNN-Shapley in discerning data quality. Tasks: We evaluate the performance of TKNN-Shapley on two standard tasks: mislabeled data detection and noisy data detection, which are tasks that are often used for evaluating the performance of data valuation techniques in prior works [KZ22, WJ23a]. Since mislabeled/noisy data often negatively affect the model performance, it is desirable to assign low values to these data points. In the experiment of mislabeled (or noisy) data detection, we randomly choose 10% of the data points and flip their labels (or add strong noise to their features). Datasets: We conduct our experiments on a diverse set of 13 datasets, where 11 of them have been used in previous data valuation studies [KZ22, WJ23a]. Additionally, we experiment on 2 NLP datasets (AG News [WSZY21] and DBPedia [ABK⁺07]) that have been rarely used in the past due to their high-dimensional nature and the significant computational resources required. Settings & Hyperparameters of TKNN-/KNN-Shapley: for both TKNN/KNN-Shapley, we use the popular cosine distance as the distance measure [Raj21], which is always bounded in $[-1,+1]$. Throughout all experiments, we use $\tau=-0.5$ and $K=5$ for TKNN-/KNN-Shapley, respectively, as we found the two choices consistently work well across all datasets. We conduct ablation studies on the choice of hyperparameters in Appendix E.