Three-nucleon system: Irreducible and reducible contributions of the three-nucleon force
Abstract
The three-nucleon bound and scattering equations are solved in momentum space for a coupled-channel Hamiltonian. The Hamiltonian couples the purely nucleonic sector of Hilbert space with a sector in which one nucleon is excited to a isobar. The interaction consists of irreducible two-baryon and irreducible three-baryon potentials. The calculation keeps only the purely nucleonic one among the irreducible three-baryon potentials. The coupled-channel two-baryon potential yields additional reducible contributions to the three-nucleon force. The Coulomb interaction between the two protons is included using the method of screening and renormalization. Three-nucleon force effects on the bound-state energies and on observables of elastic nucleon-deuteron scattering and breakup are studied.
pacs:
21.30.-x, 21.45.-v, 24.70.+s, 25.10.+sI Motivation
The notion of the three-nucleon (3N) force is not a uniquely-defined concept for the theoretical description of nuclear phenomena. The 3N force arises in the hadronic picture of nuclear systems, a model developed by theoreticians for calculational convenience. The 3N force is therefore also model-dependent and experimentally not measurable.
The microscopic degrees of freedom underlying nuclear phenomena are the quarks and gluons of quantum chromodynamics (QCD). However, a direct description of nuclear phenomena in terms of those microscopic degrees of freedom is not available yet; instead, the effective description in terms of quark-gluon clusters, i.e., in terms of hadrons and their interactions among each other and with electroweak probes is a common conceptual and often quantitatively successful approach to nuclear phenomena at low and moderate energies which we also adopt. At low energies, rigid nucleons appear to make up nuclei in bound and scattering states; after all, nuclear bound states have masses which are almost multiples of the one of a single nucleon. At energies above the pion ()-production threshold, the isobar and the meson become additional active degrees of freedom. The interactions between the hadronic constituents of nuclear systems depend on the chosen degrees of freedom, i.e., on the energy range of applicability; they are mediated by exchanged mesons. The dynamics is usually assumed to be controlled by a field theory for the effective hadronic degrees of freedom, originally by a phenomenological field theory with a zoo of mesons machleidt:87a ; at present, the favorably employed one is the chiral effective field theory (EFT) epelbaum:06 ; epelbaum:09 ; machleidt:11a , which respects the chiral symmetries of QCD and works with the nucleon and as degrees of freedom, sometimes extended by the inclusion of the isobar krebs:07 ; krebs:08 .
However for practical calculations of nuclear systems, the dynamics is chosen to follow quantum mechanics. The forces between the hadrons, arising from field-theoretic processes, have therefore to be cast into the form of hermitian potentials. That dynamic simplification is achieved by freezing some of the field-theoretic degrees of freedom. The quantum-mechanical kinematics is non-relativistic for the nucleon and the isobar, relativistic for the , if quantum-mechanically active. Quantum mechanics is advantageous, since it allows the step from two-particle to many-particle systems in a natural way. The potentials of the baryons are of two-, three- and, in general, of A-particle nature, A being the number of baryons making up the nuclear system under study. It is well established that at normal densities the many-N potentials show a hierarchy of importance: The 2N part is most important and makes the contact with the deuteron and with free two-nucleon scattering. The 3N part is the first important dynamic correction of the 2N interaction, whereas many-N interactions are more complex than the 3N one and also appear dynamically rather unimportant at normal nuclear densities. Furthermore, many-baryon contributions to the interaction, e.g., those arising from non-nucleonic baryons as the isobar, are also dynamically strongly suppressed due to their reduced weights in the nuclear wave functions. That is the reason why the present paper focuses on the 3N force in the hadronic picture of nuclear phenomena.
The present paper makes the following choice for the description of nuclear phenomena. The only active degrees of freedom are the nucleon and the isobar, all mesonic degrees of freedom are frozen. The Hilbert space consists of two sectors, a purely nucleonic one and a sector in which one nucleon is replaced by a isobar. The Hilbert space is chosen with a view on the energy domain above the -production threshold. The isobar is an important mechanism for production, but since 2 and 3 production are strongly suppressed far above their thresholds, configurations with more than one isobar should be physically less important in the energy regime up to about excitation in the c.m. system. Our goal is the description of nuclear phenomena for energies below the -production threshold. Though the is energetically not an active degree of freedom yet, the isobar is already expected to make important contributions to the nuclear dynamics. That will indeed be the case, and that is the reason for the chosen extended Hilbert space. The chosen Hilbert space is shown in Fig. 1 for the example of a three-baryon system. In the presently chosen absence of a coupling to -nucleon states the isobar is a stable baryon; its rest mass is taken to be 1.232 GeV, the resonance position of -nucleon scattering in the partial wave.

The potentials, required for the dynamics in the chosen Hilbert space, are illustrated in Fig. 2; they are irreducible and hermitian. The interaction Hamiltonian is of coupled-channel character: It consists of two-baryon parts which act in both sectors of the Hilbert space and which couple them by transition potentials. The Hamiltonian also contains three-baryon parts which also act in both sectors of the Hilbert space and couple them by transition potentials. In addition there are more complex many-baryon potentials involving more than three baryons, up to baryon number A, the baryon number of the nuclear system under study. However, we shall constrain our calculations to the three-nucleon system; thus, four-baryon forces and forces of even higher complexity do not occur.


When employing the coupled-channel Hamiltonian with an explicit isobar, illustrated in Fig. 2, the nuclear dynamics receives the irreducible contributions of the chosen Hamiltonian, but also reducible contributions to the 2N and 3N interactions arising from its iterative application in the process of solving the many-nucleon problem. The interplay between irreducible and reducible contributions to the 2N and 3N interactions is shown in Fig. 3. Some dynamic processes, in other approaches described by irreducible potentials, are already accounted for by the coupled-channel two-baryon part of the Hamiltonian as reducible processes in the Hilbert space of Fig. 1; they have therefore to be excluded from the irreducible parts of the Hamiltonian.
The 2N interaction receives an important contribution from the virtual excitation of a nucleon to the isobar contributing to the attraction at intermediate range. For example, the potential CD Bonn + , designed by us as such a coupled-channel potential in Ref. deltuva:03c and employed by us for the description of few-nucleon systems previously, artfully takes out the virtual excitation of the isobar from its irreducible part. The reducible, usually attractive contributions, illustrated in the upper row of Fig. 3, to the 2N interaction get weakened in the nuclear medium, a well-known effect, called 2N dispersion.
In the same way, the three-nucleon processes provided by the coupled-channel potential in a reduced form will have to be excluded from the employed irreducible 3N potential. The physically most important three-nucleon processes which the coupled-channel potential already provides are the Fujita-Miyazawa fujita:57a and the -ring processes, as illustrated in the lower row of Fig. 3; the importance of those processes is seen in our own calculations, but it is also confirmed in the context of other dynamic strategies in Refs. krebs:13 ; pieper:01a .


The paper studies the three-nucleon system. Its objective is twofold, it has a physics aspect and a technical aspect:
-
•
The paper extends the dynamics of our previous calculations nemoto:98a ; deltuva:03a by adding an irreducible 3N force to the employed coupled-channel two-baryon potential. Our previous calculations without such an irreducible 3N force are physically incomplete and missed the three-nucleon binding energies and the neutron-deuteron doublet scattering length. We would like to improve on both quantities with the physics question: Is their simultaneous improvement possible? How serious is the miss on those two observables for the prediction of three-nucleon scattering at higher energies?
-
•
The paper demonstrates that complete and reliable calculations including reducible and irreducible 3N forces can be done for the bound and scattering states of the three-nucleon system. As will be discussed in Subsection II.B, the chosen dynamics is not yet in all its respects up to the most modern standards. But the paper paves the way to further, dynamically more satisfactory calculations. That is the technical objective of this paper.
II Calculational apparatus
The paper calculates the three-nucleon bound and scattering states, i.e., nucleon-deuteron elastic scattering and breakup, for energies up to the -production threshold. Those calculational goals require the extension of two numerical schemes, used previously by the authors. Our standard approach to the three-nucleon system is based on a coupled-channel two-baryon potential as in Refs. nemoto:98a ; deltuva:03a ; note that Ref. deltuva:03a and all our recent calculations overcame the need for a separable expansion of the two-baryon transition matrix, still required in Ref. nemoto:98a . In contrast, Ref. deltuva:09e uses irreducible two- and three-baryon forces for the three-nucleon bound states and scattering, but the forces are purely nucleonic ones. The present paper requires the combination of those two schemes. Ref. stadler:92a already implemented such a combination of a coupled-channel two-baryon potential with an explicit -isobar and of an additional irreducible 3N force, but the application was constrained to the three-nucleon bound state; the present paper extends that approach to the three-nucleon scattering. Furthermore, the coupled-channel potential, employed in Ref. stadler:92a , was not properly fitted to the two-nucleon data.
II.1 The equations
There are different strategies for setting up the quantum-mechanical equations for obtaining the three-nucleon bound and scattering states. We work in momentum-space representation and employ integral equations of the Alt, Grassberger, and Sandhas (AGS) type alt:67a . There are three pairwise potentials , i.e.,
| (1) |
being the label of the non-interacting particle during the pairwise interaction. Each of the three potentials is summed up into the respective two-particle transition matrix , i.e.,
| (2) |
is the free three-particle resolvent with the available energy and the free Hamiltonian containing the kinetic energy of the particles and their rest mass differences, in the three-nucleon system with -isobar states the difference with respect to three nucleons. The three-particle potential
| (3) |
is also decomposed into three terms that are symmetric under the exchange of particles and and can be transformed into one another by cyclic permutations. The decomposition (3) is not unique. Often the 3N force is written such that labels the particle which is directly linked to the two others in the interaction urbana9 . However, such a decomposition is inefficient for our practical calculation, and we will therefore follow the procedure of Refs. lazauskas:phd ; deltuva:09e ; this procedure for the decomposition gets explained in Subsection II.B.
The strategy for setting up the integral equations works with the two-particle part of the potential summed into the transition matrix , but keeping the three-particle part in its potential form uniterated. The basis of states, employed for calculations in the three-nucleon system, is, in the purely nucleonic Hilbert sector, the direct product of an antisymmetrized nucleon pair and a third nucleon without antisymmetrization; thus, the basis is overcomplete. In the Hilbert sector with a isobar the same pair symmetrization is used, since the isobar can be created from any of the three nucleons in a symmetric fashion. The isospin formalism is used for distinguishing protons and neutrons including both total isospin and states. The results of the integral equations are bound-state amplitudes and multichannel transition amplitudes , connecting the initial two-body channel with the non-interacting particle of label to the final two-body channel with the non-interacting particle of label , being the final three-particle breakup channel. All multichannel transition amplitudes depend on the available energy ; that dependence is notationally suppressed. The derivation of the equations is given in Ref. deltuva:09e ; the fact, that Ref. deltuva:09e describes the three-nucleon system in terms of a completely nucleonic Hilbert space is immaterial for the derivation of equations; the resulting equations of Ref. deltuva:09e can therefore be taken over without any change.
II.1.1 Bound state
The three-particle bound-state wave function
| (4) |
is decomposed into its Faddeev components . Given the identity of nucleons, carried over to states with a isobar, the three Faddeev components are related by the permutation of the baryons. Any Faddeev component can be taken as a symmetrized Faddeev amplitude which is obtained from
| (5) |
yielding the bound-state wave function in the form with the help of the permutation operator , i.e., , being the individual permutation operator of baryons and .
II.1.2 Scattering operators
The multichannel transition amplitudes act on the two-body channel states , the eigenstates of the corresponding channel Hamiltonian with the energy eigenvalue . Due to symmetry, all three channel states are related to each other by the permutation , defined in the previous subsection. One channel can therefore be taken as characteristic for all. Its channel label will therefore be dropped as well as the label for the component of the three-nucleon potential, and one can work with a symmetrized transition operator for elastic scattering, obtained from the symmetrized AGS integral equation, i.e.,
| (6a) | |||
yielding the on-shell matrix elements , required for the calculation of observables. The breakup operator , connecting an initial two-body channel with the final breakup channel of non-interacting nucleons is then obtained by quadrature
| (6b) |
yielding the on-shell matrix elements , required for the calculation of breakup observables.
In the following elastic scattering observables are shown as functions of the center-of-mass (c.m.) scattering angle , while breakup observables as functions of the arclength along the kinematical curve. As in Ref. deltuva:09e , we obtain well-converged results by taking into account the hadronic interaction in two-baryon partial waves with the total pair angular momentum and including three-baryon states with total angular momentum ; it is fully sufficient to limit the irreducible force to states with . In all calculations of Subsection III.B for the three-nucleon system with two protons their Coulomb repulsion is added with the necessary changes in the above equations according to Refs. taylor:74a ; alt:80a ; deltuva:05a ; deltuva:05d .
II.2 Choice of the dynamics
We take over the potential CD Bonn + deltuva:03c as coupled-channel two-baryon potential, keeping its parameters unchanged in this paper. It is based on the exchange of , , , and mesons. We remind that this potential is tuned to the deuteron and to two-nucleon elastic scattering below 350 MeV lab energy, and that the potential parts, connected with the isobar, are therefore underdetermined by that procedure. Those potential parts would be physically better determined by a simultaneous fit to inelastic two-nucleon scattering, i.e., to the data of channels with a single . However, at present such a tuning procedure is too demanding for us; it would also require the addition of a Hilbert sector with a single and the corresponding additions to the Hamiltonian part of baryon number 2.
We add an irreducible 3N potential to the Hamiltonian. Among the multitude of possible three-baryon potentials, illustrated in the lower row of Fig. 2, the 3N one was argued by us in Section I to be most important.
We choose the Urbana IX 3N force urbana9 as starting point for our construction of 3N potential models, employed in this paper. This choice of a phenomenological irreducible 3N potential is against our original philosophy when developing a coupled-channel two-baryon potential: 2N and 3N forces have to be physically consistent with each other. The coupled-channel approach creates such a satisfying consistency between the 2N and the reducible 3N interactions; but this consistency is broken by the addition of a phenomenological irreducible 3N potential, as done now. The Urbana IX 3N force, chosen as starting point for the modeling in the present paper, has -exchange and phenomenological repulsive short-range terms, i.e.,
| (7) |
where curly and square brackets denote anticommutators and commutators, respectively. The strength constants were chosen in Ref. urbana9 to be MeV, , and MeV. Here is the isospin operator of the nucleon , while the potential-like pair operators and are given in coordinate space by
| (8a) | ||||
| (8b) | ||||
with being the spin operator of the nucleon , the tensor operator of the pair , the average mass, and and the Yukawa and tensor functions specified in Ref. wiringa:95a ; all operators are of range. In our calculation and the squared operators are transformed to momentum space using spherical Bessel functions. Since the decomposition of into three components according to Eq. (3) is not unique, we make the following choice: We expand the sum (7) and take as the terms where the operator acting on the final state (the operator that is on the left side in the product) is either or , i.e.,
| (9) |
gets then decomposed as in Eq. (3). This decomposition is more efficient in our practical calculations as argued in Refs. lazauskas:phd ; deltuva:09e . The numerical technique is taken over from Ref. deltuva:09e and adapted here for the context of additional non-nucleonic channels. This technical possibility of casting the 3N potential into the form (3) with of Eq. (9) was partly the reason for choosing the Urbana IX 3N force as basis for our search of a useful irreducible 3N force supplementing a given coupled-channel two-baryon potential.
The and terms in and are related to -meson exchange; the Fujita-Miyazawa mechanism, illustrated in its reducible form in Fig. 3, makes an important contribution to the 3N potential, requiring the parameter combination , as chosen in Ref. urbana9 . Since that dynamic part is provided by the employed coupled-channel two-baryon potential CD Bonn+ in a reducible form, the Fujita-Miyazawa contribution has to be taken out from the parameters in our reparametrization of an irreducible 3N potential in the Urbana-like fashion. We note in passing, that the reducible Fujita-Miyazawa process, provided by the coupled-channel two-baryon potential CD Bonn + , also includes the -meson exchange and is therefore richer than the original Fujita-Miyazawa 3N force of Ref. fujita:57a . Compared to the Urbana IX 3N force the strength of the potential should be reduced and deviations from the ratio are acceptable. In fact, that ratio got increased in Ref. stadler:92a when the Fujita-Miyazawa process was removed there from the Tucson-Melbourne 3N potential coon:79 . We therefore have to expect a similar increase of that ratio in our reparametrization of an irreducible 3N potential in the Urbana-like fashion.
The repulsion with the strength parameter in the Urbana IX 3N force was required to prevent overbinding of nuclear matter. However, that argument is not relevant in the present context any longer. The coupled-channel two-baryon potential provides repulsion due to the two-nucleon dispersion. That fact was confirmed for nuclear matter by Ref. manzke:78 . We therefore expect that our reparametrization of the irreducible 3N potential should have a smaller or even a vanishing value compared to the Urbana IX 3N force. We therefore set in our first try and retune and having in mind that the resulting dynamic model has to account for the binding energy and attempting also to fit the neutron-deuteron doublet scattering length . The potential CD Bonn + misses only by 176 keV and with fm is already pretty close to the experimental value of 0.650.04 fm dilg:71 . Thus, the required parameters in the added modified Urbana-like 3N potential should be quite mild ones.
However, with the coupled-channel two-baryon potential CD Bonn + and the modified Urbana IX 3N force as irreducible 3N force in addition, we are unable to fit the binding energy and the neutron-deuteron doublet scattering length simultaneously with weak and parameters. We therefore included also the term and tried a wide range of parameters, using a rather coarse raster, but staying within sensible limits. In the end we chose two groups of modifications only, whose parameters are listed in the Table 1 and which appear to us characteristic for our parameter search with Urbana-like 3N potentials. In the first group the ratio was set larger than by hand and not subjected to the fit.
The first group of parametrizations consists of the 3N potentials (U1, U2, U3). The two terms augmented by the parameters and yield both attraction; if repulsion is needed, it is provided by the term with the parameter . All models fit perfectly and, except for U3, underpredict the neutron-deuteron doublet scattering length . Running down this list of three modifications (U1, U2, U3) the individual strength parameters for attraction and repulsion become increasingly larger; when accounting for the neutron-deuteron doublet scattering length as in U3, the three parameters are individually largest. Furthermore, we are disturbed that the and parts of the 3N potential U3 make a massive contribution of about 5 MeV to the triton binding , which has to be balanced by a corresponding comparable repulsion due to the term, just to squeeze out the required small additional binding of 176 keV. Thus, the simultaneous account of the binding and of the neutron-deuteron doublet scattering length appears difficult. We are only able to achieve that goal with the irreducible 3N potential U3 of questionable parametrization, i.e., the attraction and repulsion required for balancing each other, are unnaturally large. However, this tuning difficulty appears not to be a feature characteristic for our special 3N force model. Indeed, in Ref. kievsky:10a another study was performed using the purely nucleonic Argonne V18 potential wiringa:95a in combination with various 3N forces; reproducing experimental values of the neutron-deuteron doublet scattering length and of 3N and 4N binding energies required a balance of attractive and repulsive 3N force contributions, individually even stronger than in the model CD Bonn + + U3 of this paper. Furthermore, Ref. epelbaum:14 used purely nucleonic 2N and 3N potentials consistently derived from EFT, thus, it uses rather different dynamics; nevertheless, the simultaneous account of the binding and of the neutron-deuteron doublet scattering length was also either impossible at all or led to unnaturally large coupling constants, quite similar to our finding. In addition, we note that all realistic purely nucleonic potentials combined with standard phenomenological 3N forces fitted to are underpredicting by a comparable amount witala:03a .
In some parameter domains we noted a surprising sensitivity for the nucleon analyzing power of elastic nucleon-deuteron scattering. We therefore created a second group of parametrizations consisting of the 3N potentials (U1, U4, U5). The repulsive term with the parameter is left out for them; attraction and, if needed, repulsion are both provided by the and terms. In the 3N potentials U4 and U5 the two parameters have opposite signs. We remind that also the 3N potential U1 has , whereas the two other parameters yield attraction; a 3N potential with both parameters and yielding repulsion is unable to account for the binding . None of the parametrizations of the second group (U1, U4, U5) is able to account for the neutron-deuteron doublet scattering length , but U5 is roughly adjusted to the neutron analyzing power of elastic neutron-deuteron scattering at 10 MeV neutron energy.
Additional modifications with further intermediate parameters appear unnecessary to be accounted in the paper, since the two groups of models for an irreducible 3N force suffice to describe the observed trends.
| CD Bonn | 8.004 | 0.932 | |||
| CD Bonn+ | 8.306 | 0.695 | |||
| CD Bonn++U1 | -0.00266 | +0.5000 | 0 | 8.482 | 0.559 |
| CD Bonn++U2 | -0.01559 | +1.0000 | 0.00625 | 8.482 | 0.606 |
| CD Bonn++U3 | -0.02598 | +1.0000 | 0.01250 | 8.482 | 0.639 |
| CD Bonn++U1 | -0.00266 | +0.5000 | 0 | 8.482 | 0.559 |
| CD Bonn++U4 | +0.06500 | -0.3995 | 0 | 8.482 | 0.576 |
| CD Bonn++U5 | -0.06500 | -0.3551 | 0 | 8.482 | 0.539 |
III Results
III.1 Observations made in the parameter search
In this subsection, we compare the predictions of interactions with the added irreducible 3N potentials, listed in the Table 1, for selected three-nucleon scattering observables; we do so separately for the two distinct groups (U1, U2, U3) and (U1, U4, U5). We choose selected observables which best illustrate the effects of the added 3N potentials in either group, desired and undesired, i.e., the neutron analyzing power of neutron-deuteron elastic scattering at 10 MeV neutron energy, the differential cross section and the deuteron analyzing power of proton-deuteron elastic scattering at 135 MeV proton energy, and the differential cross section for neutron-deuteron breakup at 13 MeV neutron lab energy in the space star configuration.


First, results for group (U1, U2, U3) are illustrated in Figs. 4 and 5. The general trend is that 3N force effects due to the irreducible U1 are insignificant, even smaller than those obtained from the reducible 3N force contributions due to the explicit -isobar excitation; they improve the agreement with the experimental data howell:87 ; ermisch:05a ; ramazani:08a ; sekiguchi:02a only slightly. In contrast, the effects due to the 3N potential U3 are larger than those due to the explicit -isobar excitation, but not beneficial for the description of the data. At 135 MeV proton-deuteron elastic scattering, they move the theoretical predictions into the right direction, but they are far too strong, often dramatically overshooting the discrepancy with data. This somehow uncontrolled behavior is not unexpected, given the individually very strong repulsive and attractive terms in U3. The results for U2 are intermediate between those for U1 and U3. We conclude that the irreducible 3N potential U1, being the softest one, appears to make most sense physically, even though it predicts fm and we have to give up our ambition to account for the experimental value precisely, when choosing U1 for further studies.
Concerning the potential CD Bonn + + U3 that is forced to fit the neutron-deuteron doublet scattering length , we observe another interesting similarity in Fig. 4 with the results of Ref. epelbaum:14 , which are obtained from EFT 2N and 3N forces, also fitted to the binding and to the neutron-deuteron doublet scattering length . In addition to the similarity found in Subsection II.B, we observe that in both cases, based on completely different dynamic models, the neutron analyzing power in neutron-deuteron elastic scattering at 10 MeV is increased at angles , but decreased , moving theoretical predictions away from the experimental data. Thus, this additional undesired effect of irreducible 3N forces on the analyzing power appears to be a general feature of presently available force models that fit 2N data, and simultaneously and points to a further aspect of the long-standing puzzle in low-energy 3N scattering. In Ref. kievsky:10a the analyzing power was studied only at 3 MeV, but the conclusions are essentially the same, i.e., improving increases the discrepancy for , except when using the Argonne V18 potential supplemented with a particular 3N force of EFT.

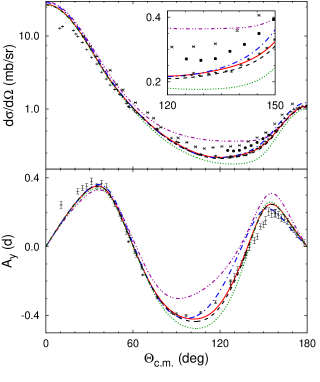
Second, the above conjecture on the general difficulty of accounting simultaneously for characteristic three-nucleon data, seen for the potential group (U1, U2, U3), is supported also by our results for the potential group (U1, U4, U5) as shown in Fig. 6. The model CD Bonn + + U5 is adjusted to reproduce the experimental data for the neutron analyzing power at 10 MeV, seemingly overcoming the long-standing puzzle. The price for this fit, however, is an increased discrepancy for the neutron-deuteron doublet scattering length , as can be seen in Table 1. The 3N potential U4 that improves compared to U1, increases the discrepancy for at the same time, much like U2 and U3 do. Thus again, the simultaneous account of 2N data, , , and appears to be impossible with the presently available force models. The models CD Bonn + + U4 and CD Bonn + + U5, although the latter is successful for low-energy , contain unusually large parameters and , which make the 3N potentials U4 and U5 as questionable as U3 before. As shown in Fig. 7 for proton-deuteron elastic scattering at 135 MeV, especially U5 yields a very strong effect that destroys the reasonable agreement with data achieved by the potentials CD Bonn + or CD Bonn + + U1.
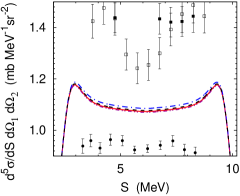
Finally, Fig. 8 studies another famous 3N puzzle, as bothersome as the problem, i.e., the fivefold differential cross section of the nucleon-deuteron breakup at 13 MeV in the space star configuration characterized by the polar and azimuthal angles of two detected nucleons . This observable is known to be quite insensitive to changes in the Hamiltonian witala:10a ; ishikawa:09a . Indeed, even the effect of the very strong 3N forces U3 and U5 is insignificant and much smaller than the discrepancy between the predictions and experimental data strate:89 ; setze:05a ; rauprich:91 . Fig. 8 presents theoretical results for neutron-deuteron scattering; the corresponding theoretical results for proton-deuteron breakup also strongly disagree with the data, despite the inclusion of Coulomb in the calculations; the proton-deuteron results overpredict the data. Thus, none of the considered 3N force models studied by us is able to cure the space star anomaly.
III.2 Overview on results obtained with the additional 3N potential U1
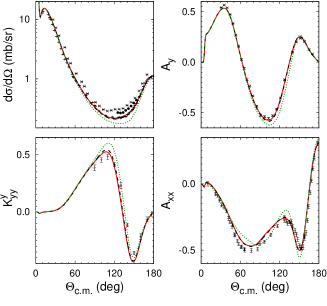


We choose the irreducible 3N potential U1 as the most reasonable one for a further comparative study of irreducible and reducible contributions to the 3N force; the addition of U1 accounts for the binding of by construction, but it also yields the - mass difference perfectly, i.e., the binding of becomes 7.718 MeV, its experimental value also being 7.718 MeV. In this subsection for a wide range of 3N scattering observables we compare the predictions of the potentials CD Bonn without any 3N force, CD Bonn + with reducible contributions to the 3N force, and of CD Bonn + + U1 with reducible and irreducible contributions to the 3N force.
In Fig. 9 we show the differential cross section and various spin observables for elastic proton-deuteron scattering at 135 MeV, in Fig. 10 the differential cross section and nucleon-to-nucleon spin transfer coefficients for elastic proton-deuteron scattering at 250 MeV, and in Fig. 11 the fivefold differential cross section and nucleon analyzing powers for proton-deuteron breakup at 135 MeV. In contrast to Subsection III.A, we carry out the calculations for proton-deuteron scattering fully and include the proton-proton Coulomb force using the method of screening and renormalization taylor:74a ; alt:80a ; deltuva:05a ; deltuva:05d , though we do not show the explicit Coulomb effects separately in the plots. In elastic scattering at these energies the Coulomb effect is irrelevant, except for small angles deltuva:05a ; it is seen in Figs. 9 and Fig. 10 as wiggles in all observables below . In breakup the Coulomb effect is most visible in configurations with low relative proton-proton energy deltuva:05d , mostly affecting the differential cross section. For example, in the configuration of Fig. 11 the proton-proton Coulomb force reduces the cross section at the peak by about 25%.
The reducible contributions to the 3N force, i.e., the explicit -isobar excitation, create the largest effects in the studied observables. The additional effects of the irreducible 3N force U1 are minor even at higher energies, and they do not destroy any achieved account of the experimental data. In proton-deuteron elastic scattering, the reducible and irreducible 3N-force contributions move the predictions quite often into the same direction such that the inclusion of irreducible 3N force U1 even slightly improves the description of the experimental data. The most prominent examples are the differential cross section around the minimum and at backward angles, the nucleon analyzing power at 135 MeV around the minimum and the nucleon-to-nucleon spin transfer coefficient at 250 MeV, as well as the deuteron vector analyzing power at 135 MeV shown in Fig. 5. In the breakup reaction the reducible and irreducible 3N forces may have effects of the same or of opposite signs as illustrated in Fig. 11, depending on the kinematical configuration and depending on the specific observable. In the considered example the Coulomb repulsion between the protons is important for the achieved gross agreement with the cross section data, but neither 3N force contribution is beneficial in accounting for the experimental data of Ref. eslami:10a , especially in the configuration.
IV Conclusions
In the present work we describe the properties of the three-nucleon system, i.e., the bound state and the nucleon-deuteron elastic scattering and breakup below the -production threshold, in an extended Hilbert space with a coupled-channel Hamiltonian containing irreducible two- and three-baryon potentials. The extension of the Hilbert space is due to a sector in which one nucleon is turned into a isobar. The Hamiltonian couples both sectors of the Hilbert space. The isobar makes important, reducible, easily calculable contributions to the 2N and 3N interactions; the most prominent contribution is the Fujita-Miyazawa mechanism to the 3N interaction, even enriched by the meson contributions. The irreducible three-baryon potential is constrained to a purely nucleonic one. The simplification of the additional Hilbert sector with a single isobar only and the constraint of the irreducible three-baryon potential to a nucleonic one only are well motivated.
We prove that calculations in such an extended Hilbert space with such an extended Hamiltonian can be computationally done with high precision. The computational technology can, in future, be extended to other and conceptually better founded forces, e.g., to those possibly provided by EFT with an explicit isobar krebs:07 ; krebs:08 , kept in a quantum-mechanical Hamiltonian still to be derived. Thus, the technical objective of the paper is reached.
We explored the effect of irreducible 3N potentials of the Urbana IX type on top of the coupled-channel two-baryon potential CD Bonn + . We found that the simultaneous precise account of the binding energy and of the neutron-deuteron doublet scattering length is extremely difficult to achieve. This finding may appear to be due to our special theoretical framework. But this is a finding encountered also in Ref. epelbaum:14 using the framework of entirely different nuclear forces of EFT and in Ref. kievsky:10a employing the Argonne V18 potential combined with variations of the Urbana IX and Tucson-Melbourne 3N forces. Thus, this finding is surprisingly more general than expected and may constitute another theoretical puzzle in the three-nucleon system. Furthermore, the simultaneous account of 2N data, of the binding , of the neutron-deuteron doublet scattering length and of the low-energy nucleon analyzing power appears to be even more difficult to achieve, and that problem also calls for new terms in the Hamiltonian, especially of the 3N nature.
We employed the irreducible 3N potential U1 of Table 1 as dynamic basis for the description of three-nucleon binding and scattering, together with the coupled-channel two-baryon potential CD Bonn + . The 3N potential U1 provides the missing contribution to the three-nucleon binding and it is weak. This is wanted, but we have to give up our original goal of also accounting for the neutron-deuteron doublet scattering length precisely. Nevertheless, the results for three-nucleon scattering at higher energies are satisfactory, since the broad range of the successful account of experimental data without an irreducible 3N potential is preserved and often even slightly improved. However, the well-known puzzles of low-energy three-nucleon scattering, i.e., the nucleon analyzing power of elastic nucleon-deuteron scattering below 20 MeV nucleon lab energy and the nucleon-deuteron breakup in the space star kinematics stay unresolved. That is a disappointing aspect of the present results, but not unexpected given the previous studies kievsky:10a ; epelbaum:14 ; witala:10a ; ishikawa:09a .
Acknowledgements.
A.D. thanks the Leibniz University Hannover for the hospitality during the completion of this work.References
- (1) R. Machleidt, K. Holinde, and C. Elster, Phys. Rep. 149, 1 (1987).
- (2) E. Epelbaum, Prog. Part. Nucl. Phys. 57, 654 (2006).
- (3) E. Epelbaum, H.-W. Hammer and U.-G. Meißner, Rev. Mod. Phys. 81, 1773 (2009).
- (4) R. Machleidt and D. R. Entem, Phys. Rep. 503, 1 (2011).
- (5) H. Krebs, E. Epelbaum and U.-G. Meißner, Eur. Phys. J. A32, 127 (2007).
- (6) E. Epelbaum, H. Krebs and U.-G. Meißner, Nucl. Phys. A806, 65 (2008).
- (7) A. Deltuva, R. Machleidt, and P. U. Sauer, Phys. Rev. C 68, 024005 (2003).
- (8) J. Fujita and H. Miyazawa, Prog. Theor. Phys. 17, 360 (1957).
- (9) H. Krebs, A. Gasparyan and E. Epelbaum, Phys. Rev. C87, 054007 (2013)
- (10) S. C. Pieper, V. R. Pandharipande, R. B. Wiringa, and J. Carlson, Phys. Rev. C 64, 014001 (2001).
- (11) S. Nemoto, K. Chmielewski, J. Haidenbauer, S. Oryu, P. U. Sauer, and N. W. Schellingerhout, Few-Body Systems 24, 213 (1998).
- (12) A. Deltuva, K. Chmielewski, and P. U. Sauer, Phys. Rev. C 67, 034001 (2003).
- (13) A. Deltuva, Phys. Rev. C 80, 064002 (2009).
- (14) A. Stadler and P. U. Sauer, Phys. Rev. C 46, 64 (1992).
- (15) E. O. Alt, P. Grassberger, and W. Sandhas, Nucl. Phys. B2, 167 (1967).
- (16) B. S. Pudliner, V. R. Pandharipande, J. Carlson, S. C. Pieper, and R. B. Wiringa, Phys. Rev. C 56, 1720 (1997).
- (17) R. Lazauskas, Ph.D. thesis, Université Joseph Fourier, Grenoble, 2003, http://tel.ccsd.cnrs.fr/documents/archives0/00/00/41/78/.
- (18) J. R. Taylor, Nuovo Cimento B 23, 313 (1974); M. D. Semon and J. R. Taylor, Nuovo Cimento A 26, 48 (1975).
- (19) E. O. Alt and W. Sandhas, Phys. Rev. C 21, 1733 (1980).
- (20) A. Deltuva, A. C. Fonseca, and P. U. Sauer, Phys. Rev. C 71, 054005 (2005).
- (21) A. Deltuva, A. C. Fonseca, and P. U. Sauer, Phys. Rev. C 72, 054004 (2005).
- (22) R. B. Wiringa, V. G. J. Stoks, and R. Schiavilla, Phys. Rev. C 51, 38 (1995).
- (23) S. A. Coon, M. D. Scadron, P. C. McNamee, B. R. Barrett, D. W. E. Blatt, and B. H. J. McKellar, Nucl. Phys. A 317, 242 (1979).
- (24) W. Manzke and M. Gari, Nucl. Phys. A 312, 457 (1978).
- (25) W. Dilg, L. Koester, and W. Nistler, Phys. Lett. 36B, 208 (1971).
- (26) A. Kievsky, M. Viviani, L. Girlanda, and L.E. Marcucci, Phys. Rev. C 81, 044003 (2010).
- (27) J. Golak et al, Eur. Phys. J. A 50, 177 (2014).
- (28) H. Witała, A. Nogga, H. Kamada, W. Glöckle, J. Golak, and R. Skibiński, Phys. Rev. C 68, 034002 (2003).
- (29) C. R. Howell et al., Few-Body Systems 2, 19 (1987).
- (30) K. Ermisch et al., Phys. Rev. C 71, 064004 (2005).
- (31) A. Ramazani-Moghaddam-Arani et al., Phys. Rev. C 78, 014006 (2008).
- (32) K. Sekiguchi et al., Phys. Rev. C 65, 034003 (2002).
- (33) H. Witała and W. Glöckle, J. Phys. G 37, 064003 (2010).
- (34) S. Ishikawa, Phys. Rev. C 80, 054002 (2009).
- (35) J. Strate et al., Nucl. Phys. A501, 51 (1989).
- (36) H. R. Setze et al, Phys. Rev. C 71, 034006 (2005).
- (37) G. Rauprich, S. Lemaitre, P. Niessen, K. R. Nyga, R. Reckenfelderbäumer, L. Sydow, H. Paetz gen. Schieck, H. Witała, and W. Glöckle, Nucl. Phys. A535, 313 (1991).
- (38) K. Hatanaka et al., Phys. Rev. C 66, 044002 (2002).
- (39) M. Eslami-Kalantari et al, EPJ Web of Conferences 3, 05010 (2010).