Thermoelectric transport and current noise through a multilevel Anderson impurity: Three-body Fermi-liquid corrections in quantum dots and magnetic alloys
Abstract
We present a comprehensive Fermi liquid description for thermoelectric transport and current noise, applicable to multilevel quantum dots (QD) and magnetic alloys (MA) without electron-hole or time-reversal symmetry. Our formulation for the low-energy transport is based on an Anderson model with discrete impurity levels, and is asymptotically exact at low energies, up to the next-leading order terms in power expansions with respect to temperature and bias voltage . The expansion coefficients can be expressed in terms of the Fermi liquid parameters, which include the three-body correlation functions defined with respect to the equilibrium ground state in addition to the linear susceptibilities and the occupation number of impurity electrons. We apply this formulation to the SU() symmetric QD and MA, and calculate the correlation functions for and , using numerical renormalization group approach. The three-body correlations are shown to be determined by a single parameter over a wide range of electron fillings for strong Coulomb interactions , and they also exhibit the plateau structures due to the SU() Kondo effects at integer values of . We find that the Lorenz number for QD and MA, defined as the ratio of the thermal conductivity to the electrical conductivity , deviates from the universal Wiedemann-Franz value as the temperature increases from , showing the dependence, the coefficient for which depends on the three-body correlations away from half filling. Furthermore, we find that the current noise for the SU(4) quantum dots and that for SU(6) show a pronounced difference at the quarter and fillings. In particular, the linear noise for exhibits a flat peak while the peak for shows a round shape, reflecting the fact that, at these filling points, the SU() Kondo effects occur for (mod ), whereas the intermediate-valence fluctuations occur for (mod ). We also demonstrate the role of three-body correlations on the nonlinear current noise and the other transport coefficients.
pacs:
71.10.Ay, 71.27.+a, 72.15.QmI Introduction
The Kondo effect is a fascinating many-body effect[1, 2], taking place in dilute magnetic alloys (MA), quantum dots (QD), and other novel quantum systems such as ultracold atomic gases [3] and quark matter [4]. It was shown in the 1970s that the low-energy behavior of the Kondo systems can be described by a quantum impurity version of the Fermi liquid (FL) theory [5, 6, 7, 8, 9]. In particular, using the numerical renormalization group (NRG) approach [10, 11, 12], Wilson et al. demonstrated that the low-lying excited states of the Kondo and the Anderson models exhibit a one-to-one correspondence with the excitations of the renormalized quasiparticles.
The quasiparticles are asymptotically free in the equilibrium ground state, where the perturbations from the environment or reservoirs, which may depend on external parameters such as frequency , temperature , bias voltages , etc., are absent. As these perturbations are adiabatically switched on, the quasiparticles capture the damping rate of order , , and through the residual interactions and this significantly affects the transport properties [5, 6, 7, 8, 9, 13, 14]. When the electron-hole or time-reversal symmetry is broken by a potential or external fields, the quasiparticles also capture the energy shift of order , , and , i.e., the corrections in the same order as the ones due to the damping rate. The contributions of these higher-order energy shifts, however, had not been fully understood until very recently.
It has recently been clarified that these higher-order energy shifts of the quasiparticles can be described exactly in terms of the three-body correlations between impurity electrons. The proof was given in two different ways, which complement each other. One is given by Mora et al. and Filippone et al. [15, 16, 17, 18], extending Nozières’ description [5] that is based on an invariance against the “floating of Kondo resonance on the Fermi sea”. The other is based on the higher-order Fermi liquid relations [19, 20, 21], which can be derived from the Ward identities for the second derivatives of the self-energy, extending Yamada-Yosida’s field-theoretical approach [6, 7, 8, 9]. These proofs enabled one to express the next-leading order terms of the transport coefficients in terms of three-body correlation functions, and these formulations have been applied to the nonlinear currents, current noise, and thermocurrent through quantum impurities without electron-hole or time-reversal symmetry [22, 23, 24, 25, 26, 27, 28, 29].
The purpose of this paper is twofold. The first one is to extend the latest version of the FL theory for treating the thermoelectric transport coefficients of multilevel quantum dots and magnetic alloys described by the Anderson model with arbitrary impurity levels. The second one is to demonstrate how the next-leading order terms of various transport coefficients vary with the impurity level and Coulomb interaction . Specifically, for the second purpose, we consider quantum dots and magnetic alloys having an SU() symmetry, and calculate the three-body correlation functions for and using the NRG approach. There have been a number of intensive works which theoretically studied low-energy transport: the nonlinear current [30, 31, 13, 32, 33, 34, 35, 14, 36, 37, 18], nonlinear current noise [38, 39, 40, 41, 16, 42, 23], and thermoelectric transport[43, 15, 44, 21]. However, the parameter space for quantum impurities is so huge that many parts are still left unexplored. In this paper, we explore the whole region of the electron fillings, , in which the occupation number of electrons in the impurity levels varies continuously across the various SU() Kondo and intermediate valence regimes.
One of the advantages of the Kondo systems realized in quantum dots is that the information about the many-body quantum states can be probed in such a highly tunable way [45, 46, 47, 48]. For instance, recent experiments have succeeded in directly probing the Kondo screening cloud [49]. Furthermore, low-energy Fermi liquid behaviors have experimentally been confirmed for nonequilibrium currents [50, 51], current noise [52, 53, 54, 55, 56], and themocurrent [57, 58]. Internal degrees of freedoms of quantum impurities also bring an interesting variety to the Kondo effect. The systems having the SU() symmetry have been realized, for instance, in the multiorbital semiconductor quantum dots and carbon nanotube (CNT) quantum dots [59], and have intensively been investigated theoretically [34, 60, 61, 62, 63, 64, 65, 15, 16, 66, 67, 26, 68, 22] and experimentally [69, 70, 71, 72, 73, 55]. Realization of the SU() Kondo effects for various has also been proposed by several authors, using triple quantum dots [74, 75] and CNT [76]. In this paper, we provide a comprehensive FL view of the low-energy transport for SU(4) and SU(6) symmetric QD and MA.
Our results reveal the fact that the three-body correlations exhibit plateau structures, caused by the SU() Kondo effects occurring at integer fillings , , . We also calculate the Lorenz number for QD and MA, defined as the ratio of the thermal conductivity to the electrical conductivity , and show how it deviates from the universal Wiedemann-Franz value as the temperature increases from . Furthermore, we demonstrate how the three-body correlations affect the order electrical conductivity, the order thermal conductivity, and the order nonlinear current and current noise. At quarter and three-quarters fillings, the SU() Kondo effects occur for (mod ) while the intermediate valence fluctuations occur for (mod ). We show that this dependence on (mod ) causes a pronounced difference appearing in the peak structures of linear noise for and .
This paper is organized as follows. In Sec. II, we describe the multilevel Anderson impurity model for quantum dots and magnetic alloys. Sections III and IV are devoted to the FL descriptions for the next-leading order terms of electrical and thermoelectric transport coefficients for quantum dots, applicable to arbitrary impurity-level structures. In Sec. V, the low-energy transport formulas for the SU() quantum dots are described in terms of the five FL parameters. We present the NRG results for the three-body correlation functions in Sec. VI. The results for nonlinear current, current noise, and thermoelectric transport through quantum dots are discussed in Secs. VII and VIII. Section IX is devoted to the FL description of the three-body correlations in thermoelectric transport of dilute magnetic alloys. In Sec. X, we discuss the results for the electrical and thermal resistivities of the SU(4) and SU(6) magnetic alloys. Summary is given in Sec. XI. In Appendix, we provide details of the derivations for the transport formulas and additional NRG results for the FL parameters in the SU() cases for , , and , for comparison.
II Model
We consider a multi-orbital Anderson impurity coupled to two noninteracting leads on the left () and right (): ,
| (1) | ||||
| (2) | ||||
| (3) |
Here, the level index runs over . The inter-electron interaction generally depends on and , with the requirements for . For , it describes the usual single-orbital Anderson model for spin fermions. The operator creates an impurity electron with spin in the impurity level of energy , and . Conduction electrons in the two lead at and obey the anti-commutation relation . The linear combination of the conduction electrons, with , couples to the impurity level. The bare level width due to the tunnel couplings is given by with . We consider the parameter region where the half band-width is much grater than the other energy scales, . We use a unit throughout this paper.
Low-energy properties of the Anderson model can be described in terms of a set of Fermi liquid parameters defined with respect to the equilibrium ground state, i.e., the phase shift , the linear susceptibilities and the three-body correlation functions between impurity electrons; see Appendix A for details. The phase shift is a primary parameter that reflects the charge distribution of impurity levels, through the Friedel sum rule: . In this paper, we explore the low-energy transport of quantum dots and magnetic alloys in the whole region of the electron fillings,
| (4) |
The current conservation, which follows from the Heisenberg equation of motion for the occupation number ,
| (5) |
also plays an essential role in the Fermi liquid description, through the Ward identities. Here, represents the current flowing from the left lead to the dot, and the current from the dot to the right lead:
| (6) | ||||
| (7) |
In the next section, we will give a brief overview of the low-energy expansion formulas for nonlinear current and current noise, obtained previously in Refs. 27, 29, to show how the formulas can be expressed in terms of the FL parameters, including the three-body correlations. This is for comparison with the formulas for thermal electric transport coefficients, which we extend to multilevel quantum dots and magnetic alloys in this paper. Specifically, we will describe the derivation of the formulas for multilevel quantum dots and magnetic alloys in Sec. IV and Appendix G, respectively.
III Fermi liquid description for nonlinear current noise of QD
We consider the nonequilibrium steady state under a finite bias voltage , applied between the two leads by setting the chemical potentials of the left and right leads to be and , respectively. The retarded Green’s function plays a central role in the microscopic description of the Fermi liquid transport:
| (8) | ||||
| (9) |
Here, represents a nonequilibrium steady-state average taken with the statistical density matrix, which is constructed at finite bias voltages and temperatures , using the Keldysh formalism [33, 13, 77].
III.1 Differential conductance
The nonequilibrium current through quantum dots can be expressed in terms of the spectral function [33, 13]:
| (10) | ||||
| (11) |
Here, for , , with the Fermi function. Specifically, in this paper, we consider the case where the chemical potentials are applied in a symmetric way:
| (12) |
choosing the Fermi level at equilibrium to be the origin of one-particle energies . Note that the role of bias and tunneling asymmetries, and , has been precisely discussed in Refs. 28, 29.
The nonlinear current can be expanded up to the next-leading order terms, using the low-energy asymptotic form of the spectral function , which has been obtained up to terms of order , , and [27], as shown in Appendix B. In particular, for symmetric junctions with and , the low-energy expansion of the differential conductance takes the form,
| (13) |
Here, the coefficients and of the next-leading order terms can be expressed in terms of the phase shift , the linear susceptibilities , and the static three-body correlation functions defined in Appendix A:
| (14) | |||
| (15) |
III.2 Nonlinear current noise
We also study the current noise [78, 26, 27], defined by
| (16) |
Here, represents fluctuations of the symmetrized current:
| (17) |
Behavior of the current noise in the low-energy Fermi liquid regime has been studied by several authors, taking into account the three-body correlations [17, 16]. In a previous work, we have derived a general formula for the current noise through the multilevel Anderson impurity model up to terms of order for symmetric junctions and [26, 27]:
| (18) |
The coefficient for the next-leading order term has been calculated by taking into account all components of the Keldysh vertex function together with the low-energy asymptotic form of . It has been shown to be expressed in the following form,
| (19) |
IV Fermi liquid description for thermoelectric transport of QD
In this section, we discuss thermoelectric transport through multilevel quantum dots in the linear-response regime, the low-energy behaviors of which can be deduced from the asymptotic form of the spectral function given in Appendix B.
The linear conductance , thermopower and thermal conductance of a quantum dot can be expressed in the form [79, 80, 81, 22, 82]:
| (20) | ||||
| (21) | ||||
| (22) |
Here, for , and is defined at with respect to the thermal equilibrium, as
| (23) |
with , the transmission probability defined in Eq. (11). Note that thermal conductance is the linear-response coefficient of the heat current , flowing from the high-temperature side toward the low-temperature side, with the temperature difference between the two sides.
The thermoelectric coefficients can be calculated, by substituting the low-energy asymptotic form of , given in Eq. (111) into . At low temperatures, the component for , which determines , is given by
| (24) |
Here, is the coefficient that we have already described in Eq. (14). The next component, for , takes the form
| (25) |
Here, is the derivative of the density of states with respect to the frequency , which can also be written in terms of the phase shift and diagonal linear susceptibility , as shown in Eq. (101). Thus, the leading-order term of thermopower for quantum dots is given by
| (26) |
The thermal conductance depends on the other component for , the low-energy asymptotic form of which is given by
| (27) |
Therefore, the thermal conductance can be calculated up to terms of order , by substituting these asymptotic forms into Eq. (22):
| (28) | |||
| (29) |
Here, the arithmetic mean (AM) of the phase shifts is defined by
| (30) |
Furthermore, the Lorenz number can be calculated up to terms of order :
| (31) | ||||
| (32) |
The Wiedemann-Franz law holds between the leading-order terms of the linear conductance and the thermal conductance , such that the Lorenz number approaches the universal value in the low-temperature limit. The Lorenz number deviates from this universal value as temperature increases, exhibiting the dependence.
V Three-body correlations in the SU() symmetric Fermi liquid
This Hamiltonian , defined in Sec. II, has an SU() symmetry in the case at which the impurity states become degenerate for all and the Coulomb interaction is isotropic for all and .
In the atomic limit of the SU() symmetric case, the total number of impurity electrons takes an integer value and exhibits the Coulomb-stair case behavior as a function of . It consists of a series of plateaus of the width and the height for , , , , emerging at around the midpoint . We will use the following notation for the shifted impurity level , which includes the Hartree-Fock energy shift defined with respect to the half filling in such a way that
| (33) |
The system has an electron-hole symmetry at . When the tunneling couplings are switched on, the stair-case structure emerges for strong interactions .
In the SU() symmetric case, the linear susceptibilities have two linearly independent components, i.e., the diagonal one and the off-diagonal one for These two components determine the essential properties of quasiparticles:
| (34) |
Here, is a characteristic energy scale of the SU() Fermi liquid, by which the -linear specific heat of impurity electrons can be expressed in the form [6, 8, 9]. The Wilson ratio corresponds to a dimensionless residual interaction between quasiparticles [83]; we will also use the rescaled ratio,
| (35) |
which is bounded in the range .
V.1 Charge and spin susceptibilities
The charge susceptibility is given by a linear combination of the two-body correlations,
| (36) | |||
| (37) |
Here, is the free energy.
Next, we consider the spin susceptibility for the SU() symmetric case, using the notation in which the internal degrees freedom are separated into two parts , where and , assuming to be even (extension to odd is straightforward). The Zeeman splitting is induced by an external field , which couples to the impurity spin :
| (38) |
The magnetization of the impurity spin is given by
| (39) |
Note that is an even function of . The spin susceptibility can be expressed in the following form,
| (40) | |||
| (41) |
where .
V.2 Three-body correlation functions
Among components of the three-body correlation , only three components become linearly independent in the SU() symmetric case. They can be expressed in terms of the derivatives of the linear susceptibilities, using Eqs. (113), (114), and (117) given in Appendix C:
| (42) | ||||
| (43) | ||||
| (44) |
for . Here,
| (45) |
and the scale factors and have been introduced for the off-diagonal three-body components in such a way that
| (46) | ||||
| (47) |
We will also use the dimensionless three-body correlations, defined by
| (48) | ||||
| (49) |
In this work, we calculate the right-hand side of Eqs. (42)–(44) with the NRG to obtain the three-body correlations for the SU() case. Note that, for noninteracting electrons at , only the diagonal components of the three-body correlation and the susceptibility remain finite due to the Pauli exclusion principle,
| (50) |
and .
V.3 Transport formulas for quantum dots in SU() Fermi liquid regime
We next consider the low-energy expansion of transport coefficients , , , and the Lorenz number . Specifically, for the junctions having tunneling and bias symmetries and , these transport coefficients take the following form in the SU() symmetric case,
| (51) | |||
| (52) | |||
| (53) | |||
| (54) |
The formulas for the coefficients , , , , and of the next-leading order terms are summarized in Tables 1 and 2. Each of these ’s can be decomposed into two parts, denoted as ’s and ’s. The part, defined in the right column of Table 2, represents the two-body contributions determined by and . The part represents the three-body contributions which can be described in terms of the dimensionless parameters defined in Eq. (48).
These transport formulas in the SU() Fermi liquid regime clarify the fact that the next-leading order terms for the symmetric tunnel junctions are completely determined by five parameters: , , , , and . The three-body correlations can be experimentally deduced through the measurements of the coefficients ’s. The other three-body component, , defined with respect to three different levels, couples to the tunnel and bias asymmetries, i.e., and , and contributes to the nonlinear current [28, 29]. The behavior of ’s depend significantly on the electron filling of the impurity levels. For instance, in the noninteracting case at , these coefficients vary with the level position as shown in Fig. 1.

In the rest of this paper, we will demonstrate the behavior of the next-leading order terms of the transport coefficients for and . To this end, we calculate the correlation functions , , and using the NRG approach [84, 26], with parameter settings described in Appendix D. Specifically, Eqs. (42)–(45) are used for obtaining the three-body correlations. We have reported part of the results for coefficient in a previous paper, studying the role of bias and tunneling asymmetries on the nonlinear terms of at [29]. In this paper, we provide a comprehensive view of the three-body Fermi liquid effect through a systematic analysis of the next-leading order terms , , and for quantum dots, and through the related coefficients for magnetic alloys, , and . In order to quickly grasp the underlying physics derived from quasiparticle properties in the SU(4) and SU(6) cases, we provide a brief review of the key characteristics of the two-body correlation functions in Appendix E, extending the interaction range up to . Additionally, we also include some new results for the renormalized impurity level there.
VI Three-body correlations in the SU(4) SU(6) Anderson impurity
In this section, we discuss the behavior of charge and spin susceptibilities defined in Eqs. (37) and (41). In particular, we focus on the derivatives and , which can also be expressed in terms of the three-body correlation functions:
| (55) | ||||
| (56) |
The NRG results reveal the fact that these derivatives in the left-hand side are suppressed in the strong-coupling region for large . This implies that the linear combinations of the three-body correlations in left-hand side of Eqs. (55) and (56) approach zero, reducing the number of independent components of the three-body correlation functions , as demonstrated below.











VI.1 Charge and spin susceptibilities: &
One of the most fundamental quantities that play a central role in the low-energy physics of quantum impurities is the characteristic energy scale , defined in Eq. (34) as an inverse of the diagonal susceptibility . We will use, in the following discussions, the Kondo temperature , defined as the value of at the electron-hole symmetric point .
The NRG results for in the SU(4) and SU(6) cases are plotted vs in Figs. 2(a) and 2(b), respectively, by multiplying them by . We see that has local maxima for strong interactions, at integer-filling points, i.e., , reflecting the oscillatory behavior of the wave function renormalization factor () described in Appendix E. At , the energy scale approaches the non-interacting value, , as the electron filling of the impurity levels approaches or .
The charge susceptibilities for and are plotted in Figs. 2(c) and 2(d), using as a normalization factor, i.e., from Eq. (37). Therefore, the normalized value is determined by the rescaled Wilson ratio , described in Appendix E. As increases, decreases in a wide region of the impurity level , where the impurity levels are partially filled . In this filling range, the charge susceptibility is significantly suppressed by the Coulomb repulsion, and it vanishes in the strong interaction limit. Outside this region, i.e., at , the charge susceptibility approaches the noninteracting value as the filling of the impurity levels approaches or .
Figures 2(e) and 2(f) show the spin susceptibilities for and , which are normalized with the same scaling factor, i.e., [see Eq. (41)]. As the interaction increases, increases from the non-interacting value . In the strong interaction limit, it approaches the value , i.e., for and for , and exhibits a wide plateau structure in the strong-coupling region . At , where the occupation number approaches or , the spin susceptibility also approaches the noninteracting value .
VI.2 Derivative of and with respect to
The three-body correlation functions can be obtained from the derivatives of with respect to and , using Eqs. (42)–(44). In particular, can be rewritten in terms of the derivatives of the charge and spin susceptibilities, as
| (57) | ||||
| (58) |
for . Figures 3(a) and 3(b) show the NRG results for for and , respectively. Similarly, the derivatives of the spin susceptibility for and are plotted in Figs. 3 (c) and 3(d). Note that in these figures, the derivatives have been multiplied by a factor of to make them dimensionless. These derivatives are significantly suppressed in the strong-coupling region for large . More specifically, : the derivative of spin susceptibility becomes much smaller than while it is still larger than the derivative of charge susceptibility. Therefore, both and are suppressed in a wide range of electron fillings for large .
We next consider , defined in Eq. (45) as a derivative of a linear combination of the two different diagonal susceptibilities with respect to the magnetic fields . Figures 3(e) and 3(f) show for and , respectively. We see that exhibits a staircase structure with a flat plateau emerging around the integer filling points , , , , for large . The magnitude becomes much larger than the derivative of the charge and spin susceptibilities, and . Therefore, dominates the terms in the right-hand side of Eqs. (42)–(44) in the strong-coupling region , and the three independent components of three-body correlations approach one another in such a way that
| (59) |
This means that the three-body correlations are described by a single parameter in a wide filling range for large .






VI.3 Three-body correlations for and
We have calculated the three-body correlation functions , and for , using Eqs. (42)–(44). Figure 4 shows the dimensionless three-body correlations , and , defined in Eqs. (48) and (49). The left and right panels describe the NRG results in the SU(4) and SU(6) cases, respectively, and three different interaction strengths (from weak to strong) are chosen for the top, middle, and bottom panels.
All components of the three-body correlation functions vanish, , at the electron-hole symmetric point , and evolve as deviates from this point. Among the three independent components, the intra-level component has the largest magnitude, and exhibits plateau structures for large at integer filling points , , , . The other components, and , involve inter-level correlations and evolve as the Coulomb interaction increases. In particular, the correlation between the three different levels becomes the weakest. In the limit of , the diagonal component approaches the noninteracting value while the other two vanish:
| (60) |
Figures 4(e) and 4(f) clearly demonstrate the relation Eq. (59), which holds at for large :
| (61) |
It means that all the three-body components are determined by a single parameter in the strong-coupling region for large , as mentioned. The dimensionless three-body correlation functions clearly exhibit the plateau structure around the integer filling points , , , , , where the SU() Kondo effect occurs. These structures reflect the behavior of , described in Figs. 3(e) and 3(f), and evolve as the interaction strength increases. We see, in Figs. 4(e) and 4(f), that the plateaus appear much clearer for than , for the same interaction strength .
We will examine, in the subsequent sections, how these three-body correlation functions affect the next-leading order terms of the transport coefficients in the low-energy Fermi liquid regime away from half filling.
VII Nonlinear current noise of
SU(4) SU(6) quantum dots
In this section, we discuss the nonlinear terms of the steady current and the current noise , specifically, the order term for symmetric junctions, i.e., and . To provide a comprehensive view of the low-bias behavior of these terms, we begin with a brief review on the previous results for the coefficient of the nonlinear conductance [29], extending slightly the interaction range up to . We will then discuss the results for , i.e., the order term of nonlinear noise.
VII.1 : order term of
The leading-order term of the conductance, at , is determined by the transmission probability , i.e., the first term in the right-hand side of Eq. (51). It exhibits the well-known Kondo plateaus, which develop in the strong-coupling region, as shown in Figs. 15(b) and 16(b) in Appendix E.
The next-leading order term of the nonlinear conductance can be decomposed into the two-body part , defined in Table 2, and the three-body part , as
| (62) |
These coefficients , and are plotted vs in Figs. 5(a)–5(f) for and .
The two-body part dominates the next-leading order term near the electron-hole symmetric point , where and the three-body part vanishes:
| (63) |
Therefore, in the strong interaction limit, the peak at reaches and for and , respectively. Note that the rescaled Wilson ratio approaches in a wide region of for large . Outside this region, the two-body and three-body parts of approach to the noninteracting values,
| (64) |
since , , and the three-body contributions approach the values given in Eq. (60).






The SU() Kondo effect occurs in the strong-coupling region at the integer filling points. The plateau structure evolves as increases, especially in the three-body part , as seen in Figs. 5(e) and 5(f). In the strong-coupling region, it can be expressed in the form due to Eq. (61). The two-body part , shown in Figs. 5(c) and 5(d) for , does not exhibit a clear plateau other than the one appearing near half filling. For , this is because the factor for vanishes at and , i.e., at the quarter and three-quarters filling points. As a sum of and , the coefficient exhibits a wide and rather flat structure in the region of for large , seen in Figs. 5(a) and 5(b). There also emerge some weak local maxima in this flat structure at the integer filling points , , , , . In particular, the peak is most pronounced at , where or .


VII.2 Order and Order terms of
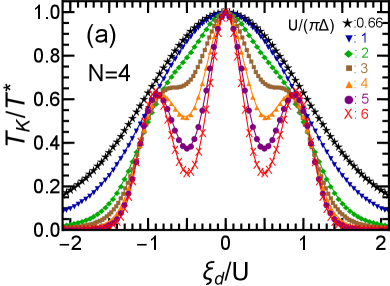
We next consider the current noise , the low-energy asymptotic form of which is given in Eq. (52) and Table 2. The leading-order term, , corresponds to the linear-response noise, the NRG results for which are shown as a function of in Figs. 6(a) and 6(b), for and , respectively. The linear noise is maximized at the points where the phase shift reaches and . It occurs at the integer filling points and for , at which the SU(4) Kondo effect makes the peaks wide and flat. In contrast, for , the peak emerges at the half-integer filling points and . More generally, the peak of the linear noise forms a flat plateau structure for (mod ), whereas the peak becomes round for (mod ) due to the fluctuations occurring between two adjacent integer filling states. For large , the quarter and three-quarters fillings occur near , at which the ground state is highly correlated for multilevel systems of . In contrast, these fillings occur at for SU(2) quantum dots, where the electron correlation becomes less important due to the valence fluctuations (see Appendix F).
The coefficient for the order term of current noise can also be decomposed into the two-body and three-body parts, as shown in Table 2:
| (65) |
The behavior of three-body part can be deduced from the one for , i.e., shown in Figs. 5(e) and 5(f), by multiplying them by a factor of “” which induces the modulations. One of the most distinctive features of , compared to the other coefficients ’s listed in Table 2, is that it depends upon the higher harmonics and with respect to the phase shift, which enter through not only through but : note that and defined in Eq. (48) are proportional to the factor . As varies, these higher harmonics evolve continuously in the range , simultaneously with the electron filling . Figures 7(a)–7(f) show results for , , and for and .

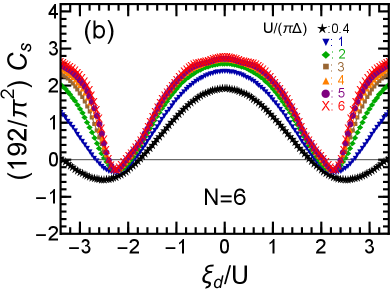




Each curve for , shown in Figs. 7(a) and 7(b), exhibits two valleys situated at the valence fluctuation regions for large . These valleys rise all around as increases. Notably, for , the bottom value of turns positive for large interactions , while for , it remains negative even for the largest interaction examined in this study.
Near the electron-hole symmetric point , where and , the two-body part dominates the nonlinear noise coefficient since the three-body correlations disappear around this point:
| (66) |
In particular, in the limit of , the rescaled Wilson ratio approaches the saturation value . Hence, the coefficient for the order term reaches for , and it reaches for : the height of this ridge decreases as increases.
In contrast, in the opposite limit , both the two-body and the three-body parts approach the noninteracting values
| (67) |
since , , and in this limit. Therefore, and contribute comparably to in the region , where the impurity levels are either almost empty or fully occupied . In particular, as seen in Figs. 7(c) and 7(d), the two-body part approaches the saturation value already at for large interactions .
In the strong-coupling region for large , the behavior of two-body part is determined by the higher-harmonic term, as
| (68) |
since the Wilson ratio is locked at in this region. As seen in Figs. 7(c) and 7(d), the two-body part has local minima at quarter and three-quarters filling points, which occur at and , or for large . At these local minima, take a positive value for , as it can be deduced from Eq. (68). This is in contrast to the SU(2) case where the local minima of take a negative value, as shown in Appendix F. In the strong-coupling region , the three-body part takes the following form, for large ,
| (69) |
due to the property described in Eq. (61). Equation (69) clearly shows that the three-body part vanishes, , at quarter and three-quarters fillings. Therefore, at these filling points, does not exhibit the plateau structures for in Fig. 7(e), despite the fact that clearly exhibits the plateau structures as seen in Fig. 5(e). In contrast, for , shows the clear plateau structures in Fig. 7(f) at the fillings of and . The three-body parts for both and cases also have pronounced local minima near the valence fluctuation regions , which cause the valley structure appearing in . A similar valley structure also emerges in for , as shown in Appendix F. However, it stems from the two-body correlations , instead of , in the SU() case.
VIII Thermoelectric transport of
SU(4) SU(6) quantum dots
We next consider the order term of the linear conductance and the order term of thermal conductance of SU() quantum dots.
VIII.1 : order term of
The coefficient for the order conductance, defined in Table 2, also consists of two-body parts and three-body part :
| (70) |
In particular, the three-body part is solely determined by the derivatives of the charge and spin susceptibilities, given in Eqs. (55) and (56), and does not depend on :
| (71) |
This is a quite distinct characteristics of from the next-leading order terms of the other transport coefficients. Figures 8(a)–8(f) show the NRG results for , , and .
We see in Figs. 8(e) and 8(f) that the three-body contribution almost vanishes, , in the wide strong-coupling region , in which the occupation number varies with , in the range of . This is because the magnitudes of the derivatives and , appearing in the right-hand side of Eq. (71), are significantly suppressed by the Coulomb repulsion in this region, as demonstrated in Figs. 3(a)–3(d).
Therefore, the two-body part dominates in the strong-coupling region , and it takes the following form for large ,
| (72) |
as the rescaled Wilson ratio reaches the saturation value . Hence, the plateau structure of is determined by the term of in Eq. (72). In particular, the plateau around the half filling point reaches the height of and for and , respectively, since in this region. The order conductance, , vanishes at , more specifically at the quarter and the three-quarter fillings where the phase shift reaches or . The zero points of emerge at integer fillings in the case of (mod ) at which the SU() Kondo effect is occurring, whereas for (mod ) the zeros emerge at half-integer filings in between the two adjacent Kondo states. This explains the reason why the SU(4) Kondo state at quarter filling exhibits universal -scaling behavior, which shows the dependence at low temperatures instead of the dependence [68].
In the valence fluctuation and empty (or fully-occupied) orbital regimes, which spread over the regions of , the three-body part becomes comparable to the two-body part . Both of these parts approach the noninteracting values in the limit of :
| (73) |










VIII.2 : order term of
The coefficient for the order term of the thermal conductance can also be decomposed into two parts, and , as shown in Table 2:
| (74) |
In contrast to of the conductance given in Eq. (71), the three-body part of the thermal conductance depends on as well as and . The contribution of enters through and , described in Eqs. (42) and (43). This component yields the plateau structure in , which reflects the staircase behavior seen in Figs. 3(e) and 3(f). Figure 9 shows the NRG results for , , and in the SU(4) and SU(6) cases.
Near half filling in the region of , the two-body part dominates as the three-body part disappears near half filling , i.e., :
| (75) |
In particular, in the strong interaction limit , the coefficient for and approach the values of and , respectively.
The rescaled Wilson ratio takes the values very close to the saturation value for large in the strong-coupling region of , as described in Appendix E. Similarly, in this region, the three-body correlations show the property described in Eq. (61), and thus and take the form
| (76) |
Therefore, the plateau structure of is determined by the term appearing in the right-hand side, while the structure of reflects the behavior of shown in Fig. 4(e) and 4(f). The coefficient changes sign in the strong-coupling region at two points of , which are incommensurate with the occupation number in contrast to that changes sign at and fillings.
In the opposite limit , both the two-body and three-body parts approach the noninteracting values,
| (77) |


VIII.3 : order term of
The Lorenz number for quantum dots is defined as the ratio of the thermal conductance to the electrical conductance . It takes the universal Wiedemann-Franz value at zero temperature: . However, as the temperature rises, it deviates from the universal value, showing the dependence described in Tables 1 and 2. The coefficient for the order term is given by , as a difference between the next-leading order terms of and .
Figure 10(a) and 10(b) show the NRG results for in the SU(4) and SU(6) cases, respectively. Near half filling , the coefficient is determined by the two-body part as the three-body part vanishes at , as seen in Fig. 4(e) and 4(f):
| (78) |
It takes a positive value and reaches for , and for , in the limit of where .
In the strong-coupling region , the coefficient exhibits the plateau structures for large , reflecting the corresponding structures of and . The coefficient changes sign at the points where the order terms of and coincide, i.e., .
In the other regions at , the impurity levels approach the empty state or fully occupied state. In particular, in the limit of , both the two-body and three-body parts approach the noninteracting values, and , and thus
| (79) |
IX Fermi liquid description for
SU() symmetric magnetic alloys
We have discussed, in the previous sections, low-energy transport properties of SU() quantum dots, by extending the Fermi liquid description to the next-leading order terms which contribute to the transport at finite temperatures or at finite bias voltages. Our formulation is applicable to a wide class of Kondo systems other than quantum dots, particularly to dilute magnetic alloys (MA) composed of , , or electrons [2]. In this and the next sections, we apply this formulation to dilute magnetic alloys away from half filling, taking into account exactly the order and energy shifts of quasiparticles that enter through the real part of the self-energy given in Appendix B.
The thermoelectric transport coefficients of magnetic alloys in the linear-response regime can be derived from the function for , , and , defined by [43]
| (80) |
Here, the inverse spectral function in the integrand represents the relaxation time of conduction electrons, which depends on as well as . The low-temperature expansion of can be deduced from the exact low-energy asymptotic of , given in Appendix B. We have presented the expansion formulas for the standard Anderson impurity model in a previous paper [21]. In this work, we extend the formulation to multi-level impurities in a general form without assuming the SU() symmetry. Details of the derivation are given in Appendix G.
In the following, we consider the behavior of the next-leading order terms of electrical conductivity and thermal conductivity of magnetic alloys in the SU() symmetric case, where for all , and for all and . In this case, the formulas given in Appendix G are simplified, and as a result, the electrical resistivity , the thermal resistivity , and the Lorenz number can be expressed in the form,
| (81) | |||
| (82) | |||
| (83) |
Here, is the unitary-limit value of electrical conductivity. The explicit expressions of the dimensionless coefficients , , and are listed in Table 2. These coefficients ’s for magnetic alloys can also be decomposed into the two-body part and the three-body part, as those for quantum dots. Note that the following relations hold between the coefficients for magnetic alloys and quantum dots:
| (84) | ||||
| (85) | ||||
| (86) |
In particular, the term appearing in the right-hand side vanishes at half filling, i.e., . In this case the coefficients for magnetic alloys in the left-hand side coincide with their quantum-dot counterparts in the right-hand side, except for the signs of and . The behavior of these coefficients for magnetic alloys also reflects the properties of low-lying energy states and significantly depends on the occupation number and the interaction strength .
X Thermoelectric transport of
SU(4) SU(6) magnetic alloys
We consider here the next-leading order terms of the electrical resistivity and thermal resistivity of SU() symmetric magnetic alloys for and . For comparison, we also provide the NRG results for these transport coefficients in the SU(2) case in Appendix F, and the analytic expressions of ’s for noninteracting magnetic alloys in Appendix H.
X.1 : order term of
The coefficient for the order resistivity, is defined in Table 2. It consists of two-body part and three-body part :
| (87) |
Note that , i.e., the three-body part for the resistivity of magnetic alloys is identical to the one for the conductance of quantum dots. Therefore, does not depend on and is determined by the derivative of the charge and spin susceptibilities through Eq. (71). Figures 11(a)–11(d) show the NRG results for , , and for both the SU(4) and SU(6) symmetric cases.
The coefficient is positive and is less sensitive to the impurity level position as compared to the quantum-dot counterpart shown in Fig. 8. This difference is caused by the first term, , appearing in the right-hand side of Eq. (84). In particular, in the noninteracting case, it becomes a constant, , independent of the level position, as all effects due to are absorbed into the characteristic energy for (see Appendix H). Therefore, it is the strong electron correlation that makes , shown in Figs. 11(a) and 11(b), deviates from the constant value.
The three-body part almost vanishes, , for large in the strong-coupling region , as mentioned for in Eq. (71). This is caused by the fact that the magnitudes of the derivatives, and , are significantly suppressed by the Coulomb repulsion in the wide range of electron filling , as demonstrated in Figs. 3(a)–3(d). Therefore, in this region , the coefficient is determined solely by the two-body part , which takes the form
| (88) |
as the rescaled Wilson ratio is saturated to . Hence, the plateaus emerging around the integer filling points , , , , reflect the structures of the Kondo ridge occurring for the transmission probability , seen in Figs. 15(b) and 16(b) in Appendix E. Among these plateaus, the one at half filling, where , takes the smallest value: and for and , respectively. As moves away from half filling, the coefficient increases in the region of . Equation (88) also indicates that the plateau becomes highest at the electron fillings of and : and for and , respectively. The NRG results for , shown in Figs. 11(a) and 11(b), clearly demonstrate these behaviors, which are quite different form the behaviors of of quantum dots. Equation (88) also shows that, in the SU(2) symmetric case where , the coefficient takes the maximum value at half filling, as demonstrated also in Appendix F.
In contrast, at , the occupation number approaches the empty or the fully occupied states as the impurity level moves further away from the Fermi level. In this region, both the two-body and three-body parts give comparable contributions to , and approach the noninteracting values:
| (89) |
and thus .




X.2 : order term of
We next consider the order term of thermal conductivity of the SU() symmetric magnetic alloys. The coefficient , defined in Tables 1 and 2, consists of two-body and three-body parts:
| (90) |
Note that , i.e., the three-body part for of magnetic alloys is identical to the one for the thermal conductance of quantum dots. The NRG results for these coefficients , , and are shown in Figs. 12(a)–12(d) for and .
The coefficient for magnetic alloys is less sensitive to as compared to for for quantum dots. This difference is caused by the contribution of the first term, , in the right-hand side of Eq. (85). The coefficient is positive and has a broad peak at , the height of which is determined by the two-body contribution as three-body part vanishes in the electron-hole symmetric case:
| (91) |
In the limit of , it reaches the maximum possible value, and for and , respectively.




In the strong-coupling region , the coefficient takes the following form for large ,
| (92) |
This is because, in this region, the rescaled Wilson ratio is almost saturated (see Appendix E) and the three-body part is parameterized by a single component, , due to the property described in Eq. (61). The plateau structures of , appearing in Figs. 12(a) and 12(b) around the integer filling points , , , , are determined by both the term in and the plateaus occurring in seen in Figs. 12(c) and 12(d).
In contrast, at , the electron filling approaches the empty or the fully occupied states as the impurity level goes very far away from the half filled point. Therefore, the order thermal conductivity for magnetic alloys also approaches the noninteracting value in this limit:
| (93) |
and thus .
X.3 : order term of
The Lorenz number for magnetic alloys is defined as the ratio of the thermal conductivity to electrical conductivity . It takes the universal Wiedemann-Franz value at zero temperature: . However, it deviates from this value as the temperature increases, showing the dependence as described in Eq. (83). The precise expansion formula for the coefficient for the order term is shown in Table 2. It is given by the difference, , between the order term of the resistivities, and , defined in Eqs. (81) and (83). The coefficient for magnetic alloys and the quantum-dot counterpart are related to each other through Eq. (86): these two coefficients tend to have opposite signs. In Appendix H, we have also provide an analytic formula for in the noninteraction case, for comparison.
The NRG results for are shown in Figs. 13(a) and 13(b) for and , respectively. Near half filling , the coefficient is determined by the two-body part as the three-body part, given by , vanishes at :
| (94) |
This coefficient attains its greatest possible negative value in the limit of where : for , and for .
In the strong-coupling region , the also exhibits the plateau structures around the integer filling points , , , for large , reflecting the structures that appear for both and . In particular, the plateaus at fillings, seen in Figs. 13(a) and 13(b) for , take a negative value for both and , whereas the other plateaus become positive for as the electrical resistivity dominates, i.e., .
As the impurity level goes far away from the Fermi level in the region , the occupation number approaches or . In the limit of , the two-body and three-body parts take the noninteracting values, and , and the coefficient converges to the positive value,
| (95) |


XI Summary
We have presented a comprehensive Fermi liquid description for nonlinear current and thermoelectric transport through quantum dots and magnetic alloys, which is asymptotically exact at low energies up to the next-leading order terms. Our formulation is based on the multilevel Anderson model and is applicable to arbitrary impurity-level structures for , , , , including the spin degrees of freedom. The coefficients for the next-leading order terms have been shown to be expressed in terms of a set of the correlation functions defined with respect to the equilibrium ground state: the phase shift , the static susceptibilities , and the three-body correlations which emerge when the system does not have both the electron-hole and time-reversal symmetries.
Extending Yamada-Yosida’s field-theoretical approach, we have obtained the formulas for the differential conductance , current noise and thermal conductance of quantum dots, and also the electrical resistivity and thermal conductivity of dilute magnetic alloys. In the SU() symmetric case, these transport coefficients take simplified forms, as listed in Tables 1 and 2, and the three-body correlations can be deduced from the derivatives of the susceptibilities: , , and through Eqs. (42)–(45).
We have also calculated the correlation functions for the SU(4) and SU(6) cases, using the NRG approach over the whole region of impurity-electron fillings , which includes the Kondo and the valence-fluctuation regimes. In the SU() case, the three-body correlations have three linearly independent components that approach each other closely as the Coulomb interaction increases: for , in a wide filling range . This is caused by the suppression of the derivatives of the charge and spin susceptibilities, occurring at large : and , with the characteristic energy scale of the SU() Fermi liquid. This property of three-body correlations is also related to a similar property of linear susceptibilities, , which reflects the suppression of charge fluctuations, , occurring at large .
The coefficients ’s for the next-leading order terms can be decomposed into the two-body part ’s and the three-body part ’s, as listed in Table 2. The NRG results show that the three-body part of the coefficient for the order term of exhibits Kondo plateau structures at integer filling points , , , for large . These plateaus of complement the two body part , which decreases away from half filling, to form a wide ridge structure in that spreads over the region of .
The linear-response term of current noise is maximized at quarter filling and three-quarters filling, and the peaks exhibit flat structures for , while they are round for . This difference is caused by the fact that, at these fillings, the SU() Kondo effects occur for (mod ), while the intermediate valence fluctuations occur for (mod ). The coefficient for the order nonlinear term of has a peak at half filling, which evolves into a plateau as increases. As the impurity level deviates from the half filling point, decreases rapidly for , whereas it varies more modestly for . This is mainly due to the higher-harmonic “” dependence of the three-body part , which vanishes at the quarter and three-quarters filling points. As increases further, has a pronounced negative minimum in the valence fluctuation regions at for both and , which yield the valley structures appearing in . This is in marked contrast to the SU(2) case, where the valley structure emerging in is caused by the two-body contributions , instead of .
We have also studied the coefficient for the order term of the linear conductance and the coefficient for the order term of thermal conductance , for SU() quantum dots. The three-body part of is determined solely by the derivatives of charge and spin susceptibilities, i.e., and , and is independent of . Therefore, is significantly suppressed and almost vanishes for strong interactions in a wide range of the electron filling . In contrast, the three-body part for thermal conductance involves and becomes comparable to the two-body part , except for the plateau region near half filling. The Lorenz number for quantum dots takes the universal Wiedemann-Franz value at and shows a dependence at low temperatures. The coefficient for the order term of is given by , i.e., the difference between the next-leading order terms of and . This coefficient also exhibits the Kondo plateau structures at integer filling points , , , .
The three-body correlations also play a significant role in the low-energy transport of magnetic alloys. We have investigated the behaviors of the coefficient for the order resistivity and for the order thermal conductivity . In the SU() symmetric case, the three-body parts of these coefficients become identical to the related ones for quantum dots, i.e., and . Therefore, the difference between the coefficients for MA and that for the QD counterparts arises from the two-body parts, more specifically, from the additional terms appearing in the right-hand side of Eqs. (84) and (85). The additional terms make the coefficients and positive definite and less sensitive to the impurity level position , compared to the QD counterparts and . The coefficient takes the maximum value at the electron fillings of and for , while in the SU(2) case has a single peak at half filling. The coefficient for the order term of the Lorenz number for magnetic alloys also becomes less sensitive to the electron filling compared to for quantum dots.
The three-body correlation functions can be determined experimentally by measuring the coefficients ’s for the next leading order terms. These experimental values can then be used to infer the behaviors of other unmeasured transport coefficients.
Acknowledgements.
This work was supported by JSPS KAKENHI Grants No. JP18K03495, No. JP18J10205, No. JP21K03415, and No. 23K03284 and JST CREST Grant No. JPMJCR1876. K. M. was supported by JST Establishment of University Fellowships towards the Creation of Science Technology Innovation Grant No. JPMJFS2138. Y. T. was supported by Sasakawa Scientific Research Grant from the Japan Science Society No. 2021-2009, and by the Shigemasa and Shigeaki Nakazawa Fellowship of Graduate School of Science, Osaka City University.Appendix A Fermi liquid parameters
A.1 Linear and nonlinear static susceptibilities
The ground-state properties and the leading Fermi liquid corrections due to the low-lying excitations can be described in terms of the occupation number and the linear susceptibilities of the impurity level, derived from the free energy :
| (96) | ||||
| (97) |
Here, , and thermal-equilibrium averages are defined as , with the inverse temperature.
In addition to the linear susceptibilities, the nonlinear susceptibilities play an essential role in the next-leading order terms of the transport coefficients when the system does not have both the electron-hole and time-reversal symmetries:
| (98) |
Here, is the imaginary-time ordering operator. This correlation function has the permutation symmetry: Specifically, in our formulation we are using the ground state values for , and , determined at .
The occupation number can be related to the phase shift through the Friedel sum rule: . The phase shift corresponds to the argument of the Green’s function, given by , at [8], and determines the value of the spectral function at :
| (99) | ||||
| (100) |
where is the nonequilibrium spectral function defined in Eq. (9). The derivative of also contributes to the next-leading order terms and can be expressed in terms of the diagonal susceptibility , using Eq. (106),
| (101) |
One of the most typical Fermi liquid corrections due to many-body scatterings arises in the -linear specific heat of impurity electrons:
| (102) |
The coefficient can be expressed in terms of the diagonal components of the linear susceptibility using the Ward identities [6, 8, 9], i.e., Eqs. (106) and (107), which follow from a relationship between the derivative of the self-energy with respect to and the derivative with respect to .
A.2 Ward identities
The local Fermi liquid state of quantum impurity systems can be microscopically described using the retarded Green’s function, defined in Eq. (8), which can also be written in the form,
| (103) |
The information about the low-lying energy states can be extracted from the equilibrium self-energy , by expanding it, step by step, around the Fermi energy . The expansion up to linear terms in describes the renormalized resonance state of the form,
| (104) |
Here, the renormalized parameters are defined by
| (105) |
The wavefunction renormalization factor can be related to the derivative of with respect to the impurity level , using the Ward identity [6, 8, 9]:
| (106) |
The coefficient determines the extent to which the susceptibility is enhanced at :
| (107) |
Recently studies have been clarified that the order real part of the self-energy can be expressed in terms of the the diagonal component of the three-body correlation function, , as [18, 19, 20, 21]
| (108) |
Physically, this coefficient determines the energy shifts of quasiparticles of order , and , which affect the low-energy transport of the next-leading order.
Appendix B Low-energy asymptotic form of spectral function
The low-energy asymptotic form of the retarded self-energy for multilevel Anderson impurity model has been derived up to terms of order , , and in the previous works [27, 29]. For symmetric tunnel junctions with () and (), it takes the form,
| (109) | ||||
| (110) |
Substituting these expansion results into Eq. (103), we obtain the asymptotic form spectral function,
| (111) |
Correspondingly, the inverse of the spectral function that determines the thermoelectric transport of magnetic alloys takes the following form, up to terms order and at ,
| (112) |
Appendix C Properties of in SU() case
We briefly describe here some relations between the three-body correlation functions and the derivative of the linear susceptibilities with respect to the center of mass coordinate of the impurity levels, .
The derivative of the diagonal susceptibility can be written as
| (113) |
where . Note that in the SU() symmetric case. Similarly, the derivative of the off-diagonal susceptibility for takes the form
| (114) |
for . In the SU(2) symmetric case, Eqs. (113) and (114) provide enough information to determine the two independent components and from the two differential coefficients and . However, for , there are three independent three-body components, i.e., , , and , so that we need additional information to determine all these components.
In order to obtain another independent relation, we consider the derivative of the susceptibilities with respect to the magnetic field , which induces the level splitting in impurity levels in a such way that and , with for and :
| (115) |
From this derivative, we obtain the following relation, taking ,
| (116) |
Here, we set the magnetic field to be zero, , in the last two lines. This relation can also be rewritten into the following form at , using the original label ,
| (117) |
for .

Appendix D NRG procedures
We have carried out NRG calculations, dividing the conduction channels into pairs and using the SU(2) spin and U(1) charge symmetries for each of the pairs, i.e., symmetries. The discretization parameter and the number of retained low-lying excited states are chosen to be for . Note that the SU(4) symmetry is preserved in our iteration scheme since the truncation of higher energy states has been carried out after adding all new states from the pairs.
For , we have also exploited the method of Stadler et al. [85]. In this case, the truncation procedure is carried out at each of the steps (1, , , ) after adding the states constructed with one of the channel pairs, by using Oliveira’s -trick [86], choosing different values for each of the steps: for the -th pair. We have carried out calculations for , taking rather large values for the NRG parameters, such that for small interactions and , and for large interactions , , , , and . This method significantly reduces the computational cost for obtaining low-lying energy states and enables us to calculate the three-body correlation functions for , although it does not faithfully preserve the SU() symmetry. We have checked whether this method reproduces the noninteracting results. Figure 14 compares the NRG result for with the exact one for ; the results show reasonable agreement. It indicates that this truncation procedure works effectively for deducing the SU(6) FL parameters.
In order to calculate defined in Eq. (45), we have also introduced a small external potential , which depends on the channel index 1, , , and shifts the impurity level from . Specifically, for , it is applied in a way equivalent to the local Zeeman field: and . For , we have extended the potential such that , , and , and have deduced from the derivatives of the channel susceptibilities with respect to .
Appendix E Two-body FL parameters for
SU(4) & SU(6) symmetric cases
We provide a quick overview of the behavior of the renormalized parameters in the SU(4) and SU(6) cases, which can be derived from the phase shift and the linear susceptibilities [87, 88, 89, 90]. Our discussion here is based on the NRG results, plotted in Figs. 15 and 16 as functions of the impurity level position , for several different interaction strengths: from weak to strong interactions up to .
The SU() Kondo effect occurs for strong interactions when the impurity levels are filled by an integer number of electrons, i.e., at the fillings of , , , . It takes place at , , …, , and gives an interesting variety in the low-energy properties. As increases, a greater interaction strength is required to clearly observe the Kondo behavior. This is because the quantum fluctuations caused by the Coulomb interaction are suppressed for large . In particular, the mean-field theory becomes exact in the limit that is taken keeping the scaled interaction constant [90].












Figures 15(a) and 16(a) show the occupation number for and , respectively. As increases, the Coulomb staircase structure emerges: varies steeply at , , , . Correspondingly, as increases, the transmission probability , shown in Figs. 15(b) and 16(b), exhibits a plateau structure that develops around , , , . In particular, the plateau at the half-filling point reaches the unitary limit value .
The renormalization factor , shown in Figs. 15(c) and 16(c) for and , exhibits a broad valley structure at , where . The valley becomes deeper as increases, and the local minima emerge for at the integer-filling points, reflecting the occurrence of the SU() Kondo effects. The renormalization factor also has local maxima at intermediate valence states in between two adjacent local minima. Note that is significantly suppressed by the strong electron correlations even at these local maxima. Figures 15(d) and 16(d) show the rescaled Wilson ratio . For large interactions, exhibits a wide flat structure at , the height of which approaches the saturation value , especially for , reflecting the suppression of charge fluctuations in this region of .
Figures 15(e) and 16(e) show the renormalized resonance-level position for and , respectively, as a function of . For strong interactions, the renormalized level is almost locked at the Fermi level, , in the strong-coupling region , which corresponds to the filling range of . Figures 15(f) and 16(f) show an enlarged view of in the vicinity of the Fermi level. We see that exhibits a fine structure which reflects the staircase behavior of the phase shift and the oscillatory behavior of the renormalization factor . Outside the strong-coupling region, approaches the bare value at , or the Hartree-Fock value at : these asymptotic forms of are shown as the dashed lines in Figs. 15(e) and 16(e).




Appendix F Current noise and thermoelectric transport for SU(2) symmetric case
We have discussed the behavior of the current noise and thermoelectric transport of the SU(4) and SU(6) Anderson model in Secs. VII, VIII, and X. For comparison, here we briefly describe the corresponding results in the SU(2) case, specifically, the current noise and the thermoelectric transport coefficients are plotted in Figs. 17 and 18, respectively.
We can see in Fig. 17(b) that the linear noise is suppressed in the strong-coupling region for large , where the transmission probability exhibits a wide Kondo plateau in Fig. 17(a). However, the linear noise increases and has the peaks, the width of which is of the order of at valence fluctuation regions near the quarter and three-quarters filling points where the phase reaches or . At these filling points, the coefficient for the order nonlinear current noise has the negative minima, as seen in Fig. 17(c). We see in Fig. 17(d) that the three-body part of , is also suppressed over a wide region . Therefore, in this strong-coupling region, the nonlinear noise is determined solely by the two-body part in the SU(2) case:
| (118) |
where is the Wilson ratio. In particular, the dip structures of at the quarter and three-quarters fillings reflect the mimina of in . In contrast, at , the three-body part becomes comparable to , and contributes to .
Figure 18 shows the results for the next-leading order terms of the thermoelectric transport coefficients for the SU(2) quantum dots (a) and (b) , and for SU(2) magnetic alloys (c) and (d) . All these coefficients exhibit the plateau structures due to the Kondo effect in the strong-coupling region for large , where the phase shit is locked at . In this region, the three-body contributions, and , almost vanish (see Ref. 28 for more details), and the height of these plateaus approach the saturation values for , i.e., , , , and . The coefficients and for charge transport show a similar behavior in the strong-coupling region. Furthermore, in this region, the coefficients for thermal conductivities, and , also show a similar behavior. In contrast, at , the coefficients and for quantum dots change sign and become negative as the occupation number approaches or , whereas the coefficients and for magnetic alloys remain positive definite.




Appendix G Three-body Fermi liquid corrections to thermoelectric transport of magnetic alloys
In this appendix, we describe the low-energy asymptotic form of the electrical resistivity , the thermopower , and the thermal conductivity of magnetic alloys:
| (119) | ||||
| (120) | ||||
| (121) |
For magnetic alloys, the response functions for and are given by
| (122) |
Equation (119) defines the electrical conductivity relative to its unitary-limit value . Correspondingly, the prefactor for is defined in such a way that the -linear thermal conductivity should take the form,
| (123) |
The asymptotic form of can be calculated, using the low-energy expansion of the inverse spectral function given in Eq. (112):
| (124) | ||||
| (125) | ||||
| (126) |
Here, the coefficients and are given by
| (127) | ||||
| (128) |
We obtain the low-temperature expressions of , and , substituting Eqs. (124)–(126) into Eqs. (119)–(121):
| (129) | ||||
| (130) | ||||
| (131) |
Here, is the harmonic mean (HM) of , defined by
| (132) |
The coefficients and of the next-leading order terms are given by
| (133) | ||||
| (134) |
Correspondingly, the electrical conductivity and the thermal conductivity take the following form,
| (135) | ||||
| (136) |
Furthermore, the Lorenz number can also be deduced up to terms of order , as
| (137) | ||||
| (138) |
In the limit of zero temperature, the Lorenz number takes a constant value , and the Wiedemann-Franz law holds. However, it deviates as temperature increases, showing the dependence.
Appendix H Thermoelectric transport coefficients for noninteracting magnetic alloys
We provide here the noninteracting results for the thermoelectric transport coefficients of magnetic alloys. For , the response functions for can be calculated, substituting the explicit form of the spectral function into Eq. (122):
| (139) | ||||
| (140) | ||||
| (141) |
The transport coefficients, defined in Eqs. (119)–(121), can be deduced from these analytic expressions for . In particular, in the SU() symmetric case where , the electrical resistivity for is given by
| (142) | ||||
| (143) |
Here, is the characteristic energy scale in the noninteracting case. The coefficient for the -resistivity is given by a constant () as the dependence is absorbed into .
The thermopower and thermal resistivity for are given by
| (144) | |||
| (145) | |||
| (146) |
Furthermore, the dimensionless coefficient for the order term of the Lorenz number is given by and it takes the form,
| (147) |
These results for the next-leading order terms in the noninterating case are plotted as functions of in Fig. 19. The coefficient takes a Lorentzian form with an offset value of (). Correspondingly, has a dip at , and vanishes at the points where and give equal contributions to the Lonrez number . As the impurity level moves further away from the Fermi level , it approaches the value of ().

References
- Kondo [1964] J. Kondo, Prog. Theor. Phys. 32, 37 (1964).
- Hewson [1993] A. C. Hewson, The Kondo Problem to Heavy Fermions (Cambridge University Press, Cambridge, 1993).
- Ono et al. [2019] K. Ono, J. Kobayashi, Y. Amano, K. Sato, and Y. Takahashi, Phys. Rev. A 99, 032707 (2019).
- Yasui and Ozaki [2017] S. Yasui and S. Ozaki, Phys. Rev. D 96, 114027 (2017).
- Nozières [1974] P. Nozières, J. Low Temp. Phys. 17, 31 (1974).
- Yamada [1975a] K. Yamada, Prog. Theor. Phys. 53, 970 (1975a).
- Yamada [1975b] K. Yamada, Prog. Theor. Phys. 54, 316 (1975b).
- Shiba [1975] H. Shiba, Prog. Theor. Phys. 54, 967 (1975).
- Yoshimori [1976] A. Yoshimori, Prog. Theor. Phys. 55, 67 (1976).
- Wilson [1975] K. G. Wilson, Rev. Mod. Phys. 47, 773 (1975).
- Krishna-murthy et al. [1980a] H. R. Krishna-murthy, J. W. Wilkins, and K. G. Wilson, Phys. Rev. B 21, 1003 (1980a).
- Krishna-murthy et al. [1980b] H. R. Krishna-murthy, J. W. Wilkins, and K. G. Wilson, Phys. Rev. B 21, 1044 (1980b).
- Hershfield et al. [1992] S. Hershfield, J. H. Davies, and J. W. Wilkins, Phys. Rev. B 46, 7046 (1992).
- Oguri [2001] A. Oguri, Phys. Rev. B 64, 153305 (2001).
- Mora [2009] C. Mora, Phys. Rev. B 80, 125304 (2009).
- Mora et al. [2009] C. Mora, P. Vitushinsky, X. Leyronas, A. A. Clerk, and K. Le Hur, Phys. Rev. B 80, 155322 (2009).
- Mora et al. [2015] C. Mora, C. P. Moca, J. von Delft, and G. Zaránd, Phys. Rev. B 92, 075120 (2015).
- Filippone et al. [2018] M. Filippone, C. P. Moca, A. Weichselbaum, J. von Delft, and C. Mora, Phys. Rev. B 98, 075404 (2018).
- Oguri and Hewson [2018a] A. Oguri and A. C. Hewson, Phys. Rev. Lett. 120, 126802 (2018a).
- Oguri and Hewson [2018b] A. Oguri and A. C. Hewson, Phys. Rev. B 97, 045406 (2018b).
- Oguri and Hewson [2018c] A. Oguri and A. C. Hewson, Phys. Rev. B 97, 035435 (2018c).
- Karki and Kiselev [2017] D. B. Karki and M. N. Kiselev, Phys. Rev. B 96, 121403(R) (2017).
- Karki et al. [2018] D. B. Karki, C. Mora, J. von Delft, and M. N. Kiselev, Phys. Rev. B 97, 195403 (2018).
- Karki and Kiselev [2018] D. B. Karki and M. N. Kiselev, Phys. Rev. B 98, 165443 (2018).
- Moca et al. [2018] C. P. Moca, C. Mora, I. Weymann, and G. Zaránd, Phys. Rev. Lett. 120, 016803 (2018).
- Teratani et al. [2020a] Y. Teratani, R. Sakano, and A. Oguri, Phys. Rev. Lett. 125, 216801 (2020a).
- Oguri et al. [2022] A. Oguri, Y. Teratani, K. Tsutsumi, and R. Sakano, Phys. Rev. B 105, 115409 (2022).
- Tsutsumi et al. [2021] K. Tsutsumi, Y. Teratani, R. Sakano, and A. Oguri, Phys. Rev. B 104, 235147 (2021).
- Tsutsumi et al. [2023] K. Tsutsumi, Y. Teratani, K. Motoyama, R. Sakano, and A. Oguri, Phys. Rev. B 108, 045109 (2023).
- Glazman and Raikh [1988] L. I. Glazman and M. E. Raikh, JETP Lett. 47, 452 (1988).
- Ng and Lee [1988] T. K. Ng and P. A. Lee, Phys. Rev. Lett. 61, 1768 (1988).
- Wingreen and Meir [1994] N. S. Wingreen and Y. Meir, Phys. Rev. B 49, 11040 (1994).
- Meir and Wingreen [1992] Y. Meir and N. S. Wingreen, Phys. Rev. Lett. 68, 2512 (1992).
- Izumida et al. [1998] W. Izumida, O. Sakai, and Y. Shimizu, Journal of the Physical Society of Japan 67, 2444 (1998).
- Izumida et al. [2001] W. Izumida, O. Sakai, and S. Suzuki, J. Phys. Soc. Jpn. 70, 1045 (2001).
- Aligia [2012] A. A. Aligia, Journal of Physics: Condensed Matter 24, 015306 (2012).
- Aligia [2014] A. A. Aligia, Phys. Rev. B 89, 125405 (2014).
- Gogolin and Komnik [2006] A. O. Gogolin and A. Komnik, Phys. Rev. Lett. 97, 016602 (2006).
- Sela et al. [2006] E. Sela, Y. Oreg, F. von Oppen, and J. Koch, Phys. Rev. Lett. 97, 086601 (2006).
- Golub [2006] A. Golub, Phys. Rev. B 73, 233310 (2006).
- Sela and Malecki [2009] E. Sela and J. Malecki, Phys. Rev. B 80, 233103 (2009).
- Sakano et al. [2011] R. Sakano, T. Fujii, and A. Oguri, Phys. Rev. B 83, 075440 (2011).
- Costi et al. [1994] T. A. Costi, A. C. Hewson, and V. Zlatić, J. Phys.: Condens. Matter 6, 2519 (1994).
- Costi [2019] T. A. Costi, Phys. Rev. B 100, 155126 (2019).
- Goldhaber-Gordon et al. [1998a] D. Goldhaber-Gordon, H. Shtrikman, D. Mahalu, D. Abusch-Magder, U. Meirav, and M. A. Kastner, Nature 391, 156 (1998a).
- Goldhaber-Gordon et al. [1998b] D. Goldhaber-Gordon, J. Göres, M. A. Kastner, H. Shtrikman, D. Mahalu, and U. Meirav, Phys. Rev. Lett. 81, 5225 (1998b).
- Cronenwett et al. [1998] S. M. Cronenwett, T. H. Oosterkamp, and L. P. Kouwenhoven, Science 281, 540 (1998).
- van der Wiel et al. [2000] W. G. van der Wiel, S. D. Franceschi, T. Fujisawa, J. M. Elzerman, S. Tarucha, and L. P. Kouwenhoven, Science 289, 2105 (2000).
- V. Borzenets et al. [2020] I. V. Borzenets, J. Shim, J. C. H. Chen, A. Ludwig, A. D. Wieck, S. Tarucha, H.-S. Sim, and M. Yamamoto, Nature 579, 210 (2020).
- Grobis et al. [2008] M. Grobis, I. G. Rau, R. M. Potok, H. Shtrikman, and D. Goldhaber-Gordon, Phys. Rev. Lett. 100, 246601 (2008).
- Scott et al. [2009] G. D. Scott, Z. K. Keane, J. W. Ciszek, J. M. Tour, and D. Natelson, Phys. Rev. B 79, 165413 (2009).
- Zarchin et al. [2008] O. Zarchin, M. Zaffalon, M. Heiblum, D. Mahalu, and V. Umansky, Phys. Rev. B 77, 241303(R) (2008).
- Delattre et al. [2009] T. Delattre, C. Feuillet-Palma, L. G. Herrmann, P. Morfin, J.-M. Berroir, G. FShu ve, B. PlaXun ais, D. C. Glattli, M.-S. Choi, C. Mora, and T. Kontos, Nature Physics 5, 208 (2009).
- Yamauchi et al. [2011] Y. Yamauchi, K. Sekiguchi, K. Chida, T. Arakawa, S. Nakamura, K. Kobayashi, T. Ono, T. Fujii, and R. Sakano, Phys. Rev. Lett. 106, 176601 (2011).
- Ferrier et al. [2016] M. Ferrier, T. Arakawa, T. Hata, R. Fujiwara, R. Delagrange, R. Weil, R. Deblock, R. Sakano, A. Oguri, and K. Kobayashi, Nat. Phys. 12, 230 (2016).
- Hata et al. [2021] T. Hata, Y. Teratani, T. Arakawa, S. Lee, M. Ferrier, R. Deblock, R. Sakano, A. Oguri, and K. Kobayashi, Nature Communications 12, 3233 (2021).
- Hsu et al. [2022] C. Hsu, T. A. Costi, D. Vogel, C. Wegeberg, M. Mayor, H. S. J. van der Zant, and P. Gehring, Phys. Rev. Lett. 128, 147701 (2022).
- Svilans et al. [2018] A. Svilans, M. Josefsson, A. M. Burke, S. Fahlvik, C. Thelander, H. Linke, and M. Leijnse, Phys. Rev. Lett. 121, 206801 (2018).
- Laird et al. [2015] E. A. Laird, F. Kuemmeth, G. A. Steele, K. Grove-Rasmussen, J. Nygård, K. Flensberg, and L. P. Kouwenhoven, Rev. Mod. Phys. 87, 703 (2015).
- Borda et al. [2003] L. Borda, G. Zaránd, W. Hofstetter, B. I. Halperin, and J. von Delft, Phys. Rev. Lett. 90, 026602 (2003).
- Choi et al. [2005] M.-S. Choi, R. López, and R. Aguado, Phys. Rev. Lett. 95, 067204 (2005).
- Eto [2005] M. Eto, Journal of the Physical Society of Japan 74, 95 (2005).
- Sakano and Kawakami [2006] R. Sakano and N. Kawakami, Phys. Rev. B 73, 155332 (2006).
- Anders et al. [2008] F. B. Anders, D. E. Logan, M. R. Galpin, and G. Finkelstein, Phys. Rev. Lett. 100, 086809 (2008).
- Weymann et al. [2018] I. Weymann, R. Chirla, P. Trocha, and C. P. Moca, Phys. Rev. B 97, 085404 (2018).
- Filippone et al. [2014] M. Filippone, C. P. Moca, G. Zaránd, and C. Mora, Phys. Rev. B 90, 121406(R) (2014).
- Mantelli et al. [2016] D. Mantelli, C. P. Moca, G. Zarand, and M. Grifoni, Physica E: Low-dimensional Systems and Nanostructures 77, 180 (2016).
- Teratani et al. [2020b] Y. Teratani, R. Sakano, T. Hata, T. Arakawa, M. Ferrier, K. Kobayashi, and A. Oguri, Phys. Rev. B 102, 165106 (2020b).
- Sasaki et al. [2000] S. Sasaki, S. De Franceschi, J. M. Elzerman, W. G. van der Wiel, M. Eto, S. Tarucha, and L. P. Kouwenhoven, Nature 405, 764 (2000).
- Jarillo-Herrero et al. [2005] P. Jarillo-Herrero, J. Kong, H. S. J. van der Zant, C. Dekker, L. P. Kouwenhoven, and S. De Franceschi, Phys. Rev. Lett. 94, 156802 (2005).
- Babić et al. [2004] B. Babić, T. Kontos, and C. Schönenberger, Phys. Rev. B 70, 235419 (2004).
- Makarovski et al. [2007] A. Makarovski, A. Zhukov, J. Liu, and G. Finkelstein, Phys. Rev. B 75, 241407(R) (2007).
- Cleuziou et al. [2013] J. P. Cleuziou, N. V. N’Guyen, S. Florens, and W. Wernsdorfer, Phys. Rev. Lett. 111, 136803 (2013).
- Kuzmenko et al. [2006] T. Kuzmenko, K. Kikoin, and Y. Avishai, Phys. Rev. B 73, 235310 (2006).
- López et al. [2013] R. López, T. Rejec, J. Martinek, and R. Žitko, Phys. Rev. B 87, 035135 (2013).
- Kuzmenko and Avishai [2014] I. Kuzmenko and Y. Avishai, Phys. Rev. B 89, 195110 (2014).
- Caroli et al. [1971] C. Caroli, R. Combescot, and P. Nozières, Phys. C: Solid State Phys 4, 916 (1971).
- Hershfield [1992] S. Hershfield, Phys. Rev. B 46, 7061 (1992).
- Guttman et al. [1995] G. D. Guttman, E. Ben-Jacob, and D. J. Bergman, Phys. Rev. B 51, 17758 (1995).
- Costi and Zlatić [2010] T. A. Costi and V. Zlatić, Phys. Rev. B 81, 235127 (2010).
- Chirla and Moca [2014] R. Chirla and C. P. Moca, Phys. Rev. B 89, 045132 (2014).
- Pérez Daroca et al. [2018] D. Pérez Daroca, P. Roura-Bas, and A. A. Aligia, Phys. Rev. B 97, 165433 (2018).
- Hewson [2001] A. C. Hewson, J. Phys.: Condens. Matter 13, 10011 (2001).
- Hewson et al. [2004] A. C. Hewson, A. Oguri, and D. Meyer, Eur. Phys. J. B 40, 177 (2004).
- Stadler et al. [2016] K. M. Stadler, A. K. Mitchell, J. von Delft, and A. Weichselbaum, Phys. Rev. B 93, 235101 (2016).
- Oliveira and Oliveira [1994] W. C. Oliveira and L. N. Oliveira, Phys. Rev. B 49, 11986 (1994).
- Nishikawa et al. [2010a] Y. Nishikawa, D. J. G. Crow, and A. C. Hewson, Phys. Rev. B 82, 115123 (2010a).
- Nishikawa et al. [2010b] Y. Nishikawa, D. J. G. Crow, and A. C. Hewson, Phys. Rev. B 82, 245109 (2010b).
- Oguri et al. [2011] A. Oguri, R. Sakano, and T. Fujii, Phys. Rev. B 84, 113301 (2011).
- Oguri [2012] A. Oguri, Phys. Rev. B 85, 155404 (2012).