Thermoelectric ratchet effect for charge carriers with hopping dynamics
Abstract
We show that the huge Seebeck coefficients observed recently for ionic conductors, arise from a ratchet effect where activated jumps between neighbor sites are rectified by a temperature gradient, thus driving mobile ions towards the cold. For complex systems with mobile molecules like water or polyethylen glycol, there is an even more efficient diffusiophoretic transport mechanism, proportional to the thermally induced concentration gradient of the molecular component. Without free parameters, our model describes experiments on the ionic liquid EMIM-TFSI and hydrated NaPSS, and it qualitatively accounts for polymer electrolyte membranes with Seebeck coefficients of hundreds of .
Introduction. – Thermoelectric materials are widely investigated in view of applications for harvesting waste heat, temperature sensors, and cooling devices Bell (2008), where the underlying conductivity mechanism may be electronic Bell (2008); Bubnova et al. (2011); Russ et al. (2016); Gregory et al. (2018); Xiao et al. (2017), ionic Zhao et al. (2016); Kim et al. (2016); Wang et al. (2017); Li et al. (2019); Zhao et al. (2019); Han et al. (2020a), or both Wang et al. (2015); Chang et al. (2016). As their fundamental property, an applied temperature difference induces an electric current or, in the ionic case, a thermoelectric field. According to the second law, heat flows towards lower temperatures; thus positive and negative charge carriers are dragged by their “heat of transport” de Groot and Mazur (1962), generating a thermopower which is quantified by the Seebeck coefficient .
Most metals and conventional semiconductors show a weak thermoelectric response, as expected for a band structure with nearly symmetric electron and hole states Fritzsche (1971). Their thermopower contributions largely cancel, resulting in . Higher values are observed for doped organic polymers Bubnova et al. (2011); Russ et al. (2016); Gregory et al. (2018), where structural disorder and electron-phonon coupling concur to hopping conductivity, with the heat of transport given by the dissociation energy Mott and Davis (1971).
In recent years Seebeck coefficients of up to were reported for ionic conductors such as hydrated polystyrene sulfonate Kim et al. (2016); Wang et al. (2017), cellulosic membranes infiltrated with electrolyte solution Li et al. (2019), ionic liquids Zhao et al. (2019) and polymer gels Zhao et al. (2016); Han et al. (2020a). The mechanisms leading to these huge Seebeck coefficients are poorly understood. Thermodiffusion in dilute electrolytes, as laid out by Nernst Nernst (1889), is not valid for such complex materials and does not account for the large values of : Ionic heats of transport in aqueous solutions are of order of the thermal energy Agar et al. (1989), resulting in , as confirmed by thermoelectric effects on colloidal suspensions Putnam and Cahill (2005); Würger (2010); Vigolo et al. (2010); Majee and Würger (2011); Eslahian et al. (2014).
Here we propose a model for the thermoelectric properties for charge carriers with hopping dynamics. We identify a ratchet mechanism which rectifies thermally activated jumps between neighbor sites and which relates the Seebeck coefficient to the enthalpy barrier. It turns out that companion fields of the temperature gradient, for example the thermally induced concentration gradient of a molecular component, may strongly enhance the thermoelectric response. We give a detailed comparison of our findings with experimental data for the above mentioned materials. We discuss a simple physical picture which could be relevant for both ionic and electronic polymer-based conductors.
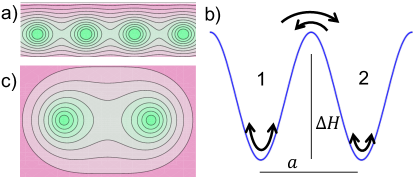
Hopping dynamics and Seebeck coefficient. – We consider carriers of charge which are trapped at well-defined sites but perform thermally activated jumps to neighbor sites. According to the Eyring model Eyring (1935), the jump rate reads as
| (1) |
where the attempt frequency is the ratio of the thermal energy and Planck’s constant. The Gibbs energy barrier consists of the activation enthalpy and entropy ; the former is given by the height of the barrier illustrated in Fig. 1, and the latter is related to the width of the valley at the saddle point. This picture is supported by conductivity measurements on amorphous polyelectrolyte complexes De et al. (2017); Ostendorf et al. (2019), which provide evidence that charge transport occurs through activated jumps of the cations between discrete sites.
The exponential factor in (1) gives the probability of a local free enthalpy fluctuation which eventually permits a mobile charge to cross the barrier. At thermal equilibrium, forward and backward jumps between two degenerate wells occur at the same rate, . In a non-uniform temperature as illustrated in Fig. 1b, however, jumps from a given site to the neighbor site occur at rate that depends on the temperature of the initial position, whereas the inverse rate reads . The difference arises mainly from the variation of the Planck-Plesset or entropy potential . Because of the very small temperature difference mK, the change of the exponent in (1) is much smaller than unity SI- . Then we may safely linearize the rate difference,
| (2) |
with mean values and . (For the sake of simplicity we consider degenerate wells; yet this result is readily generalized to the case of a finite bias energy SI- .) Thus the temperature gradient rectifies the thermal charge fluctuations due to activated hopping, as discussed previously for impurity atoms in crystals LeClaire (1954); Brinkman (1954)
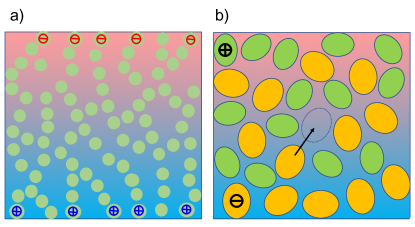
For a macroscopic network of connected paths as shown in Fig. 2a, the rate difference of backward and forward jumps results in a drift velocity . Inserting (2) we find , with the mobility and the heat of transport
| (3) |
which is positive for charges of either sign. Charge transport in ionic liquids is described by the thermally activated formation of short-lived vacancies Abbott (2004), as illustrated in Fig. 2b. Averaging over the vacancy position, we recover the above description of a connected network, albeit with comprising the (positive) barrier for ionic motion and the (negative) vacancy enthalpy. For impurity atoms in crystals, these contributions to have been determined experimentally Jaffe and Shewmon (1964).
According to the second law, the excess enthalpy has a tendency to flow towards the cold, thus dragging the ions opposite to the temperature gradient. This thermodiffusion current results in surface charges at the hot and cold sample boundaries (Fig 2a), which in turn give rise to an electric field and opposite velocity . In a closed system, the steady state is achieved if the total ion velocity vanishes, , implying generation of a thermoelectric field , with the Seebeck coefficient .
In the presence of monovalent charges of either sign , the Seebeck coefficient
| (4) |
is given by the mean heat of transport
| (5) |
weighted with the fraction of ions contributing to thermally driven charge transport Majee and Würger (2011). Note that the Hittorf transport numbers for the conductivity, , include the mobility Han et al. (2020b).
| (mV/K) | |||
| EMIM-TFSI1111-ethyl-3-methylimidazolium [EMIM] -bis(trifluoro-methylsulfonyl)imide[TFSI] | Zhao et al. (2019) | 0.27/0.26 D’Agostino et al. (2018) | |
| EMIM-TFSI-cp222Poly(vinylidene fluoride-co-hexafluoropropylene)-PEG333Polyethylene-glycol 300 Da | Zhao et al. (2019) | ||
| NaPSS-water | 4 Wang et al. (2017) | 1.2 | 0.5444Measured for (NaPSS)0.55PDADMAC0.45 De et al. (2017), see Fig. 3. De et al. (2017) |
| KCl-gelatin | 6.7 Han et al. (2020a) | 2 | |
| NaPEG-OH | 11 Zhao et al. (2016); Li et al. (2019) | 3.3 | 0.5 Zhao et al. (2016) |
| NaPEG-OH-cellulose | 24 Li et al. (2019) | 7.2 |
Eqs. (3) and (4) relate the Seebeck coefficient to the enthalpy barrier. The latter is in general much larger than the thermal energy, resulting in and thus providing a rationale for the large Seebeck coefficients of ionic conductors listed in Table 1. For the pure ionic liquid EMIM+-TFSI-, the measured heat of transport eV is very close to the activation enthalpies of cations and anions D’Agostino et al. (2018). A quantitative comparison is obtained from Eq. (5); inserting the barriers and weights , deduced from Tafur et al. (2015) and the mobility ratio Zhao et al. (2019), we obtain the theoretical value eV. This very good agreement provides evidence for the ratchet mechanism (2) being at the origin of the large Seebeck coefficient . On the other hand, in view of (5), the relation implies , thus confirming that anions are the majority carriers.
The remaining systems of Table 1 are more complex, consisting of mobile ions and polymer matrices with infiltrated water or PEG. They do not satisfy the relation (3): Though the ions move through activated jumps, the heat of transport by far exceeds the enthalpy barrier. In the following we show how the added nonionic molecular component modifies the thermodynamic response.
Non-equilibrium composition. – Polyelectrolyte materials may absorb a significant weight fraction of water De et al. (2017), which modifies both thermoelectric Kim et al. (2016); Wang et al. (2017) and transport properties Michaels et al. (1965); Varcoe (2007); De et al. (2017); Ostendorf et al. (2019). Similarly, complex polymer electrolytes are very sensitive to the composition: When adding PEG, the Seebeck coefficient of (EMIM-TFSI)-(PVDF-HFP) changes sign and increases from to mV/K Zhao et al. (2019); for KCl-gelatin, shows a strong and nonlinear variation with the salt concentration Han et al. (2020a). These observations cannot be explained in terms of (3) with a composition dependent : The measured heat of transport would imply enthalpy barriers of several eV (Table 1), which would inhibit ion diffusion and is clearly not compatible with the measured conductivity.
Yet the above description based on the rate difference (2) is valid only if the composition is not affected by the non-uniform temperature. In the general case, when evaluating the transport properties in a temperature gradient, we need to account for thermodiffusion of molecular components such as water or PEG, which gives rise to a non-uniform concentration . Then the activation enthalpy and entropy and are not the same in two neighbor wells, and the rate difference of backward and forward jumps reads
| (6) |
with and the derivates
| (7) |
Defining the gradient , we find that the ion acquires a drift velocity , in addition to defined below (2). Proceeding as above Eq. (4), we obtain the effective Seebeck coefficient
| (8) |
with
| (9) |
and the temperature derivativee
| (10) |
Here is the actual heat of transport as measured in terms of the Peltier coeffiicient de Groot and Mazur (1962), whereas the additional term in (9) accounts for the modified hopping dynamics due to the non-uniform composition.
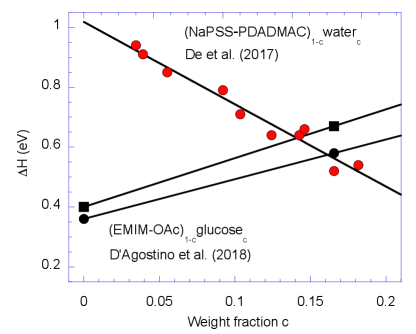
In order to obtain an estimate for the relevance of the diffusiophoretic contribution to the heat of transport (9), we plot in Fig. 3 the composition dependence of the enthalpy barrier for a hydrated polyelectrolyte complex and the ionic liquid EMIM-OAc with added sugar. The slope of the solid lines gives the derivative , which varies for these ions from to eV. There seem to be no data for the derivative . For binary liquids this parameter is related to the well-known Soret coefficient ; with typical values K-1 Wiegand (2004), we find , where either sign is possible. This estimate suggests that the composition-driven term in (9) may attain several eV.
As an example we consider hydrated NaPSS, with a maximum Seebeck coefficient of 4 mV/K Wang et al. (2017). The analysis in Ref. De et al. (2017) suggests a water content of ; as an estimate we take the enthalpy barrier of NaPSS-PDADMAC in Fig. 3, eV. The difference to the measured heat of transport eV, is met by the diffusiophoretic contribution with the above parameters, eV.
In the first part of this paper we have shown that thermodiffusion of ions with activated dynamics is much stronger than in ordinary liquids. Yet this result holds true also for non-ionic molecules such as water, PEG, and glucose – the enthalpy barrier of glucose in EMIM-OAc is 0.38 eV D’Agostino et al. (2018) –, and should result in larger values for than the above estimate. This would explain the very large Seebeck coefficients measured for the polymer electrolyte Na+PEG-OH- in cellulose matrices Li et al. (2019). In physical terms, it would imply that ion thermodiffusion in these membranes is mainly due to diffusiophoresis, at a velocity , which is driven by the thermally induced concentration gradient of water, .
Discussion. – The ratchet effect expressed by Eq. (2) and illustrated in Fig. 1, relies on two assumptions: First, the ions move through jumps between discrete positions and, second, forward and backward hopping rates and depend on the temperature of the initial well.
The first condition requires that the activated behavior is related to jumps between discrete sites, as opposed to thermodiffusion in aqueous solution, where the ion’s motion is phoretic, creating a steady backward flow in a homogeneous medium Morthomas and Würger (2008). Most systems of Table 1 are based on solid polymer matrices; adding small amounts of water, PEG, or ionic liquid, is not likely to create fluid domains, suggesting that charge carriers move through discrete jumps. Recent attempts to rationalize the structural and dynamical properties of ionic liquids like EMIM-TFSI Abbott (2004), rely on Fürth’s hole theory for liquids Fürth (1941), where conductivity arises from the formation of short-lived vacancies illustrated in Fig. 2b.
The second condition is rather obviously satisfied in Eyring’s transition state theory Eyring (1935), where barrier crossing is a mechanical problem and where the required energy is provided in the initial state by collisions with other atoms or, in a solid, with collective modes. For the case of strongly damped motion, Kramers Kramers (1940) showed that barrier crossing results from Brownian motion, and also occurs with an activated rate. The required energy is taken from thermal Langevin forces along the uphill part of the trajectory, resulting in an asymmetry of forward and backward rates similar to (2).
The discrete model studied here, provides a simple physical picture for the ratchet effect and the strong thermopower observed in ionic conductors: Each jump of the mobile ion collects energy of the order of the barrier height at the initial position and releases the same amount in the neighbor well. According to Clausius’ formulation of the second law, heat necessarily flows from the hot to the cold, implying that jumps opposite to the temperature gradient are favored, and that the rate imbalance is proportional to the enthalpy barrier. As a consequence, the heat of transport is given by .
For complex materials containing mobile molecular components, we find in addition to the thermal ratchet effect, a diffusiophoretic mechanism of ion transport: The applied temperature gradient induces a non-uniform composition , for example, a concentration gradient of hydration water or polyethylene glycol. Then the free enthalpy barrier is different for forward and backward jumps, and the effective heat of transport includes a term proportional to the concentration derivative of the free enthalpy of activation . Formally the correction term in (9) can be expressed as the difference of the enthalpy at variable and constant ,
| (11) |
The second term on the right-hand side is the usual Gibbs-Helmholtz expression for the equilibrium enthalpy, whereas the first one allows for a non-uniform concentration, which gives rise to the drift velocity , with . Similar effects are known for colloidal thermophoresis in liquids, where particle motion is often dominated by concentration gradients of added polymer Jiang et al. (2009), salt Eslahian et al. (2014), or a binary liquid at the critical point Buttinoni et al. (2012); Würger (2015).
Regarding electronic systems, the binding energy of small polarons in doped organic polymers Gregory et al. (2018) and metal oxides Xiao et al. (2017) contributes to but is absent in the heat of transport . On the other hand, the electronic heat of transport in pure silicon is dominated by the phonon-drag contribution, which accounts for electrons being nudged by long-lived thermal phonons Trzcinski et al. (1986).
Summarizing our comparison with experiments on ionic conductors, we obtain a quantitative description for the thermopower of the pure ionic liquid EMIM-TFSI, without free parameter, by identifying the heat of transport with the enthalpy of activation. Regarding the hydrated polyelectrolyte NaPSS, our results show that thermally induced diffusiophoresis largely contributes to the effective heat of transport (9) and thus to the Seebeck coefficient. An estimate of the parameters of Eq. (9), suggests that ion diffusiophoresis due to the gradient in water content, accounts for the large Seebeck coefficients measured for electrolyte infiltrated membranes.
Helpful and stimulating discussions with X. Crispin, C. Cramer and M. Schönhoff are gratefully acknowledged. This project was supported by the French National Research Agency through grant ANR-19-CE30-0012-01 and by the European Research Council (ERC) through grant no 772725.
References
- Bell (2008) L. E. Bell, Science 321, 1457 (2008).
- Bubnova et al. (2011) O. Bubnova, Z. U. Khan, A. Malti, S. Braun, M. Fahlman, M. Berggren, and X. Crispin, Nature Materials 10, 429 (2011).
- Russ et al. (2016) B. Russ, A. Glaudell, J. J. Urban, M. L. Chabinyc, and R. A. Segalman, Nature Reviews Materials 1, 16050 (2016).
- Gregory et al. (2018) S. A. Gregory, A. K. Menon, S. Ye, D. S. Seferos, J. R. Reynolds, and S. K. Yee, Advanced Energy Materials 8, 1802419 (2018).
- Xiao et al. (2017) X. Xiao, M. Widenmeyer, W. Xie, T. Zou, S. Yoon, M. Scavini, S. Checchia, Z. Zhong, P. Hansmann, S. Kilper, A. Kovalevsky, and A. Weidenkaff, Phys Chem Chem Phys 19, 13469 (2017).
- Zhao et al. (2016) D. Zhao, H. Wang, Z. U. Khan, J. C. Chen, R. Gabrielsson, M. P. Jonsson, M. Berggren, and X. Crispin, Energy Environ. Sci. 9, 1450 (2016).
- Kim et al. (2016) S. L. Kim, H. T. Lin, and C. Yu, Advanced Energy Materials 6, 1600546 (2016).
- Wang et al. (2017) H. Wang, D. Zhao, Z. U. Khan, S. Puzinas, M. P. Jonsson, M. Berggren, and X. Crispin, Advanced Electronic Materials 3, 1700013 (2017).
- Li et al. (2019) T. Li, X. Zhang, S. D. Lacey, R. Mi, X. Zhao, F. Jiang, J. Song, Z. Liu, G. Chen, J. Dai, Y. Yao, S. Das, R. Yang, R. M. Briber, and L. Hu, Nature Materials 18, 608 (2019).
- Zhao et al. (2019) D. Zhao, A. Martinelli, A. Willfahrt, T. Fischer, D. Bernin, Z. U. Khan, M. Shahi, J. Brill, M. P. Jonsson, S. Fabiano, and X. Crispin, Nature Communications 10, 1093 (2019).
- Han et al. (2020a) C.-G. Han, X. Qian, Q. Li, B. Deng, Y. Zhu, Z. Han, W. Zhang, W. Wang, S.-P. Feng, G. Chen, and W. Liu, Science 368, 1091 (2020a).
- Wang et al. (2015) H. Wang, U. Ail, R. Gabrielsson, M. Berggren, and X. Crispin, Advanced Energy Materials 5, 1500044 (2015).
- Chang et al. (2016) W. B. Chang, H. Fang, J. Liu, C. M. Evans, B. Russ, B. C. Popere, S. N. Patel, M. L. Chabinyc, and R. A. Segalman, ACS Macro Letters, ACS Macro Letters 5, 455 (2016).
- de Groot and Mazur (1962) S. de Groot and P. Mazur, Non-equilibrium Thermodynamics (North-Holland Publishing Company; Interscience Publishers, 1962).
- Fritzsche (1971) H. Fritzsche, Solid State Communications 9, 1813 (1971).
- Mott and Davis (1971) N. F. Mott and E. A. Davis, Electronic Processes in Non-Crystalline Materials (Oxford University Press, 1971).
- Nernst (1889) W. Nernst, Zeitschrift für physikalische Chemie 4, 129 (1889).
- Agar et al. (1989) J. N. Agar, C. Y. Mou, and J. L. Lin, The Journal of Physical Chemistry 93, 2079 (1989).
- Putnam and Cahill (2005) S. A. Putnam and D. G. Cahill, Langmuir 21, 5317 (2005).
- Würger (2010) A. Würger, Rep. Prog. Phys. 73, 126601 (2010).
- Vigolo et al. (2010) D. Vigolo, S. Buzzaccaro, and R. Piazza, Langmuir 26, 7792 (2010).
- Majee and Würger (2011) A. Majee and A. Würger, Phys. Rev. E 83, 061403 (2011).
- Eslahian et al. (2014) K. A. Eslahian, A. Majee, M. Maskos, and A. Würger, Soft Matter 10, 1931 (2014).
- Eyring (1935) H. Eyring, Chemical Reviews 17, 65 (1935).
- De et al. (2017) S. De, A. Ostendorf, M. Schönhoff, and C. Cramer, Polymers 9, 550 (2017).
- Ostendorf et al. (2019) A. Ostendorf, M. Schönhoff, and C. Cramer, Physical Chemistry Chemical Physics 21, 7321 (2019).
- (27) The supplementary information file discusses the case of finite bias energy and the linearization approximation .
- LeClaire (1954) A. D. LeClaire, Phys. Rev. 93, 344 (1954).
- Brinkman (1954) J. A. Brinkman, Phys. Rev. 93, 345 (1954).
- Abbott (2004) A. P. Abbott, ChemPhysChem 5, 1242 (2004).
- Jaffe and Shewmon (1964) D. Jaffe and P. Shewmon, Acta Metallurgica 12, 515 (1964).
- Han et al. (2020b) Y. K. Han, J. Y. Cheon, T. Kim, S. B. Lee, Y. D. Kim, and B. M. Jung, RSC Adv. 10, 18945 (2020b).
- D’Agostino et al. (2018) C. D’Agostino, M. D. Mantle, C. L. Mullan, C. Hardacre, and L. F. Gladden, ChemPhysChem 19, 1081 (2018).
- Tafur et al. (2015) J. P. Tafur, F. Santos, and A. J. Fernandez Romero, Membranes 5, 752 (2015).
- Michaels et al. (1965) A. S. Michaels, G. L. Falkenstein, and N. S. Schneider, The Journal of Physical Chemistry 69, 1456 (1965).
- Varcoe (2007) J. R. Varcoe, Physical Chemistry Chemical Physics 9, 1479 (2007).
- Wiegand (2004) S. Wiegand, J. Phys.: Condens. Matter 16, R357 (2004).
- Morthomas and Würger (2008) J. Morthomas and A. Würger, Eur. Phys. J. E 27 (2008).
- Fürth (1941) R. Fürth, Mathematical Proceedings of the Cambridge Philosophical Society 37, 276 (1941).
- Kramers (1940) H. A. Kramers, Physica 7, 284 (1940).
- Jiang et al. (2009) H.-R. Jiang, H. Wada, N. Yoshinaga, and M. Sano, Phys. Rev. Lett. 102, 208301 (2009).
- Buttinoni et al. (2012) I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe, and C. Bechinger, J. Phys. Condens. Matter 24, 284129 (2012).
- Würger (2015) A. Würger, Phys. Rev. Lett. 115, 188304 (2015).
- Trzcinski et al. (1986) R. Trzcinski, E. Gmelin, and H. J. Queisser, Phys. Rev. Lett. 56, 1086 (1986).