.
Thermodynamic topology of Black Holes in -Euler-Heisenberg gravity’s Rainbow
Abstract
The topology of black hole thermodynamics is a fascinating area of study that explores the connections between thermodynamic properties and topological features of black holes. It often involves analyzing critical points in the phase diagrams of black holes and assigning topological charges to these points. One significant approach is based on Duan’s topological current -mapping theory, which introduces the concept of topological charges to critical points in black hole thermodynamics. This paper has led to several significant findings: We successfully derive the field equations for -Euler-Heisenberg theory, providing a framework for studying the interplay between modified gravity and non-linear electromagnetic effects. We obtain an analytical solution for a static, spherically symmetric, energy-dependent black hole with constant scalar curvature. Also, our analysis of black holes in F(R)-Euler-Heisenberg gravity’s Rainbow reveals significant insights into their topological properties. We identified the total topological charges by examining the normalized field lines along various free parameters. Our findings indicate that the parameters and influence the topological charges. These results are comprehensively summarized in Table I. Additionally, a general overview of Tables II, III, and IV related to the photon sphere of the mentioned black hole reveals that with an increase in , the permissible range of negative in the first case gradually transitions into a non-permissible region in the third case. On the other hand, it is known that the QED parameter, which measures the strength of nonlinear effects, can be either positive or negative. A positive QED parameter reduces the electric field near the horizon and increases the black hole’s mass, whereas a negative QED parameter increases the electric field and decreases the mass. According to the two statements above, it can be concluded that the increase in actually decreases the strength of the electric field near the horizon and strengthens the effects of gravity.
I Introduction
The greatest cosmological challenges this century are early-time inflation and late-time acceleration. In precise terms, what does inflation refer to, and what does dark energy consist of? Why and how did the early universe and the late universe expand upwards so very fast? What might explain why the evolution of the universe is similar for small and large curvatures? To tackle these matters, Refs. [1, 2, 3, 4, 5] outline and investigate Einstein’s modified theories of gravity as an alternative framework. Among the various modified theories of gravity, the theory has aroused a great deal of interest because it offers an explanation for a broad series of observations. For instance, the theory of gravity provides a plausible hypothesis for the existence of dark matte [6, 7] and the universe’s rapid expansion [2, 3, 4, 5, 8, 9]. Even more, the theory can be harnessed to forecast cosmic acceleration or early universe inflation [10, 11, 12], not to mention massive compact objects [13, 14, 15, 16, 17, 18]. Another achievement in the context of gravity is the complete description of all the evolutionary epochs of the universe while maintaining consistency with Newtonian and post-Newtonian approximations [19]. Within the theory of gravity, turns out to be an arbitrary function of the scalar curvature .
Since the theory of gravity may describe a number of cosmological and astrophysical phenomena, it is vital to examine and highlight the coupling of the Euler-Heisenberg (EH) term as a matter source with gravity’s rainbow by adopting the -EH Lagrangian. Heisenberg and Euler established the non-linear electrodynamics Lagrangian making use of Dirac’s electron-positron theory [20]. Schwinger remodelled this nonperturbative one-loop Lagrangian in the context of quantum electrodynamics (QED) [21] and found that it could identify the phenomenon of vacuum polarisation successfully. Due to the one-loop nonperturbative QED, the EH Lagrangian has drawn ever-increasing scrutiny to the subject of generalised black hole solutions. A wealth of intriguing studies on black holes in the context of EH nonlinear electrodynamics are described in [22, 23, 24, 25, 26, 27, 28, 29].
In the search for the unification of general relativity and quantum mechanics, a wide range of challenges have arisen. Nowadays, in spite of a few theories such as string theory [30], loop quantum gravity [36], and space-time foam models [32] that have attempted to tackle this conundrum, the question remains devoid of any phenomenological process. A key reason for unifying gravity with quantum theory is the violation of Lorentz invariance, which we might regard as an indispensable criterion for the elaboration of a quantum theory of gravity. Another distinctive factor among unification theories is that they forecast a maximum energy value of the order at the Planck scale that a particle could attain; i.e., if a particle is qualified by the Standard Model of particle physics, then it should conform to the upper limit of the Planck energy, , which is experimentally backed up by Abraham et al [33]. A further alternative to Lorentz symmetry violation involves, in the ultraviolet limit, modifying the standard energy-moment dispersion ratio. This, in fact, has a long history in theories as diverse as discreteness space-time [39], Horava-Lifshitz [34, 35], doubly special relativity [40, 41], and loop quantum gravity [36, 37]. In the framework of doubly special relativity, the dispersion relation works out as where and are functions of , standing for the energy of the particle used to analyse space-time and for Planck’s energy. The functions and are commonly thought of as rainbow functions and are designed for phenomenological purposes [42]. On the other hand, the standard energy dispersion relation gets recurved in the limit , otherwise known as the infrared limit. As a matter of fact, Linear Lorentz transformations break the invariance of the theory [43]; nevertheless, non-linear Lorentz transformations are those that keep the theory invariant. Moreover, as well as the speed of light being a constant, the Planck energy is also a constant, and it remains impossible for a particle to rise beyond this limit.
A generalisation of doubly special relativity to what is known as rainbow gravity has been suggested by Magueijo and Smolin [44], where spacetime is mapped to a family of specified parameters in the metric that is parametrised by . Accordingly, the spacetime geometry is contingent on the energy of the particle testing it, causing a rainbow of the metric. Meanwhile, a number of studies have incorporated Magueijo and Smolin’s theory into the understanding of black holes [45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59] and into modifying theories of gravity [60, 61]. A worthy concrete illustration investigation is concerned with the work of M. Momennia et al. [62] exploiting a non-linear electrodynamics (NED) field in the context of the rainbow gravity, resulting in the validity of the first law of thermodynamics in the presence of rainbow functions. Therefore, the rainbow gravity framework has provided the avenue for the consideration of a large number of investigations, such as the derivation considering the dilatonic gravity of an exact black hole solution minimally coupled to the Born-Infeld term with an energy-dependent Liouville-type potential [63]. Similarly, incorporating the quadratic term of the Gauss-Bonnet gravity in the framework of rainbow gravity leads to modifying the appropriate constraints to work out non-singular universes [64]. It is worth noting that the study of thermodynamic properties is considered the main and impacting process regarding rainbow gravity. Thus, since the energy scale depends on the spacetime metric, entropy and temperature also have the same dependence [65]. To gain a topological perspective in thermodynamics, one effective approach is to use Duans topological current mapping theory. Wei et al. introduced two distinct methods to study topological thermodynamics based on temperature and the generalized free energy function. The first method involves analyzing the temperature function by eliminating pressure and utilizing the auxiliary and topological parameter . The potential is then constructed based on these assumptions. For further study, see [66, 67, 68, 69]. The second method assumes that black holes can be considered defects in the thermodynamic parameter space. Their solutions are investigated using the generalized off-shell free energy. In this context, the stability and instability of the obtained black hole solutions are determined by positive and negative winding numbers, respectively. Additionally, the properties of a field configuration can be deduced from the zero points of the field in space [70, 71, 72, 73]. Wei, Liu, and B. Mann asserted that for different branches of a black hole at an arbitrary temperature, the topological charge number, the sum of the winding numbers, is a universal number independent of the black hole parameters. In the range of small and large black holes, the topological charge number depends solely on the thermodynamic asymptotic behavior of the black hole temperature. Consequently, black holes can be categorized into three different groups based on the number of topological charges [70]. Following the introduction of this second method, various black holes were studied to investigate topological charges. C. H. Liu and J. Wang demonstrated that the topological number remains constant, and the charged GB black holes in the AdS space fall into the same category as the RN-AdS, sharing the same topological numbers. However, their results indicated that charge dependence is not the only effective factor [74]. Y. Du and Xi. Zhang examined the rotating charged BTZ black hole model and found that there are only two topological classes for BTZ space-time. [75]. Using the same method, Wu investigated the structure of charged Lorentzian Taub-NUT space-times and neutral Lorentzian NUT-charged space-times in 4 dimensions in two separate articles. [76]. In the second work, Wu found that the presence of the NUT charge as a parameter did not affect the structures in symptotically flat space-time but had an effect on asymptotically local AdS space-time [77]. For further study, you can see [78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95]. Building upon the above concepts, we organize the article as follows: In Section II, we provide the field equations in F(R)-Euler-Heisenberg theory. In Section III, we obtain the black hole solutions in F(R)-Euler-Heisenberg gravity’s rainbow. In Sections IV and V, we study the thermodynamics, thermodynamic topology, and photon sphere of the mentioned black holes. We obtain the thermodynamic topology and topological classification of black holes in F(R)-Euler-Heisenberg gravity’s rainbow and its photon sphere in some cases in Section VI. Finally, we present the conclusion of our paper in Section VII.
II Field equations in -Euler-Heisenberg theory
In this section, we aim to highlight the coupling of the EH term as a matter source with the gravity. To this end, we consider the -EH action
| (1) |
where , in which and , are respectively, the Ricci scalar and a general function of the Ricci scalar, is the determinant of the metric tensor , and is dedicated to being the EH Lagrangian. Throughout this study, we adopt the Newtonian gravitational constant and the speed of light as being equal to 1, i.e., . In practical terms, the EH Lagrangian can be described by considering the following expression [20]:
| (2) |
where is the EH parameter by which the intensity of the NLED contribution is regulated; is the fine structure constant; and is the mass of the electron; hence, the EH parameter is of the order of . In turn, and are, respectively, true scalars and pseudo-scalars, with the following definitions:
| (3) |
where stands for the Maxwell invariant together with is the electromagnetic field strength of which is the gauge potential. Furthermore, the invariant can be defined in terms of , where . Notably, the completely antisymmetric tensor , satisfies . It is worth pointing out that the criterion abolishes the non-linear electromagnetic character of the EH theory so that the linear electromagnetic field of the Maxwell theory arises .
As far as NLEDs are concerned, though, there are two potential frameworks: one is the usual framework (the -frame) in terms of the electromagnetic field tensor . The other frame is the frame, with the tensor as the principal field of the definition
| (4) |
where with . In the realm of the EH theory, can be defined by
| (5) |
which stands for a class of electric/magnetic fields, namely the electric induction and the magnetic field . In connection to the condensed matter fields, the EH term, according to Eq. (18), involves a duality between the vectors set such that , and the magnetic intensity and the electric field .
To better grasp the EH model by means of the frame, it is quite worthwhile to consider the two independent invariants and assigned to the frame, which are given by
| (6) |
where . In particular, the Legendre transformation of the relevant Lagrangian is exploited to provide a structural function expressed as follows:
| (7) |
where, regardless of the second and higher order terms in , this structural function can be represented as follows:
| (8) |
The equations of motion of the -EH theory of gravity can be obtained, leading to
| (9) | ||||
| (10) |
where and is the energy-momentum tensor for the EH theory in the setting, given by
| (11) |
Next, we present the spherically symmetric static solution for the -EH gravity’s rainbow.
III Black hole solutions in -Euler-Heisenberg gravity’s rainbow
Within the scope of this study, we consider a spherically, static, four-dimensional, energy-dependent spacetime, in which we adopt the procedure described in Refs. [44, 101], so that
| (12) |
and
| (13) |
where the quantities in tilde (i.e. and ) stand for energy-independent frame fields. Based upon the foregoing assumptions, we in fact may generate black holes in -EH gravity’s rainbow by considering the following static, spherically symmetric, energy-dependent, four-dimensional spacetime
| (14) |
where , and is the metric function , and rainbow functions.
Practically speaking, the field equations underlying the context of gravity with the EH matter fields (9) seem to be difficult. This means that accurate analytical solutions are proving tricky to pin down. To overcome this issue, one should consider the traceless energy-momentum tensor for the EH matter field, and then one can obtain an analytical solution from gravity coupled to a nonlinear electrodynamics field. Thus, to be able to derive the solution of a black hole with constant curvature in the theory of gravity as coupled to the EH matter field, it suffices for the trace of the stress-energy tensor to hold to zero [102, 103]. Based on the hypothesis of constant scalar curvature [104], the trace of equation (9) takes the following terms:
| (15) |
where . The constant scalar curvature is accordingly drawn from the equation (15) as follows:
| (16) |
Making use of Eq. (16) into Eq. (9), the field equations of the -EH theory could be established in the right way as
| (17) |
By way of observation, the parameter implies a gravitational redefinition concerning general relativity; in particular, imposing the condition leads to a redefinition of the general relativity. Thus, the field equation in the -EH theory (17) reduces to the EH theory of gravity.
Turning to the electromagnetic field, we have to treat only the electric field source of the EH theory so that the electromagnetic tensor is explicitly derived as
| (18) |
in which the electromagnetic invariants are given by
| (19) |
where represents an integration constant that is associated with the electric charge.
At this stage, the field equations for gravity with EH matter fields (9), in conjunction with the consideration of the metric function (14) and the tensor of the electric component (18), are explicitly expressed by the following differential equations:
| (20) | ||||
| (21) |






where , , and , are, respectively, the , , and components of the field equations (9). By implementing the above differential equation set, a definite solution to the constant scalar curvature can be provided. Following a close examination and further calculations, the metric function can now be expressed in the most precise form.
| (22) |
where is an integration constant correlated with the black hole’s geometric mass. It is worth highlighting that the obtained black hole solution (22) is exactly in conformity with the field equations (9). Therefore, to carry out a physical analysis based on the black hole solution (22), one can ensure a constraint on the parameter such that . On the other hand, the consideration of the particular partial space, namely and ), recovers the so-called Reissner-Nordstrom-(A)dS black hole defined by
| (23) |
Such application tools are needed to understand the black hole solution better. In particular, the singularity and uniqueness features can be exploited by using the scalar invariants, i.e., the Ricci scalar, the Ricci square, and the Kretschmann scalar.
The Ricci scalar for the corresponding metric is given by
| (24) |
The Ricci squared is given by
| (25) |
On the other hand, the Kretschmann scalar is formulated according to the metric function and the fucntion (22) as follows:
| (26) |
Upon thorough analysis of the expressions (24), (III), and (III), the black hole solution described by the metric (14) is singular for all the allowable values of the parameters black hole system. So investigating the limits for the scalar invariants at would result in the following:
| (27) |
By way of observation, the presence of the spacetime singularity is due to the mass , the electric charge , and the EH parameter in the black hole metric. A useful way of avoiding the singularity resulting from the mass, the charge, and the EH parameters is to outline a procedure with a non-linear charge distribution function similar to Ref. [105]. Throughout this work, we will not be thinking about such a situation and will stick to the metric function (14) for the rest of the analysis. On the other hand, examining behavior at large distances is a worthwhile adjunct, given that
| (28) |
which implies that the Ricci scalar, the Ricci squared, and the Kretschmann scalar have a finite term at a large distance. To sum up, these scalars are evidence that our black hole solution is unique, and that the EH parameter does not modify the asymptotical behavior of the spacetime
Next, the examination of the metric function allows to explore the set of corresponding real roots. On the other hand, the analysis of the appropriate set of these real roots offers the possibility to extract information on the horizons (inner and outer horizons, and even more the cosmological horizon). Thus, to proceed with this examination, such a numerical approach is needed.
Solving the equation at the event horizon leads to specifying the horizon radii spectrum. For this reason, Fig. 1 represents, either for (or AdS space if ) or for (or dS space if ), the variation of the metric function as a function of the space-time variable graphically showing the proper horizon radii. It is worth remarking that in the case of , the horizon structure provides at most four horizon radii (one of which refers to the cosmological horizon). In contrast, as we can observe, the case related to can cover only three possible horizon radii (one of which is adapted to the cosmological horizon). Roughly speaking, the sign of the parameter plays a crucial role in defining the structure of black hole horizon in the -EH gravity’s rainbow.
Analysing the impact of the electrical charge (), the parameter of EH (), and ’s parameters (, and ) and Rainbow structure (, and ) on the structure of the black hole horizon in the -EH gravity’s rainbow is also necessary. To this end, Fig. 2 depicts the behaviour of the metric function against the spacetime variable . It is observed that the appropriate horizon structure provides at most three horizon radii (one of which corresponds to the cosmological horizon) for the case where . Thus, each parameter variation affects the horizon structure in such a way that we can point out that at a critical value of the EH parameter, i.e., , there are two horizon radii, which are a root (in the extreme case) and the cosmological horizon. Further, at the range , the horizon structure admits three horizon radii, namely the inner horizon, the outer horizon, and the cosmological horizon. Whereas for , the horizon structure merely carries the cosmological horizon. Similarly, a graphical inspection of the electrical charge parameter may imply a particular pattern for the horizon structure. So, we can observe that for a certain critical value, such as , the horizon structure may entail two horizon radii, the inner horizon being the smallest among the three horizons and the other being formed by a matching between the outer horizon and the cosmological horizon. Furthermore, for , the horizon structure involves only the inner horizon, whereas for , the situation consists of three horizon radii. As far as the parameters of are concerned, namely and , the horizon structure, for instance, in terms of entails a critical value at which it exhibits two types of horizon, the inner horizon and the other being formed by a correlation between the outer horizon and the cosmological horizon. In addition, for , the black hole horizon carries three horizon radii, while in the case of , the horizon structure has only one horizon, which stands for the outer. On the other hand, it is notable that for a critical value of the parameter such that , the black hole admits in particular the extreme horizon and the cosmological horizon. For , the situation turns out to be different since the black hole’s horizon entails only the cosmological horizon. Moreover, in the case , the horizon structure exhibits three horizon radii, i.e., all the possible horizons of the black hole. Finally, it is necessary to explore the characteristic of the horizon structure concerning the variation of the set of rainbow gravity functions, such as (, ). This variation can be appreciated on the plot, in which, at a critical value of as , the horizon structure possesses the inner horizon and one that is correlated between the outer horizon and the cosmological horizon. Other scenarios can be considered to clearly assess the impact of the Rainbow function such as on the horizon, from which at , the black hole admits three horizons, whereas for , the horizon involves only the inner horizon. On the other hand, we observe that the horizon structure comprises the inner horizon and a correlated horizon between the outer horizon and the cosmological horizon in the case where , i.e., above this threshold, the black hole admits only the inner horizon, and below this threshold, the black hole presents three horizon radii.
IV Thermodynamics
The best way to approach thermodynamically the black hole solutions in gravity’s rainbow with EH matter source is to consider the first law of thermodynamics. To begin with, inspection at the event horizon of the metric solution (22) leads to providing the mass term of the black hole as follows:
| (29) |
Next, to ascertain the Hawking temperature, one has to consider primarily the surface gravity [106], which is supplied out of
| (30) |
with is a Killing vector. Achieving a correct expression of the surface gravity is carried out by exploiting the metric function (22) and by injecting the mass (29) into Eq. (30). The surface gravity of a black hole is therefore expressed by
| (31) | |||||
as well as the formula stands for the Hawking temperature, which could be expressed by an appropriate term as follows:
| (32) | |||||
It is noteworthy that all the parameters set in the black hole system, namely, , , , and perfectly affected the behavior of the Hawking temperature.
To achieve an accurate description of the Hawking temperature behavior, it is merely instructive to study the asymptotic and high-energy limits of the temperature. In this respect, the high-energy limit can be exemplified as follows
| (33) |
which proves the extent to which the parameters of the matter sector as well as the rainbow functions influence the high-energy behavior of the Hawking temperature. Accordingly, the Hawking temperature is definitely positive for at the high-energy limit.
On the other hand, the asymptotic limit of temperature remains just a dependence of , such that
| (34) |
which implies that the Hawking temperature sets to be positive (negative) whenever ().
By using Gauss’s law, the electric charge of the black hole per unit volume, , can be ascertained by the following formula
| (35) |
The EH electromagnetic potential corresponding to the black hole within the framework of the F(R)-EH gravity’s rainbow is as follows
| (36) | |||||
By applying a modified area law in the theory of gravity, we can extrapolate the corresponding entropy of black holes such as
| (37) |
with being the horizon area as
| (38) |
So now we can work out the entropy of EH black holes in gravity’s rainbow by substituting Eq. (38) into Eq. (37), thus yielding
| (39) |
which states that the law of areas cannot be held for black hole solutions in gravity .
Exploring the total mass of black holes in -EH theory would be achievable by looking at the Ashtekar-Magnon-Das (AMD) approach [107, 108], which can be expressed as follows
| (40) |
This allows us, after substituting mass (29) in Eq. (40), to obtain the total mass as follows:
| (41) |
Afterwards, inspection of the total mass at its high-energy limit can reveal the form
| (42) |
where a consistent dependency is shown only with parameters and ). Thus, at the high-energy limit, it is striking that the total mass of small black holes is always negative.
The asymptotic limit, on the other hand, of the total mass is found to be as follows:
| (43) |
where the positive (negative) branch of is consistently referred to as ().
At this stage, we may evaluate the first law of thermodynamics. Accordingly, the conserved and specific thermodynamic quantities in Eqs. (41), (32), (36) and (37) satisfy the first law of thermodynamics in the following format.
| (44) |
where , and , respectively, are in accordance with the relations achieved in the Eqs. (32) and (36).
V Thermodynamic topology and photon sphere
Thermodynamic topology involves studying the thermodynamic properties of black holes using topological methods. It helps understand the critical points and phase transitions of black holes by analyzing their topological charges and numbers. A photon sphere is a region where gravity is strong enough that photons (light particles) are forced to travel in orbits. For a black hole, this sphere lies just outside the event horizon. The existence and properties of photon spheres can be studied using topological methods, which assign topological charges to these spheres. These charges help in understanding the stability and structure of the photon sphere. In recent studies, researchers have explored the relationship between thermodynamic topology and photon spheres in various black hole models, including those with hyperscaling violation. They have found that different topological charges correspond to different physical configurations, such as black holes and naked singularities[81]. Here, we want to study the Thermodynamic topology of Black Holes in -Euler-Heisenberg gravity’s Rainbow. so we follow some route that is explained in detail in the following section
VI Thermodynamics topology of black holes
The primary concept associated with defects is the topological charge. To examine the thermodynamic topology of a black hole, we calculate the topological charge and utilize it to determine the topological classes. We employ Duan’s mapping technique to compute the topological charge. To introduce the thermodynamic properties of black holes, various quantities are utilized. For example, two distinct variables, such as mass and temperature, can describe the generalized free energy[109]. Given the relationship between mass and energy in black holes, we can reformulate our generalized free energy function as a standard thermodynamic function in the following form,
| (45) |
where, represents the Euclidean time period, and (the inverse of ) denotes the temperature of the ensemble. The generalized free energy is on-shell only when . From the expression for the off-shell free energy of a black hole, a vector field is constructed as follows,
| (46) |
where is divergent, the vector direction points outward when or . For and , the ranges are and , respectively. A topological current can be defined using Duan’s -mapping topological current theory as follows,
| (47) |
To determine the topological charge, we first identify the unit vector , where . We have and . According to Noether’s theorem, the resulting topological currents are conserved viz . It can be demonstrated that the current is non-zero only at the zero points of the vector field by utilizing the following equation,
| (48) |
where we utilize the following properties of the Jacobi tensor,
| (49) |
The Jacobi vector reduces to the standard Jacobi when , as demonstrated by . Equation (48) shows that is non-zero only when . Through some calculations, we can express the topological number or total charge in the following form,
| (50) |
where is the positive Hopf index, counting the loops of the vector in the space when is near the zero point . Meanwhile, . The quantity represents the winding number for the -th zero point of in . Note that the winding number is independent of the shape of the region where the calculation occurs. The value of the winding number is directly associated with black hole stability. The topological charge can be determined by summing the winding numbers calculated along each contour surrounding the zero points,
| (51) |
It is important to note that if the parameter region lacks zero points, the total topological charge is considered to be zero. In the following two subsections, we will explore the thermodynamic topology of black holes in Euler-Heisenberg F(R)-Rainbow gravity
VI.1 Topological classification of black holes in -Euler-Heisenberg gravity’s Rainbow
Based on equations (45), we derive the generalized Helmholtz free energy for black holes within the framework of Euler-Heisenberg F(R)-Rainbow gravity
| (52) |
From the discussion in the previous section, the form of the function is determined as follows,
| (53) |
The unit vectors and are computed using equation (53). Next, we calculate the zero points of the component by solving the equation and derive an expression for as follows,
| (54) |
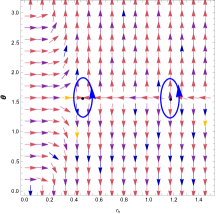
We analyze Figure (3), which pertains to the structure of black holes in Euler-Heisenberg F(R)-Rainbow gravity. The figures display the normalized field lines. As depicted in the figures, some zero points represent the model’s topological charges with various free parameters. They are proportional to the winding number and are situated inside the blue contour at the coordinates . We considered free parameters , , , to draw these contours. In Figure (3,left), we plotted the curve for . As shown in Figure (3,left), three blue loops represent the topological numbers =(-1, +1, -1) and the total topological number . Also, in Figures (3,middle) and (3,right), we plotted the curve for respectively. (3,middle) represents the topological numbers with the total topological number and Figure (3,right) represents the one topological number , so that the total topological number is . Without loss of generality, we analyzed the topological properties of these black holes in this paper by choosing for black holes in Euler-Heisenberg F(R)-Rainbow gravity. The content discusses the stability of the black holes by examining the winding numbers and specific heat capacity. We have plotted Figures (4,top;left), (4,top; middle and righr) and (4,bottom; left and right) for the mentioned model with respect to free parameters , , , and respectively, following the same approach. We plotted the normalized field vectors for these black holes in Figures (4,top;left), (4,top; middle and righr) and (4,bottom; left and right). Due to the better display of topological charges, we tried to draw two figures for each case, that is, Figure (4,top;left), Figures (4,top; middle and righr) together, and Figures (4,bottom; left and right) together are checked in the investigation of the total topological charges. As it is clear in these figures, only for Figure (4,top;left) corresponding to the free parameters , , , and , we have topological charges =(-1, +1, -1) and the total topological charge . For the other two samples with , the total topological charges are equal to . By comparing Figures (3) and (4), it is clear that the positive or negative of and parameter values of play a very important role in determining the topological charges. We summarize the results in Table I.







|
VI.2 Photon sphere
In our past papers [96, 97], we demonstrated that the topological photon sphere can play a fundamental and reciprocal role in interpreting the behavior of a black hole. More precisely, since the existence of a photon sphere or photon rings is one of the essential requirements of ultra-compact gravitational structures, particularly black holes[98], the topological photon sphere can serve as a crucial test for determining the parameter ranges of black holes and, consequently, their overall behavior, and vice versa. To achieve this, we first construct the regular H potential and the vector field [99].
| (55) |
| (56) |
which according to the length element and the following metric function:
| (57) |
| (58) |
these functions will be as follows,
| (59) |
| (60) |
| (61) |
In this work, our objective is to investigate the impact of gravitational modifications on the effective parameters of the Euler-Heisenberg model within the context of Rainbow Gravity. Therefore, we specifically focus on the influence of parameters related to these structures. Also, given the limitation on the number of equations, we are compelled to consider some parameters as predetermined. An interesting point to note at the outset is that, as can be clearly seen from equation (60), the Rainbow parameter is effectively absent in this equation. Consequently, we will concentrate our efforts on the impact of the gravitational modification parameter.
VI.2.1 Case I:

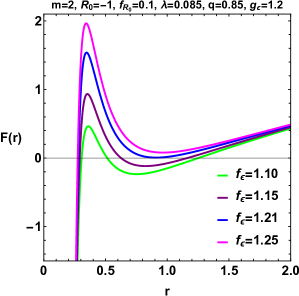
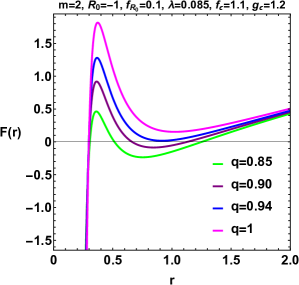
According to the assumed values , we have drawn the metric function for different , in fig (5), the metric function has a root for and the black hole has an event horizon.




|
According to the method of determining topological charges [96, 97, 100] and can be inferred from Table 2, the chosen in Figure (6) corresponds to a region where the system must possess an unstable photon sphere and a total topological charge of -1. This is confirmed by the potential function H(r) exhibiting a local maximum. Consequently, the structure will take the form of a normal black hole. However, in Figure (7), this selection pertains to a region classified as a naked singularity. As depicted in Figure (7), a global minimum appears in a space devoid of an event horizon, alongside a local maximum or the unstable photon sphere, resulting in a total topological charge of 0.
VI.2.2 Case II: =1
In the following, in order to avoid repetition, we will only mention the Figs and tables and finally we will discuss based on the tables. The metric function for different ,The structure of topological charges and the diagram of the potential function H(r) of this state can be seen in Figure (8,9,10) and the parametric classification and general conclusions about different areas can be seen in Table 3.





|
VI.2.3 Case III: =
The structure of topological charges and the diagram of the potential function H(r) of this state can be seen in Figure (11) and the parametric classification and general conclusions about different areas can be seen in Table 4.


|
VII Conclusion
The study of black hole thermodynamics delves into the intriguing connections between thermodynamic properties and the topological features of black holes. This field often involves examining critical points in black hole phase diagrams and assigning topological charges to these points. A notable approach is Duan’s topological current -mapping theory, which introduces the concept of topological charges to these critical points. This method offers a new perspective on the thermodynamic behavior of black holes and can be applied to other types of black holes, revealing more complex topological information.
In conclusion, Our research has yielded several significant findings. We have successfully derived the field equations for -Euler-Heisenberg theory, establishing a framework to explore the interaction between modified gravity and non-linear electromagnetic effects. Additionally, we have obtained an analytical solution for a static, spherically symmetric, energy-dependent black hole with constant scalar curvature. Also, our analysis of black holes in F(R)-Euler-Heisenberg gravity’s Rainbow provides significant insights into their topological properties. By examining the normalized field lines and various free parameters, we identified distinct winding and total topological numbers. Our findings suggest that the parameters and influence the topological charges. The stability of these black holes was further assessed through winding numbers, highlighting the intricate relationship between these parameters and the black holes’ topological characteristics. These results are comprehensively summarized in Table I. Additionally, an overview of Tables II, III, and IV related to the photon sphere of the mentioned black hole shows that with an increase in , the permissible range of negative in the first case gradually transitions into a non-permissible region in the third case. Furthermore, the QED parameter, which measures the strength of nonlinear effects, can be either positive or negative. A positive QED parameter reduces the electric field near the horizon and increases the black hole’s mass, whereas a negative QED parameter increases the electric field and decreases the mass. Based on these observations, it can be concluded that an increase in decreases the strength of the electric field near the horizon and enhances the effects of gravity.
References
- [1] A. De Felice and S. Tsujikawa, f(R) theories, Living Rev. Rel. 13 (2010), 3 doi:10.12942/lrr-2010-3 [arXiv:1002.4928 [gr-qc]].
- [2] V. Faraoni and S. Capozziello, Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics, Springer, 2011, ISBN 978-94-007-0164-9, 978-94-007-0165-6 doi:10.1007/978-94-007-0165-6
- [3] S. Nojiri and S. D. Odintsov, Unified cosmic history in modified gravity: from F(R) theory to Lorentz non-invariant models, Phys. Rept. 505 (2011), 59-144 doi:10.1016/j.physrep.2011.04.001 [arXiv:1011.0544 [gr-qc]].
- [4] S. Capozziello and M. De Laurentis, Extended Theories of Gravity, Phys. Rept. 509 (2011), 167-321 doi:10.1016/j.physrep.2011.09.003 [arXiv:1108.6266 [gr-qc]].
- [5] K. Bamba, S. Capozziello, S. Nojiri and S. D. Odintsov, Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests, Astrophys. Space Sci. 342 (2012), 155-228 doi:10.1007/s10509-012-1181-8 [arXiv:1205.3421 [gr-qc]].
- [6] E. Abdalla and A. Marins, The Dark Sector Cosmology, Int. J. Mod. Phys. D 29 (2020) no.14, 2030014 doi:10.1142/S0218271820300141 [arXiv:2010.08528 [gr-qc]].
- [7] S. Nojiri and S. D. Odintsov, Introduction to modified gravity and gravitational alternative for dark energy, eConf C0602061 (2006), 06 doi:10.1142/S0219887807001928 [arXiv:hep-th/0601213 [hep-th]].
- [8] A. Joyce, B. Jain, J. Khoury and M. Trodden, Beyond the Cosmological Standard Model, Phys. Rept. 568 (2015), 1-98 doi:10.1016/j.physrep.2014.12.002 [arXiv:1407.0059 [astro-ph.CO]].
- [9] S. Nojiri, S. D. Odintsov and V. K. Oikonomou, Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution, Phys. Rept. 692 (2017), 1-104 doi:10.1016/j.physrep.2017.06.001 [arXiv:1705.11098 [gr-qc]].
- [10] S. Capozziello, Curvature quintessence, Int. J. Mod. Phys. D 11 (2002), 483-492 doi:10.1142/S0218271802002025 [arXiv:gr-qc/0201033 [gr-qc]].
- [11] Y. Aditya and D. R. K. Reddy, Locally rotationally symmetric Bianchi type-I string cosmological models in f(R) theory of gravity, Int. J. Geom. Meth. Mod. Phys. 15 (2018) no.09, 1850156 doi:10.1142/S0219887818501566
- [12] W. Hu and I. Sawicki, Models of f(R) Cosmic Acceleration that Evade Solar-System Tests, Phys. Rev. D 76 (2007), 064004 doi:10.1103/PhysRevD.76.064004 [arXiv:0705.1158 [astro-ph]].
- [13] A. Cooney, S. DeDeo and D. Psaltis, Neutron Stars in f(R) Gravity with Perturbative Constraints, Phys. Rev. D 82 (2010), 064033 doi:10.1103/PhysRevD.82.064033 [arXiv:0910.5480 [astro-ph.HE]].
- [14] M. K. Cheoun, C. Deliduman, C. Güngör, V. Keleş, C. Y. Ryu, T. Kajino and G. J. Mathews, Neutron stars in a perturbative gravity model with strong magnetic fields, JCAP 10 (2013), 021 doi:10.1088/1475-7516/2013/10/021 [arXiv:1304.1871 [astro-ph.HE]].
- [15] A. V. Astashenok and S. D. Odintsov, Supermassive Neutron Stars in Axion Gravity, Mon. Not. Roy. Astron. Soc. 493 (2020) no.1, 78-86 doi:10.1093/mnras/staa214 [arXiv:2001.08504 [gr-qc]].
- [16] A. V. Astashenok, S. Capozziello, S. D. Odintsov and V. K. Oikonomou, Causal limit of neutron star maximum mass in gravity in view of GW190814, Phys. Lett. B 816 (2021), 136222 doi:10.1016/j.physletb.2021.136222 [arXiv:2103.04144 [gr-qc]].
- [17] L. Sarmah, S. Kalita and A. Wojnar, Stability criterion for white dwarfs in Palatini f(R) gravity, Phys. Rev. D 105 (2022) no.2, 024028 doi:10.1103/PhysRevD.105.024028 [arXiv:2111.08029 [gr-qc]].
- [18] S. Kalita and B. Mukhopadhyay, Gravitational wave in f(R) gravity: possible signature of sub- and super-Chandrasekhar limiting mass white dwarfs, Astrophys. J. 909 (2021) no.1, 65 doi:10.3847/1538-4357/abddb8 [arXiv:2101.07278 [astro-ph.HE]].
- [19] S. Capozziello, A. Stabile and A. Troisi, The Newtonian Limit of f(R) gravity, Phys. Rev. D 76 (2007), 104019 doi:10.1103/PhysRevD.76.104019 [arXiv:0708.0723 [gr-qc]].
- [20] W. Heisenberg and H. Euler, Consequences of Dirac’s theory of positrons, Z. Phys. 98 (1936) no.11-12, 714-732 doi:10.1007/BF01343663 [arXiv:physics/0605038 [physics]].
- [21] J. S. Schwinger, On gauge invariance and vacuum polarization, Phys. Rev. 82 (1951), 664-679 doi:10.1103/PhysRev.82.664
- [22] K. A. Bronnikov, V. N. Melnikov, G. N. Shikin and K. P. Staniukowicz, SCALAR, ELECTROMAGNETIC, AND GRAVITATIONAL FIELDS INTERACTION: PARTICLE - LIKE SOLUTIONS, Annals Phys. 118 (1979), 84-107 doi:10.1016/0003-4916(79)90235-5
- [23] K. A. Bronnikov, Regular magnetic black holes and monopoles from nonlinear electrodynamics, Phys. Rev. D 63 (2001), 044005 doi:10.1103/PhysRevD.63.044005 [arXiv:gr-qc/0006014 [gr-qc]].
- [24] H. Yajima and T. Tamaki, Black hole solutions in Euler-Heisenberg theory, Phys. Rev. D 63 (2001), 064007 doi:10.1103/PhysRevD.63.064007 [arXiv:gr-qc/0005016 [gr-qc]].
- [25] C. Corda and H. J. Mosquera Cuesta, Removing black-hole singularities with nonlinear electrodynamics, Mod. Phys. Lett. A 25 (2010), 2423-2429 doi:10.1142/S0217732310033633 [arXiv:0905.3298 [gr-qc]].
- [26] R. Ruffini, Y. B. Wu and S. S. Xue, Einstein-Euler-Heisenberg Theory and charged black holes, Phys. Rev. D 88 (2013), 085004 doi:10.1103/PhysRevD.88.085004 [arXiv:1307.4951 [hep-th]].
- [27] S. H. Hendi and M. Allahverdizadeh, Slowly Rotating Black Holes with Nonlinear Electrodynamics, Adv. High Energy Phys. 2014 (2014), 390101 doi:10.1155/2014/390101
- [28] M. Maceda and A. Macías, Non-commutative inspired black holes in Euler–Heisenberg non-linear electrodynamics, Phys. Lett. B 788 (2019), 446-452 doi:10.1016/j.physletb.2018.11.048 [arXiv:1807.05269 [gr-qc]].
- [29] J. C. Olvera and L. A. López, Scattering and absorption sections of nonlinear electromagnetic black holes, Eur. Phys. J. Plus 135 (2020) no.3, 288 doi:10.1140/epjp/s13360-020-00303-0 [arXiv:1910.03067 [gr-qc]].
- [30] D. Amati, M. Ciafaloni and G. Veneziano, Can Space-Time Be Probed Below the String Size?, Phys. Lett. B 216 (1989), 41-47 doi:10.1016/0370-2693(89)91366-X
- [31] G. Amelino-Camelia, J. R. Ellis, N. E. Mavromatos and D. V. Nanopoulos, Distance measurement and wave dispersion in a Liouville string approach to quantum gravity, Int. J. Mod. Phys. A 12 (1997), 607-624 doi:10.1142/S0217751X97000566 [arXiv:hep-th/9605211 [hep-th]].
- [32] G. Amelino-Camelia, J. R. Ellis, N. E. Mavromatos, D. V. Nanopoulos and S. Sarkar, Tests of quantum gravity from observations of gamma-ray bursts, Nature 393 (1998), 763-765 doi:10.1038/31647 [arXiv:astro-ph/9712103 [astro-ph]].
- [33] J. Abraham et al. [Pierre Auger], Measurement of the Energy Spectrum of Cosmic Rays above eV Using the Pierre Auger Observatory, Phys. Lett. B 685 (2010), 239-246 doi:10.1016/j.physletb.2010.02.013 [arXiv:1002.1975 [astro-ph.HE]].
- [34] P. Horava, Quantum Gravity at a Lifshitz Point, Phys. Rev. D 79 (2009), 084008 doi:10.1103/PhysRevD.79.084008 [arXiv:0901.3775 [hep-th]].
- [35] P. Horava, Spectral Dimension of the Universe in Quantum Gravity at a Lifshitz Point, Phys. Rev. Lett. 102 (2009), 161301 doi:10.1103/PhysRevLett.102.161301 [arXiv:0902.3657 [hep-th]].
- [36] G. Amelino-Camelia, J. R. Ellis, N. E. Mavromatos and D. V. Nanopoulos, Distance measurement and wave dispersion in a Liouville string approach to quantum gravity, Int. J. Mod. Phys. A 12 (1997), 607-624 doi:10.1142/S0217751X97000566 [arXiv:hep-th/9605211 [hep-th]].
- [37] G. Amelino-Camelia, Quantum-Spacetime Phenomenology, Living Rev. Rel. 16 (2013), 5 doi:10.12942/lrr-2013-5 [arXiv:0806.0339 [gr-qc]].
- [38] G. ’t Hooft, Quantization of point particles in (2+1)-dimensional gravity and space-time discreteness, Class. Quant. Grav. 13 (1996), 1023-1040 doi:10.1088/0264-9381/13/5/018 [arXiv:gr-qc/9601014 [gr-qc]].
- [39] G. ’t Hooft, Quantization of point particles in (2+1)-dimensional gravity and space-time discreteness, Class. Quant. Grav. 13 (1996), 1023-1040 doi:10.1088/0264-9381/13/5/018 [arXiv:gr-qc/9601014 [gr-qc]].
- [40] J. Magueijo and L. Smolin, Generalized Lorentz invariance with an invariant energy scale, Phys. Rev. D 67 (2003), 044017 doi:10.1103/PhysRevD.67.044017 [arXiv:gr-qc/0207085 [gr-qc]].
- [41] J. Magueijo and L. Smolin, Lorentz invariance with an invariant energy scale, Phys. Rev. Lett. 88 (2002), 190403 doi:10.1103/PhysRevLett.88.190403 [arXiv:hep-th/0112090 [hep-th]].
- [42] M. Dehghani, Thermodynamics of novel charged dilaton black holes in gravity’s rainbow, Phys. Lett. B 785 (2018), 274-283 doi:10.1016/j.physletb.2018.08.045
- [43] R. Garattini and E. N. Saridakis, Gravity’s Rainbow: a bridge towards Hořava–Lifshitz gravity, Eur. Phys. J. C 75 (2015) no.7, 343 doi:10.1140/epjc/s10052-015-3562-y [arXiv:1411.7257 [gr-qc]].
- [44] J. Magueijo and L. Smolin, Gravity’s rainbow, Class. Quant. Grav. 21 (2004), 1725-1736 doi:10.1088/0264-9381/21/7/001 [arXiv:gr-qc/0305055 [gr-qc]].
- [45] Y. Ling, X. Li and H. b. Zhang, Thermodynamics of modified black holes from gravity’s rainbow, Mod. Phys. Lett. A 22 (2007), 2749-2756 doi:10.1142/S0217732307022931 [arXiv:gr-qc/0512084 [gr-qc]].
- [46] P. Galan and G. A. Mena Marugan, Entropy and temperature of black holes in a gravity’s rainbow, Phys. Rev. D 74 (2006), 044035 doi:10.1103/PhysRevD.74.044035 [arXiv:gr-qc/0608061 [gr-qc]].
- [47] C. Z. Liu and J. Y. Zhu, Hawking radiation and black hole entropy in a gravity ’ rainbow, Gen. Rel. Grav. 40 (2008), 1899-1911 doi:10.1007/s10714-008-0607-7 [arXiv:gr-qc/0703055 [gr-qc]].
- [48] C. Leiva, J. Saavedra and J. Villanueva, The Geodesic Structure of the Schwarzschild Black Holes in Gravity’s Rainbow, Mod. Phys. Lett. A 24 (2009), 1443-1451 doi:10.1142/S0217732309029983 [arXiv:0808.2601 [gr-qc]].
- [49] A. F. Ali, Black hole remnant from gravity’s rainbow, Phys. Rev. D 89 (2014) no.10, 104040 doi:10.1103/PhysRevD.89.104040 [arXiv:1402.5320 [hep-th]].
- [50] A. F. Ali, M. Faizal and B. Majumder, Absence of an Effective Horizon for Black Holes in Gravity’s Rainbow, EPL 109 (2015) no.2, 20001 doi:10.1209/0295-5075/109/20001 [arXiv:1406.1980 [gr-qc]].
- [51] A. F. Ali, M. Faizal and M. M. Khalil, Absence of Black Holes at LHC due to Gravity’s Rainbow, Phys. Lett. B 743 (2015), 295-300 doi:10.1016/j.physletb.2015.02.065 [arXiv:1410.4765 [hep-th]].
- [52] Y. Gim and W. Kim, Black Hole Complementarity in Gravity’s Rainbow, JCAP 05 (2015), 002 doi:10.1088/1475-7516/2015/05/002 [arXiv:1501.04702 [gr-qc]].
- [53] S. H. Hendi, M. Faizal, B. E. Panah and S. Panahiyan, Charged dilatonic black holes in gravity’s rainbow, Eur. Phys. J. C 76 (2016) no.5, 296 doi:10.1140/epjc/s10052-016-4119-4 [arXiv:1508.00234 [hep-th]].
- [54] Y. W. Kim, S. K. Kim and Y. J. Park, Thermodynamic stability of modified Schwarzschild–AdS black hole in rainbow gravity, Eur. Phys. J. C 76 (2016) no.10, 557 doi:10.1140/epjc/s10052-016-4393-1 [arXiv:1607.06185 [gr-qc]].
- [55] Z. W. Feng and S. Z. Yang, Thermodynamic phase transition of a black hole in rainbow gravity, Phys. Lett. B 772 (2017), 737-742 doi:10.1016/j.physletb.2017.07.057 [arXiv:1708.06627 [gr-qc]].
- [56] Y. Gim, H. Um and W. Kim, Black hole complementarity with the generalized uncertainty principle in gravity’s rainbow, JCAP 02 (2018), 060 doi:10.1088/1475-7516/2018/02/060 [arXiv:1712.04444 [gr-qc]].
- [57] R. Garattini, Gravity’s Rainbow and Black Hole Entropy, J. Phys. Conf. Ser. 942 (2017) no.1, 012011 doi:10.1088/1742-6596/942/1/012011 [arXiv:1712.09729 [gr-qc]].
- [58] S. H. Hendi and M. Momennia, AdS charged black holes in Einstein–Yang–Mills gravity’s rainbow: Thermal stability and criticality, Phys. Lett. B 777 (2018), 222-234 doi:10.1016/j.physletb.2017.12.033
- [59] B. Eslam Panah, Effects of energy dependent spacetime on geometrical thermodynamics and heat engine of black holes: gravity’s rainbow, Phys. Lett. B 787 (2018), 45-55 doi:10.1016/j.physletb.2018.10.042 [arXiv:1805.03014 [hep-th]].
- [60] R. Garattini, Distorting General Relativity: Gravity’s Rainbow and f(R) theories at work, JCAP 06 (2013), 017 doi:10.1088/1475-7516/2013/06/017 [arXiv:1210.7760 [gr-qc]].
- [61] S. H. Hendi, B. Eslam Panah, S. Panahiyan and M. Momennia, F(R) gravity’s rainbow and its Einstein counterpart, Adv. High Energy Phys. 2016 (2016), 9813582 doi:10.1155/2016/9813582 [arXiv:1607.03383 [gr-qc]].
- [62] S. H. Hendi, S. Panahiyan, B. Eslam Panah and M. Momennia, Thermodynamic instability of nonlinearly charged black holes in gravity’s rainbow, Eur. Phys. J. C 76 (2016) no.3, 150 doi:10.1140/epjc/s10052-016-3994-z [arXiv:1512.05192 [gr-qc]].
- [63] S. H. Hendi, B. Eslam Panah, S. Panahiyan and M. Momennia, Dilatonic black holes in gravity’s rainbow with a nonlinear source: the effects of thermal fluctuations, Eur. Phys. J. C 77 (2017) no.9, 647 doi:10.1140/epjc/s10052-017-5211-0 [arXiv:1708.06634 [gr-qc]].
- [64] S. H. Hendi, M. Momennia, B. Eslam Panah and M. Faizal, NONSINGULAR UNIVERSES IN GAUSS–BONNET GRAVITY’S RAINBOW, Astrophys. J. 827 (2016) no.2, 153 doi:10.3847/0004-637X/827/2/153 [arXiv:1703.00480 [gr-qc]].
- [65] M. Dehghani, Thermodynamics of charged dilatonic BTZ black holes in rainbow gravity, Phys. Lett. B 777 (2018), 351-360 doi:10.1016/j.physletb.2017.12.048
- [66] S. W. Wei and Y. X. Liu, Topology of black hole thermodynamics, Phys. Rev. D 105 (2022) no.10, 104003 doi:10.1103/PhysRevD.105.104003 [arXiv:2112.01706 [gr-qc]].
- [67] P. K. Yerra and C. Bhamidipati, Topology of black hole thermodynamics in Gauss-Bonnet gravity, Phys. Rev. D 105 (2022) no.10, 104053 doi:10.1103/PhysRevD.105.104053 [arXiv:2202.10288 [gr-qc]].
- [68] N. C. Bai, L. Li and J. Tao, Topology of black hole thermodynamics in Lovelock gravity, Phys. Rev. D 107 (2023) no.6, 064015 doi:10.1103/PhysRevD.107.064015 [arXiv:2208.10177 [gr-qc]].
- [69] P. K. Yerra and C. Bhamidipati, Topology of Born-Infeld AdS black holes in 4D novel Einstein-Gauss-Bonnet gravity, Phys. Lett. B 835 (2022), 137591 doi:10.1016/j.physletb.2022.137591 [arXiv:2207.10612 [gr-qc]].
- [70] E. Witten, Anti-de Sitter space and holography, Adv. Theor. Math. Phys. 2 (1998), 253-291 doi:10.4310/ATMP.1998.v2.n2.a2 [arXiv:hep-th/9802150 [hep-th]].
- [71] S. W. Wei, Y. X. Liu and R. B. Mann, Black Hole Solutions as Topological Thermodynamic Defects, Phys. Rev. Lett. 129 (2022) no.19, 191101 doi:10.1103/PhysRevLett.129.191101 [arXiv:2208.01932 [gr-qc]].
- [72] Y. S. Duan and M. L. Ge, SU(2) Gauge Theory and Electrodynamics with N Magnetic Monopoles, Sci. Sin. 9 (1979) no.11, 1072 doi:10.1142/9789813237278_0001
- [73] Y. Duan, THE STRUCTURE OF THE TOPOLOGICAL CURRENT, SLAC-PUB-3301.
- [74] C. Liu and J. Wang, Topological natures of the Gauss-Bonnet black hole in AdS space, Phys. Rev. D 107 (2023) no.6, 064023 doi:10.1103/PhysRevD.107.064023 [arXiv:2211.05524 [gr-qc]].
- [75] Y. Du and X. Zhang, Topological classes of BTZ black holes, [arXiv:2302.11189 [gr-qc]].
- [76] D. Wu, Classifying topology of consistent thermodynamics of the four-dimensional neutral Lorentzian NUT-charged spacetimes, Eur. Phys. J. C 83 (2023) no.5, 365 doi:10.1140/epjc/s10052-023-11561-4 [arXiv:2302.01100 [gr-qc]].
- [77] D. Wu, Consistent thermodynamics and topological classes for the four-dimensional Lorentzian charged Taub-NUT spacetimes, Eur. Phys. J. C 83 (2023) no.7, 589 doi:10.1140/epjc/s10052-023-11782-7 [arXiv:2306.02324 [gr-qc]].
- [78] D. Wu, Topological classes of rotating black holes, Phys. Rev. D 107 (2023) no.2, 024024 doi:10.1103/PhysRevD.107.024024 [arXiv:2211.15151 [gr-qc]].
- [79] D. Wu and S. Q. Wu, Topological classes of thermodynamics of rotating AdS black holes, Phys. Rev. D 107 (2023) no.8, 084002 doi:10.1103/PhysRevD.107.084002 [arXiv:2301.03002 [hep-th]].
- [80] J. Sadeghi, M. R. Alipour, S. Noori Gashti and M. A. S. Afshar, Bulk-boundary and RPS thermodynamics from topology perspective, Chin. Phys. C 48 (2024) no.9, 095106 doi:10.1088/1674-1137/ad53b9 [arXiv:2306.16117 [gr-qc]].
- [81] J. Sadeghi, M. A. S. Afshar, S. Noori Gashti and M. R. Alipour, Thermodynamic topology and photon spheres in the hyperscaling violating black holes, Astropart. Phys. 156 (2024), 102920 doi:10.1016/j.astropartphys.2023.102920 [arXiv:2307.12873 [gr-qc]].
- [82] J. Sadeghi, M. A. S. Afshar, S. Noori Gashti and M. R. Alipour, Topology of Hayward-AdS black hole thermodynamics, Phys. Scripta 99 (2024) no.2, 025003 doi:10.1088/1402-4896/ad186b
- [83] J. Sadeghi, M. A. S. Afshar, S. Noori Gashti and M. R. Alipour, Thermodynamic topology of black holes from bulk-boundary, extended, and restricted phase space perspectives, Annals Phys. 460 (2024), 169569 doi:10.1016/j.aop.2023.169569 [arXiv:2312.04325 [hep-th]].
- [84] M. R. Alipour, M. A. S. Afshar, S. Noori Gashti and J. Sadeghi, Topological classification and black hole thermodynamics, Phys. Dark Univ. 42 (2023), 101361 doi:10.1016/j.dark.2023.101361 [arXiv:2305.05595 [gr-qc]].
- [85] J. Sadeghi, S. Noori Gashti, M. R. Alipour and M. A. S. Afshar, Bardeen black hole thermodynamics from topological perspective, Annals Phys. 455 (2023), 169391 doi:10.1016/j.aop.2023.169391 [arXiv:2306.05692 [hep-th]].
- [86] S. P. Wu and S. W. Wei, Thermodynamical topology of quantum BTZ black hole, Phys. Rev. D 110 (2024) no.2, 024054 doi:10.1103/PhysRevD.110.024054 [arXiv:2403.14167 [gr-qc]].
- [87] B. Eslam Panah, B. Hazarika and P. Phukon, Thermodynamic topology of topological black hole in -ModMax gravity’s rainbow, [arXiv:2405.20022 [hep-th]].
- [88] M. Y. Zhang, H. Chen, H. Hassanabadi, Z. W. Long and H. Yang, Thermodynamic topology of Kerr-Sen black holes via Rényi statistics, Phys. Lett. B 856 (2024), 138885 doi:10.1016/j.physletb.2024.138885 [arXiv:2312.12814 [gr-qc]].
- [89] D. Wu, Topological classes of thermodynamics of the four-dimensional static accelerating black holes, Phys. Rev. D 108 (2023) no.8, 084041 doi:10.1103/PhysRevD.108.084041 [arXiv:2307.02030 [hep-th]].
- [90] B. Hazarika and P. Phukon, Thermodynamic Topology of Black Holes in f(R) Gravity, PTEP 2024 (2024) no.4, 043E01 doi:10.1093/ptep/ptae035 [arXiv:2401.16756 [hep-th]].
- [91] N. J. Gogoi and P. Phukon, Thermodynamic topology of 4D Euler–Heisenberg-AdS black hole in different ensembles, Phys. Dark Univ. 44 (2024), 101456 doi:10.1016/j.dark.2024.101456 [arXiv:2312.13577 [hep-th]].
- [92] H. Chen, D. Wu, M. Y. Zhang, H. Hassanabadi and Z. W. Long, Thermodynamic topology of phantom AdS black holes in massive gravity, Phys. Dark Univ. 46 (2024), 101617 doi:10.1016/j.dark.2024.101617 [arXiv:2404.08243 [gr-qc]].
- [93] S. P. Wu and S. W. Wei, Thermodynamical topology of quantum BTZ black hole, Phys. Rev. D 110 (2024) no.2, 024054 doi:10.1103/PhysRevD.110.024054 [arXiv:2403.14167 [gr-qc]].
- [94] D. Wu, S. Y. Gu, X. D. Zhu, Q. Q. Jiang and S. Z. Yang, Topological classes of thermodynamics of the static multi-charge AdS black holes in gauged supergravities: novel temperature-dependent thermodynamic topological phase transition, JHEP 06 (2024), 213 doi:10.1007/JHEP06(2024)213 [arXiv:2402.00106 [hep-th]].
- [95] Y. Z. Du, H. F. Li, Y. B. Ma and Q. Gu, Topology and phase transition for EPYM AdS black hole in thermal potential, Nucl. Phys. B 1006 (2024), 116641 doi:10.1016/j.nuclphysb.2024.116641 [arXiv:2309.00224 [hep-th]].
- [96] J. Sadeghi and M. A. S. Afshar, The role of topological photon spheres in constraining the parameters of black holes, Astropart. Phys. 162 (2024), 102994 doi:10.1016/j.astropartphys.2024.102994 [arXiv:2405.06568 [gr-qc]].
- [97] J. Sadeghi and M. A. S. Afshar, Effective Potential and Topological Photon Spheres: A Novel Approach to Black Hole Parameter Classification, [arXiv:2405.18798 [gr-qc]].
- [98] V. Cardoso, L. C. B. Crispino, C. F. B. Macedo, H. Okawa and P. Pani, Light rings as observational evidence for event horizons: long-lived modes, ergoregions and nonlinear instabilities of ultracompact objects, Phys. Rev. D 90 (2014) no.4, 044069 doi:10.1103/PhysRevD.90.044069 [arXiv:1406.5510 [gr-qc]].
- [99] S. W. Wei, Topological Charge and Black Hole Photon Spheres, Phys. Rev. D 102 (2020) no.6, 064039 doi:10.1103/PhysRevD.102.064039 [arXiv:2006.02112 [gr-qc]].
- [100] R. Ruffini, Y. B. Wu and S. S. Xue, Einstein-Euler-Heisenberg Theory and charged black holes, Phys. Rev. D 88 (2013), 085004 doi:10.1103/PhysRevD.88.085004 [arXiv:1307.4951 [hep-th]].
- [101] J. J. Peng and S. Q. Wu, Covariant anomaly and Hawking radiation from the modified black hole in the rainbow gravity theory, Gen. Rel. Grav. 40 (2008), 2619-2626 doi:10.1007/s10714-008-0642-4 [arXiv:0709.0167 [hep-th]].
- [102] A. de la Cruz-Dombriz, A. Dobado and A. L. Maroto, Black Holes in f(R) theories, Phys. Rev. D 80 (2009), 124011 [erratum: Phys. Rev. D 83 (2011), 029903] doi:10.1103/PhysRevD.80.124011 [arXiv:0907.3872 [gr-qc]].
- [103] T. Moon, Y. S. Myung and E. J. Son, f(R) black holes, Gen. Rel. Grav. 43 (2011), 3079-3098 doi:10.1007/s10714-011-1225-3 [arXiv:1101.1153 [gr-qc]].
- [104] G. Cognola, E. Elizalde, S. Nojiri, S. D. Odintsov and S. Zerbini, One-loop f(R) gravity in de Sitter universe, JCAP 02 (2005), 010 doi:10.1088/1475-7516/2005/02/010 [arXiv:hep-th/0501096 [hep-th]].
- [105] L. Balart and E. C. Vagenas, Regular black holes with a nonlinear electrodynamics source, Phys. Rev. D 90 (2014) no.12, 124045 doi:10.1103/PhysRevD.90.124045 [arXiv:1408.0306 [gr-qc]].
- [106] D. Kubiznak, R. B. Mann and M. Teo, Black hole chemistry: thermodynamics with Lambda, Class. Quant. Grav. 34 (2017) no.6, 063001 doi:10.1088/1361-6382/aa5c69 [arXiv:1608.06147 [hep-th]].
- [107] A. Ashtekar and A. Magnon, Asymptotically anti-de Sitter space-times, Class. Quant. Grav. 1 (1984), L39-L44 doi:10.1088/0264-9381/1/4/002
- [108] A. Ashtekar and S. Das, Asymptotically Anti-de Sitter space-times: Conserved quantities, Class. Quant. Grav. 17 (2000), L17-L30 doi:10.1088/0264-9381/17/2/101 [arXiv:hep-th/9911230 [hep-th]].
- [109] S. W. Wei, Y. X. Liu and R. B. Mann, Black Hole Solutions as Topological Thermodynamic Defects, Phys. Rev. Lett. 129 (2022) no.19, 191101 doi:10.1103/PhysRevLett.129.191101 [arXiv:2208.01932 [gr-qc]].