Center for Bright Beams
Theory of Nb-Zr alloy superconductivity and first experimental demonstration for superconducting radio-frequency cavity applications
Abstract
Niobium-zirconium (Nb-Zr) alloy is an old superconductor that is a promising new candidate for superconducting radio-frequency (SRF) cavity applications. Using density-functional and Eliashberg theories, we show that addition of Zr to a Nb surface in small concentrations increases the critical temperature and improves other superconducting properties. Furthermore, we calculate for Nb-Zr alloys across a broad range of Zr concentrations, showing good agreement with the literature for disordered alloys as well as the potential for significantly higher in ordered alloys near 75%Nb/25%Zr composition. We provide experimental verification on Nb-Zr alloy samples and SRF sample test cavities prepared with either physical vapor or our novel electrochemical deposition recipes. These samples have the highest measured of any Nb-Zr superconductor to date and indicate a reduction in BCS resistance compared to the conventional Nb reference sample; they represent the first steps along a new pathway to greatly enhanced SRF performance. Finally, we use Ginzburg-Landau theory to show that the addition of Zr to a Nb surface increases the superheating field , a key figure of merit for SRF which determines the maximum accelerating gradient at which cavities can operate.
Introduction.
Superconducting radio-frequency (SRF) cavities are a key component of particle accelerators used, e.g., as light sources [1] and colliders [2]. These cavities are extremely reliant on the superconducting properties of the cavity surface. Of particular interest are the RF resistance, which determines energy dissipation and cooling costs, and the superheating field, which determines the maximum accelerating gradient and thus the number of cavities required [3, 4]. Further optimization of these quantities is necessary to enable more energy-efficient and compact accelerators and requires the exploration of superconductors beyond industry-standard niobium (Nb).
Many efforts have explored adding other elements to the SRF surface of Nb cavities, such as tin [5, 6, 7] and nitrogen [8]. One of the limitations of these materials is the difficulty of producing uniform layers of the necessary phases and compositions that achieve the desired improvements in superconducting properties. A possible material that avoids these complications is niobium-zirconium (Nb-Zr). Nb-Zr alloys retain a body-centered cubic (bcc) crystal structure, the same as Nb, across a broad compositional range up to about 50% Zr [9], and form a stable, insulating Zr native oxide which should cause little dissipation under RF conditions.
The superconducting properties of Nb-Zr alloys, however, are not as well characterized as those of other Nb-based superconductors. Literature studies [10, 11] have focused on bulk random alloy samples very different from the thin-film alloy layers necessary for SRF. Furthermore, these bulk random-alloy samples showed a relatively modest enhancement of the critical temperature compared to elemental Nb, far less than would be expected based on the rigid band shift theory proposed by early researchers [11].
As for the superheating field , previous studies have addressed homogeneous superconductors [12, 13, 14, 15, 16] and layered superconductors [17, 18, 19, 20, 21], but efforts to improve SRF cavity performance have revealed that material inhomogeneities are key factors which affect [4]. Recent studies of for inhomogeneous superconductors include materials with continuously-varying impurity concentrations [22] and the effect of spatial variations in [23].
To better understand the Nb-Zr alloy system, we use density-functional theory (DFT) and Eliashberg theory in the dilute limit (25% Zr), where the virtual crystal approximation (VCA) allows us to calculate a variety of superconducting properties. We confirm that the addition of Zr to Nb increases .
We then switch from VCA to a supercell approach in order to directly account for lattice relaxation effects, which become important at higher Zr concentrations (up to 50% Zr), and focus on . With this approach, we find good agreement with the literature for random alloys at all concentrations, and we investigate the potential for ordered alloy structures to surpass the limitations of the random alloy.
We synthesize Nb-Zr alloy surface layers of different Zr doping profiles using physical vapor and electrochemical methods and examine their material and RF superconducting properties. We find that the measured meets or exceeds literature values for Nb-Zr random alloys, in agreement with our calculations. We show that the enhanced likely translates to improved performance under RF conditions by comparing the BCS resistance of the alloyed sample to that of a reference Nb sample.
Finally, we use GL theory to investigate how Nb-Zr surface layers with different thicknesses and compositions affect . We incorporate spatial variations of multiple superconducting properties using realistic profiles of Zr concentration. We find that addition of Zr to Nb noticeably improves , making Nb-Zr an excellent candidate for SRF applications.
Superconducting properties of Nb-Zr in the dilute limit.
We calculate the superconducting properties of Nb-Zr alloys in the dilute limit using VCA. We use Quantum Espresso (QE) [24, 25, 26] to perform the DFT calculations. We use the Perdew–Burke-Ernzerhof [27] functional for the exchange-correlation energy and norm conserving pseudopotentials [28, 29]. We use the Methfessel-Paxton smearing scheme [30] to smear the electrons during lattice relaxation. For the electron-phonon calculations, we use the tetrahedron method [31] as implemented in QE, with a -mesh of and a -mesh of to calculate the Eliashberg function . Finally, we calculate the superconducting gap using isotropic Eliashberg theory, as implemented in the EPW code [32, 33].
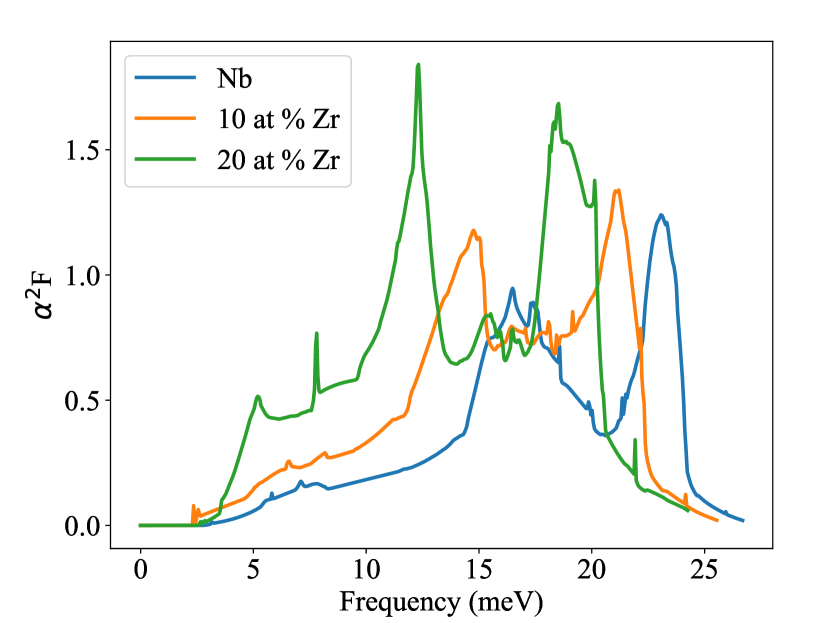
Table 1 shows the calculated superconducting properties for Zr concentrations ranging from 0 to 25%. The calculated agree well between the three methods used to calculate the critical temperature - Allen-Dynes [34], Xie [35], and isotropic Eliashberg. As Zr concentration increases, so do both the electron-phonon coupling constant and the of the alloy. This increase in can be attributed to softening of the phonons, as shown in Fig. 1, and an increase in the density of states at the Fermi level .
| Composition | (4K) (meV) | (m/s) | (states/eV/Å3) | (K) | (K) | (K) | (nm) | (nm) | (mT) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nb | 1.13 | 2.4 | 0.082 | 11.24 | 14.2 | 10.39 | 39.0 | 38.0 | 157 | 1.03 | |
| Nb0.95Zr0.05 | 1.30 | 3.0 | 0.086 | 13.60 | 16.8 | 13.46 | 39.5 | 30.3 | 195 | 1.30 | |
| Nb0.90Zr0.10 | 1.69 | 4.0 | 0.091 | 17.18 | 20.8 | 18.3 | 38.9 | 23.7 | 253 | 1.64 | |
| Nb0.80Zr0.20 | 2.37 | 5.3 | 0.103 | 21.17 | 25.3 | 24.28 | 38.0 | 18.5 | 331 | 2.05 | |
| Nb0.75Zr0.25 | 2.85 | 5.8 | 0.106 | 22.02 | 26.7 | 26.49 | 37.9 | 17.6 | 350 | 2.16 |
Superconducting properties of Nb-Zr alloys at higher Zr concentrations.
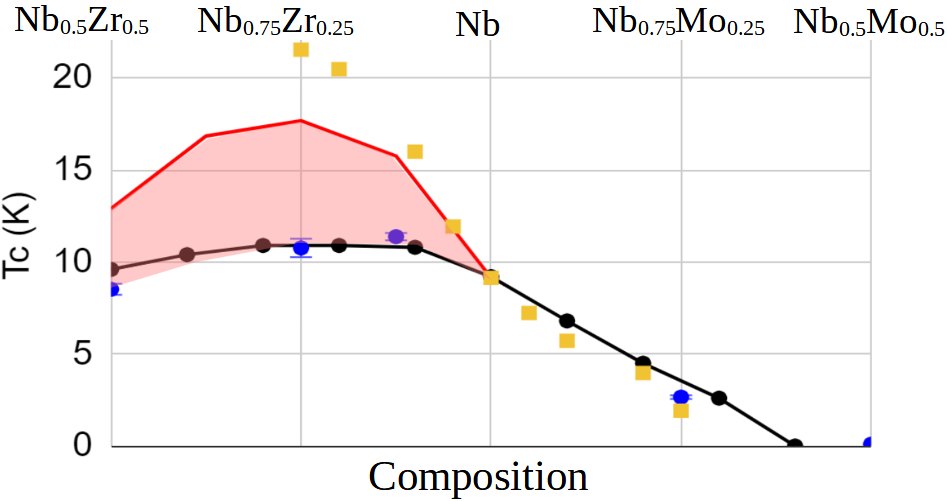
Previous experimental studies of Nb1-nZrn bcc random alloys have found moderately increased and greatly increased upper critical field compared to Nb across a broad compositional range from to [11, 10]. Alloys made with molybdenum (Mo), Nb’s other 5th row neighbor, have ’s that drop off quickly with increasing Mo concentration. This data (Fig. 2‘experiment’ curve) is in qualitative agreement with the simple alloy theory originally used to describe bcc alloy superconductivity, namely that there is a universal d-band shape, and alloying simply shifts the position of the Fermi level by adding or removing d-band electrons, thus altering and therefore [11, 36]. Quantitatively, this effect is captured in our VCA calculations (Fig. 2 ’VCA’ curve), which show good agreement with experiment for Nb-Mo, but significantly overestimate for Nb-Zr. This indicates that, while VCA may accurately describe Nb-Mo and dilute Nb-Zr alloys, it misses important nonlinear effects in the Nb-Zr system that alter the d-band shape and tend to lower .
Exploration of the full compositional range of Nb1-nZrn therefore requires an analysis of Nb-Zr which accounts fully for the effects of Zr substitutions in the Nb lattice; for this we employ the supercell method. Specifically, for each , we construct 48-atom supercells, substitute the required number of Nb atoms with Zr at random sites, and fully relax the structure, using the JDFTx software package with the PBE exchange-correlation functional and ultrasoft pseudopotentials [37, 27, 38]. Averaging the resulting density of states (DOS) over multiple configurations at each composition yields an expected macroscopic . We then estimate as a function of composition through the BCS - relationship, resulting in the ‘random alloy’ predictions displayed in Fig. 2. We find quite good agreement with the random-alloy experiments for both Nb-Mo and Nb-Zr, indicating that our calculated –composition relationship correctly captures the important nonlinear effects that determine in Nb-Zr random alloys.
Examining our supercell calculations, we find that, for atoms at their unrelaxed, ideal bcc locations, the electronic DOS for Nb-Zr alloys resemble that of Nb with a rigid band shift, similar to what would be found in VCA. However, we find that the atoms tend to move away from their ideal bcc locations in a way that significantly reduces . This final, reduced value varies only modestly with composition up to 50% Zr, explaining the modest variations that are observed in . Figure 3a illustrates this relaxation effect for the 50/50 Nb-Zr random alloy, where the initially large DOS peak near the Fermi level essentially vanishes. Moreover, consistent with our observation that simple alloy theories work well for Nb-Mo, Fig. 3b shows this relaxation effect to be absent in the Nb-Mo system.
Fundamentally, the Nb-Zr alloy minimizes its energy by lowering the energies of occupied electronic states near the Fermi level, resulting in a reduced . This relaxation does not occur in Nb-Mo, which has fewer states near the Fermi level, and thus less ability to lower its energy in this manner. The redistribution of electronic energy levels in Nb-Zr is accomplished by the relaxation of lattice degrees of freedom, i.e., by the movement of atoms away from their ideal lattice positions. This brings us to a key difference between random Nb-Zr alloys, which have been our focus so far, and ordered Nb-Zr alloys. It has been pointed out that the symmetries of highly ordered structures can effectively limit the degrees of freedom for lattice relaxation [34]. In our case, this could result in a crystal with electronic structure similar to the VCA or the unrelaxed-random-alloy electronic structure and thus a much higher . It may be possible to grow such an ordered alloy in a low-temperature thin-film process such as those often employed in SRF cavity production.
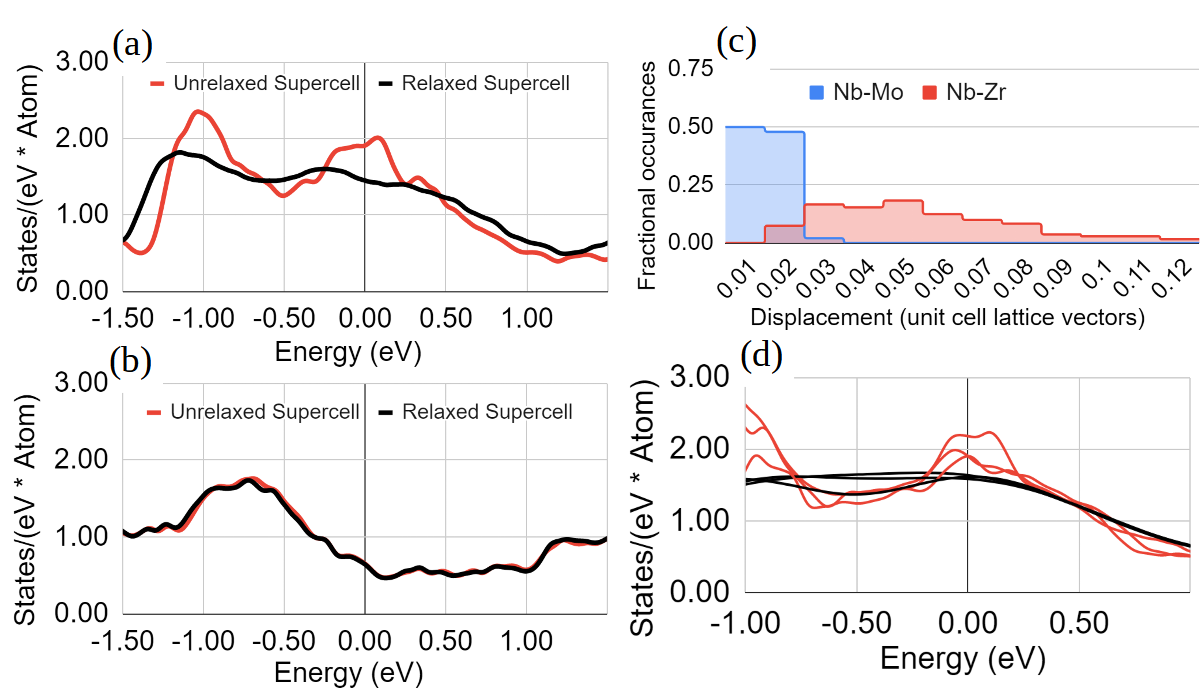
We estimate the maximum attainable of an ordered Nb-Zr alloy of a given composition as follows. We note that the same force which drives ionic displacements in the Nb-Zr random alloy tends to break the symmetries of ordered Nb-Zr structures . Indeed, this Jahn-Teller-Peierls effect has been proposed as a driving force for bcc phase instability in binary alloys, including Nb-Zr [39]. The magnitude of this driving force is directly related to the of the unrelaxed structure, which we can tune artificially by broadening the electronic states in our calculations. We then determine the limiting value of beyond which the Jahn-Teller-Peierls instability causes the structure to break its symmetry and relax to a lower-symmetry state with reduced . Fig. 3d, for example, shows the result of this process for three high symmetry structures at the same Zr concentration of , showing that they all exhibit very similar just before the onset of the instability. Finally, this stability-limited Fermi-level DOS can be used to determine the limiting as a function of composition through BCS theory. Figure 2 (‘Jahn-Teller-Peierls stability limit’ curve) displays the results of the above process. We generally expect that the values for Nb1-nZrn will all lie within the pink shaded region, between the random alloy result and the limiting Jahn-Teller-Peierls value for any special, ordered structure. For example, an Eliashberg calculation for a specific ordered structure at gives an electron-phonon coupling constant compared to a value of for Nb. To estimate the corresponding enhancement, we use the Allen-Dynes formula with and an additive shift in the parameter to account for spin-fluctuations and match the experimental of bulk Nb [34, 40]. This yields a of 15.7 K for the ordered alloy, close to our predicted stability limit of 17.7 K. This prediction represents an additional 50% enhancement over the random alloy , similar to what we indeed observe in our experiments (see below).
Experimental verification.
In order to validate our theoretical predictions, we measure the superconducting properties and RF performance of different Nb-Zr surface profiles. Samples were prepared using e-beam evaporation of a Zr target (base pressure: torr) on the Nb surface or electrochemical reaction with the Nb surface, followed by thermal annealing under torr vacuum, and a subsequent HF etch. The initial film thickness (20 – 40 nm) and post annealing conditions (600 – 1000 °C for 1/3 – 10 h) were varied to modify the surface Zr atomic concentration.
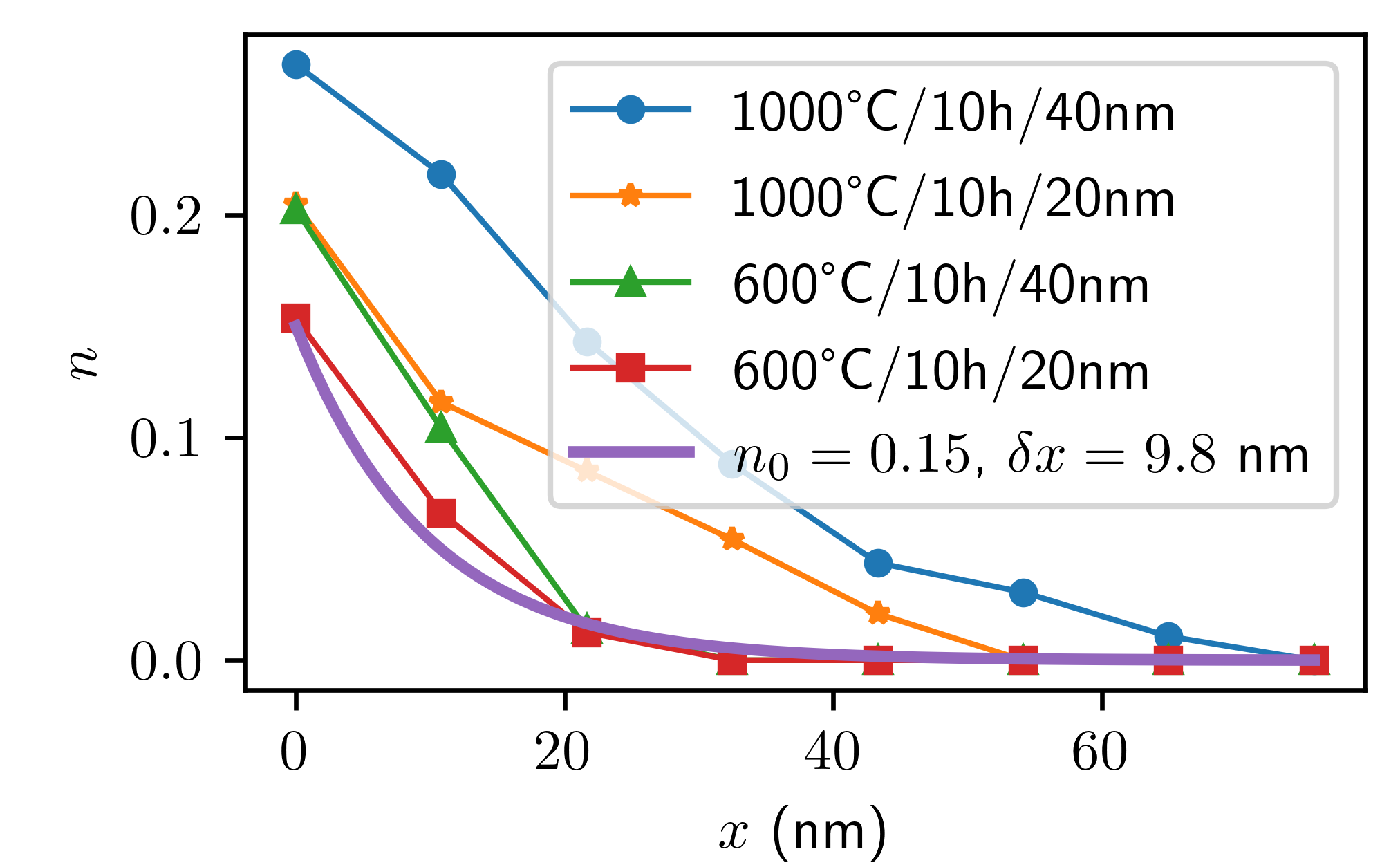
As probed by X-ray photoelectron spectroscopy, we observe 15–27 at.% Zr at the surface of evaporation-based samples (Fig. 4) as well as significant oxygen concentrations. From X-ray diffraction (Fig. 5a), we infer that substitutional Zr doping was achieved, as evidenced by the doping peaks at lower diffraction angles compared to a Nb cubic reference. Zr’s and Nb’s bcc lattice parameters are 0.354 nm and 0.330 nm, respectively [41]. Based on Vegard’s law, these doping peaks are induced by lattice enlargement when Zr dopants are incorporated into the cubic structure. Moreover, the HF etch entirely eliminates the hexagonal Zr phases that appeared on the outermost region after annealing. Note that the hexagonal and phases have low ’s of 7 K and 4 K, respectively [10, 42], so avoiding these hexagonal phases is critical to obtaining high . Additionally, the only oxide we detect is ZrO2, which is ideal for SRF applications due to its wide bandgap.
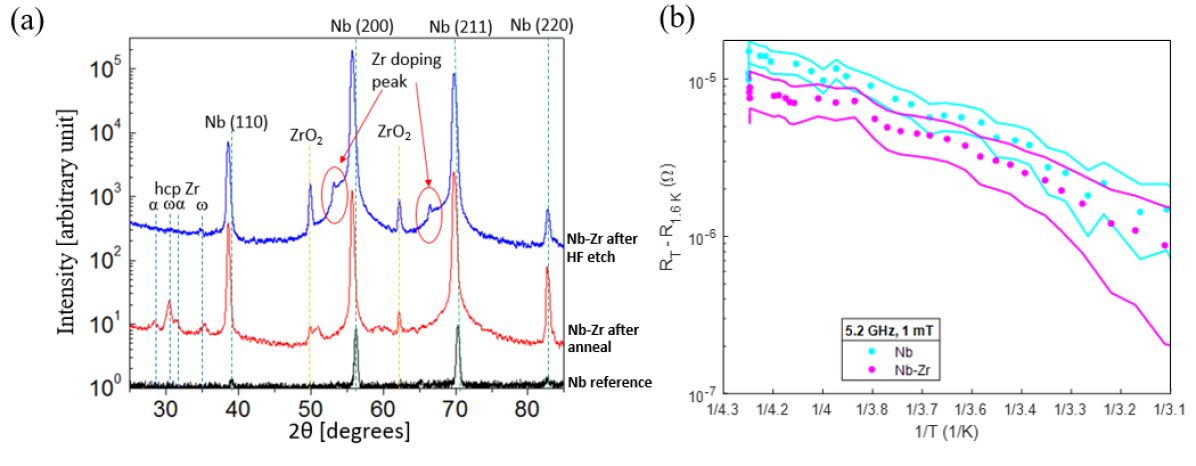
Resistance measurements using a Physical Property Measurement System under the AC transport mode demonstrate a of up to 13.5 K for evaporation-based samples that were annealed under 600 °C for 10 h. Even more impressively, the flux expulsion measurements indicate our electrochemically fabricated samples have a higher of 16 K. We point out that the 13.5 K and 16 K values are significantly higher than the literature-reported 11 K for Nb-Zr bulk alloys [10] and the 7.4 K measured in sputtered Nb-Zr thin films [43]. One can infer that retention of an ordered cubic structure is critical to achieving a higher than random alloys, which matches well with our DFT simulations.
To assess the use of Nb-Zr alloys for SRF accelerator applications, we employ an electrochemical method to scale up the alloying process to be compatible with the Cornell sample test cavity [44]. Indeed, as shown in Fig. 5b, after Nb-Zr alloying, the 5.2 GHz low-field BCS surface resistance is trending lower, which is consistent with the expected benefit of the high of the Nb-Zr material. This first RF demonstration of Nb-Zr alloys establishes a new direction for SRF cavities with high and low surface resistance. As we now show, these cavities also have the potential for high superheating fields.
GL predictions of .
To calculate , we employ GL theory to simulate Nb-Zr alloys in cavity surface layers using the data from Table 1. The main object of the theory is the free energy density of the system [45, 46, 47], which includes both an expansion in a superconducting order parameter (with phenomenological coefficients , , and ) and a contribution from the total magnetic field , where is the applied field and is the magnetic vector potential:
| (1) |
is the value of at which the superconducting Meissner state becomes unstable.
It can be shown that , , and are related to the London penetration depth , coherence length , and thermodynamic critical field :
| (2) |
We use Eq. (2) to calculate , , and for each of the compositions in Table 1. We observe a favorable increase in as Zr concentration increases.
We calculate the GL parameter for each of the compositions in Table 1 and note that addition of Zr raises . At , the type of instability which disrupts the superconducting state changes [14]. Destabilizing perturbations can be decomposed into Fourier modes with wave number . Below , the instability is due to the mode (i.e., uniform penetration of magnetic flux). Above , the instability results from a mode with . When calculating for Nb-Zr alloys, we are careful to search across perturbations with to look for this transition, so as not to overestimate .
We simulate inhomogeneous superconductors by treating the coefficients , , and as local quantities that vary spatially with material composition. For clean superconductors, these coefficients have been shown [46, 47] to depend on , , and the Fermi velocity :
| (3) |
We use these relationships to obtain , , and as follows. First, we consider a concentration profile in which Zr concentration falls off exponentially with depth in the material from a surface value on a scale set by :
| (4) |
(see Fig. 4). We then interpolate the values of , , and in Table 1 for intermediate concentrations to obtain , , and . Finally, we compose these with Eq. (3) to obtain , , and .
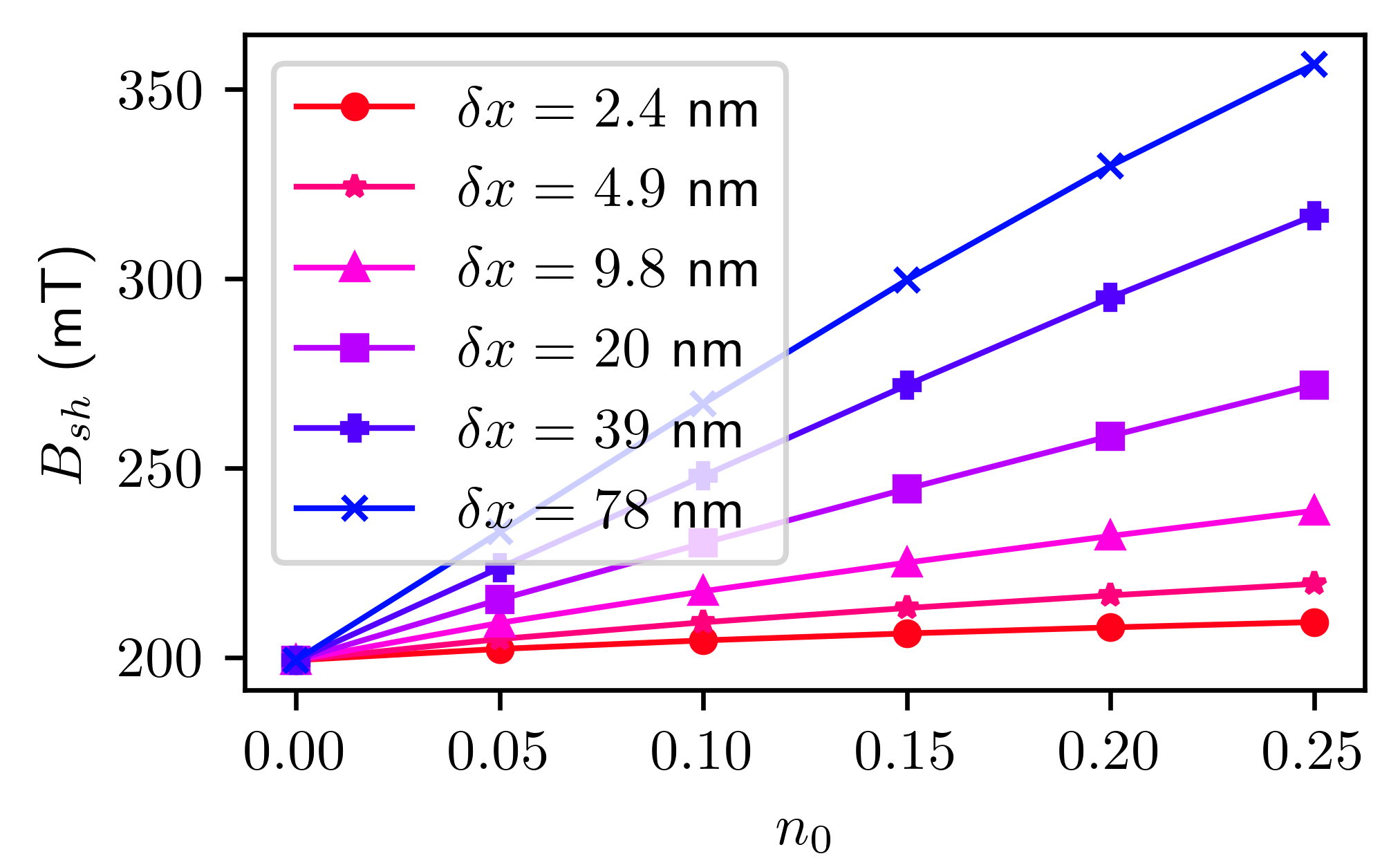
We calculate using the linear stability analysis described in [14] for various choices of and (Fig. 6). In all cases, increases as the total Zr content is increased, consistent with the improvements in other superconducting properties listed in Table 1.
Conclusion.
In summary, we have proposed and demonstrated a new type of SRF surface via Nb-Zr alloying that enables: (1) a high of 16 K that minimizes energy dissipation and cryogenic costs; (2) a promising predicted enhancement of up to 350 mT that allows approximately 85 MV/m accelerating gradients. We find an excellent match between theoretical and experimental results, which show improvement of after Zr is incorporated into the Nb lattice, and our RF results indicate a reduction of BCS resistance. Moreover, our theoretical predictions provide a viable road map to further tune and improve and . Overall, we have demonstrated that Nb-Zr alloys promise to be a new, feasible technology for accelerator physics.
Acknowledgements.
Acknowledgments.
A.H. and R.H. performed the VCA calculations. N.S.S. and T.A.A. performed the supercell alloy calculations and thank Michelle Kelley and Ravishankar Sundararaman for helpful conversations. Z.S., T.O., Z.B., D.A.M., and M.U.L. completed the experimental verification, including material growth, characterization, and RF performance evaluation. Z.S. acknowledges Dr. Darrah K. Dare and Katrina Howard for experimental assistance. B.L.F. and M.K.T. did the GL predictions of . All authors revised the manuscript. This work made use of the Cornell Center for Materials Research Shared Facilities which are supported through the NSF MRSEC program (DMR-1719875) and was performed in part at the Cornell NanoScale Facility, an NNCI member supported by NSF Grant NNCI-2025233. This work was supported by the U.S. National Science Foundation under Award PHY-1549132, the Center for Bright Beams.
References
- Decking et al. [2020] W. Decking et al., A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator, Nature Photonics 14, 391 (2020).
- Sicking and Strom [2020] E. Sicking and R. Strom, From precision physics to the energy frontier with the Compact Linear Collider, Nature Physics 16, 386 (2020).
- Padamsee et al. [1993] H. Padamsee, K. Shepard, and R. Sundelin, Physics and accelerator applications of rf superconductivity, Annual Review of Nuclear and Particle Science 43 (1993).
- Padamsee [2001] H. Padamsee, The science and technology of superconducting cavities for accelerators, Superconductor science and technology 14, R28 (2001).
- Posen et al. [2015a] S. Posen, M. Liepe, and D. Hall, Proof-of-principle demonstration of Nb3Sn superconducting radiofrequency cavities for high Q0 applications, Applied Physics Letters 106, 082601 (2015a).
- Posen and Hall [2017] S. Posen and D. L. Hall, Nb3Sn superconducting radiofrequency cavities: fabrication, results, properties, and prospects, Superconductor Science and Technology 30, 033004 (2017).
- Posen et al. [2021] S. Posen, J. Lee, D. N. Seidman, A. Romanenko, B. Tennis, O. Melnychuk, and D. Sergatskov, Advances in Nb3Sn superconducting radiofrequency cavities towards first practical accelerator applications, Superconductor Science and Technology 34, 025007 (2021).
- Burton et al. [2016] M. C. Burton, M. R. Beebe, K. Yang, R. A. Lukaszew, A.-M. Valente-Feliciano, and C. Reece, Superconducting NbTiN thin films for superconducting radio frequency accelerator cavity applications, Journal of Vacuum Science & Technology A 34, 021518 (2016).
- Smirnova and Starikov [2017] D. E. Smirnova and S. V. Starikov, An interatomic potential for simulation of Zr-Nb system, Computational Materials Science 129, 259 (2017).
- Corsan et al. [1968] J. M. Corsan, I. Williams, J. A. Catterall, and A. J. Cook, Superconductor transition temperatures of zirconium-niobium alloys, Journal of the Less-Common Metals 15, 437 (1968).
- Hulm and Blaugher [1961] J. K. Hulm and R. D. Blaugher, Superconducting solid solution alloys of the transition elements, Physical Review 123, 1569 (1961).
- Chapman [1995] S. J. Chapman, Superheating field of type II superconductors, SIAM Journal on Applied Mathematics 55, 1233 (1995).
- Dolgert et al. [1996] A. J. Dolgert, S. J. Di Bartolo, and A. T. Dorsey, Superheating fields of superconductors: Asymptotic analysis and numerical results, Physical Review B 53, 5650 (1996).
- Transtrum et al. [2011] M. K. Transtrum, G. Catelani, and J. P. Sethna, Superheating field of superconductors within Ginzburg-Landau theory, Physical Review B 83, 094505 (2011).
- Catelani and Sethna [2008] G. Catelani and J. P. Sethna, Temperature dependence of the superheating field for superconductors in the high- London limit, Physical Review B 78, 224509 (2008).
- Lin and Gurevich [2012] F. P.-J. Lin and A. Gurevich, Effect of impurities on the superheating field of type-II superconductors, Physical Review B 85, 054513 (2012).
- Liarte et al. [2016] D. B. Liarte, M. K. Transtrum, and J. P. Sethna, Ginzburg-landau theory of the superheating field anisotropy of layered superconductors, Physical Review B 94, 144504 (2016).
- Kubo et al. [2014] T. Kubo, Y. Iwashita, and T. Saeki, Radio-frequency electromagnetic field and vortex penetration in multilayered superconductors, Applied Physics Letters 104, 032603 (2014).
- Gurevich [2015] A. Gurevich, Maximum screening fields of superconducting multilayer structures, AIP Advances 5, 017112 (2015).
- Posen et al. [2015b] S. Posen, M. K. Transtrum, G. Catelani, M. U. Liepe, and J. P. Sethna, Shielding superconductors with thin films as applied to rf cavities for particle accelerators, Physical Review Applied 4, 044019 (2015b).
- Kubo [2016] T. Kubo, Multilayer coating for higher accelerating fields in superconducting radio-frequency cavities: a review of theoretical aspects, Superconductor Science and Technology 30, 023001 (2016).
- Ngampruetikorn and Sauls [2019] V. Ngampruetikorn and J. Sauls, Effect of inhomogeneous surface disorder on the superheating field of superconducting rf cavities, Physical Review Research 1, 012015 (2019).
- Pack et al. [2020] A. R. Pack, J. Carlson, S. Wadsworth, and M. K. Transtrum, Vortex nucleation in superconductors within time-dependent ginzburg-landau theory in two and three dimensions: role of surface defects and material inhomogeneities, Physical Review B 101, 144504 (2020).
- Giannozzi et al. [2009] P. Giannozzi et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, Journal of Physics: Condensed Matter 21, 395502 (2009).
- Giannozzi et al. [2020] P. Giannozzi et al., Quantum ESPRESSO toward the exascale, The Journal of Chemical Physics 152, 154105 (2020).
- Giannozzi et al. [2017] P. Giannozzi et al., Advanced capabilities for materials modelling with quantum ESPRESSO, Journal of Physics: Condensed Matter 29, 465901 (2017).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Physical Review Letter 77, 3865 (1996).
- Hamann [2013] D. R. Hamann, Optimized norm-conserving Vanderbilt pseudopotentials, Physical Review B 95, 239906 (2013).
- Schlipf and Gygi [2015] M. Schlipf and F. Gygi, Optimization algorithm for the generation of ONCV pseudopotentials, Computer Physics Communications 196, 36 (2015).
- Methfessel and Paxton [1989] M. Methfessel and A. T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Physical Review B 40, 3616 (1989).
- Kawamura et al. [2014] M. Kawamura, Y. Gohda, and S. Tsuneyuki, Improved tetrahedron method for the Brillouin-zone integration applicable to response functions, Physical Review B 89, 094515 (2014).
- Giustino et al. [2007] F. Giustino, M. L. Cohen, and S. G. Louie, Electron-phonon interaction using Wannier functions, Physical Review B 76 (2007).
- Poncé et al. [2016] S. Poncé, E. Margine, C. Verdi, and F. Giustino, EPW: Electron–phonon coupling, transport and superconducting properties using maximally localized Wannier functions, Computer Physics Communications 209, 116 (2016).
- Allen and Dynes [1975] P. B. Allen and R. C. Dynes, Transition temperature of strong-coupled superconductors reanalyzed, Physical Review B 12, 905 (1975).
- Xie et al. [2022] S. R. Xie, Y. Quan, A. C. Hire, B. Deng, J. M. DeStefano, I. Salinas, U. S. Shah, L. Fanfarillo, J. Lim, J. Kim, G. R. Stewart, J. J. Hamlin, P. J. Hirschfeld, and R. G. Hennig, Machine learning of superconducting critical temperature from eliashberg theory, npj Computational Materials 8 (2022).
- Bardeen et al. [1957] J. Bardeen, L. N. Cooper, and J. R. Schrieffer, Theory of superconductivity, Physical Review 108, 1175 (1957).
- Sundararaman et al. [2017] R. Sundararaman, K. Letchworth-Weaver, K. A. Schwarz, D. Gunceler, Y. Ozhabes, and T. A. Arias, JDFTx: Software for joint density-functional theory, SoftwareX 6, 278 (2017).
- Garrity et al. [2014] K. F. Garrity, J. W. Bennett, K. M. Rabe, and D. Vanderbilt, Pseudopotentials for high-throughput DFT calculations, Computational Materials Science 81, 446 (2014).
- Feng and Widom [2018] B. Feng and M. Widom, Band structure theory of the bcc to hcp Burgers distortion, Physical Review B 98, 174108 (2018).
- Bekaert et al. [2018] J. Bekaert, A. Aperis, B. Partoens, P. M. Oppeneer, and M. V. Milošević, Advanced first-principles theory of superconductivity including both lattice vibrations and spin fluctuations: The case of , Physical Review B 97, 014503 (2018).
- Thompson et al. [2003] G. B. Thompson, R. Banerjee, S. A. Dregia, and H. L. Fraser, Phase stability of bcc Zr in Nb/Zr thin film multilayers, Acta Materialia 51, 5285 (2003).
- Wang et al. [2011] B. T. Wang, P. Zhang, H. Y. Liu, W. D. Li, and P. Zhang, First-principles calculations of phase transition, low elastic modulus, and superconductivity for zirconium, Journal of Applied Physics 109, 063514 (2011).
- Cavalleri et al. [1989] A. Cavalleri, F. Giacomozzi, L. Guzman, and P. M. Ossi, Structure and superconductivity of Nb-Zr thin films, Journal of Physics: Condensed Matter 1, 6685 (1989).
- Oseroff et al. [2021] T. Oseroff, M. Liepe, and Z. Sun, Sample test systems for next-gen SRF surfaces, in Proceedings of 20th International Conference on RF Superconductivity (JACoW Publishing, East Lansing, MI, USA, 2021) p. 357.
- Tinkham [2004] M. Tinkham, Introduction to superconductivity (Courier Corporation, 2004).
- Kopnin [2001] N. Kopnin, Theory of nonequilibrium superconductivity, Vol. 110 (Oxford University Press, 2001).
- De Gennes and Pincus [2018] P.-G. De Gennes and P. A. Pincus, Superconductivity of metals and alloys (CRC Press, 2018).