^a^ainstitutetext: Department of Theoretical and Experimental Nuclear Physics,
Odessa National Polytechnic University, Odessa, Ukraine^b^binstitutetext: Department of Computer Technology and Applied Mathematics, Kuban State University,
Krasnodar, Russia

Theory of magnetic flux tubes in strong fields and the phenomenon of dark matter axions identical to solar axions

Vitaliy D. Rusov¹¹1Corresponding author: Vitaliy D. Rusov, [email protected] a Vladimir P. Smolyar b Margarita E. Beglaryan [email protected]

Abstract

We develop the general laws of the theory of the almost empty anchored magnetic flux tubes (MFT) with $B\sim 10^{7}~{}G$ , starting from tachocline to the surface of the Sun. The main result of this theory is the formation of the solar axions and the magnetic O-loop inside the MFT near the tachocline. In this magnetic O-loop (based on the Kolmogorov turbulent cascade) the axions are converted to photons, producing the axion origin photons near the bottom of the convective zone, i.e. near the tachocline. On the other hand, high-energy photons from the radiation zone through the axion-photon oscillations in the O-loop inside the MFT near the tachocline produce the so-called axions of photon origin under the sunspot. This means that at such strong magnetic fields the Parker-Biermann cooling effect of MFT develops due to the “disappearance” of the Parker’s convective heat transport, and consequently, the temperature in the lower part of the magnetic tube with the help of the axions of photonic origin from the photon-axion oscillations in the O-loop near the tachocline. As a result, a free path for photons of axion origin opens from the tachocline to the photosphere!

We show that the width of the ring between the magnetic wall of the flux tube and the magnetic O-loop near the tachocline, is the distance between the Parker-Biermann cooling effect, which forms the flux tube buoyancy, and the convective heating source $(dQ/dt)_{2}$ , which, despite the neutral buoyancy of the magnetic tube ring, repeats the upstream tube identically. In other words, the source of convective heating $(dQ/dt)_{2}$ appears on the surface of the Sun as a result of the initiation (due to the Parker-Biermann cooling effect) of adiabatic growth of an undulatory instability in toroidal flux tubes which initially were in mechanical equilibrium (neutral buoyancy) in the stable overshoot layer.

A very beautiful problem was solved this way. The high-energy photons passing from the radiation zone through the horizontal field of the O-loop near the tachocline turn into axions (see inverse oscillations $\gamma+\vec{B}\rightarrow\vec{B}+a$ ), which almost completely eliminates the radiation heating $(dQ/dt)_{1}$ of the almost empty magnetic flux tube. A certain flux of photons coming from the radiation zone through the tachocline, passes through the “ring” of a strong magnetic tube by virtue of convective heating $(dQ/dt)_{2}$ . It allows to determine both the velocity and the lifetime of the magnetic flux tube (with $B\sim 10^{7}~{}G$ ) before the reconnection, from tachocline to the surface of the Sun, as well as the rate of the magnetic flux tube reconnection (with $B\sim 10^{5}~{}G$ ) near the tachocline $V_{rec}$ . The latter is determined only by the rise time of the magnetic loop and the disappearance of the spot from the surface of the Sun.

Finally, we can show that the formation of sunspot cycles is equivalent to the number of cycles from the MFT, which coincides with the observational data of the Joy’s law, and that both effects are the manifestations of dark matter (DM) – solar axions in the core of the Sun, whose modulations are controlled by the anticorrelated 11-year modulation of asymmetric dark matter (ADM) density in the solar interior.

1 Introduction and motivation

It is known that the unsolved problem of energy transport by magnetic flux tubes at the same time represents another unsolved problem related to the sunspot darkness (see 2.2 in Rempel2011 ). Of all the known concepts playing a noticeable role in understanding the connection between the energy transport and sunspot darkness, let us consider the most significant theory, in our view. It is based on the Parker-Biermann cooling effect (Parker1955a, ; Biermann1941, ; Parker1979b, ) and originates from the early works of Biermann1941 and Alfven1942 .

As you know, the Parker-Biermann cooling effect (Parker1955a, ; Biermann1941, ; Parker1979b, ), which plays a role in our current understanding, originates from Biermann1941 and Alfven1942 : in a highly ionized plasma, the electrical conductivity can be so large that the magnetic fields are frozen into the plasma. Biermann realized that the magnetic field in the spots themselves can be the cause of their coolness – it is colder because the magnetic field suppresses the convective heat transport. Hence, the darkness of the spot is due to a decrease in surface brightness.

Parker (Parker1955a, ; Parker1974a, ; Parker1974b, ; Parker1974c, ; Parker1979b, ) has pointed out that the magnetic field can be compressed to the enormous intensity only by reducing the gas pressure within the flux tube relative to the pressure outside, so that the external pressure compresses the field. The only known mechanism for reducing the internal pressure sufficiently is a reduction of the internal temperature over several scale heights so that the gravitational field of the Sun pulls the gas down out of the tube (as described by the known barometric law $dp/dz=-\rho g$ ). Hence it appears that the intense magnetic field of the sunspot is a direct consequence of the observed reduced temperature (Parker1955a, ).

On the other hand, Parker (Parker1974c, ; Parker1977, ) has also pointed out that the magnetic inhibition of convective heat transport beneath the sunspot, with the associated heat accumulation below, raises the temperature in the lower part of the field. The barometric equilibrium leads to enhanced gas pressure upward along the magnetic field, causing the field to disperse rather than intensify. Consequently, Parker1974c argued that the temperature of the gas must be influenced by something more than the inhibition of heat transport!

Our unique alternative idea is that the explanation of sunspots is based not only on the suppression of convective heat transfer by a strong magnetic field (Biermann1941, ) through the enhanced cooling of the Parker-Biermann effect (Parker1974a, ), but also on the appearance of the axions of photonic origin (Fig 5, Fig. B.1 in RusovDarkUniverse2021 ) from the tachocline to the photosphere, which is confirmed by the “disappearance” of the heat, and consequently, the temperature in the lower part of the magnetic tube (Parker1974c, ; Parker1977, ) due to the axions of photonic origin from the photon-axion oscillations in the O-loop near the tachocline (see Fig. 5).

This means that the appearance of axions of photonic origin, which “remove” the problem of the temperature rise in the lower part of the magnetic tube, and the photons of axionic origin, which have the free path (Rosseland length; see Fig. B.3 in RusovDarkUniverse2021 ) from the tachocline to the photosphere, are the explanation of sunspots based not only on the suppression of convective heat transport by a strong magnetic field (Biermann1941, ), but also on the indispensable existence of the Parker-Biermann cooling effect.

On the other hand, we understand that the existence of the Parker-Biermann cooling effect is associated with the so-called thermomagnetic Ettingshausen-Nernst effect (see Apendix A in RusovDarkUniverse2021 ).

Due to the large temperature gradient in the tachocline, the thermomagnetic EN effect (Ettingshausen1886, ; Sondheimer1948, ; Spitzer1956, ; Kim1969, ) creates electric currents that are inversely proportional to the strong magnetic field of the tachocline. As we showed earlier (RusovDarkUniverse2021, ), the toroidal magnetic field of tachocline by means of the thermomagnetic Ettingshausen-Nernst effect (Appendix A) “neutralizes” the magnetic field of the solar core $\sim 5\cdot 10^{7}~{}G$ (Fowler1955, ; Couvidat2003, ). It means that, using the thermomagnetic EN effect, a simple estimate of the magnetic pressure of an ideal gas in the tachocline of e.g. the Sun,

\frac{B_{tacho}^{2}}{8\pi}=p_{ext}\approx 6.5\cdot 10^{13}\frac{erg}{cm^{3}}~{}~{}at~{}~{}0.7R_{Sun},

(1)

can indirectly prove that by using the holographic principle of quantum gravity (see Apendix C in RusovDarkUniverse2021 ), the repelling toroidal magnetic field of the tachocline exactly “neutralizes” the magnetic field in the Sun’s core (see Fig. A1 in RusovDarkUniverse2021 )

B_{tacho}^{Sun}=4.1\cdot 10^{7}~{}G=-B_{core}^{Sun},

(2)

where the projections of the magnetic fields of the tachocline and the core have equal values but opposite directions.

Such strong magnetic fields in a tachocline of e.g. the Earth, Sun, magnetic white dwarfs, accreting neutron stars and BHs can predict the exact “neutralization” of the magnetic field in the core of these stars and in a black hole (see Appendix C in RusovDarkUniverse2021 ).

Let us note another important Babcock-Leighton (BL) mechanism. On the one hand, we mark out the holographic BL mechanism (see Fig. C.1b in RusovDarkUniverse2021 ), which we often refer to as the holographic antidynamo mechanism, caused by a remarkable example of the Cowling antidynamo theorem. This theorem states that no axisymmetric magnetic field can be maintained through the self-sustaining action of the dynamo by means of an axially symmetric current (Cowling1933, ). On the other hand, the holographic BL mechanism (as a component of our solar anti-dynamo model) follows our example of a thermomagnetic EN effect, or the so-called solar holographic antidynamo, in which the poloidal field originates directly from the toroidal field, but not vice versa (see Fig. C.1a in RusovDarkUniverse2021 ).

Refer to caption — Figure 1: An illustration of the main possible processes of a magnetically active star of the Sun type. (a) $\alpha$ -effect, $\Omega$ -effect and BL mechanism as components of the solar dynamo model. The $\Omega$ -effect (blue) depicts the transformation of the primary poloidal field into a toroidal field by differential rotation. Regeneration of the poloidal field is then performed either by the $\alpha$ -effect (top) or by the BL mechanism (yellow in the middle). In case of $\alpha$ -effect, the toroidal field at the base of the convection zone is subject to cyclonic turbulence. In the BL mechanism, the main process of regeneration of the poloidal field (based on the $\Omega$ -effect (blue)) is the formation of sunspots on the surface of the Sun from the rise of floating toroidal flux tubes from the base of the convection zone. The magnetic fields of these sunspots closest to the equator in each hemisphere diffuse and join, and the field due to the spots closer to the poles has a polarity opposite to the current that initiates rotation of the polarity. The newly formed polar magnetic flux is transported by the meridional flow to deeper layers of the convection zone, thereby creating a new large-scale poloidal field. Derived from Sanchez2014 . (b) BL mechanism and holographic BL mechanism as components of our solar antidynamo model. Unlike the component of the solar dynamo model (a), the BL mechanism, which is predetermined by the fundamental holographic principle of quantum gravity, and consequently, the formation of the thermomagnetic EN effect (see Spitzer1962 ; Spitzer2006 ; Rusov2015 ), emphasizes that this process is associated with the continuous transformation of toroidal magnetic energy into poloidal magnetic energy ( $T\rightarrow P$ transformation), but not vice versa ( $P\rightarrow T$ ). This means that the holographic BL mechanism is the main process of regeneration of the primary toroidal field in the tachocline, and thus, the formation of floating toroidal magnetic flux tubes at the base of the convective zone, which then rise to the surface of the Sun. The joint connection between the poloidal and toroidal magnetic fields is the result of the formation of the so-called meridional magnetic field, which goes to the pole in the near-surface layer, and to the equator at the base of the convection zone.

Using the Babcock-Leighton mechanism (see Fig. 1), and consequently, the MFT in strong fields, we are interested in the existence of dark matter axions identical to solar axions, which strongly affects the magnetic O-loops inside the MFT near the tachocline, and is thus connected to the so-called thermomagnetic Ettingshausen-Nernst effect through the Parker-Biermann cooling effect (see Apendix A in RusovDarkUniverse2021 ).

Since the photons of axion origin cause the Sun luminosity variations, then unlike in the case of the self-excited dynamo, an unexpected yet simple question arises: is there a dark matter chronometer hidden deep in the Sun core?

In order to answer this question, let us first consider all the unexpected and intriguing implications of the 11-year modulations of the ADM density in the solar interior and around the BH (see Sect. 3 in RusovDarkUniverse2021 ).

A unique result of our model is the fact (see Sect. 3 in RusovDarkUniverse2021 ), that the periods, velocities and modulations of the S-stars are the essential indicator of the modulation of the ADM halo density in the fundamental plane of the Galaxy center, which closely correlates with the density modulation of the baryon matter near the SMBH. If the modulations of the ADM halo at the GC lead to modulations of the ADM density on the surface of the Sun (through vertical density waves from the disk to the solar neighborhood), then there is an ”experimental” anticorrelation identity between such indicators as the ADM density modulation in the solar interior and the number of sunspots. Or equivalently, between the modulation of solar axions (or photons of axion origin) and the sunspot cycles!

A hypothetical pseudoscalar particle called axion is predicted by the theory related to solving the CP-invariance violation problem in QCD. The most important parameter determining the axion properties is the energy scale $f_{a}$ of the so-called U(1) Peccei-Quinn symmetry violation. It determines both the axion mass and the strength of its coupling to fermions and gauge bosons including photons. However, in spite of the numerous direct experiments, axions have not been discovered so far. Meanwhile, these experiments together with the astrophysical and cosmological limitations leave a rather narrow band for the permissible parameters of invisible axion (e.g. $10^{-6}eV\leqslant m_{a}\leqslant 10^{-2}eV$ (ref01, ; ref02, )). The PQ mechanism, solving the strong CP problem in a very elegant way (PecceiQuinn1977, ; PecceiQuinn1977PRD, ), is especially attractive here, since the axion is also a candidate for dark matter (Preskill1983, ; Abbott1983, ; Dine1983, ; Kawasaki2013, ; Marsh2016, ; DiLuzio2020, ; Sikivie2021, ).

The following question is very important for us: Where do relict hot dark matter axions²²2 See e.g. the works Turner1987 ; Archidiacono2015 ; CAST2017 ; DiLuzio2021 . in cosmology come from?

In this regard, we will consider the remarkable model by Shafieloo, Hazra, Sahni and Starobinsky Shafieloo2017 , who proposed a new description of the cosmological constant $\Lambda$ that determines the density of dark energy (DE). A model in which (surprisingly enough!) metastable dark energy decays radioactively into dark matter, leads to lower values of the Hubble parameter at high redshifts compared to cold dark matter (CDM) in a form of the final stage of the inflation. The analogue of the model by Shafieloo, Hazra, Sahni and Starobinsky Shafieloo2017 :

\Omega_{DE}\rightarrow\Omega_{DM}=\Omega_{CDM}+\Omega_{baryon}.

(3)

Although this model provides a better fit to cosmological data of baryon acoustic oscillation (BAO) (especially data from high-redshift quasars) than concordance ( $\Lambda$ CDM) cosmology, we are also interested in real physics of dark matter.

We know that, according to the excellent work Turner1987 , the Peccei-Quinn symmetry breaking scale is calculated to be $\sim 2\cdot 10^{8}~{}GeV$ (corresponding to the axion mass of $\sim 3.2\cdot 10^{-2}~{}eV$ (see Fig. 2, and also Fig. 1 in RusovDarkUniverse2021 )), at which the thermal production of hot dark matter axions in the early Universe (through Primakoff processes ( $q+\gamma\rightarrow q+a$ ; the particle in the loop is the heavy $Q$ quark) and photoproduction on heavy quarks (see Fig. 1 in Turner1987 )) dominates over coherent production of dark matter axions as approximately $\Omega_{thermal}/\Omega_{coherent}\sim 1200\times[m_{a}/1eV]^{2.175}$ , where $\Omega_{coherent}$ was calculated in Turner1986 ; Preskill1983 ; Abbott1983 ; Dine1983 ; Kawasaki2013 ; Marsh2016 ; DiLuzio2020 ; Sikivie2021 . The photon luminosity from the decays of these relict axions leads to an upper limit of the axion mass of the order of $\sim 1~{}eV$ (see left panel in Fig. 3). If the mass of the axion saturates this bound, then it is quite possible to detect the relict axion decay.

But the most remarkable fact is that the thermal production of axions by hot dark matter in the early Universe, where inflation occurs before PQ-symmetry breaking, happens through the increasing rate of axion production and leads to a large number of axions with masses greatly exceeding $3.2\cdot 10^{-2}~{}eV$ , i.e. about $1~{}eV$ . Therefore, the thermally produced axions (with $\Omega_{HDM-axion}\sim 0.31$ , see left panel in Fig. 3) dominate the population of relic axions, and during the inflation, due to the energy of the axion field, the hot dark matter axions are converted to other fields and generate particles. The latter manifest themselves as the excess of baryons ( $\Omega_{baryon}\sim 0.049$ ) over antibaryons (see e.g. Domcke2020 ), and also in the form of asymmetric CDM Higgs³³3In contrast to the (incomplete) Standard Model, the Higgs-boson here is supposed to have integer weak isospin, which is consistent with the experimental data on its decay channels (PDG2020, ). It is considered as a bound state of $W^{+}$ and $W^{-}$ bosons – the particles with weak isospin of 1. Since the weak isospin of gauge bosons is equal to unity, the bound state can have a weak isospin of 2, 1 or 0. The state with zero isospin obviously cannot take part in weak interactions. It has zero electric charge and does not consist of strongly inteacting particles. Therefore, such a state can interact only gravitationally. On the other hand, it has all the theoretical properties of the Higgs boson. For example, in the model of multiparticle fields, the spontaneous symmetry breaking is NOT postulated as in the Standard Model (see Merkotan2017 ; Merkotan2018 ; Ptashynskiy2019 ), but is obtained as a result of the dynamic equations of the model, as a result of which it has a nonzero vacuum value. Due to these properties, it can be considered as a candidate for dark matter (Merkotan2017, ; Merkotan2018, ; Ptashynskiy2019, ). (see right panel in Fig. 3) and the formation of some remnant thermalized axions with mass $3.2\cdot 10^{-2}~{}eV$ involved in the CDM Higgs halo. We also know RusovDarkUniverse2021 that the asymmetry of the CDM Higgs boson Merkotan2017 ; Merkotan2018 ; Ptashynskiy2019 with a mass of $\sim$ 5 GeV (see Fig. 6 in Vincent2016 ) and a high density $\Omega_{CDM-Higgs}\sim 0.26$ forms in the final stage of inflationary Universe and exists till nowadays.

The main result is that the axions of hot dark matter (HDM axion; see the left panel in Fig. 3) predetermine the formation of baryon asymmetry and asymmetry of the cold dark matter Higgs boson (CDM-Higgs; see Merkotan2017 ; Merkotan2018 ; Ptashynskiy2019 ), as well as the formation of some remnants of hot dark matter axions (HDM axion) participating in the CDM Higgs halo (see analog of RusovDarkUniverse2021 ). This leads to the following description of the generalized model (which is directly related to the Starobinsky model (see $\Omega_{DE}$ in Shafieloo2017 ), the Turner model (see $\Omega_{HDM-axion}$ in Turner1987 ) and the Sharph & Rusov model (see $\Omega_{CDM-Higgs}$ in Merkotan2017 ; Merkotan2018 ; Ptashynskiy2019 ) in the form

	$\displaystyle\Omega_{DE}\rightarrow\Omega_{DM}\equiv\Omega_{HDM-axion}$	$\displaystyle=\Omega_{CDM-Higgs}+\Omega_{baryon}+\Omega_{(solar)axion}$
		$\displaystyle\cong\Omega_{CDM-Higgs}+\Omega_{baryon}$		(4)

where

$\Omega_{HDM-axion}\equiv\Omega_{HDM-axion}^{thermal}(m_{a}\sim 1eV)+{}$
${}+\Omega_{HDM-axion}^{thermal}(m_{a}\sim 3.2\cdot 10^{-2}eV)+\Omega_{HDM-axion}^{coherent}(m_{a}\sim 3.2\cdot 10^{-2}eV)=$
$=\Omega_{HDM-axion}^{thermal}(m_{a}\sim 1eV)+\Omega_{(solar)axion}(m_{a}\sim 3.2\cdot 10^{-2}eV)\cong$
$\cong\Omega_{HDM-axion}^{thermal}(m_{a}\sim 1eV)=0.31$

(see left panel in Fig. 3) when $\Omega_{CDM-Higgs}>\Omega_{baryon}\gg\Omega_{(solar)axion}$ (see Eq. 8).

The latter, surprisingly enough, are the “experimental” key to the existence of the asymmetry of CDM Higgs boson and the “remnants” of cold dark matter axions (see Eqs. (4) and (8)) – this is a direct proof of the solution to the problem of solar corona heating, which is associated with the hot dark matter axions on the Sun ( $\Omega_{(solar)axion}$ in (4)) and the asymmetry of the CDM Higgs boson halo in solar neighborhood⁴⁴4In this case, neutrinos and helioseismic information thus complement each other, especially when the presence of particles such as axions at the maximum luminosity of the Sun, and particles such as the Higgs ADM at the minimum luminosity of the Sun, affects the transfer of heat within the interior of the Sun. Therefore, the maximum and minimum of neutrino fluxes can simultaneously solve a very complex “problem of solar composition”, or otherwise called “the problem of solar abundance”, which is associated with the solar cycle. Most important here is that the neutrino flux from the subdominant CNO cycle is linearly dependent on the metallicity ( $Z$ ) of the solar core (see e.g. Gann2015 ; Borexino2020a ; Borexino2020b ; TapiaArellano2021 ). It means that the modulation of solar abundance, with high metallicity at the solar maximum ( $Z\sim 0.0170$ with $Z/X=0.023$ (Grevesse1998, )) and low metallicity at the solar minimum ( $Z\sim 0.0133$ with $Z/X=0.0178$ (Asplund2009, )), is in good agreement with the deviation of the radial sound speed profile $\delta c_{s}/c_{s}=(c_{s,obs}-c_{s,th})/c_{s,obs}$ inside the Sun (Fig. 4), which consists of two related models: for the maximum luminosity of axions (Fig. 4a) and for the minimum luminosity of axions, which is associated with the maximum luminosity of Higgs ADM (Fig. 4b). and which is anti-correlated (through vertical density waves from the disk to the Sun) with 11-year S-stars around the black hole (see Fig. 4 and Eqs. (27)-(28) in RusovDarkUniverse2021 ). Second, let us remind that the most fundamental problem of the Standard Model is the appearance of the scalar component of the two-particle gauge field in a form of the Higgs boson, scalar in interior indices, which is considered a component of dark matter (see Fig. 4)!

So what is so special about this Higgs dark matter particle? We know that the existence of dark matter in the Universe is a striking evidence that physics goes beyond the Standard Model, although its nature remains a mystery. At the same time, the closeness of the energy densities of DM and baryons $\Omega_{DM}\approx 5.3\Omega_{baryon}$ (PlanckCol2015, ; Patrignani2016, ) motivates the idea of asymmetric dark matter (ADM) (Nussinov1985, ; Chivukula1990, ; Barr1990, ; Kaplan1992, ; Hooper2005, ; Kaplan2009, ; Davoudiasl2012, ; Petraki2013, ; Zurek2014, ), based on the assumption that the current DM density is determined by the $\eta_{DM}$ asymmetry in the DM sector, similar to the baryon asymmetry $\eta_{baryon}$ . Then

\frac{\Omega_{DM}}{\Omega_{baryon}}=\frac{m_{DM}}{m_{N}}\frac{\eta_{DM}}{\eta_{baryon}}

(5)

where $m_{DM}$ is the DM mass and $m_{N}$ is the nucleon mass. If two asymmetries are generated by the same mechanism, or one dark asymmetry is responsible for the other – baryon asymmetry arising from leptogenesis, we expect $\eta_{DM}\sim\eta_{B}$ . Hence it follows that taking the value $m_{DM}=m_{ADM}\sim 5~{}GeV$ and $m_{N}\approx 0.939~{}GeV$ , one can obtain the value

\frac{\Omega_{DM}}{\Omega_{baryon}}=\frac{m_{DM}}{m_{N}}\frac{\eta_{DM}}{\eta_{baryon}}\approx\frac{m_{ADM}}{m_{N}}\approx 5.32,

(6)

which suggests that, according to Turner1987 , $\Omega_{HDM-axion}\sim 0.31$ (see Fig. 3 and Eq. (4)) coincides with the high density (thermal!) hot dark matter axions (see Fig. 3) during the Universe inflation (see right panel in Fig. 3).

Applying the equality $\Omega_{DM}=\Omega_{ADM}$ , we use, according to Eq. (4), the identity between $\Omega_{ADM}$ and $\Omega_{CDM-Higgs}$ , which allows one to obtain the following equation

	$\displaystyle\frac{\Omega_{HDM-axion}^{inflation}}{\Omega_{CDM-Higgs}}=\frac{\Omega_{CDM-Higgs}+\Omega_{baryon}+\Omega_{(solar)axion}}{\Omega_{CDM-Higgs}}\cong$
	$\displaystyle\frac{\Omega_{CDM-Higgs}+\Omega_{CDM-Higgs}/5.32}{\Omega_{CDM-Higgs}}=1.2,$		(7)

where the new physics manifests not only Eq. (7) (see right panel in Fig. 3), but also a description of the low density of hot dark matter axions (see Eq. (17) in Graham2015 ) in the final stage of the Universe inflation and till nowadays.

\Omega_{(solar)axion}\approx 2\left(\frac{6~{}\mu eV}{m_{a}}\right)^{7/6}\approx 10^{-4},

(8)

which, on the basis of “experimental” data, identically coincides with the values of the hadronic axion-photon coupling $g_{a\gamma}\sim 4.4\cdot 10^{-11}~{}GeV^{-1}$ and the mass $m_{a}\sim 3.2\cdot 10^{-2}~{}eV$ on the Sun (see Fig. 2 and Fig. 1 in RusovDarkUniverse2021 ). This means that the axions of hot dark matter on the Sun and the axions of hot dark matter in our galactic Higgs ADM halo (see Eq. (8)) are absolutely identical!

This is due to the fact that the PQ symmetry is significantly broken in the early Universe, and is caused by the production of dark matter axions. The most surprising is the fact that the thermal production of the axion of hot dark matter in early Universe (see left panel in Fig. 3) is an inflationary source of the formation of asymmetry of baryons, in which, during post-inflation, the “collisions and interactions between gas-rich galaxies are considered key stages in their formation and evolution, causing the rapid formation of new stars” Goulding2018 , and, as a consequence, emitting streams (!) of hot dark matter axions (see e.g. supernovae Hsueh2019 , Galactic Globular Clusters Gilman2019 , and the Sun RusovDarkUniverse2021 ).

But the most remarkable fact is that our data on the axions dark matter in the form of the estimates of the hadronic axion-photon coupling $g_{a\gamma}$ , the mass $m_{a}$ and the ADM Higgs mass, experimentally coincide, according to RusovDarkUniverse2021 , with the solution for the ADM Higgs chronometer in the S-stars interior, which controls the solar cycles of the dark matter axions luminosity, and consequently, is the remarkable solution for the problem of solar corona heating using photons of axion origin and ADM Higgs – a complete proof of the existence of the ADM Higgs RusovDarkUniverse2021 .

And, finally, the fundamental results in both directions make it possible to obtain (through indirect detection) the convincing evidence of the existence and nature of the asymmetry of cold dark matter Higgs halo near a black hole and, as a result, in the solar neighborhood. They also demonstrate a remarkable identity of solar axions and axions of hot dark matter in the Universe (see $m_{a}\sim 3.2\cdot 10^{-2}~{}eV$ of the thermal and cogerent axions in the left panel of Fig. 3). At the same time, it must be remembered that initially an axion with a mass of 1 eV, which is a low-energy remnant of the Peccei-Quinn solution to the strong CP problem PecceiQuinn1977 ; PecceiQuinn1977PRD ; Wilczek1978 ; Weinberg1978 , makes the main contribution to the energy density of the Universe (see $\Omega_{HDM-axion}\sim 0.31$ in Fig. 3 and Eq. (4)). Although it is not accessible for direct cosmological searches for hot dark matter axions, it is accessible for direct astrophysical experiments for axions of hot dark matter with a mass of $m_{a}\sim 3.2\cdot 10^{-2}~{}eV$ , identical to solar axions!

Taking into account the above remarks, we arranged our paper in the following way. In Section 2 we discuss the effect of virtually empty magnetic tubes and dark matter axions in the Sun’s core. In Section 2.1 we present the convective heating and buoyancy of magnetic tubes – the phenomenon of solar axions of dark matter. In Section 2.2 we discuss the physics of magnetic reconnection of the magnetic tubes in the lower layers and the observed features of the tilt angle of Joy’s law. Finally, in Section 3 we provide a summary and perspective of this work.

2 Effect of virtually empty magnetic flux tubes and solar axion in the Sun interior

The appearance of sunspots on the solar surface is one of the major manifestations of solar activity demonstrating the cyclic behavior with the period of about 11 years (see e.g. Hathaway2015 ). A very high density of the magnetic field is observed within the sunspots, which suppresses the convective heat flow from the solar interior to the surface (Biermann1941, ; Alfven1942, ; Cowling1953, ; Parker1955a, ). That is why the sunspots are cooler and darker against the background of the solar disk. More than a hundred years ago (Hale1908, ) discovered the vertical “vortices” of the magnetic field in the sunspots. About a year later British astronomer (Evershed1909, ) was conducting the observations in Kodaikanal (Tamil Nadu, India) and found that in spite of the Hale’s vertical “vortices”, the magnetic field in the penumbra is radially divergent from the center of a sunspot. The mechanism of the sunspot formation including the umbra and penumbra as well as the Evershed effect are still the subject of active discussions and studies today, and lots of fundamental questions remain unanswered (Solanki2003, ; Borrero2011, ; Tiwari2015, ; Pozuelo2015, ). We consider some possible solutions to these problems below.

We are mostly interested in effects for which the current theories, assuming that the sunspots are produced by the dynamo action at the bottom of the convection zone, fail to provide the convincing proofs and explain the dynamo action in the convection zone. This problem becomes even stronger with the recent findings. The numerical simulations of the solar dynamo have not revealed thin MFTs of the comparable strength so far (see e.g. Guerrero2011 ; Nelson2013 ; Kapyla2013 ). The helioseismology does not give any evidence of the upward MFTs existence either (Birch2013, ; Birch2016, ). This is especially important because of the recent helioseismological investigations which set the strict limitations on the velocities of large-scale convection inside the Sun and demonstrated the inconsistency with the existing global magnetoconvection e.g. ref34-3 modeling (Hanasoge2010, ; Hanasoge2012, ; Hanasoge2015, ; Gizon2012, ; Birch2013, ; Birch2016, ).

Thus, our major question is: “How are the sunspots generated by the strong magnetic field at the base of the convection zone without any dynamo action?”, or otherwise “Which fundamental processes connect the sunspot cycle with the large-scale magnetic field of the Sun?”. Or even more precisely, “What are the fundamental processes, associated with solar axions, connect the sunspot cycle to the large-scale magnetic field of the Sun?”

Of all the known concepts playing a noticeable role in understanding of the link between the energy transfer and the darkness of sunspots, let us consider the most significant one, in our opinion. It is based on the Parker-Biermann cooling effect (Parker1955a, ; Biermann1941, ; Parker1979b, ) in strong fields, which explains how the suppression of the Parker’s convective heat transport in the lower part of the magnetic tube manifests itself.

In order to understand the physics of the Parker’s suppression of the convective heat transport in strong magnetic fields, we need to tun to the dark matter axions, born in the core of the Sun. With solar axions and the existence of a magnetic O-loop inside the MFT near the tachocline, the answer becomes very simple. When a magnetic O-loop is formed inside the MFT near the tachocline through the Kolmogorov turbulent cascade (see Fig. 2), the high-energy photons from the radiation zone experience the axion-photon oscillations in this O-loop, and the so-called axions of photonic origin appear under the sunspot. This means that the cooling effect of Parker-Birmann exists due to the disappearance of barometric equilibrium (Parker1974a, ) and, as a consequence, the manifestation of the photon free path (Rosseland length; see Fig. B.3 in RusovDarkUniverse2021 ) from the tachocline to the photosphere, which is confirmed by axions of photonic origin after photon-axion oscillations in the O-loop (see Fig. 5).

On the other hand, a certain stream of high-energy photons coming from the radiation zone through the tachocline and through the “ring” (between the magnetic wall of the flux tube and the O-loop) (see Figs. 5 and 6) allows to use the barometric equilibrium (Parker1974a, ), i.e. no Parker-Birmann cooling effect, to determine the convective heating $(dQ/dt)_{2}$ (see Sect. 2.1).

This solution explicitly depends on the lifetime of the magnetic tubes rising from the tachocline to the solar surface. Therefore, because of the magnetic reconnection in the lower layers (see Fig. 4 in Parker1994 ), it is not the final stage of the simulation. The essence of a virtually empty tube which is first born without a dynamo of any kind (Fig. 7a), is related to the physics of the turbulent reconnection of magnetic bipolar structures (see Fig. 7b,c and Eq. (8) in Jabbari2016 ). It is therefore connected to a very rare model of fluctuation dynamo caused by a multiscale turbulence model (see Baggaley2009 ), but necessarily through the so-called turbulent reconnection (Loureiro2009, ; Huang2010, ; Beresnyak2017, ). In this case the turbulent pumping of the plasma from the azimuthal field is repeated in the $\Omega$ -loop again and again (Fig. 7).

As described by Spruit1987 ; Wilson1990 ; Parker1994 ; Parker2009 , the upward convection flow around the rising $\Omega$ -loop brings its “legs” together in such a way that the magnetic field reconnection occurs across this loop. This cuts off the loop from the azimuthal magnetic field, turning it into an O-loop (see Fig. 3 in Spruit1987 and Fig. 4 in Parker1994 ). After that the azimuthal magnetic field restores its initial configuration and becomes ready for another process with $\Omega$ -loop.

Let us now make some important remarks on the turbulent reconnection, the $\Omega$ -loop transformation into the O-loop by rapid “legs” closure, the restoration of the initial azimuthal field and the preconditions for another $\Omega$ -loop formation in the same place. It is also necessary to explain the physical interpretation of the overshoot process near the tachocline and estimate the velocity $v_{rise}$ and time $\tau_{rise}$ of the magnetic tube rise from the overshoot boundary layer – starting with the azimuthal magnetic flux strength of $B_{tacho}\sim 4\cdot 10^{7}~{}G$ (see Eq. A.17 in RusovDarkUniverse2021 ).

One ultimate goal of this section is to determine the general regularities in the theory of MFTs, which are generated by the magnetic buoyancy of virtually empty tubes rising from the tachocline to the surface of the Sun (Fig. 5). Another one is the physical interpretation of the process of MFTs reconnection in the lower layers of the convection zone (Fig. 7). Not only this is related to the magnetic cycles of flux tubes coinciding with the observed Joy’s law for the tilt angle, but both effects (surprisingly enough) are induced by the existence of DM – the solar axions generated in the core of the Sun.

2.1 Convective heating and the buoyant rise of magnetic flux tubes: the phenomenon of solar dark matter axions

The first problem is devoted to the study of the effect of virtually empty magnetic tubes and the phenomenon of solar dark matter axions.

The assumption that the virtually empty magnetic tubes (Fig. 5) are neutrally buoyant ( $\rho_{int}=\rho_{ext}$ (Spruit1982, )) implies that the temperature inside these tubes is lower than that of the ambient medium (Fig. 5 and Fig. 7a). This leads to the heat inflow, and consequently, the flux tube rises up (see Parker1975 or Sect. 8.8 in Parker1979a ). For a horizontal tube with a cross-section of radius $a$ the rise velocity follows from the Parker’s analysis (see Parker1975 , Eq. (60) in Ballegooijen1982 ):

v_{rise}=2\frac{H_{p}}{\tau_{d}}\frac{B^{2}}{8\pi p_{ext}}\left(-\delta+0.12\frac{B^{2}}{8\pi p_{ext}}\right)^{-1},

(9)

where $H_{p}=\Re T_{ext}/g=p_{ext}/g\rho_{ext}=0.08R_{Sun}$ (BohmVitense1958, ; Spruit1977, ; Brun2011, ) is the pressure scale height at the tachocline, $T_{ext}$ and $p_{ext}$ are the external gas temperature and pressure, $\delta\equiv Y=\nabla_{e}-\nabla_{ad}=-c_{p}^{-1}dS/d\xi=-c_{p}^{-1}H_{p}dS/dz$ is the dimensionless entropy gradient (see Ballegooijen1982 ; Smolec2008 ; Smolec2010 ), $\nabla_{e}\equiv d\ln T_{ext}/d\ln p_{ext}$ and $\nabla_{ad}\equiv(\partial\ln T/\partial\ln p)_{s}$ are the local and adiabatic temperature gradients in external and internal plasma (Spruit1974, ; Ballegooijen1982, ; Christensen1995, ), $s$ is the specific entropy, $c_{p}$ is the heat capacity at constant pressure, and $\tau_{d}$ is the radiation and/or convection diffusion time of the flux tube:

\tau_{d}=\frac{c_{p}\rho a^{2}}{k_{e}}\simeq c_{p}\rho a^{2}\left[\frac{c_{p}F_{tot}}{g}\left(1+\frac{2\ell_{ov}}{5H_{p}}\right)^{\nu}\right]^{-1}.

(10)

where for the fully ionized gas $c_{p}=2.5\Re$ ( $\Re$ is the gas constant in the ideal gas law $p=\rho\Re T$ ), $T(z)$ and $\rho(z)$ are the mean temperature and density; $k_{e}$ is the radiative heat conductivity (see Eq. (36) in Ballegooijen1982 ); $\ell_{ov}\approx 0.37H_{p}$ (Ballegooijen1982, ; Christensen2011, ) is the thickness of the overshoot layer; the total radiative energy flux $F_{tot}=L/(4\pi r^{2})$ depends on the Sun luminosity $L$ ; $g$ is the gravitational acceleration.

Next we apply the condition of hydrostatic equilibrium, $dp/dz=\rho g$ , when the adiabatic temperature gradient $(dT/dz)_{ad}=g/c_{p}$ may be used, and the neutral buoyancy of the flux tube in the overshoot zone $(|\delta T|/T_{ext})^{-1}\sim\beta\equiv 8\pi p_{ext}/B^{2}$ . This way we are able to estimate the time of the radiative and/or convective diffusion $\tau_{d}$ (see Eq. (10)) of the flux tube:

\tau_{d}=\frac{c_{p}\rho a^{2}}{k_{e}}\approx|\delta T|c_{p}\rho\frac{a^{2}}{(1.148)^{\nu}\delta zF_{tot}}\,,

(11)

where

\delta z\sim(1.148)^{-\nu}\left(\frac{a}{H_{p}}\right)^{2}H_{p}\frac{\nabla_{e}}{\nabla_{rad}},~{}~{}where~{}~{}\nu\geqslant 3.5\,,

(12)

F_{tot}=\frac{L}{4\pi R_{tacho}^{2}}=H_{p}\frac{\nabla_{rad}}{\nabla_{e}}\left(\frac{dQ}{dt}\right)_{1}.

(13)

Here $\nabla_{rad}=(\partial\ln T_{ext}/\partial\ln p_{ext})_{rad}$ is the radiative equilibrium temperature gradient; $(dQ/dt)_{1}$ is the rate of radiative heating, which only depends on the thermodynamic parameters $k_{e}$ and $T_{ext}$ of the ambient plasma, depending only on the radial distance from the Sun center (Spruit1974, ; Ballegooijen1982, ).

As a result, it is not difficult to show that the van Ballegooijen model combining equations (9)-(13) gives the final expression for the rise time by radiation and/or convective diffusion from the boundary layer of the overshoot to the solar surface,

\tau_{d}\approx\frac{2}{\beta}T_{ext}\left[\frac{1}{c_{p}\rho_{ext}}\left(\frac{dQ}{dt}\right)_{1}\right]^{-1},

(14)

and the lifting speed of the MFT from the overshoot boundary layer to the surface of the Sun,

	$\displaystyle v_{rise}=H_{p}\nabla_{ad}\frac{1}{p_{ext}}\left(\frac{dQ}{dt}\right)_{1}\left(-\delta+0.12\frac{B^{2}}{8\pi p_{ext}}\right)^{-1},$
	$\displaystyle\nabla_{ad}=\nabla_{e}\simeq 0.4,$		(15)

which are almost identical to the equations (29) and (30) of Fan1996 .

Hence, we understand that the van Ballegooijen model is a special case for magnetic fields of $B_{tacho}\leqslant 10^{5}~{}G$ , under which a magnetic dynamo can exist. On the other hand, we know that based on the holographic BL mechanism, generating (in contrast to dynamo!) the toroidal magnetic field in the tachocline, the universal model of flux tubes predetermines the existence of not only the fields of $B_{tacho}\leqslant 10^{5}~{}G$ , but also the strong magnetic fields of the order $B_{tacho}\sim 10^{7}~{}G$ .

Unlike the special van Ballegooijen model, we adopt the universal model of MFTs with

v_{rise}=2\frac{H_{p}}{\tau_{d}}\frac{B^{2}}{8\pi p_{ext}}\left(-\delta+0.12\frac{B^{2}}{8\pi p_{ext}}\right)^{-1},

where

\tau_{d}=\frac{c_{p}\rho a^{2}}{k_{e}}\left[1+\left(\frac{dQ}{dt}\right)_{2}\middle/\left(\frac{dQ}{dt}\right)_{1}\right]^{-1}.

(16)

Here $(dQ/dt)_{2}$ represents the radiative diffusion across the flux tube due to the temperature difference ( $\delta T\equiv T-T_{ext}$ ) between the tube and the external plasma (see Fan1996 ).

Using simple calculations of equations (9) and (16) for MFTs, it is easy to show that with the help of the total expression

\frac{dQ}{dt}=\left(\frac{dQ}{dt}\right)_{1}+\left(\frac{dQ}{dt}\right)_{2}

(17)

of the universal model

\tau_{d}\approx\frac{2}{\beta}T_{ext}\left[\frac{1}{c_{p}\rho_{ext}}\frac{dQ}{dt}\right]^{-1}

(18)

and

	$\displaystyle v_{rise}=H_{p}\nabla_{ad}\frac{1}{p_{ext}}\frac{dQ}{dt}\left(-\delta+0.12\frac{B^{2}}{8\pi p_{ext}}\right)^{-1},$
	$\displaystyle\nabla_{ad}=\nabla_{e}\simeq 0.4,$		(19)

which is the general case of the so-called universal model of van Ballegooijen-Fan-Fisher (vanBFF model).

On the other hand, let us remind that on the basis of the BL holographic mechanism, generating the toroidal magnetic field in the tachocline, the universal model of flux tubes is predetermined by the existence of strong magnetic fields of the order of $B_{tacho}\sim 10^{7}~{}G$ . Since the physics of the holographic BL mechanism does not involve a magnetic dynamo, we often refer to it as the universal antidynamo vanBFF model. It is determined by the following total energy rate per unit volume:

\frac{dQ}{dt}=\left(\frac{dQ}{dt}\right)_{1}+\left(\frac{dQ}{dt}\right)_{2}=\left(\frac{dQ}{dt}\right)_{1}\left[1+\frac{\alpha_{1}^{2}}{\nabla_{e}}\left(\frac{H_{p}}{a}\right)^{2}\frac{1}{\beta}\right],

(20)

where

\left(\frac{dQ}{dt}\right)_{1}=-\nabla\vec{F}_{rad}=F_{tot}\frac{\nabla_{e}}{\nabla_{rad}}\frac{1}{H_{p}}=k_{e}\nabla_{e}\frac{T_{ext}}{H_{p}^{2}},

(21)

\left(\frac{dQ}{dt}\right)_{2}=-k_{e}\frac{\alpha_{1}^{2}}{a^{2}}(T-T_{ext}),

(22)

where we used the approximate relation $|\delta T|/T_{ext}\sim 1/\beta$ ); the parameter $\alpha_{1}^{2}\approx 5.76$ (Fan1996, ; Weber2015, ); $\vec{F}_{rad}$ is the radiative energy flux (Spruit1974, ); $\nabla_{e}\sim 1.287\nabla_{rad}$ (see Table 2 in Spruit1974 ); $H_{p}/a$ is a factor for the lower convection zone (see Ballegooijen1982 ).

As a result, we understand that the heating rate of MFTs consists of the rate of radiative and convective heating (see Eqs. (17)-(22); Eq. (10) in Fan1996 and Eq. (7) in Weber2015 ):

\frac{dQ}{dt}=\rho T\frac{dS}{dt}\approx-div\vec{F}_{rad}-k_{e}\frac{\alpha_{1}^{2}}{a^{2}}(T-T_{ext}),

(23)

where $S$ is the entropy per unit mass. The first term $(dQ/dt)_{1}$ determines the mean temperature gradient between the lower convection zone and the overshoot (see Eq. (21)). It deviates from the radiative equilibrium substantially, implying the existence of the nonzero divergence of the heating radiation flux. The second term $(dQ/dt)_{2}$ (see Eq. (22)) represents the radiation diffusion through the flux tube because of the temperature difference between the tube and the external plasma. Its effect is to reduce the temperature difference.

Hence, it is clear that with strong toroidal magnetic fields in the tachocline (of the order $>10^{5}~{}G$ ) the second term $(dQ/dt)_{2}$ (in contrast to Ballegooijen1982 ; Fan1996 ; Weber2015 ; Weber2016 ) is the dominant source of convective heating. For the toroidal magnetic field $B_{tacho}\sim 4\cdot 10^{7}~{}G$ in the tachocline, our estimate of the second term

	$\displaystyle\left(\frac{dQ}{dt}\right)_{2}=\frac{\alpha_{1}^{2}}{\nabla_{e}}\frac{1}{\beta}\left(\frac{H_{p}}{a}\right)^{2}\left(\frac{dQ}{dt}\right)_{1}\geqslant$	$\displaystyle 5\cdot 10^{4}~{}erg\cdot cm^{-3}s^{-1}$
		$\displaystyle at~{}~{}\beta\simeq 1$		(24)

is related to the first term $(dQ/dt)_{1}\approx 29.7~{}erg\cdot cm^{-3}\cdot s^{-1}$ (see Eq. (18) in Fan1996 ) and the following parameters: $\alpha_{1}^{2}\approx 5.76$ (Fan1996, ; Weber2015, ), $\nabla_{e}\approx 0.4$ (see Table 2 in Spruit1974 ; Fan1996 ), $1/\beta=B_{tacho}^{2}/8\pi p_{ext}=1$ , $\nabla_{e}/\nabla_{rad}\approx 1.287$ , $a=(\Phi/\pi B_{tacho})^{1/2}\leqslant 0.1H_{p}$ (see Fan1993 ) with an average value of magnetic flux $\Phi\sim 10^{21}~{}Mx$ (see e.g. Zwaan1987 ).

Taking into account the consequences of the non-local theory of mixing length (Spruit1974, ; Spruit1982, ), it can be shown that thin, neutrally buoyant flux tubes are stable in the stably stratified medium, provided that its field strength $B$ is smaller than a critical value $B_{c}$ (Ballegooijen1982, ), which is approximately given by

\frac{B_{c}^{2}}{8\pi p_{ext}}=-\gamma\delta=-\frac{5}{3}\delta.

(25)

So, for the maximum value of the toroidal magnetic field ( $B_{tacho}\sim 4\cdot 10^{7}~{}G$ ) the estimate of the rise time of the radiation and/or convection diffusion of the flux tube (see Eq. (18))

\tau_{d}\approx\frac{2}{\beta}T_{ext}\left[\frac{1}{c_{p}\rho_{ext}}\left(\frac{dQ}{dt}\right)_{2}\,\right]^{-1}\geqslant 10^{4}~{}year

(26)

and the lifting speed of an almost empty magnetic tube (see Eqs. (24), (25))

v_{rise}\simeq\frac{H_{p}\nabla_{e}}{p_{ext}}\left(\frac{dQ}{dt}\right)_{2}\frac{1}{0.72}\leqslant 10^{-8}~{}km/s

(27)

show that the existence of MFTs on the surface of the Sun is meaningless.

In this regard, there is one more beautiful task associated with our problem of almost total suppression of radiative heating in virtually empty magnetic tubes (see Fig. 5). Let us remind that photons going from the radiation zone through the horizontal field of the O-loop near the tachocline (Fig. 5) are turned into axions, thus almost completely eliminating the radiative heating in the virtually empty magnetic tube. Some small photon flux can still pass through the “ring” between the O-loop and the tube walls (see Fig. 5) and reach the penumbra. Let us denote the area of the magnetic tube “ring” by $2\pi ra_{conv}$ , where $r$ is the magnetic tube radius, and $a_{conv}$ is the width of the “ring”.

What is the physics behind the appearance of the “ring” between the O-loop and the walls of the magnetic tube (Fig. 8)? In simple words, one can say the following. The appearance of the “ring” cross-section is the result of the production of both axion-origin photons (by converting solar axions into photons in the tachocline) and photon-origin axions (through the conversion of high-energy photons from the radiation zone to axions in the tachocline). From here, on the one hand, the axions of photonic origin are the part of the manifestation of the mean free path of axion origin photons from the tachocline to the photosphere. On the other hand, they are the part of the manifestation of magnetic tube “ring”, where the convective heating $(dQ/dt)_{2}$ dominates over the radiative heating $(dQ/dt)_{1}$ .

As a result, assuming the mean width of the “ring”

a_{conv}\sim 3.7\cdot 10^{-4}~{}H_{p},

(28)

we apply a new analysis of the universal vanBFF model (see Eq. (19) and (17) (analogous to Ballegooijen1982 ) or (19) and (25) (analogous to Eq. (29) in Fan1996 )), where the calculated values such as the magnetic flux $\Phi$ and the rise speed $(v_{rise})_{conv}$ of the MFT to the surface of the Sun, do not contradict the known observational data:

•

the value of the magnetic flux of the tube (for $r\sim 70~{}km$ )

$\Phi=2\pi ra_{conv}B_{tacho}\approx 3.7\cdot 10^{21}Mx,$ (29)

which is in good agreement with the observational data of Zwaan Zwaan1987 ;

•

the time of radiation diffusion of the flux tube (18)-(20)

	$\displaystyle(\tau_{d})_{conv}$	$\displaystyle=2T_{ext}\left\{\frac{1}{c_{p}\rho_{ext}}\left(\frac{dQ}{dt}\right)_{1}\left[1+\frac{\alpha_{1}^{2}}{\nabla_{e}}\left(\frac{H_{p}}{a_{conv}}\right)^{2}\right]\right\}^{-1}$
		$\displaystyle\approx 1.1\cdot 10^{5}~{}s~{}\sim 1.3~{}day$		(30)

and, as a consequence, the magnitude of the lifting speed of the MFT (see Eq. (9))

(v_{rise})_{conv}=\frac{2.77H_{p}}{(\tau_{d})_{conv}}\sim 1.4~{}km/s,

(31)

which are almost identical to the observational data of the known works by Kosovichev et al. Kosovichev2016 .

In order to show signatures of appearing areas of sunspots inside the Sun before they appear on the surface, we used, according to Kosovichev et al. Kosovichev2016 , the measurements of plasma flows in the upper convection zone, provided by the Time-Distance Helioseismology pipeline developed for the analysis of solar oscillation data obtained by the Helioseismic and Magnetic Imager (HMI) within the Solar Dynamics Observatory (SDO), to investigate the subsurface dynamics of the emerging active region (AR) NOAA 11726.

Figure 9c shows the distribution of the effective phase shift (“helioseismic index”) for the depth range 62-75 Mm measured on April 19, 2013, 03:00 UT, when there was no significant magnetic flux on the surface. The figure 9d shows the variations of the helioseismic perturbation associated with the emerging AR at two different depths: 62-75 Mm and 42-55 Mm depending on time. One of the greatest advantages of the remote helioseismology is that the full-disk observations of solar variations allow to build a special scheme of measurement and selection of acoustic waves signals (Fig. 9b), passing though certain sub-surface areas. For example, Ilonidis et al. Ilonidis2013 developed a special proceadure of deep focusing which is able to detect large emerging active areas more than a day before their appearance on the surface (Fig. 9). The rise velocity determined by tracking the magnetic flux declination with depth, is about 1.4 km/s, which is very close to the rise velocity in the deep layers Kosovichev2016 , e.g. near tachocline! Interestingly, the results of several attempts to detect the emerging magnetic flux before its appearance in the photosphere may be compared to our theoretical estimates (30)-(31) and demonstrate a surprising agreement in terms of the magnetic tube rising velocity and time.

At the same time, it is known that observations of the characteristic rising speed of active regions (sunspot groups) $\sim 1.0-1.4~{}km/s$ Ilonidis2013 ; Kosovichev2000 ; Zharkov2008 ; Toriumi2013 ; Kosovichev2016 , which coincides with a speed of $\sim 1.4~{}km/s$ of the universal model of van Ballegooijen-Fan-Fisher (see vanBFF model for (19)), is an order of magnitude larger than the speed of 0.1-0.25 km/s, associated with numerical models of the emerging flux (see Fan2021 ).

Below we briefly and simply show how our fundamental physics of the rise of magnetic field tubes based on solar axions of dark matter differs from the classical physics of an active region emerging flux from convective dynamos in the bulk of the solar convection zone (see e.g. Fan2021 ; Charbonneau2020 ; Hotta2020 ).

Let us first draw some attention to what the remarkable physicist Yuhong Fan says about the essence of magnetic fields in the solar convection zone: “The question of whether, or to what extent, a strong toroidal magnetic field stored in the overshoot region at the base of the convection zone, generated by a deep seated solar dynamo process, is responsible for the formation of solar active regions remains to be more rigorously investigated.” Fan2021

In contrast to the classical physics of an active region emerging flux from convective dynamos in the bulk of the solar convection zone (see e.g. Fan2021 ; Charbonneau2020 ; Hotta2020 ), we already know that:

•

first, a strong toroidal magnetic field, stored in the overshoot tachocline region, is predetermined by the thermomagnetic Ettingshausen-Nernst effect (see Apendix A in RusovDarkUniverse2021 ), which exactly (in contrast to dynamo!) coincides with $B_{tacho}=4\cdot 10^{7}~{}G$ ; at the same time, we indirectly showed that, using the holographic principle of quantum gravity (see Apendix C in RusovDarkUniverse2021 ), the repelling toroidal magnetic field of the tachocline exactly “neutralizes” the magnetic field in the Sun core Fowler1955 ; Couvidat2003 , where the projections of the magnetic fields of the tachocline and the core have the equal value but the opposite directions.
•

second, unlike the component of the solar dynamo model (see Fig. C.1a in RusovDarkUniverse2021 and Fan2021 ; Charbonneau2020 ), the Babcock-Leighton mechanism (see Fig. C.1b in RusovDarkUniverse2021 ), predefined by the the fundamental holographic principle of quantum gravity, and thermomagnetic EN effect, emphasizes that this process is associated with continuous transformation of toroidal magnetic energy into poloidal magnetic energy ( $T\rightarrow P$ transformation), but not vice versa ( $P\rightarrow T$ ). It means that the holographic BL mechanism is the main process of regeneration of the primary toroidal field in the tachocline, and thus, the formation of buoyant toroidal magnetic flux tubes at the base of the convective zone, which then rise to the surface of the Sun.
•

third, our physics of the magnetic flux tubes rise is related to the fact that if the axions, which are born in the Sun’s core, are directly converted into X-rays near the tachocline, then the axion-photon oscillations predetermine the appearance of magnetic sunspot cycles. This is due to the fact that the formation of sunspots and their cycles is a consequence, according to RusovDarkUniverse2021 , of the anticorrelation 11-year cycles of ADM density modulation inside the Sun, which, not surprisingly, are a consequence of the 11-year ADM halo density modulation in the fundamental plane of the galactic center, which closely correlates with the density modulation of baryonic matter near the supermassive black hole. From here, it is easy to show (see RusovDarkUniverse2021 ) in what way the anticorrelation identity between indicators of the ADM density modulation inside the Sun and the number of sunspots (or the correlation identity between indicators of modulation of solar axions (or photons of axion origin) and sunspot cycles) is realized.

Finally, let us show that if the rise velocity of the floating magnetic tube, determined by the magnetic field values $\sim 4.1\cdot 10^{7}~{}G$ and the “ring” width $\sim 3.7\cdot 10^{-4}~{}H_{p}$ , causes the appearance of MHT in the form of sunspots, then the parameters of the universal vanBFF model will be associated with the magnetic cycles that are almost identical to the observational data of the tilt angle of Joy’s law.

2.2 Secondary reconnection of magnetic tubes in lower layers and the observed features of the tilt angle of Joy’s Law

The problem is devoted to physics of the magnetic reconnection of a magnetic tube in the lower layers, which is associated with the so-called reconnecting dynamo and the observed features of the tilt angle of Joy’s law.

In contrast to the primary reconnection inside magnetic tubes near the tachocline, which generates the O-loops, thus participating in the formation of photons of axion origin, as well as the axions of photon origin, from the O-loop to the photosphere, here we are interested in the secondary magnetic reconnection, which, although does not depend on sunspot cycles, but is necessarily related to the process of sunspots liftoff from the surface of the Sun.

In Fig. 10 one can see the conditions for the secondary reconnection between the O-loop (green lines) and the unipolar part of the $\Omega$ -loop (blue lines) that can organize them in the lower layer (Fig. 10, left) or in the upper layer (Fig. 10, right), thereby showing the appearance of bipolar magnetic tubes in various versions (Fig. 10c,d and g,h).

Finally, let us note that we have two types of primary magnetic reconnection inside the $\Omega$ -loop near the tachocline, one of which is manifested by the existence of a free O-loop (red lines in Fig. 6, green lines in Figs. 10a and 10e), and the other one practically does not exist. In other words, magnetic reconnection inside the $\Omega$ -loop may or may not accidentally give birth to a free O-loop near the tachocline (see Fig. 6). This means that if a free O-loop is created in the $\Omega$ -loop near the tachocline via the primary reconnection, classical sunspots appear on the surface (see black tubes, Fig. 11), while the rare “transparent” bipolar tubes, not reaching the surface and having no O-loop inside, appear as “optically invisible” spots on the surface (see white bipolar tubes, Fig. 11).

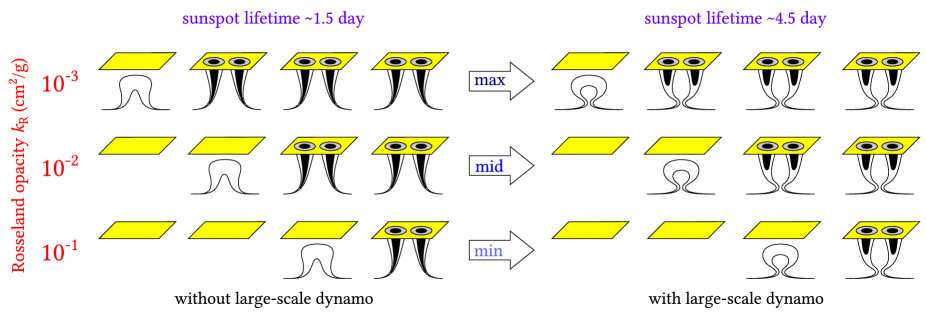
Here arises a question: How does the secondary magnetic reconnection in the lower layers of flux tubes (with magnetic field strength $\sim 10^{7}~{}G$ (see Fig. 7a) and $\sim 10^{5}~{}G$ (see Fig. 7b), respectively) explain the physics and theoretical estimates of the buoyant tubes – the time and speed of the sunspot liftoff from the solar surface, and the tendency of the tilt angle of Joy’s law?

Let us first note the physics of primary reconnection in the lower layers of the magnetic flux tubes (with $B\sim 10^{7}~{}G$ ). Based on the mechanical equilibrium model (MEQ) of Choudhuri1987 and vanBFF MEQ model (see Sect. 2.1), we showed that the results of the simulation of flux tube trajectories without adiabatic ring flux drag in the super-adiabatic zone (see Fig. 8) are well represented in Fig. 12a,b (red lines). The most intriguing results of the simulation of flux tube trajectories are a very strong basis not only for understanding the complex physics, but also for understanding the theoretical estimates of buoyant MFTs, like the rise time and speed of rising to the Sun surface (see (30)-(31), and also analogous Fig. 1 and Fig. 5 in Browning2016 ), and the explanation of the tendency of the tilt angle of Joy’s law (see Fig. 12c,d), which do not contradict the known experimental data, for example, the well-known works of DasiEspuig2010 ; DasiEspuig2013 ; Ivanov2012 ; McClintock2013 ; Pevtsov2014 ; Tlatova2015 ; Pavai2015 ; Baranyi2015 ; Wang2015 ; Wang2017 .

Further, we are interested in the second stage of modeling the trajectory of magnetic flux tubes (see Fig. 12), when a magnetic tube that reaches the solar surface above the photosphere changes its shape and structure with the topological effect of the secondary magnetic reconnection in the lower layers of the magnetic tube, see Fig. 7b and 10a-c. Moreover, we believe that the secondary magnetic reconnection of the flux tubes leads to the real decrease in the magnetic field to $B\sim 10^{5}~{}G$ at $\sim 0.8~{}R_{Sun}$ (see Fig. 14), at which the evolution of the tubes (in thermal equilibrium (TEQ) with the surroundings it is often referred to as magnetic buoyancy (Parker1975, )) is controlled by the latitudinal pressure gradient in magnetic layers on the overshoot tachocline that allows a balance between nonzero buoyancy force, curvature force and pressure force in the absence of azimuthal flow (see bottom panel in Fig. 2 in Schussler2002 ; see also review and Fig. 5b in Fan2009 ), which generally allows a balance of TEQ between four main forces: nonzero buoyancy, magnetic tension, aerodynamic drag, and Coriolis force.

Despite our complicated theoretical calculations of the trajectories (Fig. 12a,b) of the flux tubes without drag of adiabatic flux ring in the superadiabatic convection zone (red lines: based on the MEQ model by Choudhuri1987 and the vanBFF MEQ model (see Sect. 2.1)) and involving the flux ring resistance in thermal equilibrium (blue lines: based on the TEQ model by Choudhuri1987 ), below we will describe the scenario, which explains the simple physics of why the magnetic tubes emerging on the solar surface, can only be at low, and to a lesser extent at middle latitudes (see Figs. 12a,b and 13b).

The first part of the scenario consists in discussing the physics of magnetic flux buoyancy and, as a consequence, estimating the rise speed of an almost empty magnetic tube, $v_{rise}$ , based on the vanBFF model (see Sect. 2.1), which simultaneously coincides with the known expressions for the buoyancy speed, $v_{B}$ (see e.g. Parker1975 ; see also Eq. (17) and Fig. 2 in Ballegooijen1988 ; Eq. (34) in Fan1993 ; Eq. (30) in Khaibrakhmanov2017 ):

(v_{rise})_{conv}\equiv(v_{B})_{conv}\approx v_{A}\left(\frac{\pi}{C_{D}}\frac{a_{conv}}{H_{p}}\frac{z}{H_{p}}\right)^{1/2},

(32)

where $v_{A}\equiv B/(4\pi\rho_{int})^{1/2}$ is the Alfvén speed of the magnetic field (see e.g. Roberts2001 ), $C_{D}\approx 1$ is the drag coefficient, $\rho_{int}$ is the internal density of the gas in the MFT. It is assumed that the magnetic tube is formed inside the disk at an altitude $z/H_{p}\approx 1$ .

For the neutral buoyancy condition ( $\rho_{int}=\rho_{ext}\approx 0.2~{}g/cm^{3}$ ; see Figs. 6 and 11 in Rusov2015 ; RusovArxiv2019 and Fig. 5) and the strong toroidal field of the magnetic tube, $B_{tacho}^{Sun}=4.1\cdot 10^{7}~{}G$ , as well as the average width of the “thin” ring $a_{conv}\sim 3.7\cdot 10^{-4}~{}H_{p}$ (see Eq. (28) and Fig. 8) between the O-loop and the walls of the magnetic tube (see Fig. 8), it is not difficult to show that the estimate of the Alfvén speed (see Eq. (32))

v_{A}\cong 4.1\cdot 10^{6}~{}cm/s

(33)

allows us to estimate the analytical coincidence of the rise speed $v_{rise}$ (see Eq. (31)) and the magnetic buoyancy speed $v_{B}$ :

(v_{rise})_{conv}\equiv(v_{B})_{conv}\approx 1.4\cdot 10^{5}~{}cm/s,

(34)

at which for such large magnetic fields there is a significant number of rising tubes at all latitudes (see also the red lines in Figs. 13a and 12a,b).

So, for the considered case, the secondary magnetic reconnection of the flux tubes leads to the real decrease in the magnetic field to $B\sim 10^{5}~{}G$ at $\sim 0.8R_{Sun}$ (see Figs. 12a,b), and thereby reveals the nonzero magnetic buoyancy (see the blue lines in Fig. 12a,b). This means that for the condition of nonzero buoyancy ( $\rho_{ext}\approx 0.09~{}g/cm^{3}$ ) and the toroidal magnetic field of the flux tube, as well as the transverse radius of the “thin” ring $\sigma_{0}\equiv a_{conv}\sim 100~{}km\approx 4.5\times 3.7\cdot 10^{-4}H_{p}$ (see Fig. 12c,d), the estimate

v_{A}\cong 1.1\cdot 10^{4}~{}cm/s

(35)

allows us to estimate the analytical coincidence of the rise speed $v_{rise}$ (see Eq. (31)) and the magnetic buoyancy speed $v_{B}$ :

(v_{rise})_{conv}\equiv(v_{B})_{conv}\approx 7.2\cdot 10^{2}~{}cm/s,

(36)

where we assume that MFTs are formed inside the disk at a height $z\sim H_{p}$ (see e.g. Khaibrakhmanov2017 ). Below we consider the reason for the rising magnetic buoyancy only at low and middle latitudes.

The second part of the scenario, which is based on the remarkable idea of Kichatinov1991 (see also Fig. 5 in Krivodubskij2005 ), includes the generation of the magnetic field near the bottom of the convective zone (see Fig. C.1b in RusovDarkUniverse2021 for the holographic BL mechanism) and transfer of the toroidal field from the deep layers to the solar surface, where the efficiency of the magnetic buoyancy transfer is predetermined by the participation of two processes: macroscopic turbulent diamagnetism (see Zeldovich1957 ; Radler1968a ; Radler1968b ; Vainshtein1980 ; VainshteinKichatinov1983 ; Stix1989 ; Kichatinov1992 ; Kitchatinov2016 ) and rotational $\nabla\rho$ -pumping (see Drobyshevski1974 ; Vainshtein1983 ; VainshteinKichatinov1983 ; Stix1989 ; Kichatinov1991 ; Ossendrijver2002 ; Kitchatinov2012 ), which are also associated with the process of meridional circulation (see e.g. Ballegooijen1982 ; Spruit1982 ; Dudorov1985 ; Ballegooijen1988 ; Wang1991 ; Choudhuri1995 ; Caligari1995 ; Nandy2002 and also Khaibrakhmanov2017 ).

Let us note some important properties of macroscopic turbulent diamagnetism. It is known that Zeldovich1956 ; Zeldovich1957 and Spitzer1956 discovered the diamagnetism of inhomogeneously turbulent conducting liquids, in which the inhomogeneous magnetic field moves as a single whole. In this case the turbulent fluid, for example, with nonuniform effective diffusivity $\eta_{T}\approx(1/3)vl$ (see Fig. 1 in Kitchatinov2008 ; see also Fig. 14b) behaves like a diamagnetic one and carries the magnetic field with the effective velocity

\vec{v}_{dia}=-\frac{1}{2}\nabla\eta_{T},

(37)

where $l$ is the mixing length of turbulent pulsations, and $v=\sqrt{\langle v^{2}\rangle}$ is the root-mean-square velocity of turbulent motion. The minus sign on the right in Eq. (37) shows the meaning of turbulent magnetism: it is not paramagnetic magnetism, so magnetic fields repel from regions with relatively high turbulent intensity. In other words, macroscopic turbulent plasma diamagnetism and, as a consequence, the so-called macroscopic diamagnetic effect (see Radler1968a ; Radler1968b ) in the physical sense is the displacement of the averaged magnetic field $B$ from regions with increased intensity of turbulent pulsations to regions with less developed turbulence (Vainshtein1980, ; Krause1980, ).

However, there is an interesting problem of the diamagnetic process caused by inhomogeneous turbulent intensity with allowance for the total nonlinearities in the magnetic field. This is due to the fact that up to the present time analytical estimates have been obtained only for the limiting cases of weak and strong magnetic fields. For example, at strong magnetic fields of flux tubes, at $B\gg B_{eq}$ , the diamagnetic effect becomes almost negligible, in particular, strong magnetic damping of diamagnetism $\sim B^{-3}$ is obtained for super-equipartitions of fields (Kichatinov1992, ), when turbulence is close to two-dimensional (Zeldovich1957, ). On the other hand, for very weak fields the diamagnetic pumping, which is predetermined by the intensity of turbulence at $B\ll B_{eq}$ , is a very effective process (Kichatinov1992, ).

Between the known limiting cases of weak and strong magnetic fields we are interested in the average toroidal magnetic field of a flux tube, that is $B_{tacho}^{Sun}\sim 10^{5}~{}G$ , when $B\geqslant B_{eq}$ . This is due to the fact that the secondary magnetic reconnection of the flux tubes (see Figs. 10b,d,f,g) leads to the real decrease of the magnetic field to $B\sim 10^{5}~{}G$ at $\sim 0.8~{}R_{Sun}$ (see the blue lines in Fig. 12a,b). This means that the real decrease in the toroidal magnetic field of the flux tube is a consequence of the formation of the secondary reconnection, as well as the important appearance of two “anti-buoyancy” effects: the downwardly directed turbulent diamagnetic transfer and the rotational effect of the magnetic $\nabla\rho$ -pumping (VainshteinKichatinov1983, ; Krivodubskij2005, ).

In this regard, we consider turbulence with quasi-isotropic spectral tensor (Kichatinov1987, ), which is certainly the simplest representation for inhomogeneous turbulence (see Eq. (2.12) in Kichatinov1992 . As a consequence, the information on the spectral properties of turbulence (given by Eqs. (2.12)-(2.16) from Kichatinov1992 ) is sufficient to reduce the expression for the average electromotive force $\varepsilon$ (see Eq. (2.1) Kichatinov1992 ) to its traditional form, where only integrations over the wave number $k$ and frequency $\omega$ remain. After such shortening it is possible to get (see Kichatinov1992 )

\vec{F}=(\vec{v}_{dia}+\vec{v}_{dens})\times\vec{B}

(38)

with the speed of turbulent diamagnetic transfer

\vec{v}_{dia}=-\nabla\int\limits_{0}^{\infty}\Re_{dia}(k,\omega,B)\frac{\eta k^{2}q(k,\omega,x)}{\omega^{2}+\eta^{2}k^{4}}dkd\omega,

(39)

where $q$ stands for the local velocity spectrum, and the rate of rotational magnetic advection caused by the vertical heterogeneity of the fluid density in the convective zone, i.e. the magnetic $\nabla\rho$ -pumping effect,

\vec{v}_{dens}=\frac{\nabla\rho}{\rho}\int\limits_{0}^{\infty}\Re_{dens}(k,\omega,B)\frac{\eta k^{2}q(k,\omega,x)}{\omega^{2}+\eta^{2}k^{4}}dkd\omega.

(40)

The effective speeds $v_{dens}$ and $v_{dia}$ are consequences of the non-uniformity of density and of turbulence intensity, respectively, where the latter is attributed to the known diamagnetic pumping.

We are interested in the problem of reconstructing a strong toroidal field $\sim 10^{7}~{}G$ of flux tubes (see Figs. 13a and 14a), which by the secondary reconnection transform regions of the mean magnetic field $\sim 10^{5}~{}G$ in the convective zone (see Figs. 13b and 14a) and, thereby, allow the organization of the amazing balance between the magnetic buoyancy, turbulent diamagnetism, and the rotationally modified $\nabla\rho$ -effect. It can be shown that for the parameters $\beta=B/B_{eq}\sim 1$ and $\cos\varphi$ (see Eq. (3.5) in Kichatinov1992 ), the speeds (39) and (40), which depend on the magnetic field $B$ through the kernels $\Re_{dens}(\beta,\varphi)$ and $\Re_{dia}(\beta,\varphi)$ (see Eqs. (3.6) and (3.7) in Kichatinov1992 ), have the following estimates:

v_{dia}^{black}\sim 1.3\cdot 10~{}cm/s

(41)

and

v_{dens}^{light}\sim 7.2\cdot 10^{2}~{}cm/s.

(42)

This raises the question of how a certain balance appears between the speeds of magnetic buoyancy (see Eq. (36) and Fig. 13), diamagnetic pumping (see Eq. (41)), and rotating densely stratified $\nabla\rho$ -pumping (see Eq. (42) and Fig. 13b),

(v_{B}^{red})_{conv}+v_{dia}^{black}+v_{dens}^{light}\cong(v_{B}^{red})_{conv}+v_{dens}^{light}=?

(43)

In order to consider the balance Eq. (43), it is necessary to apply the widely used approximation of the mixing length (see e.g. BohmVitense1958 ; Bradshaw1974 ; Gough1977a ; Gough1977b ; Barker2014 ; Brandenburg2016 ), which, according to Kichatinov1991 , fully satisfies this goal. This approximation will be understood as the replacement of nonlinear terms along with time derivatives in the equations for fluctuating fields by means of $\tau$ -relaxation terms, i.e. instead of equations (3.1) and (3.9) from Kichatinov1991 , we now have the equation of the radial speed of the toroidal field in the convection zone

v_{dens}^{light}=\tau\langle u^{2}\rangle^{\circ}\frac{\nabla\rho}{\rho}\left[\phi_{2}(\hat{\Omega})-\cos^{2}\theta\cdot\phi_{1}(\hat{\Omega})\right]\approx

(44)

\approx 6v_{p}\left[\phi_{2}(\hat{\Omega})-\cos^{2}\theta\cdot\phi_{1}(\hat{\Omega})\right]=

(45)

=-\frac{3\kappa g}{(\gamma-1)c_{p}T}\left[\phi_{2}(\hat{\Omega})-\cos^{2}\theta\cdot\phi_{1}(\hat{\Omega})\right],

(46)

where $\tau\approx l/(\langle u^{2}\rangle^{\circ})^{1/2}$ is a typical lifetime of a convective eddy; $l$ is the mixing length; $\langle u^{2}\rangle^{\circ}$ is the mean intensity of fluctuating velocities for original turbulence; $\theta$ is the latitude; $e_{r}\nabla\rho/\rho=-e_{r}g/[(\gamma-1)c_{p}T]$ , where $e_{r}$ is the radial unit vector; $T\cong 1.35\cdot 10^{6}~{}K$ is the temperature at $0.8R_{Sun}$ ; $g=g_{0}(R_{Sun}/r)$ is the gravitational acceleration, where $g_{0}=2.74\cdot 10^{4}~{}cm/s^{2}$ is the surface value; $c_{p}=3.4\cdot 10^{8}~{}cm^{2}s^{-2}K^{-1}$ (fully ionized hydrogen) is the specific heat at constant pressure; $\gamma=5/3$ is the ratio of specific heats $c_{p}/c_{V}$ ; $3\kappa=\tau\langle u^{2}\rangle^{\circ}$ , where $\kappa\equiv\eta_{T}\approx 5\cdot 10^{13}~{}cm^{2}\cdot s^{-1}$ is turbulent diffusivity supplied by the model of non-rotating convection zone (Spruit1974, ; Gough1976, ; Stix1990, ; Parker2009, ; Karak2014, ) (see also Fig. 1 in Kitchatinov2008 ) and the mixing length relation $\langle u^{2}\rangle^{\circ}=-\nabla\Delta Tl^{2}g/(4T)$ , where the $\nabla\Delta T$ is superadiabatic temperature gradient; $v_{p}=(1/6)\tau\langle u^{2}\rangle^{\circ}(\nabla\rho/\rho)$ is the velocity of the magnetic field transfer caused by the density gradient (see Eq. (36) in VainshteinKichatinov1983 ); $\hat{\Omega}=Co=2\tau\Omega$ is the Coriolis number (reciprocal of the Rossby number), where $\Omega$ is the rotation speed, $\tau$ is the turnover time, and the functions

\phi_{n}(\hat{\Omega})=(1/8)I_{n}(\Omega,k,\omega)

(47)

(see $I_{1}$ and $I_{2}$ in Eqs. (3.12) and (3.21) in Kichatinov1991 ) are

\phi_{1}(\hat{\Omega})=\frac{1}{4\hat{\Omega}^{2}}\left[-3+\frac{\hat{\Omega}^{2}+1}{\hat{\Omega}}\arctan\hat{\Omega}\right],

(48)

\phi_{2}(\hat{\Omega})=\frac{1}{8\hat{\Omega}^{2}}\left[1+\frac{\hat{\Omega}^{2}-1}{\hat{\Omega}}\arctan\hat{\Omega}\right]

(49)

(see also analogous Eq. (19) and Fig. 2 in Kitchatinov2016 ), which describe the rotational effect on turbulent convection.

According to Kapyla2014 , the rotational effect on the flow can be measured with the local Coriolis number $\hat{\Omega}=Co=2\tau\Omega$ , especially if $\tau$ is estimated on the basis of the theory of mixing length, which predicts values of $\hat{\Omega}$ reaching more than 10 in the deep layers (see e.g. Ossendrijver2003 ; Brandenburg2005 ; Kapyla2011 ; KapylaEtAl2011 ). However, on the other hand, according to Kapyla2014 , the question of whether there are such deep layers of solar and stellar convection zones or not is still open.

At the same time, we showed that this rotating magnetic $\nabla\rho$ -pumping appears precisely in the deep layers (through reconnection of the $\Omega$ -loop (see Figs. 13b and 14) at middle and low latitudes, where the influence of the rotational gradient causes the upward magnetic pumping. The direction of the magnetic $\nabla\rho$ -pumping (up or down, see Fig. 13b) is susceptible to the sign of the factor in Eqs. (48) - (49), which depends on the polar angle (colatitude) and the behavior of the Coriolis number functions in the convection zone.

Below we show that the estimate of the Coriolis number for solar convection in the deep layer should be $\hat{\Omega}\approx 20$ . As a consequence of (47)-(49), the following values are assumed for this quantity:

\phi_{1}\cong 0.0171,~{}~{}~{}\phi_{2}\cong 0.0098,

(50)

at which the radial velocity (44) of toroidal field transport changes the sign at the latitude $\theta^{*}=\arccos\sqrt{\varphi_{2}/\varphi_{1}}\cong 41^{\circ}$ , being negative (downward) for $\theta>\theta^{*}$ and positive (upward) for $\theta<\theta^{*}$ . Using (46), we find that the value of the radial velocity in the convective zone $v_{dens}^{light}$ (see Eqs. (44)-(46)) near low latitudes (e.g. $\theta^{*}=\arccos(0.985)\cong 10^{\circ}$ ; see also Fig. 13b) almost completely coincides with the value of the speed (42), which was previously calculated with the help of the magnetic field $B$ in the kernel $\Re_{dens}(\beta,\varphi)$ .

This means that the balance of the magnetic buoyancy (see Eq. (36) and Fig. 13) and rotating density-stratified $\nabla\rho$ -pumping (see Eq. (42) and Fig. 13b) provides both the process of blocking the magnetic buoyancy at high latitudes,

\uparrow(v_{B}^{red})_{conv}+\downarrow v_{dens}^{light}\leqslant 0~{}~{}~{}at~{}high~{}latitudes,

(51)

and the process of lifting MFTs from the base of the convective zone to the solar surface at low latitudes,

\uparrow(v_{B}^{red})_{conv}+\uparrow v_{dens}^{light}>0~{}~{}~{}at~{}lower~{}latitudes,

(52)

which are simultaneously predetermined by the following rise time value:

(\tau_{B}^{red})_{conv}\sim\frac{z_{0}}{(v_{B}^{red})_{conv}+v_{dens}^{light}}\leqslant 4.5~{}~{}day,

(53)

where $z_{0}\approx 0.1~{}H_{p}$ is the length of the magnetic line at $0.8R_{Sun}$ (see the green band in Fig. 14). Here we must remember that magnetic $\nabla\rho$ -pumping of plasma from the azimuthal field through the formation of the $\Omega$ -loop is repeated again and again (see Fig. 7 and Fig. 4 in Parker2009 ). Moreover, our theoretical estimates of the rise time of the $\Omega$ -loop are in good agreement with the experimental observations by Gaizauskas1983 , who mention the repeated appearance of new $\Omega$ -loops with an interval of 5-8 days, which simultaneously indicates the continuing convective pumping of plasma.

We have shown above that the sunspots – the dark magnetic regions occurring at low latitudes on the surface of the Sun (see Fig. 13) – are indicators of the magnetic field generated not with the help of the dynamo mechanism (this is very important!), which does not exist here, but with the help of the holographic BL mechanism as components of the model of solar antidynamo (see Fig. C.1b in RusovDarkUniverse2021 ). Hence, the question arises as to how the sunspots originating from magnetic buoyancy on the surface only at low and, to a lesser extent, middle latitudes do not contradict the known observational data of the tilt angle of Joy’s law (see Fig. 12c,d).

Hence, it is very interesting that the holographic BL mechanism, which is a satisfactory alternative theory against the action of the dynamo, predetermines not only the generation of sunspots themselves on the surface at low and middle latitudes (see Fig. 13), but their coincidence with the observed slope angle of Joy’s law, where, as a consequence, the average angle of inclination of bipolar sunspots increases with latitude (see Fig. 12c,d). This is due to the fact that strong toroidal magnetic fields in the overshoot tachocline are generated by the holographic BL mechanism (see Fig. C.1 in RusovDarkUniverse2021 ), and bipolar magnetic tubes are created by lifting $\Omega$ -loops caused by magnetic buoyancy. As a result, these ascending $\Omega$ -loops, according to Choudhuri1989 , will be bent (towards the pole; see also Fig. 15) by the Coriolis force, so that they eventually appear on the surface of the Sun with the tilt angle (see Fig. 12).

Using the magnetic field strength near the bottom of the convective zone of the order of $10^{5}~{}G$ at $0.8R_{Sun}$ (see Figs. 13b and 14a), we find that the Coriolis force plays a dominant role, and the MFTs, starting from the bottom at low latitudes, deviate by $0.8R_{Sun}$ (see Figs. 12a,b and 15) and appear on the surface of the Sun at low and middle latitudes, located in the direction of the poles as sunspots. It is obvious that since the time of radiation diffusion of the flux tube (see Fig. 12a) is related to Eq. (53),

(\tau_{B}^{red})_{conv}\equiv(\tau_{d})_{conv}\leqslant 4.5~{}~{}day,

(54)

using the equations (32), (35), (36), it is possible to estimate the average width of the “ring” of the MFT:

a_{conv}\sim 100~{}km.

(55)

Here we are interested in the relationship between the speed of magnetic buoyancy, $(v_{B}^{red})_{conv}$ , and the average width of the “ring” $\sigma_{0}$ , which is identical to $a_{conv}$ based on the vanBFF model (see Sect. 2.1). Using Eq. (23) from Choudhuri1987

\frac{(v_{B}^{red})_{conv}}{4.8\cdot 10^{3}~{}cm/s}\equiv u_{t}^{\prime}=\left(\frac{4\pi}{C_{D}}\cdot\frac{\sigma_{0}}{R_{Sun}}\cdot\frac{(\Delta\rho/\rho_{ext})_{0}}{2\cdot 10^{-6}}\right)^{1/2},

(56)

which connects the cross-section of the magnetic tube “ring” $\sigma_{0}\equiv a_{conv}$ (see Eq. (21)) with the thermal velocity in dimensionless coordinates (see analogous Table 1 in Choudhuri1987 ), it is not difficult to show that for $(\Delta\rho/\rho_{ext})_{0}\sim 10^{-5}$ (or equivalently at $B_{0}=v_{A}(4\pi\rho)^{1/2}\sim 10^{5}~{}G$ ) the magnetic buoyancy values $(v_{B}^{red})_{conv}/4.8\cdot 10^{3}~{}cm/s\equiv u_{t}^{\prime}\approx 0.15$ and $\sigma_{0}\equiv a_{conv}\sim 100~{}km$ remarkably coincide with the corresponding values of Eqs. (36) and (55), respectively.

3 Summary and Outlook

The main result of the theory of magnetic flux tubes is the properties of dark matter axions identical to solar axions, the modulations of which are controlled by the anticorrelated 11-year modulation of the asymmetric dark matter (ADM) density in the solar interior (RusovDarkUniverse2021, ):

1.

The existence of anchored flux tubes with $10^{7}~{}G$ in the overshoot tachocline is a consequence of the fundamental properties of the holographic principle of quantum gravity, one of which (unlike the dynamo action!) generates a strong toroidal field in the tachocline with the help of the holographic BL mechanism (see Fig. 1b and C.1b in RusovDarkUniverse2021 ).
2.

The theory of the almost empty anchored magnetic flux tubes with $B\sim 10^{7}~{}G$ is the result of the formation of the magnetic O-loop (through the primary reconnection) inside the MFT in the lower part of the convective zone, which efficiently converts the solar axions and high-energy photons from the radiation zone into photons of axion origin and axions of photonic origin, respectively. The appearance of the axions of photonic origin is, on the one hand, the manifestation of a “ring” of a strong magnetic tube due to convective heating $(dQ/dt)_{2}$ (Fig. 8). On the other hand, it leads to a remarkable result of the “disappearance” of Parker’s convective heat transport, and consequently, to the ris of the temperature in the lower part of the magnetic tube. At the same time, the Parker-Biermann cooling effect is preserved in the convective zone, when a free path opens for the photons of axion origin from the tachocline to the photosphere! From here it is possible, for example, to obtain a solution to the problem of corona heating (RusovDarkUniverse2021, ).

The existence of magnetic buoyancy of flux tubes from the tachocline to the surface of the Sun is a consequence of the primary trajectory formation through the so-called universal model of van Ballegooijen-Fan-Fisher (vanBFF model), which is determined by the equation $dQ/dt=(dQ/dt)_{1}+(dQ/dt)_{2}$ . The first term $(dQ/dt)_{1}$ defines the average temperature gradient between the lower convective zone and the overshoot (see Eq. 27), which deviates significantly from the radiation equilibrium, which in turn suggests the presence of a nonzero divergence of the heating radiation flux. The second term $(dQ/dt)_{2}$ represents the convective diffuse radiation passing through a flux tube due to temperature differences between the tube and the ambient plasma, radiation thermal conductivity, and the mean width of the magnetic tube “ring” (see Eq. (28) and the area of the magnetic tube “ring” $2\pi ra_{conv}$ , where $r$ is the magnetic tube radius).

It was shown that at strong fields of $\sim 10^{7}~{}G$ , which are determined by the thermomagnetic EN effect (as a consequence of the holographic principle of quantum gravity), the external gas pressure is almost equal to the magnetic pressure between the tube and the ambient plasma. This leads to the virtually empty magnetic tube: $dQ/dt\approx(dQ/dt)_{2}\gg(dQ/dt)_{1}$ . It means that solar axions, which are magnetically converted from the high-energy photons of the radiation zone, on the one hand, directly suppress the radiation heating in the convective zone, and on the other hand, initiate an increase in convective heating by a sharp decrease in the average width of the magnetic tube “ring”. As a result, the convective heating $(dQ/dt)_{2}$ strongly dominates over the radiation heating $(dQ/dt)_{1}$ .

This way we apply a new analysis of the universal vanBFF model, where the calculated values such as the magnetic flux $\Phi$ , the rise time $\tau_{d}$ and the rise speed $(v_{rise})_{conv}$ of the MFT to the surface of the Sun, do not contradict the known observational data.
3.

The existence of the magnetic buoyancy of flux tubes on the surface of the Sun is a consequence of the formation of a secondary trajectory by magnetic reconnection with $B\sim 10^{5}~{}G$ (see blue lines in Fig. 12a,b), at which, on the one hand, the formation of the rotating density-stratified $\nabla\rho$ -pumping with $B\sim 10^{5}~{}G$ near the tachocline (see green bands in Figs. 13b and 14a) provides the process of blocking magnetic buoyancy at high latitudes, and on the other hand, it predetermines the existence of the dominant Coriolis force in $\nabla\rho$ -pumping with $B\sim 10^{5}~{}G$ , which ultimately generates an arched ascending loop on the surface of the Sun with a tilt in the lower and, to a lesser extent, middle latitudes (see Figs. 12 and 15a).
4.

The basic properties of an almost empty magnetic tube (see Figs. 5 and 8), characterizing thin radii of the cross-section ( $\sigma_{0}\equiv a_{conv}\sim 20~{}km$ ) and strong magnetic fields $\sim 10^{7}~{}G$ , do not contradict the existence of a thin flux tube, since a virtually empty magnetic tube, unlike thin flux tubes, has not only strong magnetic fields, but also the width of the “ring” ( $\sigma_{0}\equiv a_{conv}\sim 100~{}km$ ) of the MFT between the surface of the thick O-loop and the wall of the tube (see Figs. 5 and 8). It means that it is not the thin flux tubes with $\sim 10^{5}~{}G$ near the tachocline (see green bands in Figs. 13b and 14a) that serve as a basis for the role of the Coriolis force at a certain latitude of the rising tilt in the direction of the active region. Therefore, the mean width of the magnetic tube “ring” (see Fig. 8) and the arched ascending loop of the magnetic field lines (see the tilt angle of Joy’s law in Fig. 12c,d and Fig. 15) are allowed.
5.

The averaged theoretical estimates of the magnetic cycle of flux tubes are practically identical to the observational (averaged) data of the tilt angle of Joy’s law (see Fig. 12c,d).

In the future, we will apply the results of the theory of magnetic tubes in strong fields not only to the Sun and a black hole, which was partially obtained in our work (RusovDarkUniverse2021, ), but also consider its implications for the case of the well-known paradigm of fazzball complementarity in a black hole, which “challenges” the standard models of the central engine of a black hole for gamma-ray bursts and suggests a common physical mechanism behind GRBs, which indicates the magnetar central engine of GRBs.

References

(1) M. Rempel and R. Schlichenmaier, Sunspot modeling: From simplified models to radiative MHD simulations, Living Rev. Solar Phys. 8 (2011) .
(2) E.N. Parker, The formation of sunspot from solar toroidal field, Astrophys. J. 121 (1955) 491.
(3) L. Biermann, Der gegenwäartige stand der theorie konvektiver sonnenmodelle, Vierteljahrsschrift Astron. Gesellsch. 76 (1941) 194.
(4) E.N. Parker, Sunspots and the physics of magnetic flux tubes. I. the general nature of the sunspot, Astrophys. J. 230 (1979) 905.
(5) H. Alfvén, Existence of electromagnetic-hydrodynamic waves, Nature 150 (1942) 405.
(6) E.N. Parker, Hydraulic Concentration of Magnetic Fields in the Solar Photosphere. I. Turbulent Pumping, Astrophysical Journal 189 (1974) 563.
(7) E.N. Parker, Hydraulic Concentration of Magnetic Fields in the Solar Photosphere. II. Bernoulli Effect, Astrophysical Journal 190 (1974) 429.
(8) E.N. Parker, The nature of the sunspot phenomenon: I: Solutions of the heat transport equation, Solar Physics 36 (1974) 249–274.
(9) E.N. Parker, The generation of magnetic fields in astrophysical bodies. XI. The effect of magnetic buoyancy on the growth and migration of dynamo waves in the sun., Astrophysical Journal 215 (1977) 370.
(10) V.D. Rusov, I.V. Sharph, V.P. Smolyar, M.V. Eingorn and M.E. Beglaryan, Coronal heating problem solution by means of axion origin photons, Physics of the Dark Universe 31 (2021) 100746.
(11) A.V. Ettingshausen and W. Nernst, Ueber das auftreten electromotorischer kräfte in metallplatten, welche von einem wärmestrome durchflossen werden und sich im magnetischen felde befinden, Wied. Ann. 29 (1886) 343.
(12) E.H. Sondheimer, The theory of the galvanomagnetic and thermomagnetic effects in metals, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 193 (1948) 484.
(13) L.J. Spitzer, Physics of Fully Ionized Gases, John Wiley & Sons, Inc., New York (1956).
(14) Y.B. Kim and M.J. Stephen in Superconductivity, R. Parks, ed., vol. 2, (New York), Dekker (1969).
(15) W.A. Fowler, G.R. Burbidge and E.M. Burbidge, Nuclear reactions and element synthesis in the surface of stars., Astrophysical Journal Supplement 2 (1955) 167.
(16) S. Couvidat, S. Turck-Chièze and A.G. Kosovichev, Solar seismic models and the neutrino predictions, The Astrophysical Journal 599 (2003) 1434.
(17) T.G. Cowling, The magnetic field of sunspots, Monthly Notices of the Royal Astronomical Society 94 (1933) 39.
(18) S. Sanchez, A. Fournier and J. Aubert, The Predictability of Advection-dominated Flux-transport Solar Dynamo Models, Astrophysical Journal 781 (2014) 8.
(19) L.J. Spitzer, Physics of Fully Ionized Gases, Interscience Publishers, John Wiley & Sons, New York, 2nd ed. (1962).
(20) L.J. Spitzer, Physics of Fully Ionized Gases, Dover Publications, Inc., Mineola, New York, 2nd ed. (2006).
(21) V. Rusov, M. Eingorn, I. Sharph, V. Smolyar and M. Beglaryan, “Thermomagnetic Ettingshausen-Nernst effect in tachocline and axion mechanism of solar luminosity variations.” 2015.
(22) G.G. Raffelt, Axions and other very light bosons: Part II (astrophysical constraints), Phys. Lett. 592 (2004) 391.
(23) G.G. Raffelt, Astrophysical axion bounds, Lect. Notes Phys. 741 (2008) 51.
(24) R.D. Peccei and H.R. Quinn, Cp conservation in the presence of pseudoparticles, Physical Review Letters 38 (1977) 1440–1443.
(25) R.D. Peccei and H.R. Quinn, Constraints imposed by $\mathrm{CP}$ conservation in the presence of pseudoparticles, Phys. Rev. D 16 (1977) 1791.
(26) J. Preskill, M.B. Wise and F. Wilczek, Cosmology of the invisible axion, Physics Letters B 120 (1983) 127.
(27) L. Abbott and P. Sikivie, A cosmological bound on the invisible axion, Physics Letters B 120 (1983) 133.
(28) M. Dine and W. Fischler, The not-so-harmless axion, Physics Letters B 120 (1983) 137.
(29) M. Kawasaki and K. Nakayama, Axions: Theory and cosmological role, Annual Review of Nuclear and Particle Science 63 (2013) 69–95.
(30) D.J. Marsh, Axion cosmology, Physics Reports 643 (2016) 1 .
(31) L. Di Luzio, M. Giannotti, E. Nardi and L. Visinelli, The landscape of qcd axion models, Physics Reports 870 (2020) 1–117.
(32) P. Sikivie, Invisible axion search methods, Reviews of Modern Physics 93 (2021) 015004.
(33) M.S. Turner, Early-universe thermal production of not-so-invisible axions, Phys. Rev. Lett. 59 (1987) 2489.
(34) M. Archidiacono, T. Basse, J. Hamann, S. Hannestad, G. Raffelt and Y.Y. Wong, Future cosmological sensitivity for hot dark matter axions, Journal of Cosmology and Astroparticle Physics 2015 (2015) 050.
(35) CAST Collaboration, New cast limit on the axion–photon interaction, Nature Physics 13 (2017) 584–590.
(36) L. Di Luzio, G. Martinelli and G. Piazza, Breakdown of chiral perturbation theory for the axion hot dark matter bound, Phys. Rev. Lett. 126 (2021) 241801.
(37) A. Shafieloo, D.K. Hazra, V. Sahni and A.A. Starobinsky, Metastable dark energy with radioactive-like decay, Monthly Notices of the Royal Astronomical Society 473 (2017) 2760.
(38) M.S. Turner, Cosmic and local mass density of “invisible” axions, Phys. Rev. D 33 (1986) 889.
(39) E. Armengaud, D. Attié, S. Basso, P. Brun, N. Bykovskiy, J. Carmona et al., Physics potential of the international axion observatory (iaxo), Journal of Cosmology and Astroparticle Physics 2019 (2019) 047–047.
(40) K.M. Backes, D.A. Palken, S.A. Kenany, B.M. Brubaker, S.B. Cahn, A. Droster et al., A quantum enhanced search for dark matter axions, Nature 590 (2021) 238.
(41) B.M. Brubaker, L. Zhong, S.K. Lamoreaux, K.W. Lehnert and K.A. van Bibber, HAYSTAC axion search analysis procedure, Physical Review D 96 (2017) 123008.
(42) C. Boutan, M. Jones, B.H. LaRoque, N.S. Oblath, R. Cervantes, N. Du et al., Piezoelectrically tuned multimode cavity search for axion dark matter, Physical Review Letters 121 (2018) 261302.
(43) V. Domcke, Y. Ema, K. Mukaida and M. Yamada, Spontaneous baryogenesis from axions with generic couplings, Journal of High Energy Physics 2020 (2020) 96.
(44) Particle Data Group, Review of Particle Physics, Progress of Theoretical and Experimental Physics 2020 (2020) .
(45) K.K. Merkotan, T.M. Zelentsova, N.O. Chudak, D.A. Ptashynskyi, V.V. Urbanevich, O.S. Potiienko et al., An Alternative Method for Solving Two Problems of the Standard Model, ArXiv e-prints (2017) [1711.01914].
(46) K.K. Merkotan, T.M. Zelentsova, N.O. Chudak, D.A. Ptashynskiy, V.V. Urbanevich, O.S. Potiienko et al., Multi-particle fields and higgs mechanism, Journal of Physical Studies 22 (2018) .
(47) D.A. Ptashynskiy, T.M. Zelentsova, N.O. Chudak, K.K. Merkotan, O.S. Potiienko, V.V. Voitenko et al., Multiparticle fields on the subset of simultaneity, Ukrainian Journal of Physics 64 (2019) 732.
(48) A.C. Vincent, P. Scott and A. Serenelli, Updated constraints on velocity and momentum-dependent asymmetric dark matter, Journal of Cosmology and Astroparticle Physics 11 (2016) 007 [1605.06502].
(49) R.T. Co and K. Harigaya, Axiogenesis, Phys. Rev. Lett. 124 (2020) 111602.
(50) R.T. Co, N. Fernandez, A. Ghalsasi, L.J. Hall and K. Harigaya, Lepto-axiogenesis, Journal of High Energy Physics 2021 (2021) 17.
(51) G.D.O. Gann, Everything under the sun: A review of solar neutrinos, AIP Conference Proceedings 1666 (2015) 090003.
(52) Borexino Collaboration, Sensitivity to neutrinos from the solar CNO cycle in Borexino, The European Physical Journal C 80 (2020) 1091.
(53) Borexino Collaboration, Experimental evidence of neutrinos produced in the cno fusion cycle in the sun, Nature 587 (2020) 577.
(54) N. Tapia-Arellano and S. Horiuchi, Measuring solar neutrinos over gigayear timescales with paleo detectors, Physical Review D 103 (2021) 123016.
(55) N. Grevesse and A.J. Sauval, Standard Solar Composition, Space Science Reviews 85 (1998) 161.
(56) M. Asplund, N. Grevesse, A.J. Sauval and P. Scott, The Chemical Composition of the Sun, Annual Review of Astron and Astrophys 47 (2009) 481 [0909.0948].
(57) N. Vinyoles, A. Serenelli, F.L. Villante, S. Basu, J. Redondo and J. Isern, New axion and hidden photon constraints from a solar data global fit, Journal of Cosmology and Astroparticle Physics 10 (2015) 015 [1501.01639].
(58) A.C. Vincent, P. Scott and A. Serenelli, Possible Indication of Momentum-Dependent Asymmetric Dark Matter in the Sun, Physical Review Letters 114 (2015) 081302 [1411.6626].
(59) A.C. Vincent, A. Serenelli and P. Scott, Generalised form factor dark matter in the Sun, Journal of Cosmology and Astroparticle Physics 8 (2015) 040 [1504.04378].
(60) S. Degl’Innoccenti, W.A. Dziembowski, G. Fiorentini and B. Ricci, Helioseismology and standard solar models, Astroparticle Physics 7 (1997) 77 [astro-ph/9612053].
(61) G. Fiorentini, B. Ricci and F. Villante, Helioseismology and screening of nuclear reactions in the sun, Physics Letters B 503 (2001) 121 .
(62) Planck Collaboration, Planck 2015 results - xiii. cosmological parameters, A&A 594 (2016) A13.
(63) C. Patrignani and Particle Data Group, Review of Particle Physics, Chinese Physics C 40 (2016) 100001.
(64) S. Nussinov, Technocosmology – could a technibaryon excess provide a “natural” missing mass candidate?, Physics Letters B 165 (1985) 55–58.
(65) R. Chivukula and T.P. Walker, Technicolor cosmology, Nuclear Physics B 329 (1990) 445–463.
(66) S. Barr, R. Sekhar Chivukula and E. Farhi, Electroweak fermion number violation and the production of stable particles in the early universe, Physics Letters B 241 (1990) 387–391.
(67) D.B. Kaplan, Single explanation for both baryon and dark matter densities, Physical Review Letters 68 (1992) 741–743.
(68) D. Hooper, J. March-Russell and S.M. West, Asymmetric sneutrino dark matter and the $\omega_{b}$ / $\omega_{DM}$ puzzle, Physics Letters B 605 (2005) 228–236.
(69) D.E. Kaplan, M.A. Luty and K.M. Zurek, Asymmetric dark matter, Physical Review D 79 (2009) 115016.
(70) H. Davoudiasl and R.N. Mohapatra, On relating the genesis of cosmic baryons and dark matter, New Journal of Physics 14 (2012) 095011.
(71) K. Petraki and R.R. Volkas, Review of Asymmetric Dark Matter, International Journal of Modern Physics A 28 (2013) 1330028 [1305.4939].
(72) K.M. Zurek, Asymmetric Dark Matter: Theories, signatures, and constraints, Physics Reports 537 (2014) 91 [1308.0338].
(73) P.W. Graham, I.G. Irastorza, S.K. Lamoreaux, A. Lindner and K.A. van Bibber, Experimental searches for the axion and axion-like particles, Annual Review of Nuclear and Particle Science 65 (2015) 485–514.
(74) A.D. Goulding, J.E. Greene, R. Bezanson, J. Greco, S. Johnson, A. Leauthaud et al., Galaxy interactions trigger rapid black hole growth: An unprecedented view from the Hyper Suprime-Cam survey, Publications of the Astronomical Society of Japan 70 (2018) S37 [1706.07436].
(75) J.-W. Hsueh, W. Enzi, S. Vegetti, M.W. Auger, C.D. Fassnacht, G. Despali et al., SHARP – VII. New constraints on the dark matter free-streaming properties and substructure abundance from gravitationally lensed quasars, Monthly Notices of the Royal Astronomical Society 492 (2019) 3047.
(76) D. Gilman, S. Birrer, A. Nierenberg, T. Treu, X. Du and A. Benson, Warm dark matter chills out: constraints on the halo mass function and the free-streaming length of dark matter with eight quadruple-image strong gravitational lenses, Monthly Notices of the Royal Astronomical Society 491 (2019) 6077.
(77) F. Wilczek, Problem of strong $p$ and $t$ invariance in the presence of instantons, Phys. Rev. Lett. 40 (1978) 279.
(78) S. Weinberg, A new light boson?, Physical Review Letters 40 (1978) 223–226.
(79) D.H. Hathaway, The solar cycle, Living Reviews in Solar Physics 12 (2015) 4.
(80) T.G. Cowling, The solar system, vol. 1, (Chicago), p. 532, The University of Chicago Press (1953).
(81) G.E. Hale, On the probable existence of a magnetic field in sun-spots, Astrophysical Journal 28 (1908) 315.
(82) J. Evershed, Radial movement in sun-spots, Monthly Notices of the Royal Astronomical Society 69 (1909) 454.
(83) S.K. Solanki, Sunspots: An overview, The Astronomy and Astrophysics Review 11 (2003) 153.
(84) J.M. Borrero and K. Ichimoto, Magnetic structure of sunspots, Living Reviews in Solar Physics 8 (2011) 4.
(85) S.K. Tiwari, M. van Noort, S.K. Solanki and A. Lagg, Depth-dependent global properties of a sunspot observed by hinode using the solar optical telescope/spectropolarimeter, A&A 583 (2015) A119.
(86) S.E. Pozuelo, L.R.B. Rubio and J. de la Cruz Rodríguez, Lateral downflows in sunspot penumbral filaments and their temporal evolution, The Astrophysical Journal 803 (2015) 93.
(87) G. Guerrero and P.J. Käpylä, Dynamo action and magnetic buoyancy in convection simulations with vertical shear, A&A 533 (2011) A40.
(88) N.J. Nelson, B.P. Brown, A.S. Brun, M.S. Miesch and J. Toomre, Magnetic wreaths and cycles in convective dynamos, The Astrophysical Journal 762 (2013) 73.
(89) P.J. Käpylä, M.J. Mantere, E. Cole, J. Warnecke and A. Brandenburg, Effects of enhanced stratification on equatorward dynamo wave propagation, The Astrophysical Journal 778 (2013) 41.
(90) A.C. Birch, D.C. Braun, K.D. Leka, G. Barnes and B. Javornik, Helioseismology of pre-emerging active regions. ii. average emergence properties, The Astrophysical Journal 762 (2013) 131.
(91) A.C. Birch, H. Schunker, D.C. Braun, R. Cameron, L. Gizon, B. Löptien et al., A low upper limit on the subsurface rise speed of solar active regions, Science Advances 2 (2016) .
(92) R. Stein, Solar surface magneto-convection, Living Rev.Solar Phys. 9 (2012) 4.
(93) S.M. Hanasoge, T.L.D. Jr and M.L. DeRosa, Seismic constraints on interior solar convection, The Astrophysical Journal Letters 712 (2010) L98.
(94) S.M. Hanasoge, T.L. Duvall and K.R. Sreenivasan, Anomalously weak solar convection, Proceedings of the National Academy of Sciences 109 (2012) 11928.
(95) S. Hanasoge, M.S. Miesch, M. Roth, J. Schou, M. Schüssler and M.J. Thompson, Solar dynamics, rotation, convection and overshoot, Space Science Reviews 196 (2015) 79.
(96) L. Gizon and A.C. Birch, Helioseismology challenges models of solar convection, Proceedings of the National Academy of Sciences 109 (2012) 11896.
(97) J. Bahcall and M. Pinsonneault, Standard solar models, with and without helium diffusion, and the solar neutrino problem, Rev. Mod. Phys. 64 (1992) 885.
(98) A. Kolmogorov, The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers, Akademiia Nauk SSSR Doklady 30 (1941) 301.
(99) A.N. Kolmogorov, Local structure of turbulence in an incompressible viscous fluid at very high reynolds numbers, Soviet Physics Uspekhi 10 (1968) 734.
(100) A.N. Kolmogorov, The local structure of turbulence in incompressible viscous fluid for very large reynolds numbers, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 434 (1991) 9.
(101) E.N. Parker, Theoretical properties of $\Omega$ -loops in the connection zone of the sun. I. emerging bipolar magnetic regions, The Astrophysics Journal 433 (1994) 867.
(102) S. Jabbari, Origin of solar surface activity and sunspots, Ph.D. thesis, Stockholm University, Faculty of Science, Department of Astronomy. NORDITA., 2016.
(103) A.W. Baggaley, C.F. Barenghi, A. Shukurov and K. Subramanian, Reconnecting flux-rope dynamo, Phys. Rev. E 80 (2009) 055301.
(104) N.F. Loureiro, D.A. Uzdensky, A.A. Schekochihin, S.C. Cowley and T.A. Yousef, Turbulent magnetic reconnection in two dimensions, Monthly Notices of the Royal Astronomical Society: Letters 399 (2009) L146.
(105) Y.-M. Huang and A. Bhattacharjee, Scaling laws of resistive magnetohydrodynamic reconnection in the high-lundquist-number, plasmoid-unstable regime, Physics of Plasmas 17 (2010) 062104.
(106) A. Beresnyak, Three-dimensional Spontaneous Magnetic Reconnection, Astrophysical Journal 834 (2017) 47 [1301.7424].
(107) H.C. Spruit, A.M. Title and A.A. Van Ballegooijen, Is there a weak mixed polarity background field? theoretical arguments, Solar Physics 110 (1987) 115.
(108) P.R. Wilson, P.S. McIntosh and H.B. Snodgrass, The reversal of the solar polar magnetic fields, Solar Physics 127 (1990) 1.
(109) E.N. Parker, Solar magnetism: The state of our knowledge and ignorance, Space Sci. Rev. 122 (2009) 15.
(110) H.C. Spruit and A.A. van Ballegooijen, Stability of toroidal flux tubes in stars, Astronomy and Astrophysics 106 (1982) 58.
(111) E.N. Parker, The generation of magnetic fields in astrophysical bodies. X - Magnetic buoyancy and the solar dynamo, Astrophysical Journal 198 (1975) 205.
(112) E.N. Parker, Cosmical magnetic fields: Their origin and their activity, Oxford, Clarendon Press (1979).
(113) A.A. van Ballegooijen, The overshoot layer at the base of the solar convective zone and the problem of magnetic flux storage, Astronomy and Astrophysics 113 (1982) 99.
(114) E. Böhm-Vitense, Über die wasserstoffkonvektionszone in sternen verschiedener effektivtemperaturen und leuchtkräfte. mit 5 textabbildungen, Zeitschrift fuer Astrophysik 46 (1958) 108.
(115) H.C. Spruit, Magnetic Flux Tubes and Transport of Heat, Ph.D. thesis, Ph. D. Thesis, Utrecht University, 1977.
(116) A.S. Brun, M.S. Miesch and J. Toomre, Modeling the dynamical coupling of solar convection with the radiative interior, The Astrophysical Journal 742 (2011) 79.
(117) R. Smolec and P. Moskalik, Convective hydrocodes for radial stellar pulsation. physical and numerical formulation, Acta Astronomica 58 (2008) 193 [0809.1979].
(118) R. Smolec and P. Moskalik, Non-linear modelling of beat cepheids: resonant and non-resonant models, A&A 524 (2010) A40.
(119) H. Spruit, A model of the solar convective zone, Solar Physics 34 (1974) 277.
(120) J. Christensen-Dalsgaard, M.J.P.F.G. Monteiro and M.J. Thompson, Helioseismic estimation of convective overshoot in the sun, Monthly Notices of the Royal Astronomical Society 276 (1995) 283.
(121) J. Christensen-Dalsgaard, M.J.P.F.G. Monteiro, M. Rempel and M.J. Thompson, A more realistic representation of overshoot at the base of the solar convective envelope as seen by helioseismology, Monthly Notices of the Royal Astronomical Society 414 (2011) 1158.
(122) Y. Fan and G. Fisher, Radiative heating and the buoyant rise of magnetic flux tubes in the solar interior, Solar Phys. 166 (1996) 17.
(123) M.A. Weber and Y. Fan, Effects of radiative diffusion on thin flux tubes in turbulent solar-like convection, Solar Physics 290 (2015) 1295 [1503.08034].
(124) M.A. Weber and M.K. Browning, Modeling the rise of fibril magnetic fields in fully convective stars, The Astrophysical Journal 827 (2016) 95.
(125) Y. Fan, G.H. Fisher and E.E. Deluca, The origin of morphological asymmetries in bipolar active regions, Astrophysical Journal 405 (1993) 390.
(126) C. Zwaan, Elements and patterns in the solar magnetic field, Annual Review of Astronomy and Astrophysics 25 (1987) 83.
(127) J.E. Bailey, G.A. Rochau, R.C. Mancini, C.A. Iglesias, J.J. Macfarlane, I.E. Golovkin et al., Experimental investigation of opacity models for stellar interior, inertial fusion, and high energy density plasmas, Physics of Plasmas 16 (2009) 058101.
(128) A.G. Kosovichev, J. Zhao and S. Ilonidis, Local Helioseismology of Emerging Active Regions: A Case Study, ArXiv e-prints (2016) [1607.04987].
(129) S. Ilonidis, J. Zhao and T. Hartlep, Helioseismic investigation of emerging magnetic flux in the solar convection zone, The Astrophysical Journal 777 (2013) 138.
(130) A.G. Kosovichev and J. Duvall, T. L., Local Helioseismology and Magnetic Flux Emergence, in Subsurface and Atmospheric Influences on Solar Activity, R. Howe, R.W. Komm, K.S. Balasubramaniam and G.J.D. Petrie, eds., vol. 383 of Astronomical Society of the Pacific Conference Series, p. 59, Jan., 2008.
(131) A. Kosovichev, T. Duvall JR. and P. Scherrer, Time-distance inversion methods and results – (invited review), Solar Physics 192 (2000) 159–176.
(132) S. Zharkov and M.J. Thompson, Time – distance analysis of the emerging active region noaa 10790, Solar Physics 251 (2008) 369–380.
(133) S. Toriumi, S. Ilonidis, T. Sekii and T. Yokoyama, PROBING THE SHALLOW CONVECTION ZONE: RISING MOTION OF SUBSURFACE MAGNETIC FIELDS IN THE SOLAR ACTIVE REGION, The Astrophysical Journal 770 (2013) L11.
(134) S. Ilonidis, J. Zhao and A. Kosovichev, Response to comment on “detection of emerging sunspot regions in the solar interior”, Science 336 (2012) 296.
(135) Y. Fan, Magnetic fields in the solar convection zone, Living Reviews in Solar Physics 18 (2021) 5.
(136) P. Charbonneau, Dynamo models of the solar cycle, Living Reviews in Solar Physics 17 (2020) 4.
(137) H. Hotta and H. Iijima, On rising magnetic flux tube and formation of sunspots in a deep domain, Monthly Notices of the Royal Astronomical Society 494 (2020) 2523.
(138) S. Jabbari, A. Brandenburg, D. Mitra, N. Kleeorin and I. Rogachevskii, Turbulent reconnection of magnetic bipoles in stratified turbulence, Monthly Notices of the Royal Astronomical Society 459 (2016) 4046.
(139) K. Petrovay and L. van Driel-Gesztelyi, Making sense of sunspot decay. i. parabolic decay law and gnevyshev–waldmeier relation, Solar Physics 176 (1997) 249.
(140) A.R. Choudhuri and P.A. Gilman, The influence of the Coriolis force on flux tubes rising through the solar convection zone, Astrophysical Journal 316 (1987) 788.
(141) M.K. Browning, M.A. Weber, G. Chabrier and A.P. Massey, Theoretical Limits on Magnetic Field Strengths in Low-mass Stars, Astrophysical Journal 818 (2016) 189 [1512.05692].
(142) M. Dasi-Espuig, S.K. Solanki, N.A. Krivova, R. Cameron and T. Peñuela, Sunspot group tilt angles and the strength of the solar cycle, Astronomy and Astrophysics 518 (2010) A7 [1005.1774].
(143) M. Dasi-Espuig, Solanki, S. K., Krivova, N. A., Cameron, R. and Peñuela, T., Sunspot group tilt angles and the strength of the solar cycle (corrigendum), A&A 556 (2013) C3.
(144) V.G. Ivanov, Joy’s law and its features according to the data of three sunspot catalogs, Geomagnetism and Aeronomy 52 (2012) 999.
(145) B.H. McClintock and A.A. Norton, Recovering Joy’s Law as a Function of Solar Cycle, Hemisphere, and Longitude, Solar Physics 287 (2013) 215 [1305.3205].
(146) A.A. Pevtsov, L. Bertello, A.G. Tlatov, A. Kilcik, Y.A. Nagovitsyn and E.W. Cliver, Cyclic and Long-Term Variation of Sunspot Magnetic Fields, Solar Physics 289 (2014) 593 [1301.5935].
(147) K.A. Tlatova, V.V. Vasil’eva and A.A. Pevtsov, Long-term variations in the sunspot magnetic fields and bipole properties from 1918 to 2014, Geomagnetism and Aeronomy 55 (2015) 896.
(148) Senthamizh Pavai, V., Arlt, R., Dasi-Espuig, M., Krivova, N. A. and Solanki, S. K., Sunspot areas and tilt angles for solar cycles 7-10, A&A 584 (2015) A73.
(149) T. Baranyi, Comparison of debrecen and mount wilson/kodaikanal sunspot group tilt angles and the joy’s law, Monthly Notices of the Royal Astronomical Society 447 (2015) 1857.
(150) Y.-M. Wang, R.C. Colaninno, T. Baranyi and J. Li, Active-region Tilt Angles: Magnetic versus White-light Determinations of Joy’s Law, Astrophysical Journal 798 (2015) 50 [1412.2329].
(151) Y.-M. Wang, Surface Flux Transport and the Evolution of the Sun’s Polar Fields, Space Science Reviews 210 (2017) 351.
(152) A.R. Choudhuri, The evolution of loop structures in flux rings within the solar convection zone, Solar Physics 123 (1989) 217.
(153) S. D’Silva and A.R. Choudhuri, A theoretical model for tilts of bipolar magnetic regions, Astronomy and Astrophysics 272 (1993) 621.
(154) A.A. Pevtsov, Y.A. Nagovitsyn, A.G. Tlatov and A.L. Rybak, Long-term trends in sunspot magnetic fields, The Astrophysical Journal Letters 742 (2011) L36.
(155) M. Schüssler and M. Rempel, Structure of the magnetic field in the lower convection zone, in From Solar Min to Max: Half a Solar Cycle with SOHO, A. Wilson, ed., vol. 508 of ESA Special Publication, pp. 499–506, June, 2002.
(156) Y. Fan, Magnetic fields in the solar convective zone, Living Rev.Solar Phys. 6 (2009) 4.
(157) V.N. Krivodubskij, Turbulent dynamo near tachocline and reconstruction of azimuthal magnetic field in the solar convection zone, Astronomische Nachrichten 326 (2005) 61.
(158) A.A. van Ballegooijen and A.R. Choudhuri, The possible role of meridional flows in suppressing magnetic buoyancy, Astrophysical Journal 333 (1988) 965.
(159) S.A. Khaibrakhmanov, A.E. Dudorov, S.Y. Parfenov and A.M. Sobolev, Large-scale magnetic field in the accretion discs of young stars: the influence of magnetic diffusion, buoyancy and Hall effect, Monthly Notices of the RAS 464 (2017) 586 [1609.03969].
(160) B. Roberts and P. Murdin, Solar photospheric magnetic flux tubes: theory, 2001.
(161) V. Rusov, M. Eingorn, I. Sharph, V. Smolyar and M. Beglaryan, “Thermomagnetic ettingshausen-nernst effect in tachocline, magnetic reconnection phenomenon in lower layers, axion mechanism of solar luminosity variations, coronal heating problem solution and mechanism of dark matter spike variations around black hole.” 2019.
(162) M. Stix and D. Skaley, The equation of state and the frequencies of solar P modes, Astronomy and Astrophysics 232 (1990) 234.
(163) M. Stix, The Sun: An Introduction, Springer, Berlin (2004).
(164) L.L. Kichatinov, Turbulent transport of magnetic fields in a highly conducting rotating fluid and the solar cycle, Astronomy and Astrophysics 243 (1991) 483.
(165) Y.B. Zel’dovich, The magnetic field in two-dimensional motion of a conducting turbulent liquid, Sov. Phys. JETP 4 (1957) 460.
(166) K.-H. Rädler, Zur elektrodynamik turbulent bewegter leitender medien. i. grundzüge der elektrodynamik der mittleren felder, Zeitschrift für Naturforschung A 23 (1968) 1841.
(167) K.-H. Rädler, Zur elektrodynamik turbulent bewegter leitender medien. ii. turbulenzbedingte leitfähigkeits- und permeabilitätsänderungen, Zeitschrift für Naturforschung A 23 (1968) 1841.
(168) S.I. Vainshtein, Y.B. Zel’dovich and A.A. Ruzmaikin, The Turbulent Dynamo in Astrophysics, Nauka, Moscow (1980).
(169) S.I. Vainshtein and L.L. Kichatinov, The macroscopic magnetohydrodynamics of inhomogeneously turbulent cosmic plasmas, Geophysical & Astrophysical Fluid Dynamics 24 (1983) 273.
(170) M. Stix, The Sun. an Introduction, Springer-Verlag Berlin Heidelberg (1989), 10.1007/978-3-642-97129-7.
(171) L.L. Kichatinov and G. Ruediger, Magnetic-field advection in inhomogeneous turbulence, Astronomy and Astrophysics 260 (1992) 494.
(172) L.L. Kitchatinov and A.A. Nepomnyashchikh, Diamagnetic pumping in a rotating convection zone, Advances in Space Research 58 (2016) 1554 .
(173) E.M. Drobyshevski and V.S. Yuferev, Topological pumping of magnetic flux by three-dimensional convection, Journal of Fluid Mechanics 65 (1974) 33–44.
(174) S. Vainshtein, Magnetic Fields in Space, Nauka, Moscow (1983).
(175) M. Ossendrijver, M. Stix, A. Brandenburg and G. Rüdiger, Magnetoconvection and dynamo coefficients - ii. field-direction dependent pumping of magnetic field, A&A 394 (2002) 735.
(176) L.L. Kitchatinov and S.V. Olemskoy, Solar dynamo model with diamagnetic pumping and nonlocal $\alpha$ -effect, Solar Physics 276 (2012) 3 [1108.3138].
(177) A.E. Dudorov and A.K. Kirillov, Dynamics of magnetic flux tubes in the convection zone of the sun., Byulletin Solnechnye Dannye Akademie Nauk SSSR 1985 (1986) 85.
(178) W. Y.-M., N.R. Sheeley, Jr. and A.G. Nash, A new solar cycle model including meridional circulation, Astrophysical Journal 383 (1991) 431.
(179) A.R. Choudhuri, M. Schüssler and M. Dikpati, The solar dynamo with meridional circulation., Astronomy and Astrophysics 303 (1995) L29.
(180) P. Caligari, F. Moreno-Insertis and M. Schussler, Emerging flux tubes in the solar convection zone. 1: Asymmetry, tilt, and emergence latitude, Astrophysical Journal 441 (1995) 886.
(181) D. Nandy and A.R. Choudhuri, Explaining the latitudinal distribution of sunspots with deep meridional flow, Science 296 (2002) 1671.
(182) Y.B. Zel’dovich, Magnetic field at two-dimensional motion of conducting liquid, Sov. Phys. JETP 31 (1956) 154.
(183) L.L. Kitchatinov and G. Rüdiger, Diamagnetic pumping near the base of a stellar convection zone, Astronomische Nachrichten 329 (2008) 372.
(184) F. Krause and K.-H. Raedler, Mean-field magnetohydrodynamics and dynamo theory, Pergamon Press (1980), 10.1016/C2013-0-03269-0.
(185) L.L. Kichatinov, A mechanism for differential rotation based on angular momentum transport by compressible convection, Geophysical & Astrophysical Fluid Dynamics 38 (1987) 273–292.
(186) P. Bradshaw, Possible origin of prandt’s mixing-length theory, Nature 249 (1974) 135.
(187) D.O. Gough, Mixing-length theory for pulsating stars, Astrophysical Journal 214 (1977) 196.
(188) D. Gough, The current state of stellar mixing-length theory, in Problems of Stellar Convection, E.A. Spiegel and J.-P. Zahn, eds., vol. 71 of Lecture Notes in Physics, Berlin Springer Verlag, 1977, DOI.
(189) A.J. Barker, A.M. Dempsey and Y. Lithwick, Theory and simulations of rotating convection, The Astrophysical Journal 791 (2014) 13.
(190) A. Brandenburg, Stellar mixing length theory with entropy rain, The Astrophysical Journal 832 (2016) 6.
(191) D.O. Gough and N.O. Weiss, The calibration of stellar convection theories, Monthly Notices of the Royal Astronomical Society 176 (1976) 589.
(192) B.B. Karak, J. Jiang, M.S. Miesch, P. Charbonneau and A.R. Choudhuri, Flux transport dynamos: From kinematics to dynamics, Space Science Reviews 186 (2014) 561.
(193) Käpylä, P. J., Käpylä, M. J. and Brandenburg, A., Confirmation of bistable stellar differential rotation profiles, A&A 570 (2014) A43.
(194) M. Ossendrijver, The solar dynamo, Astronomy and Astrophysicsr 11 (2003) 287.
(195) A. Brandenburg and K. Subramanian, Astrophysical magnetic fields and nonlinear dynamo theory, Physics Reports 417 (2005) 1 .
(196) P. Käpylä, On global solar dynamo simulations, Astronomische Nachrichten 332 (2011) 43.
(197) P. Käpylä, M. Mantere and A. Brandenburg, Effects of stratification in spherical shell convection, Astronomische Nachrichten 332 (2011) 883.
(198) V. Gaizauskas, K.L. Harvey, J.W. Harvey and C. Zwaan, Large-scale patterns formed by solar active regions during the ascending phase of cycle 21, Astrophysical Journal 265 (1983) 1056.