Theoretical Prediction of High-Temperature Superconductivity in SrAuH3 at Ambient Pressure
Abstract
We present a comprehensive computational investigation of electron-phonon interactions in MXH3 hydride compounds, where represents alkali and post-transition metals, and denotes 3, 4, and 5 transition metals. Our density functional theory calculations identify 17 dynamically stable compounds. Notably, SrAuH3 and SrZnH3 emerge as theoretical ambient-pressure superconductors with predicted critical temperatures () exceeding 100 K. Analysis of the electronic structure reveals that the component dominates the density of states at the Fermi level, playing a crucial role in determining electron-phonon coupling strength and superconducting properties. We elucidate the underlying mechanisms governing these properties through detailed examination of the electronic and vibrational spectra. Our findings may challenge the prevailing notion that high- superconductivity in hydrides requires extreme pressures, potentially paving the way for practical applications. This study also provides valuable insights to guide future experimental efforts in the synthesis of ambient-pressure hydride superconductors.
I Introduction
Hydrogen-based superconductors have emerged as a major focus in condensed matter physics, distinct from iron-based and nickel-based superconductors [1, 2]. These materials, notable for their diverse structures, rich symmetry, and potential for room-temperature superconductivity, have sparked intense research aimed at reducing their stabilization pressure while maintaining high transition temperatures. This pursuit of stable high-temperature hydrogen-based superconductors under ambient or mild pressure conditions has become a cutting-edge topic in the field. The theoretical foundation for this research lies in Bardeen-Cooper-Schrieffer (BCS) theory [3], which relates the superconducting critical temperature () to the Debye temperature. Metallic hydrogen, with its exceptionally high Debye temperature and strong electron-phonon coupling, has long been predicted to be a high superconductor [4, 5], driving the exploration of hydrogen-rich compounds as potential high-temperature superconductors.
Recent decades have seen significant breakthroughs in hydride superconductors, driven by advancements in high-pressure experimental techniques [6, 7, 8] and crystal structure prediction methods [9, 10, 11]. Binary hydrides like H3S [12], LaH10 [13, 14], and YH9 [13, 15] have been experimentally confirmed to exhibit above 200 K under high pressures. Research has expanded to ternary hydrogen-rich compounds, with theoretical predictions suggesting even higher values, such as 473 K for Li2MgH16 at 250 GPa [16]. Experimentally, (La, Ce)H9,10 has demonstrated a of 176 K at 100 GPa [21]. Incorporating anharmonic corrections often significantly influences the minimum pressures required for dynamical stability. For instance, in BaSiH8 and SrSiH8, the stable pressure ranges are strongly affected [17, 18]. Similarly, the stability threshold is reduced to 77 GPa for LaBH8 [19] and to 129 GPa for LaH10 [20]. Ternary hydrides following the ABH8 template [22, 23, 24, 19] have been experimentally realized, with LaBeH8 exhibiting a of 110 K at 80 GPa [25]. Despite these advances, room-temperature superconductivity remains elusive, and the focus is shifting towards discovering materials that can achieve superconductivity at ambient or low pressures for practical applications. This evolving landscape encompasses polyhydrides, emphasizing the need for new hydrogen-based materials that balance high with feasible external pressure conditions.
Doping and elemental substitution in hydride compounds offer possible avenues for modifying atomic interactions and potentially lowering the pressure required for superconductivity. While introducing magnesium into methane produces -MgCH4 with a of 120 K under high pressure [26], incorporating iron into H3S to form Fe2SH3 drastically reduces the superconducting transition temperature to 0.3 K [27]. Recently, high-throughput computational screening predicted a metastable ambient-pressure hydride superconductor, Mg2IrH6, with a critical temperature of 160 K [28], comparable to the highest-temperature superconducting cuprates. These contrasting results highlight the complex interplay of elements in ternary hydrides and underscore the need for systematic exploration of new compositional and structural combinations. Such investigations are crucial for unlocking the potential of ternary hydrides as high-temperature superconductors that can operate at ambient pressure, a key requirement for practical applications. Future studies should focus on exploring a wider range of elemental combinations, investigating the role of crystal structure and chemical bonding, developing computational methods to predict stability and synthesizability, and experimental verification of computational predictions, with emphasis on ambient-pressure synthesis techniques.
In this study, we employ high-throughput computational methods to investigate potential superconductivity in cubic MXH3 compounds under ambient pressure. Here, represents alkali and post-transition metals (Li, Na, Mg, Al, K, Ca, Ga, Rb, Sr, and In), while encompasses 3d, 4d, and 5d transition metals. Using first-principles calculations, we systematically examine the structural stability, electronic structure, phonon spectra, and superconducting properties of these 290 compounds. In the manuscript, we focus on the strontium hydrides: SrXH3 (X = Au, Tc, Zn), which exhibit relatively high . Our screening process prioritizes stability, a crucial factor in determining the feasibility of these materials for further study and potential applications. By focusing on ambient pressure conditions, our research aims to bridge the gap between high- hydrides and practical applications, advancing the field toward viable room-temperature superconductors. This comprehensive approach allows us to explore a wide range of compositions, potentially uncovering candidates for ambient-pressure, high-temperature superconductivity in the MXH3 family.
II Methods
We performed structure optimizations using the ab initio approach implemented in the Quantum Espresso (QE) package [29]. Charge density and wave function cutoff values were set to 600 Ry and 60 Ry, respectively. Self-consistent electron density calculations employed a 242424 -point mesh with a Gaussian smearing of 0.02 Ry. Following convergence tests, we calculated dynamical matrices and vibration potentials on a 888 -point mesh using density functional perturbation theory (DFPT) [30]. An optimized tetrahedron method has been employed for the integration [31]. We utilized Standard solid-state pseudopotentials [32] throughout our calculations. Superconducting critical temperatures were estimated using the Allen-Dynes modified McMillan equation and numerical solutions of the Eliashberg equations [33]. For stable structures, we conducted high-accuracy electronic structure calculations using the full-potential linearized augmented plane wave (FP-LAPW) method implemented in the WIEN2K code [34], applying the generalized gradient approximation (GGA) [35] for exchange-correlation potentials. We visualized crystal structures using VESTA [36] and Fermi surfaces using Fermisurfer [37]. To estimate the superconducting , we employed linear response calculations for e-ph properties and applied the Allen-Dynes modified McMillan formula[38, 33]:
| (1) |
| (2) |
| (3) |
where the logarithmically averaged phonon frequency, the e-ph coupling constant, and the Coulomb pseudopotential (set to 0.13). Factors and represent strong coupling and spectral function corrections, respectively, and depend on , , , and the mean square frequency .
III Results and discussion
The crystal structure of SrAuH3 (Fig. 1(a))crystallizes in the cubic space group (No. 221). Sr, Au, and H atoms occupy 1 (0.5, 0.5, 0.5), 1 (0, 0, 0), and 3 (0, 0, 0.5) Wyckoff positions, respectively, with a calculated lattice constant of 3.828 Å at ambient pressure. The detailed structural parameters and calculated superconducting properties for all 17 dynamically stable MXH3 compounds are presented in Table S1 in Supplemental Material [39]. Figure 1(b) presents a comprehensive heatmap of the calculated superconducting critical temperatures for the MXH3 compounds. Our high-throughput calculations revealed eight dynamically stable structures with = Sr. Among these, SrAuH3, SrTcH3, and SrZnH3 emerge as particularly candidates, with Allen-Dynes predictions of 132 K, 69 K, and 107 K, respectively. The electron-phonon (e-ph) coupling constants for these compounds are 2.025, 1.303, and 1.94, respectively, indicating strong coupling regimes. Notably, SrAuH3 and SrZnH3 exhibit the highest s, surpassing the boiling point of liquid nitrogen. The logarithmic average phonon frequencies for these compounds are 806 K, 655 K, and 681 K, respectively. These results underscore the potential of Sr-based ternary hydrides as ambient-pressure high- superconductors and provide valuable insights into the interplay between electronic structure and lattice dynamics in these systems.
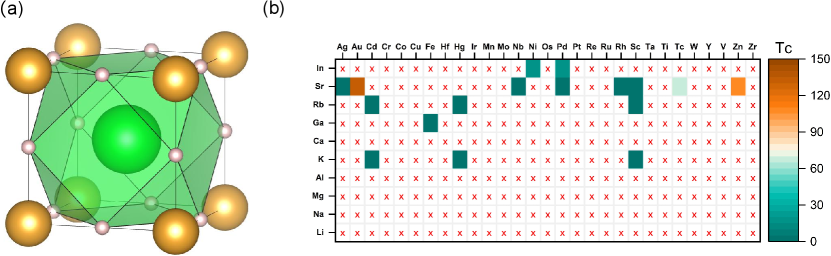
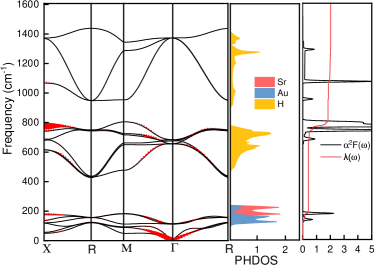
Figure 2 presents the phonon dispersions and projected phonon density of states (PHDOS) for SrAuH3 at ambient pressure. The absence of imaginary frequencies along high-symmetry paths confirms dynamical stability. The highly dispersive top group of phonon spectra, peaking at 1420 cm-1 at the point, is attributed to the hydrogen vibrations. Electron-phonon coupling coefficients are overlaid on the dispersion curves, revealing strong couplings predominantly in acoustic and low-frequency optical modes near the point, possibly due to Au atom contributions. The Eliashberg function and integrated -ph coupling are shown in the right panels. The total -ph coupling and logarithmically averaged phonon frequency are calculated. The coupling integral below 1200 cm-1 accounts for the majority of the total coupling. Phonon spectra and densities of states for SrTcH3 and SrZnH3 are provided in the Supplemental Material [39]. The primitive cell of SrAuH3 contains 5 atoms, yielding 15 phonon bands: 3 acoustic and 12 optical branches, with irreducible representation expressed as 4 1. Low-frequency acoustic branches primarily arise from Sr and Au vibrations, while modes between 200 and 1400 cm-1 are associated with H vibrations. The right panel of Figure 2 shows the Eliashberg spectral function and e-ph coupling integration . The total is predominantly contributed by low- and medium-frequency vibrations.
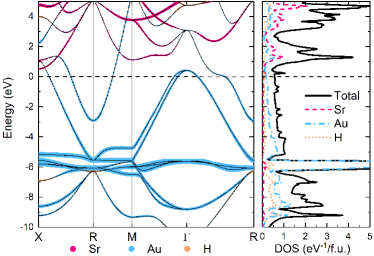
The electronic band structure and atomic projected density of states (DOS) in eV-1/formula unit (f.u.) for SrAuH3 at ambient pressure are shown in Figure 3. The band structure exhibits metallic behavior, evidenced by multiple bands crossing the Fermi level (). Near , Au predominantly contributes to the DOS, with Au orbitals dominating and forming a sharp van Hove singularity (vHs) approximately 0.2 eV above . This vHs significantly enhances the DOS, potentially boosting superconductivity as per BCS theory. The high DOS at , primarily from Au states, likely facilitates strong electron-phonon coupling, possibly explaining SrAuH3’s high critical temperature. For comparison, electronic structures of SrTcH3 and SrZnH3 are provided in the Supplemental Material [39]. Analysis of the electronic band structures reveals that the atoms predominantly contribute to DOS near the Fermi level, underscoring the critical role of the elements in determining the electronic properties of these compounds.
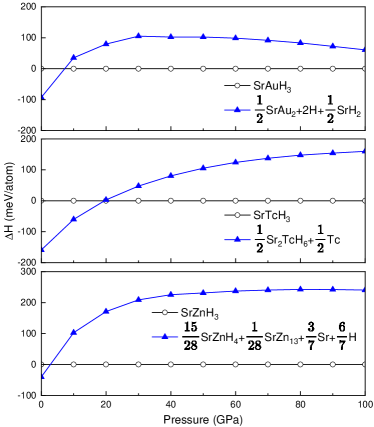
During experimental synthesis, materials can become trapped in local energy minima, known as metastable states, within the energy landscape. Figure 4 shows the calculated enthalpy as a function of pressure for Sr–X–H structures relative to the -SrXH3. SrAuH3 becomes thermodynamically stable above 7 GPa. The enthalpy difference = (SrAu2+4H + SrH2) – (SrAuH3) changes sign from negative to positive at this pressure. This crossover point delineates the stability regions of SrAuH3 with respect to different decomposing phases, elucidating its pressure-driven formation mechanism. The low synthesis pressure of 7 GPa, achievable in multi-anvil apparatus, offers a possible route for experimental realization of this potential high- superconductor. Similarly, SrTcH3 and SrZnH3 undergo phase transitions at 20 GPa and 3 GPa, respectively, with SrTcH3 possibly decomposed into Sr2TcH6 and Tc, and SrZnH3 decomposed into SrZnH4, SrZn13, Sr and H.
Detailed visualization of the Fermi surfaces for SrAuH3 at ambient pressure are shown in Figure 5. The surfaces are color-coded to represent the Fermi velocity distribution, with the spectrum transitioning from blue to red as velocity increases. This complex Fermi surface topology comprises three distinct components: (1) a nearly spherical hole-like sheet centered at the point, dominating the Brillouin zone center; (2) cross-shaped sheets extending along the principal axes, indicative of significant band dispersion in these directions; and (3) eight electron-like pockets located at the Brillouin zone corners ( points). The hole-like character of the central sphere, combined with the electron-like nature of the corner pockets, suggests a compensated metallic behavior. Analysis of the band structure near the Fermi level confirms the predominantly electronic nature of the Fermi surface, with the Au contributing significantly to the density of states at . The observed Fermi surface complexity, particularly the presence of multiple sheets with varying electron and hole characters, may enhance electron-phonon coupling through increased scattering channels. Furthermore, the high Fermi velocities, indicated by the red regions, imply large electronic bandwidths, which could contribute to the predicted high critical temperature in this system. These features collectively suggest that SrAuH3 possesses the electronic characteristics often associated with high-temperature superconductors, warranting further investigation into its superconducting properties and potential applications.

IV Conclusion
In conclusion, we present a comprehensive high-throughput investigation of superconductivity in cubic ternary hydrides MXH3 at ambient pressure. Our analysis identifies 17 dynamically stable strontium hydrides, with SrAuH3, SrTcH3 and SrZnH3 exhibiting notably high superconducting transition temperatures of 132 K, 69 K and 107 K, respectively. The exceptional of SrXH3 suggests a significant influence of atoms on superconductivity in strontium hydrides. The predicted synthesis pressures for SrXH3 compounds fall within experimentally accessible ranges ( 20 GPa), providing possible avenues for future high-pressure synthesis experiments. These findings not only reveal a rich landscape of potential high- superconductors within the MXH3 family at ambient pressure but also demonstrate an effective strategy for exploring conventional superconductivity in ternary hydrides through distinctive structural motifs. This study provides a foundation for future investigations into ambient-pressure, high- ternary hydride superconductors, potentially catalyzing new avenues in superconductor research and materials design.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grants No. 12374135, 12175107), and Nanjing University of Posts and Telecommunications Foundation (NUPTSF) (Grants No. NY219087, NY220038) and the Hua Li Talents Program of Nanjing University of Posts and Telecommunications. Some of the calculations were performed on the supercomputer in the Big Data Computing Center (BDCC) of Southeast University.
References
- Tokura et al. [1989] Y. Tokura, H. Takagi, and S. Uchida, A superconducting copper oxide compound with electrons as the charge carriers, Nature 337, 345 (1989).
- Li et al. [2019] W. M. Li, J. F. Zhao, L. P. Cao, Z. Hu, Q. Z. Huang, X. C. Wang, Y. Liu, G. Q. Zhao, J. Zhang, Q. Q. Liu, R. Z. Yu, Y. W. Long, H. Wu, H. J. Lin, C. T. Chen, Z. Li, Z. Z. Gong, Z. Guguchia, J. S. Kim, G. R. Stewart, Y. J. Uemura, S. Uchida, and C. Q. Jin, Superconductivity in a unique type of copper oxide, Proceedings of the National Academy of Sciences 116, 12156 (2019).
- Bardeen et al. [1957] J. Bardeen, L. N. Cooper, and J. R. Schrieffer, Theory of superconductivity, Phys. Rev. 108, 1175 (1957).
- Wigner and Huntington [1935] E. Wigner and H. B. Huntington, On the Possibility of a Metallic Modification of Hydrogen, The Journal of Chemical Physics 3, 764 (1935).
- Ashcroft [1968] N. W. Ashcroft, Metallic hydrogen: A high-temperature superconductor?, Phys. Rev. Lett. 21, 1748 (1968).
- Mao et al. [2018] H.-K. Mao, X.-J. Chen, Y. Ding, B. Li, and L. Wang, Solids, liquids, and gases under high pressure, Rev. Mod. Phys. 90, 015007 (2018).
- Buzea and Robbie [2004] C. Buzea and K. Robbie, Assembling the puzzle of superconducting elements: a review, Superconductor Science and Technology 18, R1 (2004).
- Rotundu et al. [2013] C. R. Rotundu, T. Ćuk, R. L. Greene, Z.-X. Shen, R. J. Hemley, and V. V. Struzhkin, High-pressure resistivity technique for quasi-hydrostatic compression experiments, Review of Scientific Instruments 84, 063903 (2013).
- Wang et al. [2012] Y. Wang, J. Lv, L. Zhu, and Y. Ma, Calypso: A method for crystal structure prediction, Computer Physics Communications 183, 2063 (2012).
- Jansen [2015] M. Jansen, Conceptual inorganic materials discovery – a road map, Advanced Materials 27, 3229 (2015).
- Liu et al. [2012] H. Liu, W. Cui, and Y. Ma, Hybrid functional study rationalizes the simple cubic phase of calcium at high pressures, The Journal of Chemical Physics 137, 184502 (2012).
- Drozdov et al. [2015] A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov, and S. I. Shylin, Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system, Nature 525, 73 (2015).
- Drozdov et al. [2019] A. P. Drozdov, P. P. Kong, V. S. Minkov, S. P. Besedin, M. A. Kuzovnikov, S. Mozaffari, L. Balicas, F. F. Balakirev, D. E. Graf, V. B. Prakapenka, E. Greenberg, D. A. Knyazev, M. Tkacz, and M. I. Eremets, Superconductivity at 250 k in lanthanum hydride under high pressures, Nature 569, 528 (2019).
- Somayazulu et al. [2019] M. Somayazulu, M. Ahart, A. K. Mishra, Z. M. Geballe, M. Baldini, Y. Meng, V. V. Struzhkin, and R. J. Hemley, Evidence for superconductivity above 260 k in lanthanum superhydride at megabar pressures, Phys. Rev. Lett. 122, 027001 (2019).
- Wang et al. [2022] Y. Wang, K. Wang, Y. Sun, L. Ma, Y. Wang, B. Zou, G. Liu, M. Zhou, and H. Wang, Synthesis and superconductivity in yttrium superhydrides under high pressure, Chinese Physics B 31, 106201 (2022).
- Sun et al. [2019] Y. Sun, J. Lv, Y. Xie, H. Liu, and Y. Ma, Route to a superconducting phase above room temperature in electron-doped hydride compounds under high pressure, Phys. Rev. Lett. 123, 097001 (2019).
- Lucrezi et al. [2022] R. Lucrezi, S. Di Cataldo, W. von der Linden, L. Boeri, and C. Heil, In-silico synthesis of lowest-pressure high-tc ternary superhydrides, npj Computational Materials 8, 119 (2022).
- Lucrezi et al. [2023] R. Lucrezi, E. Kogler, S. Di Cataldo, M. Aichhorn, L. Boeri, and C. Heil, Quantum lattice dynamics and their importance in ternary superhydride clathrates, Communications Physics 6, 298 (2023).
- Belli and Errea [2022] F. Belli and I. Errea, Impact of ionic quantum fluctuations on the thermodynamic stability and superconductivity of , Phys. Rev. B 106, 134509 (2022).
- Errea et al. [2020] I. Errea, F. Belli, L. Monacelli, A. Sanna, T. Koretsune, T. Tadano, R. Bianco, M. Calandra, R. Arita, F. Mauri, and J. A. Flores-Livas, Quantum crystal structure in the 250-kelvin superconducting lanthanum hydride, Nature 578, 66 (2020).
- Ma et al. [2022] L. Ma, K. Wang, Y. Xie, X. Yang, Y. Wang, M. Zhou, H. Liu, X. Yu, Y. Zhao, H. Wang, G. Liu, and Y. Ma, High-temperature superconducting phase in clathrate calcium hydride up to 215 k at a pressure of 172 gpa, Phys. Rev. Lett. 128, 167001 (2022).
- Di Cataldo et al. [2021] S. Di Cataldo, C. Heil, W. von der Linden, and L. Boeri, : Towards high- low-pressure superconductivity in ternary superhydrides, Phys. Rev. B 104, L020511 (2021).
- Zhang et al. [2022] Z. Zhang, T. Cui, M. J. Hutcheon, A. M. Shipley, H. Song, M. Du, V. Z. Kresin, D. Duan, C. J. Pickard, and Y. Yao, Design principles for high-temperature superconductors with a hydrogen-based alloy backbone at moderate pressure, Phys. Rev. Lett. 128, 047001 (2022).
- Liang et al. [2021] X. Liang, A. Bergara, X. Wei, X. Song, L. Wang, R. Sun, H. Liu, R. J. Hemley, L. Wang, G. Gao, and Y. Tian, Prediction of high- superconductivity in ternary lanthanum borohydrides, Phys. Rev. B 104, 134501 (2021).
- Song et al. [2023] Y. Song, J. Bi, Y. Nakamoto, K. Shimizu, H. Liu, B. Zou, G. Liu, H. Wang, and Y. Ma, Stoichiometric ternary superhydride as a new template for high-temperature superconductivity at 110 k under 80 gpa, Phys. Rev. Lett. 130, 266001 (2023).
- Tian et al. [2015] F. Tian, D. Li, D. Duan, X. Sha, Y. Liu, T. Yang, B. Liu, and T. Cui, Predicted structures and superconductivity of hypothetical mg-ch4 compounds under high pressures, Materials Research Express 2, 046001 (2015).
- Zhang et al. [2016] S. Zhang, L. Zhu, H. Liu, and G. Yang, Structure and electronic properties of fe2sh3 compound under high pressure, Inorganic Chemistry 55, 11434 (2016), pMID: 27783489.
- Dolui et al. [2024] K. Dolui, L. J. Conway, C. Heil, T. A. Strobel, R. P. Prasankumar, and C. J. Pickard, Feasible route to high-temperature ambient-pressure hydride superconductivity, Phys. Rev. Lett. 132, 166001 (2024).
- Giannozzi et al. [2009] P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, and R. M. Wentzcovitch, Quantum espresso: a modular and open-source software project for quantum simulations of materials, Journal of Physics: Condensed Matter 21, 395502 (2009).
- Baroni et al. [2001] S. Baroni, S. de Gironcoli, A. Dal Corso, and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys. 73, 515 (2001).
- Kawamura et al. [2014] M. Kawamura, Y. Gohda, and S. Tsuneyuki, Improved tetrahedron method for the brillouin-zone integration applicable to response functions, Phys. Rev. B 89, 094515 (2014).
- Prandini et al. [2018] G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet, and N. Marzari, Precision and efficiency in solid-state pseudopotential calculations, npj Computational Materials 4, 72 (2018), http://materialscloud.org/sssp.
- Allen and Dynes [1975] P. B. Allen and R. C. Dynes, Transition temperature of strong-coupled superconductors reanalyzed, Phys. Rev. B 12, 905 (1975).
- Blaha et al. [2020] P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen, and L. D. Marks, WIEN2k: An APW+lo program for calculating the properties of solids, The Journal of Chemical Physics 152, 074101 (2020).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- Momma and Izumi [2011] K. Momma and F. Izumi, Vesta 3 for three-dimensional visualization of crystal, volumetric and morphology data, Journal of Applied Crystallography 44, 1272 (2011).
- Kawamura [2019] M. Kawamura, Fermisurfer: Fermi-surface viewer providing multiple representation schemes, Computer Physics Communications 239, 197 (2019).
- McMillan [1968] W. L. McMillan, Transition temperature of strong-coupled superconductors, Phys. Rev. 167, 331 (1968).
- [39] See Supplemental Material at http://link.aps.org/supplemental/xxxxxx, which includes detailed computational results: calculated phonon spectra and electronic band structures, comprehensive tables of lattice constants, and complete calculation results for all predicted stable compounds.