Theoretical insights into the role of lattice fluctuations
on the excited behavior of lead halide perovskites
Abstract
Unravelling the role of charge-lattice interactions on the optoelectronic properties in lead halide perovskites is of great interest due to their unique photophysical properties. While there is broad consensus on the importance of the structural deformations and polar fluctuations on the behavior of charge carriers and quasiparticles, the strongly anharmonic nature of these fluctuations and their strong interactions render theoretical descriptions of lead halides challenging. In this Account, we review our recent efforts to understand how the soft, polar lattice of this class of materials alter their quasiparticle binding energies and fine structure, charge mobilities, and lifetimes of phonons and excess charges. This is reviewed in the context of the effective models we have built, and the novel theoretical methods we have developed to understand bulk crystalline materials, as well as nanostructures, and lower dimensionality lattices. The perspective we detail provides both some design principles for optoelectronic materials and a set of theoretical tools to study them when charge-lattice interactions are important.
I Introduction
Over the past 20 years, lead halide perovskites have emerged as an important material for a variety of photovoltaic and light-emitting applications. On top of their ease of synthesis, tunable optoelectronic properties and high defect tolerance, 1; 2; 3 they have small exciton binding energies, 4 long carrier lifetimes and diffusion lengths 5 despite modest charge mobilities, 6 and have demonstrated high power conversion efficiencies and quantum yields. Consisting of a lead-halide inorganic framework and counter-balancing cations, lead halide perovskites are held together with ionic bonds that localize significant charge leading to strong Coulomb interactions between photoexcited carriers and the surrounding lattice. 7 The isotropic nature of this ionic bonding results in a deformable lattice, admitting structural fluctuations and polaron formation that can protect charges from scattering with defects, 8; 9 and screen the interaction between charges. 10 Although many of the important optical properties in perovskites are presumed to arise from the interplay of electronic structure and charge-lattice interactions,2; 11 elucidating their microscopic origin has remained challenging.
The significant anharmonicity of perovskite lattices means that traditional models and perspectives on electron-phonon coupling are not appropriate. Unlike most crystalline semiconducting materials where lattice fluctuations are well described by a harmonic approximation, perovskites have rocking and tilting motions of the inorganic framework that are better described by double well potentials, 12 and they exhibit nearly free motions of their A-site cations 13. Unsurprisingly, these soft modes produce a number of competing structural phases that can be accessed over typical operating conditions or tuned through nanocrystalline size. In lower dimensional crystals, the A-site cation can be replaced with ionic ligands, which themselves can disorder and admit large fluctuations14. Even at low temperatures, where a harmonic approximation may be valid, perovskites have complex unit cells, rendering the use of traditional theoretical methods computationally intractable. There have been a growing number of studies pointing to the importance of charge-lattice effects on the properties of lead-halide perovskites, motivating analytical 15 and numerical studies 15; 16, but balancing an atomistic description of the lattice and a non-perturbative treatment of charge-lattice coupling has required that novel theoretical techniques be developed. We have developed path integral based methods in order to describe charge-lattice affects non-perturbatively 17; 18, and adapted pseudo-potential methods 19 to study nanocrystals and the role of surface relaxation on quasiparticle energetics and lifetimes 20. These tools have enabled studies on exciton binding and charge carrier renormalization from polaron formation, and an elucidation of the interplay between lattice structure and exciton energies in nanomaterials.
In this Account, we summarize these theoretical developments and how they have been used to rationalize spectroscopic and excited state dynamics in these material systems. In Sec. II, we present a discussion on static properties of excited states focusing on exciton fine structure and binding energies of excitons and biexcitons and how each depends on lattice geometry and particle morphology. We continue in Sec. III by addressing how the lattice fluctuations alter the dynamic properties such as charge mobility, and the lifetimes of charge and lattice excitations. In each subsection, we specify the types of perovskites considered, ranging from zero-dimensional nanocrystals to their three-dimensional bulk counterparts. In Sec. IV, we conclude this with a summary and active areas of continued study.
II Static properties
The generation, dissociation, and recombination of excitons determine the power conversion efficiencies and quantum yields of devices. The energetics of excitons and other quasiparticle excitations offer figures of merit for designing semiconducting materials, as they correlate with relevant dynamical properties. Details of these static properties and how they depend on the static or evolving lattice are reviewed here. In particular we review (i) how lattice distortion influences exciton fine structure in nanocrystals and (ii) how the binding energies of excitons and their complexes are modulated by confinement and polaronic effects.
II.1 Exciton fine structure
Lead halide perovskite nanocrystals are considered a promising quantum light source material as they show a remarkable brightness for photoluminescence and high quantum yield. 21 The origin of the bright emission has been a subject of debate, since there are conflicting experimental reports on the nature of the excitonic ground state, and the size of the dark-bright excitonic spittings22; 23. The excitonic fine structure of a material can be inferred in principle from spectroscopic measurements at cryogenic temperatures, though such measurements are challenging. While in bulk semiconductors the splitting of dark-bright exciton sublevels is very small, the splitting in nanocrystals can be substantial.

For materials with strong spin-orbit coupling like the lead halide perovskites, spin and angular momentum are correlated, resulting in a spin lattice coupling that can change and possibly invert the spitting of optically bright and dark states. In the bulk, lead halide perovskites undergo structural phase transitions between low temperature orthorhombic phases, intermediate tetragonal phases, and high temperature cubic phases, each with different symmetry and thus changes to the electronic band structure. 25 In nanoparticles, the locations of phase transformations are generally at different temperature than their bulk counterparts, and their significant surface-to-volume ratios can result in further complications as those surfaces relax and reconstruct.
Using an atomistic force field, 26 we studied a series of CsPbI3 perovskite nanocrystals whose relaxed structures are shown in Fig. 1(a). We observed that the local lattice structure was size-dependent, with the smallest nanocrystals stabilizing a highly symmetric cubic phase whereas the largest ones recovered a bulk-like orthorhombic structure. The degree of asymmetry was quantified in Fig. 1(b), using a lattice anisotropy parameter defined as the difference in the Pb-Pb distance between shortest and longest axis of the nanocrystal. The values for cubic structures are zero and for orthorhombic structures, the tilting of the octahedra breaks the isotropic symmetry resulting in a small constant value of the order parameter. We found that the relaxed structures did not monotonically transition between cubic and orthorhomic with increasing size, and rather exhibit a maximum anisotropy for cubes with edge lengths of 2.7 nm. These observations were broadly consistent with experimental x-ray measurements.20 This size-dependence stems from the competition between surface relaxation and the stability of the bulk orthorhombic phase. The establishment of the nanoparticle structure was only theoretically tractable with ab initio derived forcefields, as it is computationally intractable to relax geometries directly with density functional theory for such large systems.
The exciton fine structures were subsequently obtained from semiempirical pseudopotential methods 19 using the Bethe-Salpeter equation 27 developed in Ref. 24 on the geometries obtained from the forcefield calculations. The electronic pseudopotentials were parameterized to include both the effect from lattice distortion and spin-orbit coupling. Only with such a theoretical framework could the correlated electronic structure of nanoparticles be computed. With this methodology, we found the excitonic ground state to be dark with spin triplet character, exhibiting a small Rashba coupling, which is implied by the similar splitting trends as increasing nanocrystal sizes for all phases shown in Fig. 1(c, left). For cubic phases of cubic nanoparticles, the three bright states are degenerate, but deviations locally in the unit cell or morphologically in the aspect ratio of the nanocrystal could break this degeneracy. With the relaxed structure of each nanocrystal, Fig. 1(c, right panels) describes the standard deviation of splittings between bright excitonic states as a function of aspect ratio. Unlike the cubic and orthorhombic structures, the splittings with low aspect ratio are significant, unique feature of relaxed structures. This study confirmed that the lattice symmetry is vital in interpreting exciton fine structure of perovskite nanocrystals.
II.2 Exciton binding energy in bulk
While the absolute energies of excitons determine what states are populated thermally, the exciton binding energy marks the threshold to generate free charge carriers from an initial photoexcitation and determines the relative proportion of bound excitons to free charge carries. Bulk lead-halide perovskites have shown anomalously small values for exciton binding energies, typically reported as less than thermal energy at room temperature, attracting a great attention as a promising material for photovoltaic applications. 4 First principle estimates of exciton binding energies had failed to recover the anomalously small exciton binding energies,28 and while simple effective mass models could be made consistent with experiments, they typically required values of the dielectric constants that were difficult to interpret.29 The difficulty in establishing the exciton binding energy from such studies implicated the role of exciton-polarons and lattice deformation in the renormalization of observed binding energies. Such effects are not often accounted for in solid-state electronic structure.

The approach we developed was based on imaginary time path integrals33; 34; 35; 36 using an explicit atomistic representation of the lattice. Perovskites have highly dispersive bands, so the low energy band structure is well described by effective mass models. The lattice Hamiltonian was given by the previously validated atomistic force field 37 and the charge-lattice coupling was described by the sum of pseudopotentials 17; 18, in which way all orders of anharmonic features of perovskite lattice can be captured. Within this model, imaginary time path integrals could then be used to treat electron-hole correlation and charge-lattice coupling, without resorting to perturbation theory or approximate analytical results.
We found good agreement with most experimental reports for exciton binding in the methylammonium lead-iodide perovskites, MAPbI3, establishing a binding energy of 21 meV. The lattice renormalization of exciton binding occurs through two mechanisms, illustrated in Fig. 2(a). First, the lattice screens the direct interaction between charges by the static dielectric constant. This is a direct effect, weakening the Coulomb potential between the electron and hole. Second, the lattice stabilizes the free charges, altering their and the exciton’s self energy. This effect reflects in polaron formation of free charges or exciton-polaron formation of the bound electron-hole pair. We have found that exciton-polaron binding energies are relatively small, as a charge neutral object couples weakly to the lattice, but the stabilization of both the electron and hole from polaron formation is significant, and directly responsible for the attenuation of the binding energy.
We developed an effective field theory to decompose the contribution from the lattice on excitonic properties,17 through different approximations to the lattice Green’s function, . In principle, includes both a frequency, and wavevector, , dependence. In a static screening model, the electron-hole interaction is only screened by an effective dielectric constant, ignoring the dependence on both and , . In a dynamic screening model, we could incorporate the effect from harmonic phonons through a Frohlich-like model 8; 38 for a charge that is coupled with polarization field produced from the collective harmonic motions of the lattice. The models in this approximation were dispersionless, so , but whose frequency dependence admits the formation of a polaron through the quantum mechanical treatment of the lattice. Alternatively, a nonlocal screening model with spatially dependent dielectic function from the explicit MAPbI3 lattice, , was developed. In this model, the frequency dependence was ignored, which is equivalent to assuming it is well-described classically. The computed exciton binding energy under each type of lattice screening is summarized in Fig. 2(b), including the full lattice Green’s function that incorporates both non-locality and frequency dependence. Comparisons show that the inclusion of lattice effects from either dynamic or nonlocal screening reduces the attraction between electron and hole by about 10 meV, but incorporating both of these effects provides an excellent agreement with experiments, accounting for a nearly 30 meV red shift of the binding energy (21 meV) compared to the simple effective mass estimate (50 meV).39 This clarified the origin of small exciton binding energy, emphasizing the importance of anharmonic lattice fluctuations and polaron formation in lead halide perovskites.

II.3 Exciton binding in two-dimensions
Two-dimensional layered hybrid organic-inorganic perovskites have been proposed as alternatives to their bulk counterparts due to enhanced tunability and stability.42 Consequently, the photophysics of two-dimensional perovskites are different than bulk perovskites. The heterogeneous layer composition leads to a dielectric contrast that enhances the electron-hole interaction.43 The electron-hole interaction is also enhanced by quantum confinement that arises from the exciton and inorganic layer length-scales being similar in value.43 However, it remained to be understood how excitons are renormalized due to charge-phonon interactions in two-dimensional perovskites. To approach this problem, we considered two model systems with organic ligands, n-butylammonium (BTA) and phenylethylammonium (PEA), (BTA)2(MA)n-1PbnI3n+1 and (PEA)2(MA)n-1PbnI3n+1 where is the number of inorganic sublayers. A change in corresponds directly to a change in the quantum well thickness, thus also modifying the confinement. We studied both crystals formed from alternating slabs of organic and inorganic material, as well as single sheets dispersed in solution, the latter of which is report in Fig. 3.
To study the renormalization to exciton binding in these model systems and geometries, we developed a path integral framework41 similar to the one used to investigate bulk perovskites. Specifically, we employed continuum electrostatics along with the thin-film Frohlich interaction derived for a thin-film geometry.44 Figure 3 shows that the inclusion of a dynamic lattice brings exciton binding energies in reasonable agreement with experiment for both materials.40 The binding energy for the BTA ligand is much larger then the PEA ligand due to the large dielectic contrast between the organic layer and the inorganic lattice. Both exhibited a strong dependence on , illustrating the effect of dielectric confinement. When studying the polaron, we observed a non-monotonic behavior of polaron binding energy as a function of quantum well thickness . We were able to capture this non-monotonic trend with a variational bound that has two length scales: one that corresponds to an effective dielectric screening radius and another that corresponds to the polaron radius.41 To physically rationalize this trend, we consider two competing mechanisms. The first is that as increases, the amount of polar inorganic material increases, thus leading us to expect the electron-phonon interaction to strengthen. The second is that as increases, a lattice dipole becomes weakened due to stronger screening from the inorganic layer, thus leading us to expect the electron-phonon interaction to weaken. Overall, we were able to elucidate the interplay between quantum confinement, dielectric confinement, and charge-phonon coupling in two-dimensional perovskites.
II.4 Biexciton binding in cubic nanocrystals
While there is a reasonable agreement on the size of exciton binding energies in bulk perovskites, the values for perovskite nanocrystals are comparatively less established, and the understanding of multiparticle energies is even more unclear. In nanocrystals, quantum confinement can lead to strong many-body interactions among photoexcited charges and these can significantly affect the optical properties, 45 implying that it is necessary to study the behavior of exciton complexes such biexcitons. Recently, experimental studies46 proposed an anti-binding behavior of biexcitons in CsPbBr3 nanocrystals, implicating the potential lattice effect on these interactions. A number of biexciton binding energies for lead halide perovskites have been reported to date, whose values span a wide range even with opposite signs. 46; 45 However, experimental analysis is difficult because of effects from thermal broadening, spectral drifts, and the large variance in the nanocrystal sizes. 47

Adopting the same path integral approach as employed to study other perovskite systems, the energetics of quasiparticle excitations in CsPbBr3 perovskite nanocrystals are reviewed 48 where Fig. 4(a) shows the snapshots of molecular dynamics simulations of biexciton and exciton in CsPbBr3 nanocrystal with electrons and holes represented as imaginary time paths under the external potential accounting for a dielectric confinement effects. For comparison, the static and dynamic lattice screening models noted above are also considered. Over the range of nanocrystal sizes, exciton and biexciton binding energy calculations have been performed under each type of lattice screening. Shown in Fig. 4(c) is the difference in exciton and biexciton binding energies compared with results from static screening model. Even with the strong size dependence of both exciton and biexciton binding energies, the large values of imply that the inclusion of lattice effects either from dynamic or explicit CsPbBr3 lattice screening largely suppress the exciton binding energy, whereas lattice effects are negligible for biexciton binding. This observation is rationalized by the mechanism of polaron formation where instead of weakening the electron-hole interaction, lowering the self-energies of free charges contributes dominantly to reducing the binding energies in nanocrystals, which is not relevant for biexciton binding energies. Further, the calculations on biexciton binding energy, in agreement with other size-dependent measurements on CsPbBr3 nanocubes, 49 confirm that biexcitons are bound for all nanocrystal sizes considered, regardless of the type of lattice screenings.
III Dynamic properties
The dynamics of charges and the surrounding lattice play a crucial role in the functioning of semiconductor based devices. After photoexcitation, the subsequent relaxation dynamics involves a number of different processes which occur on timescales that span the picoseconds of exciton dissociation and lattice vibration, to nano- and microseconds for charge carrier lifetimes all of which conspire to determine a device’s efficiency. Establishing a microscopic understanding of these processes, and how each are influenced by the soft, polar lattice, provides means of designing materials to optimize optoelectronic properties. In this section, we focus on how lattice fluctuations alter the diffusion and lifetimes of charge carriers as well as the lifetime of lattice vibrations.
III.1 Charge carrier mobility
In the application of semiconducting materials, mobility of charge carriers is one of primary properties which limits the performance of materials. In photovoltaic devices, free charge carriers need to reach the extraction layer within their lifetime to make use of them whereas in light-emitting devices, larger mobility implies the greater brightness with low driving voltage. 50 Experimentally, the relative carrier mobility can be extracted from the photoinduced conductivity measurement using the pump-probe THz transmission dynamics after photoexcitation where the intensity of the signal is proportional to the density of free charge carriers. 6 Studying charge transport phenomena in lead halide perovskites, Wehrenfennig et al. showed that the difference in charge mobility highly affects the performance of materials. 6 Charge lattice interactions and polaronic effects in particular have been implicated in observations of renormalizing charge mobilities, as scattering off of the lattice is the primary mechanism of dissipation for excess charges16.
Using our quasiparticle path integral approach, 33; 34; 35; 36 we have estimated the relative charge carrier mobility at various electron-phonon coupling strengths using Frohlich model Hamiltonian. 8; 38 In the anti-adiabatic limit which is applicable to lead halide perovskites, the charge mobility can be obtained from their renormalized mass as 51
| (1) |
where is a longitudinal optical frequency of phonons, is a dimensionless Frohlich coupling constant, is inverse temperature times Boltzmann’s constant and is Planck’s constant. An inverse renormalized mass at a given electron-phonon coupling strength can be computed using a linear response relation 52
| (2) |
where is the distance between the first and the last beads of an open-chain imaginary time path, pictorially shown in Fig. 5(a).

Adopting the material properties of bulk lead-halide perovskites, the relative charge mobilities are described in Fig. 5(b), at various electron-phonon coupling strengths. In this parameter regime, the effective mass is well described using first order perturbation theory 9 and is consistent with Feynman’s variational method 53. Combining these two results, we were able to infer that the coupling with phonons makes the charge carriers heavier, while suppressing the carrier mobility, with a greater reduction expected for MAPbI3 compared to CsPbI3 due to its smaller Frohlich coupling constant. Molecularly, the weaker charge-lattice coupling for the inorganic lattice originates in the slightly less polarizable A-site cation.
III.2 Electron-hole recombination rate
At typical operating conditions for bulk photovoltaics, electron-hole recombination determines the lifetimes of charge carriers. Despite their modest mobilities, the lead halide perovskites exhibit large diffusion lengths, enabling exception power conversion efficiencies. Over the last decade, it has been found that the origin of the large diffusion lengths is an abnormally long free carrier lifetime, or correspondingly low radiative recombination rate.5 It had been conjectured that polaronic effects play a major role in the underlying mechanism of low electron-hole recombination rates of perovskites, 1; 10 though direct evidence theoretically or experimentally had been lacking. We were able to elucidate the molecular origin of the long charge carrier lifetime as originating in an emergent repulsion between electrons and holes mediated by the soft perovskite lattice.
In general, the charge recombination rate in the bulk is understood using a bimolecular rate expression. 6 For the reaction of , the bimolecular recombination rate can be defined as
| (3) |
where is the electron/hole density. We used quasiparticle path integral molecular dynamics simulations with an atomistic description of MAPbI3 lattice to evaluate this rate. In a bulk system, recombination is a bimolecular process, so the rate is proportional to the probability of bound electron and hole being co-localized, and a conditional probability of radiating provided they are co-localized. 18; 17 Both depend on the effective potential between charges, as mediated through a finite temperature, fluctuating lattice. Using explicit simulations, we found at 300 K a non-local lattice Green’s function, was well approximated by
| (4) |
characterized by two lengthscales, , and which are screening and correlation lengths associated with dielectric fluctuations. This functional form includes a single resonant peak that results from the double well potential of the optical mode.15
As the lattice Green’s function screens in the electron-hole interaction, in the limit that the lattice is well described classically, it implies an effective potential
| (5) |
where is the distance between two charges, , , , and . Notably this potential, shown in Fig. 6(a), includes a barrier at intermediate distances. This electron-hole repulsion significantly decreases their wavefunction overlap relative to expectations without a fluctuating lattice, , or within its dispersionaless harmonic approximation, . All three approximations to the screening from the lattice are shown in Fig. 6(b) where the electron-hole radial probability density is plotted, . Under standard approximations using either the static or harmonic approximation, the expected lifetimes of charge carriers at concentrations are on the order of 1/10 ns, while it rises to 1/200 ns when the nonlocal screening from the lattice is taken into account. This latter estimate was in very good agreement with photoluminescence lifetime measurements under similar carrier concentrations.5; 4 This study thus resolved the longstanding question concerning the anomalously long carrier lifetimes, by invoking a novel lattice mediated repulsion. This mechanism was molecular in origin, as reflective in the lengthscales , and .

III.3 Radiative recombination in nanocrystals
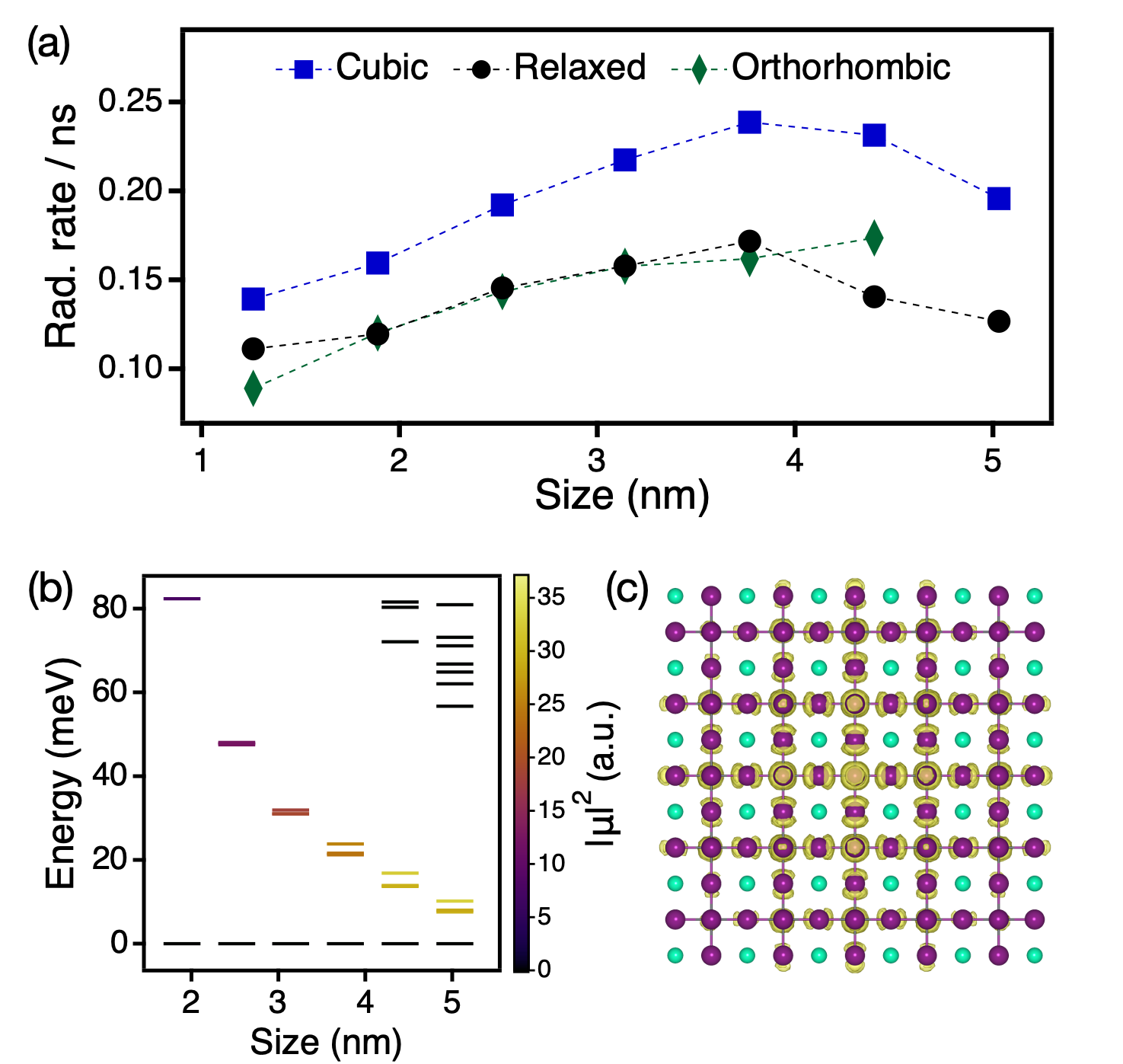
The optoelectronic properties of nanocrystals depend intricately on size-dependent confinement trends as well as lattice symmetry. A photo-generated electron-hole pair is confined to the volume of the nanocrystal and has a wavefunction that extends over the entire lattice up to the Bohr diameter, leading to radiative recombination physics governed by the nanocrystal size and lattice symmetry.54; 3 In perovskite nanocrystals at room temperature, fast radiative recombination has been observed with near-unity photoluminescence quantum yield, indicating possible applications in quantum light generation.3 In a recent work, Alivisatos et al measured a non-monotonic size-dependence to the exciton radiative recombination rates in CsPbBr3 nanocubes, which showed a maximum rate for approximately 5.5 nm, intermediately confined nanocrystals.55 Thus, a detailed understanding of how quantum confinement and lattice distortion influence radiative recombination is necessary for designing optimal platforms for perovskite nanocrystal based optical devices.
To elucidate the interplay of structural and electronic effects, we combined molecular dynamics simulations for lattice dynamics with atomistic semi-empirical pseudopotential calculations for excitonic states. The detailed theoretical framework has been described elsewhere.26; 24 A size-dependent transition was found in agreement with previous work,24 where small, approximately 2 nm CsPbX3 cubes are cubic and larger, 4 nm CsPbX3 nanocrystals (X = I, Br) have increased lattice distortion toward the orthorhombic geometry. The size regime of lattice symmetry breaking between 2 nm to 3 nm does not align with the regime of non-monotonic turnaround in the radiative rates between 4 nm and 7 nm, suggesting that the underlying lattice symmetry is not the dominant influence on radiative recombination in perovskite nanocrystals at room temperature. Rather, we found that competing size-dependent trends in the exciton oscillator strengths and density of states nicely capture the optoelectronic behavior in the correct size regime. Boltzmann thermal averaged radiative rates were computed in the time-dependent perturbation theory framework as
| (6) |
where and are the oscillator strength and Bohr frequency of exciton , , is the permittivity of free space, and is the speed of light. Radiative rates are proportional to the exciton oscillator strength, which increases with nanocrystal size due to the larger electron-hole overlap in the nanocrystal volume. From this trend, it is expected that the radiative rates increase monotonically for larger nanocrystals. However, as shown in Fig. 7(a), the radiative rates decrease for perovskite nanocrystals larger than 5.0 nm in diameter. The delayed radiative recombination is due to thermal distribution of exciton population into higher-lying, low oscillator strength ”dim” states that become accessible at ambient temperatures due to the increased density of states in large nanocrystals, as shown in Fig. 7(b). These dim states are within of the exciton ground state and show an equilibrium distribution due to the long timescale of radiative recombination compared to thermalizing nonradiative relaxation. It is clear from Eq. (6) that population of these dim states effectively decreases the Boltzmann factors of the few large oscillator strength excitons in response to reweighting by the many dim states, leading to reduced radiative rates for larger perovskite nanocrystals.
III.4 Phonon dephasing
The relaxation of excited charges proceeds through charge-phonon interactions, exciting lattice vibrations which themselves must subsequently relax. The examination of the dynamics of the lattice vibrations that charges coupled to can thus provide insight into the behavior of excited states and clarify the ways in which they are coupled. In layered perovskites, experimental observations have reported a rich lattice dynamics owing to their ionic inorganic framework together with the softness arising from the organic barrier layers. Early work by Quan et al. reported the dependence of photoluminescence quantum yield on the organic ligand environments. 14 They observed that layered perovskites with aromatic organic groups show much higher yields compared to those with alkyl groups. Delving into the role of dynamics of the lattice, with a pump-probe spectroscopy (illustrated in Fig. 8(a)), vibrational relaxation dynamics were studied through phonon dephasing rate with mainly two different organic ligands, n-butylamine (BTA) and phenylethylamine (PEA). It was found that phonon relaxation with BTA ligands is much faster than with PEA ligands. While with the faster dephasing rate over the range of temperature, contrary to the prediction from a general scattering theory, 56 the dephasing rates of BTA ligands exhibit no temperature dependence whereas the rates from PEA ligands show a linear temperature dependence. Hence, these distinct dynamics depending on the organic ligands given the same inorganic framework indicate the importance of the organic ligands in describing lattice dynamics in layered perovskites.
To obtain a molecular level understanding of vibrational dynamics of layered perovskites, molecular dynamics simulations 57 were performed. While simple, the basic physical properties such as lattice constants and mechanical properties were reasonably reproduced by the model whose simulation snapshots with BTA and PEA ligands are shown in Fig. 8(b) and (c), respectively. To effectively extract the phonon modes, the fluctuation-dissipation theorem is employed to relate displacement correlations from simulations to the dynamical matrix 58 where the analysis on the resultant vibrational frequencies and phonon modes verifies that the organic ligands largely participate in forming vibrational modes in layered perovskites. 14
For the lowest frequency optical mode, the atomistic model qualitatively captured the phonon dephasing dynamics observed experimentally in each layered perovskites. In the classical limit, derived from the Fermi’s golden rule, the relaxation rate of vibrational mode can be computed from the Fourier transform of the corresponding force-force correlation function 59 as
| (7) |
where is the optical frequency and is the force exerted on mode due to the coupling with their surrounding lattice. Figure 8(d) describes the dephasing rate in BTA and PEA layered perovskites over a range of temperatures, showing that the dephasing rates of BTA layered perovskite is higher than the one from PEA layered perovskite and are insensitive to the temperature.

Different phonon dynamics in layered perovskites were understood by comparing their packing geometry and anharmonicity of organic ligands. As deduced from Fig. 8(b) and (c), compared to PEA ligands where molecules are well aligned via strong interaction, BTA ligands hold amorphous packing geometry even at low temperature, whose dynamic disorder can rationalize the temperature insensitive relaxation rate. In terms of higher rate of BTA perovskites, this can be resolved by the large anharmonicity of BTA ligands. Based on the structural analysis of organic ligands, the local potential associated with the ligand orientation turns out to be highly anharmonic in BTA perovskite, showing a large deviation from the prediction based on fluctuation-dissipation theorem (see Ref. 14 for the detailed analysis). This is further supported by calculations showing the correlation between optical modes at different temperatures, described in Fig. 8(e) where the value ranges from 0 to 1 with the value 1 indicating that two vibrational modes are identical. While for PEA perovskites, the values are close to 1 across the whole range of temperature, the large drop in BTA perovskites as increasing the temperature implies that the optical modes are highly mixed with increasing temperature, a signal of large anharmonicity. Given the huge contribution of the organic ligands to the optical modes, the stronger anharmonicity from BTA perovskites justify the higher rate, facilitating the vibrational relaxation.
IV Concluding remarks
In this Account, we have outlined our studies describing the effects from the perovskite lattice on the excited state properties. For both static and dynamic properties, while various computational and analytical descriptions for excited states and lattice are considered in our approaches presented here, our focus has been on how to include the lattice effect and how important it is. Our calculations confirm that the lattice distortion resulting from the structural relaxation needs to be considered to properly describe the electronic states in perovskites. Further, it is found that the lattice fluctuations affect phonon dynamics itself and also dynamics of charge carriers, generically reducing the mobility, exciton binding energy, and electron-hole recombination rate, whereas there is negligible effects on biexciton bindings. We expect these results along with the strategic approaches drive the continued exploration on the role of lattice effects in elucidating the origin of properties in lead halide perovskites.
V ACKNOWLEDGMENTS
Support for this work was provided by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, under Contract No. DEAC02-05-CH11231 within the Fundamentals of Semiconductor Nanowire Program (KCPY23). Computational resources were provided in part by the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under contract no. DEAC02-05CH11231. We would like to thank other collaborators who participated in the work reviewed here including Amael Obliger, Daniel Weinberg, Peidong Yang, and Paul Alivisatos.
References
- Zhu and Podzorov (2015) X.-Y. Zhu and V. Podzorov, The Journal of Physical Chemistry Letters 6, 4758 (2015).
- Miyata et al. (2017) K. Miyata, D. Meggiolaro, M. T. Trinh, P. P. Joshi, E. Mosconi, S. C. Jones, F. D. Angelis, and X.-Y. Zhu, Science Advances 3, e1701217 (2017).
- Kovalenko et al. (2017) M. V. Kovalenko, L. Protesescu, and M. I. Bodnarchuk, Science 358, 745 (2017).
- Herz (2016) L. M. Herz, Annual Review of Physical Chemistry 67, 65 (2016).
- Quilettes et al. (2015) D. W. d. Quilettes, S. M. Vorpahl, S. D. Stranks, H. Nagaoka, G. E. Eperon, M. E. Ziffer, H. J. Snaith, and D. S. Ginger, Science 348, 683 (2015).
- Wehrenfennig et al. (2014) C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith, and L. M. Herz, Advanced Materials 26, 1584 (2014).
- Wang et al. (2016) H. Wang, L. Valkunas, T. Cao, L. Whittaker-Brooks, and G. R. Fleming, The Journal of Physical Chemistry Letters 7, 3284 (2016).
- Fröhlich (1954) H. Fröhlich, Advances in Physics 3, 325 (1954).
- Devreese (2015) J. T. Devreese, “Fröhlich polarons. lecture course including detailed theoretical derivations,” (2015), arXiv:1012.4576 [cond-mat.other] .
- Chen et al. (2016) Y. Chen, H. T. Yi, X. Wu, R. Haroldson, Y. N. Gartstein, Y. I. Rodionov, K. S. Tikhonov, A. Zakhidov, X. Y. Zhu, and V. Podzorov, Nature Communications 7, 12253 (2016).
- Limmer and Ginsberg (2020) D. T. Limmer and N. S. Ginsberg, The Journal of chemical physics 152 (2020).
- Yang et al. (2017) R. X. Yang, J. M. Skelton, E. L. d. Silva, J. M. Frost, and A. Walsh, The Journal of Physical Chemistry Letters 8, 4720 (2017), 1708.00499 .
- Brivio et al. (2015) F. Brivio, J. M. Frost, J. M. Skelton, A. J. Jackson, O. J. Weber, M. T. Weller, A. R. Goñi, A. M. A. Leguy, P. R. F. Barnes, and A. Walsh, Physical Review B 92, 144308 (2015).
- Quan et al. (2021) L. N. Quan, Y. Park, P. Guo, M. Gao, J. Jin, J. Huang, J. K. Copper, A. Schwartzberg, R. Schaller, D. T. Limmer, and P. Yang, Proceedings of the National Academy of Sciences 118, e2104425118 (2021), 2102.07957 .
- Schlipf et al. (2018) M. Schlipf, S. Poncé, and F. Giustino, Physical Review Letters 121, 086402 (2018), 1808.08130 .
- Mayers et al. (2018) M. Z. Mayers, L. Z. Tan, D. A. Egger, A. M. Rappe, and D. R. Reichman, Nano Letters 18, 8041 (2018).
- Park et al. (2022) Y. Park, A. Obliger, and D. T. Limmer, Nano Letters 22, 2398 (2022).
- Park and Limmer (2022) Y. Park and D. T. Limmer, The Journal of Chemical Physics 157, 104116 (2022), 2205.11780 .
- Rabani et al. (1999) E. Rabani, B. Hetényi, B. J. Berne, and L. E. Brus, The Journal of Chemical Physics 110, 5355 (1999).
- Zhao et al. (2020) Q. Zhao, A. Hazarika, L. T. Schelhas, J. Liu, E. A. Gaulding, G. Li, M. Zhang, M. F. Toney, P. C. Sercel, and J. M. Luther, ACS Energy Letters 5, 238 (2020).
- Rainò et al. (2019) G. Rainò, A. Landuyt, F. Krieg, C. Bernasconi, S. T. Ochsenbein, D. N. Dirin, M. I. Bodnarchuk, and M. V. Kovalenko, Nano Letters 19, 3648 (2019).
- Becker et al. (2018) M. A. Becker, R. Vaxenburg, G. Nedelcu, P. C. Sercel, A. Shabaev, M. J. Mehl, J. G. Michopoulos, S. G. Lambrakos, N. Bernstein, J. L. Lyons, T. Stöferle, R. F. Mahrt, M. V. Kovalenko, D. J. Norris, G. Rainò, and A. L. Efros, Nature 553, 189 (2018).
- Swift et al. (2024) M. W. Swift, P. C. Sercel, A. L. Efros, J. L. Lyons, and D. J. Norris, ACS Nano 18, 19561 (2024), 2310.19678 .
- Weinberg et al. (2023) D. Weinberg, Y. Park, D. T. Limmer, and E. Rabani, Nano Letters 23, 4997 (2023), 2303.00707 .
- Dastidar et al. (2017) S. Dastidar, C. J. Hawley, A. D. Dillon, A. D. Gutierrez-Perez, J. E. Spanier, and A. T. Fafarman, The Journal of Physical Chemistry Letters 8, 1278 (2017).
- Bischak et al. (2020) C. G. Bischak, M. Lai, Z. Fan, D. Lu, P. David, D. Dong, H. Chen, A. S. Etman, T. Lei, J. Sun, M. Grünwald, D. T. Limmer, P. Yang, and N. S. Ginsberg, Matter 3, 534 (2020), 1907.13509 .
- Filip et al. (2021) M. R. Filip, J. B. Haber, and J. B. Neaton, Physical Review Letters 127, 067401 (2021), 2106.08697 .
- Umari et al. (2018) P. Umari, E. Mosconi, and F. D. Angelis, The Journal of Physical Chemistry Letters 9, 620 (2018).
- Pollmann and Büttner (1977) J. Pollmann and H. Büttner, Physical Review B 16, 4480 (1977).
- Sun et al. (2013) S. Sun, T. Salim, N. Mathews, M. Duchamp, C. Boothroyd, G. Xing, T. C. Sum, and Y. M. Lam, Energy & Environmental Science 7, 399 (2013).
- Saba et al. (2014) M. Saba, M. Cadelano, D. Marongiu, F. Chen, V. Sarritzu, N. Sestu, C. Figus, M. Aresti, R. Piras, A. G. Lehmann, C. Cannas, A. Musinu, F. Quochi, A. Mura, and G. Bongiovanni, Nature Communications 5, 5049 (2014).
- Sestu et al. (2015) N. Sestu, M. Cadelano, V. Sarritzu, F. Chen, D. Marongiu, R. Piras, M. Mainas, F. Quochi, M. Saba, A. Mura, and G. Bongiovanni, The Journal of Physical Chemistry Letters 6, 4566 (2015).
- Feynman (1998) R. P. Feynman, Statistical Mechanics (Westview, 1998).
- Feynman and Hibbs (2005) R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals (Dover, 2005).
- Chandler and Wolynes (1981) D. Chandler and P. G. Wolynes, The Journal of Chemical Physics 74, 4078 (1981).
- Ceperley (1995) D. M. Ceperley, Reviews of Modern Physics 67, 279 (1995).
- Mattoni et al. (2016) A. Mattoni, A. Filippetti, and C. Caddeo, Journal of Physics: Condensed Matter 29, 043001 (2016).
- Mozafari (2016) E. Mozafari, Theoretical Description of the Electron-Lattice Interaction in Molecular and Magnetic Crystals (2016).
- Galkowski et al. (2016) K. Galkowski, A. Mitioglu, A. Miyata, P. Plochocka, O. Portugall, G. E. Eperon, J. T.-W. Wang, T. Stergiopoulos, S. D. Stranks, H. J. Snaith, et al., Energy & Environmental Science 9, 962 (2016).
- Urban et al. (2020) J. M. Urban, G. Chehade, M. Dyksik, M. Menahem, A. Surrente, G. Trippé-Allard, D. K. Maude, D. Garrot, O. Yaffe, E. Deleporte, et al., The Journal of Physical Chemistry Letters 11, 5830 (2020).
- Rana and Limmer (2024) R. Rana and D. T. Limmer, arXiv preprint arXiv:2407.08173 (2024).
- Leung et al. (2022) T. L. Leung, I. Ahmad, A. A. Syed, A. M. C. Ng, J. Popović, and A. B. Djurišić, Communications materials 3, 63 (2022).
- Hanamura et al. (1988) E. Hanamura, N. Nagaosa, M. Kumagai, and T. Takagahara, Materials Science and Engineering: B 1, 255 (1988).
- Sio and Giustino (2022) W. H. Sio and F. Giustino, Physical Review B 105, 115414 (2022).
- Zhu et al. (2023) C. Zhu, T. Nguyen, S. C. Boehme, A. Moskalenko, D. N. Dirin, M. I. Bodnarchuk, C. Katan, J. Even, G. Rainò, and M. V. Kovalenko, Advanced Materials 35, 2208354 (2023).
- Dana et al. (2021) J. Dana, T. Binyamin, L. Etgar, and S. Ruhman, ACS Nano 15, 9039 (2021).
- Lubin et al. (2021) G. Lubin, R. Tenne, A. C. Ulku, I. M. Antolovic, S. Burri, S. Karg, V. J. Yallapragada, C. Bruschini, E. Charbon, and D. Oron, Nano Letters 21, 6756 (2021), 2108.00345 .
- Park and Limmer (2023) Y. Park and D. T. Limmer, Physical Review Materials 7, 106002 (2023).
- Brennan et al. (2020) M. C. Brennan, A. Forde, M. Zhukovskyi, A. J. Baublis, Y. V. Morozov, S. Zhang, Z. Zhang, D. S. Kilin, and M. Kuno, The Journal of Physical Chemistry Letters 11, 4937 (2020).
- Sutherland and Sargent (2016) B. R. Sutherland and E. H. Sargent, Nature Photonics 10, 295 (2016).
- Martin and Frost (2023) B. A. A. Martin and J. M. Frost, Physical Review B 107, 115203 (2023), 2203.16472 .
- Kornilovitch (1998) P. E. Kornilovitch, Physical Review Letters 81, 5382 (1998).
- Marshall and Chawla (1970) J. T. Marshall and M. S. Chawla, Physical Review B 2, 4283 (1970).
- Alivisatos (1996) A. Alivisatos, Science 271, 933 (1996).
- Abbas et al. (2024) A. S. Abbas, D. Chabeda, D. Weinberg, D. T. Limmer, E. Rabani, and A. P. Alivisatos, arXiv:2409.06165 (2024).
- Verma et al. (1995) P. Verma, S. C. Abbi, and K. P. Jain, Phys. Rev. B 51, 16660 (1995).
- Hata et al. (2017) T. Hata, G. Giorgi, K. Yamashita, C. Caddeo, and A. Mattoni, J. Phys. Chem. C 121, 3724 (2017).
- Kong (2011) L. T. Kong, Comput. Phys. Commun. 182, 2201 (2011).
- Egorov et al. (1999) S. Egorov, K. Everitt, and J. Skinner, J. Phys. Chem. A 103, 9494 (1999).