Theoretical Error Analysis of Entropy Approximation
for Gaussian Mixtures
Abstract
Gaussian mixture distributions are commonly employed to represent general probability distributions. Despite the importance of using Gaussian mixtures for uncertainty estimation, the entropy of a Gaussian mixture cannot be calculated analytically. In this paper, we study the approximate entropy represented as the sum of the entropies of unimodal Gaussian distributions with mixing coefficients. This approximation is easy to calculate analytically regardless of dimension, but there is a lack of theoretical guarantees. We theoretically analyze the approximation error between the true and the approximate entropy to reveal when this approximation works effectively. This error is essentially controlled by how far apart each Gaussian component of the Gaussian mixture is. To measure such separation, we introduce the ratios of the distances between the means to the sum of the variances of each Gaussian component of the Gaussian mixture, and we reveal that the error converges to zero as the ratios tend to infinity. In addition, the probabilistic estimate indicates that this convergence situation is more likely to occur in higher-dimensional spaces. Therefore, our results provide a guarantee that this approximation works well for high-dimensional problems, such as neural networks that involve a large number of parameters.
Keywords : Gaussian mixture, Entropy approximation, Approximation error estimate, Upper and lower bounds
1 Introduction
Entropy is a fundamental measure of uncertainty in information theory with many applications in machine learning, data compression, and image processing. In machine learning, for instance, entropy is a key component in the evidence lower bound (ELBO) in the variational inference (Hinton and Van Camp, 1993; Barber and Bishop, 1998; Bishop, 2006) and the variational autoencoder (Kingma and Welling, 2013). It also plays a crucial role in the data acquisition for Bayesian optimization (Frazier, 2018) and active learning (Settles, 2009). In the real-world scenario, unimodal Gaussian distribution is widely used and offers computational advantages because its entropy can be calculated analytically, which offers computational advantages. However, unimodal Gaussian distributions are limited in the approximation ability, and in particular, they hardly approximate multimodal distributions, which are often assumed, for instance, as posterior distributions of Bayesian neural networks (BNNs) (MacKay, 1992; Neal, 2012) (see, e.g., Fort et al. (2019)). On the other hand, Gaussian mixture distribution (the superposition of Gaussian distributions) can capture the multimodality, and in general, approximate any continuous distribution in some topology (see, e.g., Bacharoglou (2010)). Unfortunately, the entropy of Gaussian mixture lacks a closed form, thereby necessitating the use of entropy approximation methods.
There are numerous approximation methods for estimating the entropy of Gaussian mixture (see Section 2). One common method for approximating the entropy of a Gaussian mixture is to compute the weighted sum of the entropies of the individual unimodal Gaussian components with mixing coefficients (see (3.2)), and this approximate entropy is easy to calculate analytically. However, despite its empirical success, this approximation lacks theoretical guarantees. The purpose of this paper is to reveal under what conditions this approximation performs well and to provide some theoretical insights on this approximation. Our contributions are as follows:
-
•
(Main result: New error bounds) We provide new upper and lower bounds of the approximation error. These bounds show that the error is essentially controlled by the ratios (which are given in Definition 4.1) of the distances between the means to the sum of the variances of each (Gaussian) component of the Gaussian mixture, and the error converges to zero as the ratios tend to infinity (Theorem 4.2). Consequently, we provide an “almost” necessary and sufficient condition for the approximate entropy to be valid (Remark 4.3).
-
•
(Probabilistic error bound) To confirm the effectiveness of the approximation for higher-dimension problems, we also provide the approximation error bound in the form of a probabilistic inequality (Corollary 4.7). In supplementary of Gal and Ghahramani (2016), it is mentioned (without mathematical proof) that this approximate entropy tends to be the true one in high-dimensional spaces when the means of the Gaussian mixture are randomly distributed. Our probabilistic inequality is a rigorous and generalized result of what they mention and shows the usefulness of this approximation in high-dimensional problems. Moreover, we numerically demonstrate this result in a simple case and show its superiority over several other methods (Section 5).
-
•
(Error bound for derivatives) For example in machine learning, not only the approximation of entropy but also its partial derivatives are required in backpropagation. Therefore, we also provide the upper bounds for the partial derivatives of the error with respect to parameters (Theorem 4.8), which ensure that the derivatives of the approximate entropy are also close enough to the true ones when the ratios are large enough.
-
•
(More detailed analysis in the special case) We conduct a more detailed analysis of the error bounds in a special case. More precisely, when all covariance matrices coincide, we provide an explicit formula on the entropy of Gaussian mixture with the integral dimension-reduced to its component number (Proposition 4.9). Then, by using this formula, we improve and simplify the upper and lower bounds of the error (Theorem 4.10) and the probabilistic inequality (Corollary 4.12). In this special case, we obtain a necessary and sufficient condition for this approximation to converge to the true entropy (Remark 4.11).
2 Related work
In numerical computation of the entropy of Gaussian mixtures, the approximation by Monte Carlo estimation is often used. However, it may require a large number of samples for high accuracy, leading to high computational costs. Furthermore, the Monte Carlo estimator gives a stochastic approximation, and hence, it does not guarantee deterministic bounds (confidence intervals may be used). There are numerous deterministic approximation methods (see, e.g., Hershey and Olsen (2007)). For example, approximation methods based on upper or lower bounds of the entropy are often used. That is, we try to obtain an approximation by estimating the upper or lower bounds of the entropy or we adopt the bounds as an approximate entropy (see, e.g., Bonilla et al. (2019); Hershey and Olsen (2007); Nielsen and Sun (2016); Zobay (2014)). A typical one is to use the lower bound of the entropy based on Jensen’s inequality (see Bonilla et al. (2019)). These approximations have the advantage of being analytically calculated in closed forms, whereas there is no theoretical guarantee that they work well in the context of machine learning such as variational inference. As another typical method, Huber et al. (2008) proposed the entropy approximation by a combination of the Taylor approximation with the splitting method of Gaussian mixture components. Recently, Dahlke and Pacheco (2023) provided new approximations using Taylor and Legendre series, and they theoretically and experimentally analyzed these approximations together with the approximation in Huber et al. (2008). Notably, Dahlke and Pacheco (2023) theoretically showed sufficient conditions for the approximations to be convergent. However, their performance remains unexplored in higher-dimensional cases. As an approximation that is easy to calculate regardless of dimensions, the sum of the entropies of unimodal Gaussian distributions is often used. For example, the approximation entropy represented as the “sum with mixing coefficients” of the entropies of unimodal Gaussian distributions (see Remark 4.5), which is equal to the true one when all Gaussian components coincide, is investigated in Melbourne et al. (2022). On the other hand, Gal and Ghahramani (2016) used the approximation represented as the sum of the entropies of “unimodal Gaussian distributions with mixture coefficients” in the context of variational inference from an intuition that this approximation tends to the true one in high-dimensional spaces when the means of the mixture are randomly distributed. In our work, we focus on the theoretical error estimation for this approximation and reveal that this approximation converges to the true one when all Gaussian components are far apart or in high-dimensional cases.
3 Entropy approximation for Gaussian mixtures
The entropy of probability distribution is defined by
| (3.1) |
Here, we choose a probability distribution as the Gaussian mixture distribution, that is,
where is the number of mixture components, and are mixing coefficients constrained by . Here, is the Gaussian distribution with a mean and (positive definite) covariance matrix , that is,
where is the determinant of matrix , and for a vector and a positive definite matrix . However, the entropy term cannot be computed analytically when the distribution is a Gaussian mixture.
We define the approximate entropy by the sum of the entropies of “unimodal Gaussian distributions with mixture coefficients”:
| (3.2) |
which can be computed analytically. It is obvious that holds for unimodal Gaussian (i.e., the case ). Moreover, it is shown that
(see (LABEL:computation1) in Appendix and Remark 4.5). These bounds show that the error does not blow up with respect to the mean , the covariance , and the dimension if the number of mixture components is fixed. In addition, these bounds imply that as the Gaussian mixture converges to a unimodal Gaussian (i.e., for some and for all ). It is natural to ask under what other conditions this approximation can be justified. In Section 4, we will provide an “almost” necessary and sufficient condition for this approximation to be valid.
4 Theoretical error analysis of the entropy approximation
In this section, we analyze the approximation error to theoretically justify the entropy approximation .
We introduce the following notation to state our results.
Definition 4.1.
For two Gaussian distributions and , we define by
| (4.1) |
and by
| (4.2) |
where and is the operator norm (i.e., the largest singular value).
Interpretation of : We can interpret that and measure distances of two Gaussian distributions in some sense respectively. Here notice that is symmetric (i.e., is always equal to ), but is not necessarily symmetric (i.e., is not always equal to ).
Figure 1 shows the geometric interpretation of in the isotropic case, that is, and . In this case, has a symmetric form with respect to as
Here, the volume of on is equal to that of on , where for and . If all distances between the means go to infinity, or all variances go to zero, etc., then go to infinity for all pairs of . Furthermore, if all means are normally distributed (variances are fixed), then an expected value of is in proportion to the dimension . That intuitively means that the expected value of becomes large as the dimension of the parameter increases.



These intuitions also hold in anisotropic case. From definition (4.2), we have
This shows that the circumsphere of circumscribes (see Figure 2 right). Moreover, by coordinate transformation , we can interpret that is a distance of and from the perspective of (see Figure 2 left), and gives a concrete form of satisfying , that is, (Lemma A.4).
4.1 General covariance case
We study the error for general covariance matrices . First, we give the following upper and lower bounds for the error.
Theorem 4.2.
Let . Then
| (4.3) |
where the coefficient is defined by
and the set is defined by
Moreover, the same upper bound holds for instead of :
| (4.4) |
The proof is given by calculations with the triangle inequality, the Cauchy-Schwarz inequality, and a change of variables. For upper bound, we use the inequality , and we split the integral region to and in order to utilize the characteristic of . While, for the lower bound, we use the concavity of function and the definition of . See Appendix A.1 for the proof of Theorem 4.2.
Remark 4.3.
Theorem 4.2 implies the following facts:
-
(i)
According to the upper bound in (4.3), the approximation is valid when
-
(a)
or for all pairs with
for . In particular, the error exponentially decays to zero when all go to zero.
-
(a)
- (ii)
-
(iii)
According to the lower bound in (4.3), if and hold for all pairs and some constant independent of , then (a) is necessary for this approximation to be valid (where we note that when , and that holds). It is unclear whether all are positive, but we can show that either or is always positive for any pair (see Remark A.6).
-
(iv)
From the above facts and the symmetry of , we conclude that (b) is a necessary and sufficient condition for the approximation to be valid if hold for all pairs and some constant independent of .
Remark 4.4.
In Theorem 4.2, the parameter plays a role of adjusting the convergence speed as follows:
-
(i)
In the case of , the upper bound does not imply the convergence, and the following bound is obtained:
-
(ii)
Consider the upper bound (focusing on the term of pair in summation) of (4.3) as a function with respect to , it is minimal on if , and monotonically increase in if . Replacing on each summation in the proof of Theorem 4.2 with minimal points , we obtain more precise upper bound
which converges to zero when dimension goes to infinity, if for all pairs .
Remark 4.5.
Melbourne et al. (2022) has explored the entropy approximation of mixtures represented as the “sum with mixing coefficients” of the entropies of unimodal Gaussian distributions (without mixing coefficients in the logarithmic term):
| (4.5) |
This approximate entropy is equal to the true entropy when all Gaussian components coincide (i.e., and for all see (Melbourne et al., 2022, Theorem I.1)), but not when all Gaussian components are far apart (i.e., for all ). In contrast, while the approximation differs from when all Gaussian components coincide, it converges to when all Gaussian components are far apart (see Theorem 4.2). This is because differs by from (refer to (3.2)). Moreover, using also Wang and Madiman (2014, Lemma XI.2), the other upper bound
| (4.6) |
is obtained, where the last inequality is justified by constraint .
Remark 4.6.
Next, we provide the probabilistic inequality for the error as a corollary of Theorem 4.2.
Corollary 4.7.
Let . Take and such that
| (4.7) |
for all pairs (), that is, the left-hand side follows a Gaussian distribution with zero mean and an isotropic covariance matrix . Then, for and ,
| (4.8) |
The proof is a combination of Markov’s inequality and the upper bound in Theorem 4.2. We also use the moment generating function of which follows the -distribution by the assumption (4.7). See Appendix A.2 for the details.
When (4.7) holds, an expected value of is . Hence, if is regarded as , then for there exists such that the upper bound in (4.3) expectedly converges to zero as the dimension goes to infinity. Furthermore, Corollary 4.7 justifies Gal and Ghahramani (2016, Proposition 1 in Appendix A), which formally mentions that tends to when means are normally distributed, all elements of covariance matrices do not depend on , and is large enough. In fact, the right-hand side of (4.8) converges to zero as for some if .
We also study the derivatives of the error with respect to learning parameters . For simplicity, we write
We give the following upper bounds for the derivatives of the error.
Theorem 4.8.
Let , , and . Then
where and is the -th and -th components of vector and matrix , respectively, and is the entry-wise matrix -norm, and is the determinant of the matrix that results from deleting -th row and -th column of matrix . Moreover, the same upper bounds hold for instead of .
The proof is given by similar calculations and techniques to the proof of Theorem 4.2. For the details, see Appendix A.3.
We observe that even in the derivatives of the error, the upper bounds exponentially decay to zero as go to infinity for all pairs with . We can also show that if means are normally distributed with certain large standard deviation , then the probabilistic inequality like Corollary 4.7 that the bound converges to zero as goes to infinity is obtained.
4.2 Coincident covariance case
We study the error for coincident covariance matrices, that is,
| (4.9) |
where is a positive definite matrix. In this case, have the form as
In this case, a more detailed analysis can be done. First, we show the following explicit form of the true entropy .
Proposition 4.9.
Let . Then
| (4.10) |
where and is some rotation matrix such that
| (4.11) |
Here, is the standard basis in , and for .
The proof is given by certain rotations and polar transformations. For the details, see Appendix A.4.
We note that the special case of (4.10) can be found in Zobay (2014, Appendix A). Using Proposition 4.9, we have the following upper and lower bounds for the error.
Theorem 4.10.
Let and . Then
| (4.12) | |||
| (4.13) |
The upper bound is proved by the argument in proof of the second upper bound in Theorem 4.2 with the explicit form (4.10) and . The lower bound is given by applying that in Theorem 4.2 in the case of for all by remarking in that case.
Remark 4.11.
Corollary 4.12.
Let and . Take and such that
for all pairs (). Then, for and ,
5 Experiment
We numerically examined the approximation capabilities of the approximate entropy (3.2) compared with Huber et al. (2008), Bonilla et al. (2019), and the Monte Carlo integration. Generally, we cannot compute the entropy (3.1) in a closed form. Therefore, we restricted the setting of the experiment to the case for the coincident covariance matrices (Section 4.2), in particular , and the number of mixture components , where we obtained the more tractable formula for the entropy (B.4). In this setting, we investigated the relative error between the entropy and each approximation method (see Figure 3). The details for the experimental setting and exact formulas for each method are shown in Appendix B.
From the result in Figure 3, we can observe the following. First, the relative error of ours shows faster decay than others in higher dimensions . Therefore, the approximate entropy (3.2) has an advantage in higher dimensions. Second, the graph for ours scales in the -axis as scales, which is consistent with the expression of the upper bound in Corollary 4.12. Finally, ours is robust against varying mixing coefficients, which cannot be explained by Corollary 4.12. Note that we can hardly conduct a similar experiment for because we cannot prepare the tolerant ground truth of the entropy. For example, even the Monte Carlo integration is not suitable for the ground truth already in the case for due to its large relative error around .


(a) , ,

(b) , ,

(c) , ,

(d) , ,
6 Limitations and future work
The limitations and future work are as follows:
-
•
When all covariance matrices coincide, a necessary and sufficient condition is obtained for the approximation to be valid (see (i) in Remark 4.11). However, in the general covariance case, it has not yet been obtained without the constraints for covariance matrices (Remark 4.3). Improving the lower bound (or upper bound) to find a necessary and sufficient condition is a future work.
-
•
There is an unsolved problem on the standard deviation in (4.7) of Corollary 4.7. According to this corollary, the approximation error almost surely converges to zero as if we take (the discussion after Corollary 4.7). However, it is unsolved whether the condition is optimal or not for the convergence. According to Corollary 4.12, the condition can be removed in the particular case for all .
-
•
The approximate entropy (3.2) is valid only when are large enough. However, since there are situations where are likely to be small, such as the low-dimensional latent space of a variational autoencoder (Kingma and Welling, 2013), it is worthwhile to propose an appropriate entropy approximation for small situation. Although approximation of (4.5) seems to be an appropriate one for small situation, the criteria (e.g., some value of ) for using either of and is unclear.
-
•
Further enrichment of experiments is important, such as the large component case, and comparison of the derivatives of entropy.
-
•
One important application of the entropy approximation is variational inference. In Appendix C, we include an overview of variational inference and an experiment on the toy task. However, these are not sufficient to determine the effectiveness of this approximation for variational inference. For instance, the variational inference maximizes the ELBO in (C.1), which includes the entropy term. Investigating how this approximate entropy dominates other terms will be interesting for future work.
Acknowledgments
TF was partially supported by JSPS KAKENHI Grant Number JP24K16949.
References
- Bacharoglou [2010] Athanassia Bacharoglou. Approximation of probability distributions by convex mixtures of Gaussian measures. Proceedings of the American Mathematical Society, 138(7):2619–2628, 2010.
- Barber and Bishop [1998] David Barber and Christopher M Bishop. Ensemble learning in Bayesian neural networks. Nato ASI Series F Computer and Systems Sciences, 168:215–238, 1998.
- Bishop [2006] Christopher M. Bishop. Pattern recognition and machine learning. Springer, 2006.
- Bonilla et al. [2019] Edwin V Bonilla, Karl Krauth, and Amir Dezfouli. Generic inference in latent Gaussian process models. J. Mach. Learn. Res., 20:117–1, 2019.
- Dahlke and Pacheco [2023] Caleb Dahlke and Jason Pacheco. On convergence of polynomial approximations to the Gaussian mixture entropy. NeurIPS 2023, 2023.
- Fort et al. [2019] Stanislav Fort, Huiyi Hu, and Balaji Lakshminarayanan. Deep ensembles: A loss landscape perspective. arXiv preprint arXiv:1912.02757, 2019.
- Frazier [2018] Peter I Frazier. A tutorial on Bayesian optimization. arXiv preprint arXiv:1807.02811, 2018.
- Gal and Ghahramani [2016] Yarin Gal and Zoubin Ghahramani. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. Proceedings of The 33rd International Conference on Machine Learning, 48:1050–1059, 20–22 Jun 2016.
- He et al. [2020] Bobby He, Balaji Lakshminarayanan, and Yee W Teh. Bayesian deep ensembles via the neural tangent kernel. Advances in Neural Information Processing Systems, 33:1010–1022, 2020.
- Hershey and Olsen [2007] John R Hershey and Peder A Olsen. Approximating the Kullback Leibler divergence between Gaussian mixture models. In 2007 IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP’07, volume 4, pages IV–317. IEEE, 2007.
- Hinton and Van Camp [1993] Geoffrey E Hinton and Drew Van Camp. Keeping the neural networks simple by minimizing the description length of the weights. In Proceedings of the sixth annual conference on Computational learning theory, pages 5–13, 1993.
- Huber et al. [2008] Marco F Huber, Tim Bailey, Hugh Durrant-Whyte, and Uwe D Hanebeck. On entropy approximation for Gaussian mixture random vectors. In 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, pages 181–188. IEEE, 2008.
- Kingma and Welling [2013] Diederik P Kingma and Max Welling. Auto-encoding variational Bayes. arXiv preprint arXiv:1312.6114, 2013.
- Kingma et al. [2015] Durk P Kingma, Tim Salimans, and Max Welling. Variational dropout and the local reparameterization trick. Advances in neural information processing systems, 28:2575–2583, 2015.
- Lakshminarayanan et al. [2017] Balaji Lakshminarayanan, Alexander Pritzel, and Charles Blundell. Simple and scalable predictive uncertainty estimation using deep ensembles. Advances in neural information processing systems, 30, 2017.
- MacKay [1992] David JC MacKay. A practical Bayesian framework for backpropagation networks. Neural computation, 4(3):448–472, 1992.
- Melbourne et al. [2022] James Melbourne, Saurav Talukdar, Shreyas Bhaban, Mokshay Madiman, and Murti V Salapaka. The differential entropy of mixtures: New bounds and applications. IEEE Transactions on Information Theory, 68(4):2123–2146, 2022.
- Neal [2012] Radford M Neal. Bayesian learning for neural networks. Springer Science & Business Media, 118, 2012.
- Nielsen and Sun [2016] Frank Nielsen and Ke Sun. Guaranteed bounds on information-theoretic measures of univariate mixtures using piecewise log-sum-exp inequalities. Entropy, 18(12):442, 2016.
- Rezende et al. [2014] Danilo J Rezende, Shakir Mohamed, and Daan Wierstra. Stochastic backpropagation and approximate inference in deep generative models. International conference on machine learning, pages 1278–1286, 2014.
- Settles [2009] Burr Settles. Active learning literature survey. 2009.
- Titsias and Lázaro-Gredilla [2014] Michalis Titsias and Miguel Lázaro-Gredilla. Doubly stochastic variational Bayes for non-conjugate inference. In International conference on machine learning, pages 1971–1979. PMLR, 2014.
- Wang and Madiman [2014] Liyao Wang and Mokshay Madiman. Beyond the entropy power inequality, via rearrangements. IEEE Transactions on Information Theory, 60(9):5116–5137, 2014.
- Zobay [2014] Oliver Zobay. Variational Bayesian inference with Gaussian-mixture approximations. Electronic Journal of Statistics, 8(1):355–389, 2014.
Appendix
Appendix A Proofs in Section 4
We recall the definitions and notations used in this appendix. Let be the Gaussian mixture distribution, that is,
where is the dimension, is the number of mixture components, are mixing coefficients constrained by , and is the Gaussian distribution with a mean and covariance matrix , that is,
Here, is the determinant of matrix , and for a vector and a positive definite matrix . The entropy of and its approximation are defined by
A.1 Proof of Theorem 4.2
Lemma A.1.
Proof.
Making the change of variables as , we write
| (A.1) |
Using the inequality and the Cauchy-Schwarz inequality, we have
| (A.3) | ||||
| (A.4) | ||||
Thus, the proof of Lemma A.1 is finished. ∎
Lemma A.2.
Let . Then
| (A.5) |
Proof.
Using the inequality (A.3) and the inequality , we decompose
Firstly, we evaluate the term . By the definition of , we have
Then it follows from properties of , and triangle inequality that
| (A.6) |
From inequality (A.1) and the Cauchy-Schwarz inequality, it follows that for ,
where we have used the change of variable as .
Secondly, we evaluate the term . In the same way as above, we have
Combining the estimates obtained now, we conclude (A.5). ∎
Lemma A.3.
Let . Then
Proof.
Lemma A.4.
for any .
Proof.
When satisfies
because
then , where . On the other hand, from the definition of , we have
and thus . Therefore, we obtain
Making the change of variables as ,
From definition (4.1), is obtained. ∎
Lemma A.5.
where the coefficient is defined by
and the set is defined by
| (A.7) |
Proof.
Using the equality in (LABEL:computation1), we write
Since is a concave function of for , we estimate that
Here, it follows from the two conditions in the definition (A.7) of that
for , where we used the cosine formula in the second step. Combining the above estimates, we have
The proof of Lemma A.5 is finished. ∎
Remark A.6.
Either or is positive. Indeed,
-
•
if has at least one positive eigenvalue, then is positive;
-
•
if all eigenvalues of are non-positive, then has at least one positive eigenvalue;
-
•
if , then because is a half-space of ,
where is the zero matrix.
A.2 Proof of Corollary 4.7
We restate Corollary 4.7 as follows:
Lemma A.7.
Let . Assume and such that
| (A.8) |
for all pairs (). Then, for and ,
| (A.9) |
A.3 Proof of Theorem 4.8
The next lemma is the same as Theorem 4.8.
Lemma A.8.
Let , , and . Then
where and is the -th and -th components of vector and matrix , respectively, and is the entry-wise matrix -norm, and is the determinant of the matrix that results from deleting -th row and -th column of matrix . Moreover, the same upper bounds hold for instead of .
Proof.
In this proof, we denote by . From the equality (LABEL:computation1), we have
| (A.10) |
(i) The derivatives of (A.10) with respect to are calculated as
| (A.11) | ||||
| (A.12) | ||||
| (A.13) |
Since for when , we estimate
| (A.15) |
and
| (A.16) |
We also calculate
| (A.17) |
and
| (A.18) |
where we denote by the -th component of vector , and and the -th component of matrix and , respectively.
By using (LABEL:derivative-mu-1)–(A.18),
where the last inequality is given by the same arguments in the proof of Lemma A.2. Similar to Lemma A.3, this evaluation holds when and are replaced with any , for example .
(ii) The derivatives of (A.10) with respect to are calculated as follows:
| (A.19) |
We calculate
| (A.20) |
and
| (A.21) |
where we denote by the -th component of vector , and and the -th component of matrix and , respectively, and is the -th component of vector , and is component-wise derivative of matrix with respect to . We also calculate , where is the matrix such that -th component is one, and other are zero. We further estimate (A.21) by
| (A.22) |
where is -th component of matrix . By using inequality of for (), and the arguments (A.19)–(A.22), we have
where the last inequality is given by the same arguments in the proof of Theorem A.2.
A.4 Proof of Proposition 4.9
Lemma A.9.
Let . Then
| (A.23) |
where and is some rotation matrix such that
| (A.24) |
Here, is the standard basis in , and for .
Proof.
First, we observe that
Using (LABEL:computation1) with the assumption (4.9), we write
We choose the rotation matrix satisfying (A.24) for each . Making the change of variables as , we write
where , that is,
We change the variables as
where (), , (), and . Because
we obtain
| (A.25) |
By the equality
we conclude (A.23) from (A.25). The proof of Proposition 4.9 is finished. ∎
Appendix B Details of Section 5
We give a detailed explanation for the relative error experiment in Section 5. We restricted the setting of the experiment to the case for the coincident covariance matrices (4.9) and the number of mixture components . Furthermore, we assumed that , , and . In this setting, we varied the dimension of Gaussian distributions from 1 to 500 for certain parameters , where we sampled 10 times for each dimension . As formulas for the entropy approximation, we employed , , and for the method of ours, Huber et al. [2008], and Bonilla et al. [2019], respectively, as follows:
| (B.1) | ||||
| (B.2) | ||||
| (B.3) | ||||
where (B.1) is the same as described in Section 3, (B.2) is based on the Taylor expansion [Huber et al., 2008, (4)], and (B.3) is based on the lower bound analysis [Bonilla et al., 2019, (14)]. In the case for the coincident and diagonal covariance matrices , (B.2) for or can be analytically computed as
where
In the following, we show the tractable formula of the true entropy, which is used in the experiment in Section 5. In the case for the coincident covariance matrices and , we can reduce the integral in (4.10) to a one-dimensional Gaussian integral as follows:
Furthermore, we can choose the rotation matrix in Proposition 4.9 such that
that is,
Hence, we have
Therefore, by making the change of variables as , we conclude that
| (B.4) |
Note that the integration of (B.4) can be efficiently executed using the Gauss-Hermite quadrature.
Appendix C Application example: Variational inference to BNNs with Gaussian mixtures
C.1 Overview: Variational inference with Gaussian mixtures
Let be the base model that is a function parameterized by weights , e.g., the neural network. Let and be the prior distribution of the weights and the likelihood of the model, respectively. For supervised learning, let be a dataset where and are the input and output, respectively, and the input-output pair is independently identically distributed. The Bayesian posterior distribution is formulated as
The goal of variational inference is to minimize the Kullback-Leibler (KL) divergence between a variational family and posterior distribution given by
which is equivalent to maximizing the evidence lower bound (ELBO) given by
| (C.1) |
(see, e.g., Barber and Bishop [1998], Bishop [2006], Hinton and Van Camp [1993]). The first term of (C.1) is the expected log-likelihood given by
the second term is the cross-entropy between a variational family and prior distribution , and the third term is the entropy of given by
Here, we choose a unimodal Gaussian distribution as a prior, that is, , and we choose a Gaussian mixture distribution as a variational family, that is,
where is the number of mixture components, and are mixing coefficients constrained by . Here, is the Gaussian distribution with a mean and covariance matrix , that is,
where is the determinant of matrix , and for a vector and a positive definite matrix .
In the following, we investigate the ingredients in (C.1). The expected log-likelihood is analytically intractable due to the nonlinearity of the function . To overcome this difficulty, we follow the stochastic gradient variational Bayes (SGVB) method [Kingma and Welling, 2013, Kingma et al., 2015, Rezende et al., 2014], which employs the reparametric trick and minibatch-based Monte Carlo sampling. Let be a minibatch set with minibatch size . By reparameterizing weights as , we can rewrite the expected log-likelihood as
By minibatch-based Monte Carlo sampling, we obtain the following unbiased estimator of the expected log-likelihood as
| (C.2) |
where we employ noise sampling once per mini-batch sampling (Kingma et al. [2015], Titsias and Lázaro-Gredilla [2014]). On the other hand, the cross-entropy between a Gaussian mixture and unimodal Gaussian distribution can be analytically computed as
| (C.3) |
For the entropy term we employ the approximate entropy (3.2), that is,
| (C.4) |
C.2 Experiment of BNN with Gaussian mixtures on toy task
We employed the approximate entropy (3.2) for variational inference to a BNN whose posterior was modeled by the Gaussian mixture, which we call BNN-GM in the following. We conducted the toy D regression task [He et al., 2020] to observe the uncertainty estimation capability of the BNN-GM. In particular, we observed that the BNN-GM could capture larger uncertainty than the deep ensemble [Lakshminarayanan et al., 2017]. The task was to learn a curve from a training dataset that consisted of points sampled from a noised curve , . Refer to Appendix C.3 for the detail of implementations. We compared the BNN-GM with the deep ensemble of DNNs, the BNN with the single unimodal Gaussian, and the deep ensemble of BNNs with the single unimodal Gaussian, see Figure 4.
From the result in Figure 4, we can observe the following. First, every method can represent uncertainty on the area where train data do not exist. However, the BNN with a single unimodal Gaussian can represent smaller uncertainty than other methods (see around ). Second, as increasing the number of components, the BNN-GM can represent larger uncertainty than the deep ensemble of DNNs or BNNs. Therefore, there is a qualitative difference in uncertainty estimation between BNN-GMs and deep ensembles. Finally, the BNN-GM of 10 components has weak learners with small mixture coefficients. We suppose that this phenomenon is caused by the entropy regularization for the Gaussian mixture. Note that we do not claim the superiority of BNN-GMs to deep ensembles.
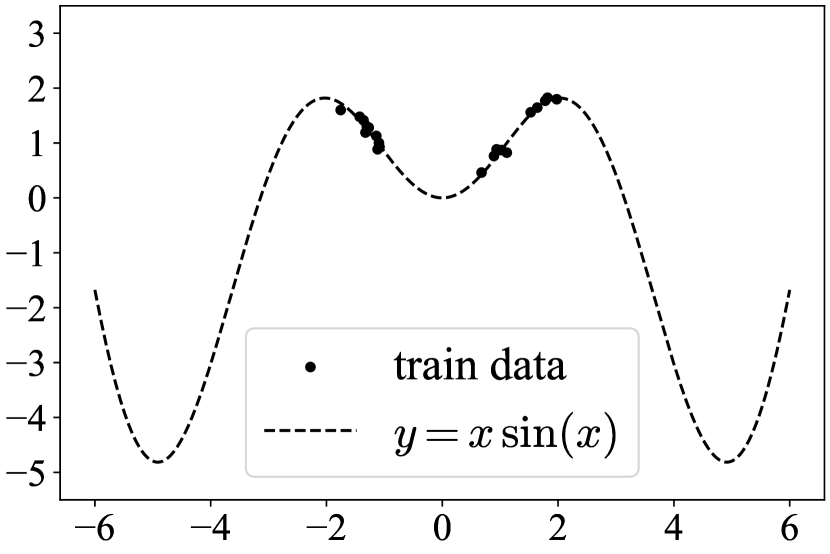
(a) Dataset

(b) Deep ensemble of 5 DNNs

(c) Deep ensemble of 10 DNNs

(d) BNN (single Gaussian)

(e) BNN-GM of 5 components

(f) BNN-GM of 10 components

(g) Deep ensemble of 5 BNNs

(h) Deep ensemble of 10 BNNs
C.3 Details of experiment
We give a detailed explanation for the toy D regression experiment in Appendix C.2. The task is to learn a curve from a training dataset that consists of points sampled from the noised curve , , see Figure 4. To obtain the regression model of the curve, we used the neural network model as the base model that had two hidden layers and hidden units in each layer with erf activation. Regarding the Bayes inference for the BNN-GM, we modeled the prior as and the variational family as the Gaussian mixture. Furthermore, we chose the likelihood function as the Gaussian distribution:
Then, we performed the SGVB method based on the proposed ELBO (C.5), where the batch size was equal to the dataset size. Hyperparameters were as follows: epochs , learning rate , , .