The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ and ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$

Shilei Fan Shilei FAN: School of Mathematics and Statistics, and Key Lab NAA–MOE, Central China Normal University, Wuhan 430079, China [email protected] , Mamateli Kadir Mamateli Kadir: School of Mathematics and Statistics & Research Center of Modern Mathematics and Applications, Kashi University, Kashi 844000, China [email protected] and Peishan Li Peishan Li: School of Mathematics and Statistics, and Hubei Key Lab–Math. Sci., Central China Normal University, Wuhan 430079, China [email protected]

Abstract.

In this paper, we provide a geometric characterization of tiles in the finite abelian groups $\mathbb{Z}_{p^{n}}\times\mathbb{Z}_{q}$ and $\mathbb{Z}_{p^{n}}\times\mathbb{Z}_{p}$ using the concept of a $p$ -homogeneous tree, which provides an intuitively visualizable criterion.

Key words and phrases:

Tiles, finite groups,

p

-homogeneous.

2010 Mathematics Subject Classification:

Primary 43A99; Secondary 05B45, 26E30.

S. L. FAN and P. S. Li are partially supported by NSFC (grants No. 12331004 and No. 12231013) and by NSF of Xinjiang Uygur Autonomous Region (Grant No. 2024D01A160). M. Kadir is supported by the NSF of China (Grant No. 12361015), the Fundamental Research Founds for Colleges of XinJiang Education Department, China (Grant No. XJEDU2023P108).

1. Introduction

Let $G$ be a locally compact abelian group. Consider a Borel measurable subset $\Omega$ in $G$ with $0<\mathfrak{m}(\Omega)<\infty$ , where $\mathfrak{m}$ denotes a Haar measure on $G$ . We say that $\Omega$ is a tile of $G$ by translation if there exists a set $T\subset G$ such that

\sum_{t\in T}1_{\Omega}(x-t)=1,\mathfrak{m}\ a.e.x\in G,

where $1_{A}$ denotes the indicator function of a set $A$ in $G$ . Such a set $T$ is called a tiling complement of $\Omega$ and $(\Omega,T)$ is called a tiling pair.

Let $\widehat{G}$ be the dual group of $G$ consisting of the continuous characters of $G$ . The set $\Omega$ is called a spectral set if there exists a set $\Lambda\subset\widehat{G}$ of continuous characters of $G$ which form a Hilbert basis of the space $L^{2}(\Omega)$ . Such a set $\Lambda$ is called a spectrum of $\Omega$ and $(\Omega,\Lambda)$ is called a spectral pair.

In harmonic and functional analysis, a fundamental question asks whether a geometric property of sets (tiling) and an analytic property (spectrality) are always two sides of the same coin. This question was initially posed by Fuglede [10] for finite-dimensional Euclidean spaces, stemmed from a question of Segal on the commutativity of certain partial differential operators.

Conjecture (Fuglede 1974).

A Borel set $\Omega\subset\mathbb{R}^{d}$ of positive and finite Lebesgue measure is a spectral set if and only if it is a tile.

The original Fuglede conjecture has been disproven in its full generality for dimensions 3 and above for both directions [8, 17, 18, 23, 28]. This means that neither implication (tiling implies spectral and vice versa) holds true in these higher dimensions. However, the connection between tiling and spectral properties remains an active area of research, particularly in lower dimensions. The conjecture is still open for the one-dimensional and two-dimensional cases ( ${\mathbb{R}}$ and ${\mathbb{R}}^{2}$ ). There might be a deeper relationship to be discovered in these simpler settings (see [3] for a focused look on dimension $1$ ).

Despite the general counterexamples, the conjecture has been successfully proven for convex sets [12, 11, 20] in all dimensions. On the other hand, there has been a growing interest in extending the Fuglede conjecture beyond the realm of Euclidean spaces. Fuglede himself hinted at the possibility of exploring the conjecture in different settings. This has led to a more general version of the conjecture applicable to locally compact abelian groups. Formally stated, Fuglede’s conjecture on a locally compact abelian group $G$ asks: Is a Borel set $\Omega\subset G$ of positive and finite Haar measure is a spectral set if and only if it is a tile?

The generalized Fuglede conjecture has been proved for different groups, particularly for finite abelian groups. These successes include groups like $\mathbb{Z}_{p^{n}}$ [19], $\mathbb{Z}_{p}^{d}$ ( $p=2$ and $d\leq 6$ ; $p$ is an odd prime and $d=2$ ; $p=3,5,7$ and $d=3$ ) [1, 5, 9, 13], $\mathbb{Z}_{p}\times\mathbb{Z}_{p^{n}}$ [13, 25, 29], $\mathbb{Z}_{p}\times\mathbb{Z}_{pq}$ [16] and $\mathbb{Z}_{pq}\times\mathbb{Z}_{pq}$ [4], $\mathbb{Z}_{p^{n}q^{m}}$ ( $p<q$ and $m\leq 9$ or $n\leq 6$ ; $p^{m-2}<q^{4}$ ) [14, 21, 22], $\mathbb{Z}_{pqr}$ [24], $\mathbb{Z}_{p^{2}qr}$ [26] and $\mathbb{Z}_{pqrs}$ [15], where $p,q,r,s$ are distinct primes. Fan et al. [6, 7] established the validity of the conjecture for the field ${\mathbb{Q}}_{p}$ of $p$ -adic numbers, and obtained the geometric structure of tiles and spectral sets in ${\mathbb{Q}}_{p}$ . The concept of $p$ –homogeneous tree structure was introduced in [7] to characterize the tile in $\mathbb{Z}_{p^{n}}$ .

It is known that spectral conjecture holds on ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ and ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . However, the geometric structures of tiles were not mentioned. In this paper, we provide a geometric characterization of tiles in the finite abelian groups ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ and ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ by the concept of $p$ -homogeneous tree.

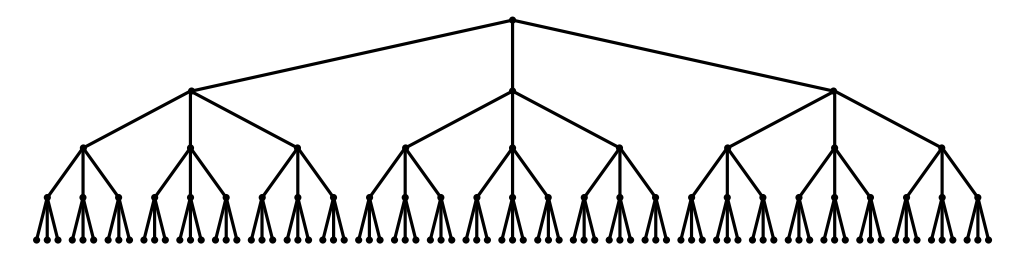
Firstly, we give a quick recall of the concept $p$ -homogeneous set in the cyclic group ${\mathbb{Z}}_{p^{n}}$ . Consider the group ${\mathbb{Z}}_{p^{n}}=\{0,1,\cdots,p^{n}-1\}$ as a finite tree $\mathcal{T}^{(n)}$ , where $n$ is an integer (see Figure 1). The vertices of $\mathcal{T}^{(n)}$ are the sets of ${\mathbb{Z}}_{p^{\gamma}},\ 0\leq\gamma\leq n$ and translations of them. The point of ${\mathbb{Z}}_{p}$ corresponding to the point of vertices at level $\gamma$ . The set of edges consists of pairs $(x,y)\in{\mathbb{Z}}_{p^{\gamma}}\times\mathbb{Z}_{p^{\gamma+1}}$ such that $x\equiv y(\bmod p^{\gamma})$ , where $0\leq\gamma\leq n-1$ . Each subset $C\subset{\mathbb{Z}}_{p^{n}}$ will determine a subtree of $\mathcal{T}^{(n)}$ , denoted by $\mathcal{T}_{C}$ , which consists of the paths from the root to the boundary points in $C$ .

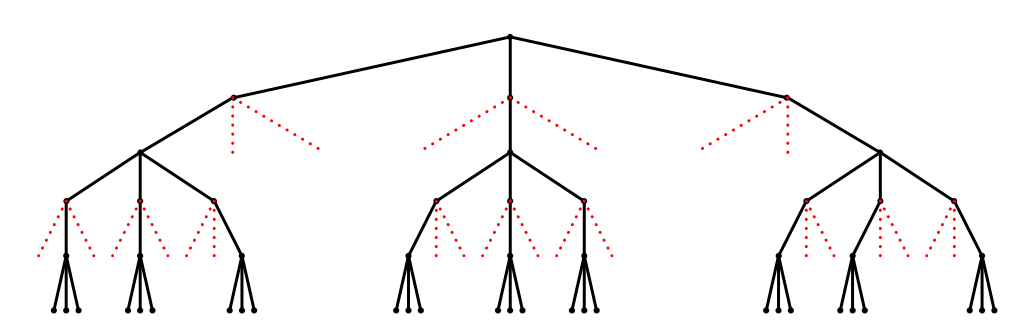
Refer to caption — Figure 1. Consider the set ${\mathbb{Z}}_{3^{4}}=\{0,1,2,\cdots,80\}$ as a tree $\mathcal{T}^{\left(4\right)}$ .

Let $I\subseteq\{0,1,2,\dots,n-1\}$ , $J\in\{0,1,2,\dots,n-1\}\backslash I$ . We say a subtree $\mathcal{T}_{C}$ of $\mathcal{T}^{(n)}$ is a $\mathcal{T}_{I}$ -form, if each point on the $I$ -th levels of the tree $\mathcal{T}_{C}$ has $p$ descendants, and the each point on the $J$ -th levels only has one descendant. A $\mathcal{T}_{I}$ -form tree is called a finite $p$ -homogeneous tree. We call a set $C\subset{\mathbb{Z}}_{p^{n}}$ a $p$ -homogeneous set, if the corresponding tree $\mathcal{T}_{C}$ is a $p$ -homogeneous tree. A special subtree $\mathcal{T}_{I}$ is shown in figure 3.

1.1. The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$

In [2], Coven and Meyerowitz introduced the so called CM conditions, which play a crucial role in characterizing a set $A$ that tiles the finite cyclic group ${\mathbb{Z}}_{N}$ by translations.

Let $A\subseteq{\mathbb{Z}}_{N}$ be a multi-set, and let $m_{a}$ denote the multiplicity of $a\in A$ . The mask polynomial of $A$ is defined as

A(x)=\sum_{a\in A}m_{a}x^{a}.

Denote by $\omega_{N}=e^{2\pi i/N}$ , which is a primitive $N$ -th root of unity.

Denote by $\Phi_{s}(x)$ the $s$ -th cyclotomic polynomial. Let $S$ denote the set of prime powers dividing $N$ , and define

S_{A}=\{s\in S:\Phi_{s}(x)\mid A(x)\}.

Consider the following algebraic conditions

(T1)

$|A|=A(1)=\prod_{s\in S_{A}}\Phi_{s}(1)$ .
(T2)

Let $s_{1},\dots,s_{m}\in S_{A}$ be powers of different primes. Then the polynomial $\Phi_{s_{1}\dotsm s_{m}}(x)$ divides $A(x)$ .

It is proved in [2] that if $A$ satisfies properties (T1) and (T2), then $A$ tiles ${\mathbb{Z}}_{N}$ by translations.

Write the cyclic group ${\mathbb{Z}}_{p^{n}q}$ as the product form ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ . We give a geometric characterization of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ by their $p$ -homogeneous structure. For a set $E$ , denote by $|E|$ the cardinality of $E$ .

Theorem 1.1.

Let $\Omega=\bigsqcup\limits_{j=0}^{q-1}(\Omega_{j}\times\left\{j\right\})$ be a tile in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ with $\Omega_{j}\subset{\mathbb{Z}}_{p^{n}}$ . Then we have the following two cases.

(1)

If $|\Omega|=p^{m}$ , then $\Omega_{0},\Omega_{1},\dots,\Omega_{q-1}$ are disjoint, and $\bigsqcup\limits_{j=0}^{q-1}\Omega_{j}$ is $p$ -homogeneous.
(2)

If $|\Omega|={p^{m}}q$ , then $|{\Omega_{i}}|={p^{m}}$ for any $i$ , and all $\Omega_{i}$ are $p$ -homogeneous with a common branched level set.

1.2. The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$

Now we shall investigate the geometric structure of tiles in the group ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . Let $\Omega$ be a tile of ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . It is evident that $|\Omega|$ divide $p^{n+1}$ . Hence, assume that $|\Omega|=p^{i}$ for some $1\leq i\leq n$ . Define a map $\pi_{1}$ from the group ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ to the group ${\mathbb{Z}}_{p^{n}}$ by

\pi_{1}(a,b)=a,\quad\hbox{ for }(a,b)\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}.

Let

\mathcal{Z}_{\Omega}=\Big{\{}g\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}:\widehat{1_{\Omega}}(g)=0\Big{\}}

be the set of zeros of the Fourier transform of the function $1_{\Omega}$ . We have the following characterization theorem of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ .

Theorem 1.2.

Assume $(\Omega,T)$ is a tiling pair in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $|\Omega|=p^{t}$ . Let

\mathcal{I}_{\Omega}=\big{\{}i\in\{0,\cdots\ n-1\}:(p^{i},0)\in\mathcal{Z}_{\Omega}\big{\}}.

We distinguish three cases.

(1)

If $|\mathcal{I}_{\Omega}|=t$ , then the set $\pi_{1}(\Omega)$ is a $p$ -homogeneous in ${\mathbb{Z}}_{p^{n}}$ with $|\pi_{1}(\Omega)|=p^{t}.$
(2)

If $|\mathcal{I}_{\Omega}|=t-1$ and $(p^{j},b)\notin\mathcal{Z}_{\Omega}$ for each $j\in\{0,1,\cdots,n\}\setminus\mathcal{I}_{\Omega}$ and $b\in{\mathbb{Z}}_{p}^{*}$ , then the sets

$\Omega_{i}=\{x\in{\mathbb{Z}}_{p^{n}}:(x,i)\in\Omega\}$

are $p$ -homogenous in ${\mathbb{Z}}_{p^{n}}$ with a same branched level set and $|\Omega_{i}|=p^{t-1}$ .

(3)

If $|\mathcal{I}_{\Omega}|=t-1$ and $(p^{j},b)\in\mathcal{Z}_{\Omega}$ for some $j\in\{0,1,\cdots,n\}\setminus\mathcal{I}_{\Omega}$ and $b\in{\mathbb{Z}}_{p}^{*}$ , then the set

\widetilde{\Omega}=\{x+b_{0}yp^{n-j_{0}-1}:(x,y)\in\Omega\}

is $p$ -homogeneous in ${\mathbb{Z}}_{p^{n}}$ with $|\widetilde{\Omega}|=p^{t}$ , where $j_{0}$ is the minimal number in $\{0,1,\cdots,n\}\setminus\mathcal{I}_{\Omega}$ such that $(p^{j_{0}},b_{0})\in\mathcal{Z}_{\Omega}$ for some $b_{0}\in{\mathbb{Z}}_{p}^{*}$ . For all $(x,y)\in\Omega$ , the sets

\Omega_{x,y}:=\{x^{\prime}\in{\mathbb{Z}}_{p^{n}}:(x^{\prime},y)\in\Omega\text{ and }x^{\prime}\equiv x\mod p^{n-j_{0}-1}\ \}

are $p$ -homogenous with a same branched level set.

2. Preliminaries

In this section, we present preliminaries for the proof of the main results. We start with the recall of the Fourier transform on finite abelian groups, basic properties of spectral sets and tiles on finite abelian groups, $p$ -homogeneous sets and ${\mathbb{Z}}$ -module generated by the $p^{n}$ -th roots of unity.

Let $G$ be a finite abelian group, and let $\mathbb{C}$ be the set of complex numbers. A character on $G$ is a group homomorphism $\chi:G\to\mathbb{C}$ . The dual group of a finite abelian group $G$ , denoted as $\widehat{G}$ , is the character group of $G$ .

For a finite abelian group $G$ , it can be written as ${\mathbb{Z}}_{n_{1}}\times{\mathbb{Z}}_{n_{2}}\times\cdots\times{\mathbb{Z}}_{n_{s}}$ with $n_{1}\mid n_{2}\mid\cdots\mid n_{s}$ . For $g=(g_{1},g_{2},\dots,g_{s})\in G$ , denote by $\chi_{g}$ the character

\chi_{g}(x_{1},\dots,x_{s})=e^{2\pi i\sum_{j=1}^{s}\frac{x_{j}g_{j}}{n_{j}}}.

For $g,h\in G$ , it is clear that

\chi_{g+h}(x)=\chi_{g}(x)\cdot\chi_{h}(x).

The dual group $\widehat{G}$ is isomorphic to itself, i.e.

\widehat{G}=\widehat{{\mathbb{Z}}}_{n_{1}}\times\widehat{{\mathbb{Z}}}_{n_{2}}\times\cdots\times\widehat{{\mathbb{Z}}}_{n_{s}}\cong{\mathbb{Z}}_{n_{1}}\times{\mathbb{Z}}_{n_{2}}\times\cdots\times{\mathbb{Z}}_{n_{s}}.

For two finite abelian groups $G_{1},G_{2}$ , let $G$ be their product $G_{1}\times G_{2}$ . It is known that $\widehat{G}=\widehat{G_{1}}\times\widehat{G_{2}}\cong G_{1}\times G_{2}$ , and each character in $\widehat{G}$ can be written as

\chi_{(g_{1},g_{2})}(x_{1},x_{2})=\chi_{g_{1}}(x_{1})\chi_{g_{2}}(x_{2}),

where $g_{1}\in G_{1}$ and $g_{2}\in G_{2}$ .

2.1. Fourier transform on the finite groups.

The Fourier transform on $G$ is a linear transformation that maps a function $f:G\rightarrow\mathbb{C}$ to a function $\widehat{f}:\widehat{G}\rightarrow\mathbb{C}$ defined as follows:

\widehat{f}(g)=\sum_{x\in G}f(x)\cdot\chi_{g}(x)

where $\chi_{g}$ is the character of $G$ corresponding to $g$ , and $f(x)$ is the value of the function $f$ at the element $x$ in $G$ .

For $A\subset G$ , denote by

\mathcal{Z}_{A}:=\big{\{}x\in\widehat{G}:\widehat{1_{A}}(x)=0\big{\}}

the set of zeros of the Fourier transform of the indicator function $1_{A}$ . It is clear that $\mathcal{Z}_{A}$ is invariant under translation.

Lemma 2.1.

For each $g\in G$ , we have

\mathcal{Z}_{A}=\mathcal{Z}_{A+g}.

Proof.

Assume that $\xi\in\mathcal{Z}_{A}$ which is equivalent to $\widehat{1_{A}}(\xi)=\sum_{x\in A}\chi_{\xi}(x)=0.$ Hence,

\widehat{1_{A+g}}(\xi)=\sum_{x\in A+g}\chi_{\xi}(x)=\sum_{x\in A}\chi_{\xi}(x+g)=\chi_{\xi}(g)\sum_{x\in A}\chi_{\xi}(x)=0.

∎

The following lemma states that the set of zeros of the Fourier transform of the indicator function of a set is invariant under special multiplication.

Lemma 2.2 ([29]).

If $g\in\mathcal{Z}_{A}$ , then $rg\in\mathcal{Z}_{A}$ for any integer $r$ with $\gcd(r,|G|)=1$ .

Let $G$ be the product of finite abelian groups $H,S$ . Let $A\subset G=H\times S$ . For each $s\in S$ , define

A_{s}=\big{\{}h\in H:(h,s)\in A\big{\}}.

Lemma 2.3.

If $(h,s)\in\mathcal{Z}_{A}$ for each $s\in S$ , then $h\in\mathcal{Z}_{A_{s}}$ for each $s\in S$ .

Proof.

Note that

A=\bigcup_{s\in S}A_{s}\times\{s\}.

Since for each $s\in S$ , $(h,s)\in\mathcal{Z}_{A}$ , it follows that

(2.1)

\displaystyle\sum_{(x,y)\in A}\chi_{(h,s)}(x,y)=\sum_{s\in S}\chi_{s}(y)\sum_{x\in A_{s}}\chi_{h}(x)=0.

Let $X_{s}=\sum_{x\in A_{s}}\chi_{h}(x)$ and let $\mathbf{X}=(X_{s})_{s\in S}$ be the row vector with elements $X_{s}$ . Let $M_{S}=(\chi_{\alpha}(s))_{\alpha,s\in S}$ be the Fourier matrix of $S$ . By Equality (2.1), we obtain the following system of linear equations

M_{S}\cdot\mathbf{X}=\begin{pmatrix}0\\ 0\\ \vdots\\ 0\end{pmatrix}.

The coefficient matrix $M_{S}$ is of full rank, therefore $X_{s}=0$ for each $s\in S$ , which implies that

\widehat{1_{A_{s}}}(h)=\sum_{x\in A_{s}}\chi_{h}(x)=X_{s}=0.

∎

2.2. Basic properties of tiles.

In this section, we give some properties of tiles in finite abelian groups. Considering a tiling pair, we have the following equivalent characterization.

Lemma 2.4 ([25]).

Let $\Omega,T\subseteq G$ . Then the following statements are equivalent:

(1)

$(\Omega,T)$ is a tiling pair.
(2)

$(T,\Omega)$ is a tiling pair.
(3)

$(\Omega+x,T+y)$ is a tiling pair for any $x,y\in G$ .
(4)

$|\Omega|\cdot|T|=|G|$ and $(\Omega-\Omega)\cap(T-T)=\{0\}.$
(5)

$|\Omega|\cdot|T|=|G|$ and $\mathcal{Z}_{\Omega}\cup\mathcal{Z}_{T}=G\setminus\{0\}.$

Lemma 2.5 ([27, Theorem 3.17]).

Assume that $(\Omega,T)$ is a tiling pair of a finite abelian group $G$ . For any integer $k$ with $(k,|T|)$ =1, $(\Omega,kT)$ is also a tiling pair.

2.3. ${\mathbb{Z}}$ -module generated by $p^{n}$ -th roots of unity.

Let $m\geq 2$ be an integer and $\omega_{m}=e^{2\pi i/m}$ , which is a primitive $m$ -th root of unity. Denote

\mathcal{M}_{m}=\Big{\{}(a_{0},a_{1},\cdots,a_{m-1})\in\mathbb{Z}^{m}:\ \sum_{j=0}^{m-1}a_{j}\omega_{m}^{j}=0\Big{\}},

which form a $\mathbb{Z}$ -module. In the following we assume that $m=p^{n}$ is a prime power.

Lemma 2.6 ([7]).

Let $(a_{0},a_{1},\cdots,a_{p^{n}-1})\in\mathcal{M}_{p^{n}}$ . Then for any integer $0\leq k\leq p^{n-1}-1$ , we have $a_{k}=a_{k+jp^{n-1}}$ for all $j=0,1,\cdots,p-1$ .

We will use Lemma 2.6 in the following two particular forms. The first one is an immediate consequence.

Lemma 2.7 ([7]).

Let $(b_{0},b_{1},\cdots,b_{p-1})\in\mathcal{M}_{p}$ . Then subject to a permutation of $(b_{0},b_{1},\cdots,b_{p-1})$ , there exist $0\leq r\leq p^{n-1}-1$ , such that

b_{j}\equiv r+jp^{n-1}\bmod p^{n}

for all $j=0,1,\cdots,p-1$ .

Lemma 2.8 ([7]).

Let $C$ be a finite subset of $\mathbb{Z}$ . If $\sum_{c\in C}e^{2\pi ic/{p^{n}}}=0$ , then $p\mid|C|$ and $C$ can be decomposed into $|C|/p$ disjoint subsets $C_{1},C_{2},\cdots,C_{|C|/p}$ , such that each subset consists of $p$ points and

\sum_{c\in C_{j}}e^{2\pi ic/{p^{n}}}=0.

2.4. $p$ -homogeneity of tiles in ${\mathbb{Z}}_{p^{n}}$

Let $n$ be a positive integer. To any finite sequence $t_{0}t_{1}\cdots t_{n-1}\in\{0,1,\dots,p-1\}^{n}$ , we associate the integer

c=c(t_{0}t_{1}\cdots t_{n-1})=\sum_{i=0}^{n-1}t_{i}p^{i}\in\{0,1,\dots,p^{n}-1\}.

This establishes a bijection between ${\mathbb{Z}}_{p^{n}}$ and $\{0,1,\dots,p-1\}^{n}$ , which we consider as a finite tree, denoted by ${\mathcal{T}}^{(n)}$ (see Figure 1).

The set of vertices of ${\mathcal{T}}^{(n)}$ is the disjoint union of the sets ${\mathbb{Z}}_{p^{\gamma}}$ , for $0\leq\gamma\leq n$ . Each vertex, except the root, is identified with a sequence $t_{0}t_{1}\cdots t_{\gamma-1}$ in ${\mathbb{Z}}_{p^{\gamma}}$ , where $0\leq\gamma\leq n$ and $t_{i}\in\{0,1,\dots,p-1\}$ . The set of edges consists of pairs $(x,y)\in{\mathbb{Z}}_{p^{\gamma}}\times{\mathbb{Z}}_{p^{\gamma+1}}$ such that $x\equiv y\pmod{p^{\gamma}}$ , where $0\leq\gamma\leq n-1$ . The points in ${\mathbb{Z}}_{p^{\gamma}}$ are corresponding to the vertices at level $\gamma$ . Each point $c$ of ${\mathbb{Z}}_{p^{n}}$ is identified with a boundary vertex $\sum_{i=0}^{n-1}t_{i}p^{i}\in\{0,1,\dots,p^{n}-1\}$ which is located at level $n$ .

Each subset $C\subset{\mathbb{Z}}_{p^{n}}$ determines a subtree of ${\mathcal{T}}^{(n)}$ , denoted by ${\mathcal{T}}_{C}$ , which consists of the paths from the root to the boundary points in $C$ . For each $0\leq\gamma\leq n$ , we denote by

C_{\bmod p^{\gamma}}:=\big{\{}x\in\{0,1,\dots,p^{\gamma}-1\}:\exists\ y\in C\text{ such that }x\equiv y\pmod{p^{\gamma}}\big{\}}

the subset of $C$ modulo $p^{\gamma}$ .

The set of vertices of ${\mathcal{T}}_{C}$ is the disjoint union of the sets $C_{\bmod p^{\gamma}}$ , for $0\leq\gamma\leq n$ . The set of edges consists of pairs $(x,y)\in C_{\bmod p^{\gamma}}\times C_{\bmod p^{\gamma+1}}$ such that $x\equiv y\pmod{p^{\gamma}}$ , where $0\leq\gamma\leq n-1$ .

For vertices $u\in C_{\bmod p^{\gamma+1}}$ and $s\in C_{\bmod p^{\gamma}}$ , we call $s$ the parent of $u$ or $u$ a descendant of $s$ if there exists an edge between $s$ and $u$ .

Now, we proceed to construct a class of subtrees of ${\mathcal{T}}^{(n)}$ . Let $I$ be a subset of $\{0,1,\dots,n-1\}$ , and let $J$ be its complement. Thus, $I$ and $J$ form a partition of $\{0,1,\dots,n-1\}$ , and either set may be empty.

We say a subtree ${\mathcal{T}}_{C}$ of ${\mathcal{T}}^{(n)}$ is of ${\mathcal{T}}_{I}$ -form if its vertices satisfy the following conditions:

(1)

If $i\in I$ and $t_{0}t_{1}\dots t_{i-1}$ is given, then $t_{i}$ can take any value in $\{0,1,\dots,p-1\}$ . In other words, every vertex in $C_{\bmod p^{i-1}}$ has $p$ descendants.
(2)

If $i\in J$ and $t_{0}t_{1}\dots t_{i-1}$ is given, we fix a value in $\{0,1,\dots,p-1\}$ that $t_{i}$ must take. That is, $t_{i}$ takes only one value from $\{0,1,\cdots,p-1\}$ , which depends on $t_{0}t_{1}\dots t_{i-1}$ . In other words, every vertex in $C_{\bmod p^{i-1}}$ has one descendant.

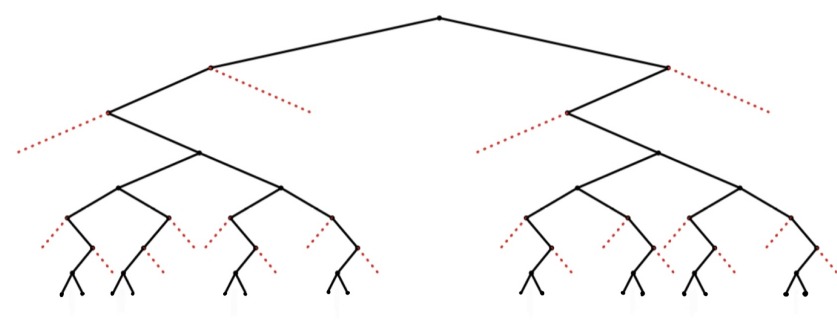
Note that such a subtree depends not only on $I$ and $J$ but also on the specific values assigned to $t_{i}$ for $i\in J$ . A ${\mathcal{T}}_{I}$ -form tree is called a finite $p$ -homogeneous tree, see Figure 4 for an example.

A set $C\subset{\mathbb{Z}}_{p^{n}}$ is said to be $p$ -homogeneous subset of ${\mathbb{Z}}_{p^{n}}$ with branched level set $I$ if the corresponding tree ${\mathcal{T}}_{C}$ is $p$ -homogeneous of form ${\mathcal{T}}_{I}$ .

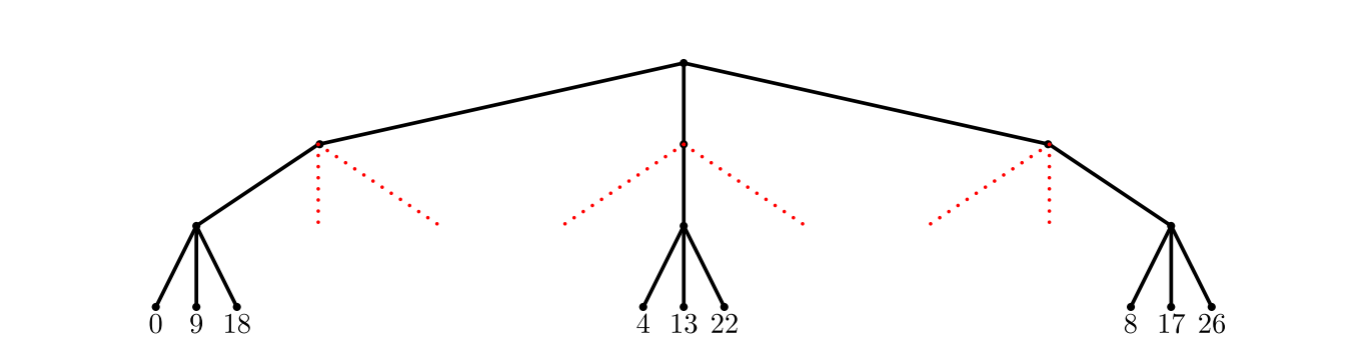
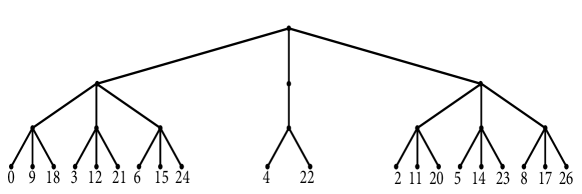
Example 2.9.

Let $p=3$ , $n=3$ , $C=\{0,4,8,9,13,17,18,22,26\}$ (see figure 5). We have:

	$\displaystyle 0$	$\displaystyle=0\cdot 1+0\cdot 3+0\cdot 3^{2},\quad 4=1\cdot 1+1\cdot 3+0\cdot 3^{2},\quad 8=2\cdot 1+2\cdot 3+0\cdot 3^{2},$
	$\displaystyle 9$	$\displaystyle=0\cdot 1+0\cdot 3+1\cdot 3^{2},\quad 13=1\cdot 1+1\cdot 3+1\cdot 3^{2},\quad 17=2\cdot 1+2\cdot 3+1\cdot 3^{2},$
	$\displaystyle 18$	$\displaystyle=0\cdot 1+0\cdot 3+2\cdot 3^{2},\quad 22=1\cdot 1+1\cdot 3+2\cdot 3^{2},\quad 26=2\cdot 1+2\cdot 3+2\cdot 3^{2}.$

A criterion for a subset $C\subset{\mathbb{Z}}_{p^{n}}$ to be $p$ -homogeneous is given in [7].

Lemma 2.10 ([7, Theorem 2.9]).

Let $n$ be a positive integer, and let $C\subset{\mathbb{Z}}_{p^{n}}$ be a multiset. Suppose that

(1)

$|C|\leq p^{k}$ for some integer $k$ with $1\leq k\leq n$ ;
(2)

there exist $k$ integers $1\leq j_{1}<j_{2}<\dots<j_{k}\leq n$ such that

$\sum_{c\in C}e^{2\pi icp^{-j_{t}}}=0\quad\text{for all }1\leq t\leq k.$

Then $|C|=p^{k}$ and $C$ is $p$ -homogeneous. Moreover, the tree ${\mathcal{T}}_{C}$ is a ${\mathcal{T}}_{I}$ -form tree with branched level set $I=\{j_{1}-1,j_{2}-1,\dots,j_{k}-1\}$ .

Lemma 2.11 ([7, Theorem 4.2]).

Let $n$ be a positive integer, and let $C\subset{\mathbb{Z}}_{p^{n}}$ . Then $C$ tiles ${\mathbb{Z}}_{p^{n}}$ if and only if $C$ is p-homogeneous.

3. The structure of tiles on ${\mathbb{Z}}_{p^{n}q}$

In this section, we primarily utilize the results established in [7] and [2] to characterize the structure of tiles on ${\mathbb{Z}}_{p^{n}q}$ .

The structural properties of tiles in ${\mathbb{Z}}_{p^{n}}$ are characterized by $p$ -homogeneity, as showed in [7]. Furthermore, the equivalence of spectral sets and tiles in ${\mathbb{Z}}_{p^{n}q}$ , where $p$ and $q$ are distinct primes, was proven in [2]. This fundamental fact serves as a cornerstone in subsequent proofs within this section.

3.1. CM condition for tiles in finite group ${\mathbb{Z}}_{N}$ .

Let $A\subseteq{\mathbb{Z}}_{N}$ be a multi-set, and let $m_{a}$ denote the multiplicity of $a\in A$ . The mask polynomial of $A$ is defined as

A(x)=\sum_{a\in A}m_{a}x^{a}.

Denote by $\omega_{N}=e^{2\pi i/N}$ , which is a primitive $N$ -th root of unity. For any $d\in\{0,1,\dots,N-1\}$ , it is straightforward to verify that $A(\omega_{N}^{d})=0$ is equivalent to $\widehat{1_{A}}(d)=0$ .

Denote by $\Phi_{s}(x)$ the $s$ -th cyclotomic polynomial.

Lemma 3.1 ([24, Lemma 2.4]).

Let $A$ be a subset of ${\mathbb{Z}}_{N}$ . Let $p$ be a prime factor of $N$ , and $a\in{\mathbb{Z}}_{N}$ . Then the following statements hold.

(1)

$A(\omega_{N}^{a})=0$ if and only if $A(\omega_{N}^{ag})=0$ for any $g\in{\mathbb{Z}}_{N}^{*}$ .
(2)

For any $d\mid N$ , $A(\omega_{N}^{d})=0$ if and only if $\Phi_{\frac{N}{d}}(X)\mid A(X).$
(3)

Suppose that $|\{p^{d}\in{\mathbb{Z}}_{N}:A(\omega_{N}^{N/p^{d}})=0\}|=k$ . Then $p^{k}\mid|A|$ .

Let $S$ denote the set of prime powers dividing $N$ , and define

S_{A}=\{s\in S:\Phi_{s}(x)\mid A(x)\}.

Coven and Meyerowitz introduced the following two properties in [2], which play a crucial role in characterizing a set $A$ that tile ${\mathbb{Z}}_{N}$ by translations:

(T1)

$|A|=A(1)=\prod_{s\in S_{A}}\Phi_{s}(1)$ .
(T2)

Let $s_{1},\dots,s_{m}\in S_{A}$ be powers of different primes. Then the polynomial $\Phi_{s_{1}\dotsm s_{m}}(x)$ divides $A(x)$ .

The following results are established in [2].

Theorem 3.2 ([2]).

Let $\Omega\subset{\mathbb{Z}}_{N}$ .

•

If $\Omega$ satisfies properties (T1) and (T2), then $\Omega$ tiles ${\mathbb{Z}}_{N}$ by translations.
•

If $\Omega$ tiles ${\mathbb{Z}}_{N}$ by translations, then (T1) holds.
•

If $\Omega$ tiles ${\mathbb{Z}}_{N}$ by translations and $|\Omega|$ has at most two prime factors, then (T2) holds.

Corollary 3.3.

For $N=p^{n}q$ , any tile $\Omega$ in ${\mathbb{Z}}_{N}$ satisfies properties (T1) and (T2).

3.2. The structure of tiles in ${\mathbb{Z}}_{p^{n}q}$

Now, let $N=p^{n}q$ with $p$ , $q$ are distinct primes. For a set $A\subset{\mathbb{Z}}_{p^{n}q}$ , denote ${\mathcal{Z}}_{A}=\{x\in{\mathbb{Z}}_{p^{n}q}:{\widehat{1_{A}}}(x)=0\}$ . Let

\mathcal{I}_{A}=\big{\{}0\leq a\leq n-1:\ p^{a}q\in{\mathcal{Z}}_{A}\big{\}}.

Lemma 3.4.

Let $(\Omega,T)$ be a tiling pair in ${\mathbb{Z}}_{p^{n}q}$ . Then the cardinality of $\Omega$ is either $p^{t}$ or $p^{t}q$ , where $0\leq t\leq n$ . In both cases $|\mathcal{I}_{\Omega}|=t$ and $\mathcal{I}_{\Omega}$ and $\mathcal{I}_{T}$ forms a disjoint union of $\{0,1,\cdots,n-1\}$ .

Proof.

Since $(\Omega,T)$ is a tiling pair in ${\mathbb{Z}}_{p^{n}q}$ , it follows that $|\Omega|\mid p^{n}q$ . Hence $|\Omega|=p^{t}$ or $|\Omega|=p^{t}q$ for some $0\leq t\leq n$ . Note that for any $0\leq a\leq n-1$ , $p^{a}q\in\mathcal{Z}_{\Omega}\cup\mathcal{Z}_{T}$ . By statement (3) of Lemma 3.1, $|\mathcal{I}_{\Omega}|=t$ , $|\mathcal{I}_{T}|=n-t$ and $\mathcal{I}_{\Omega}$ and $\mathcal{I}_{T}$ forms a disjoint union of $\{0,1,\cdots,n-1\}$ . ∎

Note that ${\mathbb{Z}}_{p^{n}q}$ is isomorphic to the group ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ by the isomorphism

x\mapsto(x_{1},x_{2})\quad\hbox{ with }x_{1}\equiv x\!\!\!\pmod{p^{n}},x_{2}\equiv x\!\!\!\pmod{q}.

Let $\pi_{1}:{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}\to{\mathbb{Z}}_{p^{n}}$ and $\pi_{2}:{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}\to{\mathbb{Z}}_{q}$ be the projection maps. In the reminder of this section, we consider the product form ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ .

For a function $f$ on ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ , the Fourier transform of $f$ is

\widehat{f}(x,y)=\sum_{(u,v)\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}}f(x,y)e^{2\pi i(\frac{ux}{p^{n}}+\frac{vy}{q})}.

Hence, it follows that $(p^{a},0)\in\mathcal{Z}_{A}$ if and only if $a\in\mathcal{I}_{A}$ .

Proof of Theorem 1.1 .

(1) Case $|\Omega|=p^{t}$ . Note that

\widehat{1_{\Omega}}(p^{a},0)=\sum_{(u,v)\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}}e^{2\pi i\frac{u}{p^{n-a}}}.

Consider $\pi_{1}(\Omega)$ as a multi-set in ${\mathbb{Z}}_{p^{n}}$ , where the multiplicity of $x\in{\mathbb{Z}}_{p^{n}}$ is given by $|\pi_{1}^{-1}(x)|$ . Therefore, $\widehat{1_{\Omega}}(p^{a},0)=0$ if and only if $\widehat{1_{\pi_{1}(\Omega)}}(p^{a})=0$ .

By Lemma 2.10, it follows that the multiplicity of each point $\pi_{1}(\Omega)$ is one and $\pi_{1}(\Omega)$ corresponds to a ${\mathcal{T}}_{I}$ -form $p$ -homogeneous tree with $I=n-1-\mathcal{I}_{\Omega}$ .

(2) Case $|\Omega|=p^{t}q$ . Assume that $(\Omega,T)$ is a tiling pair. Then we have $|T|=p^{n-t}$ . By statement (3) of Lemma 3.1, $\Omega(\omega_{N}^{p^{n}})=0$ , which is equivalent to $\Phi_{q}(X)\mid\Omega(X).$ Hence, for any $a\in I_{\Omega}$ , by Corollary 3.3 and statement (2) of Lemma 3.1, we have $\Omega(\omega_{N}^{p^{a}})=0$ , which is equivalent to $(p^{a},j)\in\mathcal{Z}_{\Omega}$ with $j\equiv p^{a}\pmod{q}.$ Actually, this implies that $(p^{a},j)\in\mathcal{Z}_{\Omega}$ for all $a\in\mathcal{I}_{\Omega}$ and $j\in\{0,\cdots,q-1\}$ . Moreover, it is clear that $(0,j)\in\mathcal{Z}_{\Omega}$ for all $j\in\{1,\cdots,q-1\}$ . Take a $p$ -homogeneous ${\mathcal{T}}_{J}$ -form subset $T_{0}\subset{\mathbb{Z}}_{p^{n}}$ . Then $(\Omega,T_{0}\times\{0\})$ forms a tiling pair, which implies that each $(\Omega_{j},T_{0})$ forms a tiling pair of ${\mathbb{Z}}_{p^{n}}$ . ∎

4. The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$

4.1. Equidistribution property

For $\textbf{x}=(x_{1},x_{2}),~{}\textbf{y}=(y_{1},y_{2})\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ , we define the inner product in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ by the formula

\langle\textbf{x},\textbf{y}\rangle=x_{1}y_{1}+p^{n-1}x_{2}y_{2}\in{\mathbb{Z}}_{p^{n}}.

We define

H(\textbf{d},t):=\{\mathbf{x}\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}:\langle\mathbf{x},\textbf{d}\rangle=t\},

for $\textbf{d}\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ and $t\in{\mathbb{Z}}_{p^{n}}$ . We call such set a plane in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ .

For $r\in{\mathbb{Z}}_{p^{n}}^{\ast}$ and $\textbf{d}=(d_{1},d_{2})\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ , we define the scalar product as:

r\textbf{d}=(\tilde{d}_{1},\tilde{{d}}_{2})\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p},

where $\tilde{{d}}_{1}\equiv r{d}_{1}\bmod p^{n}$ and $\tilde{{d}}_{2}\equiv r{d}_{2}\bmod p$ .

The following lemma provide the equidistribution property of a set $A\subset{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ .

Lemma 4.1 ([24, Lemma 3.1]).

Let $A\subseteq{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ and $\mathbf{d}\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . The following are equivalent:

(1)

$\widehat{1_{A}}(\mathbf{d})=0$ ;
(2)

$\widehat{1_{A}}(r\mathbf{d})=0$ , for any $r\in{\mathbb{Z}}_{p^{n}}^{\ast}$ ;
(3)

$|A\cap H(\mathbf{d},t)|=|A\cap H(\mathbf{d},t^{\prime})|$ , if $t\equiv t^{\prime}\bmod p^{n-1}$ .

For $\mathbf{u},\mathbf{v}\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ , we define the relation $\mathbf{u}\sim\mathbf{v}$ , if there exists $r\in{\mathbb{Z}}_{p^{n}}^{\ast}$ such that $\mathbf{u}=r\mathbf{v}$ . Thus, the equivalent classes in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ by $``\sim"$ are

(1,0),(c,p^{i})\quad\text{for all}~{}c\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}\quad\text{and}\quad i\in\{0,2,\cdots,n-1\}.

Thus, by Lemma 4.1, when we study the set of zeros $\mathcal{Z}_{A}$ of a set $A\subseteq{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ , we only need to consider the elements which have the above forms.

Now we give the divisibility property for a set in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ .

Lemma 4.2 ([29] Lemma 3.2).

Let $A\subseteq{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . If $(p^{i_{1}},a),(p^{i_{2}},0),\cdots,(p^{i_{s}},0)\in\mathcal{Z}_{A}$ for some $a\in{\mathbb{Z}}_{p^{n}}$ and $0\leq{i_{1}}<{i_{2}}<...<{i_{s}}\leq n-1$ , then $p^{s}\mid|A|$ .

4.2. Proof of the theorem 1.2

In this subsection, we are concerned tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . Let $\Omega$ be a non-trivial tile in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ , then, due to Lemma 2.4, we have that $|\Omega|\big{|}p^{n+1}$ . Thus, we can assume that $|\Omega|=p^{t}$ for some $1\leq t\leq n$ .

For a set $A\subset{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ , denote

{\mathcal{Z}}_{A}=\big{\{}(x,y)\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}:\widehat{1_{A}}(x,y)=0\big{\}}.

Let

\mathcal{I}_{A}=\big{\{}0\leq i\leq n-1:(p^{i},0)\in{\mathcal{Z}}_{A}\big{\}}.

Lemma 4.3.

Let $\Omega$ be a tile of ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $|\Omega|=p^{t}$ for some $1\leq t\leq n$ . Then $|\mathcal{I}_{\Omega}|=t-1$ or $t$ .

Proof.

Let $T$ be a tiling complement of $\Omega$ in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . Then $|T|=p^{n-t+1}$ . By Lemma 4.2, we have that $|\mathcal{I}_{\Omega}|\leqslant t$ and $|\mathcal{I}_{T}|\leqslant n-t+1$ . On the other hand, since

\mathcal{Z}_{\Omega}\cup\mathcal{Z}_{T}={\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}\backslash\{(0,0)\},

we have $|\mathcal{I}_{\Omega}|+|\mathcal{I}_{T}|\geqslant n$ . Thus, $t-1\leqslant|\mathcal{I}_{\Omega}|\leqslant t$ , that means $|\mathcal{I}_{\Omega}|=t$ or $t-1$ . ∎

Define a map $\pi_{1}$ from ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ to ${\mathbb{Z}}_{p^{n}}$ by

\pi_{1}(a,b)=a,\hbox{ for }(a,b)\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}.

Proposition 4.4.

Let $\Omega$ be a tile in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $|\Omega|=p^{t}$ and $|\mathcal{I}_{\Omega}|=t$ . Then $\pi_{1}(\Omega)$ is a $p$ -homogeneous set in ${\mathbb{Z}}_{p^{n}}$ with $|\pi_{1}(\Omega)|=p^{t}$ .

Proof.

Write $\Omega=\bigsqcup\limits_{j=0}^{p-1}(\Omega_{j}\times\left\{j\right\})$ with $\Omega_{j}\subset{\mathbb{Z}}_{p^{n}}$ . For each $i\in\mathcal{I}_{\Omega}$ , we have

	$\displaystyle\widehat{1_{\Omega}}(p^{i},0)$	$\displaystyle=\sum_{j=0}^{p-1}\widehat{1_{\Omega_{j}\times\{j\}}}(p^{i},0)$
		$\displaystyle=\sum_{j=0}^{p-1}\widehat{1_{\Omega_{j}}}(p^{i})$
		$\displaystyle=\widehat{1_{\Omega_{0}\cup\Omega_{1}\cup\cdots\cup\Omega_{p-1}}}(p^{i})$
		$\displaystyle=0.$

By Lemmas 2.10 and 2.11, $\pi_{1}(\Omega)={\Omega_{0}}\cup{\Omega_{1}}\cup\cdots\cup{\Omega_{p-1}}$ is a $p$ -homogeneous set in ${\mathbb{Z}}_{p^{n}}$ and $|\pi_{1}(\Omega)|=p^{t}$ . ∎

Now assume $|\mathcal{I}_{\Omega}|=t-1$ . Let $\mathcal{J}=\{0,1,\cdots n-1\}\backslash\mathcal{I}_{\Omega}$ .

Lemma 4.5.

Let $\Omega$ be a tile in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $|\Omega|=p^{t}$ and $|\mathcal{I}_{\Omega}|=t-1$ for some $1\leq t\leq n$ . If for each $i\in\{0,1,\cdots,n-1\}\setminus\mathcal{I}_{\Omega}$ and $b\in{\mathbb{Z}}_{p}^{*}$ , $(p^{i},b)\notin\mathcal{Z}_{\Omega}$ , then $(0,1)\in\mathcal{Z}_{\Omega}$ .

Proof.

Let $T$ be a tiling complement of $\Omega$ . By assumption, we have

\{(p^{j},b):j\in\mathcal{J},b\in{\mathbb{Z}}_{p}\}\subset\mathcal{Z}_{T}.

If $(0,1)\in\mathcal{Z}_{T}$ , we define

\Lambda=\big{\{}s_{n}(0,1)+(\sum_{j\in\mathcal{J}}s_{j}p^{j},0):s_{j},s_{n}\in\{0,1,\cdots,p-1\}\big{\}}.

Then, for any $\lambda\neq\lambda^{\prime}\in\Lambda$ , we have

\lambda-\lambda^{\prime}=r_{n}(0,1)+(\sum_{j\in\mathcal{J}}r_{j}p^{j},\ 0),

where $r_{j},r_{n}\in\{-p+1,\cdots,\ p-1\}$ . Notice that

r_{n}(0,1)+(\sum_{j\in J}r_{j}p^{j},\ 0)\sim\begin{cases}(0,1),&\text{if}\ r_{n}\neq 0\ \text{and}\ r_{j}=0\ \text{for}\ j\in\mathcal{J};\\ (p^{l},r_{l}^{-1}r_{n}),&\text{if}\ r_{n}\neq 0,r_{l}\neq 0\ \text{and}\ r_{j}=0\ \text{for}\ 1\leq j<l;\\ (p^{l},\ 0),&\text{if}\ r_{n}=0,\ r_{l}\neq 0\ \text{and}\ r_{j}=0\ \text{for}\ 1\leq j<l.\end{cases}

Therefore, $(\Lambda-\Lambda)\setminus\{(0,0)\}\subseteq\mathcal{Z}_{T}$ , which implies the characters $\{\chi_{\lambda}\}_{\lambda\in\Lambda}$ are orthogonal in $L^{2}(T)$ . However, $|\Lambda|=p^{n-t+2}>|T|$ , which is a contradiction, since the dimension of $L^{2}(T)$ is $|T|$ . Thus, $(0,1)\in\mathcal{Z}_{\Omega}$ . ∎

Note that $p^{n}=0$ in ${\mathbb{Z}}_{p^{n}}$ . Let $\Omega$ be tile of ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $|\Omega|=p^{t}$ and $|\mathcal{I}_{\Omega}|=t-1$ . Define

\gamma_{\Omega}=\min\big{\{}j\in\{0,1,\cdots,n\}\setminus\mathcal{I}_{\Omega}:(p^{j},b)\in\mathcal{Z}_{\Omega}\hbox{ for some }b\in{\mathbb{Z}}_{p}^{*}\big{\}}.

By Lemma 4.5, $\gamma_{\Omega}$ is well defined.

Lemma 4.6.

Let $\Omega$ be a tile in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $|\Omega|=p^{t}$ and $|\mathcal{I}_{\Omega}|=t-1$ for some $1\leq t\leq n$ . Then for any tiling complement $T$ , we have $(p^{i},b)\notin\mathcal{Z}_{T}$ for all $i\in\mathcal{I}_{\Omega}$ with $i<\gamma_{\Omega}$ , $b\in\{0,1,\cdots,p-1\}.$ Consequently, $(p^{i},b)\in\mathcal{Z}_{\Omega}$ .

Proof.

Let $T$ be a tiling complement of $\Omega$ and $\mathcal{J}=\{0,1,\cdots,n-1\}\setminus\mathcal{I}_{\Omega}$ . Assume that there is an $i\in\mathcal{I}_{\Omega}$ with $i<\gamma_{\Omega}$ such that $(p^{i},b)\in\mathcal{Z}_{T}$ for $b\in{\mathbb{Z}}_{p}$ . Define

\Lambda=\Big{\{}(\sum\limits_{j\in\mathcal{J}}s_{j}p^{j},0)+s_{i}(p^{i},b):s_{i},s_{j}\in\{0,1,\cdots,p-1\}\Big{\}}.

For any $\lambda\neq\lambda^{\prime}\in\Lambda$ , we have

\lambda-\lambda^{\prime}=(\sum\limits_{j\in\mathcal{J}}r_{j}p^{j},0)+r_{i}(p^{i},b),

where $r_{i},r_{j}\in\{-p+1,\cdots,p-1\}$ . Observe that

\sum_{j\in\mathcal{J}}r_{j}(p^{j},0)+~{}r_{i}(p^{i},b)\sim(p^{i},b)

if $\ r_{i}\neq 0$ and $r_{j}=0$ for $j<i$ . And

\sum_{j\in\mathcal{J}}r_{j}(p^{j},0)+~{}r_{i}(p^{i},b)\sim(p^{l},r_{l}^{-1}r_{i}b)

if $l$ is the minimal number such that $r_{l}\neq 0$ and $l<i$ . Therefore

(\Lambda-\Lambda)\backslash\{(0,0)\}\subseteq\mathcal{Z}_{T},

which implies the characters $\{\chi_{\lambda}\}_{\lambda\in\Lambda}$ are orthogonal in $L^{2}(T)$ . However, $|\Lambda|=p^{n-t+2}>|T|$ , which is a contradiction, since the dimension of $L^{2}(T)$ is $|T|$ . ∎

We distinguish two cases:

(1)\ \gamma_{\Omega}=n,\quad(2)\ \gamma_{\Omega}<n.

Firstly, we deal with the case $\gamma_{\Omega}=n$ .

Proposition 4.7.

Let $\Omega$ be tile of ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $|\Omega|=p^{t}$ , $|\mathcal{I}_{\Omega}|=t-1$ and $\gamma_{\Omega}=n.$ Then for each $b\in{\mathbb{Z}}_{p}$ , the set $\Omega_{b}=\{x\in{\mathbb{Z}}_{p^{n}}:(x,b)\in\Omega\}$ is a $p$ -homogeneous subset of ${\mathbb{Z}}_{p^{n}}$ with branched level set $n-1-\mathcal{I}_{\Omega}$ .

Proof.

By Lemmas 4.5 and 4.6, we have

\left\{(0,b):b\in{\mathbb{Z}}_{p}\right\}\subset\mathcal{Z}_{\Omega}

and

\left\{(p^{i},b):i\in\mathcal{I}_{\Omega},b\in{\mathbb{Z}}_{p}\right\}\subset\mathcal{Z}_{\Omega}.

Let $T_{0}$ be a subset of ${\mathbb{Z}}_{p^{n}}$ with $p^{j}\in\mathcal{Z}_{T_{0}}$ for $j\in\mathcal{J}=\{0,\cdots,n-1\}\setminus\mathcal{I}_{\Omega}$ . Take $T=T_{0}\times\{0\}$ , which is a subset of ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . By calculating the zero set $\mathcal{Z}_{T}$ , it follows that $(\Omega,T)$ is a tiling pair of ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . Hence, for each $b\in{\mathbb{Z}}_{p}$ , $(\Omega_{b},T_{0})$ is a tiling pair of ${\mathbb{Z}}_{p^{n}}$ , which implies $\Omega_{b}=\{x\in{\mathbb{Z}}_{p^{n}}:(x,b)\in\Omega\}$ is a $p$ -homogeneous subset of ${\mathbb{Z}}_{p^{n}}$ with branched level set $n-1-\mathcal{I}_{\Omega}$ . ∎

Now, we shall deal the case $\gamma_{\Omega}<n$ .

Proposition 4.8.

Let $\Omega$ be a tile in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ with $\gamma_{\Omega}<n$ , $|\Omega|=p^{t}$ and $|\mathcal{I}_{\Omega}|=t-1$ for some $1\leq t\leq n-1$ . Assume that $(p^{\gamma_{\Omega}},\alpha)\in\mathcal{Z}_{\Omega}$ and let $\mathcal{I}=\mathcal{I}_{\Omega}\cup\{\gamma_{\Omega}\}$ . Then the set

\widetilde{\Omega}=\left\{x+\alpha yp^{n-\gamma_{\Omega}-1}:(x,y)\in\Omega\right\}

is a $p$ -homogeneous set in ${\mathbb{Z}}_{p^{n}}$ .

Proof.

Consider the multi-set

\widetilde{\Omega}=\left\{x+\alpha yp^{n-\gamma_{\Omega}-1}:(x,y)\in\Omega\right\}\subset{\mathbb{Z}}_{p^{n}}.

It is obvious that $|\widetilde{\Omega}|=p^{t}$ . Now, we shall show that $p^{j}\in\mathcal{Z}_{\widetilde{\Omega}}$ for $j\in\mathcal{I}$ .

For $j\in\mathcal{I}_{\Omega}$ with $j>\gamma_{\Omega}$ , we have

\widehat{1_{\widetilde{\Omega}}}(p^{j})=\sum_{(x,y)\in\Omega}e^{2\pi i\frac{(x+\alpha yp^{n-\gamma_{\Omega}-1})p^{j}}{p^{n}}}=\sum_{(x,y)\in\Omega}e^{2\pi i\frac{xp^{j}}{p^{n}}}=\widehat{1_{\Omega}}(p^{j},0)=0.

For $j=\gamma_{\Omega}$ , we have

\widehat{1_{\widetilde{\Omega}}}(p^{\gamma_{\Omega}})=\sum_{(x,y)\in\Omega}e^{2\pi i\frac{(x+\alpha yp^{n-\gamma_{\Omega}-1})p^{\gamma_{\Omega}}}{p^{n}}}=\sum_{(x,y)\in\Omega}e^{2\pi i\frac{xp^{\gamma_{\Omega}}+\alpha yp^{n-1}}{p^{n}}}=\widehat{1_{\Omega}}(p^{\gamma_{\Omega}},\alpha)=0.

Now we consider the case $j<\gamma_{\Omega}$ . By the definition of $\gamma_{\Omega}$ , we have $(p^{j},b)\in\mathcal{Z}_{\Omega}$ for each $b\in{\mathbb{Z}}_{p}$ . For each $b\in{\mathbb{Z}}_{p}$ , let $\Omega_{b}=\{x\in{\mathbb{Z}}_{p^{n}}:(x,b)\in{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}\}$ . By Lemma 2.3, we have $p^{j}\in\mathcal{Z}_{\Omega_{b}}$ for each $b\in{\mathbb{Z}}_{p}$ . By the definition of $\widetilde{\Omega}$ , we have

	$\displaystyle\widehat{1_{\widetilde{\Omega}}}(p^{j})$	$\displaystyle=\sum_{(x,y)\in\Omega}e^{2\pi i\frac{(x+\alpha yp^{n-\gamma_{\Omega}-1})p^{j}}{p^{n}}}$
		$\displaystyle=\sum_{b\in{\mathbb{Z}}_{p}}\sum_{x\in\Omega_{b}}e^{2\pi i\frac{xp^{j}+\alpha bp^{n+j-1-\gamma_{\Omega}}}{p^{n}}}$
		$\displaystyle=\sum_{b\in{\mathbb{Z}}_{p}}\widehat{1_{\Omega_{b}+\alpha bp^{n+j-1-\gamma_{\Omega}}}}(p^{j}).$

By Lemma 2.1, we have $\widehat{1_{\widetilde{\Omega}}}(p^{j})=0$ . Hence, $\{p^{j}:j\in\mathcal{I}\}\subset\mathcal{Z}_{\widetilde{\Omega}}$ . Note that $|\mathcal{I}|=t$ and $|\widetilde{\Omega}|=p^{t}$ . By Lemma 2.10, $\widetilde{\Omega}$ is $p$ -homogeneous with branch level set $n-1-\mathcal{I}.$ ∎

Lemma 4.9.

Let $\Omega$ be a tile in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$ . Assume that $\mathcal{I}_{\Omega}=\{i_{1},i_{2},\cdots,i_{t-1}\}$ with $i_{1}<\cdots<i_{s}<\gamma_{\Omega}<i_{s+1}<\cdots<i_{t-1}$ . Then for each $(x,y)\in\Omega$ , the sets

\Omega_{x,y}:=\{x^{\prime}\in{\mathbb{Z}}_{p^{n}}:(x^{\prime},y)\in\Omega\text{ and }x^{\prime}\equiv x\!\!\mod p^{n-\gamma_{\Omega}-1}\ \}

is $p$ -homogenous with the branched level set $n-1-\{i_{1},i_{2}\cdots,i_{s}\}$ .

Proof.

Assume that $\mathcal{I}_{\Omega}=\{i_{1},i_{2},\cdots,i_{t-1}\}$ with $i_{1}<\cdots<i_{s}<\gamma_{\Omega}<i_{s+1}<\cdots<i_{t-1}$ .

We shall characterize the structure of the tile $\Omega$ by induction. We distinguish two cases.

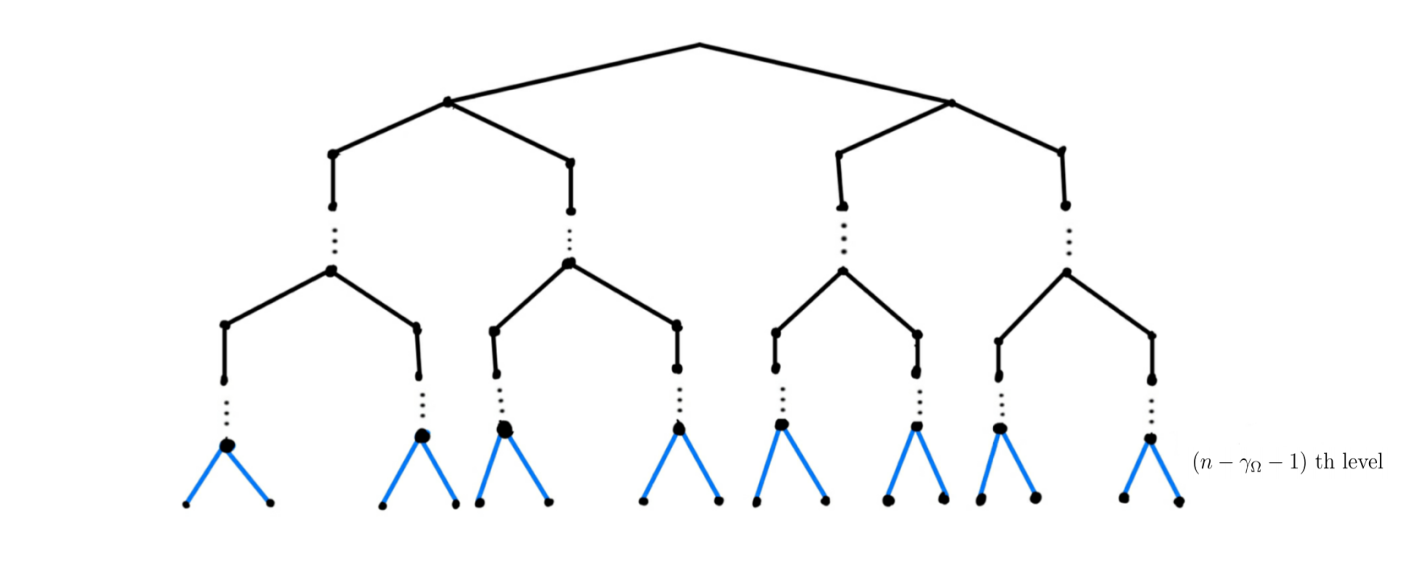
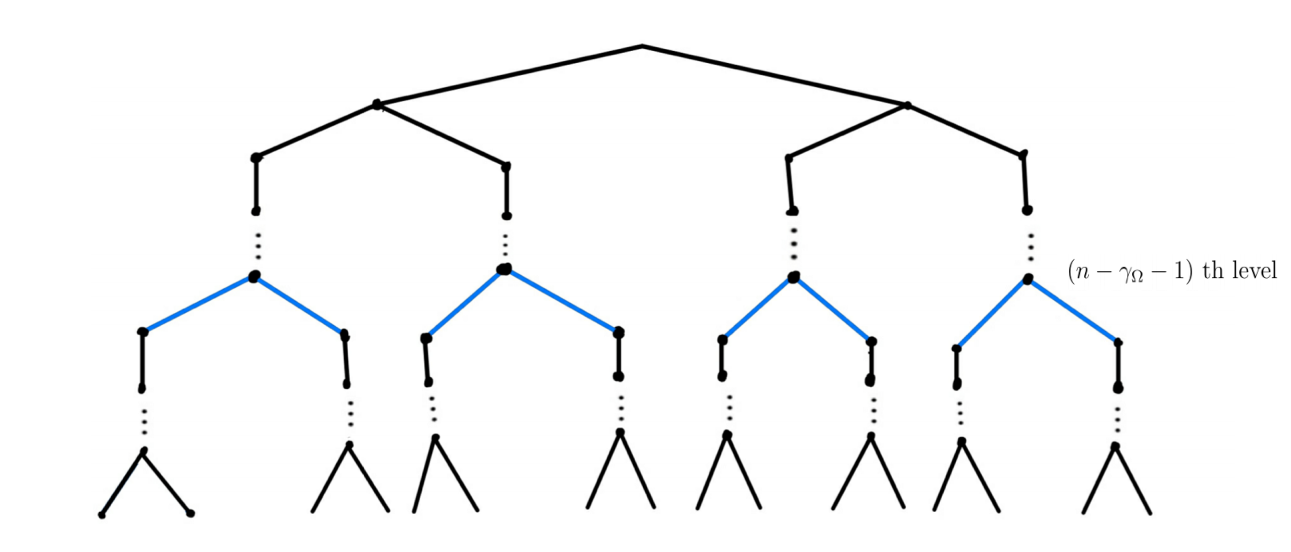
Case 1: Assume $\gamma_{\Omega}<i_{1}<i_{2}<\cdots<i_{t-1}$ . The set $\widetilde{\Omega}$ corresponding to a $p$ -homogeneous tree with branched level set

n-1-\{\gamma_{\Omega},i_{1},i_{2},\cdots,i_{t-1}\}.

The branched levels $(n-i_{1}-1),(n-i_{2}-1),\cdots(n-i_{t-1}-1)$ is determined by the projection $\pi_{1}(\Omega)$ , that is, the vertices at $(n-i_{1}-1)$ th, $(n-i_{2}-1)$ $th,\cdots$ , $(n-i_{t-1}-1)$ th levels of the corresponding tree of the set $\pi_{1}(\Omega)$ have $p$ descendants. On the other hand, there is $\alpha\in\{1,\cdots,p-1\}~{}\text{such that }~{}(p^{\gamma_{\Omega}},\alpha)\in\mathcal{Z}_{\Omega}$ . Thus, we have

\widehat{1_{\Omega}}(p^{\gamma_{\Omega}},\alpha)=\sum\limits_{(x,y)\in\Omega}{{e^{2\pi i\frac{xp^{\gamma_{\Omega}}+\alpha yp^{n-1}}{{p^{n}}}}}}=0.

By Lemma 4.1, we get

(4.1)

|\Omega\cap{H}((p^{\gamma_{\Omega}},\alpha),k)|=|\Omega\cap{H}((p^{\gamma_{\Omega}},\alpha),k+jp^{n-1})|.

By the above argument, we conclude that for $(x,y)\in\Omega$ , the sets $\Omega_{x,y}=\{x\}$ is a single point.

Case 2: Assume $i_{1}<\cdots<i_{s}<\gamma_{\Omega}<i_{s+1}\cdots<i_{t-1}$ . By Lemma 2.3, the condition $(p^{i_{1}},b)\in\mathcal{Z}_{\Omega}$ for each $b\in{\mathbb{Z}}_{p}$ implies that $p^{i_{1}}\in\mathcal{Z}_{\Omega_{b}}$ for each $b$ . Then for each $b\in{\mathbb{Z}}_{p}$ , either $\Omega_{b}=\emptyset$ , or $p\mid|\Omega_{b}|$ and $\Omega_{b}$ can decomposed into $|\Omega_{b}|/p$ subsets satisfy that each subset contains $p$ elements and each two distinct point $x,y$ in a same subset such that $p^{n-1-i_{1}}\mid(x-y)$ and $p^{n-i_{1}}\nmid(x-y)$ . By induction, for each $b\in{\mathbb{Z}}_{p}$ , either $\Omega_{b}=\emptyset$ , or $p^{s}\mid|\Omega_{b}|$ and $\Omega_{b}$ can decomposed into $|\Omega_{b}|/p^{s}$ subsets $\Omega^{s}_{b,\ell},0\leq\ell\leq|\Omega_{b}|/p^{s}$ , satisfy that each subset corresponding to a $p$ -homogenous tree with branch level set $n-1-\{i_{1},\cdots,i_{s}\}$ .

The set $\widetilde{\Omega}$ corresponding to a $p$ -homogeneous tree with branched level set

n-1-\{i_{1},\cdots,i_{s},\cdots,\gamma_{\Omega},i_{s+1},\cdots,i_{t-1}\}.

The branched levels $(n-i_{t-1}-1),(n-i_{t-2}-1),\cdots(n-i_{s+1}-1)$ is determined by the projection $\pi_{1}(\Omega)$ , that is, the vertices at $(n-i_{1}-1)$ th, $(n-i_{2}-1)$ $th,\cdots$ , $(n-i_{t-1}-1)$ th levels of the corresponding tree of the set $\pi_{1}(\Omega)$ have $p$ descendants.

On the other hand, there is $\alpha\in\{1,\cdots,p-1\}~{}\text{such that }~{}(p^{\gamma_{\Omega}},\alpha)\in\mathcal{Z}_{\Omega}$ . Thus, we have

\widehat{1_{\Omega}}(p^{\gamma_{\Omega}},\alpha)=\sum\limits_{(x,y)\in\Omega}{{e^{2\pi i\frac{xp^{\gamma_{\Omega}}+\alpha yp^{n-1}}{{p^{n}}}}}}=0.

By Lemma 4.1, we get

(4.2)

|\Omega\cap{H}((p^{\gamma_{\Omega}},\alpha),k)|=|\Omega\cap{H}((p^{\gamma_{\Omega}},\alpha),k+jp^{n-1})|.

Note that for each $\Omega^{s}_{b,\ell},0\leq\ell\leq|\Omega_{b}|/p^{s}$ , the set $\Omega^{s}_{b,\ell}\subset{H}((p^{\gamma_{\Omega}},\alpha),k)$ for some $k$ . By counting the cardinality of ${H}((p^{\gamma_{\Omega}},\alpha),k)$ . We know that $\Omega\cap{H}((p^{\gamma_{\Omega}},\alpha),k)$ is either empty or $\Omega^{s}_{b,\ell}$ for some $b$ and $\ell$ . Hence, for each $(x,y)\in\Omega$ , the sets

\Omega_{x,y}:=\{x^{\prime}\in{\mathbb{Z}}_{p^{n}}:(x^{\prime},y)\in\Omega\text{ and }x^{\prime}\equiv x\!\!\mod p^{n-\gamma_{\Omega}-1}\ \}

is $p$ -homogenous with the branched level set $n-1-\{i_{1},i_{2}\cdots,i_{s}\}$ .

∎

Theorem 1.2 follows from Propositions 4.4, 4.7, 4.8 and Lemma 4.9.

References

[1] C. Aten, B. Ayachi, E. Bau, D. FitzPatrick, A. Iosevich, H. Liu, A. Lott, I. MacKinnon, S. Maimon, S. Nan, J. Pakianathan, G. Petridis, C. Rojas Mena, A. Sheikh, T. Tribone, J. Weill, and C. Yu. Tiling sets and spectral sets over finite fields. J. Funct. Anal., 273(8):2547–2577, 2017.
[2] E. M. Coven and A. Meyerowitz. Tiling the integers with translates of one finite set. J. Algebra, 212(1):161–174, 1999.
[3] D. E. Dutkay and C.-K. Lai. Some reductions of the spectral set conjecture to integers. Math. Proc. Cambridge Philos. Soc., 156(1):123–135, 2014.
[4] T. Fallon, G. Kiss, and G. Somlai. Spectral sets and tiles in $\mathbb{Z}_{p}^{2}\times\mathbb{Z}_{q}^{2}$ . J. Funct. Anal., 282(12):109472, 2022.
[5] T. Fallon, A. Mayeli, and D. Villano. The fuglede’s conjecture holds in $\mathbb{F}_{p}^{3}$ for $p=5,7$ . Proc. Amer. Math. Soc. to appear.
[6] A. Fan, S. Fan, L. Liao, and R. Shi. Fuglede’s conjecture holds in $\mathbb{Q}_{p}$ . Math. Ann., 375(1-2):315–341, 2019.
[7] A. Fan, S. Fan, and R. Shi. Compact open spectral sets in $\mathbb{Q}_{p}$ . J. Funct. Anal., 271(12):3628–3661, 2016.
[8] B. Farkas, M. Matolcsi, and P. Móra. On Fuglede’s conjecture and the existence of universal spectra. J. Fourier Anal. Appl., 12(5):483–494, 2006.
[9] S. J. Ferguson and N. Sothanaphan. Fuglede’s conjecture fails in 4 dimensions over odd prime fields. Discrete Math., 343(1):111507, 7, 2020.
[10] B. Fuglede. Commuting self-adjoint partial differential operators and a group theoretic problem. J. Funct. Anal., 16:101–121, 1974.
[11] R. Greenfeld and N. Lev. Fuglede’s spectral set conjecture for convex polytopes. Anal. PDE, 10(6):1497–1538, 2017.
[12] A. Iosevich, N. Katz, and T. Tao. The Fuglede spectral conjecture holds for convex planar domains. Math. Res. Lett., 10(5-6):559–569, 2003.
[13] A. Iosevich, A. Mayeli, and J. Pakianathan. The Fuglede conjecture holds in $\mathbb{Z}_{p}\times\mathbb{Z}_{p}$ . Anal. PDE, 10(4):757–764, 2017.
[14] G. Kiss, R. D. Malikiosis, G. Somlai, and M. Vizer. On the discrete Fuglede and Pompeiu problems. Anal. PDE, 13(3):765–788, 2020.
[15] G. Kiss, R. D. Malikiosis, G. Somlai, and M. Vizer. Fuglede’s conjecture holds for cyclic groups of order $pqrs$ . J. Fourier Anal. Appl., 28(79), 2022.
[16] G. Kiss and G. Somlai. Fuglede’s conjecture holds on $\mathbb{Z}_{p}^{2}\times\mathbb{Z}_{q}$ . Proc. Amer. Math. Soc., 149(10):4181–4188, 2021.
[17] M. N. Kolountzakis and M. Matolcsi. Complex Hadamard matrices and the spectral set conjecture. Collect. Math., (Vol. Extra):281–291, 2006.
[18] M. N. Kolountzakis and M. Matolcsi. Tiles with no spectra. Forum Math., 18(3):519–528, 2006.
[19] I. Ł aba. The spectral set conjecture and multiplicative properties of roots of polynomials. J. London Math. Soc. (2), 65(3):661–671, 2002.
[20] N. Lev and M. Matolcsi. The Fuglede conjecture for convex domains is true in all dimensions. Acta Math., 228(2):385–420, 2022.
[21] R. D. Malikiosis. On the structure of spectral and tiling subsets of cyclic groups. Forum Math., Sigma, pages 10:e23 1–42, 2022.
[22] R. D. Malikiosis and M. N. Kolountzakis. Fuglede’s conjecture on cyclic groups of order $p^{n}q$ . Discrete Anal., pages Paper No. 12, 16, 2017.
[23] M. Matolcsi. Fuglede’s conjecture fails in dimension 4. Proc. Amer. Math. Soc., 133(10):3021–3026, 2005.
[24] R. Shi. Fuglede’s conjecture holds on cyclic groups $\mathbb{Z}_{pqr}$ . Discrete Anal., pages Paper No. 14, 14, 2019.
[25] R. Shi. Equi-distributed property and spectral set conjecture on $\mathbb{Z}_{p^{2}}\times\mathbb{Z}_{p}$ . J. Lond. Math. Soc. (2), 102(3):1030–1046, 2020.
[26] G. Somlai. Spectral sets in $\mathbb{Z}_{p^{2}qr}$ tile. Discrete Anal., pages Paper No. 5, 10, 2023.
[27] S. Szabó and A. D. Sands. Factoring groups into subsets, volume 257 of Lecture Notes in Pure and Applied Mathematics. CRC Press, Boca Raton, FL, 2009.
[28] T. Tao. Fuglede’s conjecture is false in 5 and higher dimensions. Math. Res. Lett., 11(2-3):251–258, 2004.
[29] T. Zhang. Fuglede’s conjecture holds in $\mathbb{Z}_{p}\times\mathbb{Z}_{p^{n}}$ . SIAM J. Discrete Math., 37(2):1180–1197, 2023.

The structure of tiles in ℤpn×ℤq{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q} and ℤpn×ℤp{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}

Abstract.

Key words and phrases:

2010 Mathematics Subject Classification:

1. Introduction

Conjecture (Fuglede 1974).

1.1. The structure of tiles in ℤpn×ℤq{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}

Theorem 1.1.

1.2. The structure of tiles in ℤpn×ℤp{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}

Theorem 1.2.

2. Preliminaries

2.1. Fourier transform on the finite groups.

Lemma 2.1.

Proof.

Lemma 2.2 ([29]).

Lemma 2.3.

Proof.

2.2. Basic properties of tiles.

Lemma 2.4 ([25]).

Lemma 2.5 ([27, Theorem 3.17]).

2.3. ℤ{\mathbb{Z}}-module generated by pnp^{n}-th roots of unity.

Lemma 2.6 ([7]).

Lemma 2.7 ([7]).

Lemma 2.8 ([7]).

2.4. pp-homogeneity of tiles in ℤpn{\mathbb{Z}}_{p^{n}}

Example 2.9.

Lemma 2.10 ([7, Theorem 2.9]).

Lemma 2.11 ([7, Theorem 4.2]).

3. The structure of tiles on ℤpn​q{\mathbb{Z}}_{p^{n}q}

3.1. CM condition for tiles in finite group ℤN{\mathbb{Z}}_{N}.

Lemma 3.1 ([24, Lemma 2.4]).

Theorem 3.2 ([2]).

Corollary 3.3.

3.2. The structure of tiles in ℤpn​q{\mathbb{Z}}_{p^{n}q}

Lemma 3.4.

Proof.

Proof of Theorem 1.1 .

4. The structure of tiles in ℤpn×ℤp{\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}

4.1. Equidistribution property

Lemma 4.1 ([24, Lemma 3.1]).

Lemma 4.2 ([29] Lemma 3.2).

4.2. Proof of the theorem 1.2

Lemma 4.3.

Proof.

Proposition 4.4.

Proof.

Lemma 4.5.

Proof.

Lemma 4.6.

Proof.

Proposition 4.7.

Proof.

Proposition 4.8.

Proof.

Lemma 4.9.

Proof.

References

The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$ and ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$

1.1. The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{q}$

1.2. The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$

2.3. ${\mathbb{Z}}$ -module generated by $p^{n}$ -th roots of unity.

2.4. $p$ -homogeneity of tiles in ${\mathbb{Z}}_{p^{n}}$

3. The structure of tiles on ${\mathbb{Z}}_{p^{n}q}$

3.1. CM condition for tiles in finite group ${\mathbb{Z}}_{N}$ .

3.2. The structure of tiles in ${\mathbb{Z}}_{p^{n}q}$

4. The structure of tiles in ${\mathbb{Z}}_{p^{n}}\times{\mathbb{Z}}_{p}$