The soft-mode phonons mediated unconventional superconductivity in monolayer 1T^′-WTe₂

Tuning the topological materials to be superconducting provides a highly efficient way to search and study the exotic superconductivity such as unconventional and topological superconductivity. Some methods have been developed to achieve the target, including the doping through metal intercalation hor-prl-2010 ; liu-jacs-2015 ; smylie-prb-2017 ; asaba-prx-2017 , high pressure kirshenbaum-prl-2013 ; zhang-prb-2011 , proximity effect fu-prl-2008 ; Lutchyn-prl-2010 ; xu-prl-2014 ; hao-nsr-2019 , hard and soft tip contact wang-sb-2018 ; wang-nm-2016 ; aggarwal-nm-2016 ; hou-prb-2019 ; hou-prb-2020 , and electrostatic gating Sajadi-s-2018 ; fatemi-s-2018 . Among them, the electrostatic gating has advantage to freely tune the materials in both electron- and hole-doped regimes without introducing dopant. Recently, the intrinsic superconductivity in the monolayer topological insulator 1T^′-WTe₂ have been experimentally observed by two groups through moderate electrostatic gating Sajadi-s-2018 ; fatemi-s-2018 . It is found that the superconductivity shows some interesting features. For instance, only the electron-doped regime show the superconductivity with the transition temperature ($T_{c}$) up to 1 K, whereas no superconducting signature is observed in the hole-doped regime. Furthermore, the upper critical field $H_{c2}$ shows strong anisotropy between the in-plane $H_{c2,\parallel}$ and out-of-plane $H_{c2,\perp}$, and $H_{c2,\parallel}$ is significantly larger and four times the Pauli paramagnetic limit 1.84$T_{c}$. However, the gating-dependent superconductivity and the $H_{c2}$ anisotropy have not been comprehensively understood.

In this work, we show that the phonon spectrum of 1T^′-WTe₂ dramatically softens in the electron-doped regime, but slightly stiffens in the hole-doped regime through density functional calculations. According to the phonon-mediated superconductivity theory, we reveal that the softening of the phonons with specific momentum in electron-doped regime is the driving force to give rise to the superconductivity. We also find an optimal electron-doped concentration, beyond which, the $T_{c}$ becomes to decline in accompany with the latent charge density wave (CDW) instability. Furthermore, we reveal the evolution of superconductivity coincides with the change of Fermi surface nesting condition, and predict the CDW order is quasi-one dimensional commensurate with wave vector $q_{CDW}=$(0, $\pi/b$) according to the electronic susceptibility. Thus, there exist a superconducting dome and a new CDW state in the phase diagram. Based on the symmetry classification and linearized gap equations, we find that all the superconducting pairing channels with specific irreducible representations (IRs) are degenerate without external magnetic field. However, only the pairing in $A_{u}$ channel shows the experimentally observed reasonable anisotropy between $H_{c2,\parallel}$ and $H_{c2,\perp}$. This behavior indicates that the superconductivity in 1T^′-WTe₂ probably has equal-spin-triplet pairing and belongs to unconventional type.

The first-principles calculations in this work are performed using the density functional theory (DFT) and the density functional perturbation theory (DFPT)Perdew-prb-1981 ; Ceperley-prl-1980 . We employed the QUANTUM ESPRESSO (QE) packageGiannozzi-jpcm-2009 for the electronic structure and lattice dynamics including the phonon spectrum and electron-phonon coupling. The superconducting transition temperature $T_{c}$ is calculated with the McMillan-Allen-Dynes formulaallen-prb-1975 as implemented in the QE packageGiannozzi-jpcm-2009 . The details of the calculation are presented in the supplementary materials (SM)sms .

The charge doping effect from the electrostatic gating is simulated by adding or removing electrons to the monolayer 1T^′-WTe₂ with a compensating uniform charge background. The doped carrier concentrations per 1T^′-WTe₂ is expressed as $n$ (cm^-2), with positive and negative values indicating electron and hole doping, respectively. Figure 1 shows the electronic structure of 1T^′-WTe₂ from the first-principle calculations. The Fermi surfaces in Figs. 1 (c) and (d) correspond to the hole and electron doping with carrier concentrations $n_{h}=-9.5\times 10^{13}$ cm^-2 and $n_{e}=9.5\times 10^{13}$cm^-2, respectively. Around the Fermi level, the $d$ orbitals of W and $p$ orbitals of Te are dominated. Along $\Gamma-X$ line, there are two electron pockets labeled by $K^{\prime}$ and $K$ in electron-doped case while only one hole pocket centered at $\Gamma$ point in hole-doped case. The details of calculations are presented in Section I and II in SM.

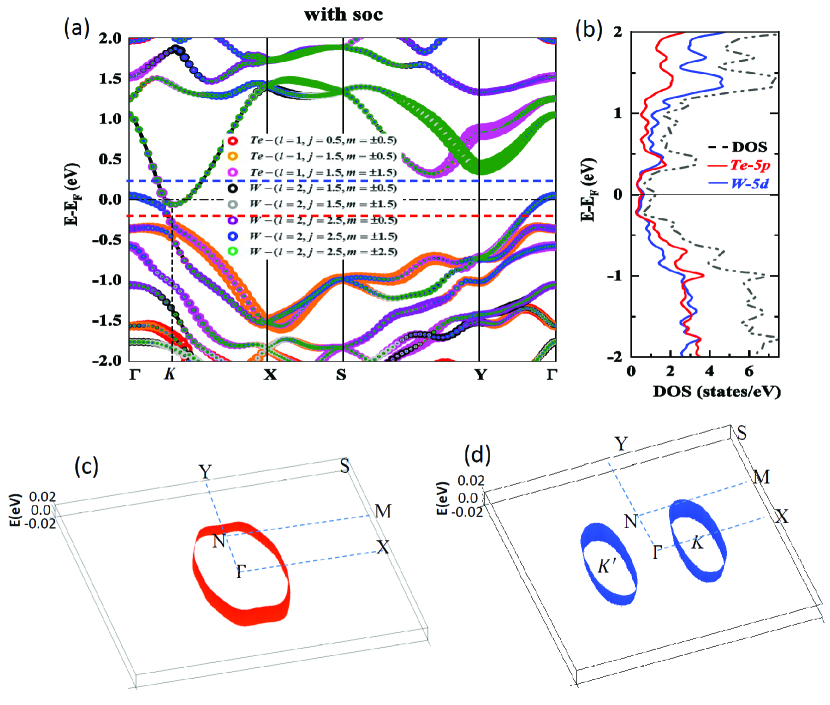
The calculated phonon spectrum $\omega_{q,\nu}$ with wave vector $q$ and mode index $\nu$ in electron-doped 1T^′-WTe₂ is shown in Fig. 2(a). Remarkably, some phonon modes at specific wave vectors $Q$ and $Q_{i}$ with $i$=1,2,3 dramatically soften in comparison with the non-doped case shown in Fig. S4 (a) in SM. However, the phonon spectrum of hole doping slightly stiffens, as shown in Fig. S4(d) in SM. This distinctly opposite trend of the phonon modes between electron doping and hole doping is clearly demonstrated in Fig. 2(c). The softening of $Q$ mode phonon is enhanced as electron doping density increases, and its frequency $\omega_{Q}$ turns to be negative when $n_{e}$ crosses $10.3\times 10^{13}$ cm^-2, as shown in the inset in Fig. 2(c). It means some long-range order instability could emerge. In the present case, such instability is probably the CDW. Furthermore, the relevant atomic displacements for the $Q$ mode phonon are mainly expressed as horizontal W-W stretching vibration and shear Te-Te tortuosing vibration, as shown in Fig. S5 in SM. These behaviors indicate the $Q$ mode phonon has the longitudinal-wave feature. We have checked that the properties of all $Q_{i}$ mode phonon are similar to those of the $Q$ mode phonon.

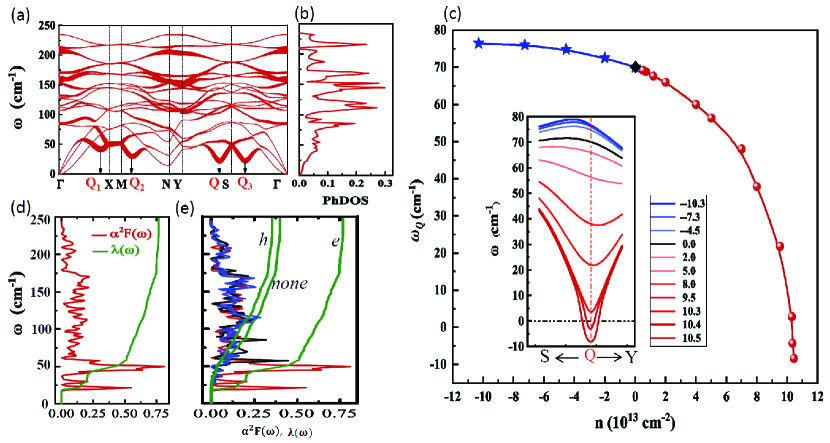
The features of phonon spectrum in Fig. 2 imply that the soft mode phonons should play a key role to induce the superconductivity in electron-doped monolayer 1T^′-WTe₂. To prove it, we also plot the linewidth of the phonon spectrum $\gamma_{q,\nu}$ shown in Fig. 2(a), the Eliashberg spectral function $\alpha^{2}F(\omega)$ and the frequency-dependent electron-phonon coupling (EPC) strength $\lambda(\omega)$ shown in Fig. 2(d) and (e). The details about $\gamma_{q,\nu}$, $\alpha^{2}F(\omega)$allen-prb-1972 , and $\lambda(\omega)$ are shown in Section III in SM. With them, one can get a crucial expression for the effective attractive interaction as follows,

Here, $N_{0}$ is the electronic density of states at the Fermi surface for both spin orientations. From Fig. 2(a), and Fig. S4 (a) and (d) in SM, one can find that some optical modes have large linewidth $\gamma_{q,\nu}$ for all three cases. The relevant frequency $\omega_{q,\nu}$, however, is very high. From Eq. (1), the $V_{q,\nu}^{ep}$ from the optical modes can be neglected. The dramatic difference occurs for the longitudinal acoustic mode. One can find that the electron doping can greatly enlarge the linewidth $\gamma_{q,\nu}$ and soften the frequency $\omega_{q,\nu}$ at the specific momenta $Q$ and $Q_{i}$. Therefore, the $\alpha^{2}F(\omega)$ and $\lambda(\omega)$ are strongly enhanced by electron doping, as shown in Figs. 2(d), 2(e) and Fig. S4(c), (f) in SM, and so is $V_{q,\nu}^{ep}$. In terms of superconductivity, only the electrons very close to the Fermi surface need to be considered. Such constraint demands the good nesting condition for the electron-doped Fermi surface in Fig. 1 (d), which can be clarified by the electron susceptibility $\chi(q)=\chi^{\prime}(q)+i\chi^{\prime\prime}(q)$ (See Section V in SM for details). The Fermi surface nesting is evaluated by the imaginary part $\chi(q)$, i.e., $\chi^{\prime\prime}(q)$. In Fig. 3 (a), we plot the pattern of $\chi^{\prime\prime}(q)$ for electron-doped case with $n_{e}=9.5\times 10^{13}$cm^-2. The nesting wave vector $q_{nest}=(0.73\pi/a,0)$, which is quite close to horizontal ordinate $\sim 0.73\pi/a$ of all $Q$ and $Q_{i}$ mode phonons. We also plot the evolution of $Q_{\Delta}=|q_{nest,x}-0.73\pi/a|$ as the doping density in Fig. 3 (b) and Fig. S6 in SM. One can find that the best nesting with $Q_{\Delta}\sim 0$ corresponds to the optimal superconductivity with the highest transition temperature $T_{c}$, as shown in Fig. 4 (a). The consistent relationship between the phonon spectrum and the electronic structure indicates that the Fermi surface nesting plays the important role to drive the superconductivity in 1T^′-WTe₂.

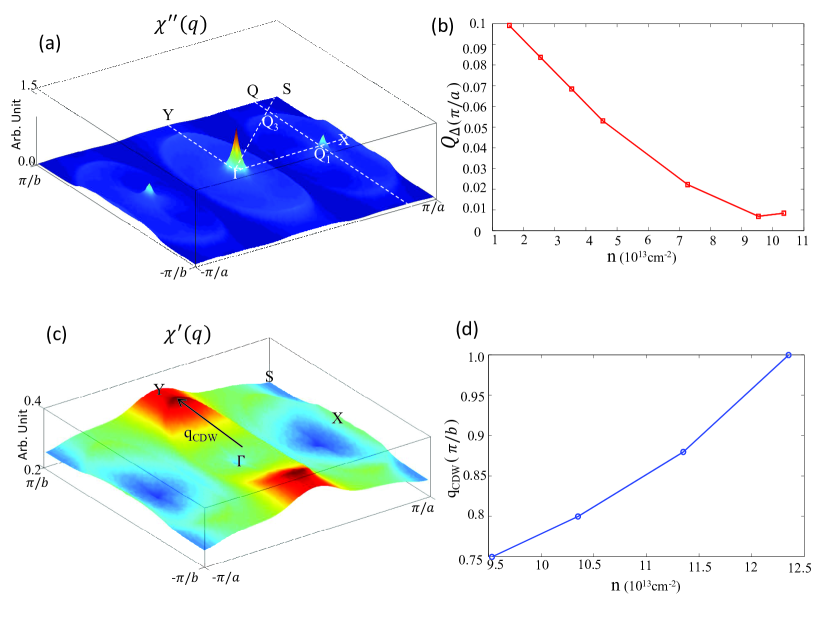
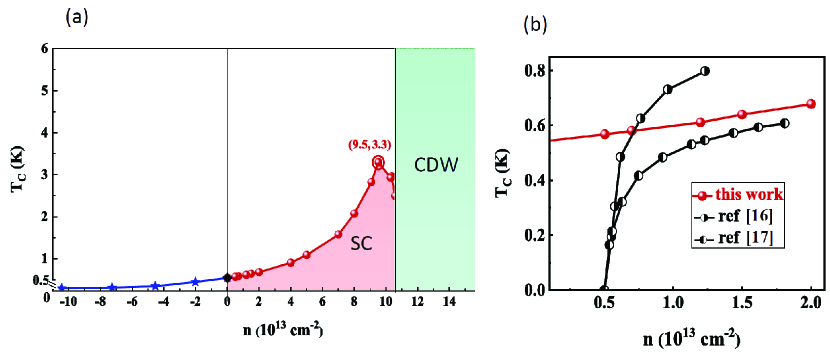
Furthermore, we calculate the superconducting transition temperature $T_{c}$ in different doping levels using the McMillan-Allen-Dynes formula allen-prb-1975 . The details are presented in Section VI in SM. The calculated results (data points) of $T_{c}$ as a function of density of electrons (red ball) and holes (blue star) are plotted in Fig. 4(a). Clearly, compared to the hole doping, the electron doping indeed strengthens the $T_{c}$ of monolayer 1T^′-WTe₂, showing significant asymmetry features. More interestingly, the $T_{c}$ curve shows two remarkable features. First, the $T_{c}$ exponentially increases as pumping electrons. The nonlinear behavior of $T_{c}$ curve is further supported by the exponential decay trend of logarithmic average frequency $\omega_{\log}$ and the exponential ascend trend of the EPC constant $\lambda^{ph}$, as shown in Fig. S8 in SM. The behavior of $T_{c}$ curve provides the possibility to obtain the quite high $T_{c}$ superconductivity through increasing electron doping, which is different from the doped graphene si-prl-2013 or doped antimonene lugovskoi-prb-2019 . Second, $T_{c}$ reaches the maximum of 3.3 K with $n_{e}=9.5\times 10^{13}$ cm^-2 corresponding to the best nesting condition, then drops, and finally disappears or merges into the possible CDW state. Here, we discuss a little more about the CDW instability. Recall that the frequency $\omega_{q}$ of $Q$ mode phonon becomes negative when $n_{e}$ increases cross $10.3\times 10^{13}$ cm^-2, as shown in Fig. 1(c). It indicates the lattices become unstable and the system undergoes a possible CDW transition. For the electronic states, the CDW instability is induced by the divergence of $\chi^{\prime}(q)$, the real part of electron susceptibility $\chi(q)$Johannes-prb-2008 . In Fig. 3 (c), we plot the pattern of $\chi^{\prime}(q)$ for electron-doped case with $n_{e}=9.5\times 10^{13}$cm^-2, whose CDW wave vector is $q_{CDW}=(0,0.75\pi/b)$. When the electron doping increases, $q_{CDW}$ is more and more close to the $(0,\pi/b)$, as shown in Fig. 3(d) and Fig. S7 in SM. We conclude that the CDW with different $q_{CDW}$ should compete with each other, and the most probable one has the wave vector $(0,\pi/b)$, which is quasi-one dimensional, commensurate $2Q$ CDW. Note that the nesting wave vector has nothing to do with the CDW wave vectorJohannes-prb-2008 . According to the above discussions, the relevant phase diagram can be plotted as shown in Fig. 4 (a), from which a superconducting dome can be found. Currently, using solid-state gates or ionic-liquid gates, typical carrier density ($10^{14}$ cm^-2) can be achieved in several two-dimensional (2D) materials Fu-npj-2017 ; Li-n-2016 ; Saito-st-2016 ; Lu-s-2015 ; Costanzo-nn-2016 , we thus expect that future experiments for electron-doped 1T^′-WTe₂ can verify our predicted maximum $T_{c}$ (3.3 K), which is about four or five times the experimental values of 0.8 K Sajadi-s-2018 or 0.6 K fatemi-s-2018 . In the range of experimental charge density, i.e., $n\in[0.7,2.1]\times 10^{13}$cm^-2, our results are in qualitatively agreement with the experimental values Sajadi-s-2018 ; fatemi-s-2018 , as shown in Fig. 4 (b). Whereas $T_{c}$ greatly deviates from the experimental value below $0.7\times 10^{13}$cm^-2. It is because the Coulomb screening effect is strongly reduced in the low density regime. Correspondingly, the constant retarded Coulomb pseudo-potential $\mu^{\ast}$ is not exact and should become large to reduce $T_{c}$ from Eq.(7) in SM.

Now, we turn to understand the superconducting properties of monolayer 1T^′-WTe₂ in the electron-doped regime. According to Fig. 1(d), there exist two separated Fermi pockets centered at momenta $\mathbf{K}^{\prime}$ and $\mathbf{K}$ which can be regarded as two valleys. The low-energy Hamiltonian can be expanded around $\mathbf{K}^{\prime}$ and $\mathbf{K}$. Define the annihilation electron operator as $c_{\mathbf{k},\eta,s}$, where $\mathbf{k}$ is the momentum measured from $\mathbf{K}^{\prime}$ and $\mathbf{K}$, $\eta=\pm$ is for two valleys and $s=\uparrow$,$\downarrow$ is for spin. On the basis of $[c_{\mathbf{k},+,\uparrow},c_{\mathbf{k},-,\uparrow},c_{\mathbf{k},+,\downarrow},c_{\mathbf{k},-,\downarrow}]$, the effective Hamiltonian is

Here, $s$ and $\tau$ are two sets of Pauli matrices for spin and valley degrees of freedom, $\varepsilon_{k}=\hslash^{2}k^{2}/2m-\mu$ is the dispersion with the chemical potential $\mu$, $g$ and $\mu_{B}$ are the Lande $g$ factor and Bohr magneton, respectively, and $\mathbf{B}=(B_{x},B_{y},B_{z})$ is the external magnetic field. Note that we only take into account the Zeeman effect of the external magnetic field, but neglect the orbital effect due to the 2D feature of 1T^′-WTe₂. In the superconducting states, the pairings should follow the IRs of the $C_{2h}$ point group of 1T^′-WTe₂. In order to consider the superconductivity for simplicity, we adopt the approximation of Fermi surface average of $V_{q,\nu}^{ep}$ to neglect the weak momentum dependence, i.e., $V^{ep}=\sum_{\nu}$ $\langle V_{\mathbf{k}-\mathbf{k}^{\prime},\nu}^{ep}\rangle_{\mathbf{k},\mathbf{k}^{\prime}\in FS}$. Thus, we only consider the momentum-independent $s$-wave pairings, which are from the constant pairing interaction $-V_{0}=V^{ep}+U_{scou}$ with $U_{scou}$ the screened Coulomb interaction. Furthermore, the soft-mode phonons have the momenta connecting the two valleys, which indicates only the inter-valley pairing is possible. Under the mean-field approximation in the Nambu basis, we can classify the pairing symmetry under the constraint of anti-commutation relation between fermion operators. The pairing function can be parameterized by the form $\hat{\Delta}=\sum_{i}\Delta_{i}\Gamma_{i}$, where $\Gamma_{i}$ is the $i$th IR matrix product from $s$ and $\tau$. The results are listed in Table 1. More details are shown in Section VII in SM.

The pairing interaction in all pairing channels in Table 1 has the same amplitude of $V_{0}/2$.

To evaluate the possible superconducting pairing in 1T^′-WTe₂, we solve the following linearized gap equations for $T_{c}$Fu-prl-2010 ; Liu-prl-2017 ,

where $\chi_{i}$ is the finite temperature superconducting susceptibility in $i$th pairing channel, and can be calculated by

Here, $\mathcal{G}_{e/h}(k,i\omega_{n})=[i\omega_{n}\mp\mathcal{H}_{0}(k)]^{-1}$ are the relevant standard electron and hole Matsubara Green functions. The details are shown in Section VII in SM, and we only list the key results here. Note that only the electron-type bands are taken into account in the electron-doped regime. With the approximation that the pairing occurs at the Fermi surface, we can get $\chi_{A_{g}}=4\chi_{0}$, $\chi_{B_{u}}=4\chi_{0}B_{z}^{2}/B^{2}$, $\chi_{A_{u}}=4\chi_{0}B_{x}^{2}/B^{2}$ or $4\chi_{0}B_{y}^{2}/B^{2}$. $\chi_{0}=N_{0}\int d\varepsilon\tanh(\frac{\varepsilon}{2k_{B}T})/\varepsilon$ is the standard superconducting susceptibility and $k_{B}$ is the Boltzmann constant. When $\mathbf{B}=0$, one can find that all the pairing channels have the same superconducting susceptibility, i.e., $4\chi_{0}$, likewise, the same $T_{c}$, i.e., $k_{B}T_{c}=\frac{2e^{\gamma}}{\pi}\hbar\omega_{D}\exp(-\frac{1}{2N_{0}V_{0}})$, where $\gamma\approx 0.5772$ is the Euler constant and $\omega_{D}$ is the Debye frequency. It indicates that all the pairing channels are degenerate and are the possible candidate for the superconducting ground state. When $\mathbf{B}\neq 0$, the $T_{c}$ of $A_{g}$ channel is robust against the magnetic field. The $T_{c}$ of $B_{u}$ or $A_{u}$ channel is magnetic-field-direction dependent. Namely, $\ln\frac{T_{c,B_{u}}(B)}{T_{c,B_{u}}(0)}=\frac{1}{2N_{0}V_{0}}(1-\frac{B^{2}}{B_{z}^{2}})$ and $\ln\frac{T_{c,A_{u}}(B)}{T_{c,A_{u}}(0)}=\frac{1}{2N_{0}V_{0}}(1-\frac{B^{2}}{B_{x/y}^{2}})$. Therefore, the $B_{u}$ channel is robust against the out-of-plane magnetic field $B=(0,0,B_{z})$ and is fragile for the in-plane magnetic field $B=(B_{x},B_{y},0)$. In other words, $B_{u}$ channel has large $H_{c2,\perp}$ and small $H_{c2,\|}$. Similarly, one can find $A_{u}$ channel has small $H_{c2,\perp}$ and large $H_{c2,\|}$. In comparison with the experimental observations, it inidicates the superconducting state should fall into the $A_{u}$ channel with the equal-spin-triplet pairing, whose $H_{c2}$ cannot be restricted by the Pauli paramagnetic limit. These results can be easily understood through the spin structure of the Cooper pairs. The $B_{u}$ and $A_{u}$ channels correspond to the three components $S_{z}$ and $S_{x}$, $S_{y}$ of the $S=1$ spin-triplet Cooper pairs, respectively. Therefore, the couplings between them and the magnetic field follow the Zeeman-type to minimize the ground state energy. For a general magnetic field with $B=B_{0}(\cos\theta\cos\varphi,\cos\theta\sin\varphi,\sin\theta)$, we can get the exact pairing form as $\hat{\Delta}\sim e^{i\varphi}c_{\mathbf{k},+\uparrow}c_{-\mathbf{k},-\uparrow}-e^{-i\varphi}c_{\mathbf{k},+\downarrow}c_{-\mathbf{k},-\downarrow}$, where the phase $\varphi$ is determined by the direction of magnetic field.

There exist several other mechanisms to result in the anisotropic $H_{c2}$ including type-I Lu-s-2015 ; Saito-np-2016 ; Xi-np-2016 , type-II Ising pairings Falson-s-2020 and spin-orbit scattering Klemm-prb-1962 . Type-I Ising pairing mechanism is related to inversion symmetry breaking and clearly is not the case in monolayer 1T^′-WTe₂, which preserves the inversion symmetry. Type-II Ising pairing mechanism relies on the band near $\Gamma$ point with out-of-plane orientation of the spin locked by the spin-orbit coupling. This mechanism can also be excluded, because no such kind of band splitting exists in monolayer 1T^′-WTe₂. For the spin-orbit scattering mechanism, there are two kinds of situations. In the clean limit of crystalline sample with high mobility, the spin-orbit coupling scattering can be discarded as it could induce the unphysically short scattering times Lu-s-2015 ; Saito-np-2016 ; Xi-np-2016 . In the dirty limit, the strong spin-orbit coupling indeed could induce the anisotropic $H_{c2}$. However, the superconductivity refers to the Fermi surface connected by the momenta relating to soft phonons. From Fig. 1 (a), the pieces of the Fermi surfaces have strong effective spin-orbit coupling is close to $\Gamma$ point, whereas the pieces of the Fermi surfaces connected by nesting wave vector has weak effective spin-orbit coupling Qian-s-2014 . This is also the reason why the simple low-energy Hamiltonian in Eq. (2) is enough and is adopted to investigate the properties of superconducting state in monolayer 1T^′-WTe₂. Thus, the spin-orbit scattering mechanism can be excluded.

In conclusion, we have determined the soft-mode phonons, the relevant enhanced electron-phonon coupling and the Fermi surface nesting are three ingredients to drive the superconductivity in electron-doped monolayer 1T^′-WTe₂. We also predict a quasi-one dimensional commensurate $2Q$ CDW emerges in the heavy electron doping regime, and a superconducting dome in the phase diagram. Furthermore, we propose an unconventional superconducting pairing with equal spin triplet to capture the experimentally observed strong anisotropic upper critical fields. Our studies provide a standard way to understand the gating-dependent superconductivity in 1T^′-WTe₂ and other transition metal dichalcogenides.