The SM expected branching ratio for and an excess for
Abstract
The recent measurements of from ATLAS and CMS show an excess of the signal strength , normalized as 1 in the standard model (SM). If confirmed, it would be a signal of new physics (NP) beyond the SM. We study NP explanation for this excess. In general, for a given model, it also affects the process . Since the measured branching ratio for this process agrees well with the SM prediction, the model is severely constrained. We find that a minimally fermion singlets and doublet extended NP model can explain simultaneously the current data for and . There are two solutions. Although both solutions enhance the amplitude of to the observed one, in one of the solutions the amplitude of flips sign to give the observ ed branching ratio. This seems to be a contrived solution although cannot be ruled out simply using branching ratio measurements alone. However, we find another solution that naturally enhances to the measured value, but keeps the amplitude of close to its SM prediction. We also comment on the phenomenology associated with these new fermions.
I Introduction
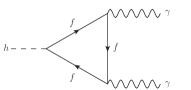
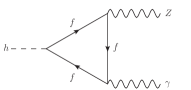
The 2012 discovery of the Higgs boson () marked a milestone in particle physics [1, 2]. Various properties of predicted by the standard model (SM) have been confirmed, but there are still many more to be tested. Notable ones are the and [3, 4, 5, 6, 7]. They are generated at loop level in both the SM and new physics (NP) [8, 9], making them ideal places to test NP theories hiding at loop level. In particular, has been measured to good precision, playing a significant role in probing the Higgs boson [10, 11]. However, has yet to be confirmed experimentally. The triangle Feynman diagrams induced by fermions are given in FIG. 1. As they involve the Yukawa couplings of Higgs boson to fermions, the potential influence of NP beyond the SM in these processes is a compelling aspect of ongoing research [12, 13, 14, 15, 16, 17, 18, 19].
To gauge how well the SM prediction fits data, it is convenient to define the signal strength, denoted as . This value represents the observed product of the Higgs boson production cross section () and its branching ratio () normalized by the SM values. When deviates from 1, it is a signal of NP beyond the SM. Recently, both ATLAS and CMS [20, 21] have obtained evidence of with the average data showing that
| (1) |
where denotes the signal strength of . The central value indicates an excess approximately twice as large as that predicted by the SM. On the other hand, the SM prediction aligns very closely with the data of the signal strength [22, 23]
| (2) |
At present, the excess for is only at 1.7. If the excess is further confirmed, it will be a signal of NP. In general, for a given NP model addressing the excess, it also affects the process . Since the measured agrees well with the SM prediction, the model is severely constrained. For a specific NP model, the literature notably shows that it is difficult to simultaneously align both and with the data within [18, 16, 15]. In this work, we study the implications from a model building point of view for the possible excess problem, the issue of the SM expected branching ratio for and an excess for .
Beyond the SM effects can come in many different ways. In the SM effective field theory, the leading CP-even dimension-six operators contributing to and are given as [24]
| (3) |
where is the Higgs doublet with quantum numbers under the SM gauge group , and the vacuum expectation value (vev) is given by after spontaneous symmetry breaking. represents the energy scale of NP, are identified as the Wilson coefficients, is the Pauli matrix. With the gauge couplings and , and are gauge field tensors for and , respectively. Here we take these operators as examples to show how the excess for can be explained. For a full basis that includes CP-violating operators, one may refer to Refs. [8, 25].
After spontaneous symmetry breaking, and , we could match the above NP operators to the effective Lagrangian responsible to and to obtain
| (4) |
with
| (5) |
In the above is the Weinberg angle, is the fine structure constant, and .
Including QCD corrections [26, 27, 28, 29, 30, 31], the amplitudes from the SM are effectively encapsulated by and with GeV. It is noteworthy that and are influenced by in distinct ways. The experimental values for and can be accomplished by fine-tuning the NP coefficients to induce a minimal but sizable . We stress that and are gauge invariant, and it suffices to exclusively consider these two for our purpose.
From the above analysis, it is clear that by tuning , and it is possible to simultaneously fit the measured data for and the excess in . Comprehensive studies on the numerical fit within the framework of the SM effective field theory have been carried out [25, 32, 33, 34]. However, it is still a challenging task to solve the excess problem for with a renormalizable model. In a renormalizable model, and are generated at one loop level as shown in Figure 1. In this work, we will focus on constructing a renormalizable model to address the problem. We find that a minimally extended model with two fermion singlets and a doublet, as shown in Table 1, can explain the problem. We only consider color-singlet fermions because, otherwise, they would lead to dramatic changes in the process and its spectrum, in contrast to the data [36, 35, 37]. Two solutions were found. One suggests that the SM amplitude is enhanced by for to the observed value, however, for , the decay amplitude is modified to to give the observed branching ratio. This solution seems to be a contrived solution, although it cannot be ruled out simply using branching ratio measurements. We, however, find another solution which naturally enhances the to the measured value, while keeping the amplitude of close to its SM prediction. The model suggests the existence of three new fermions that primarily decay into another fermion and a SM gauge boson. Additionally, it proposes a stable fermion with an electric charge close to and masses around 2 TeV.
II The model and its interactions
The new fermions can couple to the Higgs doublet and can also have bare masses. The Yukawa interaction and bare mass terms are given by
| (6) |
where . Without loss of generality, we choose the chiral basis in this work such that terms of the form vanish as detailed in Appendix A. For a general case, it is also possible to have CP-violating terms of the form . In Appendix A, we outline how the analysis can be carried out. In the following, for clarity and simplicity, we use the above Yukawa coupling to demonstrate how the SM expected branching ratio for and an excess for can be realized.
The non-zero vev of Higgs can contribute to fermion masses leading to the new fermion mass matrices in the basis with or as the following
| (7) |
The eigenstates of read
| (8) |
where the eigenvalues and mixing angles are
| (9) |
In this basis, the mass and charge-conserved Lagrangian for are given as
| (10) | |||||
where and are the Pauli matrices operating in the rotational space of . For example, . On the other hand, the -boson can induce a charge current given by
| (11) | |||||
As we will see shortly, to explain the data we need a large , which prevents them from coupling with the SM fermions. Hence, the Lagrangian remains invariant under the rotation of , and at least one of the new fermions must be stable.
III Loop-induced and in the model
We are ready to calculate the loop-induced and in the minimally extended model described previously. The one loop diagrams inducing these decays are shown in Figures 1 and 2. There are two classes of diagrams, one shown in Figure 1 in which the fermions in the loop do not change identities, which we refer to as flavor-conserving ones, and the other as shown in Figure 2 in which the fermions in the loop change identities which we refer to as flavor-changing diagrams. receives contributions from the flavor-conserving class, and receives contributions from the both classes. These features make it possible to have NP contributions of the new fermions to and differently to addressing the problem we are dealing with.
Depending on the original parameters , and , there are three classes of possible mass eigenstates: 1. both are positive; 2. one of the is positive and the other is negative; and 3. both are negative. In the last case, one can perform a chiral rotation on the fields to make all masses positive and transform , while leaving the other interaction terms unchanged. This would not change the final outcome comparing to the first case, as our final result depends on the value of . Therefore, we only need to consider the first two possibilities. These two cases can have different features for and . We proceed to discuss them in the following.
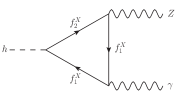
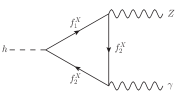
III.1 The case for both to be positive
The Feynman diagrams with flavor-conserving vertices are depicted in Figures 1 . The calculations are similar to those in the SM. The contributions with in the fermion loop are given as
| (12) |
where and . Here , and are the coupling strengths of , and to , where , , , , and . The loop functions are given as [3, 4, 5, 6, 7]
| (13) |
At , we have .
The Feynman diagrams with flavor-changing vertices are depicted in Figure 2. Due to the Ward identity, the photon vertices must conserve the flavor and hence this type of diagram is absent in . The contribution of the doublet to is
| (14) |
with the loop function given as
| (15) | |||||
Here and are the Passarino-Veltman functions [39, 40] and their analytical forms can be obtained by Package-X [40]. The coupling strengths can be read off from Eq. (II) as and .
After carrying out the four-momentum integral, we arrive at
| (16) | |||||
Since the new fermions are expected to be much heavier than the SM particles, we drop and and obtain
| (17) |
Around , we have
| (18) |
The above leads to
| (19) | |||||
around . Therefore, for the case with , we see that () constructively (destructively) interfere with (), which would lead to and for . This trend is maintained for keeping and . Hence, the scenario of is not able to explain the excess of .
III.2 The case for one of to be negative
From Eq. (19) it is observed that by setting , a destructive interference between the and doublets for can happen while leaving the second term in to constructively interfere. To rigorously address the scenario with , a rotation of is necessary to ensure the positiveness of the fermion mass. While remain unchanged, the others are modified to
| (20) | |||||
The Lagrangian is significantly modified with an extra appearing in the off-diagonal interactions. This shows that the physical quantities depend not only on the absolute values of the masses but also on their signs. This can be traced back to the fact that the mass terms in our model originate from both the bare Lagrangian and the Higgs mechanism, and the two cannot be diagonalized simultaneously with chiral rotations.
We have carried out detailed calculations and find that for and , the consequences of this rotation can be effectively modeled by substituting with in Eqs. (14), (16) and (19). It results in the favorable solution with
Before ending this section, we note that from Eq. (19) there is a second set of solutions with . By taking , and are opposite in sign and it is possible to explain the data with the feature of . In this scenario, decouples from the other fermions, and it is not necessary to include it in the model.
It is worth mentioning that Ref. [14] considered the fermions with the same representations as those in Table 2. In particular, by considering , we can reproduce the results in Ref. [14]. In this case, the only solution is where with found to be and . However, it is more natural to have a solution where .
IV Numerical results
We now provide numerical results for the case with negative . For simplicity, we adopt and the masses are given by
| (21) |
Without loss of generality, we take . Hence, we have the hierarchy of , making being the stable particle due to the energy conservation. For a meaningful perturbative calculation, we consider only the regions where and fix . We also confine the model to have the lightest new charged fermion mass be larger than GeV to satisfy the experimental lower bound for up to 7 [41].
To find the regions of parameter which fit data well, we define
| (22) |
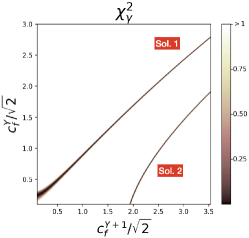
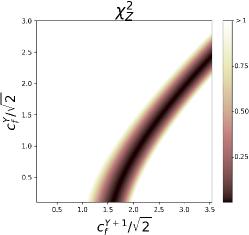
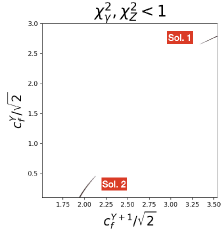
where stand for the experimental uncertainties of . In Figure 3(a), (b) and (c), we plot the allowed parameter spaces by setting , and , respectively. From Figure 3(a) and (c), it is observed that there are two sets of solutions. We name the upper line Solution 1, characterized by , while the lower line is named Solution 2, characterized by , representing the solution mentioned at the end of the last section. For depicted in Figure 3(b), there is only one set of solutions with in contrast. It is worth noting that, if we consider , there would be no solution here. In the limit of , the lines in Figure 3 exhibit a slope of , necessary to achieve a cancellation between the and doublets in Eq. (19).
We also show in Figure 3 (c), the two sets of solutions with the smallest couplings. They are
| (23) |
The corresponding predictions for other parameters are given by
| Solution 1 | |||||
| Solution 2 | (24) | ||||
We therefore have found two classes of solutions modify slightly, but enhance to the current average value. Solution 2 seems to be a contrived solution although cannot be ruled out simply using branching ratio measurements. If the current data are confirmed, we would think Solution 1 to be a better solution. It is interesting to point out that due to the large hypercharges introduced, we would encounter the Landau pole in the gauge coupling around 10 TeV in both solutions. If the excess is confirmed, our model will imply additional NP around 10 TeV, which may be detected by future experiments with higher precision and energy. It will be interesting to study which kinds of additional NP we need to remedy the situation.
Due to the smallness of the radiative corrections, we expect the large cancellation in Solution 1 to also occur after including the higher-order corrections. For instance, we consider the next-to-leading order (NLO) QED correction. In the limit, it shifts the amplitudes by
| (25) |
The formalism can be cross-checked by replacing with and comparing to the NLO QCD corrections [26, 27], as both have the same topological diagrams at NLO. Since the amplitudes are shifted homogeneously, we conclude that the large cancellations also occur at NLO.
Before ending the discussion, we would like to comment on some other phenomenological aspects at colliders. The new fermions in the model can be produced which has been discussed for smaller and masses in Ref. [14]. Since in our model the hypercharge is large, the lightest new fermion is constrained to have a mass larger than GeV [41]. The production at the current LHC may be scarce or absent. However, with higher energies and higher luminosity, the new fermions in our model may be produced. The signature of the lightest fermion will leave a charge track in the detector to be measured. While to the heavier ones, if produced they can decay into other final states. For Solution 1, except for the others will decay into plus either a -boson or -boson. But these decays will have large widths of the order of hundreds GeV, making detection difficult since there will not be a sharp resonance peak to look for. On the other hand, for Solution 2, the fermion mass differences are not high enough to form an on-shell gauge boson. They decay into an off-shell -boson, which then decays into a charged lepton and a neutrino, with the decay widths being on the order of a few tens of MeV. Similarly, the decay widths to light quark jet pairs are twice as large. Such measurements may provide information to distinguish between the two solutions.
The signal strengths for () and (), normalized to the SM predictions, are measured to be and [42], respectively. In the SM, these processes are predominantly driven by tree-level couplings, while our model influences them at the NLO through triangular fermionic loops. For both Solutions 1 and 2, the effects on are highly suppressed by and , with corrections below the one percent level. The correction to suffers the same suppression but is amplified by the large . However, in Solution 1, the destructive mechanism responsible for the small occurs also in , leading to correction below one percent. In contrast, Solution 2 delivers the largest correction, with , but is still much smaller than the current experimental precision of . To probe the footprints of NP and CP violation, it would be useful to study the spectrum of cascade decays of gauge bosons. A comprehensive analysis should be carried out once future experiments achieve the required precision.
V Conclusion
We have studied a possible explanation for the excess observed in recent measurements by ATLAS and CMS through the construction of a renormalizable model. If this excess is confirmed, it would be a signal of NP beyond the SM. For NP contribution, while modifying , in general it also affects . Since the measured agrees well with the SM prediction, there are tight constraints on theoretical models trying to simultaneously explain data on and . We find that a minimally fermion singlets and doublet extended NP model can explain simultaneously the current data on these decays. We have identified two solutions. One is the SM amplitude is enhanced by for to the observed value, but the amplitude is modified to to give the observed branching ratio. This seems to be a contrived solution, although it cannot be ruled out simply using branching ratio measurements. We, however, have found another solution which naturally enhances the to the measured value, but keeps the close to its SM prediction. With high energy colliders which can produce these new heavy fermions, by studying the decay patterns of the heavy fermions, it is possible to distinguish the two solutions we found. We eagerly await future data to provide more information.
Acknowledgements.
This work is supported in part by the National Key Research and Development Program of China under Grant No. 2020YFC2201501, by the Fundamental Research Funds for the Central Universities, by National Natural Science Foundation of P.R. China (No.12090064, 12205063, 12375088 and W2441004).Appendix A General Yukawa interaction structure in the model
In this appendix, we provide some details for a more general form for Eq. (6) in our model. The Yukawa interaction is given by
| (26) |
We note that although it is possible to rotate away by the chiral rotations of , the mass terms would acquire chiral phases of , which violates CP symmetry. Hence, would necessarily lead to a CP-violating theory. One can apply a chiral rotation to the Lagrangian to shift phases between different terms without affecting the physical results. We choose, without loss of generality, a chiral basis in which the chiral phases vanish in the mass terms.
After spontaneous symmetry breaking, we could diagonalize these mass matrices by biunitary transformation,
| (27) |
which leads to
| (28) |
We parameterize as
| (29) |
while is parameterized similarly by , , and . Solving Eq. (28), we arrive at
| (30) |
Without loss of generality, we can set and derive that
| (31) | ||||
We stress there are only two independent CP phases and , and , and are functions of them.
The Lagrangian responsible for the couplings are then given as
| (32) | ||||
where and . In the limit of , they reduce to Eq.(II).
If is non-zero, there will be two types of interactions contribute to , one is CP-conserving proportional to and another CP-violating to . For illustration, let us fine-tune so that . Taking , the effects of the novel fermions can be encapsulated by the effective Lagrangian of
| (33) |
with . At the limit of , we have a simple relation with given by Eq. (19). The signal strength of is modified to be
| (34) |
The current experiments do not reach the precision required for testing CP violation in . For simplicity, we took in Eq. (6).
References
- [1] G. Aad et al. [ATLAS collaboration], Phys. Lett. B 716, 1-29 (2012) [arXiv:1207.7214 [hep-ex]].
- [2] S. Chatrchyan et al. [CMS collaboration], Phys. Lett. B 716, 30-61 (2012) [arXiv:1207.7235 [hep-ex]].
- [3] J. R. Ellis, M. K. Gaillard and D. V. Nanopoulos, Nucl. Phys. B 106, 292 (1976).
- [4] R. N. Cahn, M. S. Chanowitz and N. Fleishon, Phys. Lett. B 82, 113-116 (1979).
- [5] M. A. Shifman, A. I. Vainshtein, M. B. Voloshin and V. I. Zakharov, Sov. J. Nucl. Phys. 30, 711-716 (1979) ITEP-42-1979.
- [6] M. B. Gavela, G. Girardi, C. Malleville and P. Sorba, Nucl. Phys. B 193, 257-268 (1981).
- [7] L. Bergstrom and G. Hulth, Nucl. Phys. B 259, 137-155 (1985) [erratum: Nucl. Phys. B 276, 744-744 (1986)].
- [8] J. Elias-Miró, J. R. Espinosa, E. Masso and A. Pomarol, JHEP 08, 033 (2013) [arXiv:1302.5661 [hep-ph]].
- [9] A. Dedes, K. Suxho and L. Trifyllis, JHEP 06, 115 (2019) [arXiv:1903.12046 [hep-ph]].
- [10] [CMS collaboration], CMS-PAS-HIG-13-005.
- [11] G. Aad et al. [ATLAS collaboration], Phys. Lett. B 726, 88-119 (2013) [erratum: Phys. Lett. B 734, 406-406 (2014)] [arXiv:1307.1427 [hep-ex]].
- [12] N. Bizot and M. Frigerio, JHEP 01, 036 (2016) [arXiv:1508.01645 [hep-ph]].
- [13] Q. H. Cao, L. X. Xu, B. Yan and S. H. Zhu, Phys. Lett. B 789, 233-237 (2019) [arXiv:1810.07661 [hep-ph]].
- [14] D. Barducci, L. Di Luzio, M. Nardecchia and C. Toni, JHEP 12, 154 (2023) [arXiv:2311.10130 [hep-ph]].
- [15] G. Lichtenstein, M. A. Schmidt, G. Valencia and R. R. Volkas, [arXiv:2312.09409 [hep-ph]].
- [16] T. T. Hong, V. K. Le, L. T. T. Phuong, N. C. Hoi, N. T. K. Ngan and N. H. T. Nha, PTEP 2024, no.3, 033B04 (2024) [arXiv:2312.11045 [hep-ph]].
- [17] R. Boto, D. Das, J. C. Romao, I. Saha and J. P. Silva, Phys. Rev. D 109, no.9, 095002 (2024) [arXiv:2312.13050 [hep-ph]].
- [18] N. Das, T. Jha and D. Nanda, [arXiv:2402.01317 [hep-ph]].
- [19] K. Cheung and C. J. Ouseph, [arXiv:2402.05678 [hep-ph]].
- [20] A. Tumasyan et al. [CMS collaboration], JHEP 05, 233 (2023) [arXiv:2204.12945 [hep-ex]].
- [21] G. Aad et al. [ATLAS and CMS collaboration], Phys. Rev. Lett. 132, no.2, 021803 (2024) [arXiv:2309.03501 [hep-ex]].
- [22] [ATLAS collaboration], ATLAS-CONF-2019-029.
- [23] A. M. Sirunyan et al. [CMS collaboration], JHEP 07, 027 (2021) [arXiv:2103.06956 [hep-ex]].
- [24] A. Y. Korchin and V. A. Kovalchuk, Phys. Rev. D 88, no.3, 036009 (2013) [arXiv:1303.0365 [hep-ph]].
- [25] A. Pomarol and F. Riva, JHEP 01, 151 (2014) [arXiv:1308.2803 [hep-ph]].
- [26] H. Q. Zheng and D. D. Wu, Phys. Rev. D 42, 3760-3763 (1990).
- [27] M. Spira, A. Djouadi and P. M. Zerwas, Phys. Lett. B 276, 350-353 (1992).
- [28] M. Spira, A. Djouadi, D. Graudenz and P. M. Zerwas, Nucl. Phys. B 453, 17-82 (1995) [arXiv:hep-ph/9504378 [hep-ph]].
- [29] A. Djouadi, Phys. Rept. 457, 1-216 (2008) [arXiv:hep-ph/0503172 [hep-ph]].
- [30] R. Bonciani, V. Del Duca, H. Frellesvig, J. M. Henn, F. Moriello and V. A. Smirnov, JHEP 08, 108 (2015) [arXiv:1505.00567 [hep-ph]].
- [31] T. Gehrmann, S. Guns and D. Kara, JHEP 09, 038 (2015) [arXiv:1505.00561 [hep-ph]].
- [32] S. Dawson and P. P. Giardino, Phys. Rev. D 97, no.9, 093003 (2018) [arXiv:1801.01136 [hep-ph]].
- [33] J. Ellis, C. W. Murphy, V. Sanz and T. You, JHEP 06, 146 (2018) [arXiv:1803.03252 [hep-ph]].
- [34] J. de Blas, Y. Du, C. Grojean, J. Gu, V. Miralles, M. E. Peskin, J. Tian, M. Vos and E. Vryonidou, [arXiv:2206.08326 [hep-ph]].
- [35] M. Battaglia, M. Grazzini, M. Spira and M. Wiesemann, JHEP 11, 173 (2021) [arXiv:2109.02987 [hep-ph]].
- [36] G. Aad et al. [ATLAS collaboration], Nature 607, no.7917, 52-59 (2022) [erratum: Nature 612, no.7941, E24 (2022)] [arXiv:2207.00092 [hep-ex]].
- [37] A. Hayrapetyan et al. [CMS], Phys. Lett. B 857, 138964 (2024) [arXiv:2403.20201 [hep-ex]].
- [38] Q. Bonnefoy, L. Di Luzio, C. Grojean, A. Paul and A. N. Rossia, JHEP 07, 189 (2021) [arXiv:2011.10025 [hep-ph]].
- [39] G. Passarino and M. J. G. Veltman, Nucl. Phys. B 160, 151-207 (1979).
- [40] H. H. Patel, Comput. Phys. Commun. 197, 276-290 (2015) [arXiv:1503.01469 [hep-ph]].
- [41] G. Aad et al. [ATLAS collaboration], Phys. Lett. B 847, 138316 (2023) [arXiv:2303.13613 [hep-ex]].
- [42] R. L. Workman et al. [Particle Data Group], PTEP 2022, 083C01 (2022).