The salient crossings of a crown diagram
Abstract.
A crown diagram of a smooth, closed oriented 4-manifold can be thought of as the projection of a link in the product of a closed surface and the circle, with chords in the circle direction connecting the strands of each crossing. This paper uses a straightforward assignment of integers to these chords to show that the smooth structures on the topological 4-manifold underlying a pair of Fintushel-Stern knot surgery 4-manifolds which are known to have the same Seiberg-Witten invariant are not isotopic. A natural question is to determine if the argument may be strengthened to show these manifolds are not diffeomorphic.
1. Introduction
Let be a smooth, closed, oriented, connected 4-manifold, and let be a closed oriented surface of genus . The construction of this paper begins with a certain type of smooth map of which is a regular fiber, a crown map, discussed in Section 2.1. The surface is decorated with a cyclically ordered collection of simple closed curves coming from , which has a natural interpretation as a -component link in using the natural embedding of additive groups , :
The condition that each component of inhabits its own slice is a rather useful one; such links are called cyclically stacked links in this paper. Analogously, a linearly stacked link lies in , with each component inhabiting its own subset . There are a few interesting sources of stacked links, such as Heegaard diagrams of closed 3-manifolds, yielding links which are linearly stacked with two levels of -component links in (or levels, after a slight perturbation), and trisection diagrams of smooth closed 4-manifolds, yielding cyclically stacked links with three levels in . These links, however, do not present an obvious distinguished collection of crossings as crown diagrams do. For crown diagrams, this collection leads to a basic smooth 4-manifold invariant, the collection of so-called salient sequences defined in Section 2.2 and established as an invariant in Section 3. Section 4 uses this to show that distinguish the smooth structures of the knot surgery manifolds and cannot be isotopic in the sense of smoothing theory, where two smooth manifolds and are isotopic smoothings of the topological 4-manifold if there is a smooth manifold and a homeomorphism to such that the projection to is regular, and diffeomorphisms sending the two ends of to and . Supposing and are diffeomorphic, the author knows of no other way to distinguish the isotopy classes of their smooth structures.
Acknowledgements
The author would like to thank José Romàn Aranda Cuevas, Yasha Eliashberg, Bob Gompf, Rob Kirby, Robert Lewis, Robert Lipshitz, Cary Malkiewich, Jeff Nye, Tim Perutz, and Lisa Piccirillo for helpful conversations during the course of this work. The author would especially like to thank Umur Çiftçi for his crucial contribution of the software EQMaker.
2. Definitions
2.1. Topological setting
A Morse 2-function is a smooth map , where is a smooth 2-manifold, such that each critical point of is locally modeled on a fold critical point,
| (1) |
or a cusp critical point,
| (2) |
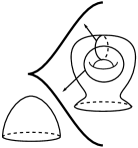
The critical locus forms a smooth 1-submanifold of , stratified into a 1-dimensional stratum of fold points and a finite stratum of cusp points. Crown diagrams come from what this paper calls crown maps, after a suggestion of R. Kirby (In previous work such as [B, BH, W1, W2], a crown diagram was called a surface diagram). A crown map is a Morse 2-function for which , the signs above are both chosen to be negative (that is, the critical points are indefinite folds and cusps), and is a single circle on which is injective (Figure 1(c)). A crown map induces a singular fiber bundle called a crown fibration on as follows. The critical values of partition into a pair of disks, the higher-genus side whose regular fibers are diffeomorphic to a closed oriented genus- surface , and the lower-genus side, which has closed oriented genus fibers. The two disks meet along the critical image of , which is a circle with corners, where each corner is the image of a cusp point.

2pt
\pinlabel at 67 80
\pinlabel at 82 53
\pinlabel at 68 25
\pinlabel at 34 25
\pinlabel at 32 80
\pinlabel at 42 53
\endlabellist
The local model for an indefinite fold point is , where is the local model for a 3-dimensional Morse critical point of index 1 or 2 (in Figure 1(a), it is index 1 with understood to increase from left to right along any horizontal arc). Such a Morse function induces a fibration of by the one- and two-sheeted hyperboloids , and each one-sheeted hyperboloid intersects the plane in a distinguished circle. In the image of a Morse 2-function, the region of regular values corresponding to is called the higher genus side of the fold arc and the distinguished circle is a simple closed curve in the regular fiber called a vanishing cycle. All of the vanishing cycles are depicted as simple closed curves in a fixed reference fiber , measured by choosing a reference path from to the image of a fold arc, and a connection for the fibration, then marking the points in the regular fiber that flow to the fold point. In general, the isotopy class of the vanishing cycle depends on these choices; however, the crown condition implies that the vanishing cycles in this paper are all non-separating and lie in a smooth, closed oriented surface of genus at least 3, and different choices of higher-genus reference fiber, connection and reference path yield isotopic vanishing cycles [BH, Section 4].
With this understood, a crown diagram of the smooth, closed oriented 4-manifold is the oriented diffeomorphism class of a pair , where is a closed, oriented surface of genus greater than 2 and is a collection of simple closed curves in which occurs as the counter-clockwise ordered sequence of vanishing cycles of a crown fibration whose oriented higher-genus fiber is . A diffeomorphism of crown diagrams is required to preserve the cyclic ordering of . According to [W1, Corollary 2], a crown diagram specifies up to orientation-preserving diffeomorphism.
The local model for an indefinite cusp is the same as the local model for the introduction via homotopy of a canceling pair of index-1 and index-2 Morse critical points in a 3-manifold (the homotopy parameter would increase from left to right in Figure 1(b)). For this reason, the vanishing cycles of the two fold arcs which meet at a cusp point can be depicted to have exactly one transverse crossing in .
Definition 2.1.
After canceling all crossings but one from each pair of consecutive vanishing cycles in a crown diagram, each unique transverse crossing between consecutive vanishing cycles is called a salient crossing.
At various points it will be useful to designate a vanishing cycle as the “first” element of , indexing with integers as , where the ordering of any three consecutive elements respects the cyclic order of . Such a choice will be called a labeling of .
Definition 2.2.
A homotopy class of is the smooth homotopy class of any crown map whose diagram is for some choice of reference fiber, connection and reference paths.
It may be possible (and would be interesting to find) that two non-homotopic crown maps have the same crown diagram. In that case, both homotopy classes of maps would be homotopy classes of the diagram.
Definition 2.3.
Two crown diagrams are isotopic if there is an isotopy of individual vanishing cycles in resulting in a crown diagram which is diffeomorphic to .
Definition 2.4.
A crown diagram is allowable if is a disjoint union of open disks whose closures are closed disks, and for every .
Proposition 2.5.
Every crown diagram with four or more vanishing cycles is isotopic to an allowable crown diagram, and two isotopic allowable crown diagrams can be made diffeomorphic using an isotopy consisting of moves taken from Figure 3, such that each move preserves allowability.
Proof.
One may apply what are generally called finger moves or point-pushing maps to individual vanishing cycles to subdivide regions until is allowable, introducing crossings between non-consecutive vanishing cycles. To convert into a different yet isotopic allowable diagram, one may add temporary finger moves at various stages of the isotopy as needed to preserve allowability at every stage.∎
2.2. The chords of a crown diagram
The cyclic ordering of gives data reminiscent of crossings in knot diagrams as follows. For , an intersection is associated with the two arcs and whose union is . These are both oriented as subspaces of , connecting the circles and . These arcs are called the chords of .
Any chord singles out the sublink of contained in and the complimentary chord singles out the sublink of contained in , because the interiors of the two intervals are disjoint positively oriented arcs in . The crossing appears in both sublinks, and if passes over in one, then passes under in the other. In either case, given a chord , one may choose a labeling of so that the under-crossing vanishing cycle at is . Then the over-crossing vanishing cycle would be for some and that corresponding sublink is
For each labeling, the two strands of each crossing in the crown diagram necessarily come from an intersection of two distinct circles, so this paper adopts the visual convention that, having chosen a crossing and a labeling, the under-crossing strand is the one with the lesser subscript. Using this convention, the corners of the disks adjacent to each crossing in a sublink can be given signs as in Figure 2.
2pt
\pinlabel at 47 47
\pinlabel at 28 28
\pinlabel at 47 28
\pinlabel at 28 47
\endlabellist
Since intersects at a unique point for each , there are distinguished chords whose associated sublinks each have two components and one crossing, which is a salient crossing. These chords are the salient chords of .
Suppose is allowable, choose a labeling of and let be the collection of disks forming the disjoint union . For any crossing there is a unique chord which does not intersect ; in other words, it is the chord which is contained in the link diagram whose over-crossing strands are designated by the labeling. Thus, a labeling gives signs to all the corners in the diagram. Given a labeling and a disk , denote by the set of chords corresponding to positive corners of and denote by the set of chords corresponding to negative corners of . Note that allowability implies and are disjoint. Assign a variable to each chord and impose the following grading equations for every labeling of and for every region :
| (3) |
The system of equations given by Equation 3 will be referred to as the grading system. It is defined as a collection of equations associated to disks, but Equation 3 also makes sense for any region whose boundary is a union of arcs of vanishing cycles that meet at crossings. The right hand side of Equation 3 assigns an integer to each , and it is not hard to check that this assignment is additive in the sense that the grading equation for a union of disks is the sum of the grading equations for the disks.
It is now possible to define the main invariant of the paper.
Definition 2.6.
A salient sequence of is a choice of values of for the salient chords of the diagram, obtained from a solution of the collection of all the grading equations for the disks in the complement of the vanishing cycles. Let denote the set of salient sequences for the diagram .
The grading system is defined as a system of equations over the integers, but it may only have solutions in a finite cyclic group, and this solution is not necessarily unique.
3. Invariance
This section contains the proof that is an invariant of the collection of crown diagrams of with any fixed genus and homotopy class.
Definition 3.1.
For two closed curves in , a slide of over is the result of replacing with the connect sum using some choice of connecting arc, which is a smooth embedded curve from one point of to one point of whose interior is disjoint from and . In this situation, is the nonstationary circle and is the stationary circle.
Theorem 3.2.
If two allowable crown diagrams of have the same genus and a common homotopy class, then .
Lemma 3.3.
If two crown diagrams of are isotopic and allowable, then .
Proof.
For any labeling, any isotopy sending to can be slightly perturbed to occur as a sequence of Reidemeister moves, chosen from Figure 3.
2pt
\pinlabelII
II-1 at 63 70
\pinlabel at 63 140
\pinlabel at 63 115
\pinlabel at 63 90
\pinlabel at 63 45
\pinlabel at 22 26
\pinlabel at 63 25
\pinlabel at 102 26
\pinlabel at 63 5
\pinlabel at 43 26
\pinlabel at 77 26
\endlabellist
2pt
\pinlabel
at 60 70
\pinlabel at 58 135
\pinlabel at 80 108
\pinlabel at 39 108
\pinlabel at 63 8
\pinlabel at 80 35
\pinlabel at 42 35
\pinlabel at 62 107
\pinlabel at 85 120
\pinlabel at 95 92
\pinlabel at 95 48
\pinlabel at 85 22
\pinlabel at 62 32
\endlabellist
2pt
\pinlabel
at 60 70
\endlabellist
Invariance of comes from examining the grading equations for those disks forming that are affected by such an isotopy, with an arbitrary fixed labeling. Except for the corners and in Figure 3(a), the crossings have unchanging labels which follow along with the isotopy, and outside of the pictured regions the disks, their corners, and their grading equations are unchanged. In the following arguments, let denote the grading equation for the disk containing the point in Figure 3, for any labeling that yields the pictured crossing data. Since relabeling yields the same pictures, possibly rotated, the following arguments are sufficient.
For the Reidemeister-II move in Figure 3(a), , , and , while all other equations for are also equations for . For this reason, . On the other hand, the chords and corresponding to the crossings and in the grading system for can be removed from all equations except for that of by rearranging the sums above for and , and by substitution for and . For , for example, the appearing in the equation for can be replaced by using the equation for , and then can be replaced by the result of solving for in the equation for , yielding the equation for . The argument for runs similarly. For this reason, appending the two grading equations in four variables coming from to the first grading system results in a grading system which is equivalent to the second, and since the variables for those two extra equations do not appear elsewhere in the first system, .
For a Reidemeister-II-1 move between consecutive vanishing cycles, it may be the case that one of the crossings that disappear is a salient crossing. This cannot happen if both diagrams are allowable, but it is possible that a sequence of slides results in a diagram which is not allowable, but becomes an allowable diagram after canceling some crossings between consecutive vanishing cycles. In that case, the relevant figure is a pair of bigons which share a corner, coming from three crossings between two vanishing cycles. In this case the two grading equations for any chosen labeling set the three associated variables to be equal.
For the Reidemeister-III moves, referring to Figure 3(b), the central triangles before and after a Reidemeister-IIIa move have the same equation . The regions opposite a corner of the triangle have equations analogous to , and regions opposite a side of the triangle have equations analogous to . There are also analogous equations for the disks in Figure 3(c). Since the reverse of a Reidemeister-IIIa move is another Reidemeister-IIIa move, and the same is true of a Reidemeister-IIIb move, the systems of grading equations before and after a Reidemeister-IIIa or Reidemeister-IIIb move are equivalent. Since the grading equations are only defined after choosing a labeling, the cases in which the central triangle has all positive or all negative corners do not occur.∎
According to [W3, Theorem 4.9], if two crown diagrams of have the same genus and homotopy class, then they are related by the so-called genus-preserving moves, which are handleslide, multislide, and shift. According to [W3, Theorem 4.3], these moves are all realized as sequences of slides of a certain form determined by which move is applied. The following lemmas show that these sequences of slides leave the salient sequence unchanged.
Lemma 3.4.
If two crown diagrams of are related by a multislide or a handleslide move, then .
Proof.
This follows from two facts. First, for any chord , the set of values taken by in the collection of solutions to the grading system is unchanged by any slide. Second, the handleslide and multislide moves can be performed in such a way that the collection of salient crossings is left unchanged.
2pt
\pinlabel at 25 62
\pinlabel at 70 62
\pinlabel at 270 62
\pinlabel at 320 78
\pinlabel at 320 46
\pinlabel at 375 95
\pinlabel at 375 28
\pinlabel
at 205 62
\endlabellist
As in the proof of Lemma 3.3, is understood to be the grading equation for the disk in the complement of the vanishing cycles containing , for some fixed labeling. To prove the first fact, in Figure 4 there are two arcs crossing the vertical vanishing cycle on the right. These could come from an arbitrary finger move, or, since this is coming from a crown diagram, they are the crossings coming from the vanishing cycles which are listed in before and after that vanishing cycle. By additivity of the grading equations, one may as well assume the regions containing are as shown, possibly with corners hidden in the dotted parts of the segments, and no other vanishing cycles passing though their interiors. With this understood, the regions containing and can be interpreted as two pieces of a single rectangle whose grading equation will be called . Then , , and the grading equations for all other regions before the slide are either unchanged or can be obtained by adding the grading equation for an appropriate rectangle in the annulus containing and . Since the inverse of any slide is another slide up to isotopy, the first fact is proved.
For the second fact, [W3] presents the sequence of slides for both multislide and handleslide as follows. Given a suitable pair of vanishing cycles for the move, choose a labeling so that they are and , and such that the set of vanishing cycles affected by the move (that is, the nonstationary set) is . Then the move is achieved by applying a diffeomorphism of to the nonstationary set whose effect is a sequence of slides applied to the nonstationary set. This fact alone is enough to show that all of the salient crossings of the crown diagram except possibly and are preserved under handleslide and multislide. As for and , the effect of the move near these crossings is depicted in Figure 8b of that paper, where the short vertical arc, contained in or in , crosses the lower circle ( or respectively) at the salient crossing or , and that crossing is unchanged by the move. ∎
Lemma 3.5.
If two crown diagrams of are related by a shift move, then .
Proof.
According to [W3, Theorem 3.1], a shift move can be realized by a sequence of slides. As in the proof of Lemma 3.4, any slide which does not change the collection of salient crossings will preserve ; however, the argument in the proof of Lemma 3.4 that the collection of salient crossings is unchanged does not apply to the shift move, so there is one further argument to make.
Applying the sequence of slides that produces a shift move can introduce new crossings between a consecutive pair of vanishing cycles and . One of those new crossings may be the only one left after canceling all the other crossings between and by Reidemeister-II-1 moves in the course of an isotopy to obtain an allowable crown diagram. In this situation the original salient crossing can be cancelled last, and since was not cancelled, it was one of the three corners in the last remaining pair of bigons, and in that situation it has already been shown that . In this way, changing the salient crossing from to does not change .∎
Proof of Theorem 3.2.
According to [W2, Theorem 1.1], any pair of crown diagrams in the same homotopy class become diffeomorphic after applying an isotopy and a sequence of moves chosen from a list of four moves called stabilization, handleslide, multislide, and shift. According to [W3, Theorem 4.9], the stabilization move can be omitted from this list because the diagrams have the same genus. According to Lemmas 3.3, 3.4, and 3.5, is unchanged by isotopy and the remaining three moves.∎
4. Examples
4.1. Relating crown diagrams of knot surgery manifolds
According to [FS, Theorem 1.9], if is a fibered knot, then is homeomorphic to the knot surgery manifold and the Seiberg-Witten invariant of is the Alexander polynomial . In the same paper, Fintushel and Stern described a Lefschetz fibration structure on . The current paper uses a monodromy factorization of this Lefschetz fibration due to Yun [Y], and it refers to KnotInfo for the Alexander polynomials and monodromy for the knots and . These are genus-2 fibered knots with the same Alexander polynomial. Genus-1 knots would have simpler diagrams, but they are not used because the two fibered genus-1 knots are the trefoil and the figure-8 knot , which are distinguished by their Alexander polynomials.
It has been known since at least the publication of [L] that one may convert a Lefschetz fibration over into a crown map by a homotopy of the fibration in which one converts the Lefschetz critical points into 3-cusped circles and performs cusp merges to unite the circles, resulting in a crown map whose crown diagram is called a coronation of the Lefschetz fibration (see [W4, Figure 7] for an example of how this looks in a crown diagram). Using the notion of surgered diagrams from [W2] to deduce properties of the resulting vanishing cycles, Behrens and Hayano gave a description of the full collection of coronations of a Lefschetz fibration in terms of mapping class groups of surfaces [BH]. In [W4] there is a fully diagrammatic interpretation of the same homotopy, yielding a single, much more explicit, member of this collection. Recording the vanishing cycles using the notation of train tracks, the weights of such a diagram reach the tens of thousands for a diagram with 22 vanishing cycles, such as the ones for knot surgery on . Instead, this paper will consider a simpler kind of diagram which is slide-equivalent to any coronation of Yun’s Lefschetz fibration. It comes with a collection of crossings that end up being the salient crossings of a coronation. Before discussing this, though, recall that the invariance of applies to crown diagrams with a common homotopy class. The manifolds and are nominally different manifolds, so it is necessary to explain how their coronations would have a common homotopy class if their corresponding smoothings were isotopic.
Lemma 4.1.
Suppose and are fibered knots in , and let , be the Lefschetz fibrations studied in [Y].
-
(1)
There is a topological manifold and homeomorphisms , such that and are homotopic maps .
-
(2)
If the two smoothings coming from these Lefschetz fibrations are isotopic, then the salient sets of their coronations are equal.
Proof.
Let be a topological 4-manifold homeomorphic to (and thus homeomorphic to the total spaces of and ). From the Pontrjagin-Thom construction, it is known that the collection of homotopy classes of maps correspond to framed cobordism classes of framed surfaces in , where the framed surface is obtained as the preimage of a neighborhood of a point in . The goal is to find homeomorphisms from to and to sending a cobordism class of surfaces in to the cobordism class of the fiber in and in , and then to deal with the framing separately. Let and be homeomorphisms, and let and be the fiber classes of and , respectively. Then neither nor are characteristic homology classes in , and both are primitive, because and each have a section whose self-intersection number is [FS, Section 6], while its intersection with the fiber class is 1. Thus, by [GS, Proposition 1.2.18], there is an automorphism of the intersection pairing of sending to . According to the topological -cobordism theorem, is realized as the induced map of a self-homeomorphism of (see for example [GS, Chapter 9]). Thus, is a homeomorphism such that , which yields the required correspondence of cobordism classes.
Having found such that is cobordant in to , let be a surface in that cobordism class. According to Theorem 2 and Example 1.3 of [KMT], there is a unique framing of up to framed cobordism because is simply connected and its intersection form is odd. For this reason, and send the unique framed cobordism class of to that of the fiber of and , respectively. For this reason, and are continuously homotopic maps . This completes the proof of Item (1).
For Item (2), since the smoothings coming from and are isotopic, there is an isotopy of converting it to be a smooth map on the total space of . Thus, and can be taken as smooth maps on the ends of connected by a continuous homotopy. That is, they share a homotopy class.
To the ends of this homotopy, append the further homotopies which convert the Lefschetz fibrations and into crown maps using [W1, Section 4]. Then, according to [W3, Section 4], these can be connected by a deformation corresponding to a sequence of genus-preserving moves on crown maps, which have equal salient sets by Theorem 3.2.∎
Question 4.2.
It seems natural to ask whether two diffeomorphic smoothings realized as the total spaces of homotopic fibration maps is enough to imply that the two smoothings are isotopic. In that case, the main result of the paper could be immediately strengthened to state that the manifolds are not diffeomorphic.
4.2. Diagrams for two knot surgery manifolds
Figure 5 depicts the relevant information to obtain Yun’s monodromy factorizations for and . Starting with the five circles in Figure 5(a), cut the surface at the four circles shown in Figure 5(b). Let denote the right Dehn twist about the circle . Then, according to KnotInfo, and using the circles shown in Figure 5(d), the monodromy of can be written as the composition of Dehn twists
applied from left to right, while the monodromy of can be written
According to [Y, Theorem 2.11], the Lefschetz monodromy factorization for is
The collection of circles that results for is a messy picture, which can be simplified considerably by applying one Dehn twist and pushing the feet of two of the handles around, switching their places in a clockwise rotation as in Figure 6. The resulting collection of Lefschetz vanishing cycles can be seen in Figures 7(a)–7(j) by deleting the pair of long rectangles and connecting the resulting ends with vertical line segments. The simplifying diffeomorphism is not used for , and the resulting collection of circles appears analogously in Figure 8. Note that in those figures, the reversal of ordering of the circles comes from the fact that the circles in the above monodromy factorization are vanishing cycles of a Lefschetz fibration, while the circles in Figures 7 and 8 get their ordering from the merging algorithm depicted in [W4, Figure 6]. In short, the so-called pseudocoronation shown in Figure 7 or Figure 8 comes from choosing an arc in the fiber of the Lefschetz fibration that crosses each of the fibration’s Lefschetz vanishing cycles exactly once, replacing that arc with a tube over which all of those vanishing cycles run, adding two more vanishing cycles in a standard way as in Figures 7(k) and 8(k), then ordering the vanishing cycles as required by [W4, Figure 6]: In that figure, or corresponds to the Lefschetz vanishing cycle. Circle 20 in Figures in Figures 7(k) and 8(k) corresponds to in [W4, Figure 6], and circle 22 in Figures 7(k) and 8(k) corresponds to in [W4, Figure 6].
2pt
\pinlabel at 100 250
\pinlabel at 135 230
\pinlabel at 135 204
\pinlabel at 135 184
\pinlabel at 135 160
\endlabellist
2pt
\pinlabel1 at 135 250
\pinlabel2 at 135 186
\pinlabel3 at 135 97
\pinlabel4 at 135 30
\endlabellist
2pt
\pinlabel at 60 222
\pinlabel at 159 200
\pinlabel at 33 192
\pinlabel at 120 108
\pinlabel at 152 24
\pinlabel1 at 95 215
\pinlabel1 at 175 215
\pinlabel2 at 95 165
\pinlabel2 at 175 165
\pinlabel3 at 95 115
\pinlabel3 at 175 115
\pinlabel4 at 95 65
\pinlabel4 at 175 65
\endlabellist
2pt
\pinlabel at 70 230
\pinlabel at 90 185
\pinlabel at 120 172
\pinlabel at 208 230
\pinlabel at 191 191
\endlabellist
According to the algorithm in [W4] and the subsequent proofs that the algorithm is realizable as a sequence of slides between vanishing cycles in the pseudocoronation, a coronation of either of the Lefschetz fibrations of or can be obtained from applying slides among the vanishing cycles in Figures 7 and 8, while keeping the staircase-shaped arrangement in Figures 7(l) and 8(l) unchanged. Since is invariant under such slides, one could instead use the grading system as given by the depicted pseudocoronations, taking the crossings between consecutive vanishing cycles in the staircase arrangement as the salient crossings: The first step in the algorithm for finding the vanishing cycle of the coronation is to repeatedly slide over along to eliminate all crossings between and other than the salient crossing in the staircase.
2pt
\pinlabel1 at 34 231
\pinlabel1 at 140 231
\pinlabel2 at 34 165
\pinlabel2 at 140 165
\pinlabel3 at 34 99
\pinlabel3 at 140 99
\pinlabel4 at 34 33
\pinlabel4 at 140 33
\pinlabel5 at 310 149
\pinlabel5 at 310 115
\pinlabel at 180 200
\pinlabel at 430 132
\endlabellist
2pt
\pinlabel1 at 34 231
\pinlabel1 at 140 231
\pinlabel2 at 34 165
\pinlabel2 at 140 165
\pinlabel3 at 75 84
\pinlabel3 at 140 99
\pinlabel4 at 34 33
\pinlabel4 at 140 33
\pinlabel5 at 310 149
\pinlabel5 at 310 115
\pinlabel at 430 132
\endlabellist
2pt
\pinlabel1 at 34 231
\pinlabel1 at 140 231
\pinlabel2 at 34 165
\pinlabel2 at 140 165
\pinlabel3 at 77 55
\pinlabel3 at 140 99
\pinlabel4 at 33 78
\pinlabel4 at 140 33
\pinlabel5 at 310 149
\pinlabel5 at 310 115
\pinlabel at -25 -25
\endlabellist
2pt
\pinlabel1 at 34 231
\pinlabel1 at 140 231
\pinlabel2 at 34 165
\pinlabel2 at 140 165
\pinlabel4 at 34 99
\pinlabel3 at 140 99
\pinlabel3 at 34 33
\pinlabel4 at 140 33
\pinlabel5 at 310 149
\pinlabel5 at 310 115
\endlabellist
2pt
\pinlabel6 at 300 195
\endlabellist
2pt
\pinlabel7 at 270 200
\endlabellist
2pt
\pinlabel8 at 270 205
\endlabellist
2pt
\pinlabel9 at 270 210
\endlabellist
2pt
\pinlabel10 at 270 215
\endlabellist
2pt
\pinlabel11 at 330 175
\endlabellist
2pt
\pinlabel12 at 325 175
\endlabellist
2pt
\pinlabel13 at 320 175
\endlabellist
2pt
\pinlabel14 at 315 175
\endlabellist
2pt
\pinlabel15 at 310 175
\endlabellist
2pt
\pinlabel20 at 30 30
\endlabellist

2pt
\pinlabel6 at 300 195
\endlabellist
2pt
\pinlabel7 at 270 200
\endlabellist
2pt
\pinlabel8 at 270 205
\endlabellist
2pt
\pinlabel9 at 270 210
\endlabellist
2pt
\pinlabel10 at 270 215
\endlabellist
2pt
\pinlabel11 at 330 175
\endlabellist
2pt
\pinlabel12 at 325 175
\endlabellist
2pt
\pinlabel13 at 320 175
\endlabellist
2pt
\pinlabel14 at 315 175
\endlabellist
2pt
\pinlabel15 at 310 175
\endlabellist
2pt
\pinlabel20 at 345 30
\endlabellist

4.3. Equations and calculations
The number of regions in the pseudocoronations given by Figures 7 and 8 is large, and each region has multiple equations coming from the different choices of labeling. For this reason, there is software written by Umur Çiftçi, called EQMaker, which produces the grading system as a text file, and there is a list of Mathematica commands for extracting from this system a new system of equations which expresses the salient set as a sum of formal parameters, all available at the author’s website. The grading systems for these diagrams both have integer solutions, the rank of the system for is 21, and the rank of the system for is 20. For this reason, the salient sets are not equal, so the corresponding smoothings are not isotopic.
References
- [B] S. Behrens, On 4-manifolds, folds and cusps, Pac. J. Math 264(2) (2013), 257-306. doi:10.2140/pjm.2013.264.257 MR3089398
- [BH] S. Behrens and K. Hayano, Elimination of cusps in dimension 4 and its applications, Proc. London Math Soc. 113 (5), 674-724. doi:10.1112/plms/pdw042 MR3570242
- [FS] R. Fintushel and R. Stern, Knots, links and 4-manifolds, Invent. Math. 134 (1998), no. 2, 363-400. doi 10.1007/s002220050268 MR1650308
- [GS] R. Gompf and A. Stipsicz, 4-manifolds and Kirby Calculus, Graduate Studies in Math. 20, Amer. Math. Soc., Providence, RI (1999). MR1707327
- [KMT] R. Kirby, P. Melvin, and P. Teichner, Cohomotopy sets of 4-manifolds, Geom. Topol. Monographs 18 (2012), 161-190.
- [L] Y. Lekili, Wrinkled fibrations on near-symplectic manifolds, Geom. Topol. 13 (2009), 277-318. doi:10.2140/gt.2009.13.277 MR2469519
- [Wa] G. Wassermann, Stability of unfoldings in space and time, Acta. Math., 135 (1975), 58-128. doi:10.1007/BF02392016
- [W1] J. Williams, The -principle for broken Lefschetz fibrations, Geom. Topol. 14 no. 2 (2010), 1015-1061. doi:10.2140/gt.2010.14.1015 MR2629899
- [W2] J. Williams, Uniqueness of crown diagrams of smooth -manifolds, 2011 preprint (submitted).
- [W3] J. Williams, Existence of 2-parameter crossings, with applications, Geom. Ded. 207, 265–286(2020). doi:10.1007/s10711-019-00499-1
- [W4] J. Williams, Depicting a generalized shift move in crown diagrams, 2020 preprint.
- [Y] K-H Yun, Twisted fiber sums of Fintushel-Stern’s knot surgered 4-manifolds, Trans. AMS 360, no. 11 (2008), 5853-5868. doi: 0002-9947(08)04623-0