The role of high-order anharmonicity and off-diagonal terms in thermal conductivity: a case study of multi-phase CsPbBr3
Abstract
We investigate the influence of three- and four-phonon scattering, perturbative anharmonic phonon renormalization, and off-diagonal terms of coherent phonons on the thermal conductivity of CsPbBr3 phase change perovskite, by using advanced implementations and first-principles simulations. Our study spans a wide temperature range covering the entire structural spectrum. Notably, we demonstrate that the interactions between acoustic and optical phonons result in contrasting trends of phonon frequency shifts for the high-lying optical phonons in orthorhombic and cubic CsPbBr3 as temperature varies. Our findings highlight the significance of wave-like tunneling of coherent phonons in ultralow and glass-like thermal conductivity in halide perovskites.
I I. Introduction
Phonons are crucial for understanding thermal transport in semiconductors and dielectrics. In the traditional approach of first-principles calculations, important quantities such as the mode-Grüneisen parameter, thermal expansion, phonon group velocity, three-phonon lifetime, and linewidth can be obtained by using anharmonic lattice dynamics under the quasi-harmonic approximation through the linearized phonon Boltzmann transport equation Togo et al. (2015); Carrete et al. (2014); van Roekeghem et al. (2016).
However, the traditional approach, in which some important factors have been overlooked, is facing several challenges:
1) the higher-order interatomic interactions like the fourth-order have been ignored for a long time like in BAs in which the four-phonon scattering is responsible for around 40% suppression of compared to that with only three-phonon interactions;
2) interatomic anharmonicity increases as temperature is raised. However, the perturbation approach is difficult to deal with highly anharmonic systems, such as cubic ABX3 perovskites with imaginary frequencies of harmonic phonons Tadano and Tsuneyuki (2015); Zhao et al. (2021). Therefore, we should illustrate the significance of anharmonic phonon renormalization, by utilizing the self-consistent phonon (SCPH) with temperature-dependent frequencies in several systems Xia et al. (2020); Kang et al. (2019);
3) the off-diagonal terms in the heat flux operator representing the heat transfer through the tunneling of wave-like coherent phonons could provide a potential method to bridge the gap between the traditional Peierls-Boltzmann transport equation and the experimental measurement in ultralow thermal conductivity materials and glass-like materials Simoncelli et al. (2019). Items 1) and 2) are related but independent from 3).
CsPbBr3 is a classical chalcogenide material and a promising candidate for thermoelectric application, garnering significant attention in recent years. However, current studies have mainly focused on the thermal transport properties of individual phase Simoncelli et al. (2019); Tadano and Saidi (2022), often considering only three-phonon scattering and calculating the lattice thermal conductivity with zero temperature phonon dispersion Hu et al. (2021); Lee et al. (2017).
The systematic investigation of all three phases of CsPbBr3, considering both renormalization effects and four-phonon scattering, as well as the contribution of off-diagonal terms, remains largely unexplored. Previous studies have primarily focused on phase transitions, vibrational mechanisms, and dielectric properties Lanigan-Atkins et al. (2021); Svirskas et al. (2020). To the best of our knowledge, no systematic studies have been conducted to date that encompass all three phases while considering renormalization, four-phonon scattering, and off-diagonal contributions.
In this study, we conduct a systematic investigation of the influence of quartic anharmonicity on the lattice dynamics and thermal transport properties of the three distinct phases of CsPbBr3. We employ recent advancements in first-principles simulations, incorporating: (i) efficient construction of high-order interatomic force constants (IFCs) from the CSLD method Zhou et al. (2014, 2019a, 2019b); (ii) rigorous calculations of temperature-dependent phonons through SCPH theory and higher-order multi-phonon scattering rates Tadano and Tsuneyuki (2015); Feng and Ruan (2016); (iii) evaluation of the lattice thermal conductivity by using a unified theory that considers both diagonal terms from the standard Peierls contribution and off-diagonal terms from the coherent Wigner distribution Simoncelli et al. (2019); Isaeva et al. (2019).
II II. COMPUTATIONAL METHODS
For the Peierls-Boltzmann transport equation, the lattice thermal conductivity can be calculated as
| (1) |
where , , , , are the reduced Planck constant, Boltzmann constant, absolute temperature, primitive unit cell volume, and the total number of sampled phonon wave vectors in the first Brillouin zone, respectively. , , , and are the equilibrium component of the phonon population, frequency, group velocity, and lifetime for the mode (wave vector and branch index ), respectively. Except for , all the above parameters can be obtained from harmonic approximation (HA). Usually, can be obtained from the perturbation theory by consideration of three-phonon scattering Debernardi et al. (1995); Gao et al. (2018).
The temperature-dependent phonon dispersion could be considered by the anharmonic phonon renormalization (APRN) at finite temperatures Li et al. (2010); Souvatzis et al. (2008); Errea et al. (2011, 2014); Xia (2018); Ravichandran and Broido (2020). Among various existing approaches, SCPH Tadano and Tsuneyuki (2015); Xia et al. (2020) approximation is one effective method that can rigorously account for the first-order correction of phonon frequencies from the quartic anharmonicity. It can better describe the soft phonon modes and strong anharmonicity. In brief, under the SCPH approximation, the temperature-dependent renormalized phonon frequency can be obtained from the following equation
| (2) |
where is the original phonon frequency from the harmonic approximation. The scalar can be obtained as,
| (3) |
in which is the fourth-order IFCs in the reciprocal representation. The phonon population satisfies Bose-Einstein distribution as a function of temperature. Both Eq. (2) and Eq. (3) have parameters and in common, and thus the SCPH equation can be solved iteratively. Note that can be interpreted as the interaction between a pair of phonon modes, and including the temperature effects Tadano and Tsuneyuki (2015); Xia et al. (2020).
Moreover, if one considers the off-diagonal terms of the heat-flux operator, which depicts the tunneling of coherent phonons, an additional contribution of lattice thermal conductivity, , needs to be considered Semwal and Sharma (1972); Knauss and Wilson (1974); Srivastava and Prasad (1981). Usually, is neglected in simple crystals because of well-separated phonon dispersions and slight broadening as a function of temperature. However, it could dominate in disordered and glass-like amorphous compounds where phonon and related group velocities cannot be clearly defined, and heat transfer is mediated by diffusons and locons Allen and Feldman (1989, 1993); Cepellotti and Marzari (2016).
Recent studies show that is substantial for materials with ultralow thermal conductivity, such as Mn4Si7 with twisting phonons Chen et al. (2015), Ba7.81Ge40.67Au5.33 clathrate Lory et al. (2017), and Tl3VSe4 Mukhopadhyay et al. (2018). Therefore, in all-inorganic halide perovskite CsPbBr3, we incorporate as follows,
| (4) |
where the phonon lifetime in Eq. (1) is substituted as , including three-phonon (3ph) and four-phonon (4ph) scattering. The group velocity is replaced with a generalized form containing off-diagonal elements Simoncelli et al. (2019); Allen and Feldman (1993),
| (5) |
in which and are the polarization vector and the phonon dynamical matrix, respectively. When , it stands for the phonon band diagonal terms, while , corresponds to the off-diagonal terms.
Therefore, the total lattice thermal conductivity . Note that in order to compute the generalized group velocity correctly, we used the phase convention that accounts for atomic positions within its lattice point to construct the dynamical matrix, as adopted in earlier studies Auerbach and Allen (1984). The details of the calculation are shown within the Supplemental Material sup ; Kresse and Furthmüller (1996); Blöchl (1994); Kresse and Joubert (1999); Esfarjani and Stokes (2008); Togo and Tanaka (2015); Candes and Wakin (2008).
III III. RESULTS AND DISCUSSION
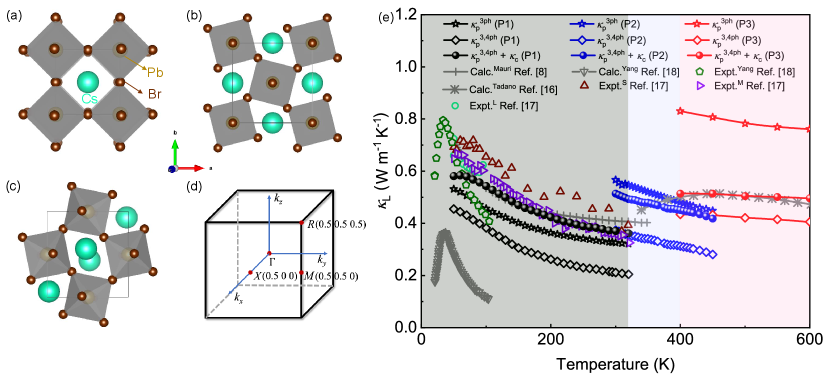
CsPbBr3 is a typical phase change material of ABX3 perovskite. One can discriminate the transition temperature by the dynamical instability of the appearance of soft acoustic phonons from anharmonic potential energy surfaces He et al. (2020); Krapivin et al. (2022). Specifically for CsPbBr3, a second-order phase transition occurs at about 318 K, and the transition temperature may vary, up to 361 K, depending on different samples. At about 373 K, there is another first-order phase transition. The critical temperature was also found at a higher temperature of about 401 K due to different experimental conditions Natarajan and Prakash (1971); Malyshkin et al. (2020). Here, we have chosen an intermediate temperature by considering the above different experimental values Natarajan and Prakash (1971); Malyshkin et al. (2020). Accordingly, the estimated temperatures for the first-order and second-order phase transitions are 320 K and 400 K, respectively. The high-temperature phase remains a cubic symmetry. The temperature reduction induces symmetry-breaking, leading to anisotropic structures from the cubic to the tetragonal at mid-temperature and finally to the orthorhombic crystals at low temperature Lanigan-Atkins et al. (2021); Bechtel et al. (2019); Malyshkin et al. (2020); Natarajan and Prakash (1971). All three crystal structures are depicted in Fig. 1 (a-c).
Fig. 1(e) shows the effects of SCPH, 4ph, and on the calculated lattice thermal conductivity of CsPbBr3. In the following, we neglect the SCPH notation for simplicity. Different primitive cells are used to calculate the corresponding temperature range. Due to the different crystal symmetry, we find that increases from the orthorhombic to the tetragonal and the cubic phases. Moreover, + in each phase decreases as temperature increases because of the enhanced phonon scattering. Since P1 and P2 are anisotropic, we use the arithmetic mean value in the figure.
Compared with , is smaller due to the additional 4ph scattering. Moreover, the gap between them () is growing significantly from P1 to P2 and finally to P3 based on Eq. (1). For instance, is 0.114, 0.168, and 0.361 W m-1 K-1 for temperature 300 K, 400 K, and 500 K, respectively. It is usually attributed to the different scaling laws of 4ph () and 3ph () scatterings in which is the relaxation time Feng et al. (2017). Therefore, 4ph scattering is more critical than 3ph scattering at high-temperature and is proportional to the temperature.
Since the ABX3 perovskite has ultralow and off-diagonal terms contribute significantly Lee et al. (2017); Simoncelli et al. (2019), we include calculation of CsPbBr3 based on Eq. (4) and Eq. (5). At 300 K, the value of of CsPbBr3 for P1 phase is 0.158 W m-1 K-1. At 400 K and 500 K, of CsPbBr3 for both P2 and P3 phases are 0.138 and 0.084 W m-1 K-1, respectively. More details of the values can be found in Supplemental Material S3 sup .
Our results of agree reasonably well with the one reported by Simoncelli, Marzari, and Mauri Simoncelli et al. (2019), while the minor deviations might come from the size of the supercell used in the calculation of harmonic phonon as well as additional effects arising from quartic anharmonicity. For the P3 phase, the value of () is 0.501 W m-1 K-1 at 500 K, which is quite close to the result of 0.50 W m-1 K-1 from the recent quasiparticle nonlinear theory (QP-NL) Tadano and Saidi (2022).
Next, we investigate the influence of anharmonic renormalization on phonon dispersion among orthorhombic, tetragonal, and cubic phases of CsPbBr3. Phonon-phonon interaction and lattice anharmonicity are ascribable to the cubic, quartic, and even higher-order IFCs.
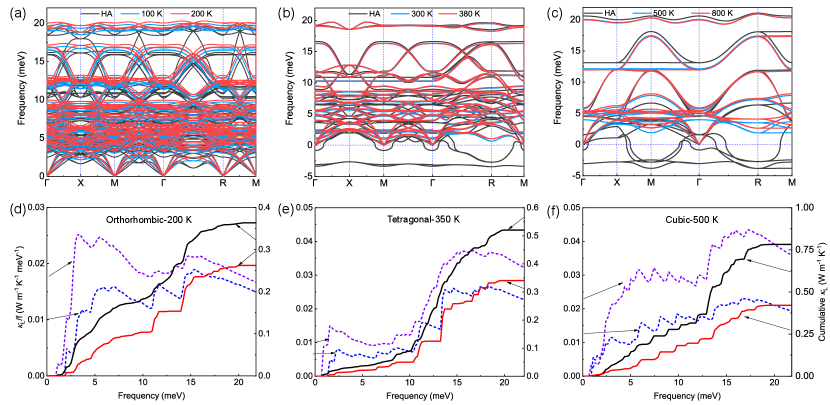
The phonon spectra at different temperatures in three phases are shown in Fig. 2. Unexpectedly, we notice that the acoustic and optical phonon branches become hardened as temperature increases for the low-temperature orthorhombic phase of CsPbBr3, shown in Fig. 2(a). Nevertheless, it is indisputable for the high-temperature cubic phase that the acoustic branches stiffen, whereas the top three optical branches soften with increasing temperature, shown in Fig. 2(c). For the tetragonal phase of CsPbBr3 in Fig. 2(b), the high-lying optical phonons is almost temperature independent. We also plot the off-diagonal term contribution for CsPbBr3 heat transport of three phases, which can be found in the Supplemental Material sup .
We also analyze the frequency-resolved (dashed lines) and cumulative (solid lines) lattice thermal conductivity at different temperatures for cubic CsPbBr3, shown in Fig. 2(d-f). Since 4ph has proved to be additional scattering, of 3ph (the upper one) is more significant than that of 4ph (the lower one).
Traditionally, acoustic phonons are the main heat carriers. However, in cubic CsPbBr3, it is found that optical phonons, ranging from 13.0 to 16.0 meV, dominate the heat transport, no matter whether or not the 4ph scatterings processes are accounted for. Furthermore, 4ph scattering reduces of the cubic CsPbBr3 by almost 40 on top of 3ph.
It is noticed that phonons of various frequencies dominate among different phases. Optical phonons above the frequency of 15.0 meV control the heat transport of 3ph and 4ph for the orthorhombic phase. In comparison, acoustic and optical phonons among the frequency of 3.0 meV and 6.0 meV are also important for 3ph transport. However, for the tetragonal phase, we can find that optical phonons among the frequency from 13.0 meV to 19.0 meV dominate the phonon transport of 3ph and 4ph as well.
Different phonon-temperature tendencies is an interesting phenomenon that has yet to be thoroughly investigated. Previous work only found consistently softened or hardened phonons Zheng et al. (2022); Zhao et al. (2021) in different materials. For the first time, we unveiled the multi-tendency of high-frequency phonon modes variation occurring in different phases of the same material. We reveal in the following that such an opposite tendencies of optical phonon modes of cubic CsPbBr3 as a function of temperature is sourced from the interaction between the top three opticals and other phonon modes.
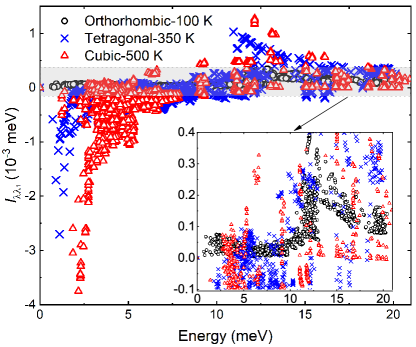
In order to understand the underlying physical mechanism of the optical branches with high frequencies of different CsPbBr3 phases have opposite temperature dependence in their phonon spectra, we have systematically studied the strength of 4ph interaction matrix elements that have been introduced in Eq. (2) and Eq. (3). We set for the highest optical phonon mode as any mode of the three highest optical phonon branches (index of mode=13-15 for cubic and 58-60 for the orthorhombic phase) and change from the lowest acoustic phonon (index of mode =1) to all other optical phonons, gradually scrutinizing the interaction between phonon population , quartic-anharmonicity , phonon frequencies , and , respectively. Here we use the imode parameter to label the index of the phonon branches.
Interestingly, is mainly positive for the orthorhombic phase, as is shown in Fig. 3. It can be both positive and negative for the tetragonal phase, and they almost cancel with each other leading to a small net frequency change. In contrast, it is found that the highest three optical branches have strong coupling with phonons in the low-frequency region, and the interaction is even negative in the cubic CsPbBr3, shown in Fig. 3. We further examine the wave vector position behind the negative and discover that most negative stem from the low-energy acoustic phonon modes, especially around and high-symmetry points.
In Supplemental Material S9-S11 sup , we also show the between imode=3, 57 at 100 K for the P1 phase, imode=3, 27 at 350 K for the P2 phase, and imode=3, 12 at 500 K for the P3 phase, respectively. Since can be either positive or negative, the renormalized phonon frequency as a function of temperature can either increase or decrease according to Eq. (2). Based on Eq. (3), only when is negative for the three highest optical phonons of cubic phase, leading to a negative and a reduced renormalization phonon frequency based on Eq. (2). On the contrary, is positive as a function of temperature for the orthorhombic phase, and finally results in an increased . Owing to the strong interaction between low-energy phonon modes around and and high-frequency optical phonons, the three highest optical phonon frequencies, with the temperature increasing, are softening for the cubic phase while hardening for the orthorhombic phase. More details can be found in the Supplemental Material sup .
To further understand the effects of anharmonic phonon renormalization and 4ph scattering on the thermal transport properties of CsPbBr3, we continue to examine several parameters related to the lattice thermal conductivity, i.e., phonon phase space and scattering rates, respectively.
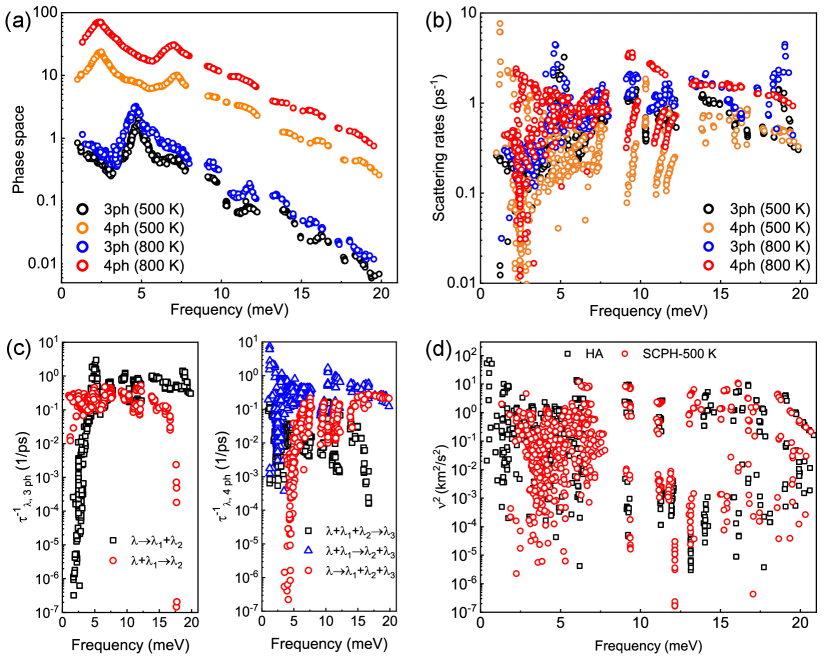
All available 3ph and 4ph scattering phase spaces need to satisfy the energy and quasi-momentum conservation simultaneously Lindsay and Broido (2008); Gao et al. (2018), shown in Fig. 4(a). The phase space of 3ph and 4ph scatterings increases as the temperature rises from 500 K to 800 K. Since the unit of phase space of 3ph and 4ph is different, one cannot compare them directly. Nevertheless, the larger phase space means more available scattering channels. The scattering strength in each accessible channel determines the final phonon relaxation time. Therefore, by including 4ph scattering, the lattice thermal conductivity is generally smaller than that of with only 3ph scattering.
The phonon scattering rates of the cubic phase are shown in Fig. 4(b). It displays that 4ph scattering has the same order of phonon scattering strength as that of 3ph. The scattering rates and phase space results for the orthorhombic and the tetragonal structures also show the same trends in Supplemental Material S5-S8 sup .
Fig. 4(c) displays the absorption and emission processes of the 3ph and 4ph as a function of frequency at 500 K, respectively. For the 3ph scattering, we consider the phonon splitting () and combination (). For the 4ph situation, we count both phonon splitting (), and combination (), as well as redistribution () processes. In the low-frequency region wherein acoustic modes dominate, 3ph combination processes are stronger than the splitting situation, while the redistribution processes of 4ph are the dominant ones. However, in the high-frequency region that is dominated by optical modes, the splitting process of 3ph becomes more important. For 4ph scattering, the splitting process also increases to a dominating portion and has the same order as the redistribution process.
Fig. 4(d) shows the temperature effect on , where is the group velocity at different temperatures for the cubic phase. Interestingly, of 800 K is higher than that of 500 K for most frequencies but almost the same for the acoustic phonons. It stems from the renormalized phonon dispersions at finite temperatures. Besides, we distinguish phonon group velocity for the cases with and without considering SCPH in Supplemental Material S4 sup .
Besides, for the ABX3 perovskites, we find that dynamical stability is in line with the thermodynamic stability Yang and Li (2022); Sun and Yin (2017). Previous work also used finite-temperature phonon dispersion of different phases of perovskites to predict the phase transition temperature Tadano and Saidi (2022). But for other materials, dynamical stability and thermodynamical stability have no direct connection.
In general, the higher the lattice constant, the weaker the interatomic interaction in materials, which will usually lead to a lower lattice thermal conductivity. On the one hand, the calculation of three-phonon scattering including thermal expansion in lower temperature phases (orthorhombic phase and tetragonal phase) is computationally prohibitive since they have lower symmetry and more atoms in the primitive cell compared with the cubic phase. On the other hand, based on the experimental investigations, the coefficient of thermal expansion for CsPbBr3 is 3.8 10-5 K-1, 6.5 10-5 K-1, 2.6 10-5 K-1 for orthorhombic, tetragonal, and cubic phase, respectively Haeger et al. (2020). The effect of the lattice constant on the thermal conductivity might be neglected in a moderate temperature range. Therefore, in our calculation, we neglect the thermal expansion like previous works Simoncelli et al. (2019); Lee et al. (2017); Lanigan-Atkins et al. (2021). Most recently, an effective one-body Hamiltonian that well represents the quasiparticle-peak have been developed. In this method, the thermal expansion in the calculation is included Tadano and Saidi (2022).
IV IV. CONCLUSIONS
In summary, our study reveals the significant contributions of four-phonon scattering and the off-diagonal terms of the heat flux operators in calculating the thermal conductivity in systems with harmonic phonons exhibiting imaginary frequencies and temperature renormalization.
Specifically, our investigation of CsPbBr3 halide perovskites in orthorhombic, tetragonal, and cubic phases yields the following key findings:
(i) For materials with ultralow lattice thermal conductivity , the inclusion of high-order anharmonicity and off-diagonal terms bridge the gap between experimental observations and theoretical predictions;
(ii) The strong coupling between high-frequency optical phonons and overdamped acoustic phonons (), provides insights into the intriguing phonon renormalization phenomena observed in strongly anharmonic systems as a function of temperature;
(iii) Beyond the conventional phonon-phonon scattering perspective, phenomena such as electron-phonon coupling, polaron formation, and entropy in halide perovskites warrant further theoretical advancements Zhou et al. (2018); Lanigan-Atkins et al. (2021).
Our study that presents an effective approach to understand the ultralow observed in halide perovskites, might inspire further experimental investigations exploring materials with glass-like thermal conductivity.
V ACKNOWLEDGMENTS
We acknowledge the support from the National Natural Science Foundation of China (No.12104356 and No.52250191). Z.G. acknowledges the support of China Postdoctoral Science Foundation (No.2022M712552), the Opening Project of Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology (No.Ammt2022B-1), and the Fundamental Research Funds for the Central Universities. We also acknowledge the support by HPC Platform, Xi’an Jiaotong University. Y.X. acknowledges Portland State University Lab Setup Fund.
References
- Togo et al. (2015) Atsushi Togo, Laurent Chaput, and Isao Tanaka, “Distributions of phonon lifetimes in Brillouin zones,” Phys. Rev. B 91, 094306 (2015).
- Carrete et al. (2014) Jesús Carrete, Wu Li, Natalio Mingo, Shidong Wang, and Stefano Curtarolo, “Finding unprecedentedly low-thermal-conductivity half-heusler semiconductors via high-throughput materials modeling,” Phys. Rev. X 4, 011019 (2014).
- van Roekeghem et al. (2016) Ambroise van Roekeghem, Jesús Carrete, Corey Oses, Stefano Curtarolo, and Natalio Mingo, “High-throughput computation of thermal conductivity of high-temperature solid phases: The case of oxide and fluoride perovskites,” Phys. Rev. X 6, 041061 (2016).
- Tadano and Tsuneyuki (2015) Terumasa Tadano and Shinji Tsuneyuki, “Self-consistent phonon calculations of lattice dynamical properties in cubic SrTiO3 with first-principles anharmonic force constants,” Phys. Rev. B 92, 054301 (2015).
- Zhao et al. (2021) Yinchang Zhao, Shuming Zeng, Geng Li, Chao Lian, Zhenhong Dai, Sheng Meng, and Jun Ni, “Lattice thermal conductivity including phonon frequency shifts and scattering rates induced by quartic anharmonicity in cubic oxide and fluoride perovskites,” Phys. Rev. B 104, 224304 (2021).
- Xia et al. (2020) Yi Xia, Vinay I. Hegde, Koushik Pal, Xia Hua, Dale Gaines, Shane Patel, Jiangang He, Muratahan Aykol, and Chris Wolverton, “High-throughput study of lattice thermal conductivity in binary rocksalt and zinc blende compounds including higher-order anharmonicity,” Phys. Rev. X 10, 041029 (2020).
- Kang et al. (2019) Joon Sang Kang, Huan Wu, Man Li, and Yongjie Hu, “Intrinsic low thermal conductivity and phonon renormalization due to strong anharmonicity of single-crystal tin selenide,” Nano Lett. 19, 4941–4948 (2019).
- Simoncelli et al. (2019) Michele Simoncelli, Nicola Marzari, and Francesco Mauri, “Unified theory of thermal transport in crystals and glasses,” Nat. Phys. 15, 809–813 (2019).
- Tadano and Saidi (2022) Terumasa Tadano and Wissam A. Saidi, “First-principles phonon quasiparticle theory applied to a strongly anharmonic halide perovskite,” Phys. Rev. Lett. 129, 185901 (2022).
- Hu et al. (2021) Sile Hu, Zhilin Ren, Aleksandra B Djurisic, and Andrey L Rogach, “Metal halide perovskites as emerging thermoelectric materials,” ACS Energy Lett. 6, 3882–3905 (2021).
- Lee et al. (2017) Woochul Lee, Huashan Li, Andrew B. Wong, Dandan Zhang, Minliang Lai, Yi Yu, Qiao Kong, Elbert Lin, Jeffrey J. Urban, Jeffrey C. Grossman, and Peidong Yang, “Ultralow thermal conductivity in all-inorganic halide perovskites,” Proc. Natl Acad. Sci. USA 114, 8693–8697 (2017).
- Lanigan-Atkins et al. (2021) T. Lanigan-Atkins, X. He, M. J. Krogstad, D. M. Pajerowski, D. L. Abernathy, Guangyong N. M. N. Xu, Zhijun Xu, D.-Y. Chung, M. G. Kanatzidis, S. Rosenkranz, R. Osborn, and O. Delaire, “Two-dimensional overdamped fluctuations of the soft perovskite lattice in CsPbBr3,” Nat. Mater. 20, 977–983 (2021).
- Svirskas et al. (2020) Sarunas Svirskas, Sergejus Balciunas, Mantas Simenas, Gediminas Usevicius, Martynas Kinka, Martynas Velicka, Dominik Kubicki, Marianela Escobar Castillo, Andrei Karabanov, Vladimir V. Shvartsman, Maria de Rosario Soares, Valdas Sablinskas, Andrei N. Salak, Doru C. Lupascu, and Juras Banys, “Phase transitions, screening and dielectric response of CsPbBr3,” J. Mater. Chem. A 8, 14015–14022 (2020).
- Zhou et al. (2014) Fei Zhou, Weston Nielson, Yi Xia, and Vidvuds Ozoliņš, “Lattice anharmonicity and thermal conductivity from compressive sensing of first-principles calculations,” Phys. Rev. Lett. 113, 185501 (2014).
- Zhou et al. (2019a) Fei Zhou, Weston Nielson, Yi Xia, and Vidvuds Ozoliņš, “Compressive sensing lattice dynamics. i. general formalism,” Phys. Rev. B 100, 184308 (2019a).
- Zhou et al. (2019b) Fei Zhou, Babak Sadigh, Daniel Åberg, Yi Xia, and Vidvuds Ozoliņš, “Compressive sensing lattice dynamics. ii. efficient phonon calculations and long-range interactions,” Phys. Rev. B 100, 184309 (2019b).
- Feng and Ruan (2016) Tianli Feng and Xiulin Ruan, “Quantum mechanical prediction of four-phonon scattering rates and reduced thermal conductivity of solids,” Phys. Rev. B 93, 045202 (2016).
- Isaeva et al. (2019) Leyla Isaeva, Giuseppe Barbalinardo, Davide Donadio, and Stefano Baroni, “Modeling heat transport in crystals and glasses from a unified lattice-dynamical approach,” Nat. Commun. 10, 3853 (2019).
- Debernardi et al. (1995) Alberto Debernardi, Stefano Baroni, and Elisa Molinari, “Anharmonic phonon lifetimes in semiconductors from density-functional perturbation theory,” Phys. Rev. Lett. 75, 1819–1822 (1995).
- Gao et al. (2018) Zhibin Gao, Fang Tao, and Jie Ren, “Unusually low thermal conductivity of atomically thin 2D tellurium,” Nanoscale 10, 12997–13003 (2018).
- Wang et al. (2018) Yuxi Wang, Renxing Lin, Pengchen Zhu, Qinghui Zheng, Qianjin Wang, Deyu Li, and Jia Zhu, “Cation dynamics governed thermal properties of lead halide perovskite nanowires,” Nano Lett. 18, 2772–2779 (2018).
- Li et al. (2010) Nianbei Li, Baowen Li, and Sergej Flach, “Energy carriers in the fermi-pasta-ulam lattice: solitons or phonons?” Phys. Rev. Lett. 105, 054102 (2010).
- Souvatzis et al. (2008) P. Souvatzis, O. Eriksson, M. I. Katsnelson, and S. P. Rudin, “Entropy driven stabilization of energetically unstable crystal structures explained from first principles theory,” Phys. Rev. Lett. 100, 095901 (2008).
- Errea et al. (2011) Ion Errea, Bruno Rousseau, and Aitor Bergara, “Anharmonic stabilization of the high-pressure simple cubic phase of calcium,” Phys. Rev. Lett. 106, 165501 (2011).
- Errea et al. (2014) Ion Errea, Matteo Calandra, and Francesco Mauri, “Anharmonic free energies and phonon dispersions from the stochastic self-consistent harmonic approximation: application to platinum and palladium hydrides,” Phys. Rev. B 89, 064302 (2014).
- Xia (2018) Yi Xia, “Revisiting lattice thermal transport in PbTe: The crucial role of quartic anharmonicity,” Appl. Phys. Lett. 113, 073901 (2018).
- Ravichandran and Broido (2020) Navaneetha K. Ravichandran and David Broido, “Phonon-phonon interactions in strongly bonded solids: selection rules and higher-order processes,” Phys. Rev. X 10, 021063 (2020).
- Semwal and Sharma (1972) B. S. Semwal and P. K. Sharma, “Thermal conductivity of an anharmonic crystal,” Phys. Rev. B 5, 3909–3914 (1972).
- Knauss and Wilson (1974) Donald C. Knauss and Robert S. Wilson, “Theory of thermal conductivity of anharmonic crystals: nondiagonal peierls contribution,” Phys. Rev. B 10, 4383–4387 (1974).
- Srivastava and Prasad (1981) G. P. Srivastava and Mahendra Prasad, “Diagonal and nondiagonal peierls contribution to the thermal conductivity of anharmonic crystals,” Phys. Rev. B 23, 4273–4275 (1981).
- Allen and Feldman (1989) Philip B. Allen and Joseph L. Feldman, “Thermal conductivity of glasses: theory and application to amorphous si,” Phys. Rev. Lett. 62, 645–648 (1989).
- Allen and Feldman (1993) Philip B. Allen and Joseph L. Feldman, “Thermal conductivity of disordered harmonic solids,” Phys. Rev. B 48, 12581–12588 (1993).
- Cepellotti and Marzari (2016) Andrea Cepellotti and Nicola Marzari, “Thermal transport in crystals as a kinetic theory of relaxons,” Phys. Rev. X 6, 041013 (2016).
- Chen et al. (2015) Xi Chen, Annie Weathers, Jesús Carrete, Saikat Mukhopadhyay, Olivier Delaire, Derek A Stewart, Natalio Mingo, Steven N Girard, Jie Ma, Douglas L Abernathy, Jiaqiang Yan, Raman Sheshka, Daniel P Sellan, Fei Meng, Song Jin, Jianshi Zhou, and Li Shi, “Twisting phonons in complex crystals with quasi-one-dimensional substructures,” Nat. Commun. 6, 6723 (2015).
- Lory et al. (2017) Pierre-François Lory, Stéphane Pailhes, Valentina M Giordano, Holger Euchner, Hong Duong Nguyen, Reiner Ramlau, Horst Borrmann, Marcus Schmidt, Michael Baitinger, Matthias Ikeda, Petr Tomeš, Marek Mihalkovič, Céline Allio, Mark Robert Johnson, Helmut Schober, Yvan Sidis, Frédéric Bourdarot, Louis Pierre Regnault, Jacques Ollivier, Silke Paschen, Yuri Grin, and Marc de Boissieu, “Direct measurement of individual phonon lifetimes in the clathrate compound Ba7.81Ge40.67Au5.33,” Nat. Commun. 8, 491 (2017).
- Mukhopadhyay et al. (2018) Saikat Mukhopadhyay, David S Parker, Brian C Sales, Alexander A Puretzky, Michael A McGuire, and Lucas Lindsay, “Two-channel model for ultralow thermal conductivity of crystalline Tl3VSe4,” Science 360, 1455–1458 (2018).
- Auerbach and Allen (1984) Assa Auerbach and Philip B. Allen, “Universal high-temperature saturation in phonon and electron transport,” Phys. Rev. B 29, 2884–2890 (1984).
- (38) See Supplemental Material at [URL will be inserted by publisher] for the details of calculated lattice constants using different exchange-correlation functionals compared with the experimental data; convergence test with sampling grid; matrix parameters for the phonon-phonon interaction; off-diagonal term contribution for three phases of CsPbBr3 .
- Kresse and Furthmüller (1996) G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set,” Phys. Rev. B 54, 11169–11186 (1996).
- Blöchl (1994) P. E. Blöchl, “Projector augmented-wave method,” Phys. Rev. B 50, 17953–17979 (1994).
- Kresse and Joubert (1999) G. Kresse and D. Joubert, “From ultrasoft pseudopotentials to the projector augmented-wave method,” Phys. Rev. B 59, 1758–1775 (1999).
- Esfarjani and Stokes (2008) Keivan Esfarjani and Harold T. Stokes, “Method to extract anharmonic force constants from first principles calculations,” Phys. Rev. B 77, 144112 (2008).
- Togo and Tanaka (2015) Atsushi Togo and Isao Tanaka, “First principles phonon calculations in materials science,” Scr. Mater. 108, 1–5 (2015).
- Candes and Wakin (2008) Emmanuel J. Candes and Michael B. Wakin, “An introduction to compressive sampling,” IEEE Signal Process. Mag. 25, 21–30 (2008).
- He et al. (2020) Xing He, Dipanshu Bansal, Barry Winn, Songxue Chi, Lynn Boatner, and Olivier Delaire, “Anharmonic eigenvectors and acoustic phonon disappearance in quantum paraelectric ,” Phys. Rev. Lett. 124, 145901 (2020).
- Krapivin et al. (2022) Viktor Krapivin, Mingqiang Gu, D. Hickox-Young, S. W. Teitelbaum, Y. Huang, G. de la Peña, D. Zhu, N. Sirica, M.-C. Lee, R. P. Prasankumar, A. A. Maznev, K. A. Nelson, M. Chollet, James M. Rondinelli, D. A. Reis, and M. Trigo, “Ultrafast suppression of the ferroelectric instability in ,” Phys. Rev. Lett. 129, 127601 (2022).
- Natarajan and Prakash (1971) M Natarajan and B Prakash, “Phase transitions in ABX3 type halides,” Phys. Status Solidi (a) 4, K167–K172 (1971).
- Malyshkin et al. (2020) Dmitry Malyshkin, Vladimir Sereda, Ivan Ivanov, Maksim Mazurin, Anton Sednev-Lugovets, Dmitry Tsvetkov, and Andrey Zuev, “New phase transition in CsPbBr3,” Mater. Lett. 278, 128458 (2020).
- Bechtel et al. (2019) Jonathon S. Bechtel, John C. Thomas, and Anton Van der Ven, “Finite-temperature simulation of anharmonicity and octahedral tilting transitions in halide perovskites,” Phys. Rev. Materials 3, 113605 (2019).
- Feng et al. (2017) Tianli Feng, Lucas Lindsay, and Xiulin Ruan, “Four-phonon scattering significantly reduces intrinsic thermal conductivity of solids,” Phys. Rev. B 96, 161201(R) (2017).
- Zheng et al. (2022) Jiongzhi Zheng, Dongliang Shi, Yuewang Yang, Chongjia Lin, He Huang, Ruiqiang Guo, and Baoling Huang, “Anharmonicity-induced phonon hardening and phonon transport enhancement in crystalline perovskite ,” Phys. Rev. B 105, 224303 (2022).
- Lindsay and Broido (2008) Lucas Lindsay and DA Broido, “Three-phonon phase space and lattice thermal conductivity in semiconductors,” J. Phys.: Condens. Matter 20, 165209 (2008).
- Yang and Li (2022) Jack Yang and Sean Li, “An atlas of room-temperature stability and vibrational anharmonicity of cubic perovskites,” Mater. Horiz. 9, 1896–1910 (2022).
- Sun and Yin (2017) Qingde Sun and Wan-Jian Yin, “Thermodynamic stability trend of cubic perovskites,” J. Am. Chem. Soc. 139, 14905–14908 (2017).
- Haeger et al. (2020) Tobias Haeger, Ralf Heiderhoff, and Thomas Riedl, “Thermal properties of metal-halide perovskites,” J. Mater. Chem. C 8, 14289–14311 (2020).
- Zhou et al. (2018) Jin-Jian Zhou, Olle Hellman, and Marco Bernardi, “Electron-phonon scattering in the presence of soft modes and electron mobility in perovskite from first principles,” Phys. Rev. Lett. 121, 226603 (2018).