The role of anharmonicity in single-molecule spin-crossover
Abstract
We exploit the system-bath paradigm to investigate vibrational-anharmonicity effects on spin-crossover in a single molecule. Focusing on weak coupling, we use the linear response approximation to deal with the nonlinear vibrational bath and propagate the Redfield master equation to obtain the equilibrium high spin fraction. We take both the anharmonicity in the bath potentials and the nonlinearity in the spin-vibration coupling into account and find a strong interplay between these two effects. Further, we show that the spin-crossover in a single molecule is always a gradual transition and the anharmonicity-induced phonon drag greatly affects the transition behavior.
I Introduction
Octahedral first-row transition-metal complexes of 3-3 may switch between the high-spin (HS) and the low-spin (LS) states under external perturbations, such as temperature change Gütlich et al. (1994), light irradiation Hauser (1986), pressure Molnár et al. (2003), magnetic field Bousseksou et al. (2002), and electric field Prins et al. (2011). Such a spin-crossover (SCO) Cambi and Szegö (1931); Brooker (2015); Bousseksou et al. (2011) usually comes up with changes in magnetic moment, color Kahn et al. (1992), structure, dielectric constant Bousseksou et al. (2003), and even catalytic capacity Zhong et al. (2018). Because of the rich physics and phenomena, SCO has wide potential applications in molecular switches Bhandary et al. (2021), memory devices Kahn and Martinez (1998), sensors Linares et al. (2012), actuators Molnár et al. (2018) and has aroused extensive research interests.
Among various SCO phenomena, the temperature-induced ones Shongwe et al. (2007) are of special interest, in which energy splitting between the HS and the LS states are close to the thermal energy. In practical applications, the transition is required to be abrupt and occur at room temperature. In this case the vibrations will play a key role due to the energy matching Ronayne et al. (2006); Zhang (2014). Various models have been proposed to understand the role of vibrations, including the Ising model extended with lattice vibration Zimmermann and König (1977), the atom-phonon model Nasser et al. (2011), and the stretching-bending model Ye et al. (2015).
Note that in metal-organic compounds, vibrations often assume strong anharmonicity due to the presence of hydrogen bonding or other intermolecular interactions. Shelest studied the thermodynamics of SCO with an anharmonic model and revealed that anharmonicity is one important parameter controlling the SCO transition Shelest et al. (2016). Nicolazzi et al. used the Lennard-Jones potential to model intermolecular interactions and found that anharmonicity can reduce the transition temperature and make the HS state more stable Nicolazzi et al. (2008, 2013); Mikolasek et al. (2017). These authors further demonstrated that anharmonicity in intermolecular interactions is pivotal to understand SCO in nanostructures which allows atoms to undergo large displacements away from their equilibrium positions Fahs et al. (2023). Boukheddaden proposed an anharmonic coupling model and showed that change in anharmonicity drastically alters the SCO transition Boukheddaden (2004). However, there are controversial conclusions in the literature. For instance, Wu et al. performed density functional theory calculations for the effects of anharmonicity on the zero-point energy and the entropy in Fe(II) and Fe(III) complexes and found a rather small contribution to SCO Wu et al. (2019).
Besides in metal-organic compounds, anharmonicity exists in a wide variety of systems and has been attracting increasing research interests. Even though suppressed in crystals by the crystal symmetry, lattice anharmonicity can still significantly affect crystal’s kinetics, dynamics, and thermodynamics Cowley (1963); Manley et al. (2019). This issue becomes more profound on surfaces Wertheim et al. (1994) or in disordered systems, including polar liquids Fleming and Cho (1996), glasses Baldi et al. (2014), and molecular systems Yan and Kühn (2011); Galestian Pour et al. (2017). For example, Lunghi and coworkers found that the anharmonicity in single molecule magnets is responsible for fast under-barrier spin relaxation Lunghi et al. (2017). Now the anharmonicity-induced nonlinear effects and the underlying origin can be accessed with linear and ultrafast IR and Raman spectroscopies thanks to their tremendous progress in the past three decades Passino et al. (1997); Tayagaki and Tanaka (2001); Okumura et al. (2001); Fulmer et al. (2004); Ould-Hamouda et al. (2018); Beć et al. (2018); Lada (2022).
When dealing with anharmonicity, available studies were based on either a classical description or the noninteracting, independent quantum oscillator model. Here we suggest a consistent quantum approach by using nonlinear quantum dissipation. In order to obtain a clear picture of the anharmonic effect itself and to avoid discussing complicated interplays between anharmonicity, spin pairing, energy splitting, and interactions among transition-metal centers, we focus on the single-molecule SCO transition in the weak spin-vibration coupling regime. A numerically exact simulation of an intrinsic nonlinear dissipation system is expensive. For the weak dissipation under study, we can approximate the bath with the anharmonic influence functional approach suggested by Makri et al. Ilk and Makri (1994); Makri (1999a, b). Eventually, the anharmonic influence functional approach maps the anharmonic bath to a harmonic one with the help of an effective spectral density function. After doing so, we can follow the quantum master equation (QME) approach developed for the linear dissipation to investigate single-molecule SCO. Note that simulations of SCO with QME was recently used by Orlov et al. Orlov et al. (2021, 2022).
At first glance the use of a nonlinear bath model is ad hoc because the bath is always linear in the open system paradigm at any given temperature. Note that the dissipation theory is a phenomenological description of open systems based on the quantum fluctuation-dissipation theorem Mori (1965); Kubo (1966). One of the key points is the system-bath separation which implies that the system-bath interaction is weak and the effect of a single bath mode on the system is negligibly small. The effect of the bath, therefore, is a collective behavior and the system only feels the overall environmental fluctuation that follows the Gaussian statistics. The fluctuation of the bath is characterized by its spectral density function and can be reproduced with the linear-dissipation Caldeira-Leggett model Caldeira and Leggett (1981). This framework, however, only holds at a fixed temperature and in principle the spectral density functions at different temperatures are not the same. In reality, all baths, especially for low-dimensional and molecular systems, are intrinsically anharmonic. The use of linear dissipation for simulating physics of an anharmonic system will have to adopt a different spectral density function, hence a different bath, for each temperature and therefore loses the predictive power for any temperature-dependent behavior. A remedy is the above-mentioned nonlinear dissipation model, in which the same bath is used to consistently yield the effective spectral density functions for all temperatures.
The rest of the paper are organized as follows. In Sec. II, we outline the anharmonic influence functional method in the linear response regime. In Sec. III, we present calculations with different anharmonic settings to check their effects on SCO. A concise summary and outlook are provided in Sec. IV.
II Theoretical model
We only investigate the one-step SCO transition which is dictated by the Hamiltonian
| (1) |
where is the spin-orbital coupling, are the electronic energy, and with and describe the vibrations of the LS and the HS states, respectively. Here we discuss the anharmonic effects without considering the Duschinsky rotation and mode-mode coupling. Furthermore, we assume that the LS and the HS states have the same anharmonicity. With these approximations and up to the fourth order, the vibrational Hamiltonians can be extracted from separate, ab initio anharmonic force constant calculations at the LS and the HS states Giese et al. (2006), yielding with and .
The Hamiltonian in Eq. (1) can be re-expressed in terms of the system-plus-bath model
| (2) |
Here we set the Planck constant and the Boltzmann constant to unity. The Hamiltonian for a two-state system in Eq. (2) can be represented as , where is the energy bias between the LS and the HS states and are the spin-1/2 Pauli matrices. Meanwhile, the Hamiltonian for the thermal bath is given by , where is the potential of the thermal bath, with and being coefficients characterizing bath anharmonicity. The Hamiltonian for the system-bath interaction is , where denotes the coupling constant between the system and the environment, the operator with being the nonlinear strength in the spin-vibration coupling, and denotes the equilibrium expectation of the operator .
Utilizing the linear response approximation, the effect of the bath is encapsulated by its correlation function Ilk and Makri (1994); Makri (1999a, b)
| (3) |
where with being the temperature, and is the effective spectral density function
| (4) |
Here is the index of the bath mode, denotes the th eigen-energy, represents the partition function, and stands for the transition frequency for . In the weak spin-vibration coupling regime under investigation, the Redfield equation can be used to obtain the equilibrium expectation
| (5) |
where the operator is defined as
| (6) |
Equation (5) is the working equation of this work. Some remarks are in order. First, Eq. (5) and the underlying system-bath paradigm are based on the assumption of a weak spin-vibration coupling. A natural question arises: How weak is weak enough to be handled with the above scheme? The answer depends on specific systems. Here we discuss this issue with a specific setting mimicking the typical temperature-induced SCO, i.e., meV, K, and with a high-frequency cutoff of 800 cm-1 for the heat bath. Analog to the linear dissipation, we adopt the renormalization energy to characterize the overall coupling strength. Model simulations show that in the absence of anharmonicity, calculations with meV can produce reliable results. In the presence of significant anharmonicity, we should be more cautious and limit the dissipation strength up to 10 meV.
In realistic SCO systems the spin-vibration coupling is not necessarily weak. For instance, in the two-dimensional layer [Fe((3,5-(CH3)2Pz)3BH)2] (Pz = pyrazolyl), the spin-vibration coupling constants of one or two modes lie between 20 meV and 50 meV and the rest are below 10 meV Bairagi et al. (2016). Such a separation that the spin-vibration coupling is dominated by one or two particular modes is not unique for [Fe((3,5-(CH3)2Pz)3BH)2] but widely exists in many SCO complexes Lemke et al. (2017); Svensson Grape et al. (2024). In this case we can follow the treatments adopted in the context of exciton dynamics to include these modes into the system and treat the rest modes as a heat bath Kühn et al. (1996). The remaining spin-vibration coupling then becomes sufficiently weak to allow a QME treatment. The above procedure is therefore applicable with a direct enlargement of the system.
Second, beyond the weak coupling regime, a universal nonlinear-dissipation theory is yet to be developed but methods are available for specific cases. For systems that can be reasonably modeled with the lowest-level nonlinearity (harmonic potentials with linear plus quadratic spin-vibration couplings), more advanced methods, such as the hierarchical equation of motion Xu et al. (2018) and the quantum stochastic Liouville equation Yan (2019) are useful to tackle the physics.
Third and the last, here we focus on transitions in a single molecule and therefore not include cooperative interactions between metal centers which are pivotal to implement practical SCO materials. However, the open system paradigm, as a generic framework to tackle quantum dissipative dynamics, can be straightforwardly extended to oligomers or lattices. To be specific, the Hamiltonian can be generalized to a nonlinearly-dissipated quantum Ising model Jin et al. (2018); Le Hur et al. (2018), that is, and . Here (), , and denote the Pauli matrices, the energy bias, and the spin-orbital coupling on site , respectively, stands for the coupling constant between the th spin and the th vibration, and refers to the nearest neighbor interaction along -direction. In this model the cooperative effects are encoded in the effective direct spin-spin interaction and the coupling of different spins to the same vibrational modes. As illustrated by Wolny and coworkers Rackwitz et al. (2013); Wolny et al. (2016), the parameters can again be extracted from ab initio calculations.
III Numerical results and discussions
Here we adopt a discretized description for the anharmonic bath Wang and Thoss (2007). To this end, we determine the parameters and upon discretizing the spectral density function with 20 000 modes, where is the linear dissipation strength and is the high frequency cutoff. For the anharmonic coefficients, we set , , where with . Here and are two parameters controlling anharmonicity. Under these conditions, the bath modes with assume a double-well potential.
In this study we set K, meV, , cm-1, , and . The parameters will be set to the same value for all vibrations, varying from 0 to 0.05 in step of 0.01. The calculated correlation functions for temperatures from 0 K to 500 K with intervals of 10 K are substituted into the Redfield equation to obtain the equilibrium distributions.
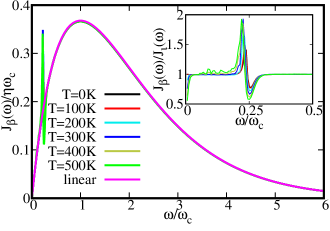
In Fig. 1 we present the effective spectral density functions for temperatures from 0 K to 500 K in step of 100 K. In the simulations, we first calculate the bath correlation function and perform the Fourier transform of its imaginary part to obtain the effective spectral density functions. For comparison we also plot the ratio . As illustrated in Fig. 1, we observe that the effective spectral density function becomes temperature-dependent and deviates from the linear one. The overwhelming feature is that a sharp peak appears around besides the original peak of the linear spectral density function. The anharmonic results merge to linear dissipation when .
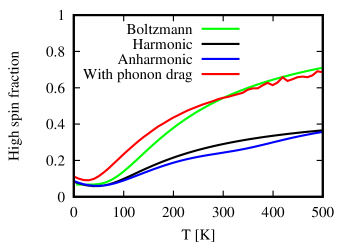
We now discuss the effect of the anharmonicity in the bath potentials without the nonlinearity in the spin-vibration coupling. The results with linear dissipation are also presented. As shown in Fig. 2, with the anharmonic model, the HS fraction first decreases and then gradually increases with temperature. Even at a temperature as high as 500 K, the HS fraction is still less than one half. The harmonic model assumes roughly the same trend as the anharmonic one. However, subtle differences exist between the two trends, mainly in the temperature range from 100 K to 300 K, which is exactly the region in which the effective spectral density function deviates from its linear counterpart. It seems that the presence of the anharmonicity in the bath potential alone slows down the LS to the HS transition. For comparison we show the results obtained from the Boltzmann distribution. It is interesting to note that even for such a weak dissipation, the results from QME are significantly different from the Boltzmann distribution.
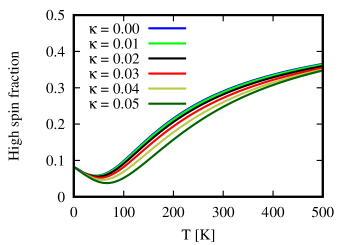
Next we investigate the effect of the nonlinearity in the spin-vibration coupling without the potential anharmonicity. The results are shown in Fig. 3, which depicts the same overall trend as that in Fig. 2. For different nonlinear intensities characterized with , the differences are pretty small and only obvious between 100 K and 300 K.
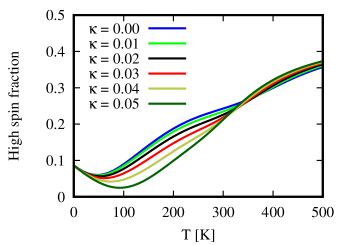
In the presence of both the anharmonicity in the bath potential and the nonlinearity in spin-vibration coupling, there may have strong interplay between these two effects. As shown in Fig. 4, now the temperature dependence are much more significant than that in Figs. 2 and 3, especially in the temperature range from 100 K to 300 K. With such an interplay, the HS fraction changes much abrupter with temperature for stronger nonlinear spin-vibration coupling.
The vibrational anharmonicity will affect SCO via another mechanism. When the system jumps between the HS and the LS states, the vibrational environment the spin feels is switched between and that are specified in Eq. (1). From the view point of reduced dynamics, the energy splitting between HS and LS is in principle . The thermal equilibrium expectations ( = , ) differ for different spin states in the presence of potential anharmonicity, and the molecular structure will be distorted according to the spin change. This equilibrium shift, which is absent for harmonic baths, introduces an additional energy splitting to SCO. Such a back-action mechanism of spin-induced molecular structure distortion is essentially the phonon drag effect observed in thermoelectric transportation Frederikse (1953); Herring (1954); Gurevich and Mashkevich (1989). However, there are subtle differences between these two cases. In thermoelectric transportation the phonon drag stems from the phonon motion against the temperature gradient and is mostly evidenced at low temperatures. In temperature-induced SCO the key role of drag effects is due to the temperature-dependent energy splitting reflecting the temperature-dependent distortion of the molecular structure. It is expected that the drag effects in SCO are manifested for temperatures under which the average molecular structures are significantly different between the HS and the LS configuration. To characterize this phonon drag effect, we set all coefficients to positive in the bath discretization and add the thermal average to . Note that in calculating the thermal average , the quadratic term always assumes a temperature-dependent result. In order to simplify the analysis and focus on the phonon drag effect we use to exclude the effect of nonlinear spin-vibration coupling. The corresponding results are demonstrated in Fig. 2, which shows that the phonon drag leads to a more pronounced and much abrupter temperature-dependence of the HS fraction.
IV Summary and outlook
In metal-organic compounds, vibrations may assume strong anharmonicity. To take account of the anharmonicity effect on the temperature-induced SCO, a linear dissipation model has to adopt a separate spectral density function at each temperature and thus fails to describe the temperature-dependent transition. Here an anharmonic vibrational bath model is used to simulate single-molecule SCO. With the linear response approximation, we are able to obtain the effective spectral density functions for all temperatures consistently with the same bath that can be extracted from ab initio calculations. To scrutinize the anharmonicity effect itself, we focus on the weak spin-vibration coupling to avoid further complications caused by strong interaction. Propagating the Redfield equation to sufficiently long time, we can obtain the equilibrium distribution of the spin.
With specific double-well potentials for low-frequency vibrations, we have shown that the effective spectral density functions assume significant temperature dependency. We have performed four series of calculations with the obtained temperature-dependent spectral density functions: (1) anharmonicity in the bath potentials only; (2) nonlinearity in spin-vibration couplings only; (3) anharmonic bath potentials together with nonlinear spin-vibration couplings; (4) including the energy difference associated with the spin-induced molecular structure distortion. We have revealed that nonlinearities in the couplings or the potentials alone produce weak effects but their combination yields much stronger influence. Further, we have demonstrated that in the presence of anharmonicity, the SCO is drastically affected by the spin- and temperature-dependent thermal-average of vibrational degrees of freedom and becomes much abrupter. We have called it the phonon drag effect because it is essentially the same mechanism first found in thermoelectric transportation.
Here we only consider single-molecule transitions in the weak spin-vibration coupling regime. With the nonlinearly-dissipated quantum Ising model, our approach can be extended to study the cooperative effects in a molecular chain or lattice. Further, we can go beyond weak coupling assumption for those systems in which the spin-vibration interaction is dominated by one particular mode. Such a mode can be approximately included in QME as a two-level system because it is generally a breathing vibration and its second- and higher-excited states are only slightly populated at temperatures under 300 K. Then, with today’s moderate computational resources, we can simulate the physics of a system up to 8 sites if this particular vibration is explicitly treated with QME and up to 16 sites otherwise. As such, we can have a consistent quantum description to scrutinize the interplay between anharmonicity, center-center cooperative interactions, and other factors.
Acknowledgments
The authors acknowledge the support from the National Natural Science Foundation of China under grant No. 21973036.
References
- Gütlich et al. (1994) P. Gütlich, A. Hauser, and H. Spiering, Thermal and optical switching of Iron(II) complexes, Angew. Chem. Int. Ed. 33, 2024 (1994).
- Hauser (1986) A. Hauser, Reversibility of light-induced excited spin state trapping in the Fe(ptz)6(BF4)2, and the Zn1-xFex(ptz)6(BF4)2 spin-crossover systems, Chem. Phys. Lett. 124, 543 (1986).
- Molnár et al. (2003) G. Molnár, V. Niel, J.-A. Real, L. Dubrovinsky, A. Bousseksou, and J. J. McGarvey, Raman spectroscopic study of pressure effects on the spin-crossover coordination polymers Fe(Pyrazine)[M(CN)4] 2H2O (M= Ni, Pd, Pt). First observation of a Piezo-Hysteresis loop at room temperature, J. Phys. Chem. B 107, 3149 (2003).
- Bousseksou et al. (2002) A. Bousseksou, K. Boukheddaden, M. Goiran, C. Consejo, M.-L. Boillot, and J.-P. Tuchagues, Dynamic response of the spin-crossover solid Co(H2(fsa)2en)(py)2 to a pulsed magnetic field, Phys. Rev. B 65, 172412 (2002).
- Prins et al. (2011) F. Prins, M. Monrabal-Capilla, E. A. Osorio, E. Coronado, and H. S. J. van der Zant, Room-temperature electrical addressing of a bistable spin-crossover molecular system, Adv. Mater. 23, 1545 (2011).
- Cambi and Szegö (1931) L. Cambi and L. Szegö, Über die magnetische susceptibilität der komplexen verbindungen, Ber. Dtsch. Chem. Ges. (A and B Ser.) 64, 2591 (1931).
- Brooker (2015) S. Brooker, Spin crossover with thermal hysteresis: Practicalities and lessons learnt, Chem. Soc. Rev. 44, 2880 (2015).
- Bousseksou et al. (2011) A. Bousseksou, G. Molnár, L. Salmon, and W. Nicolazzi, Molecular spin crossover phenomenon: Recent achievements and prospects, Chem. Soc. Rev. 40, 3313 (2011).
- Kahn et al. (1992) O. Kahn, J. Kröber, and C. Jay, Spin transition molecular materials for displays and data recording, Adv. Mater. 4, 718 (1992).
- Bousseksou et al. (2003) A. Bousseksou, G. Molnár, P. Demont, and J. Menegotto, Observation of a thermal hysteresis loop in the dielectric constant of spin crossover complexes: Towards molecular memory devices, J. Mater. Chem. 13, 2069 (2003).
- Zhong et al. (2018) W. Zhong, Y. Liu, M. Deng, Y. Zhang, C. Jia, O. V. Prezhdo, J. Yuan, and J. Jiang, C2N-supported single metal ion catalysts for HCOOH dehydrogenation, J. Mater. Chem. A 6, 11105 (2018).
- Bhandary et al. (2021) S. Bhandary, J. M. Tomczak, and A. Valli, Designing a mechanically driven spin-crossover molecular switch via organic embedding, Nanoscale Adv. 3, 4990 (2021).
- Kahn and Martinez (1998) O. Kahn and C. J. Martinez, Spin-transition polymers: From molecular materials toward memory devices, Science 279, 44 (1998).
- Linares et al. (2012) J. Linares, E. Codjovi, and Y. Garcia, Pressure and temperature spin crossover sensors with optical detection, Sensors 12, 4479 (2012).
- Molnár et al. (2018) G. Molnár, S. Rat, L. Salmon, W. Nicolazzi, and A. Bousseksou, Spin crossover nanomaterials: From fundamental concepts to devices, Adv. Mater. 30, 1703862 (2018).
- Shongwe et al. (2007) M. S. Shongwe, B. A. Al-Rashdi, H. Adams, M. J. Morris, M. Mikuriya, and G. R. Hearne, Thermally induced two-step, two-site incomplete 6A1T2 crossover in a mononuclear Iron(III) phenolate- pyridyl Schiff-base complex: A rare crystallographic observation of the coexistence of pure =5/2 and 1/2 metal centers in the asymmetric unit, Inorg. Chem. 46, 9558 (2007).
- Ronayne et al. (2006) K. L. Ronayne, H. Paulsen, A. Höfer, A. C. Dennis, J. A. Wolny, A. I. Chumakov, V. Schünemann, H. Winkler, H. Spiering, A. Bousseksou, P. Gütlich, A. X. Trautwein, and J. J. McGarvey, Vibrational spectrum of the spin crossover complex [Fe(phen)2(NCS)2] studied by IR and Raman spectroscopy, nuclear inelastic scattering and DFT calculations, Phys. Chem. Chem. Phys. 8, 4685 (2006).
- Zhang (2014) Y. Zhang, Predicting critical temperatures of Iron (II) spin crossover materials: Density functional theory plus approach, J. Chem. Phys. 141, 214703 (2014).
- Zimmermann and König (1977) R. Zimmermann and E. König, A model for high-spin/low-spin transitions in solids including the effect of lattice vibrations, J. Phys. Chem. Solids 38, 779 (1977).
- Nasser et al. (2011) J. A. Nasser, S. Topçu, L. Chassagne, M. Wakim, B. Bennali, J. Linares, and Y. Alayli, Two-dimensional atom-phonon coupling model for spin conversion: Role of metastable states, Eur. Phys. J. B 83, 115 (2011).
- Ye et al. (2015) H.-Z. Ye, C. Sun, and H. Jiang, Monte-Carlo simulations of spin-crossover phenomena based on a vibronic Ising-like model with realistic parameters, Phys. Chem. Chem. Phys. 17, 6801 (2015).
- Shelest et al. (2016) V. V. Shelest, A. V. Khristov, and G. G. Levchenko, The role of anharmonicity in the systems with spin crossover, Low Temp. Phys. 42, 505 (2016).
- Nicolazzi et al. (2008) W. Nicolazzi, S. Pillet, and C. Lecomte, Two-variable anharmonic model for spin-crossover solids: A like-spin domains interpretation, Phys. Rev. B 78, 174401 (2008).
- Nicolazzi et al. (2013) W. Nicolazzi, J. Pavlik, S. Bedoui, G. Molnár, and A. Bousseksou, Elastic Ising-like model for the nucleation and domain formation in spin crossover molecular solids, Eur. Phys. J. Spec. Top. 222, 1137 (2013).
- Mikolasek et al. (2017) M. Mikolasek, W. Nicolazzi, F. Terki, G. Molnár, and A. Bousseksou, Surface transition in spin crossover nanoparticles, Chem. Phys. Lett. 678, 107 (2017).
- Fahs et al. (2023) A. Fahs, S. Mi, W. Nicolazzi, G. Molnár, and A. Bousseksou, Disentangling surface energy and surface/interface stress effects in spin crossover nanomaterials, Adv. Phys. Res. 2, 2200055 (2023).
- Boukheddaden (2004) K. Boukheddaden, Anharmonic model for phonon-induced first-order transition in 1-D spin-crossover solids, Prog. Theor. Phys. 112, 205 (2004).
- Wu et al. (2019) J. Wu, C. Sousa, and C. de Graaf, The role of vibrational anharmonicity in the computational study of thermal spin crossover, Magnetochemistry 5, 49 (2019).
- Cowley (1963) R. A. Cowley, The lattice dynamics of an anharmonic crystal, Adv. Phys. 12, 421 (1963).
- Manley et al. (2019) M. E. Manley, O. Hellman, N. Shulumba, A. F. May, P. J. Stonaha, J. W. Lynn, V. O. Garlea, A. Alatas, R. P. Hermann, J. D. Budai, H. Wang, B. C. Sales, and A. J. Minnich, Intrinsic anharmonic localization in thermoelectric PbSe, Nat. Commun. 10, 1928 (2019).
- Wertheim et al. (1994) G. K. Wertheim, D. M. Riffe, and P. H. Citrin, Anharmonic surface vibrations in photoemission from alkali metals, Phys. Rev. B 49, 2277 (1994).
- Fleming and Cho (1996) G. R. Fleming and M. Cho, Chromophore-solvent dynamics, Ann. Rev. Phys. Chem. 47, 109 (1996).
- Baldi et al. (2014) G. Baldi, V. M. Giordano, B. Ruta, R. Dal Maschio, A. Fontana, and G. Monaco, Anharmonic damping of terahertz acoustic waves in a network glass and its effect on the density of vibrational states, Phys. Rev. Lett. 112, 125502 (2014).
- Yan and Kühn (2011) Y.-A. Yan and O. Kühn, Unraveling the correlated dynamics of the double hydrogen bonds of nucleic acid base pairs in solution, J. Phys. Chem. B 115, 5254 (2011).
- Galestian Pour et al. (2017) A. Galestian Pour, C. N. Lincoln, V. Perlík, F. Šanda, and J. Hauer, Anharmonic vibrational effects in linear and two-dimensional electronic spectra, Phys. Chem. Chem. Phys. 19, 24752 (2017).
- Lunghi et al. (2017) A. Lunghi, F. Totti, R. Sessoli, and S. Sanvito, The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets, Nat. Commun. 8, 14620 (2017).
- Passino et al. (1997) S. A. Passino, Y. Nagasawa, and G. R. Fleming, Three pulse stimulated photon echo experiments as a probe of polar solvation dynamics: Utility of harmonic bath models, J. Chem. Phys. 107, 6094 (1997).
- Tayagaki and Tanaka (2001) T. Tayagaki and K. Tanaka, Photoinduced phase transition to a new macroscopic spin-crossover-complex phase, Phys. Rev. Lett. 86, 2886 (2001).
- Okumura et al. (2001) K. Okumura, D. M. Jonas, and Y. Tanimura, Two-dimensional spectroscopy and harmonically coupled anharmonic oscillators, Chem. Phys. 266, 237 (2001).
- Fulmer et al. (2004) E. C. Fulmer, P. Mukherjee, A. T. Krummel, and M. T. Zanni, A pulse sequence for directly measuring the anharmonicities of coupled vibrations: Two-quantum two-dimensional infrared spectroscopy, J. Chem. Phys. 120, 8067 (2004).
- Ould-Hamouda et al. (2018) A. Ould-Hamouda, B. Viquerat, J. Degert, S. F. Matar, J. F. Létard, F. Guillaume, and E. Freysz, Impact of spin state transition on vibrations of [Fe-(PM-BiA)2(NCS)2] and [Fe-(PM-PEA)2(NCS)2] spin crossover compounds: Experimental and theoretical far IR and Raman study, Eur. J. Inorg. Chem. 2018, 385 (2018).
- Beć et al. (2018) K. B. Beć, J. Grabska, and Y. Ozaki, Advances in anharmonic methods and their applications to vibrational spectroscopies, in Frontiers of Quantum Chemistry, edited by M. J. Wójcik, H. Nakatsuji, B. Kirtman, and Y. Ozaki (Springer, Singapore, 2018) pp. 483–512.
- Lada (2022) Z. G. Lada, The investigation of spin-crossover systems by Raman spectroscopy: A review, Magnetochemistry 8, 108 (2022).
- Ilk and Makri (1994) G. Ilk and N. Makri, Real time path integral methods for a system coupled to an anharmonic bath, J. Chem. Phys. 101, 6708 (1994).
- Makri (1999a) N. Makri, The linear response approximation and its lowest order corrections: An influence functional approach, J. Phys. Chem. B 103, 2823 (1999a).
- Makri (1999b) N. Makri, Iterative evaluation of the path integral for a system coupled to an anharmonic bath, J. Chem. Phys. 111, 6164 (1999b).
- Orlov et al. (2021) Y. S. Orlov, S. V. Nikolaev, A. I. Nesterov, and S. G. Ovchinnikov, Light-induced ultrafast dynamics of spin crossovers under high pressure, J. Exp. Theor. Phys. 132, 399 (2021).
- Orlov et al. (2022) Y. S. Orlov, S. V. Nikolaev, and S. G. Ovchinnikov, Light-induced ultrafast dynamics of spin crossovers in LaCoO3, arXiv: 2211.01300 (2022).
- Mori (1965) H. Mori, Transport, collective motion, and Brownian motion, Prog. Theo. Phys. 33, 423 (1965).
- Kubo (1966) R. Kubo, The fluctuation-dissipation theorem, Rep. Prog. Phys. 29, 255 (1966).
- Caldeira and Leggett (1981) A. O. Caldeira and A. J. Leggett, Influence of dissipation on quantum tunneling in macroscopic systems, Phys. Rev. Lett. 46, 211 (1981).
- Giese et al. (2006) K. Giese, M. Petković, H. Naundorf, and O. Kühn, Multidimensional quantum dynamics and infrared spectroscopy of hydrogen bonds, Phys. Rep. 430, 211 (2006).
- Bairagi et al. (2016) K. Bairagi, O. Iasco, A. Bellec, A. Kartsev, D. Li, J. Lagoute, C. Chacon, Y. Girard, S. Rousset, F. Miserque, Y. J. Dappe, A. Smogunov, C. Barreteau, M.-L. Boillot, T. Mallah, and V. Repain, Molecular-scale dynamics of light-induced spin cross-over in a two-dimensional layer, Nat. Commun. 7, 12212 (2016).
- Lemke et al. (2017) H. T. Lemke, K. S. Kjær, R. Hartsock, T. B. van Driel, M. Chollet, J. M. Glownia, S. Song, D. Zhu, E. Pace, S. F. Matar, M. M. Nielsen, M. Benfatto, K. J. Gaffney, E. Collet, and M. Cammarata, Coherent structural trapping through wave packet dispersion during photoinduced spin state switching, Nat. Commun. 8, 15342 (2017).
- Svensson Grape et al. (2024) E. Svensson Grape, A. M. Davenport, and C. K. Brozek, Dynamic metal-linker bonds in metal—organic frameworks, Dalton Trans. 53, 1935 (2024).
- Kühn et al. (1996) O. Kühn, T. Renger, and V. May, Theory of exciton-vibrational dynamics in molecular dimers, Chem. Phys. 204, 99 (1996).
- Xu et al. (2018) R. X. Xu, Y. Liu, H. Zhang, and Y. J. Yan, Theories of quantum dissipation and nonlinear coupling bath descriptors, J. Chem. Phys. 148, 114103 (2018).
- Yan (2019) Y.-A. Yan, Stochastic simulation of anharmonic dissipation. II. Harmonic bath potentials with quadratic couplings, J. Chem. Phys. 150, 074106 (2019).
- Jin et al. (2018) J. Jin, A. Biella, O. Viyuela, C. Ciuti, R. Fazio, and D. Rossini, Phase diagram of the dissipative quantum Ising model on a square lattice, Phys. Rev. B 98, 241108(R) (2018).
- Le Hur et al. (2018) K. Le Hur, L. Henriet, L. Herviou, K. Plekhanov, A. Petrescu, T. Goren, M. Schiro, C. Mora, and P. P. Orth, Driven dissipative dynamics and topology of quantum impurity systems, C. R. Phys. 19, 451 (2018).
- Rackwitz et al. (2013) S. Rackwitz, W. Klopper, V. Schünemann, and J. A. Wolny, Quantification of intramolecular cooperativity in polynuclear spin crossover Fe(II) complexes by density functional theory calculations, Phys. Chem. Chem. Phys. 15, 15450 (2013).
- Wolny et al. (2016) J. A. Wolny, I. Faus, J. Marx, R. Rüffer, A. I. Chumakov, K. Schlage, H. Wille, and V. Schünemann, Vibrational coupling of nearest neighbors in 1-D spin crossover polymers of rigid bridging ligands. A nuclear inelastic scattering and DFT study, Magnetochemistry 2, 19 (2016).
- Wang and Thoss (2007) H. Wang and M. Thoss, Quantum dynamical simulation of electron-transfer reactions in an anharmonic environment, J. Phys. Chem. A 111, 10369 (2007).
- Frederikse (1953) H. P. R. Frederikse, Thermoelectric power of germanium below room temperature, Phys. Rev. 92, 248 (1953).
- Herring (1954) C. Herring, Theory of the thermoelectric power of semiconductors, Phys. Rev. 96, 1163 (1954).
- Gurevich and Mashkevich (1989) Y. G. Gurevich and O. L. Mashkevich, The electron-phonon drag and transport phenomena in semiconductors, Phys. Rep. 181, 327 (1989).