The rates of growth in an acylindrically hyperbolic group

Koji Fujiwara [email protected] Department of Mathematics, Kyoto University, Kyoto, 606-8502, Japan

Abstract.

Let $G$ be an acylindrically hyperbolic group on a $\delta$ -hyperbolic space $X$ . Assume there exists $M$ such that for any finite generating set $S$ of $G$ , the set $S^{M}$ contains a hyperbolic element on $X$ . Suppose that $G$ is equationally Noetherian. Then we show the set of the growth rates of $G$ is well-ordered (Theorem 1.1). The conclusion was known for hyperbolic groups, and this is a generalization.

Our result applies to all lattices in simple Lie groups of rank-1 (Theorem 1.3), and more generally, some family of relatively hyperbolic groups (Theorem 1.2). It also applies to the fundamental group, of exponential growth, of a closed orientable $3$ -manifold except for the case that the manifold has Sol-geometry (Theorem 5.7). A potential application is a mapping class group, to which the theorem applies if it is equationally Noetherian.

The author is supported in part by Grant-in-Aid for Scientific Research (No. 15H05739, 20H00114).

1. Introduction

1.1. Definitions and results

Let $G$ be a finitely generated group with a finite generating set $S$ . We always assume that $S=S^{-1}$ . Let $B_{n}(G,S)$ be the set of elements in $G$ whose word lengths are at most $n$ with respect to the generating set $S$ . We also denote $S^{n}$ instead of $B_{n}(G,S)$ . Let $\beta_{n}(G,S)=|B_{n}(G,S)|$ . The exponential growth rate of $(G,S)$ is defined to be:

e(G,S)=\lim_{n\to\infty}\beta_{n}(G,S)^{\frac{1}{n}}.

A finitely generated group $G$ has exponential growth if there exists a finite generating set $S$ such that $e(G,S)>1$ . The group $G$ has uniform exponential growth if there exists $c>1$ , such that for every finite generating set $S$ , $e(G,S)\geq c$ .

Given a finitely generated group $G$ , we define:

e(G)=\inf_{|S|<\infty}e(G,S),

where the infimum is taken over all the finite generating sets $S$ of $G$ . Since there are finitely generated groups that have exponential growth, but do not have uniform exponential growth [W], the infimum, $e(G)$ , is not always obtained by a finite generating set of a finitely generated group.

Given a finitely generated group $G$ , we further define the following set in $\mathbb{R}$ :

\xi(G)=\{e(G,S)||S|<\infty\},

where $S$ runs over all the finite generating sets of $G$ . The set $\xi(G)$ is always countable.

A non-elementary hyperbolic group contains a non-abelian free group, hence, it has exponential growth. In fact, a non-elementary hyperbolic group has uniform exponential growth [K]. Recently it is proved that $\xi(G)$ of a non-elementary hyperbolic group $G$ is well-ordered (hence, in particular, has the minimum), [FS]. It was new even for free groups.

In this paper, we deal with larger classes of groups. We state a main result. See Definition 1.8 for the definition of acylindricity. See Definition 1.9 for the definition of equational Noetherianity.

Theorem 1.1 (Well-orderedness for acylindrical actions).

Suppose $G$ acts on a $\delta$ -hyperbolic space $X$ acylindrically, and the action is non-elementary. Assume that there exists a constant $M$ such that for any finite generating set $S$ of $G$ , the set $S^{M}$ contains a hyperbolic element on $X$ . Assume that $G$ is equationally Noetherian. Then, $\xi(G)$ is a well-ordered set.

In particular, $\inf\xi(G)$ is realized by some $S$ , ie, $e(G)=e(G,S)$ .

The theorem holds under a weaker assumption, namely, we may replace the acylindricity of the action by that $S^{M}$ contains a hyperbolic and WPD element (Theorem 3.1). See Definition 2.1 for the definition of WPD. Theorem 1.1 is an immediate consequence of Theorem 3.1 by Lemma 2.3. See the explanation at the beginning of the section 3.

We give some applications.

Theorem 1.2 (Theorem 5.4).

As examples of this theorem, we prove:

Theorem 1.3 (Rank-1 lattices, Theorem 5.5).

Let $G$ be one of the following groups:

(1)

A lattice in a simple Lie group of rank-1.
(2)

The fundamental group of a complete Riemannian manifold $M$ of finite volume such that there exist $a,b>0$ with $-b^{2}\leq K\leq-a^{2}<0$ , where $K$ denotes the sectional curvature.

Then $\xi(G)$ is well-ordered.

Another family of examples are $3$ -manifold groups.

Theorem 1.4 (Theorem 5.7).

Let $M$ be a closed orientable $3$ -manifold, and $G=\pi_{1}(G)$ . If $M$ is one of the following, then $G$ has exponential growth and $\xi(G)$ is well-ordered.

(1)

$M$ is not irreducible and $G$ is not isomorphic to $\mathbb{Z}_{2}*\mathbb{Z}_{2}$ .
(2)

$M$ is irreducible, not a torus bundle over a circle, and $M$ has a non-trivial JSJ-decomposition.
(3)

$M$ admits hyperbolic geometry.
(4)

$M$ is Seifert fibered such that the base orbifold is hyperbolic.

Potential examples of application of the main theorem are mapping class groups. We discuss this class in Section 5.3. See Example 1.12 for non-examples.

We also show some finiteness result as follows. This was known for hyperbolic groups too, [FS].

Theorem 1.5 (Theorem 7.1).

Suppose the same assumption holds for $G$ as in Theorem 1.1. Then for any $\rho\in\xi(G)$ , up to the action of $Aut(G)$ , there are at most finitely many finite generating sets $S$ such that $e(G,S)=\rho$ .

As a part of the proof of the main result, we show a basic result on the growth of a group, generalizing a result known for hyperbolic group in [AL]. Given a group $G$ that satisfies the assumption in Theorem 1.1, where we do not need that $G$ is equationally Noetherian, there exists a constant $A>0$ such that for any finite generating set $S$ of $G$ , we have

e(G,S)\geq A|S|^{A}.

The constant $A$ depends only on $\delta$ and the acylindricity constants. See Proposition 2.10 for the statement. Examples include mapping class groups and rank-1 lattices, see Example 2.11.

We also discuss the set of growth of subgroups in a finitely generated group $G$ . Define

\Theta(G)=\{e(H,S)|S\subset G,|S|<\infty,H=\langle S\rangle,e(H,S)>1\}.

The set $\Theta(G)$ is countable and contains $\xi(G)$ . If $G$ is a hyperbolic group, it is known by [FS, Section 5] that $\Theta(G)$ is well-ordered.

Similarly, we prove:

Theorem 1.6 (Theorem 6.6).

Suppose $G$ is one of the groups in Theorem 1.3. Then $\Theta(G)$ is a well-ordered set.

We also prove:

Theorem 1.7 (Finiteness, Theorem 7.15).

Let $G$ be one of the groups in Theorem 1.3. Then for each $\rho\in\Theta(G)$ , there are at most finitely many $(H,S)$ , up to isomorphism, such that $S$ is a finite generating set of $H<G$ with $e(H,S)=\rho$ .

This kind of finiteness is known for hyperbolic groups [FS], and we generalize it (Theorem 7.1), which implies the above theorem as examples.

Some more definitions are in order in the following section.

1.2. Acylindrical actions

To generalize the properness of an action, Bowditch [Bo] introduced the following definition.

Definition 1.8 (acylindrical action).

An action of a group $G$ on a metric space $X$ is acylindrical if for any $\epsilon>0$ , there exist $R=R(\epsilon)>0$ and $N=N(\epsilon)>0$ such that for all $x,y\in X$ with $d(x,y)\geq R$ , the set

\{g\in G|d(x,g(x))\leq\epsilon,d(y,g(y))\leq\epsilon\}

contains at most $N$ elements.

A group $G$ is called an acylindrically hyperbolic group, [O], if it acts on some $\delta$ -hyperbolic space $X$ such that the action is acylindrical and non-elementary. Here, we say the action is elementary if the limit set of $G$ in the Gromov boundary $\partial X$ has at most two points. If the action is non-elementary, it is known that $G$ contains hyperbolic isometries. Non-elementary hyperbolic groups and non-virtually-abelian mapping class groups are examples of acylindrically hyperbolic groups, [Bo]. There are many other examples.

1.3. Limit groups and equational Noetherianity

Let $G$ be a group and $\Gamma$ a finitely generated (or countable) group. Let $\text{Hom}\,(\Gamma,G)$ be the set of all homomorphisms from $\Gamma$ to $G$ .

A sequence of homomorphisms $\{f_{n}\}$ from $\Gamma$ to $G$ is stable if for each $g\in\Gamma$ , either $f_{n}(g)=1$ for all sufficiently large $n$ ; or $f_{n}(g)\not=1$ for all sufficiently large $n$ . If the sequence is stable, then the stable kernel of the sequence, $\underrightarrow{\ker}(f_{n})$ , is defined by

\underrightarrow{\ker}(f_{n})=\{g\in\Gamma|f_{n}(g)=1\text{ for all sufficiently large }n\}.

We call the quotient $\Gamma/\underrightarrow{\ker}(f_{n})$ a $G$ -limit group, or the limit group over $G$ , associated to $\{f_{n}\}$ , and the homomorphism $f:\Gamma\to\Gamma/\underrightarrow{\ker}(f_{n})$ the limit homomorphism. We say the sequence $\{f_{n}\}$ converges to $f$ .

Let $G$ be a group and $F(x_{1},\cdots,x_{\ell})$ the free group on $X=\{x_{1},\cdots,x_{\ell}\}$ . For an element $s\in F(x_{1},\cdots,x_{\ell})$ and $(g_{1},\cdots,g_{\ell})\in G^{\ell}$ , let $s(g_{1},\cdots,g_{\ell})\in G$ denote the element after we substitute every $x_{i}$ with $g_{i}$ and $x_{i}^{-1}$ by $g_{i}^{-1}$ in $s$ . Given a subset $S\subset F(x_{1},\cdots,x_{\ell})$ , define

V_{G}(S)=\{(g_{1},\cdots,g_{\ell})\in G^{\ell}|s(g_{1},\cdots,g_{\ell})=1\text{ for all }s\in S\}.

$S$ is called a system of equations (with $X$ the set of variables), and $V_{G}(S)$ is called the algebraic set over $G$ defined by $S$ . We sometimes suppress $G$ from $V_{G}(S)$ .

Definition 1.9 (Equationally Noetherian).

A group $G$ is equationally Noetherian if for every $\ell\geq 1$ and every subset $S$ in $F(x_{1},\cdots,x_{\ell})$ , there exists a finite subset $S_{0}\subset S$ such that $V_{G}(S_{0})=V_{G}(S)$ .

Remark 1.10.

This definition appears in for example [GrH]. There is another version of the definition that considers $S\subset G*F(x_{1},\cdots,x_{\ell})$ , which is originally in [BMR] and also in [RW]. They are equivalent, see [RW, Lemma5.1].

Examples of equationally Noetherian groups include free groups, [Gu]; linear groups, [BMR]; hyperbolic groups without torsion, [S], then possibly with torsion, [RW]; and hyperbolic groups relative to equationally Noetherian subgroups, [GrH].

What is important for us is the following general principle.

Lemma 1.11 (Basic principle).

Let $\eta:F\to L$ be the limit map of a sequence of homomorphisms, $f_{n}:F\to G$ . Suppose $G$ is equationally Noetherian. Then for sufficiently large $n$ , $f_{n}$ factors through $\eta$ , namely, there exists a homomorphism $h_{n}:L\to G$ such that $h_{n}\circ\eta=f_{n}$ .

Proof.

Let $X=\{x_{1},\cdots,x_{\ell}\}$ and suppose $F=F(X)$ . Let $R=\{r_{i}\}\subset F(X)$ be a set of defining relations for $L$ . In general this is an infinite set. Each $r_{i}$ is a word on $X$ , so that we can see $R$ as a system of equations with $X$ the variable set. Since $G$ is equationally Noetherian, there is a finite subset $R_{0}\subset R$ such that $V(R)=V(R_{0})$ , namely, every solution (an element in $G^{\ell}$ ) for $R_{0}$ is a solution for $R$ .

Now, since $\eta(r_{1})=1$ in $L$ for a large enough $n$ , we have $f_{n}(r_{1})=1$ in $G$ since $\eta$ is the limit of $\{f_{n}\}$ . By the same reason, since $R_{0}$ is a finite set, there exists $N$ such that for every $n\geq N$ , we have $f_{n}(r_{i})=1$ in $G$ for all $r_{i}\in R_{0}$ . In other words, if $n\geq N$ , then $(f_{n}(x_{1}),\cdots,f_{n}(x_{\ell}))\in V(R_{0})$ . But since $V(R_{0})=V(R)$ , this implies that if $n\geq N$ , then $(f_{n}(x_{1}),\cdots,f_{n}(x_{\ell}))\in V(R)$ , namely, $f_{n}(r_{i})=1$ in $G$ for all $r_{i}\in R$ . Since $R$ is a system of defining relations for $L$ , it implies that each $f_{n}$ with $n\geq N$ factors through $\eta:F\to L$ . ∎

Regarding Theorem 1.1, there exists a finitely generated group $G$ that acylindrically acts on a $\delta$ -hyperbolic space, in fact a simplicial tree $T$ , in the non-elementary way such that for any finite generating set $S$ , the set $S^{2}$ contains a hyperbolic isometry on $T$ ; and that there is no finite generating set $S$ with $e(G)=e(G,S)>1$ . In particular $\xi(G)$ is not well-ordered.

The following example is pointed out by Ashot Minasyan. A group $G$ is called Hopfian if every surjective homomorphism $f:G\to G$ is an isomorphism.

Example 1.12.

Take a finitely generated non-Hopfian group, $G$ , for example $BS(2,3)$ , (a Baumslag-Solitar group). Put $H=G*\mathbb{Z}$ . Then $H$ is non-Hopfian, ie, there exists a surjection $f:H\to H$ that is not an isomorphism. It is a standard fact that a finitely generated equationally Noetherian group is Hopfian, therefore $H$ is not equationally Noetherian, so that Theorem 1.1 does not apply to $H$ .

But all other assumptions in the theorem are satisfied. Let $T$ be the Bass-Serre tree for $G*\mathbb{Z}$ . The tree $T$ is 0-hyperbolic. The action of $H$ on $T$ is acylindrical and non-elementary. Also, for any finite generating set $S$ of $H$ , it is a well-known lemma (due to Serre, cf. [BrF]) that $S^{2}$ contains a hyperbolic isometry on $T$ .

On the other hand, it is known, [Sa], that a finitely generated group $K$ that is a free product is growth-tight, namely, for any surjective homomorphism $h:K\to K$ that is not an isomorphism, and for any finite generating set $S$ of $K$ , $e(K,S)>e(K,h(S))$ . Now, it follows that $e(H)$ is not achieved by any $S$ , since if it did, then take such $S$ . But then, the non-isomorphic, surjective homomorphism $f$ in the above would imply $e(H,S)>e(H,f(S))$ , a contradiction.

Acknowledgement. This work is a continuation of [FS]. The author would like to thank Zlil Sela for generously offering numerous comments and suggestions throughout the work. He is grateful to Mladen Bestvina, Emmanuel Breuillard, Thomas Delzant, Daniel Groves and Wenyuan Yang for useful comments.

He would like to thank the referee for reading the paper thoroughly and making many suggestions, by which the paper significantly improved not only in terms of the presentation, but also mathematically, for example on Proposition 7.2.

2. Lower bound of a growth rate

Although most statements in the paper are for geodesic spaces $X$ , we consider a graph for $X$ instead of a geodesic space in the arguments throughout the paper unless we indicate otherwise. The advantage is that an infimum is achieved for various notions, for example, $L(S)$ , in the arguments. But, we do not lose generality if we assume $X$ to be a graph since we can consider the $1$ -skeleton of a Rips complex of a geodesic space with a group action. Also, the various assumptions we consider (such as the hyperbolicity of the space, acylindricity of the action) remain valid, maybe with slightly difference constants.

2.1. Hyperbolic isometries and axes

Suppose a group $G$ acts on a geodesic space $X$ by isometries. Choose a base point $x\in X$ and for $g\in G$ , put

L(g)=\inf_{x\in X}|x-g(x)|,\lambda(g)=\lim_{n\to\infty}\frac{|x-g^{n}(x)|}{n}.

$L(g)$ is called the minimal displacement. $\lambda(g)$ is called the translation length, and does not depend on the choice of $x$ , and for any $n>0$ we have $\lambda(g^{n})=n\lambda(g)$ . We also have

\lambda(g)\leq L(g)\leq\lambda(g)+7\delta.

The first inequality is trivial and we leave the second as an exercise (for example, use [AL, Corollary 1]). For a finite set $S\subset G$ and $x\in X$ , define

L(S,x)=\max_{s\in S}|x-s(x)|,

then define

L(S)=\inf_{x\in X}L(S,x).

We recall a few definitions and facts from $\delta$ -hyperbolic spaces. An isometry $g$ of a hyperbolic space $X$ is called elliptic if the orbit of a point by $g$ is bounded, and hyperbolic if there are $x\in X$ and $C>0$ such that for any $n>0$ , we have $|x-g^{n}(x)|>Cn$ . The element $g$ is hyperbolic iff $\lambda(g)>0$ .

A hyperbolic isometry $g$ is associated with a bi-infinite quasi-geodesic, $\gamma$ , called an axis in $X$ . If there exists a bi-infinite geodesic $\gamma$ that is invariant by $g$ , that would be an ideal choice for an axis, but that is not always the case.

As a remedy, if $L(g)\geq 10\delta$ , take a point $x\in X$ where $L(g)$ is achieved. Then take a geodesic $[x,g(x)]$ between $x$ and $g(x)$ and consider the union of its $g$ -orbit, which defines a $g$ -invariant path, (see for example [De]). If $L(g)<10\delta$ , then take $n>0$ such that $L(g^{n})\geq 10\delta$ and apply the construction to $g^{n}$ , and use this path for $g$ , which is not $g$ -invariant. We denote this axis as $A(g)$ in this paper. Also, for $g^{n}$ with $g\not=0$ , we may also take $A(g)$ as an axis for $g^{n}$ .

For $g$ , an axis $A(g)$ is not unique, but uniformly (over all hyperbolic $g$ ) quasi-geodesic, such that for any two points $x,y\in A(g)$ , the Hausdorff distance between the segment between $x,y$ on $A(g)$ and a geodesic between $x,y$ , $[x,y]$ , is at most $10\delta$ . Also, if $Hd(A(g),h(A(g))$ for $h\in G$ is finite, then it is bounded by $10\delta$ , where $Hd$ is the Hausdorff distance. We sometimes call $A(g)$ a $10\delta$ -axes. We consider a direction on the $10\delta$ -axis using the action of $g$ .

A hyperbolic isometry $g$ defines two limit points in $\partial X$ , the visual(Gromov) boundary of $X$ , by $g^{\infty}=\lim_{n\to\infty}g^{n}(x),g^{-\infty}=\lim_{n\to-\infty}g^{n}(x)$ , where $x$ is a base point. We say two hyperbolic isometries $g,h$ are independent if $\{g^{\pm\infty}\}$ and $\{h^{\pm\infty}\}$ are disjoint. If the Hausdorff distance between two axes is finite, then we say they are parallel.

2.2. WPD elements

We consider another version of properness of a group action that is weaker than acylindricity.

Definition 2.1 (WPD, uniformly WPD, $D$ -WPD).

Let $G$ act on a $\delta$ -hyperbolic space $X$ . Suppose that $g\in G$ is hyperbolic on $X$ . We say $g$ is WPD if there is a $10\delta$ -axis, $\gamma$ , of $g$ such that for any $\epsilon>0$ , there exists $D=D(\epsilon)>0$ such that for any $x,y\in\gamma$ with $|x-y|\geq D\lambda(g)$ , the number of the elements in the following set is at most $D$ :

(1)

\{h\in G||h(x)-x|\leq\epsilon,|h(y)-y|\leq\epsilon\}.

In application we often take $y=g^{D}(x)$ . If we want to make the function $D$ explicit, we say that $g$ is $D$ -WPD, or WPD w.r.t. $D$ . We say that $D$ is a function for WPD.

If there is a function $D$ such that if a set of hyperbolic elements in $G$ are $D$ -WPD, then we say they are uniformly WPD, or uniformly $D$ -WPD. If all hyperbolic elements in $G$ are uniformly $D$ -WPD, then we say the action is uniformly ( $D$ -)WPD.

Some remarks are in order. The notion of WPD (weak proper discontinuity) was introduced in [BeF], where the function $D$ is not used, but the definitions are equivalent.

If $g$ is $D$ -WPD, then it is $D^{\prime}$ -WPD for any function $D^{\prime}$ such that $D^{\prime}(\epsilon)\geq D(\epsilon)$ for all $\epsilon$ . So, without loss of generality, we assume that $D(\epsilon)$ does not decrease when we increase $\epsilon$ . We often use the value $D(100\delta)$ in this paper, for example, see Lemma 2.2. For convenience we also assume that $D(100\delta)\geq 50$ , which we use in the proof of Lemma 7.4.

The choice of a $10\delta$ -axis is not important in the definition. Also, one can use $C$ -axis for any $C>0$ . It only changes the function $D(\epsilon)$ . Uniformly WPD is related to but weaker than the notion of weak acylindricity in [De]. See also [De, Example 1] for the difference between acylindricity and variations of WPD.

For an acylindrical action, it is known ([F, Lemma 2.1]) that there exists $T>0$ such that for any hyperbolic element $g$ , we have $\lambda(g)\geq T$ . This holds for uniformly WPD actions too, and the argument is same, but for the readers’ convenience, we prove it.

Lemma 2.2 (Lower bound on $\lambda(g)$ ).

Suppose $G$ acts on a $\delta$ -hyperbolic space $X$ . Let $g\in G$ be hyperbolic with a $10\delta$ -axis $\gamma$ .

(1)

If $g$ is $D$ -WPD, then $\lambda(g)\geq\frac{50\delta}{D(100\delta)}$ .
(2)

If the action is acylindrical, then $\lambda(g)\geq\frac{50\delta}{N(150\delta)}$ .

Proof.

(1) Set $\mathcal{D}=D(100\delta)$ . Let $x,y\in\gamma$ with $|x-y|\geq\mathcal{D}\lambda(g)$ . Then there must be some $n$ with $0\leq n\leq\mathcal{D}$ such that $|x-g^{n}(x)|>100\delta$ or $|y-g^{n}(y)|>100\delta$ . This is because otherwise, all the elements $1,g,\cdots,g^{\mathcal{D}}$ , which are $\mathcal{D}+1$ distinct elements, are contained in the set

\{h\in G||h(x)-x|\leq 100\delta,\text{ and }|h(y)-y|\leq 100\delta\}.

This is impossible since the contains at most $\mathcal{D}$ elements. Now suppose, say, $x$ satisfies $|x-g^{n}(x)|>100\delta$ . Then it implies that $\lambda(g^{n})\geq 50\delta$ . Since $n\leq\mathcal{D}$ , we have $\lambda(g)\geq\frac{50\delta}{\mathcal{D}}$ .

(2) The argument is similar to (1). Take $x,y\in\gamma$ with $|x-y|=R(150\delta)$ . If $|x-g^{n}(x)|\leq 100\delta$ for some $n$ , then $|y-g^{n}(y)|\leq 150\delta$ . This implies, by acylindricity, there must be $n$ with $1\leq n\leq N(150\delta)$ s.t. $|x-g^{n}(x)|>100\delta$ . It follows $\lambda(g^{n})\geq 50\delta$ , so that $\lambda(g)\geq\frac{50\delta}{N(150\delta)}$ . ∎

For a function $D(\epsilon)$ , put

T=\frac{50\delta}{D(100\delta)},

then by Lemma 2.2 (1) we have $\lambda(g)\geq T$ for a $D$ -WPD element $g$ .

The following lemma is straightforward.

Lemma 2.3 (Acylindricity implies uniform WPD).

If an action of $G$ on a $\delta$ -hyperbolic space $X$ is acylindrical, then it is uniformly WPD.

Proof.

Suppose $g\in G$ is hyperbolic on $X$ , and let $\gamma$ be a $10\delta$ -axis. Let $R(\epsilon),N(\epsilon)$ be the acylindricity constants. Also, let $T>0$ be a uniform bound for $\lambda(g)\geq T$ by Lemma 2.2 (2). $T$ does not depend on $g$ nor $\epsilon$ . Suppose $\epsilon$ is given. Let $K=K(\epsilon)$ be a smallest integer with $K\geq\frac{R(\epsilon)}{T}$ . Then $\lambda(g^{K})\geq R(\epsilon)$ . The constant $K$ does not depend on $g$ . Then for any $x\in\gamma$ and $n\geq K$ , we have $|x-g^{n}(x)|\geq R(\epsilon)$ . By acylindricity, there are at most $N(\epsilon)$ elements which simultaneously move each of $x,g^{n}(x)$ by at most $\epsilon$ . Put $D(\epsilon)=\max\{K(\epsilon),N(\epsilon)\}$ , then the action is uniformly $D$ -WPD. ∎

We state a lemma which is useful for us.

Lemma 2.4.

Suppose there are at most $D$ elements that satisfies the condition (1) in the definition 2.1 for $\epsilon=100\delta$ if $|x-y|\geq D\lambda(g)$ . Then $g$ is WPD, and moreover, there is a function $D^{\prime}$ with $D^{\prime}(100\delta)=D$ that depends only on $D,\delta$ such that $g$ is $D^{\prime}$ -WPD.

Proof.

Let $\gamma$ be a $10\delta$ -axis of $g$ . Suppose $\epsilon>0$ is given. We may assume $\epsilon>100\delta$ . Take $x,y\in\gamma$ such that $|x-y|\geq D\lambda(g)+2\epsilon+1000\delta$ . Take $p,q\in\gamma$ between $x$ and $y$ with $|x-p|=|y-q|=\epsilon+50\delta$ . Then $|p-q|\geq D\lambda(g)+800\delta$ .

Let $J$ be the collection of elements in $G$ such that $|x-j(x)|\leq\epsilon$ and $|y-j(y)|\leq\epsilon$ . If $j\in J$ , then $|p-j(p)|\leq\epsilon+30\delta$ and $|q-j(q)|\leq\epsilon+30\delta$ ; and $j(p),j(q)$ are in the $15\delta$ -neighborhood of $\gamma$ . It implies that $J$ contains a subset $J_{0}$ that contains at most $(2\epsilon+200\delta)/(10\delta)$ elements such that for any $j\in J$ , one can find $j_{0}\in J_{0}$ with $|p-j^{-1}j_{0}(p)|\leq 70\delta$ . To see it, consider points $p_{1},p_{2}\in\gamma$ with $|p_{1}-p_{2}|=2\epsilon+200\delta$ such that $p$ is the mid point of the segment between $p_{1},p_{2}$ on $\gamma$ , which we denote by $[p_{1},p_{2}]$ . Then the points $j(p)$ with $j\in J$ is contained in the $30\delta$ -neighborhood of $[p_{1},p_{2}]$ . One should imagine that this neighborhood is a narrow tube around $[p_{1},p_{2}]$ . Now by a pigeon hole argument, one can find a desirable subset $J_{0}$ . (Notice that $|p-j^{-1}j_{0}(p)|=|j(p)-j_{0}(p)|$ , so that one needs to find a point $j_{0}(p)$ near (i.e. at most $70\delta$ ) a given point $j(p)$ , which is possible.)

But $|p-j^{-1}j_{0}(p)|\leq 70\delta$ implies $|q-j^{-1}j_{0}(q)|\leq 100\delta$ . This is because $|p-q|\geq 800\delta$ and both $[j(p),j(q)]$ and $[j_{0}(p),j_{0}(q)]$ are contained in the $20\delta$ -neighborhood of $\gamma$ . We have shown that the element $j^{-1}j_{0}$ moves both $p,q$ by at most $100\delta$ . By our assumption, there are at most $D$ possibilities for such element. In conclusion, $J$ contains at most $D\times(2\epsilon+200\delta)/(10\delta)$ elements. We proved that $g$ is WPD.

We compute a WPD-function for $g$ , which we denote by $D^{\prime}$ . By assumption, we may set $D^{\prime}(100\delta)=D$ . First,

D\times(2\epsilon+200\delta)/(10\delta)=D\times(\epsilon/(5\delta)+20).

Next,

D+(2\epsilon+1000\delta)/\lambda(g)\geq D+D(2\epsilon+1000\delta)/(50\delta)=D(21+\epsilon/(25\delta))

by Lemma 2.2 (1). So, if $\epsilon>100\delta$ , we set

D^{\prime}(\epsilon)=D\max\{20+\epsilon/(5\delta),21+\epsilon/(25\delta)\}=D\times(21+\epsilon/(5\delta)).

∎

2.3. Elementary closure

Suppose $G$ acts on a hyperbolic space $X$ and let $g\in G$ be a hyperbolic isometry with an axis $\gamma$ . The elementary closure of $g$ is defined by

E(g)=\{h\in G|Hd(\gamma,h(\gamma))<\infty\}.

It turns out that $E(g)$ is a subgroup of $G$ . Clearly, $\langle g\rangle<E(g)$ .

We denote the $a$ -neighborhood of a subset $Y\subset X$ by $N_{a}(Y)$ .

Lemma 2.5 (parallel axes).

Suppose $G$ acts on a $\delta$ -hyperbolic space $X$ . Let $g\in G$ be hyperbolic with a $10\delta$ -axis $\gamma$ . Let $h\in G$ , then

(1)

If $h\in E(g)$ , then $Hd(\gamma,h(\gamma))\leq 50\delta$ .
(2)

Assume that $g$ is $D$ -WPD. If $h\not\in E(g)$ , then the diameter of $h(\gamma)\cap N_{50\delta}(\gamma)$ is at most

$2D(100\delta)L(g)+100\delta.$

This lemma is well-known in slightly different versions, for example [F, Lemma 2.2] for acylindrical actions, so the proof will be brief.

In general if two axes have finite Hausdorff distance, then we say they are parallel.

Proof.

(1) By definition, $Hd(\gamma,h(\gamma))<\infty$ . Since both $\gamma,h(\gamma)$ are $10\delta$ -axes, we have a desired bound.

(2) Suppose not. Suppose that the direction of $\gamma,h\gamma$ coincide along the parallel part. Set $\mathcal{D}=D(100\delta)$ . Take $x\in h(\gamma)$ near one end of the intersection such that $g^{n}(x)$ for $0\leq n\leq 2\mathcal{D}$ are in the $50\delta$ -neighborhood of the intersection. This is possible since the intersection is long enough. Consider the points $x,g^{\mathcal{D}}(x)$ . Then $|x-g^{\mathcal{D}}(x)|\geq\mathcal{D}\lambda(g)$ . Letting $(hgh^{-1})^{-n}g^{n}$ with $0\leq n\leq\mathcal{D}$ act on $x,g^{\mathcal{D}}(x)$ , we have

|x-(hgh^{-1})^{-n}g^{n}(x)|\leq 100\delta,\,\,|g^{\mathcal{D}}(x)-(hgh^{-1})^{-n}g^{n}(g^{\mathcal{D}}(x))|\leq 100\delta

for all $0\leq n\leq\mathcal{D}$ .

But since $g$ is $D$ -WPD, there are at most $\mathcal{D}$ such elements, so that it must be that for some $n\not=m$ , we have $(hgh^{-1})^{-n}g^{n}=(hgh^{-1})^{-m}g^{m}$ , so that $g^{n-m}$ and $h$ commute. It implies that $\gamma$ and $h(\gamma)$ are parallel, a contradiction.

If the direction for $\gamma$ and $h\gamma$ are opposite, consider $(hgh^{-1})^{n}g^{n}$ instead of $(hgh^{-1})^{-n}g^{n}$ , and the rest is same. ∎

We quote a fact.

Proposition 2.6 (elementary closure).

Suppose $G$ acts on a $\delta$ -hyperbolic space $X$ . Let $g\in G$ be a hyperbolic element on $X$ . Assume $g$ is $D$ -WPD. Then,

(1)

$E(g)$ is virtually $\mathbb{Z}$ , and contains $\langle g\rangle$ as a finite index subgroup.
(2)

If $h\in G$ is a hyperbolic element such that $g$ and $h$ are independent, then $E(g)\cap E(h)$ is finite.

Proof.

(1) This is [DGO, Lemma 6.5].

(2) If $E(g)\cap E(h)$ is infinite, then it contains $\langle g^{N}\rangle$ for some $N>0$ . But since $g$ and $h$ are independent, for a sufficiently large $m$ , we have $g^{m}\not\in E(h)$ , impossible. ∎

Note that under the assumption of the proposition, the action of $G$ is elementary if and only if $G$ is virtually $\mathbb{Z}$ , which is equivalent to that $G=E(g)$ in this case.

In general, if a group $H$ is virtually $\mathbb{Z}$ , then there exists an exact sequence

1\to F\to H\to C\to 1,

where $C$ is either $\mathbb{Z}$ or $\mathbb{Z}_{2}*\mathbb{Z}_{2}$ , and $F$ is finite. In the case that $H$ is $E(g)$ in the above, we denote the finite group $F$ by $F(g)$ . If $C=\mathbb{Z}$ , $F(g)$ is the set of elements of finite order in $E(g)$ .

The axis $\gamma$ defines two points in the ideal boundary of $X$ , which we denote $\{\gamma(\infty),\gamma(-\infty)\}$ . $E(g)$ is exactly the set of elements that leaves this set invariant. If $h\in E(g)$ swaps those two points, we say it flips the axis since it flips the direction of the axis $\gamma$ .

If the action of $G$ on $X$ is $D$ -uniform WPD, then for any hyperbolic $g$ , we have $|F(g)|\leq 2D(100\delta)$ . Moreover, if $C=\mathbb{Z}$ , then $|F(g)|\leq D(100\delta)$ .

Note that $\langle g\rangle<E(g)$ . If the action is non-elementary, then $E(g)\not=G$ , which is equivalent to that $G$ is not virtually $\mathbb{Z}$ , so that $G$ contains two independent hyperbolic isometries.

We say a hyperbolic element $g$ is primitive if $C=\mathbb{Z}$ and each element $h\in E(g)$ is written as $h=fg^{n}$ for some $f\in F(g)$ and $n\in\mathbb{N}$ .

2.4. About the constants

From now on, there will be many constants to make the argument concrete and precise. In the argument we consider a sequence of generators $S_{n}$ . It would be a good idea to keep in mind that there are two kinds of constants.

The first kind are those that are fixed once the constants $\delta,D(100\delta),M$ are given by the action:

\delta,D(100\delta),M;T,k,m,b.

The constants $k,m$ will appear in Lemma 2.8 and $b$ in the proof of Lemma 4.2.

The second kind are those that depend on a generating set $S_{n}$ of $G$ :

L(S_{n}),\lambda(g),L(g),\lambda(u),L(S_{n}^{2MD}),\Delta_{n}.

If $L(S_{n})$ is bounded, then all of the constants in the second will be bounded, but if not, then, roughly they all diverge in the same order as $L(S_{n})$ .

We remark that if $L(S_{n})$ diverges, then one way to argue is to rescale $X$ by $\frac{1}{L(S_{n})}$ , then go to the limit, which is a tree, and use the geometry of the tree. This approach is the one taken in [FS], where only this case happens. But in our setting, the new feature is that possibly, $L(S_{n})$ is bounded. In this paper, we use a unified approach.

For convenience, we assume $\delta>0$ from now on.

2.5. Lower bound of a growth rate

Lemma 2.7 (hyperbolic element of large displacement).

Let $X$ be a $\delta$ -hyperbolic space and $S$ a finite set of isometries of $X$ . Suppose that $L(S)\geq 30\delta$ . Let $x\in X$ be such that $L(S)=L(S,x)$ . Then there is a hyperbolic element $g\in S^{2}$ such that

L(S)-8\delta\leq|x-g(x)|

and

|x-g(x)|-16\delta\leq L(g).

This is exactly same as a part of [AL, Lemma 7] (in that paper, our element $g$ is denoted as $b$ in the proof), although their setting is that $X$ is a Cayley graph of a hyperbolic group $G$ and $S\subset G$ .

The proof is same verbatim after a suitable translation of notions, so we omit it (cf. [BrF, Theorem 1.4] for somewhat similar result).

Note that if $s\in S$ then $|x-s(x)|\leq L(S)$ ; and if $s\in S^{2}$ then $L(s)\leq|x-s(x)|\leq 2L(S)$ by the definition of $L(S)$ and the choice of $x$ .

We summarize the properties of $g$ we use later:

•

$L(S)-24\delta\leq L(g)\leq 2L(S).$
•

The distance between $x$ and the $10\delta$ -axis of $g$ is at most $20\delta$ .

The second one follows from $L(g)=\min_{y\in X}|y-g(y)|\geq|x-g(x)|-16\delta$ .

Lemma 2.8 (free subgroup with primitive hyperbolic elements).

Let $X$ be a $\delta$ -hyperbolic geodesic space and $G$ a group acting on $X$ . Assume $G$ is not virtually cyclic. Let $D(\epsilon)$ be a function for WPD. Set

k=60D(200\delta),m=66k+4=3960D(200\delta)+4.

Let $S$ be a finite set that generates $G$ with $L(S)\geq 50\delta$ , and $x\in X$ with $L(S)=L(S,x)$ . Suppose $g\in S^{2}$ is a hyperbolic element with a $10\delta$ -axis $\gamma$ with $d(x,\gamma)\leq 20\delta$ such that

L(g)\geq|x-g(x)|-16\delta\geq L(S)-24\delta.

Assume that $g$ is $D$ -WPD.

Then there exists $s\in S$ such that $g^{k},sg^{k}s^{-1}$ are independent and freely generate a rank- $2$ free group $F<G$ with the following property. There is a WPD-function $D^{\prime}(\epsilon)$ with

D^{\prime}(100\delta)=D(200\delta)

such that every non-trivial element $h\in F$ is hyperbolic on $X$ and $D^{\prime}$ -WPD. Also, $h$ satisfies:

\lambda(h)\geq 10(2D(200\delta)L(g)+100\delta)\geq 10L(S).

Moreover, there is an element $u\in F$ that satisfies:

(1)

$u$ has a $10\delta$ -axis $\alpha$ with $d(x,\alpha)\leq 50\delta$ .
(2)

$u$ is primitive, namely, there exists

$1\to F(u)\to E(u)\to\mathbb{Z}\to 1$

such that any element $h\in E(u)$ is written as $h=fu^{p}$ with $f\in F(u)$ and $p\in\mathbb{Z}$ .
(3)

$|F(u)|\leq D^{\prime}(100\delta)=D(200\delta)$ .
(4)

$u\in S^{m}$ .

By $L(S)\geq 50\delta$ , we have $L(g)\geq 26\delta$ , $2L(g)\geq L(S)$ , and $2\lambda(g)\geq L(g)$ .

Remark 2.9.

In the proof of Proposition 2.10 we will apply Lemma 2.8 to $S^{MD(200\delta)}$ instead of a generating set $S$ itself. In that case, the element $s\in S^{MD(200\delta)}$ that appears in the above lemma can be chosen from $S$ itself. We choose such $s$ in the beginning of the proof of the lemma and the rest of the argument is exactly same.

Proof.

Set $\mathcal{D}=D(200\delta)$ and $T=\frac{50\delta}{\mathcal{D}}$ . Since $g$ is $D$ -WPD, by Lemma 2.2 (1), we have $\lambda(g)\geq T$ . Remember that by our assumption, we always have $D(100\delta)\leq D(200\delta)$ , so that the estimate in the lemma holds for $D(200\delta)$ as well.

Since $G$ is not virtually cyclic, there is an element $s\in S$ with $s\not\in E(g)$ . By Lemma 2.5(2), the diameter of the intersection $s(\gamma)\cap N_{50\delta}(\gamma)$ is at most

2\mathcal{D}L(g)+100\delta.

In view of this, set

k=10\left(4\mathcal{D}+\frac{100\delta}{T}\right)=60\mathcal{D}\geq 10.

Then

	$\displaystyle\lambda(g^{k})\geq k\lambda(g)$	$\displaystyle\geq 10(4\mathcal{D}\lambda(g)+100\delta)$
		$\displaystyle\geq 10(2\mathcal{D}L(g)+100\delta).$

Here, we used $2\lambda(g)\geq L(g),\lambda(g)\geq T$ .

Note that $sgs^{-1}$ is hyperbolic and $D$ -WPD with a $10\delta$ -axis $s(\gamma)$ . Since $\lambda(g^{k})$ is at least 10 times longer than the above intersection, $g^{k}$ and $sg^{k}s^{-1}$ freely generate a free group, $F$ . Also, its non-trivial elements $h$ are hyperbolic and

\lambda(h)\geq\lambda(g^{k})\geq 10(2\mathcal{D}L(g)+100\delta)\geq 10L(S).

For the last inequality, we used $2L(g)\geq L(S)$ .

We argue that there is a function $D^{\prime}(\epsilon)$ with $D^{\prime}(100\delta)=D(200\delta)$ such that every non-trivial $h\in F$ is uniformly $D^{\prime}$ -WPD. We only need to argue for $\epsilon=100\delta$ to check WPD by Lemma 2.4. Let $\gamma$ be a $10\delta$ -axis of $h$ . We will show that for any $y,z\in\gamma$ with $|y-z|\geq 3\lambda(h)$ , there are at most $D(200\delta)$ elements $j\in G$ satisfying

|j(y)-y|\leq 100\delta\text{ and }|j(z)-z|\leq 100\delta.

We denote the collection of those elements $j$ by $J$ . We will use the fact that the axis of $h$ is, roughly speaking, a concatenation of some translates of the segment $[x,g^{k}(x)]$ by elements in $F$ (cf. a more precise description of the axis of the element $u$ below.) Also, we point out that without loss of generality, one may take a conjugate of $h$ in $G$ in the argument. Since $h$ is a word on $g^{k}$ and $sg^{k}s^{-1}$ , by taking a conjugate of $h$ in $G$ , one may assume that the segment $[x,g^{k}(x)]$ is contained in the $30\delta$ -neighborhood of the segment $[y,z]$ except for some small neighborhood of $x$ and $g^{k}(x)$ . Taking a further conjugate of $h$ if necessary, one may assume that the segment $[x,g^{k/2}(x)]$ is contained in the $30\delta$ -neighborhood of $[y,z]$ . Here, we used $|y-z|\geq 3\lambda(h)$ .

That implies that one can find points $p,q\in[x,g^{k/2}(x)]$ with $|p-q|\geq\frac{k}{4}\lambda(g)=15\mathcal{D}\lambda(g)$ such that $|p-j(p)|\leq 150\delta$ and $|q-j(q)|\leq 150\delta$ if $j\in J$ .

But since $g$ is $D$ -WPD where $\mathcal{D}=D(200\delta)$ , the set $J$ contains at most $D(200\delta)$ elements. (Strictly speaking the points $p$ and $q$ are maybe not exactly on a $10\delta$ -axis of $g$ , but one can choose nearby points of $p$ and $q$ on the axis and argue.) We showed that $h$ is uniformly WPD.

Refer to caption — Figure 1. The thick line is $\bar{\alpha}$ . It is a broken geodesic from $x$ to $u(x)$ with four short “gaps”. The first gap is $[g^{k}(x),g^{k}s(x)]$ .

Now we argue for the moreover part. We define an element $u$ by

u=g^{k}(sg^{10k}s^{-1})g^{20k}(sg^{k}s^{-1})g^{k}.

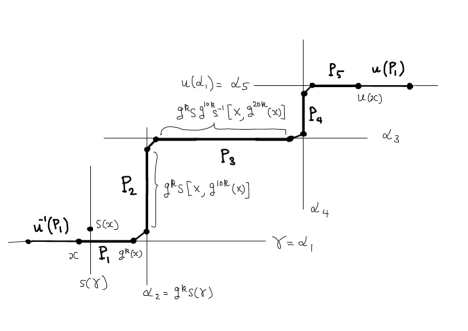
(1) To construct an axis $\alpha$ of $u$ , consider the following (see Figure 1):

	$\displaystyle[x,g^{k}(x)]\cup$	$\displaystyle g^{k}s[x,g^{10k}(x)]\cup g^{k}(sg^{10k}s^{-1})[x,g^{20k}(x)]$
	$\displaystyle\cup$	$\displaystyle g^{k}(sg^{10k}s^{-1})g^{20k}s[x,g^{k}(x)]\cup g^{k}(sg^{10k}s^{-1})g^{20k}(sg^{k}s^{-1})[x,g^{k}(x)],$

which consists of five geodesic segments, which we call pieces. We name them as $P_{1},\cdots,P_{5}$ . Their length are $U,10U,20U,U,U$ for some constant $U>0$ maybe with some error up to $100\delta$ . Remember that

U\geq\lambda(g^{k})\geq 10L(S).

Note that $P_{1}$ is contained in $\gamma$ , which is the axis of $g$ . Put $\alpha_{1}=\gamma$ . Similarly, $P_{2},\cdots,P_{5}$ are contained in the axes of the conjugates of $g$ by $g^{k}s,g^{k}(sg^{10k}s^{-1}),g^{k}(sg^{10k}s^{-1})g^{20k}s,g^{k}(sg^{10k}s^{-1})g^{20k}(sg^{k}s^{-1})$ , respectively. We will call those axes $\alpha_{2},\alpha_{3},\alpha_{4},\alpha_{5}$ .

There are four short ( $\leq L(S)$ ) gaps between $P_{i}$ and $P_{i+1}$ . We put (short) geodesics between the gaps and obtain a path, $\bar{\alpha}$ . Then take the union of the $u$ -orbit of $\bar{\alpha}$ , which we call $\hat{\alpha}$ . This is an axis for $u$ since $g$ and $sgs^{-1}$ are independent and their $10\delta$ -axes stay close ( $\leq 50\delta$ ) to each other along a short (compared to $U$ ) segment.

We call the image of a piece $P_{i}$ by $u^{p}(p\in\mathbb{Z})$ also a piece. The axis $\hat{\alpha}$ is a sequence of pieces (with short gaps in between).

By construction, $x\in\hat{\alpha}$ , but maybe $\hat{\alpha}$ is not exactly a $10\delta$ -axis for $u$ , so we take a $10\delta$ -axis, $\alpha$ . One can check that $d(x,\alpha)\leq 20\delta$ . (This is the reason we put $g^{k}$ at the end of $u$ . Without $g^{k}$ at the end, $u$ is still hyperbolic.) Also, $\hat{\alpha}$ and $\alpha$ stay close to each other in the sense that most part of each piece in $\hat{\alpha}$ , except for some short parts near the two ends, is in the $20\delta$ -neighborhood of $\alpha$ .

(2) If two axes $\beta,\beta^{\prime}$ are parallel, we write $\beta\sim\beta^{\prime}$ . Since $s\not\in E(g)$ , $\alpha_{1}\not\sim\alpha_{2}$ . Also, $\alpha_{2}\not\sim\alpha_{3}$ , $\alpha_{3}\not\sim\alpha_{4}$ , and $\alpha_{4}\not\sim\alpha_{5}$ .

We first argue that $E(u)$ maps to $\mathbb{Z}=C$ in the exact sequence after Proposition 2.6. Suppose $h\in E(u)$ . By definition, $\alpha\sim h(\alpha)$ . It suffices to show that $h$ does not flip the direction of $\alpha$ . For that, we examine the sequence of the lengths of the pieces on $\alpha$ and on $h(\alpha)$ . Here, we say that $h(P)$ is a piece if $P$ is a piece in $\alpha$ .

The sequence for the part $P_{1},\cdots,P_{5}$ is $U,10U,20U,U,U$ , so that on $\alpha$ , the sequence is (from the left to the right in Figure 2):

\cdots;U,10U,20U,U,U;\,\,U,10U,20U,U,U;\cdots

Now, if the direction of $h(\alpha)$ was opposite to $\alpha$ , then the sequence on $h(\alpha)$ would be (from the left to the right in the figure):

\cdots;U,U,20U,10U,U;\,\,U,U,20U,10U,U;\cdots

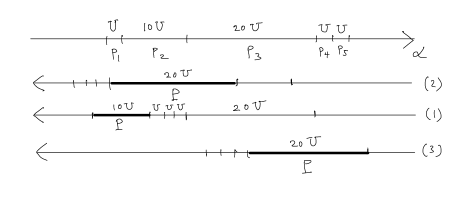
From those two sequences we observe that one of the followings must hold:

(1)

there is a piece $P$ on $h(\alpha)$ that intersects both $N_{50\delta}(P_{1})$ and $N_{50\delta}(P_{2})$ at least $\frac{U}{2}$ in diameter, or
(2)

there is a piece $P$ on $h(\alpha)$ that intersects both $N_{50\delta}(P_{2})$ and $N_{50\delta}(P_{3})$ at least $\frac{U}{2}$ in diameter, or
(3)

there is a piece $P$ on $h(\alpha)$ that intersects both $N_{50\delta}(P_{3})$ and $N_{50\delta}(P_{4})$ at least $\frac{U}{2}$ in diameter.

In the above, $P$ has length (approximately) $5U$ or $10U$ .

Let $\beta$ be the axis that contains the piece $P$ . Then, since $\frac{U}{2}$ is at least $5(2\mathcal{D}L(g)+100\delta)$ , Lemma 2.5(2) would imply that either (1) $\alpha_{1}\sim\beta\sim\alpha_{2}$ , (2) $\alpha_{2}\sim\beta\sim\alpha_{3}$ , or (3) $\alpha_{3}\sim\beta\sim\alpha_{4}$ , respectively. In either case, we obtain a contradiction since $\alpha_{1}\not\sim\alpha_{2}$ , $\alpha_{2}\not\sim\alpha_{3}$ and $\alpha_{3}\not\sim\alpha_{4}$ . We showed that $h$ does not flip $\alpha$ .

By the same reason, ie, the constrain from the combinatorics, $h(x)$ must be close to $u^{p}(x)$ for some $p\in\mathbb{Z}$ , namely, the distance is at most $2\mathcal{D}L(g)+100\delta$ . This implies that $\alpha_{1}\sim(hu^{-p})(\alpha_{1})$ and also, $\alpha_{2}\sim(hu^{-p})(\alpha_{2})$ . It then follows that

hu^{-p}\in E(g),hu^{-p}\in E(g^{n}sgs^{-1}g^{-n}),

which implies $g^{k}(hu^{-p})g^{-k}\in(E(g)\cap E(sgs^{-1}))$ . But the right hand side is a finite group, so that $hu^{-p}$ has finite order, therefore $hu^{-p}\in F(g)$ . And, of course, $hu^{-p}\in F(u)$ namely, there is $f\in F(u)$ with $h=fu^{p}$ .

(3). This is a consequence of the $D^{\prime}$ -uniform WPD, and is mentioned in the paragraphs following Proposition 2.6.

(4). Since $g\in S^{2}$ and $s\in S$ , we have $u\in S^{14k+4}$ . We are done since $m=66k+4$ . ∎

Proposition 2.10 (Lower bound of growth).

Suppose $G$ acts on a $\delta$ -hyperbolic space $X$ . Let $D(\epsilon)$ be a function for WPD. Assume that there exists a constant $M$ such that for any finite generating set $S$ of $G$ , the set $S^{M}$ contains a hyperbolic element $h$ that is $D$ -WPD.

Set

A=\frac{1}{79220M(D(200\delta))^{3}}>0.

Then for any finite generating set $S$ of $G$ , we have $e(G,S)\geq A|S|^{A}$ .

This result is a generalization of the result on hyperbolic groups by [AL]. We adapt their argument to our setting, which is straightforward.

Proof.

Set $\mathcal{D}=D(200\delta)$ . Since the element $h\in S^{M}$ is $D$ -WPD, we have $\lambda(h)\geq\frac{50\delta}{\mathcal{D}}$ by Lemma 2.2 (1). It implies that $\lambda(h^{\mathcal{D}})\geq 50\delta$ . Since $h^{\mathcal{D}}\in S^{M\mathcal{D}}$ , we have $L(S^{M\mathcal{D}})\geq 50\delta$ .

Lemma 2.7 applies to $S^{M\mathcal{D}}$ since $L(S^{M\mathcal{D}})\geq 50\delta$ . By Lemma 2.7 applied to $S^{M\mathcal{D}}$ with $x$ such that $L(S^{M\mathcal{D}})=L(S^{M\mathcal{D}},x)$ , there is $g\in S^{2M\mathcal{D}}$ such that

L(S^{M\mathcal{D}})-8\delta\leq|x-g(x)|

and the $10\delta$ -axis $\gamma$ of $g$ satisfies $d(x,\gamma)\leq 20\delta$ .

Then Lemma 2.8 applies to $S^{M\mathcal{D}}$ and $g\in S^{2M\mathcal{D}}$ . By Lemma 2.8 applied to $S^{M\mathcal{D}}$ and $g$ , there exists $s\in S^{M\mathcal{D}}$ such that $\langle g^{k},sg^{k}s^{-1}\rangle=F$ and $F$ contains $u$ that is primitive such that

|F(u)|\leq\mathcal{D};\,u\in S^{M\mathcal{D}m};\,L(u)\geq 10L(S^{M\mathcal{D}}),

where $k=60\mathcal{D},m=3960\mathcal{D}+4$ , and that $u$ is $D^{\prime}$ -WPD, where $D^{\prime}(100\delta)=D(200\delta)$ .

We note that the element $s$ can be chosen from $S$ since $G$ is not virtually cyclic. This can be easily seen in the proof of Lemma 2.8 since we only need to choose $s$ such that $s\not\in E(g)$ . See Remark 2.9.

Now, take a maximal subset $W\subset S$ such that any two distinct elements $w,v\in W$ are in different $F(u)$ -(right) cosets. Then, $|W|\geq\frac{|S|}{\mathcal{D}}$ .

Let $\alpha$ be a $10\delta$ -axis of $u$ with $d(x,\alpha)\leq 50\delta$ .
Claim 1. For distinct $v,w\in W$ , $v\alpha,w\alpha$ are not parallel. Indeed, if they were parallel, then $w^{-1}v\in E(u)$ . Moreover, we will argue $w^{-1}v\in F(u)$ , which is a contradiction since $w,v$ are in distinct $F(u)$ -cosets. The reason for $w^{-1}v\in F(u)$ is that since $w^{-1}v\in S^{2}\subset S^{M\mathcal{D}}$ , we have

L(w^{-1}v)\leq|w^{-1}v(x)-x|\leq L(S^{M\mathcal{D}}).

But on the other hand, since $u$ is primitive, if $w^{-1}v\not\in F(u)$ , then

L(w^{-1}v)\geq L(u)-100\delta\geq 6L(S^{M\mathcal{D}}).

The last inequality is from $L(u)\geq 10L(S^{M\mathcal{D}})$ . Those two estimates contradict. We showed the claim.

It implies that for distinct $v,w\in W$ , the intersection of $v\alpha$ and the $50\delta$ -neighborhood of $w\alpha$ is bounded by

2D^{\prime}(100\delta)L(u)+100\delta

by Lemma2.5 (2) since $u$ is $D^{\prime}$ -WPD. Remember that $D^{\prime}(100\delta)=D(200\delta)=\mathcal{D}$ . So, this bound is $2\mathcal{D}L(u)+100\delta$ .

Set $U=u^{20\mathcal{D}}$ . Then $U\in S^{20M\mathcal{D}^{2}m}$ and $L(U)\geq 19\mathcal{D}L(u)$ (maybe not quite $20\mathcal{D}L(u)$ ). $\alpha$ is an axis for $U$ as well. Set

B=\{wUw^{-1}|w\in W\}.

Claim 2. We have $|B|=|W|$ and $B$ freely generates a free group of rank $|W|$ .

This is because for any $w\in W$ , we have $|x-w(x)|\leq L(S^{M\mathcal{D}})$ since $W\subset S^{M\mathcal{D}}$ , which means the axis of $wUw^{-1}$ , $w\alpha$ , is close to $x$ . To be precise, close means that the distance is much smaller than $L(u)$ since $L(u)\geq 10L(S^{M\mathcal{D}})$ . Also, for the axes $w\alpha$ and $v\alpha$ of any distinct $v,w\in W$ , the intersection of one with the $50\delta$ -neighborhood of the other is $9$ times shorter than $L(U)$ since $L(U)\geq 19\mathcal{D}L(u)$ . In this setting, the usual ping-pong argument shows the claim.

Since $w\in S$ , we have $B=\{wUw^{-1}|w\in W\}\subset S^{20M\mathcal{D}^{2}m+2}$ . It follows that for any $n\in\mathbb{N}$ ,

|S^{(20M\mathcal{D}^{2}m+2)n}|\geq|B^{n}|\geq|B|^{n}=|W|^{n}\geq\frac{|S|^{n}}{\mathcal{D}^{n}}.

It implies

e(G,S)\geq\mathcal{D}^{-\frac{1}{20M\mathcal{D}^{2}m+2}}|S|^{\frac{1}{20M\mathcal{D}^{2}m+2}}.

Since

\min\left\{\mathcal{D}^{-\frac{1}{20M\mathcal{D}^{2}m+2}},\frac{1}{20M\mathcal{D}^{2}m+2}\right\}=\frac{1}{20M\mathcal{D}^{2}m+2},

which is at least $\frac{1}{79220M\mathcal{D}^{3}}$ , since $m=3960\mathcal{D}+4$ . Setting

A=\frac{1}{79220M\mathcal{D}^{3}},

we have $e(G,S)\geq A|S|^{A}$ . This is a desired conclusion since $\mathcal{D}=D(200\delta)$ . ∎

Example 2.11.

Proposition 2.10 applies to the following examples:

(1)

Non-elementary hyperbolic groups (the original case in [AL]).
(2)

The mapping class groups of a compact orientable surface $\Sigma_{g,p}$ with $3g+p\geq 4$ . See Section 5.3, where the assumptions are checked.
(3)

A lattice in a simple Lie group of rank-1. See Theorem 5.5.
(4)

The fundamental group of a complete Riemannian manifold of finite volume whose sectional curvature is pinched by two negative constants. See Theorem 5.5.

3. Well-orderedness

3.1. Main theorem

We prove the following theorem. Note that Theorem 1.1 immediately follows from this theorem combined with Lemma 2.3, since the lemma says that an acylindrical action is uniformly WPD, so that every hyperbolic element is WPD.

Theorem 3.1 (Well-orderedness for uniform WPD actions).

Suppose $G$ acts on a $\delta$ -hyperbolic space $X$ , and $G$ is not virtually cyclic. Let $D(\epsilon)$ be a function for WPD. Assume that there exists a constant $M$ such that for any finite generating set $S$ of $G$ , the set $S^{M}$ contains a hyperbolic element on $X$ that is $D$ -WPD. Assume that $G$ is equationally Noetherian. Then, $\xi(G)$ is a well-ordered set.

Proof.

We will prove that $\xi(G)$ does not contain a strictly decreasing convergent sequence. To argue by contradiction, suppose that there exists a sequence of finite generating sets $\{S_{n}\}$ , such that $\{e(G,S_{n})\}$ is a strictly decreasing sequence and $\lim_{n\to\infty}e(G,S_{n})=d$ , for some $d>1$ .

By Proposition 2.10, we may assume that the cardinality of the generating sets $|S_{n}|$ from the decreasing sequence is bounded, and by possibly passing to a subsequence we may assume that the cardinality of the generating sets is fixed, $|S_{n}|=\ell$ .

Let $S_{n}=\{x_{1}^{(n)},\cdots,x_{\ell}^{(n)}\}$ . Let $F$ be the free group of rank $\ell$ with a free generating set: $S=\{s_{1},\ldots,s_{\ell}\}$ . For each index $n$ , we define a map: $f_{n}:F\to G$ , by setting: $f_{n}(s_{i})=x_{i}^{(n)}$ . Since $S_{n}$ are generating sets, the map $f_{n}$ is an epimorphism for every $n$ . Note that $e(G,S_{n})=e(G,f_{n}(S))$ .

Since $F$ is countable, the sequence $\{f_{n}:F\to G\}$ subconverges to a surjective homomorphism $\eta:F\to L$ . $L$ is called a limit group over the group $G$ .

By assumption, $G$ is equationally Noetherian. By the general principle (Lemma 1.11), there exists an epimorphism $h_{n}:L\to G$ such that by passing to a subsequence we may assume that all the homomorphisms $\{f_{n}\}$ factor through the limit epimorphism: $\eta:F\to L$ , ie, $f_{n}=h_{n}\circ\eta$ .

Notice that since $f_{n}=h_{n}\circ\eta$ for every index $n$ , we have $e(G,f_{n}(S))\leq e(L,\eta(S))$ .

We will show the following key result:

Proposition 3.2.

Suppose $G$ satisfies the assumption in Theorem 3.1. Let $(L,\eta(S))$ be the limit group over $G$ of a sequence $f_{n}:(F,S)\to(G,f_{n}(S))$ , where $F$ is a free group with a free generating set $S$ and $f_{n}(S)$ are generating sets of $G$ . Then $\lim_{n\to\infty}e(G,f_{n}(S))=e(L,\eta(S))$ .

We postpone proving this proposition until the next section and finish the proof of the theorem.

We assumed that the sequence $\{e(G,f_{n}(S))\}$ is strictly decreasing, hence, it can not converge to an upper bound of the sequence, $e(L,\eta(S))$ . But the proposition says that it must converge to $e(L,\eta(S))$ , a contradiction. Theorem 3.1 is proved. ∎

4. Continuity of the growth rate

We prove Proposition 3.2. We already know that $e(L,\eta(S))\geq e(G,f_{n}(S))$ from the existence of the surjections $h_{n}$ , which follows from that $G$ is equationally Noetherian.

It suffices to show that given $\epsilon>0$ , for a large enough $n$ ,

\log e(L,\eta(S))-\epsilon\leq\log e(G,f_{n}(S)).

The strategy of the proof of this is same as [FS]. We note that from now on, we do not use that $G$ is equationally Noetherian in the proof.

Since the proof is long and complicated, we first informally describe the idea, which already appeared in [FS]. We want to show $e(G,f_{n}(S))$ is almost equal to $e(L,\eta(S))$ for a large enough $n$ . First of all, if we take a large enough $r$ , then $B_{r}(L,\eta(S))$ contains elements roughly as many as $e(L,\eta(S))^{r}$ by the definition. Fix such $r$ . Then if we take $n$ large enough, $B_{r}(L,\eta(S))$ and $B_{r}(G,f_{n}(S))$ are idential via the map $h_{n}$ since $L$ is a limit group. But it does not mean that $e(G,f_{n}(S))$ is almost equal to $e(L,\eta(S))$ since the growth of the balls in $(G,f_{n}(S))$ may decay if we take the radius larger. But it turns out that if we take $r$ large enough, then roughly speaking, the growth of the ball of radius $r$ in $(G,f_{n}(S))$ is almost equal to $e(G,f_{n}(S))$ . This is due to the well-known “local-to-global” principle in hyperbolic groups, and it is implemented by inserting “separators” in our argument. The threshold for the radius is given by $m$ in the proof (see Section 4.5).

We explain the idea more in detail. By the definition of the growth rate, we have for all $r$ ,

\log e(L,\eta(S))\leq\frac{1}{r}\log|B_{r}(L,\eta(S))|.

This is because the sequence $\{\log|B_{r}(L,\eta(S))|\}$ is sub-additive.

Fix $r$ (we will choose $r$ sufficiently large in the argument we will give later). Then choose $n$ large enough such that $h_{n}:B_{r}(L,\eta(S))\to B_{r}(G,f_{n}(S))$ is injective. The following map is naturally induced from $h_{n}$ for each $q\in\mathbb{N}$ :

B_{r}(L,\eta(S))^{q}\to B_{qr}(G,f_{n}(S))\subset G

by mapping $(w_{1},\cdots,w_{q})$ to $h_{n}(w_{1}\cdots w_{q})$ . If there is an $r$ such that this map is injective for all $q$ , then an easy computation would show the desired inequality for the $n$ by letting $q\to\infty$ .

But of course this map is not injective in general. For example, the concatenation of $h_{n}(w_{1}),h_{n}(w_{2}),\cdots,h_{n}(w_{q})$ may have lots of backtracks at the concatenation points. As a remedy, we insert elements $u_{i}$ of bounded length, called separators, and define a new map sending $(w_{1},\cdots,w_{q})$ to $h_{n}(w_{1}u_{1}w_{2}u_{2}\cdots w_{q}u_{q})$ . This map is denoted by $\Phi_{n}$ . The separators are constructed in Lemma 4.2. We arrange that the concatenation of elements, after we insert $h_{n}(u_{i})$ ’s, is a uniform quasi-geodesic in $G$ . This follows from that $G$ is a hyperbolic group.

But it is still not the case that the map $\Phi_{n}:B_{r}(L,\eta(S))^{q}\to B_{q(r+b)}(G,f_{n}(S))$ is injective, where $b$ is the bound of the length of the separators. What we actually show is that $\Phi_{n}$ is injective if we restrict it to the $q$ -tuples in some fixed portion of $B_{r}(L,\eta(S))$ , (see Lemma 4.8), which is enough for our purpose. This part is very technical. To argue that $\Phi_{n}$ is injective on the certain fixed portion, we use the action of $G$ on $X$ , ie, we map a tuple by $\Phi_{n}$ to $G$ , then let it act on $X$ . Then we analyze the orbit of a base point in $X$ .

4.1. Separators

We review the setting. $X$ is a $\delta$ -hyperbolic space, and $G$ acts on it. We assume $\delta\geq 1$ . For each $n$ , $S_{n}$ is a finite generating set of $G$ such that $S_{n}^{M}$ contains a hyperbolic element that is $D$ -WPD. Using the homomorphism $h_{n}:L\to G$ , we let $L$ act on $X$ . We first construct separators as elements in $G$ then pull them back to $L$ by $h_{n}$ .

Let $g\in S_{n}^{M}$ be a hyperbolic element that is $D$ -WPD. Set

\mathcal{D}=D(200\delta).

Then $\lambda(g)\geq\frac{50\delta}{\mathcal{D}}$ by Lemma 2.2(1). It implies

100\delta\leq\lambda(g^{2\mathcal{D}})\leq L(S_{n}^{2\mathcal{D}M}).

Fix $n$ . Let $y_{n}\in X$ be a point where $L(S_{n}^{2\mathcal{D}M})$ is achieved. Put

\Delta_{n}=100\delta+4\mathcal{D}L(S_{n}^{2\mathcal{D}M}).

We define a germ w.r.t. the constant $\Delta_{n}$ . Recall that given three points $x,y,z\in X$ , the Gromov product, $(y,z)_{x}$ , is defined as follows:

(y,z)_{x}=\frac{|x-y|+|x-z|-|y-z|}{2}.

Definition 4.1 (germs, equivalent and opposite germs).

Let $[x,y]$ be a (directed) geodesic segment in $X$ . Suppose that $|x-y|\geq 10\Delta_{n}$ . Then, the initial segment of $[x,y]$ of length $10\Delta_{n}$ is called the germ of $[x,y]$ at $x$ , denoted by $germ([x,y])$ . If $|x-y|<10\Delta_{n}$ , then we define the germ to be empty.

We say two non-empty germs, $[x,y],[x,z]$ , at a common point $x$ , are equivalent if $(y,z)_{x}\geq 4\Delta_{n}$ , and opposite if $(y,z)_{x}\leq 2\Delta_{n}$ .

We sometimes call the germ of $[y,x]$ at $y$ as the germ of $[x,y]$ at $y$ . If $\gamma$ is the germ of $[x,y]$ at $x$ , then for $g\in G$ , the segment $g(\gamma)$ is the germ of $[g(x),g(y)]$ at $g(x)$ . For $g\in G$ , we consider the germ of $[y_{n},g(y_{n})]$ and call it the germ of $g$ at $y_{n}$ , and write $\text{germ\,}(g)$ .

Recall from Lemma 2.8 that $k=60\mathcal{D},m=3964\mathcal{D}+4$ .

We consider germs w.r.t. $\Delta_{n}$ .

Lemma 4.2 (The constant $b$ and separators. c.f. Lemma 2.4 [FS]).

There exists a constant $b$ with the following property, where $b$ depends only on $\delta,M$ and $D(\epsilon)$ . For every $n$ , there exist primitive, hyperbolic elements $u_{1},u_{2},u_{3},u_{4}\in S_{n}^{b}$ ; and mutually opposite germs $\gamma_{1},\gamma_{2},\gamma_{3},\gamma_{4}$ of some elements in $S_{n}^{2\mathcal{D}M}$ at $y_{n}$ that satisfy:

(i)
The germs are all at $y_{n}$ in the following.
- •
  
  The germ of $[y_{n},u_{1}(y_{n})]$ is equivalent to $\gamma_{1}$ . The germ of $[y_{n},u_{1}^{-1}(y_{n})]$ is equivalent to $\gamma_{3}$ .
- •
  
  The germ of $[y_{n},u_{2}(y_{n})]$ is equivalent to $\gamma_{1}$ . The germ of $[y_{n},u_{2}^{-1}(y_{n})]$ is equivalent to $\gamma_{4}$ .
- •
  
  The germ of $[y_{n},u_{3}(y_{n})]$ is equivalent to $\gamma_{2}$ . The germ of $[y_{n},u_{3}^{-1}(y_{n})]$ is equivalent to $\gamma_{3}$ .
- •
  
  The germ of $[y_{n},u_{4}(y_{n})]$ is equivalent to $\gamma_{2}$ . The germ of $[y_{n},u_{4}^{-1}(y_{n})]$ is equivalent to $\gamma_{4}$ .
(ii)

For all $i$ ,

$\lambda(u_{i})\geq 100\Delta_{n},$

and the distance from $y_{n}$ to the $10\delta$ -axis of $u_{i}$ is at most $\Delta_{n}$ .
(iii)

For every $w\in G$ , and all $i,j$ (possibly $i=j$ ), if the $20\delta$ -neighborhood of $[y_{n},u_{i}(y_{n})]$ intersects the segment $[w(y_{n}),wu_{j}(y_{n})]$ , then the diameter of the intersection is bounded by: $\frac{1}{10}d(y_{n},u_{i}(y_{n}))$ and $\frac{1}{10}d(y_{n},u_{j}(y_{n}))$ . If $i=j$ , we assume in addition that $w\not\in F(u_{i})$ , where $F(u_{i})$ is the finite normal subgroup in $E(u_{i})$ .

Remark 4.3.

(1) Regarding Lemma 4.2 (iii), if $w\in F(u_{i})$ then the Hausdorff-distance between $[y_{n},u_{i}(y_{n})]$ and $[w(y_{n}),wu_{i}(y_{n})]$ is at most $\Delta_{n}+100\delta$ since $w$ moves any point on a $10\delta$ -axis of $u_{i}$ by at most $50\delta$ since otherwise $w$ would be hyperbolic.
(2) As we will see in the proof it suffices to take $b$ to be

(2)

b=343440M(D(200\delta))^{2}+22.

The elements $u_{i}$ are called separators and the property (iii) is called the small cancellation property of separators.

Note that we have $L(S_{n}^{2M\mathcal{D}})\geq L(S_{n})$ .

Proof.

Since $L(S_{n}^{2M\mathcal{D}})\geq 100\delta$ and $y_{n}$ is a point where $L(S_{n}^{2M\mathcal{D}})$ is achieved, by Lemma 2.7 (also see the properties at the bullets after the lemma), there is a hyperbolic element $g\in S_{n}^{4M\mathcal{D}}$ such that

2L(S_{n}^{2M\mathcal{D}})\geq L(g)\geq L(S_{n}^{2M\mathcal{D}})-24\delta\geq\frac{1}{2}L(S_{n}^{2M\mathcal{D}})

and the $10\delta$ -axis of $g$ , $\gamma$ , is at distance at most $10\delta$ from $y_{n}$ .

By Lemma 2.8 applied to $S_{n}^{2M\mathcal{D}}$ and $g$ and the $10\delta$ -axis $\gamma$ , there exists $s\in S_{n}$ (see the remark 2.9) such that $g^{k}$ and $sg^{k}s^{-1}$ are independent hyperbolic elements, which freely generate a free group $F$ whose non-trivial element, $h$ , satisfies

\lambda(h)\geq 10(2\mathcal{D}L(g)+100\delta)\geq 5\Delta_{n}.

Recall that $k=60D(200\delta)=60\mathcal{D}$ . Note that $g^{k},sg^{k}s^{-1}\in S_{n}^{4M\mathcal{D}k+2}$ . The distance from $y_{n}$ to $s\gamma$ is at most $40\delta+L(S_{n}^{2M\mathcal{D}})$ . Also, the intersection of $\gamma$ and the $50\delta$ -neighborhood of $s\gamma$ is at most $2\mathcal{D}L(g)+100\delta$ in length, which is $\leq\Delta_{n}$ , by Lemma 2.5 since $\gamma$ and $s\gamma$ are not parallel.

Consider the following four germs at $y_{n}$ w.r.t. the constant $\Delta_{n}$ :

\gamma_{1}=\text{germ\,}(g^{k}),\gamma_{2}=\text{germ\,}(sg^{k}s^{-1}),\gamma_{3}=\text{germ\,}(g^{-k}),\gamma_{4}=\text{germ\,}(sg^{-k}s^{-1}).

Note that any two of them are mutually opposite.

Then, there exist separators $u_{i}\in F$ such that $u_{i}\in S_{n}^{b}$ , where

b=1431\cdot 4\mathcal{D}Mk+22=343440\mathcal{D}^{2}M+22.

For example, set $w=g^{k},z=sg^{k}s^{-1}$ and:

	$\displaystyle u_{1}$	$\displaystyle=wzw^{2}zw^{3}z\cdots w^{19}zw^{20},$
	$\displaystyle u_{2}$	$\displaystyle=w^{21}zw^{22}z\cdots w^{39}zw^{40}z,$
	$\displaystyle u_{3}$	$\displaystyle=zw^{41}zw^{42}zw^{43}z\cdots w^{59}zw^{60},$
	$\displaystyle u_{4}$	$\displaystyle=zw^{61}zw^{62}zw^{63}z\cdots w^{79}zw^{80}z.$

We compute that they are in $S_{n}^{b}$ since $w\in S_{n}^{4\mathcal{D}Mk},z\in S_{n}^{4\mathcal{D}Mk+2}$ . It will be important that this number $b$ does not depend on $S_{n}$ . (See the proof of Proposition 3.2.)

Because of the combinatorial reason, they are primitive hyperbolic elements. The argument is similar to the one we used to showed that $u$ is primitive hyperbolic, using $\gamma$ and $s\gamma$ are not parallel, in the proof of Lemma 2.8(2). We omit it.

(i) By definition of $u_{i}$ ,

\text{germ\,}[y_{n},u_{1}(y_{n})]=\text{germ\,}[y_{n},u_{2}(y_{n})]=\text{germ\,}(w)=\gamma_{1};

\text{germ\,}[y_{n},u_{3}(y_{n})]=\text{germ\,}[y_{n},u_{4}(y_{n})]=\text{germ\,}(z)=\gamma_{2};

u_{1}^{-1}\text{germ\,}[u_{1}(y_{n}),y_{n}]=u_{3}^{-1}\text{germ\,}[u_{3}(y_{n}),y_{n}]=\gamma_{3};

u_{2}^{-1}\text{germ\,}[u_{2}(y_{n}),y_{n}]=u_{4}^{-1}\text{germ\,}[u_{4}(y_{n}),y_{n}]=\gamma_{4}.

Here, we mean that the four germs in each line are same or equivalent to each other.

(ii). The estimate for $\lambda(u_{i})$ is straightforward from the definitions of $u_{i}$ . The claim on the axes are also shown similarly to the case of $u$ in Lemma 2.8(1) and we omit it. We remark that the distance estimate on the axes differ since it comes from the fact that some of the separators start or end in $w$ , so that distance becomes larger.

(iii) follows from the definition of $u_{i}$ , namely, the combinatorial structure of the words. The argument is similar to show that $u$ in Lemma 2.8 is primitive (Lemma 2.8(2)), so we will be brief. Suppose $i\not=j$ , and the intersection was longer. Then, because of the combinatorial structure of the words $u_{i}$ and $u_{j}$ , it follows the axes $\gamma$ and $s\gamma$ would be parallel, by Lemma 2.5, which is impossible. We are done. Suppose $i=j$ , and the intersection was longer. Then since $w\not\in F(u_{i})$ , by the same reason, $\gamma$ and $s\gamma$ would be parallel, a contradiction. So we are done in this case too. ∎

Remember $u_{i}\in G$ depend on the index $n$ of $S_{n}$ , so let’s write them as $u_{i}(n)$ . Now, since $h_{n}$ is surjective, let $\hat{u}_{i}(n)\in L$ be an element with $h_{n}(\hat{u}_{i}(n))=u_{i}(n)$ . Note that the word length of $\hat{u}_{i}(n)$ in terms of $\eta(S)$ is also bounded by $b$ . The elements $\hat{u}_{i}(n)\in L$ are also called the separators for $h_{n}$ .

In the following we may just write $u$ (instead of $\hat{u}$ ) to denote a separator for $h_{n}$ to simplify the notation. We note that $|F(h_{n}(u))|\leq\mathcal{D}$ for any separator $u$ for any $h_{n}$ since $h_{n}(u)$ is primitive (see the comment after Proposition 2.6).

4.2. Forbidden elements

Given $m$ , choose and fix $n$ large enough such that the map $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ . This is possible since this set is finite in the limit group $L$ . Remember

\Delta_{n}=100\delta+4\mathcal{D}L(S_{n}^{2\mathcal{D}M}).

Given $w\in B_{m}(L,\eta(S))$ we choose one of the separators, $u\in L$ , for $h_{n}$ s.t. the germ of $[y_{n},h_{n}(w)(y_{n})]$ at $h_{n}(w)(y_{n})$ and the germ of $[h_{n}(w)(y_{n}),h_{n}(wu)(y_{n})]$ at $h_{n}(w)(y_{n})$ are opposite. (Geometrically, it implies that the concatenation $[y_{n},h_{n}(w)(y_{n})]\cup[h_{n}(w)(y_{n}),h_{n}(wu)(y_{n})]$ is almost a geodesic.) Such a separator $u$ exists by the property (i) in Lemma 4.2. Here, if $|y_{n}-h_{n}(w)(y_{n})|<10\Delta_{n}$ , then we choose any separator $u$ . We say $u$ is admissible for $w$ . Note that

|y_{n}-h_{n}(wu)(y_{n})|\geq|y_{n}-h_{n}(w)(y_{n})|+|h_{n}(w)(y_{n})-h_{n}(wu)(y_{n})|-4\Delta_{n}.

Also, the Hausdorff distance between $[y_{n},h_{n}(wu)(y_{n})]$ and $[y_{n},h_{n}(w)(y_{n})]\cup[h_{n}(w)(y_{n}),h_{n}(wu)(y_{n})]$ is at most $2\Delta_{n}+10\delta$ .

Moreover, given $w,w^{\prime}\in B_{m}$ then we can choose a separator $u$ such that $u$ is admissible for $w$ and $u^{-1}$ is admissible for $w^{\prime-1}$ . We say $u$ is admissible for $w,w^{\prime}$ . Note that

	$\displaystyle\|y_{n}-h_{n}(wuw^{\prime})(y_{n})\|\geq$	$\displaystyle\|y_{n}-h_{n}(w)(y_{n})\|+\|h_{n}(w)(y_{n})-h_{n}(wu)(y_{n})\|$
		$\displaystyle+\|h_{n}(wu)(y_{n})-h_{n}(wuw^{\prime})(y_{n})\|-8\Delta_{n}.$

As before, the Hausdorff distance between $[y_{n},h_{n}(wuw^{\prime})(y_{n})]$ and $[y_{n},h_{n}(w)(y_{n})]\cup[h_{n}(w)(y_{n}),h_{n}(wu)(y_{n})]\cup[h_{n}(wu)(y_{n}),h_{n}(wuw^{\prime})(y_{n})]$ is at most $2\Delta_{n}+10\delta$ .

For $q>0$ , we define a map

\Phi_{n}:B_{m}(L,\eta(S))^{q}\to B_{q(m+b)}(G,f_{n}(S))\subset G

by sending $(w_{1},\cdots,w_{q})$ to $h_{n}(w_{1}u_{1}\cdots w_{q}u_{q})$ , where $u_{i}\in L$ are separators we choose that are admissible for $w_{i},w_{i+1}$ for $h_{n}$ . Remember that $u_{i}\in B_{b}(L,\eta(S))$ .

It is easy to show that $\Phi_{n}$ maps an element $\not=(1,\cdots,1)$ to a non-trivial element in $G$ using the property of the separators, but what we need is more. We will argue that on a large portion, called the set of “feasible elements”, $\Phi_{n}$ is injective by showing the image of the base point $y_{n}\in X$ by those elements are all distinct.

For the given $m$ , we will define forbidden elements in $B_{m}(L,\eta(S))$ , which depend on $n$ . We are assuming that $n$ is large enough so that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ .

Definition 4.4 (forbidden elements and tails).

Given $w\in B_{m}(L,\eta(S))$ , if there exist $w^{\prime}\in B_{m}(L,\eta(S))$ and a separator $u(n)$ which is admissible for $w$ such that

(3)

|h_{n}(w^{\prime})(y_{n})-h_{n}(wu(n))(y_{n})|\leq\frac{1}{5}|y_{n}-h_{n}(u(n))(y_{n})|

then we say $w$ is forbidden w.r.t. $n$ (or in terms of $h_{n})$ . We call the segment $[h_{n}(w)(y_{n}),h_{n}(wu(n))(y_{n})]$ a tail of $w$ . The tail depends on the choice of $u$ , so if we want to specify it, we say the tail of the pair $(w,u)$ .

Let $w_{1},w_{2}$ be two (forbidden) elements and $u_{1},u_{2}$ admissible separators , respectively. If $u_{1}=u_{2}$ and $h_{n}(w_{1}^{-1}w_{2})\in F(h_{n}(u_{1}))$ , then the Hausdorff-distance between the two tails $[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u)(y_{n})]$ and $[h_{n}(w_{2})(y_{n}),h_{n}(w_{2}u)(y_{n})]$ is at most $\Delta_{n}+100\delta$ . This is an immediate consequence of Remark 4.3. In this case, we say that the tails of $(w_{1},u_{1})$ and $(w_{2},u_{2})$ are parallel.

On the other hand, if two tails $(w_{1},u_{1})$ and $(w_{2},u_{2})$ are not parallel, then the intersection of one of the tails with the $20\delta$ -neighborhood of the other tail is bounded by the $\frac{1}{10}$ of the length of each tail. This is by the small cancellation property of the separators (Lemma 4.2 (iii)),

We record one immediate consequence we use later.

Lemma 4.5 (Parallel tails).

Assume that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ . Suppose $w\in B_{m}(L,\eta(S))$ is forbidden w.r.t. $n$ , and $u$ is a separator admissible for $w$ . Then there are at most $\mathcal{D}$ possibilities for $w_{1}\in B_{m}$ , including $w=w_{1}$ , such that $w_{1}$ is forbidden, $u$ is admissible for $w_{1}$ , and the tails for $(w,u)$ and $(w_{1},u)$ are parallel.

Proof.

Since the two tails are parallel, we have $h_{n}(w_{1}^{-1}w)\in F(h_{n}(u))$ by the definition that two tails are parallel. Recall that (see the paragraphs after Proposition 2.6.)

|F(h_{n}(u))|\leq\mathcal{D}

for all separators $u$ since $u$ is primitive. Therefore, we have at most $\mathcal{D}$ possibilities for $h_{n}(w_{1}^{-1}w)$ . But since $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ , we have at most $\mathcal{D}$ possibilities for $w_{1}^{-1}w\in B_{2m}(L,\eta(S))$ , and we are done. ∎

4.3. Ratio of forbidden elements

The proof of the following lemma occupies this subsection.

Lemma 4.6.

Assume that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ . Consider the forbidden/non-forbidden elements in $B_{m}(L,\eta(S))$ w.r.t. $n$ . Then

|\{\text{the forbidden elements}\}|\leq\mathcal{D}|\{\text{the non-forbidden elements}\}|.

We denote $B_{m}(L,\eta(S))$ as $B_{m}$ . The strategy of the proof is to show that if $w\in B_{m}$ is forbidden, it will force some other elements in $B_{m}$ to be non-forbidden.

Proof.

The proof has three parts.
Part I. We first construct a subset $C(w)$ in $B_{m}$ and a tree like graph $T(w)$ in $X$ . The construction is inductive. In each step, a subset and a tree like graph grows, which will end in finite steps.

Suppose $w\in B_{m}$ is forbidden. We explain the inductive steps to construct $C(w)$ and $T(w)$ .
Step 0. Set $C_{0}(w)=w$ and $T_{0}(w)=[y_{n},h_{n}(w)(y_{n})]$ .
Step 1. Since $w$ is forbidden, there exist $w^{\prime}\in B_{m}$ and a separator $u$ that is admissible for $w$ that satisfy (3). Let $w^{\prime}=s_{1}\cdots s_{r},s_{i}\in\eta(S),r\leq m$ be a shortest representative w.r.t. the word metric by $\eta(S)$ . Then this defines a sequence of points in $X$ , which we call a path, $\gamma$ , from $y_{n}$ to $h_{n}(w^{\prime})(y_{n})$ as follows:

y_{n},h_{n}(s_{1})(y_{n}),h_{n}(s_{1}s_{2})(y_{n}),\cdots,h_{n}(s_{1}\cdots s_{r})(y_{n}).

The distance between any two adjacent points on $\gamma$ is at most $L(S_{n}^{2MD})$ since it is achieved at $y_{n}$ and $h_{n}(s_{i})\in S_{n}\subset S_{n}^{2MD}$ .

Consider the nearest point projection, denoted by $\pi$ , from a point $x\in\gamma$ to the tail $[h_{n}(w)(y_{n}),h_{n}(wu)(y_{n})]$ . The nearest points may not be unique, but we choose one for $\pi(x)$ . Then the distance between the projection of any two adjacent points on $\gamma$ is $\leq L(S_{n}^{2MD})+100\delta\leq\frac{\Delta_{n}}{4}$ . Note that $|\pi(y_{n})-h_{n}(w)(y_{n})|\leq 2\Delta_{n}+150\delta$ since $u$ is admissible for $w$ . Also, $|\pi(h_{n}(w^{\prime})(y_{n}))-h_{n}(wu)(y_{n})|\leq\frac{1}{5}|h_{n}(w)(y_{n})-h_{n}(wu)(y_{n})|+10\delta$ by (3).

By Lemma 4.2 (ii), the length of a tail is at least $100\Delta_{n}$ . Let $P,Q$ be the two points on the tail that trisect the tail into three pieces of equal length, where $P$ is closer to $h_{n}(w)(y_{n})$ than $Q$ is. Each of the three pieces has lengh at least $33\Delta_{n}$ . Let $h_{n}(s_{1}\cdots s_{p})(y_{n})$ be a point on $\gamma$ whose projection is closest to $P$ , and $h_{n}(s_{1}\cdots s_{q})(y_{n})$ a point whose projection is closest to $Q$ . Then

|\pi(h_{n}(s_{1}\cdots s_{p})(y_{n}))-P|\leq L(S_{n}^{2MD})\leq\frac{\Delta_{n}}{4},

|\pi(h_{n}(s_{1}\cdots s_{q})(y_{n}))-Q|\leq L(S_{n}^{2MD})\leq\frac{\Delta_{n}}{4}.

We denote $s_{1}\cdots s_{p},s_{1}\cdots s_{q}\in B_{m}$ as $w_{0},w_{1}$ and call them the candidates for non-forbidden elements obtained from $w$ . They depend on $u,w^{\prime}$ too. See Figure 3.

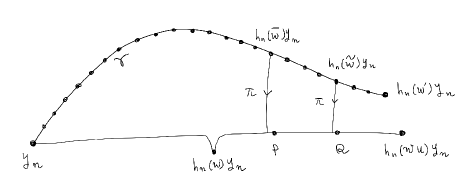
Consider the union of the three segements as follows:

	$\displaystyle\Pi(w)=[h_{n}(w)(y_{n}),h_{n}(wu)(y_{n})]$	$\displaystyle\cup[h_{n}(w_{0})(y_{n}),\pi(h_{n}(w_{0})(y_{n}))]$
		$\displaystyle\cup[h_{n}(w_{1})(y_{n}),\pi(h_{n}(w_{1})(y_{n}))].$

This depends not only $w$ , but also $u,w^{\prime}$ . $\Pi(w)$ is a tree embedded in $X$ . We call $\pi(h_{n}(w_{0})(y_{n}))$ and $\pi(h_{n}(w_{1})(y_{n}))$ the branch points of $\Pi(w)$ , and $P,Q$ the trisecting points of (the tail of) $\Pi(w)$ . This union is a disjoint union except for the two branch points. The distance betwee the branch points is at least $32\Delta_{n}$ . This in particular implies that $w_{0}\not=w_{1}$ .

We set $C_{1}(w)=\{w,w_{0},w_{1}\}\subset B_{m}$ , and $T_{1}(w)=[y_{n},h_{n}(w)(y_{n})]\cup\Pi(w)$ . If both $w_{0},w_{1}$ are non-forbidden, this is the end of the construction, and put $C(w)=C_{1}(w),T(w)=T_{1}(w)$ . Otherwise we go to the second step.

$T_{1}(w)$ is a tree like graph in the sense that it is the union of two trees, $[y_{n},h_{n}(w)(y_{n})]$ and $\Pi(w)$ attached at the point $h_{n}(w)(y_{n})$ , and the intersection is contained in the $(2\Delta_{n}+100\delta)$ -neighborhood of this point since $u$ is admissible for $w$ .

Step 2. By assumption, at least one of $w_{0}$ and $w_{1}$ is forbidden. For example, assume that $w_{1}$ is forbidden. Then $w_{1}$ has a separator $u_{1}$ admissible for $w_{1}$ , and an element $w_{1}^{\prime}\in B_{m}$ that satisfy (3). Let $\pi_{1}$ denote the nearest point projection to the tail $[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u_{1})(y_{n})]$ .

Then as in the first step, there is a path (a sequence of points obtained from a shortest expression of $w_{1}^{\prime}$ in $\eta(S)$ ) between $y_{n}$ and $h_{n}(w_{1}^{\prime})(y_{n})$ in $X$ , from which we obtain two elements, $w_{10},w_{11}\in B_{m}$ , using the projection $\pi_{1}$ from the path to the tail $[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u_{1})(y_{n})]$ . Also, we obtain a tree embedded in $X$ :

	$\displaystyle\Pi(w_{1})=[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u_{1})(y_{n})]$	$\displaystyle\cup[h_{n}(w_{10})(y_{n}),\pi(h_{n}(w_{10})(y_{n}))]$
		$\displaystyle\cup[h_{n}(w_{11})(y_{n}),\pi(h_{n}(w_{11})(y_{n}))].$

We point out that $([y_{n},h_{n}(w)(y_{n})]\cup\Pi(w))\cap N_{10\delta}(\Pi(w_{1}))$ is contained in the $(2\Delta_{n}+100\delta)$ -neighborhood of $h_{n}(w_{1})(y_{n})$ . The reason is because $u$ is admissible to $w$ , and $u_{1}$ is admissible to $w_{1}$ , while the tails of $(w,u)$ and $(w_{1},u_{1})$ are both at least $100\Delta_{n}$ long.

Also, the trisecting points $P_{1},Q_{1}$ and the branch points on the tail $[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u_{1})(y_{n})]$ are out of the $10\Delta_{n}$ -neighborhood of the tail $[h_{n}(w)(y_{n}),h_{n}(wu)(y_{n})]$ .

It follows that $w,w_{1},w_{10},w_{11}$ are distinct elements in $B_{m}$ . If $w_{0}$ is not forbidden, then we put $C_{2}(w)=C_{1}(w)\cup\{w_{10},w_{11}\}$ and

T_{2}(w)=T_{1}(w)\cup\Pi(w_{1}).

If $w_{0}$ is forbidden, then we do the same construction as we did to $w_{1}$ and obtain two candidates: $w_{00},w_{01}\in B_{m}$ , and a tree $\Pi(w_{0})$ which intersects the previously obtained treelike graph $[y_{n},h_{n}(w)(y_{n})]\cup\Pi(w)\cup\Pi(w_{1})$ only in the $(2\Delta_{n}+100\delta)$ -neighborhood of $h_{n}(w_{0})(y_{n})$ . In particular, $w,w_{0},w_{00},w_{01},w_{1},w_{10},w_{11}$ (if they exist) are all distinct. See Figure 4

We set $C_{2}(w)=C_{1}(w)\cup\{w_{00},w_{01},w_{10},w_{11}\}$ and

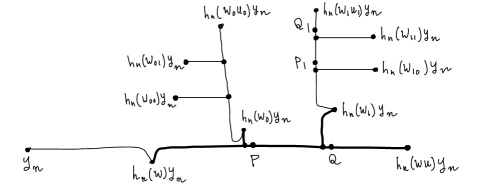
T_{2}(w)=T_{1}(w)\cup\Pi(w_{0})\cup\Pi(w_{1}).

If all of the elements $w_{00},w_{01}$ and also $w_{10},w_{11}\in B_{m}$ (if they exist) are non-forbidden, we stop here and set $C(w)=C_{2}(w),T(w)=T_{2}(w)$ , otherwise we go to the third step.

In the third step, we do the same construction to the forbidden elements among $w_{00},w_{01},w_{10},w_{11}\in B_{m}$ For example, if $w_{00}$ is forbidden, then we obtain two elements $w_{000},w_{001}$ and a tree $\Pi(w_{00})$ . This tree intersects the tree like graph $T_{2}(w)$ in the $(2\Delta_{n}+100\delta)$ -neighborhood of $h_{n}(w_{00})(y_{n})$ . We define $C_{3}(w)$ from $C_{2}(w)$ by adding a pair of elements that are obtained from each forbidden element $w_{**}$ in this step. Also, we define $T_{3}(w)$ be adding the trees $\Pi(w_{**})$ for forbidden elements $w_{**}$ .

We formally describe the $(N+1)$ -th step. In the $N$ -step, we have $C_{N}(w),T_{N}(w)$ . If all of the elements in $C_{N}(w)\backslash C_{N-1}$ are non-forbidden, then we stop and put $C(w)=C_{N}(w),T(w)=T_{N}(w)$ . Otherwise, we go to the $(N+1)$ -th step.

$(N+1)$ -th step. By assumption, at least one element in $C_{N}(w)\backslash C_{N-1}$ , $w_{i_{1}\cdots i_{N}}$ , is forbidden. Then we do the same construction as in the step 1, and obtain the tree $\Pi(w_{i_{1}\cdots i_{N}})$ ; two elements, $w_{i_{1}\cdots i_{N}0}$ and $w_{i_{1}\cdots i_{N}1}$ . We add those two elements to $C_{N}(w)$ , and also add $\Pi(w_{i_{1}\cdots i_{N}})$ to $T_{N}(w)$ . We do this all forbidden elements in $C_{N}(w)\backslash C_{N-1}(w)$ , and get $C_{N+1}(w)$ and $T_{N+1}(w)$ . Note that the trees $\Pi(w_{I})$ we added in this step are disjoint from each other, moreover, the distance between two $\Pi(w_{I}),\Pi(w_{I^{\prime}}$ with $I\not=I^{\prime}$ is at least $30\Delta_{n}$ , where $I,I^{\prime}$ are multi-subscripts of length $N$ .

Since $C_{n}(w)\subset B_{m}$ for all $n$ , and the set $C_{n}(w)$ gets bigger at least by two as $n$ increases by one, so the process must end in finite steps since $B_{m}$ is finite. At the end of the process, we have a set $C(w)$ in $B_{m}$ , and a tree like graph $T(w)$ . We remark that $C(w),T(w)$ depend on the choice of separators in the construction, but it is not important.

No that by construction, in $C(w)$ , we have

|\{\text{forbidden elements}\}|+1=|\{\text{non-forbidden elements}\}|.

Also, the orbit of $y_{n}$ by the elements in $C(w)$ appears as vertices of $T(w)$ .

Part II. Let $w_{1},w_{2}\in B_{m}$ be two forbidden elements, and we analyze how the sets $C(w_{1})$ and $C(w_{2})$ are related. In the construction of $C(w)$ , for each forbidden element, $v$ , we chose a separator $u$ and an element $v^{\prime}\in B_{m}$ . The pair $(v,u)$ defines the tail $[h_{n}(v)(y_{n}),h_{n}(vu)(y_{n})]$ , which is an arc of $T(w)$ .

Claim. Let $w_{1},w_{2}\in B_{m}$ be forbidden elements and $u_{2}$ the separator we chose for $w_{2}$ to construct $T(w_{2}),C(w_{2})$ . Assume that the tail $\tau=(w_{2},u_{2})$ is not parallel to any of $(v,u)$ that appears to construct $T(w_{1}),C(w_{1})$ . Then, $C(w_{1})\cap C(w_{2})$ is empty or $\{w_{2}\}$ .

Let $P,Q\in\tau$ be the trisecting points of $\Pi(w_{2})$ . Then neither of them is in the $10\Delta_{n}$ -neighborhood of any trisecting point that appears in $T(w_{1})$ . Indeed, suppose it was, and let $R$ be a trisecting point of the tail, $\sigma$ , in $T(w_{1})$ such that $|P-R|$ or $|Q-R|$ is $\leq 10\Delta_{n}$ . Then, since $T(w_{1}),T(w_{2})$ have $y_{n}$ as the common “root” vertex that they start from, the intersection of $\sigma$ and the $20\delta$ -neighborhood of $\tau$ is at least $\frac{1}{5}$ of $\sigma$ , which contradicts the small cancellation property.

This implies that not only the branch points on $\tau$ , but also all branch points of $T(w_{2})$ are outside of the $9\Delta_{n}$ -neighborhood of $T(w_{1})$ . This is because both $T(w_{1}),T(w_{2})$ are tree like graphs. It then follows that $C(w_{1})\cap C(w_{2})$ is empty or just $w_{2}$ because all other points in $C(w_{2})$ appear on $T(w_{2})$ after the first two branch points on $\tau$ , that are close to $P,Q$ . We showed the claim.

Part III. It follows from the claim that there is a finite collection of forbidden elements $w$ in $B_{m}$ such that the $C(w)$ ’s are mutually disjoint, and that any forbidden element $v\in B_{m}$ is either contained in the union of those $C(w)$ ’s, or $v$ has an admissible separator $u$ such that the pair (tail) $(v,u)$ is parallel to one of the tails that appears in one of the $C(w)$ ’s.

To see that, order the forbidden elements in $B_{m}$ as $w_{1},w_{2},\cdots$ . Choose admissible separators $u_{1},u_{2},\cdots$ . First, construct $C(w_{1})$ using the separators we chose. Next, if $w_{2}$ is already contained in $C(w_{1})$ , then disregard it. Also, if $(w_{2},u_{2})$ is parallel to one of the tails in $T(w_{1})$ , then disregard $w_{2}$ also. Otherwise, construct $C(w_{2})$ and keep it. If $w_{3}$ is contained in $C(w_{1})$ or $C(w_{2})$ ; or $(w_{3},u_{3})$ is parallel to one of the tails of $T(w_{1})$ or $T(w_{2})$ , then disregard $w_{3}$ . Otherwise, construct $C(w_{3})$ and keep it, and so on. By the claim we have shown, those $C(w)$ ’s are mutually disjoint such that for any forbidden element $v\in B_{m}$ , either $v$ is contained in one of the $C(w)$ ’s we have, or $(v,u)$ is parallel to one of the tails of the $T(w)$ ’s.

To finish the proof, by Lemma 4.5, the union of those $C(w)$ ’s contains at least $\frac{1}{\mathcal{D}}$ of the forbidden elements in $B_{m}$ . But since in each $C(w)$ , there are more non-forbidden elements than forbidden elements (by one), we conclude that in $B_{m}$ ,

|\{\text{forbidden elements}\}|\leq\mathcal{D}|\{\text{non-forbidden elements}\}|.

Lemma 4.6 is proved. ∎

4.4. Feasible elements

By the lemma 4.6, at least $\frac{1}{\mathcal{D}+1}$ of $B_{m}(L,\eta(S))$ consists of non-forbidden elements.

Now, we choose a maximal subset in the set of non-forbidden elements in $B_{m}(L,\eta(S))$ such that for any two distinct elements $w,w^{\prime}$ in the set, $h_{n}(w),h_{n}(w^{\prime})$ are not in the same coset w.r.t. $F(h_{n}(u_{i}))$ for any separator $u_{i}$ . We call an element in this set an adequate element. Then, in $B_{m}(L,\eta(S))$ ,

\frac{|\{\text{non-forbidden elements}\}|}{\mathcal{D}^{4}}\leq|\{\text{adequate elements}\}|.

This is because there are only four separators, $u$ , and $|F(h_{n}(u))|\leq\mathcal{D}$ for each $u$ . Combining this with Lemma 4.6 we get:

(4)

\frac{|B_{m}(L,\eta(S))|}{\mathcal{D}^{4}(\mathcal{D}+1)}\leq|\{\text{adequate elements in }B_{m}(L,\eta(S))\}|.

Definition 4.7 (feasible elements).

Fix $m$ , then $n$ . An element of the form $w_{1}u_{1}\cdots w_{q}u_{q}$ with $w_{i}\in B_{m}(L,\eta(S))$ are called feasible of type $q$ if all $w_{i}$ are adequate and each $u_{i}$ is admissible for $w_{i},w_{i+1}$ . We define $q=0$ for the empty element.

For this feasible elements, we consider the following broken geodesic:

	$\displaystyle\alpha$	$\displaystyle=[y_{n},h_{n}(w_{1})(y_{n})]\cup[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u_{1})(y_{n})]\cup\cdots$
		$\displaystyle\cup[h_{n}(w_{1}u_{1}\cdots w_{q})(y_{n}),h_{n}(w_{1}u_{1}\cdots w_{q}u_{q})(y_{n})].$

The Hausdorff-distance between $\alpha$ and the geodesic $[y_{n},h_{n}(w_{1}u_{1}\cdots w_{q}u_{q})(y_{n})]$ is at most $2\Delta_{n}+100\delta$ .

Lemma 4.8 (cf. [FS],Lemma 2.6).

For every $q$ , the map $\Phi_{n}$ is injective on the set of $q$ -tuples of adequate elements in $B_{m}(L,\eta(S))$ .

By definition, given a $q$ -tuples of adequate elements, we choose admissible separators (they are not unique) and form a feasible element of type $q$ , then map it by $\Phi_{n}$ .

Proof.

We argue by induction on the type $q$ . If $q=0$ then nothing to prove since the element is empty.

Assume the conclusion holds for $q\geq 0$ . Suppose $(q+1)$ -tuples of adequate elements $w_{1},w_{2},\cdots,w_{q+1}$ and $w_{1}^{\prime},w_{2}^{\prime},\cdots,w_{q+1}^{\prime}$ are given. Let $W=w_{1}u_{1}w_{2}u_{2}\cdots w_{q+1}u_{q+1}$ and $W^{\prime}=w_{1}^{\prime}u_{1}^{\prime}w_{2}^{\prime}u_{2}^{\prime}\cdots w_{q+1}^{\prime}u_{q+1}^{\prime}$ be two feasible elements of type $q+1$ . We assume that $h_{n}(W)=h_{n}(W^{\prime})$ and want to show $w_{i}=w_{i}^{\prime}$ for all $i$ .

The elements $W,W^{\prime}$ define two broken geodesics $\alpha,\alpha^{\prime}$ between $y_{n}$ and $h_{n}(W)(y_{n})=h_{n}(W^{\prime})(y_{n})$ . Look at the initial parts of $\alpha,\alpha^{\prime}$ : $[y_{n},h_{n}(w_{1})(y_{n})]\cup[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u_{1})(y_{n})]$ and $[y_{n},h_{n}(w_{1}^{\prime})(y_{n})]\cup[h_{n}(w_{1}^{\prime})(y_{n}),h_{n}(w_{1}^{\prime}u_{1}^{\prime})(y_{n})]$ . We first show that $u_{1}=u_{1}^{\prime}$ . Suppose not. Then it would imply that either $w_{1}$ or $w_{1}^{\prime}$ is forbidden. We explain the reason. First, by the small cancellation property of the separators (Lemma 4.2 (iii)), either $[y_{n},h_{n}(w_{1})(y_{n})]\cup[h_{n}(w_{1})(y_{n}),h_{n}(w_{1}u_{1})(y_{n})]$ is contained in the $10\Delta_{n}$ -neighborhood of $[y_{n},h_{n}(w_{1}^{\prime})(y_{n})]$ , or $[y_{n},h_{n}(w_{1}^{\prime})(y_{n})]\cup[h_{n}(w_{1}^{\prime})(y_{n}),h_{n}(w_{1}^{\prime}u_{1}^{\prime})(y_{n})]$ is contained in the $10\Delta_{n}$ -neighborhood of $[y_{n},h_{n}(w_{1})(y_{n})]$ , since $u_{1}$ is admissible for $w_{1}$ and $u_{1}^{\prime}$ is admissible for $w_{1}^{\prime}$ . Suppose we are in the first case. Then $w_{1}$ would be forbidden since there is a subword of $w_{1}^{\prime}$ , denoted by $\overline{w_{1}^{\prime}}$ , such that

|h_{n}(\overline{w_{1}^{\prime}})(y_{n})-h_{n}(w_{1}u_{1})(y_{n})|\leq\frac{1}{5}|h_{n}(w_{1})(y_{n})-h_{n}(w_{1}u_{1})(y_{n})|.

Such a subword exists because $L(S_{n})\leq\frac{\Delta_{n}}{4}$ and $|h_{n}(w_{1})(y_{n})-h_{n}(w_{1}u_{1})(y_{n})|\geq 100\Delta_{n}$ . We got a contradiction since $w_{1}$ is not forbidden. Similarly, if we are in the second case, then $w_{1}^{\prime}$ would be forbidden, which is a contradiction. We showed that $u_{1}=u_{1}^{\prime}$ .

Next we show $w_{1}=w_{1}^{\prime}$ . We first show that $h_{n}(w_{1}w_{1}^{\prime-1})\in F(h_{n}(u_{1}))$ . Suppose not. Then, as in the previous paragraph, the small cancellation property of the separators implies that either $w_{1}$ or $w_{1}^{\prime}$ is forbidden, a contradiction. We are left with the case that $h_{n}(w_{1}w_{1}^{\prime-1})\in F(h_{n}(u_{1}))$ . But, this means that $h_{n}(w_{1})$ and $h_{n}(w_{1}^{\prime})$ are in the same (right) coset w.r.t. $F(h_{n}(u_{1}))$ . Since both $w_{1}$ and $w_{1}^{\prime}$ are adequate, it implies $w_{1}=w_{1}^{\prime}$ .

Since $u_{1}=u_{1}^{\prime},w_{1}=w_{1}^{\prime}$ , it follows that $W_{1}=w_{2}u_{2}\cdots w_{q+1}u_{q+1}$ and $W_{1}^{\prime}=w_{2}^{\prime}u_{2}^{\prime}\cdots w_{q+1}^{\prime}u_{q+1}^{\prime}$ are feasible elements of type $q$ with $h_{n}(W_{1})=h_{n}(W_{1}^{\prime})$ . By the induction hypothesis, we have $w_{i}=w_{i}^{\prime}$ for all $i\geq 2$ , and we are done. ∎

4.5. Proof of Proposition 3.2

We prove Proposition 3.2.

Proof.

Recall that $D(\epsilon)$ is the WPD function and we set $\mathcal{D}=D(100\delta)$ . Recall that for every $m$ , we have

\frac{1}{m}\log(|B_{m}(L,\eta(S))|\geq\log e(L,\eta(S)).

Given $\epsilon>0$ , choose and fix a large enough $m$ such that

\frac{1}{m+b}\left(\log|B_{m}(L,\eta(S))|-\log(D^{4}(D+1)\right)\geq\frac{1}{m}\log|B_{m}(L,\eta(S))|-\epsilon.

The constant $b$ is from Lemma 4.2. Such $m$ exists since $\lim_{m\to\infty}\frac{\log|B_{m}(L,\eta(S))|}{m}=\log e(L,\eta(S))$ , and $b$ does not depend on $n,m$ . (We will choose $n$ right after this.)

Choose $n$ large enough such that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ , which defines the forbidden elements in $B_{m}(L,\eta(S))$ . Then for all $q$ :

|B_{q(m+b)}(G,f_{n}(S))|\geq\left(\frac{|B_{m}(L,\eta(S))|}{\mathcal{D}^{4}(\mathcal{D}+1)}\right)^{q}

because the number of adequate elements in $B_{m}(L,\eta(S))$ is at least $\frac{|B_{m}(L,\eta(S))|}{\mathcal{D}^{4}(\mathcal{D}+1)}$ by the estimate (4), and $\Phi_{n}$ is injective on the set of feasible elements of type $q$ by Lemma 4.8.

Then by the above three inequalities,

	$\displaystyle\log(e(G,f_{n}(S))$	$\displaystyle=\lim_{q\to\infty}\frac{1}{q(m+b)}\log\|B_{q(m+b)}(G,f_{n}(S))\|$
		$\displaystyle\geq\frac{1}{m+b}\log\left(\frac{\|B_{m}(L,\eta(S))\|}{\mathcal{D}^{4}(\mathcal{D}+1)}\right)\geq\frac{1}{m}\log(\|B_{m}(L,\eta(S))\|-\epsilon$
		$\displaystyle\geq\log e(L,\eta(S))-\epsilon.$

Since we have this for all large enough $n$ , and $\epsilon>0$ is arbitrary, we have

\lim_{n\to\infty}\log(e(G,f_{n}(S))\geq\log e(L,\eta(S)).

As we said the other direction is trivial, hence the equality holds. ∎

4.6. A family version

We state a family version of Proposition 3.2. We do not use this proposition in this paper, but it would be useful in the future.

We explain the setting. Let $\delta>0$ be a constant, $M>0$ an integer and $D(\epsilon)$ a function for WPD. Suppose we have a family of finitely generated groups $\{G_{\alpha}\}$ such that each $G_{\alpha}$ is not virtually cyclic and acts on a $\delta$ -hyperbolic space $X_{\alpha}$ . Assume that for any finite generating set $S$ of any $G_{\alpha}$ , the set $S^{M}$ contains a hyperbolic element on $X_{\alpha}$ that is $D$ -WPD.

Now suppose that $S_{n}$ is a finite generating set of $G_{n}$ that is in the family for $n>0$ . Assume that the (infinite) sequence $e(G_{n},S_{n})$ is bounded from above. Then by Proposition 2.10, there is a constant $A>0$ that depends only on $M,\delta$ and the function $D$ such that $e(G_{n},S_{n})\geq A|S_{n}|^{A}$ , therefore, the sequence $|S_{n}|$ is bounded from above.

As before, passing to a subsequence, we may assume that there exists $\ell>0$ with $|S_{n}|=\ell$ for all $n$ . This gives a sequence of surjections $f_{n}:(F,S)\to(G_{n},f_{n}(S))$ with $f_{n}(S)=S_{n}$ , where $(F,S)$ is a pair of free group $F$ and a free generating set $S$ with $|S|=\ell$ .

Passing to a further subsequence if necessary, we may assume that the sequence $f_{n}$ converges to a limit epimorphism $\eta:(F,S)\to(L,\eta)$ .

Then we have:

Proposition 4.9.

Assume that there exists an epimorphism $h_{n}:L\to G_{n}$ for all $n$ such that all the homomorphisms $\{f_{n}\}$ factor through the limit epimorphism: $\eta:F\to L$ , ie, $f_{n}=h_{n}\circ\eta$ . Then,

\lim_{n\to\infty}e(G_{n},f_{n}(S))=e(L,\eta(S)).

Before we explain the proof, we point out that in Proposition 3.2, the assumption on the existence of $h_{n}$ is a consequence of that $G$ is equationally Noetherian. In the current setting, we state it as an assumption and avoid an assumption related to equational Noetherianity.

That said, the proof is identical to the argument for Proposition 3.2. We recall that by the existence of $h_{n}$ , we immediately have $\lim_{n}e(G_{n},f_{n}(S))\leq e(L,\eta(S))$ . The main issue was to show the other inequality $\lim_{n}e(G_{n},f_{n}(S))\geq e(L,\eta(S))$ by constructing separators for each action of $L$ on $X$ , via $h_{n}:L\to G_{n}$ . That argument applies without change to the current setting since the constants $\delta,M$ and the function $D(\epsilon)$ are common for all $(G_{n},S_{n})$ and $X_{n}$ .

5. Examples

An obvious example for Theorem 1.1 is a non-elementary hyperbolic group, $G$ . Let $X$ be a Cayley graph of $G$ , then it is $\delta$ -hyperbolic, and the action by $G$ is (uniformly) proper, so that acylindrical, and non-elementary. The existence of the constant $M$ is known ([K]). As we said $G$ is equationally Noetherian ([S], [RW]). Therefore, $\xi(S)$ is well-ordered. This is proved in [FS] and we adapted their argument to prove Theorem 3.1 in this paper. In this section we discuss some other examples.

5.1. Relatively hyperbolic groups

We treat a relatively hyperbolic group. For example see [Bo1] for the definition and basic properties. Suppose $G$ is hyperbolic relative to a collection of finitely generated subgroups $\{P_{1},\cdots,P_{n}\}$ . Suppose $G$ is not virtually cyclic and not equal to any $P_{i}$ . Then it acts properly discontinuously on a proper $\delta$ -hyperbolic space $X$ such that [Bo1, Proposition 6.13]:

(1)

There is a $G$ -invariant collection of points, $\Pi\subset\partial X$ , with $\Pi/G$ finite. For each $i$ , there is a point $p_{i}\in\Pi$ such that the stabilizer of $p_{i}$ is $P_{i}$ . The union of the $G$ -orbits of the $p_{i}$ ’s is $\Pi$ .
(2)

For every $r>0$ , there is a $G$ -invariant collection of horoballs $B(p)$ at each $p\in\Pi$ such that they are $r$ -separated, ie, $d(B(p),B(q))\geq r$ for every distinct $p,q\in\Pi$ .
(3)

The action of $G$ on $X\backslash\cup_{p\in\Pi}{\rm int}B(p)$ is co-compact.

A subgroup $H<G$ is called parabolic if it is infinite, fixes a point in $\partial X$ , and contains no hyperbolic elements. The fixed point is unique and called a parabolic point. In fact, $\Pi$ is the set of parabolic points ([Bo1, Proposition 6.1 and 6.13]).

For this action, we have:

Lemma 5.1 (Proposition 5.1[X]).

Let $G$ and $X$ be as above. Then there exists $M$ such that for any finite generating set $S$ of $G$ , the set $S^{M}$ contains a hyperbolic element on $X$ .

Also we have the following:

Lemma 5.2.

Let $G$ and $X$ be as above. Then the action is uniformly WPD.

Proof.

Given $\epsilon>0$ , take a $G$ -invariant collection of horoballs that are $(10\epsilon+100\delta)$ -separated in $X$ . Let $\mathcal{B}$ denote the union of the interior of the horoballs in the collection. Then since the action of $G$ on $X\backslash\mathcal{B}$ is co-compact, there exists a constant $D(\epsilon)$ such that for any $y\in X\backslash\mathcal{B}$ , the cardinality of the following set is at most $D(\epsilon)$ :

\{h\in G||y-h(y)|\leq\epsilon+10\delta\}.

We argue that the action is uniformly WPD w.r.t. $D=D(\epsilon)$ . Let $g\in G$ be hyperbolic with an $10\delta$ -axis $\gamma$ . Let $x,y\in\gamma$ with $|x-y|\geq\lambda(g)$ . It suffices to show that the following set contains at most $D(\epsilon)$ elements:

\{h\in G||x-h(x)|\leq\epsilon,|y-h(y)|\leq\epsilon\}.

We divide the case into four:
(1) $x\not\in\mathcal{B}$ . Then there are at most $D(\epsilon)$ elements $h\in G$ s.t. $|x-h(x)|\leq\epsilon$ , and we are done.
(2) $y\not\in\mathcal{B}$ . This is same as (1).
(3) $x,y\in\mathcal{B}$ such that $x\in B(p)$ and $y\in B(q)$ with $p\not=q$ . Then, there must be $z\in[x,y]$ with $z\not\in N_{5\epsilon+30\delta}(\mathcal{B})$ since the horoballs in $\mathcal{B}$ are $(10\epsilon+100\delta)$ -separated. Then $|z-h(z)|\leq\epsilon+10\delta$ . But there are at most $D(\epsilon)$ such elements.
(4) $x,y\in B(p)$ for some $p$ . Then $g(x)\in B(q)$ for some $q\not=p$ , since $g$ is hyperbolic and does not preserve any horoball. Since horoballs are $(10\epsilon+100\delta)$ -separated, we have $|x-g(x)|\geq 10\epsilon+100\delta$ . So, $\lambda(g)\geq 10\epsilon+50\delta$ . Now, there are two possibilities: one is that $g(x)\in\gamma$ is between $x$ and $y$ . Then, as in (3), there must be $z\in[x,y]$ with $z\not\in N_{5\epsilon+30\delta}(\mathcal{B})$ , and we are done. The other possibility is that $y$ is between $x$ and $g(x)$ on $\gamma$ . But in this case, since $|x-y|\geq\lambda(g)$ , we have $|y-g(x)|\leq 50\delta$ . Then the distance between $B(p)$ and $B(q)$ is at most $50\delta$ since $y\in B(p)$ and $g(x)\in B(q)$ . But it contradicts the separation of horoballs, so this case does not happen. ∎

We quote a theorem, [GrH, Theorem D].

Theorem 5.3 (Equationally Noetherian, [GrH]).

If $G$ is hyperbolic relative to equationally Noetherian subgroups, then $G$ is equationally Noetherian.

We are ready to state a theorem.

Theorem 5.4 (Well-orderedness for relatively hyperbolic groups).

Proof.

$G$ is equationally Noetherian by Theorem 5.3. Take a hyperbolic space $X$ with a $G$ action as above. The action is non-elementary since $G$ contains a hyperbolic isometry and is not virtually $\mathbb{Z}$ . Then Theorem 3.1 applies by Lemma 5.1 and Lemma 5.2. ∎

5.2. Rank-1 lattices

There are many examples of relatively hyperbolic groups, but we mention one standard family that Theorem 5.4 applies to.

Let $G$ be a lattice in a simple Lie group of rank-1. It is always finitely generated and has exponential growth, and in fact uniform exponential growth, [EMO]. If it is a uniform lattice, then it is hyperbolic, so that $\xi(G)$ is well-ordered. We prove the following as an immediate application of Theorem 5.4.

Theorem 5.5 (Rank-1 lattices).

Let $G$ be one of the following groups:

(1)

A lattice in a simple Lie group of rank-1.
(2)

The fundamental group of a complete Riemannian manifold $M$ of finite volume such that there exist $a,b>0$ with $-b^{2}\leq K\leq-a^{2}<0$ , where $K$ denotes the sectional curvature.

Then $\xi(G)$ is well-ordered.

Proof.

We only need to argue for non-uniform lattices since otherwise, $G$ is a non-elementary hyperbolic group and the conclusion holds. Suppose that $G$ is a non-uniform lattice. Then, it is known that $G$ is relatively hyperbolic w.r.t. the the parabolic subgroups, called peripheral subgroups $\{H_{i}\}$ that are associated to the cusps, [Fa], [Bo1]. Moreover $G$ is not virtually cyclic, and not equal to any $H_{i}$ . Also, those $H_{i}$ are finitely generated virtually nilpotent groups (see for example, [Fa]). It is known that finitely generated virtually nilpotent groups are equationally Noetherian, [Br], so that $H_{i}$ are equationally Noetherian. With those facts, Theorem 5.4 applies to $G$ and the conclusion holds. ∎

We remark that it is known that if $G$ is linear over a field, then it is equationally Noetherian, [BMR]. For lattices in a simple Lie group, one can apply this result as well to see that $G$ is equationally Noetherian (consider the adjoint representation on its Lie algebra. It’s faithful since the Lie group is simple).

5.3. Mapping class groups

We discuss mapping class groups as another possible application. Let $MCG(\Sigma)$ be the mapping class group of a compact oriented surface $\Sigma=\Sigma_{g,p}$ with genus $g$ , punctures $p$ , and complexity $c(\Sigma)=3g+p$ . It is known that it is either virtually abelian or has exponential growth, and then uniform exponential growth ([Ma2]). Let $\mathcal{C}(\Sigma)$ be the curve graph of $\Sigma$ . The graph $\mathcal{C}(\Sigma)$ has vertex set representing the non-trivial homotopy classes of simple closed curves on $\Sigma$ , and edges joining vertices representing the homotopy classes of disjoint curves. The group $MCG(\Sigma)$ naturally acts on it by isometries.

We assume $c(\Sigma)>4$ . Then $MCG(\Sigma)$ has exponential growth. We recall some facts:

(1)

The graph $\mathcal{C}(\Sigma)$ is $\delta$ -hyperbolic, and any pseudo-Anosov element in $MCG(\Sigma)$ acts hyperbolically on $\mathcal{C}(\Sigma)$ , [MM1].
(2)

The action of $MCG(\Sigma)$ on $\mathcal{C}(\Sigma)$ is acylindrical, [Bo]. It is non-elementary.
(3)

There exists $T(\Sigma)>0$ such that for any pseudo-Anosov element $g$ , $\lambda(g)\geq T(\Sigma)>0$ for the action on $\mathcal{C}(\Sigma)$ , [MM1]. (This follows from the acylindricity as we pointed out.)
(4)

There exists $M(\Sigma)$ such that for any finite $S\subset MCG$ such that $\langle S\rangle$ contains a pseudo-Anosov element, then $S^{M}$ contains a pseudo-Anosov element, [Ma].

In summary, the action of $MCG(\Sigma)$ on $\mathcal{C}(\Sigma)$ is known to satisfy all the assumptions of Theorem 1.1 except we do not know if $MCG(\Sigma)$ is equationally Noetherian or not. We expect it to hold (for example, see an announcement by Daniel Groves in [GrH]), but it does not exist in the literature yet. Once that is verified, it will imply that $\xi(MCG(\Sigma))$ is well-ordered if $c(\Sigma)>4$ .

We remark that for $\Sigma_{1,1},\Sigma_{1,0},\Sigma_{0,4}$ , the conclusion holds by [FS] since $MCG(\Sigma)$ is hyperbolic (a well-known fact, for example, [MM1]).

Question 5.6.

Let $G=MCG(\Sigma)$ . Is $\xi(G)$ well-ordered? If so, the infimum is attained. It would be interesting to know its value and generating sets that attain the minimum for each $\Sigma$ .

5.4. Three manifold groups

We discuss three manifold groups. Let $M$ be a closed, orientable $3$ -manifold. $M$ is called irreducible if $\pi_{1}(M)$ does not admit a non-trivial splitting over the trivial group.

Let $M$ be a closed, orientable, irreducible 3-manifold which is not a torus bundle over a circle. Then there is a finite collection of embedded disjoint essential tori $T_{i}$ in $M$ such that each connected component of $M\backslash\cup_{i}T_{i}$ is geometric, ie, either Seifert fibred, or admitting hyperbolic or Sol-geometry. Such a collection of smallest number of tori is called the JSJ decomposition of $M$ . A JSJ-decomposition in this sense exists by the solution of the geometrization conjecture of 3-manifolds. The collection of tori is maybe empty. Otherwise we say $M$ has non-trivial JSJ-decomposition. A non-trivial JSJ-decomposition gives a graph of groups decomposition of $\pi_{1}(M)$ along subgroups isomorphic to $\mathbb{Z}^{2}$ , and $\pi_{1}(M)$ has exponential growth. Its Bass-Serre tree is called the JSJ-tree, $T_{M}$ . An action of a group $G$ on a tree $T$ is called $k$ -acylindrical if for every non-trivial element $g$ , the subtree of fixed points by $g$ is either empty or of diameter at most $k$ . It is proved that the action of $\pi_{1}(M)$ on $T_{M}$ is $4$ -acylindrical, [WZ, Proposition 4.2]. It implies that the action is uniformly $4$ -WPD. It is known that if an action of $G$ on a tree $T$ is $k$ -acylindrical for some $k$ , then it is acylindrical [MO, Lemma 5.2], therefore it is uniformly WPD (Lemma 2.3). Moreover, the acylindricity constants $R(\epsilon),N(\epsilon)$ and the uniformly WPD constant $D(\epsilon)$ depend only on $k$ and $\epsilon$ . The moreover part easily follows from the proof of Lemma 5.2in [MO].

Theorem 5.7.

Let $M$ be a closed orientable $3$ -manifold, and $G=\pi_{1}(M)$ . If $M$ is one of the following, then $G$ has exponential growth and $\xi(G)$ is well-ordered.

(1)

$M$ is not irreducible such that $G$ is not isomorphic to $\mathbb{Z}_{2}*\mathbb{Z}_{2}$ .
(2)

$M$ is irreducible such that it is not a torus bundle over a circle, and that it has a non-trivial JSJ-decomposition.
(3)

$M$ admits hyperbolic geometry.
(4)

$M$ is Seifert fibered such that the base $2$ -orbifold is hyperbolic.

Proof.

First, every three manifold group is equationally Noetherian, [GHL].

(1) In this case, $G$ is a non-trivial free product $A*B$ . Since it is not $\mathbb{Z}_{2}*\mathbb{Z}_{2}$ , it has exponential growth. $G$ acts on the Bass-Seree tree $T$ of this free product. Then for any finite generating set $S$ , the set $S^{2}$ contains a hyperbolic element on $T$ , [Se]. The action of $G$ on $T$ is $0$ -acylindrical, so that the action is uniformly $D$ -WPD for some $D$ . Since $T$ is hyperbolic, Theorem 3.1 applies with $M=2$ .

(2) In this case, let $T_{M}$ be the JSJ-tree of $M$ . Then the action of $G$ on $T_{M}$ is $4$ -acylindrical, so that it is uniformly $D$ -WPD for some $D$ . Theorem 3.1 applies with $M=2$ .

(3) If $M$ is hyperbolic, then $G$ is a non-elementary, hyperbolic group. Then $\xi(G)$ is well-ordered by [FS].

(4) In this case, we have the following exact sequence:

1\to\mathbb{Z}\to G\to H\to 1,

where $H$ is the orbifold-fundamental group of the base 2-orbifold, and $\mathbb{Z}$ is the fundamental group of the fiber circle. We denote this subgroup $C$ . By assumption, $H$ is a non-elementary, hyperbolic group.

We claim that $\xi(G)=\xi(H)$ . To see it, let $S$ be a finite generating set of $G$ . Let $\bar{S}$ be the image of $S$ by the projection $G\to H$ . We have $|\bar{S}^{n}|\leq|S^{n}|$ . But it is known that the subgroup $C$ is not distorted in $G$ in the sense that there is a constant $K>0$ such that for any $n>0$ , we have $|S^{n}\cap C|\leq Kn$ , [NS, Proposition 1.2 (2)]. It implies that for all $n$ , we have $|S^{n}|\leq Kn|\bar{S}^{n}|$ . It follows that $e(G,S)=e(H,\bar{S})$ , therefore $\xi(G)\subset\xi(H)$ . On the other hand, if $S$ is a finite generating set of $H$ , then there is a finite generating set $\tilde{S}$ of $G$ which projects to $S$ , by lifting each element of $S$ to $G$ , then adding a generator of $C$ , which gives $\tilde{S}$ . Then as we saw, $e(G,\tilde{S})=e(H,S)$ , which implies $\xi(H)\subset\xi(G)$ . We proved the claim.

But by [FS], $\xi(H)$ is well-ordered, therefore so is $\xi(G)$ . ∎

A torus bundle over a circle either admits Sol-geometry, or it is Seifert fibered (see for example, [WZ]). Therefore the theorem covers all closed, orientable $3$ -manifolds with fundamental groups of exponential growth except that $M$ has Sol-geometry. We leave it as a question.

Question 5.8.

Let $M$ a closed, orientable $3$ -manifold that has the geometry of three dimensional solvable group, Sol. Then is $\xi(\pi_{1}(M))$ well-ordered ? Also, in view of Proposition 2.10, is it true that if $|S|\to\infty$ then $e(\pi_{1}(M),S)\to\infty$ ?

6. The set of growth of subgroups

We discuss the set of growth of subgroups in a finitely generated group $G$ . Define

\Theta(G)=\{e(H,S)|S\subset G,|S|<\infty,H=\langle S\rangle,e(H,S)>1\}.

The set $\Theta(G)$ is countable and contains $\xi(G)$ as a subset. If $G$ is a hyperbolic group, it is known by [FS, Section 5] that $\Theta(G)$ is well-ordered.

6.1. Subgroups with hyperbolic elements

As usual, suppose $G$ acts on a $\delta$ -hyperbolic space $X$ . We introduce a subset in $\Theta(G)$ as follows:

\Theta_{X}(G)=\{e(H,S)|S\subset G,|S|<\infty,H=\langle S\rangle,e(H,S)>1\},

where in addition we only consider $S$ such that $\langle S\rangle$ contains a hyperbolic element on $X$ . This set depends on the action on $X$ .

Theorem 6.1 (cf. Theorem 3.1).

Suppose $G$ acts on a $\delta$ -hyperbolic space $X$ , and $G$ is not virtually cyclic. Let $D(\epsilon)$ be a function for WPD. Assume that there exists a constant $M$ such that if $\langle S\rangle$ contains a hyperbolic element on $X$ for a finite subset $S\subset G$ , then $S^{M}$ contains a hyperbolic element that is $D$ -WPD. Assume that $G$ is equationally Noetherian. Then, $\Theta_{X}(G)$ is a well-ordered set.

Proof.

The proof is nearly identical to Theorem 3.1.

Let $\{S_{n}\}$ be a sequence of finite generating sets of subgroups of exponential growth in $G$ , $\{H_{n}\}$ , such that each $H_{n}=\langle S_{n}\rangle$ contains a hyperbolic element on $X$ and that $\{e(H_{n},S_{n})\}$ is a strictly decreasing sequence with $\lim_{n\to\infty}e(H_{n},S_{n})=d$ , for some $d\geq 1$ .

By our assumption, Proposition 2.10 applies to $H_{n}$ . Therefore, $|S_{n}|$ is uniformly bounded from above. By passing to a subsequence we may assume that $|S_{n}|$ is constant, $|S_{n}|=\ell$ , for the entire sequence.

Let $S_{n}=\{x_{1}^{(n)},\cdots,x_{\ell}^{(n)}\}$ . Let $F$ be the free group of rank $\ell$ with a free generating set: $S=\{s_{1},\ldots,s_{\ell}\}$ . For each index $n$ , we define a map: $f_{n}:F\to G$ , by setting: $f_{n}(s_{i})=x_{i}^{(n)}$ . By construction: $e(H_{n},S_{n})=e(H_{n},f_{n}(S))$ .

Then, as before, the sequence $\{f_{n}:F\to G\}$ subconverges to a surjective homomorphism $\eta:F\to L$ , where $L$ is a limit group over $G$ .

Then, we have

Proposition 6.2 (cf. Proposition 3.2).

\lim_{n\to\infty}e(H_{n},f_{n}(S))=e(L,\eta(S)).

Remark 6.3.

This proposition is a special case of Proposition 4.9, when all $\delta$ -hyperbolic spaces $X_{n}$ are $X$ .

Proof.

The proof is identical to Proposition 3.2. As in the beginning of the argument (Section 4.1), for each $n$ , we pick one hyperbolic isometry $g\in S_{n}^{M}$ on $X$ that is $D$ -WPD to start with. This is possible since $H_{n}=\langle S_{n}\rangle$ contains a such hyperbolic element by the definition of $\Theta_{X}(G)$ . The rest is same, and we omit it. ∎

We continue the proof of the theorem. As in the proof of Theorem 3.1, Proposition 6.2 proves that there is no strictly decreasing sequence of rates of growth, $\{e(H_{n},S_{n})\}$ , since a strictly decreasing sequence can not approach its upper bound, a contradiction. Hence, $\Theta_{X}(G)$ is well-ordered. The theorem is proved. ∎

6.2. Relatively hyperbolic groups

We apply Theorem 6.1 relatively hyperbolic groups. Let $(G,\{P_{i}\})$ be a relatively hyperbolic group with $P_{i}$ finitely generated. Define

\Theta_{{\rm non-elem.}}(G)=\{e(H,S)|S\subset G,|S|<\infty,H=\langle S\rangle,e(H,S)>1\},

where in addition we only consider $H$ that is not conjugate into any $P_{i}$ . This is a subset in $\Theta(G)$ .

We first characterize the subgroups $H$ that appear in the definition in terms of the action on a $\delta$ -hyperbolic space $X$ that we described in Section 5.1. Fix such $X$ and an action by $G$ .

We recall a lemma. This is straightforward from the classification of subgroups that act on a hyperbolic space, [G, Section 3.1].

Lemma 6.4.

Let $H<G$ be a subgroup. Then the following two are equivalent:

(1)

$H$ has an element $g$ that is hyperbolic on $X$ , and $H$ is not virtually $\mathbb{Z}$ .
(2)

$H$ is infinite, not virtually $\mathbb{Z}$ and not conjugate into any $P_{i}$ .

The lemma implies:

\Theta_{{\rm non-elem.}}(G)=\Theta_{X}(G).

We prove:

Theorem 6.5.

Let $G$ be a group that is hyperbolic relative to a collection of subgroups $\{P_{1},\cdots,P_{n}\}$ . Suppose $G$ is not virtually cyclic, and not equal to $P_{i}$ for any $i$ . Suppose each $P_{i}$ is finitely generated and equationally Noetherian. Then $\Theta_{{\rm non-elem.}}(G)$ is well-ordered.

Proof.

It suffices to argue that $\Theta_{X}(G)$ is well-ordered. For that, we apply Theorem 6.1 to the action of $G$ on $X$ . We already checked the assumptions in the proof of Theorem 5.4, except that Lemma 5.1 holds for subgroups. Namely, there is a constant $M$ such that for any finite set $S\subset G$ such that $\langle S\rangle$ contains a hyperbolic isometry on $X$ , then $S^{M}$ contains a hyperbolic isometry. But this is true and the argument is identical to the proof of [X, Proposition 5.1], and we omit it. ∎

As an example of Theorem 6.5 we prove:

Theorem 6.6.

Let $G$ be a group in Theorem 5.5. Then $\Theta(G)$ is a well-ordered set.

Proof.

As we said in the proof of Theorem 5.5, $G$ is relatively hyperbolic w.r.t. the parabolic subgroups $\{H_{i}\}$ , which are associated to the cusps, and $H_{i}$ are virtually nilpotent. By applying Theorem 6.5 to $(G,\{H_{i}\})$ , we have that $\Theta_{{\rm non-elem}}(G)$ is well-ordered. But if a subgroup $H=\langle S\rangle$ is conjugate into one of $H_{i}$ , then it is virtually nilpotent, so that $H$ has polynomial growth. It follows that $\Theta_{{\rm non-elem}}=\Theta(G)$ holds for $G$ , so that $\Theta(G)$ is well-ordered. ∎

6.3. Subgroups in mapping class groups

We discuss mapping class groups. A subgroup $H<MCG(\Sigma)$ is called large if it contains two independent pseudo-Anosov elements. Such $H$ has exponential growth.

We define:

\Theta_{{\rm large}}(MCG(\Sigma))=\{e(H,S)|S\subset MCG(\Sigma),|S|<\infty,\langle S\rangle=H,e(H,S)>1\},

where in addition $H<MCG(\Sigma)$ is large. Note that $\xi(MCG(\Sigma))\subset\Theta_{{\rm large}}(MCG(\Sigma))$ .

Theorem 6.7.

Assume that $G=MCG(\Sigma)$ is equationally Noetherian. Then $\Theta_{{\rm large}}(MCG(\Sigma))$ is well-ordered.

Proof.

We suppress $\Sigma$ and denote $MCG$ . Let $X$ the curve graph of $\Sigma$ . Then, as we said, Theorem 6.1 applies to the action of $MCG$ on $X$ . We conclude that $\Theta_{X}(MCG)$ is well-ordered. Now, we claim $\Theta_{X}(MCG)=\Theta_{{\rm large}}(MCG)$ . Indeed, given $S\subset MCG$ , if $H=\langle S\rangle$ contains a hyperbolic element on $X$ , then it is a pseudo-Anosov element, and moreover, from $e(H,S)>1$ , $H$ must be large. We showed $\Theta_{X}(MCG)\subset\Theta_{{\rm large}}(MCG)$ . On the other hand, for $S\subset MCG$ if $H=\langle S\rangle$ is large in $MCG$ , then $H$ contains hyperbolic isometries on $X$ , so that $\Theta_{{\rm large}}(MCG)\subset\Theta_{X}(MCG)$ . ∎

It is natural to ask the following question. To deal with a non-large subgroup, considering the action on the curve graph does not seem to be enough.

Question 6.8.

Is $\Theta(MCG(\Sigma))$ well-ordered ?

7. Finiteness

7.1. Finiteness of equal growth generating sets

If $G$ is a hyperbolic group, it is known by [FS, Section 3] that for $\rho\in\xi(G)$ , there are only finitely many generating sets $S$ of $G$ , up to $\text{Aut\,}(G)$ , such that $\rho=e(G,S)$ . We discuss this issue.

Theorem 7.1 (Finiteness. cf. Theorem 3.1 in [FS]).

Suppose a finitely generated group $G$ acts on a $\delta$ -hyperbolic space $X$ and $G$ is not virtually cyclic. Let $D(\epsilon)$ be a WPD-function. Assume that there exists a constant $M$ such that if $S$ is a finite generating set of $G$ , then $S^{M}$ contains a hyperbolic element that is $D$ -WPD. Assume that $G$ is equationally Noetherian.

Then for any $\rho\in\xi(G)$ , up to the action on $\text{Aut\,}(G)$ , there are at most finitely many finite generating set $S$ such that $e(G,S)=\rho$ .

Proof.

We argue by contradiction. Suppose that there are infinitely many finite sets of generators $\{S_{n}\}$ that satisfy: $e(G,S_{n})=\rho$ , and no pair of generating sets $S_{n}$ is equivalent under the action of the automorphism group $\text{Aut\,}(G)$ . As in the proof of Theorem 3.1, by Proposition 2.10, the cardinality of the generating sets $\{S_{n}\}$ is bounded, so we may pass to a subsequence that have a fixed cardinality $\ell$ . Hence, each generating set $S_{n}$ corresponds to an epimorphism, $f_{n}:F\to G$ , where $S$ is a fixed free generating set of $F$ , and $f_{n}(S)=S_{n}$ .

By passing to a further subsequence, we may assume that the sequence of epimorphisms $\{f_{n}\}$ converges to a limit group $L$ with $\eta:F\to L$ the associated quotient map. As in the proof of Theorem 3.1, since $G$ is equationally Noetherian, by Lemma 1.11, for large $n$ , $f_{n}=h_{n}\circ\eta$ , where $h_{n}:L\to G$ is an epimorphism. In particular, $S_{n}=h_{n}(\eta(S))$ . We pass to a further subsequence such that for every $n$ , $f_{n}=h_{n}\circ\eta$ .

Since for every index $n$ , $h_{n}$ is an epimorphism from $L$ onto $G$ that maps $\eta(S)$ to $f_{n}(S)$ , $e(G,f_{n}(S))\leq e(L,\eta(S))$ . We prove:

Proposition 7.2 (cf. Proposition 3.2 [FS]).

If $\ker(h_{n_{0}})$ is infinite for some $n_{0}$ , then $e(G,f_{n_{0}}(S))<e(L,\eta(S))$ .

We postpone the proof of the proposition until the next section, and proceed. We prove a lemma.

Lemma 7.3.

The group $L$ contains a finite normal subgroup $N=N_{L}$ that contains all finite normal subgroups in $L$ , such that $|N|\leq 2D(100\delta)$ .

We recall one fact we use in the proof. If a finitely generated group $G$ acts on a $\delta$ -hyperbolic space $X$ such that $G$ is not virtually cyclic and $G$ contains a hyperbolic element on $X$ that is $D$ -WPD, then $G$ contains a maximal finite normal subgroup $N<G$ . Moreover, $|N|\leq 2D(100\delta)$ . We sometimes denote $N$ by $N_{G}$ .

The existence of such $N$ is known for an acylindrically hyperbolic group [DGO, Theorem 6.14], and the same proof applies to our setting, which we briefly recall. Indeed, $N$ is the intersection of $E(g)$ for all hyperbolic elements $g\in G$ on $X$ . It is obvious that $N$ is normal. By assumption, there must be a hyperbolic and WPD element, $g$ . Also, there is another element $h$ such that $g$ and $h$ are independent. Then, by Proposition 2.6, $E(g)\cap E(h)$ is finite, so that $N$ is finite. On the other hand, if $N^{\prime}$ is a finite normal subgroup in $G$ , then for every hyperbolic element $g\in G$ , there is $n>0$ such that $N^{\prime}$ is contained in the centralizer of $g^{n}$ , so that $N^{\prime}<E(g)$ . It implies that $N^{\prime}<N$ . We showed that $N$ is maximal.

Lastly, to see $|N|\leq 2D(100\delta)$ , consider the exact sequence $1\to F(g)\to E(g)\to C\to 1$ for the hyperbolic and $D$ -WPD element $g$ . Recall that $|F(g)|\leq D(100\delta)$ if $C$ is cyclic. From this we have $|N|\leq 2D(100\delta)$ .

We prove the lemma.

Proof.

Let $N<L$ be a finite normal subgroup. Since $h_{n}$ is surjective, $h_{n}(N)<G$ is a finite normal subgroup, therefore $h_{n}(N)<N_{G}$ for any $h_{n}$ . Also, for sufficiently large $n$ , the surjection $h_{n}:L\to G$ is injective on $N$ . But since $|N_{G}|\leq 2D(100\delta)$ , we have $|N|\leq 2D(100\delta)$ .

If $N_{1},N_{2}<L$ are two finite normal subgroups, then $N_{1}N_{2}$ is a finite normal subgroup. Combined with the fact in the previous paragraph, there must be the maximal finite normal subgroup $N_{L}$ in $L$ with $|N_{L}|\leq 2D(100\delta)$ . ∎

By Proposition 3.2, $\lim_{n\to\infty}e(G,S_{n})=e(L,\eta(S))$ . By our assumption, for every index $n$ , $e(G,S_{n})=\rho$ . Hence, $e(L,\eta(S))=\rho$ , so that for every $n$ , $e(G,S_{n})=e(L,\eta(S))$ .

It follows from Proposition 7.2 that for every $n$ , $\ker(h_{n})$ is finite. Since $\ker(h_{n})$ is a normal subgroup in $L$ , by Lemma 7.3, $\ker(h_{n})<N_{L}$ . Since $N_{L}$ is a finite group, there are only finitely many possibilities for $\ker(h_{n})$ . It follows that there must be $N_{0}<N_{L}$ such that $\ker(h_{n})=N_{0}$ for infinitely many $n$ .

The map $h_{n}$ induces an isomorphism from $L/\ker(h_{n})$ to $G$ . Notice that this gives an isomorphism from $(L/\ker(h_{n}),\eta(S))$ to $(G,S_{n})$ since $h_{n}$ gives a bijection between $\eta(S)$ and $S_{n}$ . (Here, we may assume that each $S_{n}$ consists of distinct elements, so that no two elements in $\eta(S)$ are identifies by $h_{n}$ .) But this implies that $(L/N_{0},\eta(S))$ is isomorphic to $(G,S_{n})$ for infinitely many $n$ by $h_{n}$ , ie, those $(G,S_{n})$ are isomorphic to each other. This is a contradiction since all of them must be non-isomorphic. Theorem 7.1 is proved. ∎

7.2. Idea of the proof of Proposition 7.2

We prove Proposition 7.2. The argument is long and complicated, but the main idea is same as the proof of [FS, Proposition 3.2], and we adapt it to our setting. Also, the proof is similar to the proof of Proposition 3.2, which also follows the counterpart in the paper [FS]. The difference between this paper and [FS] is that while they use the action of the limit group $L$ on a limit object, called a limit tree, while in our paper we use the actions of $L$ on $X$ induced from the maps $h_{n}:L\to G$ . But this approach is already taken in the proof of Proposition 3.2.

So, rather than giving a full formal proof, we first explain the strategy of the proof, then give all definitions and intermediate claims, which appear in the proof of [FS, Proposition 3.2], then explain the part where we need to make technical modifications, most of which already appeared in Section 4. One advantage of not using the action of $L$ on a limit object is that one does not need to deal with the degeneration of the action on the limit object. A trade-off is that we need to keep attention to the various constants related to the actions induced by $h_{n}$ through the argument.

Strategy of the proof. We start with an informal description of the idea. The constant $n_{0}$ is given as the assumption, which gives the homomorphism $h_{n_{0}}:(L,\eta(S))\to(G,f_{n_{0}}(S))$ with an infinite kernel. To show that $e(G,f_{n_{0}}(S))<e(L,\eta(S))$ , we will produce not only infinitely many (which is obvious by the assumption), but “exponentially many” elements in the preimage of $g$ by $h_{n_{0}}$ for each $g\in G$ . Those elements are given by the map $\phi_{n}$ . They are exponentially many in terms of the word length of $g$ w.r.t. $f_{n_{0}}(S)$ . See the estimate (6).

In the proof two constants $m$ and $n$ appear. They will be chosen and fixed around the end of the proof. The constant $m>1$ is first chosen. It will be used to measure the gap between $e(G,f_{n_{0}}(S))$ and $e(L,\eta(S))$ . The constant $n$ depends on $m$ , so that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ . Also, a positive integer $q$ is used to make the word length of $g$ , which is $mq$ longer and take a limit at the end of the proof.

We now explain more concretely. Similar to $B_{m}(G,S_{n})$ , the ball of radius $m$ in $Cayley(G,S_{n})$ centered at the identity, let $\text{Sph\,}_{m}(G,S_{n})$ denote the sphere of radius $m$ . It is an elementary fact that if $e(G,S_{n})>1$ , then

e(G,S_{n})=\limsup_{m\to\infty}|\text{Sph\,}_{m}(G,S_{n})|^{\frac{1}{m}}.

Given $m>0$ , for a large enough $n>0$ depending on $m$ , we will define a “map” $\phi_{n}$ :

\phi_{n}:\text{Sph\,}_{mq}(G,S_{n_{0}})\to B_{q(m+2b)}(L,\eta(S))

for all $q>0$ , where $b$ is a constant that does not depend on $n,m,q$ . The map $\phi_{n}$ is similar to the map $\Phi_{n}$ in the section 4.2, but strictly speaking $\phi_{n}$ is not a map, but $\phi_{n}(g)$ is a finite set of elements in $B_{q(m+2b)}(L,\eta(S))$ for each $g$ . But we abuse the notation and call them maps in the following account.

It satisfies for every $g\in\text{Sph\,}_{mq}(G,S_{n_{0}})$ to have the following two properties. Set $\mathcal{D}=D(200\delta)$ .

(i).

$\left(\frac{m-1}{\mathcal{D}^{4}(\mathcal{D}-1)}\right)^{q}\leq|\phi_{n}(g)|,$

see the estimate (5).
(ii).

$h_{n_{0}}\circ\phi_{n}(g)=g,$ which implies that for $g\not=h$ , we have $\phi_{n}(g)\cap\phi_{n}(h)=\emptyset$ .

Once we have such a map $\phi_{n}$ , we argue as follows: fix a (large) $m$ . Since $\phi_{n}(g)\subset B_{q(m+2b)}(L,\eta(S))$ , we have from (i) and (ii) that

|\text{Sph\,}_{mq}(G,S_{n_{0}})|\left(\frac{m-1}{\mathcal{D}^{4}(\mathcal{D}-1)}\right)^{q}\leq|B_{q(m+2b)}(L,\eta(S))|.

Taking $\log$ , dividing by $mq$ , and letting $q\to\infty$ , we have as the limsup

\log e(G,S_{n_{0}})+\frac{\log(m-1)-\log(\mathcal{D}^{4}(\mathcal{D}-1))}{m}\leq\frac{m+2b}{m}\log e(L,\eta(S)).

Since $b$ does not depend on $m$ , choosing $m$ large enough, this inequality implies

\log e(G,S_{n_{0}})<\log e(L,\eta(S)).

Roughly speaking, the construction of $\phi_{n}$ is as follows. As in the construction of $\Phi_{n}$ , we first construct separators. To define separators in $L$ , we use a non-trivial element $r_{n}\in\ker h_{n_{0}}$ . Separators will be products of conjugates of $r_{n}$ , so that they are also in $\ker h_{n_{0}}$ , which will imply the property (ii) in the above. The separators depend on $n$ .

For each $n$ , the map $h_{n}:(L,\eta(S))\to(G,S_{n})$ gives a canonical bijection between $\eta(S)$ and $S_{n}=f_{n}(S_{n})$ . This gives a bijection between the words on $\eta(S)$ (not elements in $L$ ) and the words on $S_{n}$ .

Let $m,q>0$ be integers. We will fix $m$ and let $q\to\infty$ later. Given an element $g\in\text{Sph\,}_{mq}(G,S_{n_{0}})$ , we choose a word $w(g)$ of length $mq$ on $S_{n_{0}}$ that represents $g$ . We divide $w(g)$ into $q$ subwords of length $m$ . As we said, each subword of length $m$ canonically gives a word of length $m$ on $\eta(S)$ via the map $h_{n_{0}}$ . We further subdivide each of the subwords of length $m$ on $\eta(S)$ into two words of length $k$ and $m-k$ . We choose $k$ to satisfy $1\leq k\leq m-1$ . In this way, for each choice of a $q$ -tuple of such $k$ ’s, we divided the word on $\eta(S)$ corresponding to $w(g)$ into $2q$ subwords. There are $(m-1)^{q}$ ways to subdivide it.

To each of such subdivision, we insert separators to the $(2q-1)$ break points and obtain an element in $B_{q(m+2b)}(L,\eta(S))$ since the word length of each separator is at most $b$ . We obtain $(m-1)^{q}$ such elements. Since separators are in $\ker(h_{n_{0}})$ , those elements (words) are mapped to $g$ by $h_{n_{0}}$ .

But we do not know if they are all distinct as elements in $L$ , but we will show that there are at least $(\frac{m-1}{\mathcal{D}^{4}(\mathcal{D}-1)})^{q}$ elements that are distinct. They are called feasible elements. This collection of feasible elements is denoted by $\phi_{n}(g)$ . They are significantly many, so that $e(L,\eta(S))$ is strictly larger than $e(G,S_{n_{0}})$ as we computed in the above.

Lastly, to show that those feasible elements in $L$ defined for each $g$ are distinct, as in Section 4, we let them act on the space $X$ via the map $h_{n}$ for a large enough $n$ (We choose $n$ such that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ .) We then argue that the images of the base point $y_{n}\in X$ by those elements are distinct. In the paper [FS], they use a limit tree $Y$ on which $L$ acts to argue that feasible elements are distinct. Here, we use the action on $X$ . This difference already appeared in Section 4.

7.3. Proof

We prove Proposition 7.2.

Proof.

As in Section 4.1, set $\mathcal{D}=D(200\delta)$ , and for each $n$ let $y_{n}\in X$ be a point where $L(S_{n}^{2\mathcal{D}M})$ is achieved and put

\Delta_{n}=100\delta+4\mathcal{D}L(S_{n}^{2\mathcal{D}M}).

We consider germs w.r.t. $\Delta_{n}$ .

As we did in Lemma 4.2, in the next lemma we construct separators $u_{i}\in G$ , which give $\hat{u}_{1},\hat{u}_{2},\hat{u}_{3},\hat{u}_{4}\in L$ by pulling them back by $h_{n}$ . In addition to the properties in Lemma 4.2 they satisfy $h_{n_{0}}(\hat{u}_{i})=1$ in $G$ . We state it as a lemma. The constant $b$ is different from the constant $b$ in Lemma 4.2, and it depends on $\ker(h_{n_{0}})$ but not on $n$ .

Lemma 7.4 (cf Lemma 3.3 and Lemma 3.9 in [FS]).

Suppose $\ker(h_{n_{0}})$ is infinite. Then there exists a constant $b$ with the following property: if $n$ is sufficiently large, then there are elements $u_{1},u_{2},u_{3},u_{4}\in S_{n}^{b}$ that satisfy the conditions (i), (ii) and (iii) in Lemma 4.2, and in addition to that, all $u_{i}$ satisfy

(iv)

$u_{i}\in h_{n}(\ker h_{n_{0}})$ .

Moreover, those elements are such that there are elements $\hat{u}_{1},\hat{u}_{2},\hat{u}_{3},\hat{u}_{4}\in\eta(S)^{b}$ with $h_{n}(\hat{u}_{i})=u_{i}$ and $u_{i}\in\ker(h_{n_{0}})$ for each $i$ .

We remark that the moreover part is rather than an additional property, but immediate from the construction, ie, we first construct $\hat{u}_{i}$ then map them by $h_{n}$ . We will call both $u_{i}$ and $\hat{u}_{i}$ separators.

Proof.

In the proof there will be several constants $b_{i}$ , for which we do not try to give explicit values. The important property of those constants is that they do not depend on $n$ .

First, since $\ker(h_{n_{0}})$ is infinite, choose distinct elements $r_{1},\cdots,r_{\mathcal{D}+1}\in L$ that are in the kernel. Let $b_{1}$ be the maximum of the word lengths of the $r_{i}$ in terms of $\eta(S)$ . If $n$ is large enough, then the image of those $\mathcal{D}+1$ elements by $h_{n}$ are all distinct. From now on, we only consider such $n$ . In the following we fix each such $n$ and argue. We have $\mathcal{D}+1$ distinct elements $\{h_{n}(r_{i})\}$ and the word lengths of those w.r.t. $S_{n}$ are bounded by $b_{1}$ .

Secondly, choose an element $g_{n}\in S_{n}^{M}$ that is hyperbolic on $X$ such that its $10\delta$ -axis is at distance at most $10\delta$ from the point $y_{n}$ . By assumption, such an element exists. Also there is $s\in S_{n}$ such that $g_{n}$ and $sg_{n}s^{-1}$ are independent. Choose such $s$ .

Thirdly, we choose one element, $r$ , from the $r_{i}$ ’s as follows: if there is $r_{i}$ such that
(I) The element $h_{n}(r_{i})$ is hyperbolic on $X$ ,
then choose one of such $r_{i}$ and set $r=r_{i}$ . Otherwise choose $r_{i}$ with
(II) $h_{n}(r_{i})\not\in F(g_{n})$
and set $r=r_{i}$ . This is clearly possible since $|F(g_{n})|\leq\mathcal{D}$ .

Note that the element $r$ depends on $n$ . From now on we suppress $n$ and write $g_{n}$ as $g$ .

Now we divide the case into two depending on (I) or (II) in the above. Suppose we are in the case (I). We consider the power $g^{k}$ with $k=60\mathcal{D}$ , then we have (see Lemma 2.8)

\langle g^{k},sg^{k}s^{-1}\rangle=\langle g^{k}\rangle*\langle sg^{k}s^{-1}\rangle.

Note that we have

\lambda(g^{k})\leq\Delta_{n}-100\delta.

This is because since $k=60\mathcal{D}$ and $g\in S_{n}^{M}$ , we have

\lambda(g^{k})=30\lambda(g^{2\mathcal{D}})\leq 30L(S_{n}^{2\mathcal{D}M})\leq\Delta_{n}-100\delta.

The last inequality is by $\mathcal{D}\geq 10$ and $\Delta_{n}=100\delta+4\mathcal{D}L(S_{n}^{2\mathcal{D}M}).$

Recall that the axes of $g^{k},sg^{k}s^{-1}$ are at at most $40\delta+L(S_{n}^{2M\mathcal{D}})$ from $y_{n}$ .

In the proof of Lemma 4.2, we set $w=g^{k},z=sg^{k}s^{-1}$ and produce $u_{i}$ as words on $w,z$ , but this time we take into account the germs of the element $h_{n}(r)$ and choose $z,w\in\langle g^{k}\rangle*\langle sg^{k}s^{-1}\rangle$ as follows.

Notice that 6 elements $g^{k},g^{-k},sg^{k}s^{-1},sg^{-k}s^{-1},g^{k}sg^{k}s^{-1},g^{k}sg^{-k}s^{-1},$ define six germs at $y_{n}$ that are mutually opposite since $\lambda(g^{k})\leq\Delta_{n}-100\delta$ as we noted. From the six, choose four distinct germs that are opposite to the germs for $h_{n}(r)$ and $h_{n}(r)^{-1}$ . If those two germs are empty, then ignore this condition. Denote those four germs as $\gamma_{1},\gamma_{2},\gamma_{3},\gamma_{4}$ . Now choose $w,z\in\langle g^{k},sg^{k}s^{-1}\rangle$ such that the germ for $w,w^{-1},z,z^{-1}$ is equivalent to $\gamma_{1},\gamma_{3},\gamma_{2},\gamma_{4}$ , respectively, such that the axes of $w,z$ are at at most $60\delta+L(S_{n}^{2\mathcal{D}M})$ from $y_{n}$ .

We also arrange that the axes of $w,z$ are not parallel to each other, and no element of $G$ flips the axes of $w$ or $z$ . This is achieved by a similar technique to the one we used to prove Lemma 2.8, so we do not repeat. As in the proof of Lemma 4.2, there exists a constant $b_{2}$ that depends only on $\delta,M$ and $\mathcal{D}=D(200\delta)$ such that the word lengths of $w,z$ w.r.t. $S_{n}$ are bounded by $b_{2}$ . The constant $b_{2}$ does not depend on $n$ , nor the choice of $r$ .

Now, choose $\hat{z},\hat{w}\in L$ with $h_{n}(\hat{z})=z,h_{n}(\hat{w})=w$ , whose word length w.r.t. $\eta(S)$ are also bounded by $b_{2}$ . Using $\hat{z},\hat{w},r$ we define $\hat{u}_{i}\in L$ as follows:

	$\displaystyle\hat{u}_{1}$	$\displaystyle=\hat{w}r\hat{w}^{-1}\cdot\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{2}r\hat{w}^{-2}\cdot\hat{z}r\hat{z}^{-1}\cdots\hat{w}^{19}r\hat{w}^{-19}\cdot\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{-20}r\hat{w}^{20},$
	$\displaystyle\hat{u}_{2}$	$\displaystyle=\hat{w}^{21}r\hat{w}^{-21}\cdot\hat{z}^{-1}r\hat{z}\cdot\hat{w}^{22}r\hat{w}^{-22}\cdot\hat{z}^{-1}r\hat{z}\cdots\hat{w}^{40}r\hat{w}^{-40}\cdot z^{-1}r\hat{z},$
	$\displaystyle\hat{u}_{3}$	$\displaystyle=\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{-41}r\hat{w}^{41}\cdot\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{-42}r\hat{w}^{42}\cdot\hat{z}r\hat{z}^{-1}\cdots\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{-60}r\hat{w}^{60},$
	$\displaystyle\hat{u}_{4}$	$\displaystyle=\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{61}r\hat{w}^{-61}\cdot\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{62}r\hat{w}^{-62}\cdots\hat{z}r\hat{z}^{-1}\cdot\hat{w}^{80}r\hat{w}^{-80}\cdot\hat{z}^{-1}r\hat{z}.$

The word length of $\hat{u}_{i}$ in terms of $\eta(S)$ is at most $b_{3}$ , which does not depend on $n$ . Indeed, we may set $b_{3}=21b_{1}+1420b_{2}$ .

Clearly, $\hat{u}_{i}$ are in $\ker h_{n_{0}}$ since they are products of conjugates of $r\in\ker h_{n_{0}}$ . Finally, define $u_{i}=h_{n}(\hat{u}_{i})\in S_{n}^{b_{3}}$ . Then, they satisfy the property (iv).

We need to check those elements satisfy the other properties, (i), (ii) and (iii) in Lemma 4.2. Regarding (i), the germ $\gamma_{1}$ is the germ of $w$ , the germ $\gamma_{3}$ is the germ of $w^{-1}$ , the germ $\gamma_{2}$ is the germ of $z$ , and the germ $\gamma_{4}$ is the germ of $z^{-1}$ . Then $u_{1},u_{2},u_{3},u_{4}$ satisfy (i). The property (iii) is a consequence of that the axes of $w$ and $z$ are not parallel to each other. We skip details of the arguments since it is similar to Lemma 4.2. We point out that some of the argument slightly differs depending if the germs for $h_{n}(r),h_{n}(r)^{-1}$ are defined or empty. In the empty case, we use the property that the axes of $w,z$ are not flipped by any element of $G$ .

In conclusion, those are desired elements, so in this case we take $b=b_{3}$ and we are done.

Suppose we are in the case (II) when we chose $r$ . In this case, we replace $r$ with another element $r^{\prime}$ such that $h_{n}(r^{\prime})$ is hyperbolic on $X$ . We explain how we produce such an $r^{\prime}$ . First choose an element $\hat{g}\in L$ with $h_{n}(\hat{g})=g$ , where the word length of $\hat{g}$ is at most $M$ in terms of $\eta(S)$ . Then we consider an element of the form:

r^{\prime}=r\hat{g}^{Q}r\hat{g}^{-Q}.

We will show that if $Q\geq 40\mathcal{D}$ , $h_{n}(r^{\prime})$ is hyperbolic. See Lemma 7.6. Also, since $r\in\ker h_{n_{0}}$ , we have $r^{\prime}\in\ker h_{n_{0}}$ . It is a well-known method to produce a hyperbolic element as a product of two non-hyperbolic elements, and we postpone an explanation on this, and proceed.

But, then the word length of $r^{\prime}$ in terms of $\eta(S)$ is at most $b_{5}$ , where $b_{5}=2b_{1}+60\mathcal{D}M$ , which does not depend on $n$ .

With the element $r^{\prime}$ we repeat the same argument as we did for $r$ in the case (I) and obtain desired $u_{i}$ with a bound on the word length, uniformly over all $n$ , which will finish the proof of Lemma 7.4.

We now explain some details on how to produce $r^{\prime}$ from $r$ . For an element $k\in Isom(X)$ , define a set

Min(k)=\{x\in X||x-k(x)|\leq 100\delta\}.

This is a $k$ -invariant set. We state a few standard facts on this set.

(M1)

If $k$ is not hyperbolic then $Min(k)$ is not empty, since if it is empty, then $L(k)>100\delta$ , which implies $k$ is hyperbolic, a contradiction.
(M2)

If $k$ is not hyperbolic, then for any point $y\in X$ , we have

$|y-k(y)|\geq 2(d(y,Min(k))-400\delta).$

We prove (M2). If $d(y,Min(k))\leq 400\delta$ , then nothing to show so suppose $d(y,Min(k))>400\delta$ . Let $x\in Min(k)$ be a point with $d(x,y)=d(Min(k),y)$ .

Let $z\in[x,y]$ be the point with $|x-z|=350\delta$ . We claim that $z\not\in N_{10\delta}([k(x),k(y)])$ and $k(z)\not\in N_{10\delta}([x,y])$ . To prove the first claim, suppose not, ie, $z\in N_{10\delta}([k(x),k(y)])$ . Let $v,w\in[x,y]$ be with $|x-v|=150\delta$ and $|x-w|=200\delta$ . Then we have $k([v,w])\subset N_{10\delta}([x,y])$ since $|x-k(x)|\leq 100\delta$ and $z\in N_{10\delta}([k(x),k(y)])$ . Then we have $|v-k(v)|\leq 50\delta$ since $k$ is not hyperbolic. (Otherwise, $v$ is “pushed” along the geodesic $[x,y]$ by at least $40\delta$ by $k$ , which implies that $k$ is hyperbolic, impossible.) But it implies that $v\in Min(k)$ , which is a contradiction. We showed $z\not\in N_{10\delta}([k(x),k(y)])$ .

By the same argument, we can show $k(z)\not\in N_{10\delta}([x,y])$ .

Having those two claims, we have

|y-k(y)|\geq|y-z|+|z-k(z)|+|k(z)-k(y)|-100\delta\geq 2(|y-x|-350\delta)-100\delta=2(|y-x|-400\delta).

We showed (M2).

We go back to the explanation. For a hyperbolic isometry $g$ and its $10\delta$ -axis $Ax(g)$ , we consider the nearest points projection in $X$ to $Ax(g)$ . We denote the projection by $\pi_{g}$ . For every point $x\in X$ , although $\pi_{g}(x)$ is not a point, the diameter of $\pi_{g}(x)$ is bounded by $100\delta$ . The following lemma is well-known. See Figure 5.

Lemma 7.5 (Bounded projection).

If $g\in G$ is hyperbolic and $D$ -WPD; and $k\in G\backslash E(g)$ and $k$ is not hyperbolic, then the image of $Min(k)$ in $Ax(g)$ by the projection $\pi_{g}$ is bounded by $2D(100\delta)L(g)+200\delta$ in diameter.

We prove the lemma for readers’ convenience.

Proof.

Let $x,y\in Min(k)$ and suppose $p\in\pi_{g}(x),q\in\pi_{g}(y)$ . Assume that $|p-q|$ is larger than $200\delta$ , since otherwise there is nothing to show. Then $[x,p]\cup[p,q]\cup[q,y]$ is a uniform quasi-geodesic and every point on it is moved by $k$ by at most $200\delta$ . Moreover, each point $x$ on $[p,q]$ with $|x-p|,|x-q|\geq 50\delta$ is moved by $k$ by at most $20\delta$ since $k$ is not hyperbolic.

Now, consider the points $p^{\prime},q^{\prime}\in[p,q]$ with $|p-p^{\prime}|=|q-q^{\prime}|=50\delta$ . Then since $g$ is $D$ -WPD, we have $|p^{\prime}-q^{\prime}|\leq 2D(100\delta)L(g)+100\delta$ by Lemma 2.5 (2). This is because, otherwise, $k\in E(g)$ , impossible. It follows that $|p-q|\leq 2D(100\delta)L(g)+200\delta$ . ∎

The following lemma is also standard, and this is what we need for our purpose. See Figure 5.

Lemma 7.6 (Producing hyperbolic element).

For $g,k$ as in the lemma 7.5, the element $kg^{Q}kg^{-Q}$ is hyperbolic if $Q\geq 40D(100\delta)$ .

We also give a brief proof.

Proof.

Set $\mathcal{D}=D(100\delta)$ . (Or one can set $\mathcal{D}=D(200\delta)$ as usual. It does not matter since $D(100\delta)\leq D(200\delta)$ .) In general, $Ax(g)$ is not exactly $g$ -invariant, but if $L(g)\geq 10\delta$ by definition. We also know that $L(g)\geq 50\delta/\mathcal{D}$ by Lemma 2.2 (1) for our $g$ . So, if necessary, by replacing $g$ by $g^{\mathcal{D}}$ , we may assume that $Ax(g)$ is $g$ -invariant. For simplicity, in the following argument, we assume that $Ax(g)$ is $g$ -invariant.

Consider the set $Min(g^{Q}kg^{-Q})$ , which is equal to the set $g^{Q}(Min(k))$ . We consider the projection of those two sets by $\pi_{g}$ . Then since $Ax(g)$ is $g$ -invariant, the projection $\pi_{g}$ is $g$ -equivariant. It implies that $\pi_{g}(Min(g^{Q}kg^{-Q}))=g^{Q}(\pi_{g}(Min(k)))$ .

Then by Lemma 7.5, the distance between $\pi_{g}(Min(g^{Q}kg^{-Q}))$ and $\pi_{g}(Min(k)))$ is at least

QL(g)-(2\mathcal{D}L(g)+200\delta)\geq 38\mathcal{D}L(g)-200\delta\geq 1700\delta

since $L(g)\geq 50\delta/\mathcal{D}$ . It follows that the distance between $Min(g^{Q}kg^{-Q})$ and $Min(k)$ is at least $1600\delta$ . It follows that the product of $k$ and $g^{Q}kg^{-Q}$ is hyperbolic (this is a well-known fact in $\delta$ -hyperbolic geometry, ie, if the distance between $Min(a)$ and $Min(b)$ is at least $1000\delta$ , then $ab$ is hyperbolic since both $Min(a),Min(b)$ satisfy the property (M2)). ∎

This finishes the explanation for the part to produce $r^{\prime}$ from $r$ , and the case (ii) is done. We proved Lemma 7.4. ∎

We go back to the proof of Proposition 7.2. With Lemma 7.4, the rest is very similar to [FS]. Fix $n$ that is large enough to apply Lemma 7.4. We explain how we define the map $\phi_{n}$ .

Let $g\in\text{Sph\,}_{m}(G,S_{n_{0}})$ . Choose a shortest representative word $w(g)$ of length $m$ on $S_{n_{0}}$ for $g$ . By the bijection $h_{n_{0}}$ between $S_{n_{0}}$ and $\eta(S)$ , $w(g)$ canonically gives a word $w$ of length $m$ on $\eta(S)$ .

From this word $w$ , we construct a collection of elements in $L$ . Given a positive integer $k$ with $1\leq k\leq m-1$ , we divide the word $w$ into a prefix of length $k$ , and a suffix of length $m-k$ . The prefix corresponds to an element in $L$ that we denote $w^{k}_{p}$ , and the suffix corresponds to an element in $L$ that we denote $w^{k}_{s}$ .

Now, from the four separators we constructed in Lemma 7.4 we choose a separator $\hat{u}$ for $h_{n}$ such that $\hat{u}$ is admissible for $w^{k}_{p}$ and $u^{-1}$ is admissible for $(w^{k}_{s})^{-1}$ , after we map them to $G$ by $h_{n}$ . We are writing $\hat{u}$ instead of $u$ to indicate that the separator is in $L$ .

To the pair $w^{k}_{p},w^{k}_{s}$ , we associate the following element in $L$ : $w_{p}^{k}\hat{u}w_{s}^{k}\in B_{m+b}(L,\eta(S))$ .

w\leadsto w_{p}^{k}w_{s}^{k}\leadsto w_{p}^{k}\hat{u}w_{s}^{k}

Note that $h_{n_{0}}(w_{p}^{k}\hat{u}w_{s}^{k})=h_{n_{0}}(w)$ for all $k$ since $\hat{u}\in\ker(h_{n_{0}})$ .

In this way, we obtain $m-1$ “words” in $L$ from $w$ , but possibly, some of them represent the same elements in $L$ . To address this issue, we define a subcollection of words, called forbidden words (in somewhat similar way to what we did in Section 4).

Given $m$ , take $n$ large enough such that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ from now on.

Definition 7.7 (Forbidden words. cf. Def 3.4 in [FS]).

Let $w$ be a word of length $m$ on $\eta(S)$ in the above explanation. We say that a word $w^{k}_{p}\hat{u}w^{k}_{s}$ , from the collection that is built from $w$ , is forbidden if there exists $f$ , $1\leq f\leq m$ such that:

d_{X}(h_{n}(w^{k}_{p}\hat{u})(y_{n}),h_{n}(w^{f}_{p})(y_{n}))\leq\frac{1}{5}d_{X}(y_{n},h_{n}(\hat{u})(y_{n})).

We give a bound on the number of forbidden words.

Lemma 7.8 (cf. Lemma 3.5, [FS]).

For $m$ and each word $w$ as in Definition 7.7, there are at most $\frac{1}{\mathcal{D}+1}m$ forbidden words of the form: $w^{k}_{p}\hat{u}w^{k}_{s}$ for $k=1,\ldots,m-1$ .

In the proof of this lemma we use the assumption that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ as we did in the proof of Lemma 4.6.

Proof.

The strategy of the proof is same as the proof of Lemma 4.6. In there, we ran the argument in $B_{m}(L,\eta(S))$ , but here, we do it in the set $Z(w)=\{w^{k}_{p}\hat{u}w^{k}_{s}|k=1,\cdots,m-1\}$ . Namely, if $w^{k}_{p}\hat{u}w^{k}_{s}\in Z(w)$ is forbidden for some $k$ , then there are two other elements in $Z(w)$ that are candidates for non-forbidden elements. Then if at least one of them is forbidden, then there are two other elements in $Z(w)$ that are candidates for non-forbidden elements, and so on. We omit details. ∎

Then we have:

Lemma 7.9 (cf. Lemma 3.6 [FS]).

For $m$ and the word $w$ as above, the non-forbidden words: $w^{k}_{p}\hat{v}_{i,j}w^{k}_{s}$ , for all $k$ , $1\leq k\leq m-1$ , are distinct elements in $L$ .

Proof.

The proof is nearly identical to the proof of Lemma 3.6 in [FS], and we omit it. ∎

As in Section 4, we define adequate elements in $Z(w)$ . We choose a maximal subset in the set of non-forbidden elements in $Z(w)$ such that for any two distinct elements $z_{1},z_{2}$ in the subset, $h_{n}(z_{1}),h_{n}(z_{2})$ are not in the same coset w.r.t. $F(h_{n}(u_{i}))$ for any separator $u_{i}$ . We call those elements adequate elements. This notion depends on $n$ . Then, as before,

\frac{|\{\text{non-forbidden elements}\}|}{\mathcal{D}^{4}}\leq|\{\text{adequate elements}\}|.

This is because, as we explained, there are only four separators, $\hat{u}$ , and $|F(h_{n}(\hat{u}))|\leq\mathcal{D}$ . In conclusion, since $|Z(w)|=m-1$ ,

(5)

\frac{m-1}{\mathcal{D}^{4}(\mathcal{D}+1)}\leq|\{\text{adequate elements in }Z(w)\}|.

Using adequate elements, we construct a collection of feasible words in $L$ .

Definition 7.10 (Feasible words in $L$ . cf. Definition 3.7 [FS]).

Let $m,q$ be positive integers. Let $w$ be a word of length $mq$ on $\eta(S)$ that is associated to an element $g\in\text{Sph\,}_{mq}(G,S_{n_{0}})$ as in the above discussion. We present $w$ as a concatenation of $q$ subwords of length $m$ : $w=w(1)\ldots w(q)$ .

Then for any choice of integers: $k_{1},\ldots,k_{q}$ with $1\leq k_{t}\leq m-1$ , and $t=1,\ldots,q$ , for which all the elements, $w(t)^{k_{t}}_{p}v^{t}w(t)^{k_{t}}_{s}$ , are adequate (here we drop the “hat” from $v^{t}$ deliberately although they are in $L$ to avoid confusion since we want to use it right in the below) , we associate a feasible word (of type $q$ ) on $\eta(S)$ (in $L$ ):

w(1)^{k_{1}}_{p}v^{1}w(1)^{k_{1}}_{s}\,\hat{v}^{1}\,w(2)^{k_{2}}_{p}v^{2}w(2)^{k_{2}}_{s}\,\hat{v}^{2}\,\ldots w(q)^{k_{q}}_{p}v^{q}w(q)^{k_{q}}_{s},

where for each $t$ , $1\leq t\leq q-1$ , $\hat{v}^{t}$ is one of the separators from Lemma 4.2 such that $\hat{v}^{t}$ is admissible for $w(t)^{k_{t}}_{s}$ and $(\hat{v}^{t})^{-1}$ is admissible for $\left(w(t+1)^{k_{t+1}}_{p}\right)^{-1}$ .

Finally we define the map $\phi_{n}$ . Suppose positive integers $m,q$ are given. Then for $g\in\text{Sph\,}_{mq}(G,S_{n_{0}})$ , choose one shortest representative $w(g)$ of length $mq$ on $S_{n_{0}}$ , which defines a word $\tilde{w}(g)$ of length $mq$ on $\eta(S)$ as in the definition 7.10. From $\tilde{w}(g)$ we produce feasible words on $\eta(S)$ , which define feasible elements in $L$ . Note that those elements are in $B_{q(m+2b)}(L,\eta(S))$ and mapped to $g$ by $h_{n_{0}}$ . We denote this collection as $\phi_{n}(g)$ .

We have :

Lemma 7.11 (cf. Lemma 3.8 [FS]).

For any positive integers $m,q$ , the feasible elements in the collection $\phi_{n}(g)$ we obtain for each $g\in\text{Sph\,}_{mq}(G,S_{n_{0}})$ are all distinct in $L$ .

Moreover, all the feasible elements obtained from all the elements $g$ in $\text{Sph\,}_{mq}(G,S_{n_{0}})$ are all distinct in $L$ .

In this lemma, $n$ must be large enough in the sense that Lemma 7.4 applies and also, for the given $m$ , the map $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ (cf. Lemma 4.5). We will choose such $n$ in the proof.

Proof.

The proof of the first sentence is similar to the proof of Lemma 4.8. So we omit it. (cf. the proof of Lemma 3.8 [FS].) Then the moreover part immediately follows. ∎

We note that for each $g$ , we have

(6)

\left(\frac{m-1}{\mathcal{D}^{4}(\mathcal{D}-1)}\right)^{q}\leq\phi_{n}(g).

This is from the lower bound (5) on the number of adequate elements and the lemma.

We finish the proof of the proposition 7.2. We review the setting. The constant $n_{0}$ is given to start with. We want to show $e(G,f_{n_{0}}(S))<e(L,\eta(S))$ . Then the constant $b$ is given by Lemma 7.4, which does not depend on $n$ . Choose $n$ large enough so that we can apply Lemma 7.4.

Then choose $m$ such that

\log(m-1)>2b\log(e(L,\eta(S))+\log(\mathcal{D}^{4}(\mathcal{D}-1)).

This implies:

\log(m-1)>2b\log(e(G,S_{n_{0}}))+\log(\mathcal{D}^{4}(\mathcal{D}-1)).

Then choose $n>0$ larger if necessary such that $h_{n}$ is injective on $B_{2m}(L,\eta(S))$ . We need this to apply Lemma 7.9.

Now, for all $q>0$ , by combining the lower bound (6) and (the moreover part of) Lemma 7.11, we have

|\text{Sph\,}_{mq}(G,S_{n_{0}})|\left(\frac{m-1}{\mathcal{D}^{4}(\mathcal{D}-1)}\right)^{q}\leq|B_{q(m+2b)}(L,\eta(S))|.

From this,

	$\displaystyle\log e(L,\eta(S))$	$\displaystyle\geq\lim_{q\to\infty}\frac{\log(\|\text{Sph\,}_{mq}(G,S_{n_{0}})\|(\frac{m-1}{\mathcal{D}^{4}(\mathcal{D}-1)})^{q})}{q(m+2b)}$
		$\displaystyle=\lim_{q\to\infty}\frac{\log(\|\text{Sph\,}_{mq}(G,S_{n_{0}})\|)}{q(m+2b)}+\frac{q(\log(m-1)-\log(\mathcal{D}^{4}(\mathcal{D}-1)))}{q(m+2b)}$
		$\displaystyle=\log(e(G,S_{n_{0}}))\frac{m}{m+2b}+\frac{\log(m-1)-\log(\mathcal{D}^{4}(\mathcal{D}-1))}{m+2b}$
		$\displaystyle>\log(e(G,S_{n_{0}})).$

The last inequality is by the way we chose $m$ . Hence, $e(L,\eta(S))>e(G,S_{n_{0}})$ . We proved Proposition 7.2. ∎

7.4. Family version

We state a family version of Proposition 7.2. Let $\delta,M$ be constants and $D(\epsilon)$ a function for WPD. Suppose $X_{n}$ is $\delta$ -hyperbolic, a group $G_{n}$ acts on $X_{n}$ and $S_{n}$ is a finite generating set of $G_{n}$ such that $S_{n}^{M}$ contains a hyperbolic element on $X_{n}$ that is $D$ -WPD.

Suppose that $|S_{n}|=\ell$ for all $n$ , and let $F$ be a free group of rank $\ell$ with a free generating set $S$ . Let $f_{n}:(F,S)\to(G_{n},S_{n})$ be a surjection with a bijection $f_{n}(S)=S_{n}$ . Assume that the sequence $\{f_{n}\}$ converges to $\eta:(F,S)\to(L,\eta(S))$ .

Also, assume that for all $n$ , there is a surjection $h_{n}:(L,\eta(S))\to(G_{n},S_{n})$ with $f_{n}=h_{n}\circ\eta$ . As in Proposition 4.9, we put this as an assumption. Then we have the following generalizing Proposition 7.2. The proof is identical and we omit it.

Proposition 7.12.

Assume that for all $n$ , there is a surjection $h_{n}:(L,\eta(S))\to(G_{n},S_{n})$ with $f_{n}=h_{n}\circ\eta$ . If $\ker(h_{n_{0}})$ is infinite for some $n_{0}$ , then

e(G_{n_{0}},f_{n_{0}}(S))<e(L,\eta(S)).

7.5. Finiteness for $\Theta_{X}(G)$

A finiteness result similar to Theorem 7.1 holds for subgroups. It is known for hyperbolic groups, [FS, Theorem 5.3].

Let $S_{1},S_{2}\subset G$ be two finite subsets. Let $H_{i}=\langle S_{i}\rangle<G$ be the subgroup generated by $S_{i}$ . We say $(H_{1},S_{1})$ and $(H_{2},S_{2})$ are isomorphic if there is a bijection between $S_{1},S_{2}$ that induces an isomorphism between $H_{1},H_{2}$ .

Theorem 7.13 (Finiteness in the subgroups case).

Assume the same condition on $G$ as in Theorem 7.1. Moreover, we assume that if $S$ is a finite set of $G$ such that $\langle S\rangle$ contains a hyperbolic isometry on $X$ , then $S^{M}$ contains a hyperbolic isometry that is $D$ -WPD. Let $\rho\in\Theta_{X}(G)$ , Then there are at most finitely many $(H,S)$ , up to isomorphism, such that $S\subset G$ is finite, $H=\langle S\rangle$ , $H$ contains a hyperbolic element on $X$ , and $\rho=e(H,S)$ .

The proof is nearly identical to the proof of Theorem 7.1 and we only need to modify the setting from the entire group $G$ to subgroups.

Proof.

To argue by contradiction, let $\rho\in\Theta_{X}(G)$ and suppose that there are infinitely many distinct, up to isomorphism, $(H_{n},S_{n})$ with $e(H_{n},S_{n})=\rho$ such that $H_{n}$ contains a hyperbolic isometry on $X$ . Note that by assumption, $S_{n}^{M}$ contains a hyperbolic isometry that is $D$ -WPD.

As before, by Proposition 2.10, passing to a subsequence, one may assume that there is $\ell$ with $|S_{n}|=\ell$ for all $n$ . Then we obtain $f_{n}:F\to G$ with $f_{n}(S)=S_{n}$ , where $F$ is the free group on $S$ with $|S|=\ell$ . Then, passing to a subsequence again, $f_{n}$ converges to a limit group $(L,\eta(S))$ with $\eta:F\to L$ . Since $G$ is equationally Noetherian, by Lemma 1.11, passing to a further subsequence, we may assume that there are $h_{n}:L\to H_{n}<G$ with $h_{n}\circ\eta=f_{n}$ for all $n$ .

First, by Proposition 6.2, we have that $e(H_{n},S_{n})=e(L,\eta(L))$ for all $n$ .

On the other hand, we prove a version of Proposition 7.2 for subgroups: if $\ker(h_{n_{0}})$ is infinite for some $n_{0}$ , then $e(H_{n_{0}},S_{n_{0}})<e(L,\eta(S))$ . The proof is same and we only outline it. As before set $\mathcal{D}=D(100\delta)$ . First, since $H_{n}$ contains a hyperbolic isometry on $X$ that is $D$ -WPD, each $H_{n}$ contains the maximal finite normal subgroup, which we denote by $N_{H_{n}}$ with $|N_{H_{n}}|\leq 2\mathcal{D}$ , (by Lemma 7.3).

The key step is to prove a lemma similar to Lemma 7.4. The argument is same. We use that $S_{n}^{M}$ has a hyperbolic and $D$ -WPD element for all $n$ . Then, as before, for all sufficiently large $n$ , there exists an element $r(n)\in\ker(h_{n_{0}})$ such that $h_{n}(r(n))$ is hyperbolic on $X$ , and that the word length of $r(n)$ in terms of $\eta(S)$ is bounded uniformly on $n$ . Then then rest is same as proving the lemma. Once we have the lemma, the rest is same to show the proposition. (We point out that this is a special case of Proposition 7.12, where $X_{n}$ are common. But we did not describe the details of the argument for that.)

Combining those two, we conclude that $\ker(h_{n})$ is finite for all $n$ .

Finally, there are only finitely many possibilities for $\ker(h_{n})$ since it is contained in $N_{L}$ and $|N_{L}|\leq 2\mathcal{D}$ . It implies that the desired finiteness for $(H_{n},S_{n})$ holds as before. ∎

7.6. Examples

We give some examples of Theorem 7.1 and Theorem 7.13. We start with relatively hyperbolic groups.

Theorem 7.14 (Finiteness for relatively hyperbolic groups).

Moreover, for each $\rho\in\Theta_{{\rm non-elem.}}(G)$ , there are at most finitely many $(H_{n},S_{n})$ , up to isomorphism, s.t. $e(H_{n},S_{n})=\rho$ , where $S_{n}\subset G$ is finite and $H_{n}=\langle S_{n}\rangle$ is not conjugate into any $P_{i}$ .

Proof.

Let $X$ be a hyperbolic space on which $G$ acts as we explained in Section 5.1. We also verified that all the assumption of Theorem 7.1 for $G$ and the action of $G$ on $X$ . Recall that the action of $G$ on $X$ is uniformly WPD by Lemma 5.2. It implies the first part of the theorem.

For the moreover part, we apply Theorem 7.13. As Lemma 6.4 shows, $\Theta_{{\rm non-elem.}}(G)=\Theta_{X}(G)$ , which implies the conclusion. ∎

Theorem 7.14 immediately implies the following as Theorem 6.5 implies Theorem 6.6:

Theorem 7.15 (Finiteness for lattices).

Let $G$ be a group in Theorem 5.5. Then for each $\rho\in\xi(G)$ there are at most finitely many finite generating sets $S_{n}$ , up to $\text{Aut\,}(G)$ , s.t. $e(G,S_{n})=\rho$ .

Moreover, for each $\rho\in\Theta(G)$ , there are at most finitely many $(H_{n},S_{n})$ , up to isomorphism, s.t. $e(H_{n},S_{n})=\rho$ , where $S_{n}\subset G$ is finite and $H_{n}=\langle S_{n}\rangle$ .

Lastly we record the following (potential) example:

Theorem 7.16 (Finiteness for MCG).

Let $MCG=MCG(\Sigma)$ be the mapping class group of a compact orientable surface $\Sigma$ . Assume that it is equationally Noetherian.

Then for each $\rho\in\xi(MCG)$ there are at most finitely many finite generating sets $S_{n}$ , up to $\text{Aut\,}(MCG)$ , such that $e(MCG,S_{n})=\rho$ .

Moreover, for each $\rho\in\Theta_{{\rm large}}(MCG)$ , there are at most finitely many $(H_{n},S_{n})$ , up to isomorphism, such that $e(H_{n},S_{n})=\rho$ , where $S_{n}\subset MCG$ is finite and $H_{n}=\langle S_{n}\rangle$ is a large subgroup.

Proof.

As we explained in Section 5.3, the action of $MCG(\Sigma)$ on the curve graph $X=\mathcal{C}(\Sigma)$ satisfies the assumption of Theorem 7.1. It is uniformly WPD.

For the moreover part, the conclusion holds for $\Theta_{X}(MCG)$ by Theorem 7.13. But, as we said in the proof of Theorem 6.7, we have $\Theta_{X}(MCG)=\Theta_{{\rm large}}(MCG)$ , so that the conclusion holds. ∎

References

[AL] G. N. Arzhantseva and I. G. Lysenok, A lower bound on the growth of word hyperbolic groups, Jour. of the LMS 73 (2006), 109-125.
[BMR] Gilbert Baumslag, Alexei Myasnikov, Vladimir Remeslennikov, Algebraic geometry over groups. I. Algebraic sets and ideal theory. J. Algebra 219 (1999), no. 1, 16–-79.
[BMR2] Gilbert Baumslaga, Alexei Myasnikov, Vitaly Roman’kov. Two Theorems about Equationally Noetherian Groups. Journal of Algebra Volume 194, Issue 2, Pages 654-664
[BeF] Mladen Bestvina, Koji Fujiwara, Bounded cohomology of subgroups of mapping class groups. Geom. Topol. 6 (2002), 69-–89.
[BeF2] Mladen Bestvina, Koji Fujiwara. Handlebody subgroups in a mapping class group. In the Tradition of Ahlfors–Bers, VII. Contemporary Mathematics Volume 696, 2017, Pages 30-50. AMS.
[Bo1] B. H. Bowditch, Relatively hyperbolic groups. Internat. J. Algebra Comput. 22 (2012), no. 3, 66 pp.
[Bo] Brian H. Bowditch, Tight geodesics in the curve complex. Invent. Math. 171 (2008), no. 2, 281-–300.
[BrF] E. Breuillard, K. Fujiwara. On the joint spectral radius for isometries of non-positively curved spaces and uniform growth. to appear in Annales de l’institut Fourier.
[Br] Roger M. Bryant, The verbal topology of a group. J. Algebra 48 (1977), no. 2, 340–-346.
[DGO] F. Dahmani, V. Guirardel, D. Osin, Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces. Mem. Amer. Math. Soc. 245 (2017), no. 1156, 152 pp.
[De] Thomas Delzant, Kaehler groups, $\mathbb{R}$ -trees, and holomorphic families of Riemann surfaces. Geom. Funct. Anal. 26 (2016), no. 1, 160-–187.
[DrS] Cornelia Druţ̧u, Mark Sapir, Tree-graded spaces and asymptotic cones of groups. With an appendix by Denis Osin and Mark Sapir. Topology 44 (2005), no. 5, 959-–1058.
[EMO] Alex Eskin, Shahar Mozes, Hee Oh, On uniform exponential growth for linear groups. Invent. Math. 160 (2005), no. 1, 1-–30.
[Fa] B. Farb, Relatively hyperbolic groups. Geom. Funct. Anal. 8 (1998), no. 5, 810-–840.
[F] K. Fujiwara, Subgroups generated by two pseudo-Anosov elements in a mapping class group. I. Uniform exponential growth. Groups of diffeomorphisms, 283–-296, Adv. Stud. Pure Math., 52, Math. Soc. Japan, 2008.
[FS] K. Fujiwara, Z. Sela. The rates of growth in a hyperbolic group. to appear in Invent. Math.
[G] M. Gromov. Hyperbolic groups. Essays in group theory, 75–263, Math. Sci. Res. Inst. Publ., 8, Springer, New York, 1987.
[GHL] Daniel Groves, Michael Hull, Hao Liang. Homomorphisms to 3-manifold groups. arXiv:2103.06095
[GrH] D. Groves, M. Hull, Homomorphisms to acylindrically hyperbolic groups I: Equationally noetherian groups and families. Trans. Amer. Math. Soc. 372 (2019), no. 10, 7141-–7190.
[Gu] Victor S. Guba. Equivalence of infinite systems of equations in free groups and semigroups to finite subsystems. Mat. Zametki, 48(3):321-–324, 1986.
[K] M. Koubi, Croissance uniforme dans les groupes hyperboliques, Ann. Inst. Fourier 48 (1998), 1441–1453.
[Ma] Johanna Mangahas, A recipe for short-word pseudo-Anosovs. Amer. J. Math. 135 (2013), no. 4, 1087–-1116.
[Ma2] Johanna Mangahas, Uniform uniform exponential growth of subgroups of the mapping class group. Geom. Funct. Anal. 19 (2010), no. 5, 1468-–1480.
[MM1] Howard A. Masur, Yair N. Minsky, Geometry of the complex of curves. I. Hyperbolicity. Invent. Math. 138 (1999), no. 1, 103-–149.
[MO] Ashot Minasyan, Denis Osin. Acylindrical hyperbolicity of groups acting on trees. Mathematische Annalen 362, (2015), 1055–1105
[NS] Hoang Thanh Nguyen, Hongbin Sun, Subgroup distortion of 3-manifold groups. Trans. Amer. Math. Soc. 373 (2020), no. 9, 6683–-6711.
[O] D. Osin. Acylindrically hyperbolic groups. Trans. Amer. Math. Soc. 368 (2016), no. 2, 851–-888.
[RW] C. Reinfeldt, R. Weidmann, Makanin-Razborov diagrams for hyperbolic groups. Ann. Math. Blaise Pascal 26 (2019), no. 2, 119-–208.
[Sa] A. Sambusetti. Growth tightness of free and amalgamated products. Ann. Sci. Ecole Norm. Sup. serie 35 (2002), no. 4, 477–-488.
[S] Z. Sela, Diophantine geometry over groups I: Makanin-Razborov diagrams, Publication de la IHES 93 (2001), 31-105.
[Se] Jean-Pierre Serre, Trees. Translated from the French by John Stillwell. Springer-Verlag, Berlin-New York, 1980.
[Si] A. Sisto. Projections and relative hyperbolicity. Enseign. Math. (2) 59 (2013), no. 1-2, 165-–181.
[W] J. S. Wilson, On exponential growth and uniformly exponential growth for groups, Inventiones math. 155 (2004), 287-303.
[WZ] Henry Wilton, Pavel Zalesskii, Profinite detection of 3-manifold decompositions. Compos. Math. 155 (2019), no. 2, 246–259.
[X] Xiangdong Xie, Growth of relatively hyperbolic groups. Proc. Amer. Math. Soc. 135 (2007), no. 3, 695–-704.

The rates of growth in an acylindrically hyperbolic group

Abstract.

1. Introduction

1.1. Definitions and results

Theorem 1.1 (Well-orderedness for acylindrical actions).

Theorem 1.2 (Theorem 5.4).

Theorem 1.3 (Rank-1 lattices, Theorem 5.5).

Theorem 1.4 (Theorem 5.7).

Theorem 1.5 (Theorem 7.1).

Theorem 1.6 (Theorem 6.6).

Theorem 1.7 (Finiteness, Theorem 7.15).

1.2. Acylindrical actions

Definition 1.8 (acylindrical action).

1.3. Limit groups and equational Noetherianity

Definition 1.9 (Equationally Noetherian).

Remark 1.10.

Lemma 1.11 (Basic principle).

Proof.

Example 1.12.

2. Lower bound of a growth rate

2.1. Hyperbolic isometries and axes

2.2. WPD elements

Definition 2.1 (WPD, uniformly WPD, DD-WPD).

Lemma 2.2 (Lower bound on λ​(g)\lambda(g)).

Proof.

Lemma 2.3 (Acylindricity implies uniform WPD).

Proof.

Lemma 2.4.

Proof.

2.3. Elementary closure

Lemma 2.5 (parallel axes).

Proof.

Proposition 2.6 (elementary closure).

Proof.

2.4. About the constants

2.5. Lower bound of a growth rate

Lemma 2.7 (hyperbolic element of large displacement).

Lemma 2.8 (free subgroup with primitive hyperbolic elements).

Remark 2.9.

Proof.

Proposition 2.10 (Lower bound of growth).

Proof.

Example 2.11.

3. Well-orderedness

3.1. Main theorem

Theorem 3.1 (Well-orderedness for uniform WPD actions).

Proof.

Proposition 3.2.

4. Continuity of the growth rate

4.1. Separators

Definition 4.1 (germs, equivalent and opposite germs).

Lemma 4.2 (The constant bb and separators. c.f. Lemma 2.4 [FS]).

Remark 4.3.

Proof.

4.2. Forbidden elements

Definition 4.4 (forbidden elements and tails).

Lemma 4.5 (Parallel tails).

Proof.

4.3. Ratio of forbidden elements

Lemma 4.6.

Proof.

4.4. Feasible elements

Definition 4.7 (feasible elements).

Lemma 4.8 (cf. [FS],Lemma 2.6).

Proof.

4.5. Proof of Proposition 3.2

Proof.

4.6. A family version

Proposition 4.9.

5. Examples

5.1. Relatively hyperbolic groups

Lemma 5.1 (Proposition 5.1[X]).

Lemma 5.2.

Proof.

Theorem 5.3 (Equationally Noetherian, [GrH]).

Theorem 5.4 (Well-orderedness for relatively hyperbolic groups).

Proof.

5.2. Rank-1 lattices

Theorem 5.5 (Rank-1 lattices).

Proof.

Definition 2.1 (WPD, uniformly WPD, $D$ -WPD).

Lemma 2.2 (Lower bound on $\lambda(g)$ ).

Lemma 4.2 (The constant $b$ and separators. c.f. Lemma 2.4 [FS]).

Definition 7.10 (Feasible words in $L$ . cf. Definition 3.7 [FS]).

7.5. Finiteness for $\Theta_{X}(G)$