Present address ]Department of Physics, Faculty of Science, King Khalid University, Abha, Kingdom of Saudi Arabia
Present address ]GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany, and Helmholtz-Institut Mainz, Mainz, Germany
Present address ]IFIC, CSIC-Universitat de Valéncia, Valéncia, Spain
Present address ]Institute of Nuclear Research, MTA ATOMKI, Debrecen, Hungary
The radiative width of the Hoyle state from -ray spectroscopy
Abstract
The cascading 3.21 MeV and 4.44 MeV electric quadrupole transitions have been observed from the Hoyle state at 7.65 MeV excitation energy in 12C, excited by the 12C(p,p′) reaction at 10.7 MeV proton energy. From the proton-- triple coincidence data, a value of was obtained for the radiative branching ratio. Using our results, together with from Eriksen et al. 2020Eriksen_PRC and the currently adopted values, the radiative width of the Hoyle state is determined as eV. This value is about 34% higher than the currently adopted value and will impact on models of stellar evolution and nucleosynthesis.
The triple-alpha reaction, which produces stable 12C in the universe, is a fundamental processes of helium burning stars. The entry state of the triple-alpha process, the second excited state in 12C, is a state at 7.65 MeV. It has attracted significant attention 2014Fr14 ; 2020Sm01 ; 2016Fu07 since it was first proposed in 1953 by Fred Hoyle 1953Ho81 . The existence of the state was confirmed in the same year from the analysis of the -spectrum from the 14N(d,)12C reaction 1953Du23 . The Hoyle state is unbound and the dominant decay process (%) is through the emission of an alpha particle, leading to the very short lived isotope, 8Be, which then disintegrates into two alpha particles. Stable carbon will only be produced either if the Hoyle state decays directly to the ground state via an electric monopole (E0) transition or by a cascade of two electric quadrupole (E2) transitions.
Due to its unusual structure, the Hoyle state has attracted continuous attention; see the recent review of Freer and Fynbo 2014Fr14 and other recent works 2013Zi03 ; 2015Fu09 ; 2020Sm01 . The discussion includes nuclear clustering, a spacial arrangement of the three particle clusters of which the state is believed to be composed, and discussion on a new form of nuclear matter, in analogy with the Bose-Einstein condensates. The characterization of the and states on top of the 7.65 MeV state, forming the Hoyle band 2018Garg_JPC , together with much improved ab initio calculations 2018Launey_AIP are important steps forward.
The production rate of stable carbon in the universe is cardinal for many aspects of nucleosynthesis. The reaction rate is closely related to the decay properties of the Hoyle state. The triple-alpha reaction rate can be expressed as: 1988RolfsRodney . Here is the total electromagnetic (radiative) decay width, is the energy release in the three breakup of the Hoyle state, and T is the stellar temperature. has contributions from the 3.21-MeV E2 and the 7.65-MeV E0 transitions. The contributions of electron conversion are negligible, so including photon () and pair conversion (), . Based on current knowledge, 98.4% of the electromagnetic decay width is from the E2 photon emission and 1.5% is from the E0 pair decay 2009KiZZ . The contribution is less than 0.1%.
The value of cannot be directly measured. It is usually evaluated as a product of three independently measured quantities:
| (1) |
where is the total decay width of the Hoyle state, which includes the , as well as the E2 and E0 electromagnetic decays.
The only absolute quantity in Eq. (1) is , which has been measured 8 times 1956Fr27 ; 1964Cr01 ; 1965Gu04 ; 1967Cr01 ; 1968St20 ; 1970St10 ; 2005Cr03 ; 2010Ch17 . The two most recent measurements 2005Cr03 ; 2010Ch17 are the most precise; however they disagree by more than 5. Following the recommendation of Freer and Fynbo 2014Fr14 , we have adopted a value of 62.3(20) eV from the latter study.
The least precisely known quantity is . Combining all previous measurements 1960Al04 ; 1960Aj04 ; 1972Ob01 ; 1977Al31 ; 1977Ro05 , a value of was adopted 2014Fr14 . This value has been further improved by a new pair conversion measurement at the ANU 2020Eriksen_PRC and a ratio of was recommended.
The third term, , has been measured 8 times between 1961 and 1976 1961Al23 ; 1963Se23 ; 1964Ha23 ; 1974Ch03 ; 1975Da08 ; 1975Ma34 ; 1976Ma46 ; 1976Ob03 . By excluding the value of 2.8(3) by Seeger and Kavanagh 1963Se23 , the weighted mean value is 4.13(11). In Ref. 2014Fr14 , a slightly higher value of 4.19(11) was recommended. is claimed to be the most precise term in Eq. (1).
In the present paper we report a new measurement of , which was deduced from the rate of proton-- triple coincidences, , corresponding to the de-excitation of the Hoyle state through the emission of the 3.21 and 4.44 MeV -cascade, to the rate of singles proton events, , exciting the Hoyle state:
| (2) |
where and are the photon detection efficiencies, and is the angular correlation correction for a 0-2-0 cascade. Our approach is similar to that of Obst and Braithwaite 1976Ob03 , but with much improved experimental apparatus and analysis techniques.
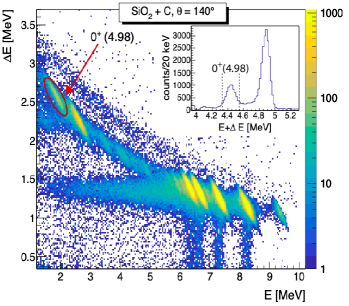
The experiments were carried out at the Cyclotron Laboratory of the University of Oslo. The Hoyle state was populated in inelastic scattering of 10.7 MeV protons on a 180 g/cm2 natural carbon target. This energy was slightly higher than the notional optimum energy of 10.5 MeV, where the 12C(p,p′) reaction has a relatively broad resonance 1971Da36 . The higher proton energy was employed to shift the inelastically scattered protons to 1.5 MeV, well above the detecting threshold. Proton angular distribution measurements 2020Eriksen_PRC suggest that the ratio of the excitation of the 4.44 MeV and 7.65 MeV states is essentially the same at 10.5 and 10.7 MeV. In the present experiments a beam intensity of 5 nA was used, keeping the total count rate below 3 kHz. Additional experiments were carried out using a target consisting of a layer of 140 g/cm2 SiO2 on a 32 g/cm2 natural carbon backing. The 28Si(p,p′) reaction was used to determine the photon detection efficiencies. The state at 4.98 MeV in 28Si decays with a 100% branching ratio to the ground state through the emission of a 3.20 MeV - 1.78 MeV cascade. In addition, the 4.50 MeV - 1.78 MeV cascade from the 6.28 MeV state was also analyzed. The branching ratio of this cascade is 2013Ba53 .
Proton-- coincidences were measured with the SiRi particle telescope 2011Guttormsen and the CACTUS -ray detector array 1990Guttormsen . The 64 telescopes of SiRi were placed in the backward direction covering angles between and relative to the beam direction. The solid angle of the particle detection was around 6% of 4. The front () and back () particle detectors have thicknesses of m and m, respectively. -rays were recorded with the CACTUS array consisting of 26 collimated 5” 5” NaI(Tl) detectors, placed at 22 cm from the target. Each detector had a 10 cm lead collimator to ensure illumination of the center of the detector. The total photon efficiency of the array is 14.2% of 4 at 1.33 MeV energy.
Signals in the detectors were used as triggers and to start the time-to-digital-converter (TDC). The stop signal was generated when any NaI(Tl) detector fired. In this way prompt proton-- coincidences could be sorted from the event-by-event data. Fig. 1 shows the energy deposition in the vs. detectors recorded with the SiO2 plus carbon target. The fraction of the particle energy deposited in the front detector depends on , and the particle energy. This relation, visible in Fig. 1 as a “banana” shaped region, can be used to identify the detected particles, and also to filter events of incomplete energy deposition (horizontal and vertical bands), as well as other beam related background events. The spectrum can be used to select the population of specific states. Protons exciting the Hoyle state fully stop in the detector. In this case the telescope was operated in anti-coincidence to reject high energy particle events depositing only partial energy in the detector.
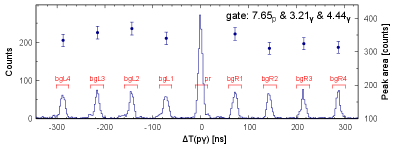
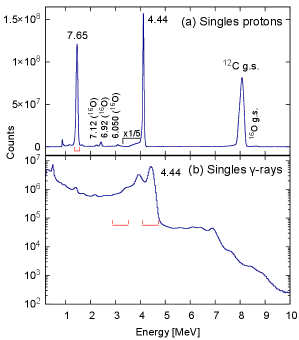
Fig. 2 shows the spectra of singles proton and -ray events from the 12C(p,p′) reaction collected over a period of 12 days. The peak at 1.5 MeV proton energy, labelled as “7.65”, represents the excitation of the Hoyle state. It contains events, however only 1 out of 2500 proton excitations is expected to result in electromagnetic transitions leading to the ground state of 12C. In comparison, the number of protons exciting the 4.44 MeV state is about 4.7 times higher, and this state always decays to the ground state with an E2 -ray transition. The singles -ray spectrum, shown in panel (b) of Fig. 2, is dominated by the 4.44 MeV photon events. Beside the full energy peak, there is a broad distribution of events of single (at 3.9 MeV) and double (at 3.4 MeV) escapes, as well as Compton scattering. The 3.21 MeV transition is expected to be about 10000 times weaker and it partially overlaps with second escape peak of the 4.44 MeV line. In this energy region the photon energy resolution was around 0.19 MeV. Excitation of the 4.44 MeV state will only produce a single photon event. However, we estimated that the probability of two 4.44 MeV -rays produced by two unrelated reactions and observed in prompt coincidence is per second, which is about three times lower than the true coincidence rate and can be considered as high.
Fig. 3 shows the time differences between protons exciting the Hoyle state and a pair of 3.21 and 4.44 MeV -rays. The main peak at = 0 ns (“pr”) corresponds to -rays in prompt coincidence with protons. The secondary peaks (“bgLx” and “bgRx”) occurring every 72 ns are from accidental coincidences where one of the two gamma-rays was produced in another beam burst. The 4 background gates either side of the prompt and equal width to the prompt peak were averaged over.
Panel (a) of Fig. 4 shows protons (“7.65”) in prompt coincidence with a 3.21 and a 4.44 MeV -rays without subtraction of accidental coincidences. In the same spectrum , the number of protons exciting the state (“4.44”), is due to accidental coincidences and is nearly 50 times higher. Using TDC gates of “pr-pr”, “pr-bgLx”, “pr-bgRx” and “bgLx-bgRx” the numbers of events in the corresponding proton spectra are 8251(91), 7697(88), 7914(89) and 54(9), respectively. Protons exciting the state will only produce single photon events, therefore the rates can be used to remove the random events. Using the above rates the scaling factor was obtained as . The rates in the same TDC gates were 249(16), 158(13), 197(14) and 66(8), respectively. This gives counts. The final proton spectrum in triple coincidence with the 3.21 and 4.44 MeV -rays is shown in panel (b) of Fig. 4.
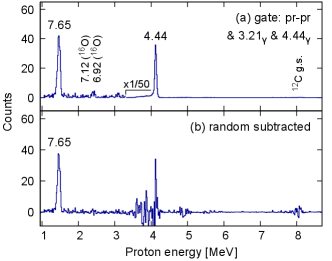
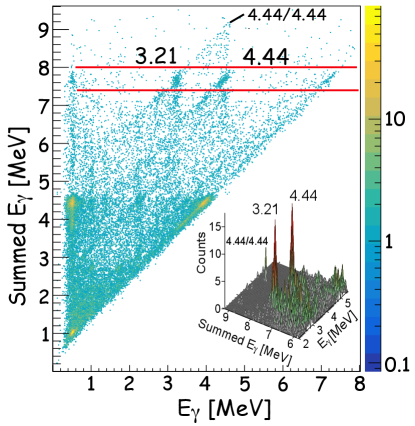
Fig. 5 shows the - coincidence events gated by protons exciting the Hoyle state, where the horizontal axis is the -ray energy and the vertical axis is the summed energy of the two gamma-rays in coincidence. The number of random events has been evaluated using the accidental coincidences of the 4.44 MeV gamma-ray with itself, indicated as “4.44/4.44”. The number of such events in the various TDC gates were 131(12), 157(13), 134(12), 63(8), which gives a subtraction factor of 1.15(11), a value consistent with the one obtained from the proton spectra. To deduce the final coincidence spectra, the scaling factor of 1.061(12) was adopted. Fig. 5 also shows the final matrix of coincidence events. A small residue of the 4.44-4.44 random coincidences is visible, but the number of related events under the peaks of interest is negligible.
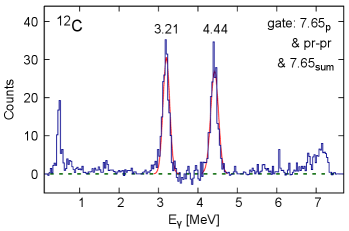
The final -ray spectrum of the 3.21-4.44 MeV cascade is shown in Fig. 6. The areas of the 3.21 and 4.44 MeV photon peaks, 208(21) and 213(21) counts, were obtained by fitting Gaussian functions to these data.
Using the scaling factor of 1.061(12), the true triple coincidence events in the prompt peak in Fig. 3 was evaluated as . The adopted value of the was obtained as the weighted mean of the three values deduced from the different projections.
The absolute photon detection efficiency, , was evaluated using the Penelope code 2008Savat . The same simulations were used to evaluate the correction factors, and , for the -ray angular correlation, including geometrical attenuation coefficients 1953Rose , listed in Table 1. To confirm the accuracy of the simulations, the proton gated spectrum of the 1.78 and 4.50 MeV -rays from the 6.28 MeV state in 28Si was used. The ratio of the peak areas of the 1.78 MeV and 4.50 MeV transitions is 1.58(3), which after applying the 1.0170(15) correction for the angular correlation, is very close to the value of 1.63(4) from the simulations.
By evaluating Eq. 2 with values from Table 1 and considering all 325 NaI detector combinations, we obtained .
To reduce dependence on the Monte Carlo evaluation of the absolute efficiencies and perform an analysis similar to that of Obst and Braithwaite 1976Ob03 , the ratio was deduced using:
| (3) |
The symbols are as given for Eq. (1). An alternative equation can be obtained using the 6.28 MeV state in 28Si. Using the singles proton and triple coincidence rates of the 4.98 MeV and 6.28 MeV states, the ratio of the proton to photon efficiencies could be determined. Combining the results from Eq. 3 and using numerical values from Table 1, we again obtain =6.1(6).
Using the theoretical total conversion coefficient, 2008Ki07 and the recommended value of 2020Eriksen_PRC , we obtain . This value is more than 3 away from the currently recommended value 2014Fr14 . Most of the previous measurements 1974Ch03 ; 1975Da08 ; 1975Ma34 ; 1976Ma46 were based on counting the number of 12C atoms surviving after the Hoyle state was formed in various nuclear reactions. To achieve high statistics, the particle detection was carried out without magnetic selection and often with reported count rates above 10 kHz. Under these conditions the elimination of accidental coincidences is very challenging.
The investigation by Obst and Braithwaite 1976Ob03 deduced the ratio using a similar procedure to the present study. Their final result, which was obtained using Eq. (14) of their paper, contains five ratios ( to ). Despite some differences between their experiment and ours, various combinations of these ratios should agree within a few percent. The largest difference occurs for , Ref. 1976Ob03 reports 0.409(15) whereas our value is 0.80(4). Thus most of the difference between Obst and Braithwaite 1976Ob03 and our work stems from the ratio in the 28Si calibration data. Our results were independently checked in Canberra and Oslo using different analysis software.
| (7.65 ) | (4.98) | (6.28) | |
|---|---|---|---|
| 217(21) | 2233(68) | 6295(106) | |
| -ray | =0.221(3) | =0.222(3) | =0.186(3) |
| efficiency [%] | =0.187(3) | =0.304(3) | |
| 0.9582(15) | 0.9623(15) | 1.0170(15) | |
Moreover, the data of Obst and Braithwaite for are not self consistent. Using the photon efficiencies, the correction factors for the angular correlations and the -ray branching ratio from the , state we have:
| (4) |
The data of 1976Ob03 are in disagreement with Eq. (4) by a factor of two; the present data (Table 1) agree within 2%.
Finally, using the recommended 2020Eriksen_PRC , the adopted and our values, the radiative width of the Hoyle state is . This result suggests a significantly higher radiative width than currently adopted.
The triple-alpha reaction together with 12C() are the two most important helium burning nuclear reactions with a significant impact on nucleosynthesis and the evolution of massive stars 2007Tur_Apj ; 2013West_Apj ; 2018Fields_Apj . In the core-He burning cycle these reactions compete to determine the relative carbon and oxygen abundances before the core-C burning starts. The uncertainties due to production rates grow at every step. This makes the uncertainty of the triple-alpha and the 12C() reaction rates crucial for the production of heavy elements. Recent calculations 2013West_Apj ; 2018Fields_Apj have explored variations within the uncertainties of the production rates: for the triple-alpha and for the 12C() reactions. West, Heger and Austin 2013West_Apj pointed out that a 25% increase in the triple alpha rate would be consistent with a 33% larger 12C() rate. Here we report a 34% change in the triple-alpha reaction rate, which is outside of the parameter space of the calculations. This scenario needs to be explored, as it could change many of the model predictions.
In summary, a new measurement of the ratio of the
Hoyle state has been performed using a much improved experimental setup than used in the last
study, more than 40 years ago, giving a value that is significantly higher.
The accurate determination of the triple-alpha rate remains a challenge for low energy nuclear physics.
The present experiment only focused on one of the three terms defined in Eq. (1).
Confirmation of the new result, using higher resolution photon spectrometers is well warranted.
Additional experiments of the ratio, as well as
of the E0 width, are equally important.
Acknowledgements.
The project was supported by the Australian Research Council Discovery Grants DP140102986, DP170101673 and by the Research Council of Norway, Grant 263030. TK, BA and AES acknowledge the hospitality of the University Oslo during the experiments. ACL gratefully acknowledges funding from the European Research Council through ERC-STG-2014, Grant Agreement no. 637686.References
- (1) T.K. Eriksen, T. Kibédi, M.W. Reed, A.E. Stuchbery, K.J. Cook, A. Akber, et al., Phys. Rev. C102, 024320 (2020).
- (2) M. Freer, H.O.U. Fynbo, Prog. Part. Nucl. Phys. 78, 1 (2014).
- (3) R. Smith, M. Gai, M.W. Ahmed, M. Freer, H.O.U. Fynbo, D. Schweitzer, S.R. Stern, Phys. Rev. C101, 021302(R) (2020).
- (4) Y. Funaki, Phys. Rev. C94, 024344 (2016).
- (5) F. Hoyle, Astrophys. J. Suppl. Ser. 1, 12 (1953).
- (6) D.N.F. Dunbar, R.E. Pixley, W.A. Wenzel, W. Whaling, Phys. Rev. 92, 649 (1953).
- (7) Y. Funaki, Phys. Rev. C92, 021302(R) (2015).
- (8) W.R. Zimmerman et al., Phys. Rev. Lett. 110, 152502 (2013).
- (9) R. Garg, et al., J. Phys. Conf. Ser. 940, 012043 (2018)
- (10) K.D. Launey, A. Mercenne, G.H. Sargsyan, H. Shows, R.B. Baker, M.E. Miora, T. Dytrych, J.P. Draayer AIP Conference Proceedings 2038, 020004 (2018)
- (11) C.E. Rolfs and W.S. Rodney, Cauldrons in the cosmos: nuclear astrophysics, Chicago, University of Chicago Press, (1988).
- (12) T. Kibédi, A.E. Stuchbery, G.D. Dracoilis, A. Devlin, A. Teh, K. Robertson, AIP Conf. Proc. 1109, 66 (2009).
- (13) J.H. Fregeau, Phys. Rev. 104, 225 (1956).
- (14) H.L. Crannell and T.A. Griffy, Phys. Rev. 136, 1580 (1964).
- (15) F. Gudden and P. Strehl, Z. Phys. 185, 111 (1965).
- (16) H. Crannell, T.A. Griffy, L.R. Suelzle, M.R. Yearian, Nucl. Phys. A 90, 152 (1967).
- (17) P. Strehl and T.H. Schucan, Phys. Lett. B 27, 641 (1968).
- (18) P. Strehl, Z. Phys. 234, 416 (1970).
- (19) H. Crannell, X. Jiang, J.T. O’Brien, D.I. Sober, E. Offermann, Nucl. Phys. A 758, 399 (2005).
- (20) M. Chernykh, H. Feldmeier, T. Neff, P. von Neumann-Cosel, A. Richter, Phys. Rev. Lett. 105, 022501 (2010).
- (21) F. Ajzenberg-Selove, P.H. Stelson, Phys. Rev. 120, 500 (1960).
- (22) D.E. Alburger, Phys. Rev. 118, 235 (1960).
- (23) A.W. Obst, T.B. Grandy, J.L. Weil, Phys. Rev. C5, 738 (1972).
- (24) D.E. Alburger, Phys. Rev. C16, 2394 (1977).
- (25) R.G.H. Robertson, R.A. Warner, S.M. Austin, Phys. Rev. C15, 1072 (1977).
- (26) D.E. Alburger, Phys. Rev. 124, 193 (1961).
- (27) P.A. Seeger, R.W. Kavanagh, Nucl. Phys. 46, 577 (1963).
- (28) I. Hall, N.W. Tanner, Nucl. Phys. 53, 673 (1964).
- (29) D. Chamberlin, D. Bodansky, W.W. Jacobs, D.L. Oberg, Phys. Rev. C9, 69 (1974).
- (30) C.N. Davids, R.C. Pardo, A.W. Obst, Phys. Rev. C11, 2063 (1975).
- (31) H.-B. Mak, H.C. Evans, G.T. Ewan, A.B. McDonald, T.K. Alexander, Phys. Rev. C12, 1158 (1975).
- (32) R.G. Markham, S.M. Austin, M.A.M. Shahabuddin, Nucl. Phys. A270, 489 (1976).
- (33) A.W. Obst, W.J. Braithwaite, Phys. Rev. C13, 2033 (1976).
- (34) C.N. Davids and T.I. Bonner, Astrophys J. 166, 405 (1971).
- (35) M.S. Basunia, Nucl. Data Sheets, 114, 1189 (2013).
- (36) M. Guttormsen, A. Bürger, T.E. Hansen, N. Lietaer, Nucl. Instr. and Meth, in Phys. Res. 648, 168 (2011).
- (37) M. Guttormsen, A. Atac, G. Løvhøiden, S. Messelt, T. Ramsøy, J. Rekstad, T.F. Thorsteinsen, T.S. Tveter, Z. Zelazny, Physica Scripta T52, 54 (1990).
- (38) F. Salvat, J.M. Fernández-Varea, J. Sempau, PENELOPE-2011: A Code System for Monte Carlo Simulation of Electron and Photon Transport, NEA 6416 (2011).
- (39) M.E. Rose, Phys. Rev. 91, 610 (1953).
- (40) T. Kibédi, T.W. Burrows, M.B. Trzhaskovskaya, P.M. Davidson, C.J. Nestor, Nucl. Inst. and Meth. in Phys. Res. A 589, 202 (2008).
- (41) C. Tur, A. Hager, S.M. Austin, Astrophys. J. 671, 821 (2007).
- (42) C. West, A. Heger, S.M. Austin, Astrophys. J. 769, 2 (2012).
- (43) C.F. Fields, F.X. Timmes, R. Farmer, I. Petermann, W.M. Wolf, S.M. Couch, Astrophys. J. Suppl. 234, 19 (2018).