The quasi-reversibility method to numerically solve an inverse source problem for hyperbolic equations
Abstract
We propose a numerical method to solve an inverse source problem of computing the initial condition of hyperbolic equations from the measurements of Cauchy data. This problem arises in thermo- and photo- acoustic tomography in a bounded cavity, in which the reflection of the wave makes the widely-used approaches, such as the time reversal method, not applicable. In order to solve this inverse source problem, we approximate the solution to the hyperbolic equation by its Fourier series with respect to a special orthonormal basis of . Then, we derive a coupled system of elliptic equations for the corresponding Fourier coefficients. We solve it by the quasi-reversibility method. The desired initial condition follows. We rigorously prove the convergence of the quasi-reversibility method as the noise level tends to 0. Some numerical examples are provided. In addition, we numerically prove that the use of the special basic above is significant.
Key words: inverse source problem, hyperbolic equation, quasi-reversibility method
AMS subject classification: 35R30, 65M32
1 Introduction
We consider an inverse source problem arising from biomedical imaging based on the photo-acoustic and thermo-acoustic effects, which are named as photo-acoustic tomography (PAT) and thermo-acoustic tomograpy (TAT) respectively. In PAT, [1, 2], non-ionizing laser pulses are sent to a biological tissue under inspection (for instance, woman’s breast in mamography). A part of the energy will be absorbed and converted into heat, causing a thermal expansion and a subsequence ultrasonic wave propagating in space. The ultrasonic pressures on a surface around the tissue are measured. The experimental set up for TAT, [3], is similar to PAT except the use of microwave other than laser pulses. Finding some initial information of the pressures from these measurements yields structure inside this tissue.
Due to the important real-world applications, the inverse source problem PAT/TAT has been studied intensively. There are several methods to solve them available. In the case when the waves propagate in the free space, one can find explicit reconstruction formulas in [4, 5, 6, 7], the time reversal method [8, 9, 10, 11, 12], the quasi-reversibility method [13] and the iterative methods [14, 15, 16]. The publications above study PAT/TAT for simple models for non-damping and isotropic media. The reader can find publications about PAT/TAT for more complicated model involving a damping term or attenuation term [17, 18, 19, 20, 21, 22, 23, 24, 25]. The time reversibility requires an approximation of the wave at a “final stage” in the whole medium. This “internal data” might be known assuming that the reflection of the wave on the measured surface is negligible. However, there are many circumstances where this assumption is no longer true. For example, when the biological tissue under consideration is located inside glass, the waves reflects as in a resonant cavity [26, 27, 28]. In this case, measuring or approximating final stage of the wave inside the tissue is impossible. We draw the reader’s attention to [29] for a method to solve PAT/TAT in a bounded cavity with wave reflection. Our contribution in this paper is to apply the quasi-reversibility method to solve the inverse source problem of PAT/TAT for damping and nonhomogeneous media. In this case, the model is a full hyperbolic equation in a bounded domain. By this, the reflection of the waves at the measurement sites is allowed.
The uniqueness and the stability for the inverse source problem for general hyperbolic equations in the damping and inhomogeneous media can be proved by using a Carleman estimate. These important results are the extensions of the uniqueness and stability for the inverse problem for a simple hyperbolic equation in [13] in the non-damping case. However, since the arguments are very similar to the ones in that paper using Carleman estimate for hyperbolic operators, for the brevity, we do not write the proof here.
Instead of using the direct optimal control method, to find the initial value of general hyperbolic equations, we derive a system of elliptic partial differential equations, which are considered as an approximation model for our method. Solution of this system is the vector consisting of Fourier coefficients of the wave with respect to a special basis. This system and the given Cauchy boundary data can be solved by the quasi-reversibility method. The quasi-reversibility method was first proposed by Lattès and Lions [30] in 1969. Since then it has been studied intensively [31, 32, 33, 34, 13, 35, 36, 37]. The application of Carleman estimates for proofs of convergence of those minimizers was first proposed in [38] for Laplace’s equation. In particular, [39] is the first publication where it was proposed to use Carleman estimates to obtain Lipschitz stability of solutions of hyperbolic equations with lateral Cauchy data. We draw the reader’s attention to the paper [40] that represents a survey of the quasi-reversibility method. Using a Carleman estimate, we prove Lipschitz-like convergence rate of regularized solutions generated by the quasi-reversibility method to the true solution of that Cauchy problem.
It seems, in theory, that our method of approximation works for any orthonormal basis of . However, this observation is not true in the numerical sense. That means, the special basis we use to establish the approximation model is crucial. The basis we use in this paper was first introduced by Klibanov in [48], called . It has a very important property that is not identically in an open interval while other bases; for e.g., trigonometric functions and orthonormal polynomials, do not. In this paper, we prove numerically that choosing this basis is optimal for our method.
As mentioned, we establish in this paper the Lipschitz convergence of the quasi-reversibility method. Our main contribution to this field is to relax a technical condition on the noise. In our previous works [41, 42, 43, 44, 45] and references therein, we assumed that the noise contained in the boundary data can be “smoothly extended” as a function defined on the domain . This condition implies that the noise must be smooth. Motivated by the fact that this assumption is not always true, we employ a Carleman estimate involving the boundary integrals to obtain the new convergence without imposing this “extension” condition of the noise function.
The paper is organized as follows. In Section 2, we state the inverse problems under consideration and derive an approximation model whose solution directly yields their solutions. In Section 3, we introduce some auxiliary results and prove the Carleman estimate, which plays an important role in our analysis. In Section 4, we implement the quasi-reversibility method to solve the system of elliptic equations and prove the convergence of the solution as the noise level tends to . Section 5 is for the numerical studies. Section 6 is to provide some numerical results for problem and to show the significance of the used orthonormal basis. Finally, section 7 is for the concluding remarks.
2 The Problem statements and a numerical approach
Let be a smooth and bounded domain in , where is the spatial dimension, and be a positive number. Let , and be functions defined on . Let be a -dimensional vector valued function in Define the elliptic operator
| (2.1) |
for all . Let represent a source, we consider the problems of solving generated by the source and subjected to either homogeneous Dirichlet or Neumann boundary condition, which are given by
| (2.2) |
or
| (2.3) |
respectively. Our interest is to determine the source , , from some boundary observation of the wave. More precisely, the inverse source problems are formulated as:
Problem 2.1.
Problem 2.2.
The unique solvability of problems (2.2) and (2.3) can be obtained by Garlerkin approximations and energy estimates as in Chapter 7, Section 7.2 in [46]. We now focus on our approach for solving these two inverse problems.
Let be an orthonormal basis of The function can be represented as:
| (2.6) |
where
| (2.7) |
Consider
| (2.8) |
for some cut-off number . This number is chosen numerically such that well-approximates the function , see Section 5.1 for more details. We have,
| (2.9) |
Plugging (2.8) and (2.9) into the first equation of problem (2.2), we get
| (2.10) |
for all .
Remark 2.1.
Equation (2.10) is actually an approximation model. We only solve Problem 2.1 and Problem 2.2 in this approximation context. Studying the behavior of (2.10) as is extremely challenging and out of the scope of the paper. In case of interesting, the reader could follow the techniques in [47] to investigate the accuracy of (2.11) as tends to
Since is an orthonormal basis of , multiplying to both sides of (2.10) and then integrating the resulting equation with respect to , for each yields
| (2.11) |
where
Furthermore, from (2.7) we have
Therefore, the Cauchy data of , for all on the boundary are determined by:
The system of elliptic partial differential equations (2.11) together with Cauchy data either (2.12) or (2.13) is our approximation model, see Remark 2.1. It allows to determine coefficients , for all , and then the approximation of . The source term will be given by In summary, the numerical method for solving Problem 2.1 and Problem 2.1 is described in Algorithm 1 and Algorithm 2 below respectively.
Remark 2.2.
In Step 1 of Algorithm 1 and Algorithm 2, we choose the basis taken from [48]. The cut-off number is chosen numerically. More details will be discussed in Section 5. In Step 2 of these algorithms, we apply the quasi-reversibility method to solve (2.11) and (2.12) and (2.11) and (2.13). The analysis about about the quasi-reversibility method and its convergence as the noise in the given data tends to are discussed in Section 4.
As mentioned in Remark 2.2 that solving (2.11) and (2.12) for Problem 2.1 and solving (2.11) and (2.13) for Problem 2.2 are interesting when the given data in (2.4) and (2.5) contain noise. We employ the quasi-reversibility method to do so. Let be a small positive number playing the role of the regularization parameter. To solve (2.11) and (2.12) we minimize the following mismatch functional
| (2.14) |
where is in satisfying for all . To solve (2.11) and (2.13), we minimize the following mismatch functional
| (2.15) |
where is in satisfying for all .
3 A Carleman estimate
Let be a number in . We denote
Then, there exists such that the function
| (3.1) |
We have the following lemma.
Lemma 3.1.
There are two positive constants and depending only on such that for all and , we have
| (3.2) |
for all function where the vector satisfies
| (3.3) |
Lemma 3.3 is a direct consequence of [49, Chapter 4, §1, Lemma 3] in which the function is independent of the time variable. Let be a positive number such that , where denotes a ball of the center at and the radius . Let and be two positive numbers such that
| (3.4) |
where is the unit direction vector of axis. For any , we define , then (3.4) yields . By modifying constant in Lemma 3.3 (using instead of ) we have that the Lemma 3.3 holds true in domain . From now on, we apply Lemma 3.3 for all function in the space . The following result plays an important role in our analysis.
Proposition 3.1 (Carleman estimate).
There exist , , both of which only depend on and such that for all and for all , we have
| (3.5) |
where is a generic constant depending only on , , and .
Proof.
The Carleman estimate (3.5) plays a key role for us to estimate the error of the solution to the inverse problem assuming that the given data contains noise.
4 The quasi-reversibility method
As mentioned in section 2, we only prove the convergence of the quasi-reversibility method to solve (2.11) with Cauchy boundary data (2.12). In this case, the objective functional , now named as , see (2.14), is written as
| (4.1) |
subject to the constraint on . Let
be a closed subspace of . It is clear that is strictly convex in . We now prove that is has a unique minimizer in .
Proposition 4.1.
The functional has a unique minimizer in .
Proof.
Let
and be a sequence satisfying
Then is bounded in . In fact, by contradiction, assume that is unbounded. Then, there exists a subsequence, still named as , satisfying Hence,
which is impossible. Due to the boundedness of in , there exists a subsequence of , still named as , which weakly converges to a function in . That implies weakly converges to in , and therefore, strongly converges to in by the compact imbedding of into . Furthermore, the fact that weakly converges in implies weakly converges to in . As a result,
Therefore
Thus is a minimizer of The uniqueness of is deduced from the strict convexity of . ∎
Definition 4.1.
We now assume that the measured data contain noise, with a noise level . We next study the convergence of as noise level tends to 0. Let denote the noisy data and the corresponding noiseless data, . By noise level , we mean
Since the truncation number is a finite number, we can write
| (4.2) |
where is a generic constant depending only on and . For each , define
| (4.3) |
for all The following theorem guarantees the Lipschitz stability of the reconstructed method with respect to noise.
Theorem 4.1.
Let be the minimizer of the functional
| (4.4) |
Assume that the system
| (4.5) |
has the unique solution Then,
| (4.6) |
where is a generic constant depending only on and . As a result, let and be the functions obtained by (2.8) with replaced by and respectively and let and be and respectively, . We have
| (4.7) |
Proof.
Due to (2.8), we have
. Hence, (4.6) implies (4.7). It is sufficient to prove (4.6). Since is the minimizer of , for all
| (4.8) |
Since is the true solution to (4.5), for all
| (4.9) |
Hence, by subtracting (4.8) from (4.9) and setting , we have
Equivalently,
Using the inequality , we have
| (4.10) |
It follows from (4.2), (4.3) and (4.10) that
| (4.11) |
for a constant It follows from (4.11) that
| (4.12) |
Since on , , the tangent derivative of on is . Hence, by (4.12)
| (4.13) |
Recall , as in Lemma 3.3 and the function as in (3.1). Fix . Applying the inequality , we have for all
Thus, by (4.11),
Applying the Carleman estimate (3.5), we have
Since fixed, choosing sufficiently large,we have
| (4.14) |
Since , on Hence, we obtain (4.6) by using (4.13) and (4.14). ∎
Remark 4.1.
The conclusion of Theorem 4.7 is similar to some theorems about the quasi-reversibility method we have developed, see e.g. [41, Theorem 5.1] and [42, Theorem 4.1]. The main difference is that in Theorem 4.7, we relax a technical condition that there exists an error vector valued function , well-defined in the whole , such that and
5 Numerical studies
In this section, we set the dimension and with . Define a grid of points on as
where with We set . On , we also define the uniform partition
where . In our computation, . To generate the simulated data, we solve (2.2) with
by the finite difference method in the implicit scheme. Let , and , be the obtained numerical solution. We can extract the data and on . These functions serve as the data without noise. For , the noisy data are given by
where is the function taking uniformly distributed random numbers in
5.1 Implementation
We present in details the implementation of Steps 1 and 2 of Algorithm 1 to solve Problem 2.1 while the other steps can be implemented directly. The implementation for Problem 2.2 can be done in the same manner.
Step 1 in Algorithm 1. In our numerical studies, we employ the basis that was first introduced by Klibanov in [48]. For each we define The set is complete in . We apply the Gram-Schmidt orthonormalization process on this set to obtain the orthonormal basis of
Remark 5.1.
The basis was successfully used very often in our research group to solve a long list of inverse problems including the nonlinear coefficient inverse problems for elliptic equations [50] and parabolic equations [51, 43, 44, 52], and ill-posed inverse source problems for elliptic equations [41] and parabolic equations [42], transport equations [45] and full transfer equations [53]. Another reason for us to employ this basis rather than the well-known basis of the Fourier series is that the first elements of this basis is a constant. Hence, when we plug (2.9) into (2.2), the information of will be lost. As a result, the contribution of in (2.11) is less than the that of the corresponding obtained by the basis .
To choose , we numerically compare and for where is the true solution to (2.2) and the source is given in Example 1 below. The number is chosen such that the error
is small enough. We perform this procedure and choose , see Figure 1. This cut off number is used for all numerical examples in the paper.



Step 2 in Algorithm 1. In this step, we apply the quasi-reversibility method to solve the system (2.11) with Cauchy data (2.12). That means, we minimize the functional defined in (2.14). The finite difference version of , still called , is
| (5.1) |
Here, instead of imposing the constraint on , we add additional term: to the right hand side of (5.1). This technique significantly reduces the efforts in the implementation. We now identify the vector value function with it “line up” version
for and . The data is also line-up in the same manner.
for , or , It is not hard to rewrite in term of as
| (5.2) |
for some matrices , , , , and . The matrix is such that
with and The matrix and are the matrices such that and respectively correspond to the Neumann and Dirichlet values of where is on , The matrix , and are such that , and correspond to , and , , The explicit forms of these matrices can be written similarly to [42, Section 5.1]. For the brevity, we do not repeat the details here.
Since is the minimizer of defined in (5.2), satisfies
where the superscript indicates the transpose of matrices. This linear system can be solve by any linear algebra package. We employ the command “lsqlin” of MATLAB for this purpose. In all following examples, the regularization parameter is chosen to be .
5.2 Numerical examples
Example 1. We consider the true source function given by



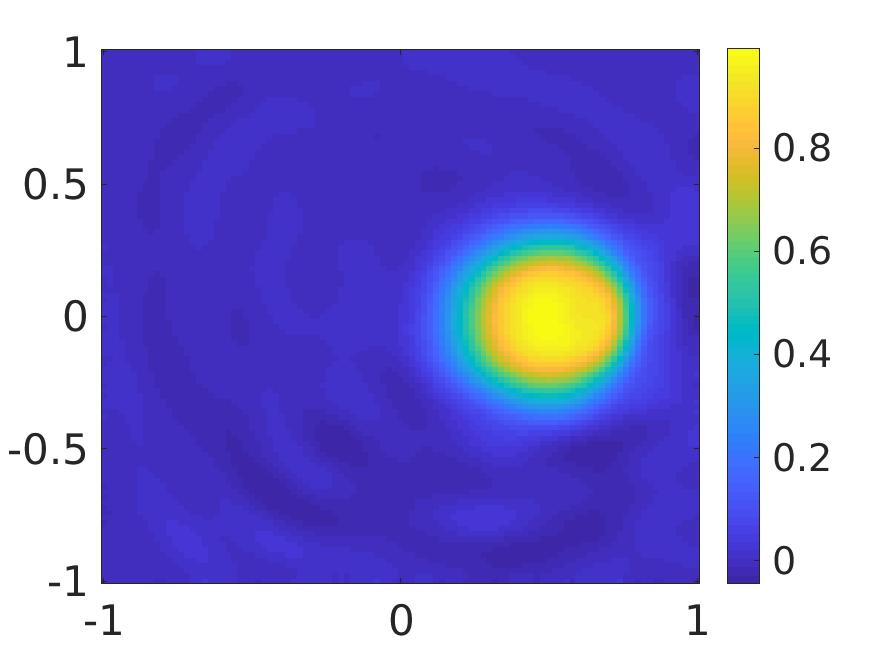

The numerical solutions are displayed in Figure 2, which show the accurate reconstructions of the shape and location of the source. The computed values of the source functions for both Problem 2.1 and Problem 2.2 are quite accurate. Regarding to Problem 2.1, in the case the maximal computed value of the source is 0.96115 (relative error 3.9%) while in the case the maximal computed value of the source is 1.01114 (relative error 1.1%). Regarding to Problem 2.2, in the case the maximal computed value of the source is 0.99389 (relative error 0.6%) while in the case the maximal computed value of the source is 0.98797 (relative error 1.2%).
Example 2. We consider a more complicated source function
where the support of the source function consists of a disk and a square, see Figure 3 (a).





The reconstructions of source are displayed in Figure 3, which show the accurate reconstructions of the square and the disk. The computed values of the source function are quite accurate. Regarding to Problem 2.1, in the case the maximal computed values of the source in the square and the disk are 1.97386 (relative error 1.3%) and 0.9608 (relative error 3.9%) respectively while in the case the corresponding maximal computed values of the source are 2.19941 (relative error 9.9%) and 1.157 (relative error 15.7%) . Regarding to Problem 2.2, in the case , the maximal computed values of the source in the square and the disk are 2.01843 (relative error 0.9%) and 0.9994 (relative error 0.0%) while in the case , the corresponding maximal computed values of the source are 2.11776 (relative error 5.9%) and 0.9733 (relative error 2.3%). We observe that when the noise level is 100%, the values of the source are well computed while and the reconstructed shapes of the inclusions start to break out.
Example 3. We next test the case where the support of the source has more complicated geometries than the one in Example 2, and the source has both positive and negative values.
The support of the source involves a rectangle with a void and an ellipse, see Figure 4(a).





The numerical solutions of Example 3 are displayed in Figure 4, which show the accurate reconstructions of the rectangle with the void and the ellipse. The computed values of the source function are quite accurate. Regarding to Problem 2.1, in the case the maximal and minimal computed values of the source is 3.22793 (relative error 7.6%) and (relative error 8.2%) respectively while in the case the maximal and minimal computed values of the source are 3.21003 (relative error 7.0%) and (relative error 1.4%) respectively. Regarding to Problem 2.2, in the case , the maximal and minimal computed values of the source are 3.04546 (relative error 1.5%) and (relative error 3.1%) respectively while in the case , the maximal and minimal computed values of the source are 3.15653 (relative error 5.2%) and (relative error 3.9%) respectively. We observe that when the noise level is 100%, the reconstructed values of the source are almost exact and the shapes of the inclusions are still acceptable. However, some artifacts are present.
Example 4. In this example, the true source function is the characteristic function of the letter .





The numerical solutions of Example 4 are displayed in Figure 5, which show the accurate reconstructions of the letter . The computed values of the source function are quite accurate. Regarding to Problem 2.1, in the case the maximal computed value of the source are 0.97705 (relative error 2.3%) while in the case the maximal computed value of the source is 0.93572 (relative error 6.4%). Regarding to Problem 2.2, in the case , the maximal computed value of the source is 1.00401 (relative error 0.4%) and in the case , the maximal computed value of the source is 0.94551 (relative error 5.4%). We observe that when the noise level is 100%, the reconstructed values and the -shape of the source meet the expectation.
6 Numerical examples in 1D and the efficiency of the basis
As mention in Remark 5.1, we choose the basis rather than the the “sin and cosine” basis of the well-known Fourier series. To numerically verifying that this choice is important, we compare some 1D numerical solutions to Problem 2.1 obtained by our method with respect to two bases: (1) the trigonometric Fourier expansion and (2) the basis . We will show that the numerical results in case (1) do not meet the expectation while the numerical results in case (2) do.
For the simplicity, we drop the damping term in the governing equation. The governing model is
| (6.1) |
Here, we choose . The aim of Problem 2.1 is to compute the initial condition from the measurement of
| (6.2) |
We now try the trigonometric Fourier expansion to solve Problem 2.1. In this section, we display the numerical results with the cut-off number . We have tried the cases when and but the quality of the computed sources does not improve. For each , we approximate by the partial sum of its Fourier series
| (6.3) |
where
Differentiate (6.3) with respect to , we have
| (6.4) |
Plugging (6.3) and (6.4) into (6.1) gives
| (6.5) |
for all Hence, we have
| (6.6) |
for The boundary constraints of and are
| (6.7) |
We solve (6.6)–(6.7) for for . Then, the function initial condition is given by where is given by (6.3). We skip presenting the implementation for this method. The implementation is similar but simpler than the implementation for the 2D case.
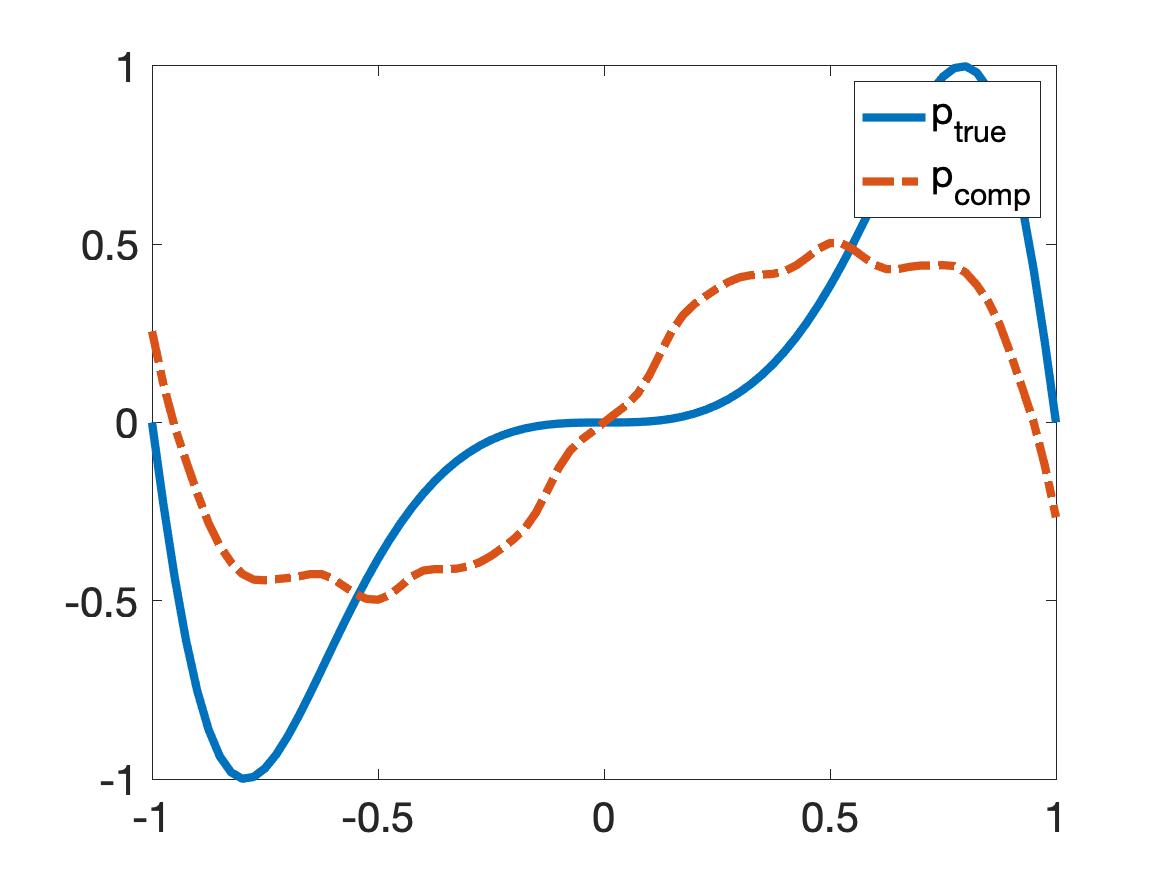
In the numerical tests, we set , and for In this section, we perform three (3) tests. The source functions , and correspond to Test 1, Test 2 and Test 3 are given below:
We compute these source functions with noise level 5%. The numerical examples are displayed in Figure 6. It is evident that approximating with the basis provides much better solutions to Problem 2.1 in comparison to approximating with the popular “sin and cosine” basis.





7 Concluding remarks
In this paper, we introduced a new approach to numerically compute the source function for general hyperbolic equations from the Cauchy boundary data. In the first step, by truncating the Fourier series of the solution to this hyperbolic equation, we derive an approximation model, who solution directly provides the knowledge of the source. We then apply the quasi-reversibility method to solve this system. The convergence of the quasi-reversibility method is rigorously proved. Satisfactory numerical examples illustrates the efficiency of our method.
Acknowledgments
Thuy Le and Loc Nguyen are supported by US Army Research Laboratory and US Army Research Office grant W911NF-19-1-0044. The authors would like to thank Dr. Michael V. Klibanov for many fruitful discussions.
References
- [1] R. A. Kruger, P. Liu, Y. R. Fang, and C. R. Appledorn. Photoacoustic ultrasound (PAUS)–reconstruction tomography. Med. Phys., 22:1605, 1995.
- [2] A. Oraevsky, S. Jacques, R. Esenaliev, and F. Tittel. Laser-based optoacoustic imaging in biological tissues. Proc. SPIE, 2134A:122, 1994.
- [3] R. A. Kruger, D. R. Reinecke, and G. A. Kruger. Thermoacoustic computed tomography: technical considerations. Med. Phys., 26:1832, 1999.
- [4] N. Do and L. Kunyansky. Theoretically exact photoacoustic reconstruction from spatially and temporally reduced data. Inverse Problems, 34(9):094004, 2018.
- [5] M. Haltmeier. Inversion of circular means and the wave equation on convex planar domains. Comput. Math. Appl., 65:1025–1036, 2013.
- [6] F. Natterer. Photo-acoustic inversion in convex domains. Inverse Probl. Imaging, 6:315–320, 2012.
- [7] L. V. Nguyen. A family of inversion formulas in thermoacoustic tomography. Inverse Probl. Imaging, 3:649–675, 2009.
- [8] V. Katsnelson and L. V. Nguyen. On the convergence of time reversal method for thermoacoustic tomography in elastic media. Applied Mathematics Letters, 77:79–86, 2018.
- [9] Y. Hristova. Time reversal in thermoacoustic tomography–an error estimate. Inverse Problems, 25:055008, 2009.
- [10] Y. Hristova, P. Kuchment, and L. V. Nguyen. Reconstruction and time reversal in thermoacoustic tomography in acoustically homogeneous and inhomogeneous media. Inverse Problems, 24:055006, 2008.
- [11] P. Stefanov and G. Uhlmann. Thermoacoustic tomography with variable sound speed. Inverse Problems, 25:075011, 2009.
- [12] P. Stefanov and G. Uhlmann. Thermoacoustic tomography arising in brain imaging. Inverse Problems, 27:045004, 2011.
- [13] C. Clason and M. V. Klibanov. The quasi-reversibility method for thermoacoustic tomography in a heterogeneous medium. SIAM J. Sci. Comput., 30:1–23, 2007.
- [14] C. Huang, K. Wang, L. Nie, L. V. Wang, and M. A. Anastasio. Full-wave iterative image reconstruction in photoacoustic tomography with acoustically inhomogeneous media. IEEE Trans. Med. Imaging, 32:1097–1110, 2013.
- [15] G. Paltauf, R. Nuster, M. Haltmeier, and P. Burgholzer. Experimental evaluation of reconstruction algorithms for limited view photoacoustic tomography with line detectors. Inverse Problems, 23:S81–S94, 2007.
- [16] G. Paltauf, J. A. Viator, S. A. Prahl, and S. L. Jacques. Iterative reconstruction algorithm for optoacoustic imaging. J. Opt. Soc. Am., 112:1536–1544, 2002.
- [17] H. Ammari, E. Bretin, E. Jugnon, and V. Wahab. Photoacoustic imaging for attenuating acoustic media. In H. Ammari, editor, Mathematical Modeling in Biomedical Imaging II, pages 57–84. Springer, 2012.
- [18] H. Ammari, E. Bretin, J. Garnier, and V. Wahab. Time reversal in attenuating acoustic media. Contemp. Math., 548:151–163, 2011.
- [19] M. Haltmeier and L. V. Nguyen. Reconstruction algorithms for photoacoustic tomography in heterogeneous damping media. Journal of Mathematical Imaging and Vision, 61:1007–1021, 2019.
- [20] S. Acosta and B. Palacios. Thermoacoustic tomography for an integro-differential wave equation modeling attenuation. J. Differential Equations, 5:1984–2010, 2018.
- [21] P. Burgholzer, H. Grün, M. Haltmeier, R. Nuster, and G. Paltauf. Compensation of acoustic attenuation for high-resolution photoa- coustic imaging with line detectors. Proc. SPIE, 6437:643724, 2007.
- [22] A. Homan. Multi-wave imaging in attenuating media. Inverse Probl. Imaging, 7:1235–1250, 2013.
- [23] R. Kowar. On time reversal in photoacoustic tomography for tissue similar to water. SIAM J. Imaging Sci., 7:509–527, 2014.
- [24] R. Kowar and O. Scherzer. Photoacoustic imaging taking into account attenuation. In H. Ammari, editor, Mathematics and Algorithms in Tomography II, Lecture Notes in Mathematics, pages 85–130. Springer, 2012.
- [25] A. I. Nachman, J. F. Smith III, and R.C. Waag. An equation for acoustic propagation in inhomogeneous media with relaxation losses. J. Acoust. Soc. Am., 88:1584–1595, 1990.
- [26] B. Cox, S. Arridge, and P. Beard. Photoacoustic tomography with a limited-aperture planar sensor and a reverberant cavity. Inverse Problems, 23:S95, 2007.
- [27] B. Cox and P. Beard. Photoacoustic tomography with a single detector in a reverberant cavity. The Journal of the Acoustical Society of America, 123:3371–3371, 2008.
- [28] L. Kunyansky, B. Holman, and B. Cox. Photoacoustic tomography in a rectangular reflecting cavity. Inverse Problems, 29:125010, 2013.
- [29] L. V. Nguyen and L. Kunyansky. A dissipative time reversal technique for photo-acoustic tomography in a cavity. SIAM J. Imaging Sci., 9:748–769, 2016.
- [30] R. Lattès and J. L. Lions. The Method of Quasireversibility: Applications to Partial Differential Equations. Elsevier, New York, 1969.
- [31] E. Bécache, L. Bourgeois, L. Franceschini, and J. Dardé. Application of mixed formulations of quasi-reversibility to solve ill-posed problems for heat and wave equations: The 1d case. Inverse Problems & Imaging, 9(4):971–1002, 2015.
- [32] L. Bourgeois. A mixed formulation of quasi-reversibility to solve the Cauchy problem for Laplace’s equation. Inverse Problems, 21:1087–1104, 2005.
- [33] L. Bourgeois. Convergence rates for the quasi-reversibility method to solve the Cauchy problem for Laplace’s equation. Inverse Problems, 22:413–430, 2006.
- [34] L. Bourgeois and J. Dardé. A duality-based method of quasi-reversibility to solve the Cauchy problem in the presence of noisy data. Inverse Problems, 26:095016, 2010.
- [35] J. Dardé. Iterated quasi-reversibility method applied to elliptic and parabolic data completion problems. Inverse Problems and Imaging, 10:379–407, 2016.
- [36] M. V. Klibanov , A. V. Kuzhuget, S. I. Kabanikhin, and D. Nechaev. A new version of the quasi-reversibility method for the thermoacoustic tomography and a coefficient inverse problem. Applicable Analysis, 87:1227–1254, 2008.
- [37] M. V. Klibanov. Carleman estimates for global uniqueness, stability and numerical methods for coefficient inverse problems. J. Inverse and Ill-Posed Problems, 21:477–560, 2013.
- [38] M. V. Klibanov and F. Santosa. A computational quasi-reversibility method for Cauchy problems for Laplace’s equation. SIAM J. Appl. Math., 51:1653–1675, 1991.
- [39] M. V. Klibanov and J. Malinsky. Newton-Kantorovich method for 3-dimensional potential inverse scattering problem and stability for the hyperbolic Cauchy problem with time dependent data. Inverse Problems, 7:577–596, 1991.
- [40] M. V. Klibanov. Carleman estimates for the regularization of ill-posed Cauchy problems. Applied Numerical Mathematics, 94:46–74, 2015.
- [41] L. H. Nguyen, Q. Li, and M. V. Klibanov. A convergent numerical method for a multi-frequency inverse source problem in inhomogenous media. Inverse Problems and Imaging, 13:1067–1094, 2019.
- [42] Q. Li and L. H. Nguyen. Recovering the initial condition of parabolic equations from lateral Cauchy data via the quasi-reversibility method. Inverse Problems in Science and Engineering, 28:580–598, 2020.
- [43] M. V. Klibanov and L. H. Nguyen. PDE-based numerical method for a limited angle X-ray tomography. Inverse Problems, 35:045009, 2019.
- [44] V. A. Khoa, M. V. Klibanov, and L. H. Nguyen. Convexification for a 3D inverse scattering problem with the moving point source. SIAM J. Imaging Sci., 13(2):871–904, 2020.
- [45] M. V. Klibanov, T. T. Le, and L. H. Nguyen. Convergent numerical method for a linearized travel time tomography problem with incomplete data. to appear on SIAM Journal on Scientific Computing, see also https://arxiv.org/abs/1911.04581, 2020.
- [46] L. C. Evans. Partial Differential Equations. Graduate Studies in Mathematics, Volume 19. Amer. Math. Soc., 2010.
- [47] M. V. Klibanov and D-L. Nguyen. Convergence of a series associated with the convexification method for coefficient inverse problems. preprint, arXiv:2004.05660, 2020.
- [48] M. V. Klibanov. Convexification of restricted Dirichlet to Neumann map. J. Inverse and Ill-Posed Problems, 25(5):669–685, 2017.
- [49] M. M. Lavrent’ev, V. G. Romanov, and S. P. Shishatskiĭ. Ill-Posed Problems of Mathematical Physics and Analysis. Translations of Mathematical Monographs. AMS, Providence: RI, 1986.
- [50] V. A. Khoa, G. W. Bidney, M. V. Klibanov, L. H. Nguyen, L. Nguyen, A. Sullivan, and V. N. Astratov. Convexification and experimental data for a 3D inverse scattering problem with the moving point source. Inverse Problems, accepted for publication, see https://iopscience.iop.org/article/10.1088/1361-6420/ab95aa/meta, 2020.
- [51] L. H. Nguyen. A new algorithm to determine the creation or depletion term of parabolic equations from boundary measurements. preprint, arXiv:1906.01931, 2019.
- [52] V. A. Khoa, G. W. Bidney, M. V. Klibanov, L. H. Nguyen, L. Nguyen, A. Sullivan, and V. N. Astratov. An inverse problem of a simultaneous reconstruction of the dielectric constant and conductivity from experimental backscattering data. to appear on Inverse Problems in Science and Engineering, see also Arxiv:2006.00913, 2020.
- [53] A. V. Smirnov, M. V. Klibanov, and L. H. Nguyen. On an inverse source problem for the full radiative transfer equation with incomplete data. SIAM Journal on Scientific Computing, 41:B929–B952, 2019.