The prolonged decay of RKKY interactions by interplay of relativistic and non-relativistic electrons in semi-Dirac semimetals

Over the past decades, the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction has been extensively studied in a variety of materials, e.g., graphenegraphene1 ; graphene2 ; graphene3 ; graphene4 ; graphene5 ; graphene6 , $\alpha$-$\mathcal{T}_{3}$ modelalpha , Dirac/Weyl semimetals (DSMs/WSMs)Weyl1 ; Weyl2 ; Dirac0 , phosphorenephosphorene2 , edge/surface bands of topological materialstopo2 ; Dirac1 ; surface1 ; surface2 ; surface3 ; surface4 and so on. These researches have showed a potential application for the RKKY interaction to realize magnetization in non-magnetic materials. A typical example is the realization of quantized anomalous Hall effect in topological insulatorsanous ; topo2 . Moreover, the RKKY interaction has been proven to characterize the intrinsic properties of materials, e.g., the band topologysurface1 ; NLSM , rich spin texturesWeyl1 , and the Rashba splittingShiranzaei . Although the RKKY interaction has wide prospect in the area of spintronics, there are still many obstacles to overcome. One is that the RKKY interaction is too weak to be detected since it usually decays fast with the increased impurity distance $R$. For example, in materials with isotropic linear dispersion, the RKKY interaction presents a fast decaying law as $\mathrm{sin}\left(2k_{F}R\right)/R^{d}$ ($1/R^{2d-1}$) at finite (zero) Fermi energy. To overcome this obstacle, new research perspectives are expected. In addition to some special devices (e.g., the PN junctionpn ), materials with peculiar dispersions are promising candidates to realize the prolonged RKKY interaction.

Recently, semi-Dirac semimetals (S-DSMs) have attracted more and more attention in condensed matter physics due to their highly anisotropic electronic structure. Different from the isotropic linear dispersions around the Dirac points, the low-energy model of S-DSM exhibits a linear dispersion in some directions but disperses quadratically in the others, which allows the coexistence of relativistic and non-relativistic electrons. This peculiar dispersion leads to many new physical properties, such as the anisotropic transportsAdroguer ; SPark , nonsaturating large magnetoresistanceNiu , unique optical propertiesMawrie1 ; Carbotte ; Dai , and quantum thermoelectricsMawrie2 . Nevertheless, the magnetic property, especially the RKKY interaction between magnetic impurities, with respect to S-DSMs receives no attention. It is expected that the strong anisotropic dispersion of the S-DSMs will affect the RKKY interaction significantly.

In this Letter, we theoretically investigate the influence of anisotropic dispersion on the RKKY interaction, and take S-DSMs as examples of anisotropic structure and compare them with isotropic DSMs/WSMs. We find that the decaying rate of the RKKY interaction in S-DSMs, including all types of two or three dimensions, can be highly prolonged along the relativistic axis, in contrast to the fast-decaying RKKY interaction in DSMs/WSMs. Furthermore, we propose a general formula to determine the decaying rate of the RKKY interaction for anisotropic DSMs with arbitrary dimensions.

RKKY theory- RKKY interaction describes an indirect exchange interaction, mediated by itinerant electrons, between two impurities embedded in the material. We start from the Hamiltonian

where $H_{0}$ stands for the host materials and $\lambda$ is spin exchange between the itinerant electron spin $\mathrm{\mathbf{s}}_{i}$ and the impurity spin $\mathrm{\mathbf{S}}_{i}$, located at $\mathbf{r}_{i}$. For weak coupling $\lambda$, we can use the standard perturbation theoryrkky1 ; rkky2 ; rkky3 , and up to the second order of $\lambda$, the RKKY interaction at zero temperature can be calculated by,

where $G\left(\pm\mathbf{R},\omega\right)$ is the retarded Green’s function with respect to $H_{0}$ in real space and $u_{F}$ is the Fermi energy. After tracing the spin degrees of freedom in Eq. (2), the RKKY interaction can be written in the form of

with

where we denote matrix of Green’s function as $G\left(\pm\mathbf{R},\omega\right)=\sum_{i=0,x,y,z}G_{i}\left(\pm\mathbf{R},\omega\right)\sigma_{i}$ and $\Lambda_{ij}\left(\mathbf{R},\omega\right)=G_{i}\left(\mathbf{R},\omega\right)G_{j}\left(-\mathbf{R},\omega\right)$. In Eq. (4), the trace part determines the spin exchange type and $\Lambda_{ij}\left(\mathbf{R},\omega\right)$ determines the decaying rate with impurity distance $\mathbf{R}=\mathbf{r_{2}}-\mathbf{r}_{1}$. Physically, $\Lambda_{ij}\left(\mathbf{R},\omega\right)$ characterizes the spin $\sigma_{i}$ disturbancedensity of site $\mathbf{r}_{1}$ as a response to the spin $\sigma_{j}$ of site $\mathbf{r}_{2}$.

Universal RKKY decay for isotropic materials- Obviously, the decay of the RKKY interaction is determined by $\Lambda_{ij}\left(\mathbf{R},\omega\right)$, which is closely related to material type. Considering a $d$-dimensional system with linear Dirac cone, $H_{\mathrm{0}}=v\mathbf{k}\cdot\mathbf{\sigma}$, where $v$ is the Fermi velocity, we have

with $R=|\mathbf{R}|$. The resulting RKKY interaction is

where $\zeta=d-1$ is the exponent of the density of states (DOS) of DSMs. The above laws have been extensively reported in isotropic systems with linear dispersion, such as graphenegraphene1 ; graphene2 ; graphene3 ; graphene4 ; graphene5 ; graphene6 , and DSMs/WSMsWeyl1 ; Weyl2 ; Dirac0 . If the isotropic system is usual quadratical dispersion $H_{0}=v^{\prime}k^{2}\sigma_{0}$, the RKKY interaction follows a laweletrongas1 ; eletrongas2 as $J^{\alpha\beta}\left(u_{F}=0\right)=0$ and $J^{\alpha\beta}\left(u_{F}\neq 0\right)\propto\mathrm{sin}\left(2R\sqrt{u_{F}/v^{\prime}}\right)/R^{d}$ which shares a same decaying rate but with a different oscillation as compared to Eq. (6).

Universal RKKY decay for S-DSM materials- The above argument is valid only for isotropic systems since $e^{i\omega R/v}$ in Eq. (5) is obtained under the $\theta_{R}$-independent condition [$\mathrm{tan}\left(\theta_{R}\right)=R_{y}/R_{x}$]. In S-DSMs with anisotropic dispersions, the corresponding Green’s function is direction-dependent.

We employ a general Hamiltonian of a minimal low-energy model of S-DSM

which collects all S-DSM models in 2D and 3D materials: (1) Case I: for $\xi_{1}=0$ and $\xi_{2}=0,$ it reduces to S-DSM in $2D$ caseVictor1 ; Victor2 ; Banerjee ; Banerjee2 ; Qiuzi ; Zhai . (2) Case II: for $\xi_{1}=0$ and $\xi_{2}=1$, it is linear momentum along two directions and square along the other one, called as $3D$-type I. (3) Case III: For $\xi_{1}=1$ and $\xi_{2}=0,$ it is linear momentum along one direction and square along other two directions, called as $3D$-type II. Noting that the Pauli matrices $\sigma_{x,y,z}$ in Eq. (8) can act either in pseudo-spin basisVictor1 ; Victor2 ; Banerjee or real-spin basisBanerjee2 ; Qiuzi ; Zhai , depending on specific materials. For example, the pseudo-spin 2D S-DSM can be extracted from $\left({\rm TiO_{2}}\right)_{5}/\left({\rm VO_{2}}\right)_{3}$ multilayer systemVictor1 ; Victor2 ; Banerjee , and the real-spin one can be obtained from the topological surface band under the effect of a helical spin density waveQiuzi or a spiral magnetization superlatticeZhai . Without loss of generality, we firstly assume that the Hamiltonian of Eq. (8) is written in real-spin basis. Later in this paper, the effect of the pseudo-spin case on the RKKY interaction would be discussed.

Different from the numerous candidates for 2D S-DSM, few literatures focus on 3D S-DSMs. The two types of 3D S-DSMs used in our paper can be obtained by applying linearly polarized light in WSMsphotoWSM1 and nodal-line semimetalsWeiChen (NLSMs), respectively. For example, one can consider a low-energy model of WSM with broken time-reversal symmetry asphotoWSM1 ,

where $\sigma_{x,y,z}$ refer to the Pauli matrices of the spin degrees of freedom, and two Weyl points are located at $(\pm m,0,0)$. After introducing a beam of linearly polarized light of frequency $\omega$, a vector potential $A=A(1,0,0){\rm cos}\left(\omega t\right)$ with period $T=2\pi/\omega$ is generated. By applying the Peierls substitution $\hbar k$$\rightarrow$$\hbar k+eA$, the system Hamiltonian becomes time-dependent. Using the Floquet theoryfloquet3 with the off-resonant condition of $A^{2}/\omega\gg 1$, the modified part of the Hamiltonian induced by light reads as $V_{0}+\sum_{n\geq 1}\left[V_{+n},V_{-n}\right]/\hbar\omega+O\left(1/\omega^{2}\right)$ with $V_{n}=\frac{1}{T}\int_{0}^{T}H(t)e^{-in\hbar\omega t}$, and the effective Hamiltonian can be written as

where the term related to $A$ refers to the photoinduced modification. By setting proper amplitude $A$ of the vector potential with $e^{2}A^{2}/2=m^{2}$, the Weyl partners are merged into a point, i.e., the WSM is changed to be the type I of 3D S-DSM [$\xi_{1}=0$ and $\xi_{2}=1$ in Eq. (8)]. Similarly, the type II of 3D S-DSM can also be obtained when the nodal ring of NLSM is shrunk into a point by the linearly polarized light.

The Green’s function with respect to $H_{\mathrm{S-DSM}}$ of Eq. (8) reads as,

with $E_{\mathrm{S-DSM}}$ denoting the eigenenergy of the Hamiltonian $H_{\mathrm{S-DSM}}$. The analytical results of $G_{i}\left(\pm\mathbf{{R},\omega}\right)$ for different S-DSMs can be obtained after some algebraic calculations (see the supplemental materialappendix ).

A: along relativistic direction- Firstly, we perform the calculations for impurities deposited along the relativistic axis (see the supplemental materialappendix ), and depict the results in Table I. For this case, the decaying rate of the interaction ($u_{F}\neq 0$) with the distance $R$ between impurities can be expressed as a general form

where $k_{F}=u_{F}/v_{l}$. Similar oscillation $\mathrm{sin}\left(2Ru_{F}/v_{l}\right)$ is also found in DSM-type materialsgraphene1 ; graphene2 ; graphene3 ; graphene4 ; graphene5 ; Weyl1 ; Weyl2 ; Dirac0 . The index $s$ in the above equation labels the number of dimension of square momentum, namely, $s=0,1,2$ correspond to the DSMs, 2D DSM (or 3D-type I S-DSM), and 3D-type II S-DSM, respectively. For $u_{F}\neq 0$, we focus on the slowest-decaying RKKY components ($1/R^{d-s/2}$). Obviously, the positive number $s$ could reduce the decaying rate as compared with isotropic systems $J_{l}^{\alpha\beta}\propto 1/R^{d}$ in Eq. (6). Specifically, for finite Fermi energy, the RKKY component of 2D S-DSM falls off as $R^{-3/2}$, which decays much more slowly than that of doped phosphorenephosphorene1 ; phosphorene2 or 2D DSM where $J_{2D}^{\alpha\beta}\propto R^{-2}$ [Eq. (6)]. Compared to the fast decaying rate of $R^{-3}$ in 3D DSMs/WSMsWeyl1 ; Weyl2 ; Dirac0 with $s=0$, the interaction in S-DSM exhibits a slowest decaying rate as $R^{-2}$ for the type II of 3D S-DSMs with $s=2$ and as $R^{-5/2}$ for the type I of 3D S-DSMs with $s=1$. This is attributed to the non-relativistic term, which enters into the anisotropic energy $E_{\mathrm{S-DSM}}$ of Eq. (9) and competes with the relativistic term to contribute a slowly-decaying rate. This law is unexpected since the slowly-decaying RKKY interaction is usually only realized by the edge/surface statetopo2 ; Dirac1 ; surface1 ; surface2 ; surface3 ; surface4 , the strainphosphorene2 , the PN junctionpn , etc. So far, few reports have discussed the slowly-decaying (or prolonged) RKKY interaction just mediated by the bulk states, without using any other means.

For zero Fermi energy, we find

Compared to the case of $u_{F}\neq 0$, there are two changes: (1) the spatial oscillation $\mathrm{sin}\left(2Ru_{F}/v_{l}\right)$ vanishes; (2) the decaying rate of the interaction is increased by the exponent $\zeta=d-1-s/2$ of the DOS $|\omega|^{\zeta}$. Similar effect also have been stated in DSMs/WSMsWeyl1 ; Weyl2 ; Dirac0 but with $s=0$. Thus, $J_{l}^{\alpha\beta}(u_{F}=0)$ always decays more slowly than that of DSM-type materialsgraphene1 ; graphene2 ; graphene3 ; graphene4 ; graphene5 ; Weyl1 ; Weyl2 ; Dirac0 , where $J^{\alpha\beta}(u_{F}=0)\propto 1/R^{2d-1}$ in Eq. (7). Noting that the relation between the decaying rate and the dimension $s$ of non-relativistic terms is still similar to the case of $u_{F}\neq 0$, i.e, S-DSMs with larger $s$ would result in a slower decaying rate, as listed in Table I.

B: along non-relativistic direction- Compared to the case with impurities in the relativistic axis, a faster decaying-rate is exhibited for the RKKY component $J_{p}^{\alpha\beta}$ when impurities are deposited in the non-relativistic axis. Performing the similar calculations, we find

where $k^{\prime}_{F}=\sqrt{u_{F}}/\sqrt{v_{p}}$. All the results for different S-DSM models are shown in Table II. For $u_{F}\neq 0$, we focus on the slowest-decaying RKKY components ($1/R^{d}$). It is found that the decay of the interaction $J_{p}^{\alpha\beta}(u_{F}\neq 0)$ in S-DSMs is only related to the dimensionality $d$, i.e., $R^{-2}$ ($R^{-3}$) for 2D (3D) S-DSMs, independent on the dimension $s$ of the non-relativistic terms. The reason is that, in this impurity configuration, the interplay of relativistic and non-relativistic electrons is eliminated by the finite Fermi energy. This would result in the same decaying rate and the same oscillation $\mathrm{sin}\left(2R\sqrt{u_{F}}/\sqrt{v_{p}}\right)$ as that of isotropic systemseletrongas1 ; eletrongas2 with quadratical dispersion. For $u_{F}=0$, all RKKY components of S-DSMs decays faster as compared to the case of $u_{F}\neq 0$. The reasons are: (1) Similar to $J^{\alpha\beta}_{l}$, the exponent $\zeta=d-1-s/2$ of the DOS $|\omega|^{\zeta}$ would result in a fast decaying rate for $J^{\alpha\beta}_{p}$; (2) Compared to the phase factor $e^{i\omega R/v_{l}}$ of the Green’s function $G_{l}$ [or $G_{i}$ in DSMs of Eq. (5)], the modified phase factor $e^{i\sqrt{\omega}R/\sqrt{v_{p}}}$ of $G_{p}$ induced by the non-relativistic term would further accelerate the decaying rate of $J^{\alpha\beta}_{p}$. As a result, $J_{p}^{\alpha\beta}(u_{F}=0)$ exhibits a fastest decaying rate than that of $J^{\alpha\beta}_{l}(u_{F}=0)$ and $J^{\alpha\beta}(u_{F}=0)$ in isotropic systems [Eq. (7)]. Noting that the anisotropic decaying laws shown in Table I and Table II are peculiar as compared to the case of doped phosphorenephosphorene1 , where the RKKY interaction follows a same decaying law ($R^{-2}$) whether in armchair direction or zigzag direction although the dispersion of the phosphorene is highly anisotropic.

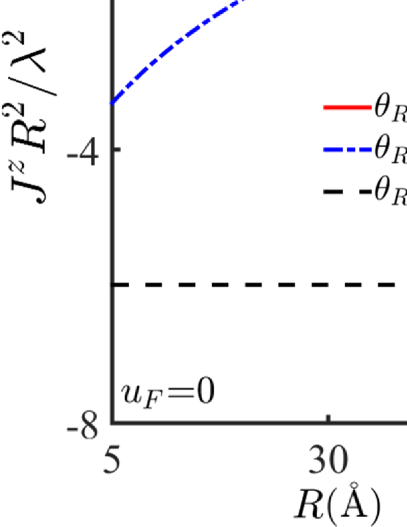
C: along non-principal directions-For impurities deposited in non-principal directions, deviating from relativistic and non-relativistic axes, the decay of the RKKY interaction can be analyzed only with numerical calculations. From the above discussions, we know that the decaying rate of the interaction can be affected heavily by the interplay of relativistic and non-relativistic electrons, leading to the slower decay in the relativistic direction than that in the non-relativistic direction. Thus, when impurities are deposited in a non-principal direction, the intermediate decaying rate would arise, as shown in Fig. 1, where the interaction decays more fast than $J_{l}^{\alpha\beta}$ ($\theta_{R}=\pi/2$) but more slowly than $J_{p}^{\alpha\beta}$ ($\theta_{R}=0$).

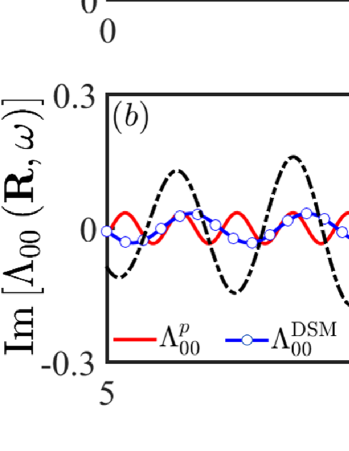
D: Underlying physics- To more deeply understand the anisotropic RKKY interaction, we employ the direction-dependent DOS $\rho\left(\omega,\theta\right)$, which is defined as $\rho\left(\omega,\theta\right)=-(1/\pi){\rm Im}\mathrm{Tr}\int G\left(\mathbf{k},\omega\right)kdk$ for 2D case. We obtain $\rho_{{}_{\mathrm{DSM}}}\left(\omega,\theta\right)$ $=|\omega|/(\pi^{2}v_{l}^{2})$ for 2D DSMs and $\rho_{{}_{\mathrm{S-DSM}}}(\omega,\theta)=\sqrt{|\omega|}/\left[2\pi^{2}v_{l}\sqrt{v_{p}{\rm cos}(\theta)}\right]$ for 2D S-DSMs. Obviously, different from the isotropic DSMs, the DOS for S-DSMs is significantly anisotropic, especially along the linear-momentum direction, i.e., $\theta=\pi/2$, where the DOS of S-DSMs is much larger than that of DSMs, as shown in Fig. 2(a). The large DOS in the relativistic direction should naturally result in a slower decaying rate in the real space. To see it, we consider an electron scattering off a magnetic impurity, whose full electronic Green’s function under Born approximation is modified to be

The change of real-space local DOS readsMitchell

in which the decay of $\delta\rho(\mathbf{R},\omega)$ is determined by ${\rm Im}[\Lambda_{ij}\left(\mathbf{R},\omega\right)]$. We illustrates the change of ${\rm Im}\left[\Lambda_{00}\left(\mathbf{R},\omega\right)\right]$ with the impurity distance $R$ in Fig. 2(b), which shows that the anisotropic decaying rate in the real space is close related to the anisotropic DOS [Fig. 2(a)]. From above expressions, one also can see that physically, the RKKY interaction characterizes the change of spin density of itinerant electrons at site $\mathbf{r}_{1}$ caused by a magnetization at site $\mathbf{r}_{2}$ when electrons complete a round trip from $\mathbf{r}_{1}$ to $\mathbf{r}_{2}$, similar to the semiclassical picture of charge density of isotropic materialsrkky6 . For certain direction, large spin density will remain more electrons participating the exchange interaction between magnetic impurities and so prolong the RKKY decay.

Anisotropic spin model and DM spin exchange interaction- The general form of RKKY interaction in Eq. (3) can divide into Heisenberg type $J^{i}$ and Dzyaloshinskii-Moriya (DM) type $J^{DM}$,

where $\mathbf{e=}(\hat{x},\hat{y},\hat{z})$ is the unit vector and the spin-frustrated terms $\sum_{i\neq j=x,y,z}J^{fr}(S_{1}^{i}S_{2}^{j}+S_{1}^{j}S_{2}^{i})$ vanish if the impurities are distributed along principle axes.

The detailed spin textures for the RKKY interaction of S-DSMs, as well as DSMs, are shown in supplemental materialappendix . Compared to the case of DSMs, there exists a significant difference for the short-range (or weak $u_{F}$) behavior of the RKKY interaction, i.e., a stronger magnetic anisotropy would arise in S-DSMs in the condition of small $k_{F}R$ as impurities are deposited on the relativistic axis. Specifically speaking, the RKKY components $J^{i}_{l}$ are anisotropic with $J^{x}_{l}\neq J^{z}_{l}\neq J^{y}_{l}$, which would generate the $XYZ$ spin model for all S-DSMs and distinguishes itself from the $XXY$ (e.g., $J^{x}_{l}=J^{z}_{l}\neq J^{y}_{l}$) spin model of DSMs. The underlying physics is attributed to the competition of the RKKY interactions with different decaying rates. Taking 2D S-DSM as an example, the RKKY components of finite Fermi energy in the long-range limit exhibits an anisotropy of $J^{x}_{l}=J^{z}_{l}\neq J^{y}_{l}$ [see Eq. (11) of the supplemental materialappendix ], where $J^{x,z}_{l}$ falls off as $R^{-3/2}$ and $J^{y}_{l}\propto R^{-2}$. When the short-range limits (small $R$) is considered, the higher-order terms $R^{-2}$ with different coefficients in $J^{x,z}_{l}$ become considerable, which compete with the term of $R^{-3/2}$ and lead to $J^{x}_{l}\neq J^{z}_{l}\neq J^{y}_{l}$.

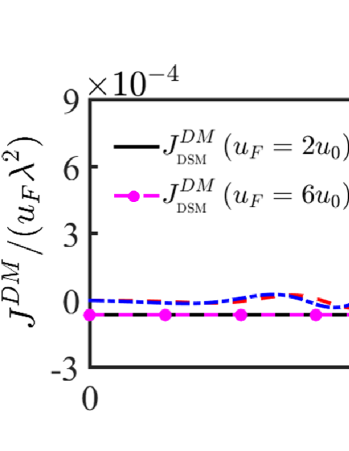
Next, we focus on the influence of the anisotropic dispersion on the DM term. Starting from Eq. (4), the DM coefficient can be obtained with

Here, the appearance of DM term must satisfy two conditions: (1) Finite Fermi energy. If $u_{F}=0$, all the models show the vanished DM interaction due to the protected electron-hole symmetry, similar to the case of WSMsWeyl1 ; Weyl2 . (2) Breaking the symmetry of spatial inversion. Note that $G\left(\mathbf{R},\omega\right)=\sum_{i=0,x,y,z}G_{i}\left(\mathbf{R},\omega\right)\sigma_{i}$. If impurities are distributed along the square-momentum direction, only diagonal components $G_{0}$ and $G_{z}$ in the spin space are nonzero, i.e., $G\left(\mathbf{R},\omega\right)=G_{0}\sigma_{0}+G_{z}\sigma_{z}$. It is easy to confirm $G\left(-\mathbf{R},\omega\right)=G\left(\mathbf{R},\omega\right)$ and so $J^{DM}=0$. Once the impurities are deposited along the linear-momentum direction, the nondiagonal components $G_{x}$ and $G_{y}$ are included, which breaks the inversion symmetry, $G\left(-\mathbf{R},\omega\right)\neq G\left(\mathbf{R},\omega\right)$, and so finite DM interaction emerges. In Fig. 3, we plot the dependence of DM exchange interaction for 2D on impurity direction $\theta_{R}$. Compared with isotropic DM interaction for the DSMs, the DM interaction for S-DSMs exhibits strong anisotropic, which is largest for linear-momentum direction ($\theta_{R}=\pi/2$) and vanishes for $\mathbf{k}^{2}$ direction ($\theta_{R}=\pi/2$). These results also are in agreement with derived analytical expressions for limit cases (see derivation in supplemental materialappendix ). Also, the introduction of non-relativistic contribution in the S-DSMs can reduces the dependence of DM interaction on $u_{F}$, in comparison with the case of DSMs.

If the Hamiltonian of Eq. (8) is expressed in the pseudospin space [$\sigma_{i}\rightarrow\tau_{i}$ in Eq. (8)], taking orbital space as an example, the term ${\rm Tr}[\sigma_{\alpha}\sigma_{i}\sigma_{j}\sigma_{\beta}]$ in Eq. (4) have to be rewritten as ${\rm Tr}[\sigma_{\alpha}\sigma_{\beta}]{\rm Tr}[\tau_{i}\tau_{j}]$ according to the Refs.Dirac1 ; Weyl1 . Thus, the DM terms would vanish and only the Heisenberg-type RKKY interaction survives with an isotropic $XXX$ ($J^{x}_{l(p)}=J^{y}_{l(p)}=J^{z}_{l(p)}$) spin model, similar to the case of graphenegraphene1 ; graphene2 ; graphene3 ; graphene4 ; graphene5 . But the decay of the RKKY interaction still follows the law shown in Eqs. (10-13).

Conclusions- We have theoretically explored the RKKY interaction between magnetic impurities in S-DSMs including all 2D and 3D models. Due to the coexistence of the relativistic and non-relativistic electrons, the RKKY interaction of S-DSMs is anisotropic and violates the decaying law proposed in isotropic systems. We find that the introduction of non-relativistic electrons in the S-DSMs can significantly prolong the decay of the RKKY interaction along relativistic direction, in comparison with the case of isotropic DSMs. For example, the decaying rate $R^{-5}$ for 3D DSMs is reduced to be $R^{-3}$ for type-II 3D S-DSMs, which can greatly facilitate the experiment detection and magnetic doping technology. The underlying physics is ascribed to the interplay of relativistic and non-relativistic electrons. Furthermore, we give a general formula to determine the decaying rate from the system dimension and the non-relativistic dimension. In addition, we find that the anisotropy of S-DSMs can greatly affect the DM component of the RKKY interaction, which is largest for impurities in the relativistic direction but vanishes in non-relativistic direction.

All these peculiar magnetic characteristics implies that the S-DSMs are a powerful platform to detect and control the magnetic exchange interaction, superior to extensively adopted isotropic systems. Experimentally, a variety of candidates for S-DSMs with different approaches have been proposed, such as multilayer $(\mathrm{TiO_{2}})_{m}/(\mathrm{VO_{2}})_{n}$ nanostructuresVictor1 ; Victor2 ; Banerjee , deformed graphenepress2 , and silicene oxideoxide . The RKKY interactions can be probed experimentally with present techniques, e.g., spin-polarized scanning tunneling spectroscopyLaplane , which can measure the magnetization curves of individual atoms, or the electron-spin-resonance technique coupled with an optical detection schemeWiebe1 ; Wiebe2 .