The Population III origin of GW190521
Abstract
We explore the possibility that the recently detected black hole binary (BHB) merger event GW190521 originates from the first generation of massive, metal-free, so-called Population III (Pop III), stars. Based on improved binary statistics derived from N-body simulations of Pop III star clusters, we calculate the merger rate densities of Pop III BHBs similar to GW190521, in two evolution channels: classical binary stellar evolution and dynamical hardening in high-redshift nuclear star clusters. Both channels can explain the observed rate density. But the latter is favoured by better agreement with observation and less restrictions on uncertain parameters. Our analysis also indicates that given the distinct features of the two channels (with merger rates peaked at and , respectively), future observation of BHB mergers similar to GW190521 with third-generation gravitational wave detectors will greatly improve our knowledge of the evolution of Pop III BHBs, especially for their dynamics during cosmic structure formation.
1 Introduction
The black hole binary (BHB) merger event GW190521 detected at a redshift of during the third observing run (O3) of LIGO/Virgo has unusual BH masses and (Abbott et al., 2020a, b), right within the mass gap predicted by standard pulsational pair-instability supernova (PPISN) models (e.g., Heger et al. 2003; Belczynski et al. 2016; Woosley 2017; Marchant et al. 2019). After its announcement, many studies explored the properties and origin of this unique event, including its statistical interpretation and implication (Fishbach & Holz, 2020; Wang et al., 2020), highly eccentric orbit (Gayathri et al., 2020), uncertainty of the mass gap (Costa et al., 2020), repeated BH mergers and stellar collisions in dense star clusters (e.g., Fragione et al. 2020; Romero-Shaw et al. 2020; Kremer et al. 2020; Renzo et al. 2020), mergers of ultra dwarf galaxies (Palmese & Conselice, 2020), accretion in dense molecular clouds (Rice & Zhang, 2020), and primordial BHs (De Luca et al., 2020).
Particularly, as discussed in Farrell et al. (2020); Tanikawa et al. (2020a), the first generation of stars in the universe, so-called Population III (Pop III) stars with zero or very low metallicities, are promising progenitors of the BHs found in GW190521, because Pop III stars, with small sizes and little mass loss, are likely to retain most of their hydrogen envelopes until the pre-SN stage, avoid the PPISN regime and form BHs in the mass gap (reaching up to ) with fallback (see Fig. 1). Actually, Kinugawa et al. (2020b) show that classical binary stellar evolution models for isolated binaries can explain the observed merger rate density of events like GW190521, under certain assumptions (Kinugawa et al., 2020a).
However, the uncertainties in binary stellar evolution models are significant, for (initial) binary statistics, common envelope (CE) parameters and SN kicks, leading to up to two orders of magnitude discrepancy in the BHB merger rate (e.g., Kinugawa et al. 2014; Belczynski et al. 2017). It remains unknown whether a Pop III star can keep its hydrogen envelope to reach and meanwhile experience close binary interactions (Farrell et al., 2020).
Furthermore, as Pop III stars are mostly formed at high redshifts (peaked at ; e.g., Johnson et al. 2013; Xu et al. 2016; Liu & Bromm 2020a), their remnants will be affected by the entire process of cosmic structure formation, and it is necessary to consider the effect of environment for the evolution of Pop III BHs/BHBs. For instance, it is shown that Pop III BHs with initial masses below the mass gap can grow to via rapid gas accretion, and thus form BHBs similar to GW190521, in centers of atomic-cooling halos (Safarzadeh & Haiman, 2020), protoglobular clusters with early ( Myr) growth before gas depletion (Roupas & Kazanas, 2019), and nuclear star clusters with wind-fed supra-exponential accretion (Natarajan, 2020). Moreover, interactions with surrounding stars can allow initially wide binaries to merge within a Hubble time, without undergoing close binary interactions. In light of this, we explore the possible Pop III origin of GW190521, focusing on an alternative channel of dynamical hardening in dense star clusters.

2 Pop III BH binary models
Our analysis is based on improved binary statistics derived from N-body simulations of Pop III star clusters, employing a novel physically-motivated model for the initial cluster configuration, described in Liu et al. (2020). The main advantage of our approach is the consideration of the (nearly) self-similar nature of disc evolution and fragment properties during hierarchical fragmentation, inferred from small-scale hydrodynamic simulations of Pop III protostellar systems (e.g., Hirano & Bromm 2017; Susa 2019; Sugimura et al. 2020). Previous studies (e.g., Kinugawa et al. 2014; Belczynski et al. 2017; Kinugawa et al. 2020a) apply the binary parameters of present-day stars or Pop III protostars (of only a few ) to much more massive newly formed Pop III systems (after gas removal by feedback), resulting in smaller clusters than expected from angular-momentum conservation, and thus likely overestimate the fraction of stars in close binaries.
We adopt the fiducial (FD) model, tf1e2ta1e5a1m1, fully described in Liu et al. (2020), in which Pop III BHBs with primary masses and total masses are identified as candidate progenitors for GW190521, according to the 90% probability intervals for these parameters inferred from observation. We use the fitting formulae for Pop III stellar evolution at a metallicity of from Tanikawa et al. (2020c) to map zero-age main sequence (ZAMS) to BH mass, including two extreme cases (Fig. 1). In the optimistic case, there is no pulsational pair-instability (PPI) effect, such that . In the pessimistic case, a star with PPI () will lose its envelope, such that . We consider two channels for Pop III BHB mergers: classical binary stellar evolution for close binaries with CE evolution, and dynamical hardening (DH) for wide binaries in dense star clusters.
2.1 Classical binary stellar evolution
For simplicity, we here estimate the efficiency of producing BHB mergers like GW190521 from Pop III stars via classical binary stellar evolution without detailed modelling of the mass transfer and CE evolution, as well as SN kicks. Instead, we identify all binaries with Roche lobe overflow of either one of the two stars that is massive enough (, Kinugawa et al. 2020a) to have a convective envelope. We assume that these binaries will undergo CE evolution due to unstable mass transfer, and merge within a Hubble time, Gyr, following a power-law delay time distribution with a slope of -1 in the range of 3 to Myr, based on previous studies (e.g., Belczynski et al. 2017)111The results are not sensitive to the detailed shape of as long as it is dominated by mergers with short delay times (a few Myr), which is a common outcome in classical binary stellar evolution models (e.g., Belczynski et al. 2017; Kinugawa et al. 2020a; Tanikawa et al. 2020b)..
Because close binaries with AU in the FD model are rare, the efficiency of Pop III BHB mergers222The efficiency of BHB mergers for a stellar population is defined as the average number of BHBs that can merge within a Hubble time per unit stellar mass. similar to GW190521 via CE evolution with PPI is low, . Considering other models in Liu et al. (2020) with much (a factor of ) smaller cluster sizes and more close binaries, we obtain an extreme upper limit of in the optimistic case. Note that we do not include SN kicks for the primary, which can enhance the chance of CE evolution by shrinking the binary orbit, especially important for BHBs in the PPISN mass gap (see fig. 33 of Tanikawa et al. 2020b). Therefore, we may have underestimated the efficiency of BHB mergers driven by CE evolution.
2.2 Dynamical hardening in dense star clusters
We next consider how BHB evolution depends on environment, which can drive initially wide binaries to merge without a CE phase that is only available for initially close binaries. Actually, the dynamics of BHB coalescence via environmental effects is very complex, involving various astrophysical aspects such as a clumpy interstellar medium, dark matter distribution, nuclear star clusters (NSCs), supermassive BHs and AGN discs (e.g., Roškar et al. 2015; Antonini & Rasio 2016; Tamfal et al. 2018; Leigh et al. 2018; Choksi et al. 2019; Ogiya et al. 2019; Zhang et al. 2019; Secunda et al. 2019). For simplicity, we focus on one mechanism particularly important for massive Pop III BHBs: the dynamical hardening (DH) by 3-body interactions with surrounding (low-mass) stars in dense star clusters (Antonini & Rasio, 2016; Leigh et al., 2018). Below we estimate the delay time for a BHB merger with DH.
Following Liu & Bromm (2020b), the evolution of the semi-major axis for a BHB driven by 3-body interactions with surrounding stars and gravitational wave (GW) emission, can be written as (Sesana & Khan, 2015)
| (1) |
The first term represents 3-body interactions, the second the energy and angular momentum loss via GWs, and
| (2) | ||||
Here, and are the masses of the primary and secondary, , and are the velocity dispersion and stellar density around the BHB, given the eccentricity , and is a dimensionless parameter, which we set to for simplicity.
The binary system first undergoes a phase dominated by DH with a characteristic semimajor axis, estimated by imposing : . We assume a constant eccentricity in the DH-dominated phase for simplicity. The duration of this stage for to reach , the DH timescale, can be estimated with
| (3) |
where is the initial semi-major axis. We set , for .
After the DH-dominated phase (), the evolution is dominated by GW emission. The time spent in GW-driven inspiral before the final coalescence can be estimated with
| (4) | ||||
The total time of inspiral in the dense star cluster is then given by . Other than the binary parameters (, , and ), the key parameters that determine are and . Besides, only hard binaries will be further hardened (instead of destroyed) by 3-body interactions, which must satisfy in order to survive disruptions close to the apocenter, where is the typical mass of surrounding stars.
2.3 Pop III BHBs in high- NSC hosts
To apply the DH machinery to Pop III BHBs, we need to know the properties of host clusters ( and ), initial binary parameters and dynamics of Pop III BHs/BHBs falling into dense star clusters. Here we consider Pop III BHBs in nuclear star clusters (NSCs), which occupy the innermost regions of most galaxies (Neumayer et al. 2020), and are also common in high- atomic-cooling halos with (e.g., Devecchi & Volonteri 2009; Devecchi et al. 2010, 2012).
For NSC properties, we explore three cases with , , corresponding to NSCs in halos with masses , respectively, which dominate the halo populations at and 4 for peaks. These three models are meant to cover most () of the region occupied by observed NSCs with masses for (see fig. 7 of Neumayer et al. 2020) in the parameter space. In reality, the host NSC properties exhibit scatters and also evolve with redshift. The realistic situation will be a mixture of our models. To populate the - space with observed NSCs (see Fig. 4 in Appendix A), we estimate with , given the half-mass(light) radius . We set to the stellar density within a characteristic radius where the enclosed stellar mass is twice the mass of the infalling BHB (), assuming that the stars follow the Dehnen profile (Dehnen, 1993) with an inner slope of (see Sec. 4.1.2 in Liu & Bromm 2020b)333 is a conservative choice, which is also consistent with the trend (Neumayer et al., 2020).. Here describes how deep the BHB can sink into the cluster by mass segregation.
We substitute the candidate BHB progenitors of GW190521 from the FD model into the DH scheme (Equ. 1-4), in which only hard binaries without CE evolution are considered. In this way, we derive the NSC inspiral time distributions for the three NSC models. The results with PPI can be well fitted by with , 4 and 8, in the ranges of Gyr, Gyr and Myr, for , respectively (see Fig. 5 in Appendix A). The corresponding efficiencies of mergers are , and . Turning off PPI will enhance by a factor of , with almost unchanged. The final efficiency is given by , where (Neumayer et al., 2020) is the fraction of galaxies that host NSCs.
Now, taking into account the BH/BHB dynamics in host halos during cosmic structure formation, the final delay time can be written as , where and are the timescales for the BHB to fall into the final host halo and sink into the NSC via dynamical friction of gas. In general, Pop III star formation peaks at in low-mass halos () at peaks, and the host halos of Pop III BHs will then grow or merge into more massive halos, in which the Pop III BHs can further sink into NSCs. The halo growth/merger process is captured by the timescale . Given the mass of the final host halo, can be estimated with , where is the age of the universe as a function of redshift, and is the redshift at which matches the critical mass at peaks. We have , 0.56 and 1.06 Gyr, for , respectively.
The (gas) dynamical friction timescale depends on the (initial) distance of the BHB to the galaxy center and the gas density profile. We adopt the formula in Boco et al. (2020, see their equ. 18 and table 1) with fixed Coulomb logarithm and assuming circular orbits for the BHBs. This formula can be applied to different density profiles, parameterized by the gas mass and half-mass radius . For the model at , which is a typical high- atomic cooling halo, the singular isothermal sphere (SIS) is a good approximation to the density profiles found in simulations at pc (see equ. 2 in Safarzadeh & Haiman 2020). We consider the entire halo444The formula in Boco et al. 2020 does not include the effect of dark matter, which is valid for the inner regions ( kpc) of massive halos (). However, in our case with at , one has to consider dark matter even for kpc, as the virial radius is kpc. Therefore, we boost the initial specific angular momentum of the BHB by a factor of to include the gravity of dark matter. The dynamical friction timescale obtained in this way is consistent with that in Safarzadeh & Haiman (2020) within a factor of 2. with and kpc, which gives . For the model at , as a typical progenitor for local early-type galaxies, we follow Boco et al. (2020) to focus on the gas-dominated inner region with kpc and , under a Sersic profile with index , such that . Finally, for the intermediate case with at , we adopt the Hernquist profile, which is between the aforementioned SIS and Sersic models in terms of compactness. Again, we consider the gas-dominated inner region with kpc and , leading to . Although our modelling of gas distributions is highly idealized, it captures the trend that gas is more concentrated due to stronger cooling (with higher metallicities) in more massive halos at lower redshifts.
Finally, we consider the distribution of Pop III BHs/BHBs in high- galaxies. We derive the fraction of Pop III BHs enclosed within around galaxy centers in atomic-cooling halos (), from the cosmological simulation in Liu & Bromm (2020b, see Fig. 6 in Appendix A), where the dynamical friction of gas is unresolved. Then the (normalized) distribution of takes the form , where we adopt pc and pc, since at pc is negligible (), and for pc. The resulting distributions are shown in Fig. 2.

3 Resulting merger rate
Once the efficiency and delay time distribution of Pop III BHBs similar to GW190521 are known from a given evolution model, the merger rate density can be calculated by convolving with the input Pop III star formation rate density (SFRD) :
| (5) |
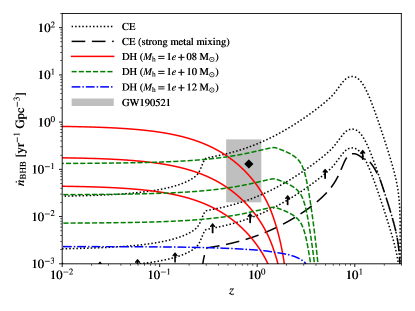
where is the age of the universe, and Myr (corresponding to ) marks the onset of Pop III star formation. We apply the optimistic Pop III SFRD model in Liu & Bromm (2020a, see the thick solid line in their fig. 13) to the Pop III BHB evolution models discussed above. For the optimal CE evolution model, we further consider a pessimistic SFRD case under strong metal mixing (see the long-dashed curve in fig. 13 of Liu & Bromm 2020a), where late-time () Pop III star formation is suppressed. The resulting evolution of in a variety of models is shown in Fig. 3.
It turns out that the CE model can only marginally reproduce the merger rate inferred from GW190521 with the optimistic efficiency from the FD model and Pop III SFRD, or with significant enhancement by SN kicks. However, if strong metal mixing is present, the merger rate from the CE channel is lower than the observed rate by a factor of , even with the optimistic efficiency from the FD model. If Pop III clusters are much (a factor of ) smaller than in the FD model, a better agreement can be achieved. But such cases seem unlikely to occur (Liu et al., 2020). The NSC DH models for at agree well with the observational constraint. While the model fails to drive enough Pop III BHBs into NSCs, and thus, underpredicts the meger rate even in the optimistic case.
4 Summary and Conclusions
We explore the possible Pop III origin of the recently reported BHB merger event GW190521 with BH masses in the pulsational pair-instability supernova (PPISN) mass gap (Abbott et al., 2020a). In particular, we consider the channel of dynamical hardening (DH) in high- nuclear star clusters (NSCs) for initially wide Pop III BHBs to merge within a Hubble time, in difference from the classical binary stellar evolution channel via common envelope (CE) evolution of close binaries (Kinugawa et al., 2020b). Based on improved binary statistics derived from N-body simulations of Pop III star clusters (Liu et al., 2020), we find that both channels can explain the merger rate of events like GW190521.
However, agreement with observation in the CE channel can only be (marginally) achieved with no PPI effect, or SN kicks to shrink the binary orbits (Tanikawa et al., 2020b), or much smaller Pop III cluster sizes than expected from small-scale simulations of Pop III protostar systems, and also requires significant late-time () Pop III star formation. For the NSC DH channel, on the other hand, the observed merger rate is naturally explained with typical populations of NSCs in dark matter halos with formed at . Besides, as pointed out in Gayathri et al. (2020) and Romero-Shaw et al. (2020), GW190521 resulted from a system that was either strongly precessing or eccentric, which is unlikely for CE evolution. However, these features are possible for initially wide Pop III binaries resulting from Pop III star cluster dynamics which later fall into NSCs, especially when considering the effect on binary orbits by central massive BHs likely co-existing with NSCs (e.g., Zhang et al. 2019). Therefore, we emphasize the importance of alternative BHB evolution channels, including environmental effects in addition to the classical binary stellar evolution channel for isolated binaries. Our results based on simplified modelling of the dynamics of Pop III BHBs in high- galaxies should be regarded as broad estimations for the range of possible outcomes. We call for more advanced theoretical models to reduce the uncertainties, and further take into account halo growth and mergers, gas accretion and central massive BHs.
Although our analysis favours the NSC DH channel, the CE channel cannot be ruled out, due to significant uncertainties in the two channels. Both may have non-negligible contributions to the BHB mergers in the PPISN mass gap. Moreover, as the former has typical long delay times of a few Gyr, while the latter is dominated by short delay times of a few Myr. Therefore, most of the corresponding BH mergers happen at and , respectively. With the third generation of gravitational wave detectors such as the Einstein telescope (Punturo et al., 2010), we will be able to measure the merger rate density of BHBs in the PPISN mass gap up to . If such sources are dominated by Pop III progenitors, this will enable us to evaluate the relative importance of the two channels of Pop III BHB mergers, providing a novel probe of early cosmic structure formation.
Acknowledgments
The authors acknowledge the Texas Advanced Computing Center (TACC) for providing HPC resources under XSEDE allocation TG-AST120024.
References
- Abbott et al. (2020a) Abbott, R., Abbott, T., Abraham, S., et al. 2020a, Phys. Rev. Lett., 125, 101102
- Abbott et al. (2020b) —. 2020b, ApJ, 900, L13
- Antonini & Rasio (2016) Antonini, F., & Rasio, F. A. 2016, ApJ, 831, 187
- Belczynski et al. (2017) Belczynski, K., Ryu, T., Perna, R., et al. 2017, MNRAS, 471, 4702
- Belczynski et al. (2016) Belczynski, K., Heger, A., Gladysz, W., et al. 2016, A&A, 594, A97
- Boco et al. (2020) Boco, L., Lapi, A., & Danese, L. 2020, ApJ, 891, 94
- Choksi et al. (2019) Choksi, N., Volonteri, M., Colpi, M., Gnedin, O. Y., & Li, H. 2019, ApJ, 873, 100
- Costa et al. (2020) Costa, G., Bressan, A., Mapelli, M., et al. 2020, arXiv preprint arXiv:2010.02242
- De Luca et al. (2020) De Luca, V., Desjacques, V., Franciolini, G., Pani, P., & Riotto, A. 2020, arXiv preprint arXiv:2009.01728
- Dehnen (1993) Dehnen, W. 1993, MNRAS, 265, 250
- Devecchi & Volonteri (2009) Devecchi, B., & Volonteri, M. 2009, ApJ, 694, 302
- Devecchi et al. (2010) Devecchi, B., Volonteri, M., Colpi, M., & Haardt, F. 2010, MNRAS, 409, 1057
- Devecchi et al. (2012) Devecchi, B., Volonteri, M., Rossi, E., Colpi, M., & Portegies Zwart, S. 2012, MNRAS, 421, 1465
- Farrell et al. (2020) Farrell, E. J., Groh, J. H., Hirschi, R., et al. 2020, arXiv preprint arXiv:2009.06585
- Fishbach & Holz (2020) Fishbach, M., & Holz, D. E. 2020, arXiv preprint arXiv:2009.05472
- Fragione et al. (2020) Fragione, G., Loeb, A., & Rasio, F. A. 2020, arXiv preprint arXiv:2009.05065
- Gayathri et al. (2020) Gayathri, V., Healy, J., Lange, J., et al. 2020, arXiv preprint arXiv:2009.05461
- Heger et al. (2003) Heger, A., Fryer, C., Woosley, S., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288
- Hirano & Bromm (2017) Hirano, S., & Bromm, V. 2017, MNRAS, 470, 898
- Johnson et al. (2013) Johnson, J. L., Dalla, V. C., & Khochfar, S. 2013, MNRAS, 428, 1857
- Kinugawa et al. (2014) Kinugawa, T., Inayoshi, K., Hotokezaka, K., Nakauchi, D., & Nakamura, T. 2014, MNRAS, 442, 2963
- Kinugawa et al. (2020a) Kinugawa, T., Nakamura, T., & Nakano, H. 2020a, arXiv e-prints, arXiv:2005.09795
- Kinugawa et al. (2020b) Kinugawa, T., Nakamura, T., & Nakano, H. 2020b, arXiv preprint arXiv:2009.06922
- Kremer et al. (2020) Kremer, K., Spera, M., Becker, D., et al. 2020, arXiv preprint arXiv:2006.10771
- Leigh et al. (2018) Leigh, N. W., Geller, A. M., McKernan, B., et al. 2018, MNRAS, 474, 5672
- Liu & Bromm (2020a) Liu, B., & Bromm, V. 2020a, MNRAS, 497, 2839
- Liu & Bromm (2020b) —. 2020b, MNRAS, 495, 2475
- Liu et al. (2020) Liu, B., Meynet, G., & Bromm, V. 2020, arXiv e-prints, arXiv:2010.05824
- Marchant et al. (2019) Marchant, P., Renzo, M., Farmer, R., et al. 2019, ApJ, 882, 36
- Natarajan (2020) Natarajan, P. 2020, arXiv preprint arXiv:2009.09156
- Neumayer et al. (2020) Neumayer, N., Seth, A., & Böker, T. 2020, A&A Rev., 28, 1
- Ogiya et al. (2019) Ogiya, G., Hahn, O., Mingarelli, C. M. F., & Volonteri, M. 2019, arXiv e-prints, arXiv:1911.11526
- Palmese & Conselice (2020) Palmese, A., & Conselice, C. J. 2020, arXiv e-prints, arXiv:2009.10688
- Punturo et al. (2010) Punturo, M., Abernathy, M., Acernese, F., et al. 2010, Classical and Quantum Gravity, 27, 194002
- Renzo et al. (2020) Renzo, M., Cantiello, M., Metzger, B., & Jiang, Y.-F. 2020, arXiv preprint arXiv:2010.00705
- Rice & Zhang (2020) Rice, J. R., & Zhang, B. 2020, arXiv e-prints, arXiv:2009.11326
- Romero-Shaw et al. (2020) Romero-Shaw, I. M., Lasky, P. D., Thrane, E., & Bustillo, J. C. 2020, arXiv preprint arXiv:2009.04771
- Roškar et al. (2015) Roškar, R., Fiacconi, D., Mayer, L., et al. 2015, MNRAS, 449, 494
- Roupas & Kazanas (2019) Roupas, Z., & Kazanas, D. 2019, A&A, 632, L8
- Safarzadeh & Haiman (2020) Safarzadeh, M., & Haiman, Z. 2020, arXiv e-prints, arXiv:2009.09320
- Secunda et al. (2019) Secunda, A., Bellovary, J., Mac Low, M.-M., et al. 2019, ApJ, 878, 85
- Sesana & Khan (2015) Sesana, A., & Khan, F. M. 2015, MNRAS, 454, L66
- Sugimura et al. (2020) Sugimura, K., Matsumoto, T., Hosokawa, T., Hirano, S., & Omukai, K. 2020, ApJ, 892, L14
- Susa (2019) Susa, H. 2019, ApJ, 877, 99
- Tamfal et al. (2018) Tamfal, T., Capelo, P. R., Kazantzidis, S., et al. 2018, ApJ, 864, L19
- Tanikawa et al. (2020a) Tanikawa, A., Kinugawa, T., Yoshida, T., Hijikawa, K., & Umeda, H. 2020a, arXiv preprint arXiv:2010.07616
- Tanikawa et al. (2020b) Tanikawa, A., Susa, H., Yoshida, T., Trani, A. A., & Kinugawa, T. 2020b, arXiv preprint arXiv:2008.01890
- Tanikawa et al. (2020c) Tanikawa, A., Yoshida, T., Kinugawa, T., Takahashi, K., & Umeda, H. 2020c, MNRAS, 495, 4170
- Wang et al. (2020) Wang, Y.-Z., Tang, S.-P., Liang, Y.-F., et al. 2020, arXiv e-prints, arXiv:2009.03854
- Woosley (2017) Woosley, S. 2017, ApJ, 836, 244
- Xu et al. (2016) Xu, H., Norman, M. L., O’Shea, B. W., & Wise, J. H. 2016, ApJ, 823, 140
- Zhang et al. (2019) Zhang, F., Shao, L., & Zhu, W. 2019, ApJ, 877, 87
Appendix A Justification of the DH models for high- NSCs
In this section, we further justify our choices of parameters in Sec. 2.3 for NSC properties and dynamics of Pop III BHs/BHBs in high- galaxies. The NSC properties adopted in our three models are based on the mass-size scaling relation for NSCs observed in the local Universe (see fig. 7 of Neumayer et al. 2020). We assume that high- NSCs have similar properties as the relaxation timescales in NSCs are usually large (a few Gyr). The distributions of observed NSCs in the - and - space are shown in Fig. 4. It turns out that our models capture typical halos with , which cover 93% of the observed NSC sample in the distribution555According to Equations 1-4, is the one single parameter that reflects NSC properties in the DH scheme. of . Here we estimate with the circular velocity at the half-mass(light) radius. As Pop III BHs/BHBs are much more massive than typical stars in the NSC, they will quickly segregate into the cluster center, so that we need to set to the central density. However, central volume densities of NSCs are only measured in a few nearby galaxies due to limitation of resolution. To capture the typical stellar density felt by the Pop III BHB in the cluster center, we set to the stellar density within a characteristic radius where the enclosed stellar mass is twice the mass of the infalling BHB (). In our case, pc, with a median of 0.02 pc. The values of obtained in this way are consistent with observation (i.e., at pc, Neumayer et al. 2020).
Fig. 5 shows the inspiral time distribution for the three models with . These distributions can be well-approximated with power-laws of positive slopes , which are quite different from the inspiral time distributions for the CE channel with negative slopes (e.g., Belczynski et al. 2017; Tanikawa et al. 2020b). The reason is that for the CE channel, the negative slope is associated with the distribution of initial separation , while in the DH channel, the inspiral time is insensitive to . As shown in Equ. 3, the term involving is negligible for wide binaries ( is typically a few AU, much smaller than ). Therefore, by DH is determined by the distributions of eccentricity and mass. In general, higher eccentricity and higher total mass lead to smaller . For the FD model, the distributions of total mass and eccentricity are both (quasi-)uniform (see fig. 9 in Liu et al. 2020). In this way, binaries with small must be massive and meanwhile highly eccentric, which are rare, such that is dominated by binaries with large , and therefore have positive slopes.
Finally, Fig. 6 shows the enclosed fraction of Pop III BHs in terms of the physical distance to the galaxy center and the ratio , given the halo viral radius , for atomic-cooling halos (, including sub-halos), measured from the cosmological simulation FD_box_Lseed in Liu & Bromm (2020b), at , 5.5 and 4, corresponding to the NSC models with , respectively. In general, at fixed , increases with redshift. The reason is that most Pop III BHs are formed in low-mass (sub)halos () at . These low-mass halos then grow or merge into more massive halos at later times, which tend to have larger physical sizes and longer dynamical timescales, such that an increased fraction of Pop III BHs will not be able to settle into the inner region of kpc. Note that dynamical fricition is not resolved at small scales ( pc) in FD_box_Lseed, so that the results in Fig. 6 can be regarded as initial distributions of BHs in which the effect of dynamical friction has not kicked in.


