The Overlap Gap Property: a Topological Barrier to Optimizing over Random Structures
Abstract
The problem of optimizing over random structures emerges in many areas of science and engineering, ranging from statistical physics to machine learning and artificial intelligence. For many such structures finding optimal solutions by means of fast algorithms is not known and often is believed not possible. At the same time the formal hardness of these problems in form of say complexity-theoretic -hardness is lacking.
In this introductory article a new approach for algorithmic intractability in random structures is described, which is based on the topological disconnectivity property of the set of pair-wise distances of near optimal solutions, called the Overlap Gap Property. The article demonstrates how this property a) emerges in most models known to exhibit an apparent algorithmic hardness b) is consistent with the hardness/tractability phase transition for many models analyzed to the day, and importantly c) allows to mathematically rigorously rule out large classes of algorithms as potential contenders, in particular the algorithms exhibiting the input stability (insensitivity).
Optimization problems involving uncertainty emerge in many areas of science and engineering, including statistics, machine learning and artificial intelligence, computer science, physics, biology, management science, economics and social sciences. The exact nature and the sources of uncertainty vary from field to field. The modern paradigm of Big Data brought forward optimization problems involving in particular many dimensions, thus creating a new meta-field of ”high dimensional probability” and ”high-dimensional statistics” [Ver18],[BVDG11],[FR13]. Two recent special semester programs at the Simons Institute for the Theory of Computing were devoted to this burgeoning topic 111https://simons.berkeley.edu/programs/si2021, https://simons.berkeley.edu/programs/hd20, among a multitude of other conferences and workshops. This paper is based on several lectures given by the author in a reading group during the first of these events. While many of the optimization problems involving randomness can be solved to optimality by fast, and in fact sometimes border-line trivial algorithms, other problems have resisted decades of attempts and slowly it has been accepted that these problems are likely non-amenable to fast algorithms, with polynomial time algorithms broadly considered to be the gold standards for what constitutes fast algorithms. The debate surrounding the actual algorithmic hardness of these problems though is by no means settled, unlike its ”worst-case” algorithmic complexity-theoretic counterparts, expressed in the form of the widely believed conjecture.
What is the ”right” algorithmic complexity theory explaining the persistent failure to find tractable algorithms for these problems? We discuss in this paper some existing theories and explain their shortcomings in light what we know now about the state of the art algorithms. We then propose an approach, largely inspired by the field of statistical physics, which offers a new topological/geometric theory of algorithmic hardness that is based on the disconnectivity of the overlaps of near optimal solutions, dubbed the ”Overlap Gap Property” (OGP). The property has been rigorously verified for many concrete models, and, importantly can be used to mathematically rule out large classes of algorithms as potential contenders, specifically algorithms exhibiting a form of input stability. This includes both classical and quantum algorithms, the latter class including algorithms called QAOA (Quantum Approximate Optimization Algorithm), [FGG20a],[FGG20b] which gained recently a lot of attention as the most realistic algorithm to be implementable on quantum computers [FGG14]. A widely studied random Number Partitioning problem will be used to illustrate both the OGP and the mechanics by which this property manifests itself as a barrier for tractable algorithms.
The Largest Clique of a Random Graph: the Most ”Embarrassing” Open Problem in Random Structures
Imagine a club with members in which about 50% of the member pairs know each other personally, and the remaining 50% of the members do not. You want to find a largest clique in this club, namely the largest group of members out of the members who all know each other. What is the typical size of such a clique? How easy is it to find one? This question can be modeled as the problem of finding a largest fully connected sub-graph (formally called a ”clique”) in a random Erdös-Rényi graph , which is a graph on nodes where every pair of nodes is connected with probability , independently for all pairs. The first question regarding the largest clique size is a textbook example of the so-called probabilistic method, a simple application of which tells us that is likely to be near with high degree of certainty as gets large [AS04]. A totally different matter is the problem of actually finding such a clique and this is where the embarrassment begins. Richard Karp, one of the founding fathers of the algorithmic complexity theory, observed in his 1976 paper [Kar76] that a very simple algorithm, both in terms of the analysis and the implementation, finds a clique of roughly half-optimum size, namely with about members, and challenged to do better. The problem is still open and this is embarrassing for two reasons: (a) The best known algorithm, namely the one above, is also an extremely naive one. So it appears that the significant progress that the algorithmic community has achieved over the past decades in constructing ever more clever and powerful algorithms, is totally helpless in improving upon this extremely simple and naive algorithm; (b) We don’t have a workable theory of algorithmic hardness which rigorously explains why finding cliques of size half-optimum is easy, and improving on it does not seem possible within the realm of polynomial time algorithms. The classical paradigm and its variants is of no help here, more on this below. An approach based on the solution space landscape can be used to rule out Markov Chain Monte Carlo (MCMC) algorithms for finding cliques larger than half-optimum by showing that the associated chain mixes at scale larger than polynomial time, and thus ruling out the MCMC algorithm [Jer92]. The method however does not appear extendable to other types algorithms which are not based on MCMC method.
The largest clique problem turns out to be one of very many other problems exhibiting a similar phenomena: using non-constructive analysis method one shows that the optimal value of some optimization problem involving randomness is some value , the best known polynomial time algorithm achieves value , and there is a significant gap between the two: . A partial list (but one growing seemingly at the speed of the Moore’s Law) is the following: randomly generated constraint satisfaction problem (aka the random K-SAT problem), largest independent set in a random graph, proper coloring of a random graph, finding a ground state of a spin glass model in statistical mechanics, discovering communities in a network (the so-called community detection problem), group testing, statistical learning of a mixture of Gaussian distributions, sparse linear regression problem, sparse covariance estimation, graph matching problem, spiked tensor problem, the Number Partitioning problem, and many other problems.
The Number Partitioning problem is motivated in particular by the statistical problem of designing a randomized control study with two groups possessing roughly ”equal” attributes. It is also a special case of the bin-packing problem, and also has been widely studied in the statistical physics literature. The Number Partitioning problem will serve as one of the running example in this article, illustrating our main ideas, so we introduce it now. Given items with weights , the goal is to split it into two groups so that the difference of total weights in two groups is the smallest possible. Namely, the goal is finding a subset such that is as small as possible. An NP-hard problem in the worst case [GJ79], it is more tractable in presence of randomness. Suppose, the weights are generated independently according to the standard Gaussian distribution . A rather straightforward application of the same probabilistic method shows that the optimum value is typically for large . Namely, the value of in our context is . An algorithm proposed by Karmarkar and Karp in 1982 [KK82] achieves the value of order , with value predicted (though not proven) to be [BM08]. The multiplicative gap between the two is thus very significant (exponential): . While multidimensional extensions of this algorithm have been considered recently [TMR20],[HSSZ19], no improvement of this result is known to the date, and no algorithmic hardness result is known either.
In Search of the ”Right” Algorithmic Complexity Theory
We now describe some existing approaches for understanding the algorithmic complexity and discuss their shortcomings in explaining the existential/algorithmic gap exhibited by the multitude of problems described above. Starting with the classical algorithmic complexity theory based on the algorithmic complexity classes such as , , etc. this theory is of no help, since these complexity classes are based on the worst-case assumptions on the problem description. For example, assuming the widely believed conjecture that , finding a largest clique in a graph with nodes within a multiplicative factor is not possible by polynomial time algorithms [Has99] for any constant if . This is a statement, however, about the algorithmic problem of finding large cliques in all graphs, and it is in sharp contrast with the factor achievable by polynomial time algorithms for random graphs , according to the discussion above.
A significant part of the algorithmic complexity theory does in fact deal with problems with random input and here an impressive random-case to worst-case reductions are achievable for some of the problems. These problems enjoy wide range applications in cryptography, where the average case hardness property is paramount for designing secure cryptographic protocols. For example, if there exists a polynomial time algorithm for computing the permanent of a matrix with i.i.d. random inputs, then, rather surprisingly, one can use it to design a polynomial time algorithm for all matrices [Lip91]. The latter problem is known to be in the complexity class which subsumes . A similar reduction exists [GK18] for the problem of computing the partition function of a Sherrington-Kirkpatrick model described below, thus implying that computing partition functions for spin glass models is not possible by polynomial time algorithms unless . Another problem admitting average-case to worst-case reduction is the problem of finding a shortest vector in a lattice [Ajt96]. The random to worst case types of reduction described above would be ideal for our setting, as they would provide the most compelling evidence of hardness of these problems. For example, it would be ideal to show that finding a clique of size at least say in implies a polynomial time algorithm with the same approximation guarantee for all graphs. Unfortunately, such a result appears out of reach for the existing proof techniques.
Closer to the approach described in this paper, and the one which in fact has largely inspired the present line of work, is a range of theories based on the solution space geometry of the underlying optimization problem. This approach emerged in the statistical physics literature, specifically the study of spin glasses, and more recently found its way to questions above and beyond statistical physics, in particular questions arising in the context of studying neural networks as [CHM+15]. The general philosophy of this take on the algorithmic complexity is that when the problem appears to be algorithmically hard, this somehow should be reflected in the non-trivial geometry of optimal or near optimal solutions. One of the earliest such approaches was formulated for the decision problems, such as random constraint satisfaction problems (aka random K-SAT problem). It links the algorithmic hardness with the proximity to the satisfiability phase transition threshold [FA86], [KS94], and the order (first vs second) of the associated phase transition [MZK+99]. To elaborate, we need to introduce the random K-SAT problem first. It is a Boolean constraint satisfaction problem involving variables defined as a conjunction of clauses , where each clause is a disjunction of exactly variables from or their negation. Thus, each is of the form . An example of such a formula with , and is say . A formula is called satisfiable if there exists an assignment of Boolean variables to values and such that the value of the formula is .
A random instance of a K-SAT problem is obtained by selecting variables into each clause uniformly at random, independently for all and applying the negation operation with probability independently for all variables. Random K-SAT problem is viewed by statistical physicists as a problem exhibiting the so-called frustration property, which is of great interest to physics of spin glasses, and hence it has enjoyed a great deal of attention in the statistical physics literature [MPV87],[MM09].
As it turns out, for each there is a conjectured critical threshold for the satisfiability property, which was rigorously proven [DSS15] for large enough . In particular, for every , the formula admits a satisfying assignment when , and for every , the formula does not admit a satisfying assignment when , both with overwhelming probability as . The sharpness of this transition was established rigorously earlier by general methods in [Fri99]. The algorithmic counterparts, however, came short of achieving the value for every (more on this below). Even before the results in [DSS15] and [Fri99], it was conjectured in the physics literature that perhaps the existence of the sharp phase transition property itself is the culprit for the algorithmic hardness [KS94], [MZK+99]. This was argued by studying the heuristic running times of finding the satisfying solutions or demonstrating non-existence of ones for small values of , and observing that the running time explodes near , and subsides when is far from on either side. The values of are known thanks to the powerful machinery of the replica symmetry methods developed in a seminal works of Parisi [Par80],[MPV87]. These methods give very precise predictions for the values of for every . For example is approximately when . An in depth analysis of the exponent of the running times was reported in [KS94].
The theory postulating that the algorithmic hardness of the K-SAT problem is linked with the satisfiability phase transition however appears inconsistent with the later rigorous discoveries obtained specifically for large values of . In particular, while is known to be approximately for large values of , all of the known algorithms stall long before that, and specifically at [CO10]. Furthermore, there is an evidence that breaking this barrier might be extremely challenging. This was argued by proving that the model undergoes the so-called clustering phase transition near [ART06],[MMZ05] (more on this below), but and also by ruling out various families of algorithms. These algorithms include sequential local algorithms and algorithms based on low-degree polynomials (using the Overlap Gap Property discussed in the next section) [GS17b],[BH21], the Survey Propagation algorithm [Het16], and a variant of a random search algorithm called WalkSAT [COHH17]. The Survey Propagation algorithm is a highly effective heuristics for finding satisfying assignments in random K-SAT and many other similar problems. It is particularly effective for low values of and beats many other existing approaches in terms of the running times and sizes of instances it is capable to handle [MPZ02] (see also [GS02] for the perspective on the approach). It is entirely possible that this algorithm and even its more elementary version, the Belief Propagation guided decimation algorithm solves the satisfiability problem for small values of . An evidence of this can be found in [RTS09], and rigorous analysis of this algorithm was conducted by Coja-Oghlan in [CO11], which shows it to be effective when . However, the analysis by Hetterich in [Het16] rules out the Survey Propagation algorithm for sufficiently large values of , beyond the threshold, which we recall is . Additionally, the theory of algorithmic hardness based on the existence of the satisfiability type phase transition does not appear to explain the algorithmic hardness associated with optimization problems, such as the largest clique problem in .
The clustering property was rigorously established [ART06],[MMZ05] for random K-SAT for values of above , which is known to be close to for large . We specifically refer to this as weak clustering property in order to distinguish it from the strong clustering property, both of which we now define. (While the distinction between weak and strong clustering was discussed in many prior works, the choice of the terminology is entirely by the author). The model exhibits the weak clustering property if there exists a subset of satisfying assignments which contains all but exponentially small in fraction of the satisfying assignments, and which can be partitioned into subsets (clusters) separated by order distances, such that within each cluster one can move between any two assignments by changing at most constantly many bits. In other words, by declaring two assignments and connected if can be obtained from by flipping the values of at most variables, the set consists of several disconnected components separated by linear in distances. This is illustrated on Figure 1 where blue regions represent clusters in . The grey ”tunnel” like sets depicted on the figure are part of the complement (exception) subset of the set of satisfying assignments, which may potentially connect (tunnel between) the clusters. Furthermore, the clusters are separated by exponentially large in cost barriers, meaning that any path connecting two solutions from different clusters, (which then necessarily contains assignments violating at least some of the constraints), at some point contains in it assignments which in fact violate order constraint. For this reason the clustering property is sometimes referred to as ”energetic” barrier.
As mentioned earlier, for large values of the onset of weak clustering occurs near , and in fact the suggestion that this value indeed corresponds to the algorithmic threshold was partially motivated by this discovery of weak clustering property around this value. See also [RT10] for the issues connecting the clustering property with the algorithmic hardness. Below the bulk of the set of satisfying assignments constitutes one connected subset.
On the other hand, the strong clustering property is the property that all satisfying assignments can be partitioned into clusters like the ones above, however, with no exceptions. Namely is the set of all satisfying assignments. This can be visualized from Figure 1 where the grey ”tunnels” are removed. It turns out that for large values of , the model does exhibit the strong clustering property as well, but the known lower bounds for it are of the order as opposed to , for large . While not proven formally, it is expected though that the onset of the strong clustering property indeed occurs at values order as opposed to for large . Namely the weak and strong clustering properties appear at different in scales.
The existence of the strong clustering property is established as an implication of the Overlap Gap Property, (which is the subject of this paper) and this was the approach used in [ART06],[MMZ05]. In contrast the weak clustering property is established by using the so-called planting solution which amounts to consider the solution space geometry from the perspective of a uniformly at random selected satisfying assignment.
The necessity of distinguishing between the two modes of clustering described above is driven by algorithmic implications. Solutions generated by most algorithms typically are not generated uniformly at random and thus in principle can easily fall into the exception set . Thus the obstruction arguments based somehow on linear separations between the clusters and exponentially large energetic barriers might simply be of no algorithmic relevance. This is elaborated further in later section devoted to the relationship between clustering and the Overlap Gap Property using specifically the binary perceptron model example. In contrast, the strong clustering property implies that every solution produced by the algorithm belongs to one of the clusters. Thus if two implementations of the algorithm produce solutions in different clusters, then informally the algorithm is capable of ”jumping” over large distances between the clusters. In fact this intuition is formalized using the Overlap Gap Property notion by means of extending the strong clustering property to an ensemble of correlated instances (which we call ensemble Overlap Gap Property) pitted against the stability (input insensitivity) of algorithms. This is discussed in depth in the next section.
As the notion of ”exception” size in the definition of weak clustering property hinges on the counting measure associated with the space of satisfying assignments (and the uniform measure was assumed in the discussion above) a potential improvement might stem from changing this counting measures and introducing solution specific weights. Interestingly, for small values of this can be done effectively delaying the onset of weak clustering, as was shown by Budzynski et al in [BRTS19]. Unfortunately, though, for large the gain is only in second order terms, and up to those orders, the threshold for the onset of weak clustering based on biased counting measures is still as shown by Budzynski and Semerjian in [BS20]. This arguably, provides an even more robust evidence that this value marks a phase transition point of fundamental nature.
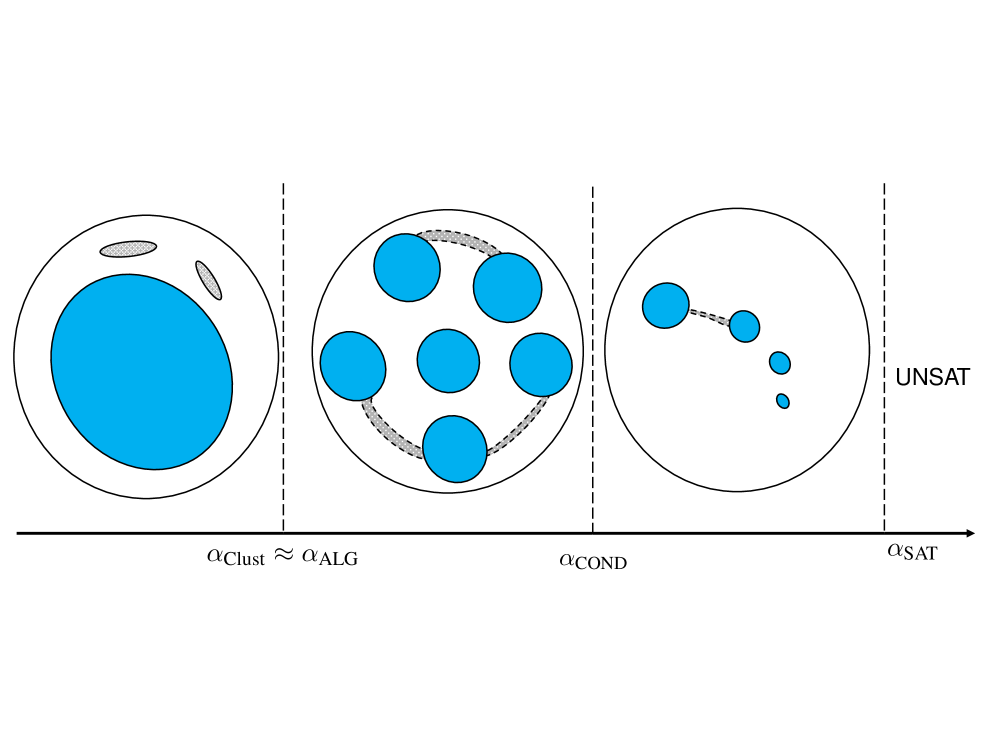
More recently algorithmic barriers were suggested to be linked with refined properties of the clustering phase transition, specifically the so-called condensation phase transition [KMRT+07] and the emergence of so-called frozen variables. Algorithmic implications of both are discussed in [MPRT16]. Using again a powerful machinery of the replica symmetry breaking, providing non-rigorous, though highly believable predictions, one identifies another phase transition satisfying for large . As the value passes through the number of solution clusters covering the majority of satisfying assignment in the random K-SAT problem drops dramatically from the exponentially many to only constantly many ones, with the largest cluster containing a non-trivial fraction of all of the assignments [KMRT+07], see Figure 1. At this stage a long-range dependence between the spin magnetization (appropriately defined) emerges and furthermore at this stage the random overlaps (inner products) of pairs of assignments generated according to the associated Gibbs measure have a non-trivial limiting distribution, described by the so-called Parisi measure.
Even before the value exceeds the value for large , each cluster contains a non-trivial fraction of the frozen variables, which are variables always taking the same values within a given cluster of satisfying assignment. The authors in [MPRT16] conjecture that the emergence of frozen variables is the primary culprit of the algorithmic hardness and construct a variant of the Survey Propagation algorithm called Backtracking Survey Propagation algorithm which is conjectured to be effective all the way up to . Numerical simulations demonstrate an excellent performance of this algorithm on randomly generated instances of K-SAT for small values of .
The conjecture linking the emergence of frozen variables with algorithmic hardness stumbles however upon similar challenges as the theory based on the existence of the phase transition. A rigorous evidence has been established that when is large, is of the order for some (explicitly computable) value which does not depend on . In particular is substantially above the value at which all known algorithms fail and furthermore classes of algorithms, including the standard Survey Propagation algorithm, are ruled out as discussed above. Of course the non-existence of evidence is not necessarily the evidence of non-existence, and it is very much possible that in future successful polynomial time algorithms will be constructed in the regime . But there is another limitation of the theory of algorithmic hardness based on the emergence of frozen variables: just like the notion of satisfiability phase transition, the notion of frozen variables does not apply to problems of optimization type, such as the largest clique problem, or optimization problem appearing in the context of spin glass models, for example the problem of finding a ground state of a spherical -spin glass model. In this model spins take values in a continuous range and thus the notion of frozenness, which is exclusively discrete, is lost.
Topological Complexity Barriers. The Overlap Gap Property
We now introduce a new approach for predicting and proving algorithmic complexity for solving random constraint satisfaction problems and optimization problems on random structures, such as the ones introduced in earlier sections. The approach bears a lot of similarity with the predictions based on the clustering property described in the earlier section, but has important and nuanced differences, which allows us to rule out large classes of algorithms, something that did not seem possible before. An important special case of such algorithms are stable algorithms, namely algorithms exhibiting low sensitivity to the data input. A special yet very broad and powerful class of such algorithms are algorithms based on low-degree polynomials. A fairly recent stream of research [HS17],[HKP+17],[Hop18] puts forward an evidence that in fact algorithms based on low-degree polynomials might be the most powerful class of polynomial time algorithms for optimization problem on random structures, such as problems discussed in this paper.
A generic formulation of the optimization problem
To set the stage, we consider a generic optimization problem . Here encodes the objective function (cost) to be minimized. The solutions lie in some ambient solution space , which is typically very high dimensional, often discrete, with encoding its dimension. The space is equipped with some metric (distance) defined for each pairs of solutions . For the max-clique problem we can take . For the Number Partitioning problem we can take . is intended to denote the associated randomness of the problem. So, for example, for the max-clique problem, encodes the random graph , and encodes a set of nodes constituting a clique, with if node is in the clique and otherwise. We denote by an instance generated according to the probability law of . In the present context, is any graph, the likelihood of generating of which is . Finally, is the number of ones in the vector . Now, if does not actually encode a clique (that is for at least one of the edges of the graph we have ) we can easily augment the setup by declaring for such ”non-clique” encoding vectors. For the Number Partitioning problem, is just the probability distribution associated with an -vector of independent standard Gaussians. For each and each instance of , the value of the associated partition is . Here denotes an inner product between vectors and . Thus, for the largest clique problem we have that the random variable is approximately with high degree of likelihood. For the Number Partitioning problem we have that is approximately with high degree of likelihood as well.
The OGP and its variants
We now introduce the Overlap Gap Property (abbreviated as OGP) and its several variants. The term was introduced in [GL18], but the property itself was discovered by Achlioptas and Ricci-Tersenghi [ART06], and Mezard, Mora and Zecchina [MMZ05]. The definition of the OGP pertains to a particular instance of the randomness . We say that the optimization problem exhibits the OGP with values if for every two solutions which are -optimal in the additive sense, namely satisfy , it is the case that either or . Intuitively, the definition says that every two solutions which are ”close” (within an additive error ) to optimality, are either ”close” (at most distance ) to each other, or ”far” (at least distance ) from each other, thus exhibiting a fundamental topological discontinuity of the set of distances of near optimal solutions. In the case of random instances we say the the problem exhibits the OGP if the problem exhibits the OGP with high likelihood when is generated according to the law . An illustration of the OGP is depicted on Figure 2. The notion of the ”overlap” refers to the fact that distances in normed space are directly relatable to inner products, commonly called overlaps in the spin glass theory, via , and the fact that solutions themselves often have identical or close to identical norms. The OGP is of interest only for certain choices of parameters which is always problem dependent. Furthermore, all of these parameters along with the optimal value are usually dependent on the problem size, such as the number of Boolean variables in the K-SAT model or number of nodes in a graph. In particular, the property is of interest only if there are pairs of -optimal solutions satisfying both and property. The first case is trivial as we can take , but the existence of pairs with distance at least needs to be verified. Establishing the OGP rigorously can be either straightforward or technically very involved, again depending on the problem. It is should not be surprising that the presence of the OGP presents a potential difficulty in finding an optimal solution, due to the presence of multiple local minima, similarly to the lack of convexity property. An important distinction should be noted, however, between the OGP and the lack of convexity property. The function can be non-convex, but not exhibiting the OGP, as depicted on Figure 3. Thus the ”common” intractability obstruction presented by non-convexity is not identical with the OGP. Also, the solution space is often discrete (such as the binary cube) rendering the notions of convexity non-applicable.

We now extend the OGP definition to the so-called ensemble Overlap Gap Property, abbreviated as the e-OGP, and the multi-overlap gap property, abbreviated as the m-OGP. We say that a set of problem instances satisfies the e-OGP with parameters if for every pair of instances , for every -optimal solution of the instance (namely ), and every -optimal solution of the instance (namely ), it is the case that either or , and in the case when instances and are probabilistically independent, the former case (i.e. ) is not the possible. The set represents a collection of problem instances over which the optimization problem is considered. For example might represent a collection of correlated random graphs , or random matrices or random tensors. Indeed, below we will provide an example of a family of correlated random graphs as a main example of the case when the e-OGP holds. We see that the OGP is the special case of the e-OGP when consist of a single instance .
Finally, we say that a family of instances satisfies the m-OGP with parameters and , if for every -collection of instances and every collection of solutions that are -optimal with respect to , at least one pair satisfies or . Informally, the m-OGP means that one cannot find near optimal solutions for instances such that all pairs of distances lie in the interval . Clearly the case boils down to the e-OGP discussed earlier. In many applications the difference between and is often significantly smaller than the value of itself, that is . Thus, roughly speaking the m-OGP means that one cannot find near optimal solutions so that all pairwise distances are . The first usage of OGP as an obstruction to algorithms was adopted by Gamarnik and Sudan in [GS17a]. The first application of m-OGP as an obstruction to algorithms was adopted by Rahman and Virag in [RV17]. While their variant of m-OGP proved useful for some applications as in Gamarnik and Sudan [GS17b], and Coja-Oghlan, Haqshenas and Hetterich [COHH17], since then the definition of m-OGP has been extended to ”less symmetric” variants as one by Wein in [Wei20] and by Bresler and Huang in [BH21]. We will not discuss the nature of these extensions and instead refer to the aforementioned references for further details. e-OGP was introduced in Chen et al. [CGPR19].

OGP is an obstruction to stability
Next we discuss how the presence of variants of the OGP constitutes an obstruction to algorithms. The broadest class of algorithms for which such an implication can be established are algorithms that are stable with respect to a small perturbation of instances . An algorithm is viewed here simply as a mapping from instances to solutions , which we abbreviate as . Suppose, we have a parametrized collection of instances with discrete parameter taking values in some interval . We say that the algorithm is stable or specifically -stable with respect to the family if for every , . Informally, if we think of as an instance obtained from by a small perturbation, the output of the algorithm does not change much: the algorithm is not very sensitive to the input. Continuous versions of such stability have been considered as well, specifically in the context of models with Gaussian distribution. Here is a continuous parameter, and the algorithm is stable with sensitivity value if for every . Often these bounds are established only with probabilistic guarantees, both in the case of discrete and continuously valued .
Now assume that the e-OGP holds for a family of instances . Assume two additional conditions: (a) the regime for -optimal solutions of , and -optimal solutions of is non-existent (namely every -optimal solution of is ”far” from every -optimal solution of ; and (b) . The property (a) is typically verified since the end points and of the interpolated sequence are often independent, and (a) can be checked by straightforward moment arguments. The verification of condition (b) typically involves technical and problem dependent arguments. The conditions (a) and (b) above plus the OGP allow us to conclude that any -stable algorithm fails to produce a -optimal solution. This is seen by a simple contradiction argument based on continuity: consider the sequence of solutions , produced by the algorithm . We have for every and by the OGP and assumption (a) above. Suppose, for the purposes of contradiction, that every solution produced by the algorithm is -optimal for every instance . Then by the OGP it is the case that, in particular, is either at most or at least for every . Since , there exists , possibly , such that and . Then , which is a contradiction with the assumption (b).
Simply put, the crux of the argument is that the algorithm cannot ”jump” over the gap , since the incremental distances, bounded by are two small to allow for it. This is the main method by which stable algorithms are ruled out in presence of the OGP and is illustrated on Figure 4. On this figure the smaller circle represent all of the -optimal solutions which are at most distance from , across all instances . The complement to the larger circle represents all of the -optimal solutions which are at least distance from , again across all instances . All -optimal solutions across all instances should fall into one of these two regions, according to the e-OGP. As the sequence of solutions has to cross between these two regions, at some point the distance between and will have to exceed , contradicting the stability property.


Suppose the model does not exhibit the OGP, but does exhibit the m-OGP (ensemble version). We now describe how this can also be used as an obstruction to stable algorithms. As above, the argument is based on first verifying that for two independent instance and the regime is not possible with overwhelming probability. Consider independent instances and consider an interpolated sequence with the property that and for all . In other words the sequence starts with identical copies of instance and slowly interpolates towards instance . The details of such a construction are usually guided by concrete problems. Typically, such constructions are also symmetric in distribution, so that, in particular, all pairwise expected distances between the algorithmic outputs are the same, say denoted by . Furthermore, in some cases a concentration around the expectation can be also established. As an implication this set of identical pairwise distances spans values from to value larger than by the assumption (a). But the stability of the algorithm also implies that at some point it will be the case that , contradicting the m-OGP. This is illustrated on Figure 5. The high concentration property discussed above was established using standard methods in [GS17b] and [Wei20], but the approach in [GK21] was based on a different arguments employing methods from Ramsey extremal combinatorics field. Here the idea is to generate many more independent instances than the value of arising in m-OGP and showing using Ramsey theory results that there should exist a subset of -instances such that all pairwise distances fall into interval .
OGP for concrete models
We now illustrate the OGP and its variants for the Number Partitioning problem and the maximum clique problem as examples. The discussion will be informal and references containing detailed derivations will be provided. The instance of the Number Partitioning problem is a sequence of independent standard normal random variables. For every binary vector , the inner product is a mean zero normal random variable with variance . The likelihood that takes value in an interval around zero with length is roughly times the length of the interval, namely times . Thus the expected number of such vectors is of constant order since there are choices for . This gives an intuition for why there do exist vectors achieving value . Details can be found in [KK82]. Any choice of order magnitude smaller length interval leads to expectation converging to zero and thus non-achievable with overwhelming probability. Now, to discuss the OGP, fix constants and consider pairs of vectors which achieve objective value and have the scaled inner product . The expected number of such pairs is roughly times the area of the square with side length approximately , namely . This is because the likelihood that a pair of correlated gaussians falls into a very small square around zero is dominated by the area of this square up to a constant. Approximating as , where is the standard binary entropy, the expectation of the number of such pairs evaluates to roughly . As the largest value of is , we obtain an important discovery: for every there is a region of of the form for which the expectation is exponentially small in , and thus the value is not achievable by pairs of partitions and with scaled inner products in , with overwhelming probability. Specifically, for every pair of -optimal solutions with , it is the case that is either or at most . With this value of and , we conclude that the model exhibits the OGP.
Showing the ensemble version of OGP (namely e-OGP) can be done using very similar calculations, but what about values of smaller than ? After all, the state of the art algorithms achieve only order which corresponds to at scale. It turns out [GK21] that in fact the m-OGP holds for this model for all strictly positive with a judicious choice of constant value . Furthermore, the m-OGP extends all the way to by taking growing with , but not beyond that value, at least using the available proof techniques. Thus, at this stage we may conjecture that the problem is algorithmically hard for objective values smaller than order , but beyond this value we don’t have a plausible predictions either for hardness or tractability. In conclusion, at least at the exponential scale we see that the OGP gives a theory of algorithmic hardness consistent with the state of the art algorithms.
The largest clique problem is another example where the OGP based predictions are consistent with the state of the art algorithms. Recall from the earlier section, that while the largest clique in is roughly , the largest size clique achievable by known algorithm is roughly half-optimal with size approximately . Fixing consider pairs of cliques with sizes roughly . This range of corresponds to clique sizes known to be present in the graph existentially with overwhelming probability, but not achievable algorithmically. As it turns out, see [GS17a],[GJW20a], the model exhibits the OGP for and overlap parameters , both of which are at the scale . Specifically, every two cliques of size have intersection size either at least or at most , for some values , both at scale . This easily implies OGP with . The calculations in [GS17a] and [GJW20a] were carried out for a similar problem of finding a largest independent set (a set with no internal edges) in sparse random graphs with of the order , but the calculation details for the dense graph are almost identical. The end result is that , where and are the two roots of the quadratic equation , namely , and roots exist if and only if . For recent algorithmic results for the related problem on random regular graphs with small degree see [MK20].
To illustrate the ensemble version of the OGP, consider an ensemble of random graphs, constructed as follows. Generate according to the probability law of . Introduce a random uniform order of pairs of nodes and generate graph from by resampling the pair – the -th pair in the order , and leaving other edges of intact. This way each graph individually has the law of , but neighboring graphs and differ by at most one edge. The beginning and the end graphs and are clearly independent. Now fix and A simple calculation shows that the expected number of size cliques in and same size cliques in , such that the size of the intersection of and is is approximately given by , where is the (rescaled) number of edges of which were resampled from . Easy calculation shows that the function has two roots in the interval given by , when the larger root is smaller than , namely when . On the other hand, when , including the extreme case corresponding to , there is only one root in . The model thus not only does exhibit the e-OGP for the ensemble . Additionally the value represents a new type of phase transition, not known earlier to the best of the author’s knowledge. When every two cliques with size have intersection size either at least or at most . On the other hand, when , the second regime disappears, and any two such cliques have intersection size only at most . The situation is illustrated on the Figure 6 for the special case and . This phase transition is related to the so-called chaos property of spin glasses which we discuss below, but has qualitatively different behavior. In particular, the analogous parameter in the context of spin glass models has value . More on this below.
The value is not tight with respect to the apparent algorithmic hardness which occurs at as discussed earlier. This is where the multi-OGP comes to rescue. A variant of an (assymetric) m-OGP has been established recently in [Wei20], building on an earlier symmetric version of m-OGP, discovered in [RV17], ruling out the class of stable algorithms as potential contenders for solving the Independent Set problem above . More specifically, in both works (for the case of local algorithms in [RV17] and for the case of low-degree polynomials based algorithms in [Wei20]) it is shown that for every fixed there exists a constant such that the model exhibits m-OGP with this value of for independent sets corresponding to . While, it has not be formally verified, it appears based on the first moment argument that value growing with is needed, in the sense that no fixed value of achieves the OGP all the way down to , but constant values of which are -dependent do. It is interesting to contrast this with the Number Partitioning problem where it was crucial to take growing with in order the bridge the gap between the algorithmic and existential thresholds.

Stability of low-degree polynomials
How does one establish the link of the form OGP implies Class of algorithms fails, and what classes of algorithms can be proven to fail in presence of the OGP? As discussed earlier, the failure is established by showing stability (insensitivity) of the algorithms in class C to the changes of the input. This stability forces the algorithm to produce pairs of outputs with overlap falling into a region ”forbidden” by the OGP. The largest class of algorithms to the day which is shown to be stable is the class of algorithms informally dubbed as ”low-degree polynomials”. Roughly speaking this is a class of algorithms where the solution is obtained by constructing an -sequence of multi-variate polynomials with variables evaluated at entries of the instance . The largest degree of the polynomial is supposed to be low, though depending on the problem it can take even significantly high value. Algorithms based on low-degree polynomials gained a lot of prominence recently due to connection with the so-called Sum-of-Squares method and represent arguably the strongest known class of polynomial time algorithms [HS17],[HKP+17],[Hop18]. What can be said about this method in the context of the problems exhibiting the OGP? It was shown in [GJW20a],[Wei20] and [BH21] that degree- polynomial based algorithms are stable for the problems of finding a ground state of a p-spin model, finding a large independent set of a sparse Erdös-Rényi graph , and for the problem of finding a satisfying assignment of a random K-SAT problem. This is true even when is as large as . Thus algorithms based on polynomials even with degree fail to find near optimum solutions for these problems due to the presence of the OGP. Many algorithms can be modeled as special cases of low degree polynomials, and therefore ruled out by OGP, including the so-called Approximate Message Passing algorithms [GJ19],[GJW20a], local algorithms considered in [GS17a],[RV17] and even quantum versions of local algorithms known as Quantum Approximate Optimization Algorithm (QAOA) [FGG20a].
OGP and the problem of finding ground states of p-spin models
In addition to the maximum clique problem, there is another large class of optimization problem for which the OGP approach provides a tight classification of solvable vs not yet solvable in polynomial time problems. It is the problem of finding ground states of p-spin models – the very class of optimization problems which led to studying the overlap distribution and overlap gap type properties to begin with. The problem is described as follows: suppose one is given a -order tensor of side length . Namely, is described as a collection of real values where range between and . Given the solution space , the goal is finding a solution (called ground state) which minimizes the inner product . The randomness in the model is derived from the randomness of the entries of . A common assumption, capturing most of the structural and algorithmic complexity of the model, is that the entries are independent standard normal entries. Two important special cases of the solution space include the case when is a binary cube , and when it is a sphere of a fixed radius (say ) in the -dimensional real space, the latter case being referred to as spherical spin glass model. The special case and is the celebrated Sherrington-Kirkpatrick model [SK75] – the centerpiece of the spin glass theory. The problem of computing the value of this optimization problem above was at the core of the spin glass theory in the past four decades, which led to the replica symmetry breaking technique first introduced in the physics literature by Parisi [Par80], and then followed by a series of mathematically rigorous developments, including those by Talagrad [Tal10] and Panchenko [Pan13].
The algorithmic progress on this problem, however, is quite recent. While the power of the Monte Carlo based simulation results have been tested numerous times, the first rigorous progress has appeared only in the past few years. In the important development by Subag [Sub18] and Montanari [Mon19] a polynomial time algorithms were constructed for finding near ground states in these models. Remarkably, this was done precisely for regimes where the model does not exhibit the OGP as per a detailed analysis of the so-called Parisi measure of the associated Gibbs distribution. A follow-up development in [AMS20] extended this to models which do exhibit OGP, but in this case near ground states are not reached. Instead, one constructs the best solution within the part of the solution space not exhibiting the OGP. To put it differently, the algorithms produce a -optimal solution for the smallest value of for which the OGP does not hold. Conversely, as shown in a series of recent developments [GJ19],[GJW20b],[Sel20], the optimization problem problem associated with finding near ground states cannot be solved within some classes of algorithms, the largest of which is the class of algorithms based on low-degree polynomials. The failure of this class of algorithms was established exactly along the lines described above: verifying stability of the algorithms of interest, and verifying the presence of OGP which presents an obstruction to stability. Interestingly, a class of algorithms, which is not described by low-degree polynomials but which is still ruled out by the OGP is the Langevin dynamics at a linear in scale, as shown in [GJW20b]. The Langevin dynamics is continuous version of the Markov Chain Monte Carlo type algorithm. Its stability stems from the Gronwald’s type bound stating that two time dependent Langevin trajectories associated with the Langevin dynamics run on two instances and , diverge at the rate order for some constant . Thus when is of order and and are at distance which is exponentially small in , one can control this divergence. One then uses e-OGP for an interpolated sequence with discrete values of with increments to argue stability. The approach fails at time scales larger than , since the required concentration bounds underlying OGP hold only modulo exponentially in small probability, and as a result the union bound over more than terms is no longer effective. It is a very plausible conjecture, though, that the Langevin dynamics indeed still fails unless it is ran for exponentially long time. We leave this conjecture as an interesting open problem.
The analogue of the phase transition discussed in the context of the largest clique problem takes place in the p-spin model as well in the more extreme form called the chaos property: any non-trivial perturbation of the instance whereby any fixed positive fraction of entries of are flipped, results in the instance for which every near ground state is nearly orthogonal to every near ground state of . To put it differently is effectively zero for this model. This has been established in a series of works [Cha09],[CHL18],[Eld20]. Notably, the chaos property itself is not a barrier to polynomial time algorithms since the Sherrington-Kirkpatrick model is known to exhibit the chaos property, yet, it is amenable to poly-time algorithms as in [Sub18] and [Mon19]. The chaos property however is used as a tool to establish the ensemble version of the OGP (e-OGP) as was done in [CGPR19] and [GJ19].
OGP, the clustering property, and the curious case of the perceptron model
We now return to the subject of weak and strong clustering property, and discuss it now from the perspective of the OGP and the implied algorithmic hardness. The relationship is interesting, non-trivial and perhaps best exemplified by yet another model which exhibits statistical to computation gap: the binary perceptron model. The input to the model is matrix of i.i.d. standard normal entries . A fixed parameter is fixed. The goal is to find a binary vector such that for each . In vector notation we need to find such that , where for any vector . This is also known as binary symmetric perceptron model, to contrast it with assymetric model, where the requirement is that , for some fixed parameter (positive or negative), with inequalities interpreted coordinate-wise. In the assymetric case the a typical choice is . Replica symmetry breaking based heurstic methods developed in this context by Krauth and Mezard [KM89] predict a sharp threshold at for the case , so that when and such a vector exists, and when such a vector does not exist, both with high probability as . This was confirmed rigorously as an upper bound in [DS19]. For the symmetric case a similar sharp threshold is known rigorously as a dependent constant , as established in [PX21] and [ALS21].
The known algorithmic results however are significantly weaker and scarce. The algorithm by Kim and Rouche [KR98] finds for the assymetric case when . While the algorithm has not been adopted to the symmetric case, it is quite likely that a version of it should work here as well for some positive sufficiently small -dependent constant . Heuristically, the message passing algorithm was found to be effective at small positive densities, as reported in [BZ06]. Curiously, though, it is known that the symmetric model exhibits the weak clustering property at all positive densities , as was rigorously verified recently in [PX21] and [ALS21]. Furthermore, quite remarkably, each cluster consist of singletons! Namely the cardinality of each cluster is one, akin to ”needles in the haystack” metaphor. A similar picture was established in the context of the Number Partitioning problem [GK21]. This interesting entropic (due to the subextensive cardinality of clusters) phenomena is fairly novel and its algorithmic implications have been also discussed in [BRTS21] in the context of another constraint satisfaction problem – the random K-XOR model. Thus at this stage, assuming the extendability of the Kim-Roche algorithm and/or validity of the message passing algorithm, we have an example of a model exhibiting weak clustering property, but amenable to polynomial time algorithms. This stands in in contrast to the random K-SAT model and in fact all other models known to the author. As an explanation of this phenomena, the aforementioned references point out that to the ”non-uniformity” in algorithmic choices of the solutions allowing it somehow to bypass the overwhelming clustering picture exhibited by the weak clustering property.
What about the strong clustering property and the OGP? First let us elucidate the relationship between the two properties. The pair-wise () OGP which holds for a single instance clearly implies the strong clustering property: if every pair of -optimal solutions is at distance at most or at least , and the second case is non-vacuous, clearly the set of solutions is strongly clustered. It furthermore, indicates that the diameter of each cluster is strictly smaller (at scale) than the distances between the clusters, see Figures 2,3. In fact this is precisely how the strong clustering property was discovered to begin with in [ART06] and [MMZ05]. However, the converse does not need to be the case, as one could not rule out an example of a strong clustering property where the cluster diameters are larger than the distances between them, and, as a result, the overlaps of pairs of solutions span a continuous intervals. At this stage we are not aware of any such examples.
Back to the symmetric perceptron model, it is known (rigorously, based on the moment computation), that it does exhibit the OGP, at a value strictly smaller than the critical threshold [BDVLZ20]. As a result the strong clustering property holds as well above this . Naturally, we conjecture that the problem of finding a solution is hard in this regime, and it is very likely that classes of algorithms, such as low-degree polynomial based algorithm and their implications can be ruled out by the OGP method along the lines discussed above.
Finally, as the strong clustering property appears to be the most closely related to the OGP, it raises a question as to whether it can be used as a ”signature” of hardness in lieu of OGP and/or whether it can be used as a method to rule out classes of algorithm, similarly to the OGP based method. There are two challenges associated with this proposal. First we are not aware of any effective method of establishing the strong clustering property other than the one based on the OGP. Second, and more importantly, it is not entirely clear how to link meaningfully the strong clustering property with m-OGP, which appears necessary for many problems in order to bridge the computational gaps to the known algorithmically achievable values. Likewise, it is not entirely clear what is the appropriate definition of either weak or strong clustering property in the ensemble version, when one considers a sequence of correlated instances, which is again another important ingredient in the implementation of the refutation type arguments. Perhaps some form of dynamically evolving clustering picture is of relevance here. Some recent progress on the former question regarding the geometry of the m-OGP was obtained recently in [BAJ21] in the context of the spherical spin glass model. We leave both questions as interesting open venues for future investigation.
Discussion
In this introductory article we have described a new approach to computational complexity arising in optimality studies of random structures. The approach, which is based on topological disconnectivity of the overlaps of near optimal solutions, called the Overlap Gap Property, is both a theory and a method. As a theory it predicts the onset of algorithmic hardness in random structures at the onset of the OGP. The approach has been verified at various levels of precision in many classes of problems and the summary of the state of the art is presented in Table 1. In this table the current list of models known to exhibit an apparent algorithmic hardness is provided, along with references and notes indicating whether the OGP based method matches the state of the art algorithmic knowledge. The ”Yes” indicates this to be the case, and ”Not known” indicates that the formal analysis has not been completed yet. Remarkably, to the day we are not aware of a model which does not exhibit the OGP, but which is known to exhibit some form of an apparent algorithmic hardness.
| Problem description | OGP matches known algorithms | References |
| Cliques in Erdös-Rényi graphs | Yes | Based on references below |
| Independent Sets in sparse Erdös-Rényi graphs | Yes | [GS17a],[RV17], [GJW20a],[Wei20],[FGG20a] |
| Random K-SAT | Yes | [GS17b],[COHH17],[BH21] |
| Largest submatrix problem | Not known | [GL18] |
| Matching in random hypergraphs | Not known | [CGPR19] |
| Ground states of spin glasses | Yes | [GJ19],[GJW20b][Sub18],[Mon19], [AMS20], |
| Number partitioning | Yes (up to sub-exponential factors) | [GK21] |
| Hidden Clique problem | Yes | [GZ19] |
| Sparse Linear Regression | Yes (up to a constant factor) | [GI17] |
| Principal submatrix recovery | Not known | [GJS19],[AWZ20] |
The OGP based approach also provides a concrete method for rigorously establishing barriers for classes of algorithms. Typically such barriers are established by verifying certain stability (input insensitivity) of algorithms making them inherently incapable of overcoming the gaps appearing in the overlap structures. While the general approach for ruling out such classes of algorithm is more or less problem independent, the exact nature of such stability as well as the OGP itself is very much problem dependent, and the required mathematical analysis varies from borderline trivial to extremely technical, often relying on the state of the art development in the field of mathematical theory of spin glasses.
Acknowledgements
The support from the NSF grant DMS-2015517 is gratefully acknowledged.
References
- [Ajt96] Miklós Ajtai, Generating hard instances of lattice problems, Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, ACM, 1996, pp. 99–108.
- [ALS21] Emmanuel Abbe, Shuangping Li, and Allan Sly, Proof of the contiguity conjecture and lognormal limit for the symmetric perceptron, arXiv preprint arXiv:2102.13069 (2021).
- [AMS20] Ahmed El Alaoui, Andrea Montanari, and Mark Sellke, Optimization of mean-field spin glasses, arXiv preprint arXiv:2001.00904 (2020).
- [ART06] Dimitris Achlioptas and Federico Ricci-Tersenghi, On the solution-space geometry of random constraint satisfaction problems, Proceedings of the thirty-eighth annual ACM symposium on Theory of computing, 2006, pp. 130–139.
- [AS04] Noga Alon and Joel H Spencer, The probabilistic method, John Wiley & Sons, 2004.
- [AWZ20] Gérard Ben Arous, Alexander S Wein, and Ilias Zadik, Free energy wells and overlap gap property in sparse pca, Conference on Learning Theory, PMLR, 2020, pp. 479–482.
- [BAJ21] Gérard Ben Arous and Aukosh Jagannath, Shattering versus metastability in spin glasses, arXiv e-prints (2021), arXiv–2104.
- [BDVLZ20] Carlo Baldassi, Riccardo Della Vecchia, Carlo Lucibello, and Riccardo Zecchina, Clustering of solutions in the symmetric binary perceptron, Journal of Statistical Mechanics: Theory and Experiment 2020 (2020), no. 7, 073303.
- [BH21] Guy Bresler and Brice Huang, The algorithmic phase transition of random -sat for low degree polynomials, arXiv preprint arXiv:2106.02129 (2021).
- [BM08] Stefan Boettcher and Stephan Mertens, Analysis of the karmarkar-karp differencing algorithm, The European Physical Journal B 65 (2008), no. 1, 131–140.
- [BRTS19] Louise Budzynski, Federico Ricci-Tersenghi, and Guilhem Semerjian, Biased landscapes for random constraint satisfaction problems, Journal of Statistical Mechanics: Theory and Experiment 2019 (2019), no. 2, 023302.
- [BRTS21] Matteo Bellitti, Federico Ricci-Tersenghi, and Antonello Scardicchio, Entropic barriers as a reason for hardness in both classical and quantum algorithms, arXiv preprint arXiv:2102.00182 (2021).
- [BS20] Louise Budzynski and Guilhem Semerjian, Biased measures for random constraint satisfaction problems: larger interaction range and asymptotic expansion, Journal of Statistical Mechanics: Theory and Experiment 2020 (2020), no. 10, 103406.
- [BVDG11] Peter Bühlmann and Sara Van De Geer, Statistics for high-dimensional data: methods, theory and applications, Springer Science & Business Media, 2011.
- [BZ06] Alfredo Braunstein and Riccardo Zecchina, Learning by message passing in networks of discrete synapses, Physical review letters 96 (2006), no. 3, 030201.
- [CGPR19] Wei-Kuo Chen, David Gamarnik, Dmitry Panchenko, and Mustazee Rahman, Suboptimality of local algorithms for a class of max-cut problems, The Annals of Probability 47 (2019), no. 3, 1587–1618.
- [Cha09] Sourav Chatterjee, Disorder chaos and multiple valleys in spin glasses, arXiv preprint arXiv:0907.3381 (2009).
- [CHL18] Wei-Kuo Chen, Madeline Handschy, and Gilad Lerman, On the energy landscape of the mixed even p-spin model, Probability Theory and Related Fields 171 (2018), no. 1-2, 53–95.
- [CHM+15] Anna Choromanska, Mikael Henaff, Michael Mathieu, Gérard Ben Arous, and Yann LeCun, The loss surfaces of multilayer networks, Artificial intelligence and statistics, 2015, pp. 192–204.
- [CO10] Amin Coja-Oghlan, A better algorithm for random k-sat, SIAM Journal on Computing 39 (2010), no. 7, 2823–2864.
- [CO11] A. Coja-Oghlan, On belief propagation guided decimation for random k-SAT, Proceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, 2011, pp. 957–966.
- [COHH17] Amin Coja-Oghlan, Amir Haqshenas, and Samuel Hetterich, Walksat stalls well below satisfiability, SIAM Journal on Discrete Mathematics 31 (2017), no. 2, 1160–1173.
- [DS19] Jian Ding and Nike Sun, Capacity lower bound for the ising perceptron, Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, 2019, pp. 816–827.
- [DSS15] Jian Ding, Allan Sly, and Nike Sun, Proof of the satisfiability conjecture for large k, Proceedings of the forty-seventh annual ACM symposium on Theory of computing, 2015, pp. 59–68.
- [Eld20] Ronen Eldan, A simple approach to chaos for p-spin models, Journal of Statistical Physics 181 (2020), no. 4, 1266–1276.
- [FA86] Yaotian Fu and Philip W Anderson, Application of statistical mechanics to np-complete problems in combinatorial optimisation, Journal of Physics A: Mathematical and General 19 (1986), no. 9, 1605.
- [FGG14] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann, A quantum approximate optimization algorithm, arXiv preprint arXiv:1411.4028 (2014).
- [FGG20a] Edward Farhi, David Gamarnik, and Sam Gutmann, The quantum approximate optimization algorithm needs to see the whole graph: A typical case, arXiv preprint arXiv:2004.09002 (2020).
- [FGG20b] , The quantum approximate optimization algorithm needs to see the whole graph: Worst case examples, arXiv preprint arXiv:2005.08747 (2020).
- [FR13] Simon Foucart and Holger Rauhut, A mathematical introduction to compressive sensing, Springer, 2013.
- [Fri99] E. Friedgut, Sharp thresholds of graph proprties, and the -SAT problem, J. Amer. Math. Soc. 4 (1999), 1017–1054.
- [GI17] David Gamarnik and Zadik Ilias, High dimensional regression with binary coefficients. estimating squared error and a phase transtition, Conference on Learning Theory, 2017, pp. 948–953.
- [GJ79] Michael R Garey and David S Johnson, Computers and intractability, vol. 174, freeman San Francisco, 1979.
- [GJ19] David Gamarnik and Aukosh Jagannath, The overlap gap property and approximate message passing algorithms for -spin models, Ann. Appl. Probab. To appear (2019).
- [GJS19] David Gamarnik, Aukosh Jagannath, and Subhabrata Sen, The overlap gap property in principal submatrix recovery, arXiv preprint arXiv:1908.09959 (2019).
- [GJW20a] David Gamarnik, Aukosh Jagannath, and Alexander S Wein, Low-degree hardness of random optimization problems, 61st Annual Symposium on Foundations of Computer Science, 2020.
- [GJW20b] , Low-degree hardness of random optimization problems, arXiv preprint arXiv:2004.12063 (2020).
- [GK18] David Gamarnik and Eren Kizildag, Computing the partition function of the sherrington-kirkpatrick model is hard on average, arXiv preprint arXiv:1810.05907 (2018).
- [GK21] , The landscape of the number partitioning problem and the overlap gap property, In preparation (2021).
- [GL18] David Gamarnik and Quan Li, Finding a large submatrix of a gaussian random matrix, The Annals of Statistics 46 (2018), no. 6A, 2511–2561.
- [GS02] Carla P Gomes and Bart Selman, Satisfied with physics, Science 297 (2002), no. 5582, 784–785.
- [GS17a] David Gamarnik and Madhu Sudan, Limits of local algorithms over sparse random graphs, Annals of Probability 45 (2017), 2353–2376.
- [GS17b] , Performance of sequential local algorithms for the random nae-k-sat problem, SIAM Journal on Computing 46 (2017), no. 2, 590–619.
- [GZ19] David Gamarnik and Ilias Zadik, The landscape of the planted clique problem: Dense subgraphs and the overlap gap property, arXiv preprint arXiv:1904.07174 (2019).
- [Has99] J. Hastad, Clique is hard to approximate within , Acta Math. 182 (1999), 105–142.
- [Het16] Samuel Hetterich, Analysing survey propagation guided decimationon random formulas, 43rd International Colloquium on Automata, Languages, and Programming (ICALP 2016), Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2016.
- [HKP+17] Samuel B Hopkins, Pravesh K Kothari, Aaron Potechin, Prasad Raghavendra, Tselil Schramm, and David Steurer, The power of sum-of-squares for detecting hidden structures, 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS), IEEE, 2017, pp. 720–731.
- [Hop18] Samuel Hopkins, Statistical inference and the sum of squares method, Ph.D. thesis, Cornell University, 2018.
- [HS17] Samuel B Hopkins and David Steurer, Efficient bayesian estimation from few samples: community detection and related problems, 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS), IEEE, 2017, pp. 379–390.
- [HSSZ19] Christopher Harshaw, Fredrik Sävje, Daniel Spielman, and Peng Zhang, Balancing covariates in randomized experiments using the gram-schmidt walk, arXiv preprint arXiv:1911.03071 (2019).
- [Jer92] Mark Jerrum, Large cliques elude the metropolis process, Random Structures & Algorithms 3 (1992), no. 4, 347–359.
- [Kar76] Richard M Karp, The probabilistic analysis of some combinatorial search algorithms, Algorithms and complexity: New directions and recent results 1 (1976), 1–19.
- [KK82] Narendra Karmarkar and Richard M Karp, The differencing method of set partitioning, Computer Science Division (EECS), University of California Berkeley, 1982.
- [KM89] Werner Krauth and Marc Mézard, Storage capacity of memory networks with binary couplings, Journal de Physique 50 (1989), no. 20, 3057–3066.
- [KMRT+07] F. Krzakała, A. Montanari, F. Ricci-Tersenghi, G. Semerjian, and L. Zdeborová, Gibbs states and the set of solutions of random constraint satisfaction problems, Proceedings of the National Academy of Sciences 104 (2007), no. 25, 10318–10323.
- [KR98] Jeong Han Kim and James R Roche, Covering cubes by random half cubes, with applications to binary neural networks, Journal of Computer and System Sciences 56 (1998), no. 2, 223–252.
- [KS94] Scott Kirkpatrick and Bart Selman, Critical behavior in the satisfiability of random boolean expressions, Science 264 (1994), no. 5163, 1297–1301.
- [Lip91] Richard Lipton, New directions in testing, Distributed Computing and Cryptography 2 (1991), 191–202.
- [MK20] Raffaele Marino and Scott Kirkpatrick, Large independent sets on random -regular graphs with small, arXiv preprint arXiv:2003.12293 (2020).
- [MM09] M. Mezard and A. Montanari, Information, physics and computation, Oxford graduate texts, 2009.
- [MMZ05] M. Mézard, T. Mora, and R. Zecchina, Clustering of solutions in the random satisfiability problem, Physical Review Letters 94 (2005), no. 19, 197205.
- [Mon19] Andrea Montanari, Optimization of the sherrington-kirkpatrick hamiltonian, 2019 IEEE 60th Annual Symposium on Foundations of Computer Science (FOCS), IEEE, 2019, pp. 1417–1433.
- [MPRT16] Raffaele Marino, Giorgio Parisi, and Federico Ricci-Tersenghi, The backtracking survey propagation algorithm for solving random k-sat problems, Nature communications 7 (2016), no. 1, 1–8.
- [MPV87] M. Mezard, G. Parisi, and M. A. Virasoro, Spin-glass theory and beyond, vol 9 of Lecture Notes in Physics, World Scientific, Singapore, 1987.
- [MPZ02] Marc Mézard, Giorgio Parisi, and Riccardo Zecchina, Analytic and algorithmic solution of random satisfiability problems, Science 297 (2002), no. 5582, 812–815.
- [MZK+99] Rémi Monasson, Riccardo Zecchina, Scott Kirkpatrick, Bart Selman, and Lidror Troyansky, Determining computational complexity from characteristic ?phase transitions?, Nature 400 (1999), no. 6740, 133–137.
- [Pan13] Dmitry Panchenko, The sherrington-kirkpatrick model, Springer Science & Business Media, 2013.
- [Par80] Giorgio Parisi, A sequence of approximated solutions to the sk model for spin glasses, Journal of Physics A: Mathematical and General 13 (1980), no. 4, L115.
- [PX21] Will Perkins and Changji Xu, Frozen 1-rsb structure of the symmetric ising perceptron, Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing, 2021, pp. 1579–1588.
- [RT10] Federico Ricci-Tersenghi, Being glassy without being hard to solve, Science 330 (2010), no. 6011, 1639–1640.
- [RTS09] Federico Ricci-Tersenghi and Guilhem Semerjian, On the cavity method for decimated random constraint satisfaction problems and the analysis of belief propagation guided decimation algorithms, Journal of Statistical Mechanics: Theory and Experiment 2009 (2009), no. 09, P09001.
- [RV17] Mustazee Rahman and Balint Virag, Local algorithms for independent sets are half-optimal, The Annals of Probability 45 (2017), no. 3, 1543–1577.
- [Sel20] Mark Sellke, Approximate ground states of hypercube spin glasses are near corners, arXiv preprint arXiv:2009.09316 (2020).
- [SK75] David Sherrington and Scott Kirkpatrick, Solvable model of a spin-glass, Physical review letters 35 (1975), no. 26, 1792.
- [Sub18] Eliran Subag, Following the ground-states of full-rsb spherical spin glasses, arXiv preprint arXiv:1812.04588 (2018).
- [Tal10] M. Talagrand, Mean field models for spin glasses: Volume I: Basic examples, Springer, 2010.
- [TMR20] Paxton Turner, Raghu Meka, and Philippe Rigollet, Balancing gaussian vectors in high dimension, Conference on Learning Theory, PMLR, 2020, pp. 3455–3486.
- [Ver18] Roman Vershynin, High-dimensional probability: An introduction with applications in data science, vol. 47, Cambridge University Press, 2018.
- [Wei20] Alexander S Wein, Optimal low-degree hardness of maximum independent set, arXiv preprint arXiv:2010.06563 (2020).