The Origin of Weakened Magnetic Braking in Old Solar Analogs
Abstract
The rotation rates of main-sequence stars slow over time as they gradually lose angular momentum to their magnetized stellar winds. The rate of angular momentum loss depends on the strength and morphology of the magnetic field, the mass-loss rate, and the stellar rotation period, mass, and radius. Previous observations suggested a shift in magnetic morphology between two F-type stars with similar rotation rates but very different ages (88 Leo and CrB). In this Letter, we identify a comparable transition in an evolutionary sequence of solar analogs with ages between 2–7 Gyr. We present new spectropolarimetry of 18 Sco and 16 Cyg A & B from the Large Binocular Telescope, and we reanalyze previously published Zeeman Doppler images of HD 76151 and 18 Sco, providing additional constraints on the nature and timing of this transition. We combine archival X-ray observations with updated distances from Gaia to estimate mass-loss rates, and we adopt precise stellar properties from asteroseismology and other sources. We then calculate the wind braking torque for each star in the evolutionary sequence, demonstrating that the rate of angular momentum loss drops by more than an order of magnitude between the ages of HD 76151 and 18 Sco (2.6–3.7 Gyr) and continues to decrease modestly to the age of 16 Cyg A & B (7 Gyr). We suggest that this magnetic transition may represent a disruption of the global dynamo arising from weaker differential rotation, and we outline plans to probe this phenomenon in additional stars spanning a wide range of spectral types.
The Astrophysical Journal Letters
1 Introduction
Fifty years after Skumanich (1972) used the Sun and a few young star clusters to infer that rotation slows with the square-root of age, it is clear that rotational evolution is anything but smooth in solar-type stars. Detailed characterization of some of the same clusters considered by Skumanich recently identified a mass-dependent pause in the spin-down of stars that can last from 100 Myr to a few Gyr (Curtis et al., 2019, 2020). This pause may signal a redistribution of angular momentum from the radiative interior to the convective envelope (Spada & Lanzafame, 2020), temporarily compensating for the gradual loss of angular momentum to magnetized stellar winds. The extrapolation of the Skumanich spin-down relation beyond the solar age also appears to be unreliable, with old field stars observed by the Kepler space telescope rotating substantially faster than expected (Angus et al., 2015). This behavior may reflect a weakening of magnetic braking beyond a critical Rossby number (), when the ratio of the rotation period to the convective overturn timescale becomes comparable to the solar value (van Saders et al., 2016, 2019). This conclusion was reinforced by stars with ages and rotation rates both determined from asteroseismology (Hall et al., 2021), and the resulting accumulation of stars with a broad range of ages at similar rotation periods was identified in stellar samples with precise effective temperatures (David et al., 2022).
The evidence for a reduced torque is powerful, but to understand the cause we need to tie it to a physical mechanism. Weakened magnetic braking in middle-aged stars may result from either a shift in magnetic morphology from larger to smaller spatial scales (Réville et al., 2015; Garraffo et al., 2016), an abrupt change in the mass-loss rate (Ó Fionnagáin & Vidotto, 2018), or both. The global dipole can sustain more open magnetic flux where stellar wind can escape—giving it the longest effective lever arm—so a disruption of the largest-scale organization of the magnetic field can dramatically reduce the efficiency of angular momentum loss. However, very few constraints are available for old inactive stars from existing spectropolarimetric data sets (e.g., See et al., 2019). Additional observations of specific evolutionary sequences of stars can help elucidate the origin of weakened magnetic braking. Finley & Matt (2018) used a set of magnetohydrodynamic wind simulations to develop a parametrization of the wind braking torque based on the strength and morphology of the magnetic field, the mass-loss rate, and the stellar rotation period, mass, and radius. By comparing stars along an evolutionary sequence, this parametrization allows us to evaluate the relative importance of various contributions to the total change in angular momentum loss. Metcalfe et al. (2019, 2021) used this approach to identify a shift in magnetic morphology between two F-type stars with similar rotation rates but very different ages (88 Leo and CrB).
In this Letter, we identify a comparable transition in an evolutionary sequence of solar analogs with ages between 2–7 Gyr. In Section 2, we describe the new and archival observations that allow us to constrain the input parameters of the wind braking prescription. In Section 3, we calculate the rate of angular momentum loss for each of the stars in the evolutionary sequence, and we determine the most important changes that influence the wind braking torque at different ages. Finally, in Section 4 we speculate on the physical mechanisms that might be responsible for the inferred magnetic transition, and we outline future tests that can further characterize the nature and timing of this phenomenon.


2 Observations
2.1 Spectropolarimetry
We observed 18 Sco and 16 Cyg A & B in 2021 May at = 130,000 with the Potsdam Echelle Polarimetric and Spectroscopic Instrument (PEPSI; Strassmeier et al., 2015) on the 28.4 m Large Binocular Telescope (LBT), using the same instrumental setup and data reduction methods described in Metcalfe et al. (2019). We applied the least-squares deconvolution technique (LSD; Kochukhov et al., 2010) to these observations in order to derive precise mean intensity and polarization profiles. The line data required for the LSD analysis were obtained from the VALD database (Ryabchikova et al., 2015), adopting stellar atmospheric parameters from Brewer et al. (2016). By combining information from between 1150–1300 metal lines deeper than 10% of the continuum, we obtained mean Stokes profiles with an uncertainty of 10-5 (see Figure 1). The data yielded a definite detection of the polarization signature for 18 Sco on both observing nights, with a mean longitudinal magnetic field = G and G on 2021 May 24 and 25, respectively. These Stokes profiles are similar to those obtained by Petit et al. (2008), but with a much higher signal-to-noise ratio. No significant polarization signatures were detected in the LSD profiles for 16 Cyg A & B, which yielded = G and G, respectively. Following the line profile modeling methodology described in Metcalfe et al. (2019), we estimated upper limits on the strengths of axisymmetric dipole, quadrupole, and octupole magnetic fields that are compatible with the observed polarization profiles for 16 Cyg A & B (see Table 2.1).
To complement these new observations, we reanalyzed the Zeeman Doppler imaging (ZDI) maps for HD 76151 and 18 Sco published in Petit et al. (2008), which were obtained near the mean activity level and near cycle maximum, respectively. These ZDI maps were obtained with an = 65,000 spectropolarimeter attached to a 2 m telescope. The wind braking prescription of Finley & Matt (2018) was constructed using simulations that only contained axisymmetric magnetic fields. However, the observed ZDI maps contain both axisymmetric and non-axisymmetric components. We therefore need a method of calculating the equivalent axisymmetric dipole, quadrupole, and octupole fields to use in the wind braking prescription for these stars. This can be done by considering the magnetic flux of each component of the ZDI map, since it is the radial dependence of the magnetic flux that is important for determining angular momentum loss. Specifically, we calculated the magnetic flux associated with just the dipole field in each ZDI map, accounting for both axisymmetric and non-axisymmetric components. We then determined the polar field strength () required for an axisymmetric dipole field to match the total magnetic flux associated with all dipole components in the ZDI map. We repeated this procedure for the analysis of the quadrupole () and octupole () components of the ZDI maps, and the resulting polar field strengths were all used for the wind braking torque calculations. The results are shown in Table 2.1.
| HD 76151 | 18 Sco | 16 Cyg A | 16 Cyg B | |
|---|---|---|---|---|
| (K) | ||||
| M/H (dex) | ||||
| (dex) | ||||
| (mag) | ||||
| (dex) | ||||
| (days) | ||||
| Inclination (∘) | ||||
| (G) | ||||
| (G) | ||||
| (G) | ||||
| ( erg s-1) | ||||
| Mass-loss rate () | ||||
| Mass () | ||||
| Radius () | ||||
| Luminosity () | ||||
| Age (Gyr) | ||||
| Sources | 1, 3, 4, 7, 8, 9 | 2, 3, 4, 7, 10, 11 | 2, 3, 5, 6, 7, 12 | 2, 3, 5, 6, 7, 12 |
| Torque ( erg) | –0.494 | –0.375 |
2.2 X-ray Data
We determined the X-ray luminosity () for each of our targets following the procedures described in Ayres & Buzasi (2022), using archival observations from several missions. The ROSAT All-Sky Bright Source Catalog (Boller et al., 2016) included observations of HD 76151 from 1990–1991 (slightly below the mean activity level), while Chandra observed 18 Sco with the ACIS-S instrument in 2011 (ObsID 12393, near magnetic minimum) and 16 Cyg A & B using the HRC-I instrument in 2020 (ObsID 21167 & 23188, constant activity). All four targets were identified in a catalog of serendipitous point sources observed by XMM-Newton (Traulsen et al., 2020), providing an independent estimate of the X-ray luminosity when converted to the standard 0.1–2.4 keV energy band. The modeling approach entails convolving the empirical emission measure distributions (EMD) from Wood et al. (2018) with temperature-dependent energy conversion factors (ECF) for each particular instrument. The EMD models correspond to a range of X-ray surface fluxes, while each model-derived ECF implies an empirical surface flux, given the net count rate of the observation and the stellar parameters based on Gaia EDR3 (Gaia Collaboration et al., 2021). When the predicted surface flux agrees with the input model value, this indicates the self-consistent choice for the ECF. After modeling each individual observation, we adopted the consensus estimates shown in Table 2.1. The conservative errors are intended to reflect possible temporal variations due to activity cycles as well as inter-instrumental calibration inconsistencies, including uncertainties in energy band conversion factors. We estimated mass-loss rates using the scaling relation (Wood et al., 2021), calculating surface fluxes from the X-ray luminosities and stellar radii shown in Table 2.1.
2.3 Stellar Properties
In addition to the magnetic field strength and morphology from spectropolarimetry and the mass-loss rate from X-ray fluxes, the other parameters that are required to calculate the wind braking torque are the stellar rotation period, mass, and radius. For HD 76151 and 18 Sco we adopted the rotation periods and inclinations from Petit et al. (2008), while for 16 Cyg A & B we adopted the asteroseismic determinations of both parameters from Hall et al. (2021). Aside from HD 76151, stellar masses and radii for our targets are available from asteroseismology. For 18 Sco we adopted the values from Bazot et al. (2011), while for 16 Cyg A & B we adopted those from Creevey et al. (2017). For HD 76151 we determined the stellar radius from an analysis of the spectral energy distribution, following Metcalfe et al. (2021) with procedures adapted from Stassun et al. (2017, 2018), and we estimated the stellar mass from the empirical eclipsing-binary-based relations of Torres et al. (2010). Stellar ages are from gyrochronology for HD 76151 (Barnes, 2007), and asteroseismology for 18 Sco (Li et al., 2012) and 16 Cyg A & B (Creevey et al., 2017). Table 2.1 includes a complete listing of the adopted and computed stellar properties.
3 Wind Braking Torque
With all of the observational inputs determined, we can now estimate the wind braking torque for each of the stars in the evolutionary sequence using the prescription of Finley & Matt (2018)111https://github.com/travismetcalfe/FinleyMatt2018. For HD 76151 and 18 Sco we have the equivalent polar field strengths derived in Section 2.1 from the ZDI maps. For 16 Cyg A & B we only have upper limits, each of which assumes that all of the field is in a single component, so we calculate the range of torques resulting from the three upper limits on polar field strength. Combining the information from spectropolarimetry with the other stellar properties , we find that the wind braking torque for 18 Sco (3.7 Gyr) and 16 Cyg A & B (7 Gyr) are all more than an order of magnitude smaller than for HD 76151 (2.6 Gyr). The calculated wind braking torques are listed in Table 2.1. The large change in wind braking torque between HD 76151 and 18 Sco is comparable to the inferred change between the F-type stars 88 Leo (2.4 Gyr) and CrB (9.8 Gyr) by Metcalfe et al. (2021) at roughly the same Rossby number. Identical methods applied to these stars yields a torque of erg for 88 Leo, and a range of upper limits –0.337 erg for CrB.
Evolutionary changes in magnetic field strength, mass-loss rate, rotation period, and radius are all expected on Gyr timescales, so it’s important to evaluate the influence of each input parameter on the total change in wind braking torque. Following Metcalfe et al. (2021), we assess the various contributions by modifying one parameter at a time between the adopted values for two stars along the evolutionary sequence, ranking their influence by the associated decrease in the absolute wind braking torque. The magnetic field strength is indicated by the absolute values of , while the field morphology is reflected in their relative values. These two contributions are not easily separable without additional assumptions, so we calculate their combined influence by changing simultaneously. Comparing the fiducial models for HD 76151 and 18 Sco, we find that the change in wind braking torque (2.6–3.7 Gyr) is dominated by the evolution of the mass-loss rate (69%) and magnetic field strength and morphology (65%), with additional contributions from differences in the rotation period (10%) and stellar radius (4%). The small difference in stellar mass between the two stars slightly offsets (+0.4%) the overall decrease in wind braking torque.
To isolate the evolutionary changes that occur between the ages of 18 Sco and 16 Cyg A & B, we repeated the procedure above using the fiducial models for these stars. For simplicity, we adopt the upper limits on for 16 Cyg A & B with the remaining field components set to zero, yielding the strongest constraints on the wind braking torque. Once again we rank the influence of each parameter by the decrease in absolute wind braking torque, grouping the associated changes in parentheses for 16 Cyg A & B, respectively. We find that beyond the age of 18 Sco (3.7–7 Gyr) the wind braking torque continues to weaken modestly for 16 Cyg A & B (17%, 20%). Importantly, the decrease in wind braking torque becomes dominated by the evolution of magnetic field strength and morphology (59%, 31%), with smaller contributions from differences in the mass-loss rate (+3%, 20%) and stellar mass (1%, 0.4%). These reductions are substantially offset by evolutionary changes in stellar radius (+83%, +36%) and by small differences in rotation period (+11%, +7%).
We can forward model the rotation periods of the evolutionary sequence to provide supporting evidence for weakened magnetic braking near the age of 18 Sco, following the same approach described in Metcalfe et al. (2021). Using , [M/H], and radius as constraints, and adopting priors on mass, age, and bulk metallicity, the standard spin-down model predicts rotation periods of , , , and days for HD 76151, 18 Sco, 16 Cyg A & B, respectively. By contrast, the weakened magnetic braking model predicts rotation periods of , , , and days, much closer to the observed periods for 16 Cyg A & B.
4 Discussion
By combining spectropolarimetric measurements for an evolutionary sequence of solar analogs with the wind braking prescription of Finley & Matt (2018), we have placed new constraints on the nature and timing of weakened magnetic braking in middle-aged stars. In particular, we have shown that the wind braking torque decreases by more than an order of magnitude between the ages of HD 76151 and 18 Sco (2.6–3.7 Gyr), substantially exceeding theoretical expectations. Angular momentum losses during this epoch are dominated by evolutionary changes in both the mass-loss rate and magnetic field strength and morphology. The wind braking torque continues to decrease modestly between the ages of 18 Sco and 16 Cyg A & B (3.7–7 Gyr) primarily from changes in the magnetic field strength and morphology, despite being substantially offset by evolutionary changes in the stellar radius. Unfortunately, constraints on the magnetic morphology at the intermediate age of Cen A (5.4 Gyr) are relatively weak due to an unfavorable stellar inclination (Kochukhov et al., 2011). Our results corroborate previous indications of a magnetic transition from F-type stars (Metcalfe et al., 2019, 2021).
With growing observational evidence of a magnetic transition in middle-aged stars, we can now speculate on the physical mechanisms that might be responsible. Large-scale magnetic fields in stars are thought to be generated by a global dynamo process, in which differential rotation provides the shear to transform poloidal field into toroidal field (Charbonneau, 2020). Metcalfe et al. (2016) suggested a fundamental shift in the character of differential rotation for middle-aged stars, based on the observed concentration of field into the poloidal component for young solar analogs (Petit et al., 2008), as well as the theoretical transition to anti-solar differential rotation in global convection simulations at high Rossby number (Gastine et al., 2014). Some of the details of this suggestion were misguided by differences in how the Rossby number is calculated for three-dimensional simulations of convection compared to one-dimensional stellar models that adopt mixing-length theory (Brun et al., 2017), but qualitatively it remains a viable explanation. Subsequent observational evidence supporting this suggestion came from Benomar et al. (2018), who attempted to measure latitudinal differential rotation from the asteroseismic mode splittings of Kepler targets and found two-thirds of the sample consistent with uniform rotation. The absence of significant differential rotation at high Rossby number in this sample is consistent with the notion that weaker differential rotation may be related to the observed onset of weakened magnetic braking. Bazot et al. (2019) applied a similar analysis to 16 Cyg A & B and found weak differential rotation comparable to the Sun, but with the highest stellar latitudes largely unconstrained by observations. This limitation could be addressed with additional analysis of the octupole modes observed in these stars.
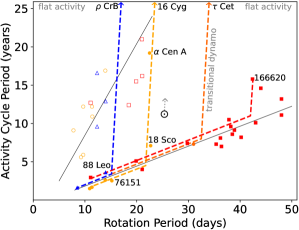
If a diminishing large-scale field is responsible for weakened magnetic braking, then a coincident shift in the underlying dynamo might be found in observations of stellar activity cycles. Metcalfe & van Saders (2017) attempted to identify such a signature, and proposed an evolutionary thread connecting younger stars that show a clear relationship between rotation rate and activity cycle period (like HD 76151), to older stars that appear to be outliers from this relationship or exhibit constant activity on decadal timescales. The template for this evolutionary thread included the solar analogs 18 Sco at 3.7 Gyr, Cen A at 5.4 Gyr, and 16 Cyg A & B near 7 Gyr (see Figure 2). These stars all have comparable rotation periods, but the 7 yr activity cycle in 18 Sco (Hall et al., 2007) will apparently become longer and weaker by the age of Cen A (Ayres, 2014) before disappearing entirely by the age of 16 Cyg A & B (Radick et al., 2018). Similar patterns were found in hotter stars with faster rotation and among cooler stars with slower rotation, at roughly the same critical Rossby number identified by van Saders et al. (2016). Within this context, the Maunder minimum in the Sun can be interpreted as intermittency in the solar cycle as it grows longer and weaker on stellar evolutionary timescales. Additional evidence for this interpretation comes from the recent observation of HD 166620 apparently entering a grand minimum (Baum et al., 2022), after showing clear cyclic behavior during the Mount Wilson survey (Baliunas et al., 1995). This star has a Rossby number similar to the solar value and appears slightly above the so-called inactive sequence of stellar activity cycles, an outlier comparable to the Sun (Böhm-Vitense, 2007).
We can further characterize the nature and timing of the magnetic transition by combining
spectropolarimetry of carefully selected targets with reliable stellar ages from
asteroseismology. We have already obtained new LBT snapshots of the solar analogs
HD 126053 and Ser, and future observations will target Cet and
HD 166620 along with some active comparison stars at similar rotation periods (CF UMa
and 40 Eri). Most of these stars have recently been observed at 20-second cadence with
the Transiting Exoplanet Survey Satellite (TESS; Ricker et al., 2014), allowing a search
for solar-like oscillations to help constrain the stellar properties (e.g.,
see Metcalfe et al., 2021). Results from the initial reconnaissance with LBT will help guide
the longer-term spectropolarimetry that is required to reconstruct complete Zeeman
Doppler images for these targets, reducing the ambiguities that are inherent in snapshot
observations. Within a few years, we should be able to apply the methodology outlined
above to new observations spanning a wide range of spectral types, which sample
different convective overturn timescales.
Special thanks to Wayne Rosing and Kenneth Kulju for supporting this project, and to Sean Matt and Keith MacGregor for helpful suggestions. T.S.M. acknowledges support from the Vanderbilt Initiative in Data-intensive Astrophysics (VIDA). A.J.F. is supported by the ERC Synergy grant “Whole Sun,” No. 810218. O.K. acknowledges support by the Swedish Research Council (project 2019-03548). V.S. acknowledges support from the European Space Agency (ESA) as an ESA Research Fellow. The LBT is an international collaboration among institutions in the United States, Italy and Germany. LBT Corporation partners are: The University of Arizona on behalf of the Arizona Board of Regents; Istituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, The Leibniz Institute for Astrophysics Potsdam, and Heidelberg University; The Ohio State University, and The Research Corporation, on behalf of The University of Notre Dame, University of Minnesota and University of Virginia.
References
- Angus et al. (2015) Angus, R., Aigrain, S., Foreman-Mackey, D., & McQuillan, A. 2015, MNRAS, 450, 1787
- Ayres (2014) Ayres, T. R. 2014, AJ, 147, 59
- Ayres & Buzasi (2022) Ayres, T. R., & Buzasi, D. 2022, ApJ, submitted
- Baliunas et al. (1995) Baliunas, S. L., et al. 1995, ApJ, 438, 269
- Barnes (2007) Barnes, S. A. 2007, ApJ, 669, 1167
- Baum et al. (2022) Baum, A. C., Wright, J. T., Luhn, J. K., & Isaacson, H. 2022, AJ, 163, 183
- Bazot et al. (2019) Bazot, M., Benomar, O., Christensen-Dalsgaard, J., Gizon, L., Hanasoge, S., Nielsen, M., Petit, P., & Sreenivasan, K. R. 2019, A&A, 623, A125
- Bazot et al. (2011) Bazot, M., et al. 2011, A&A, 526, L4
- Benomar et al. (2018) Benomar, O., et al. 2018, Science, 361, 1231
- Böhm-Vitense (2007) Böhm-Vitense, E. 2007, ApJ, 657, 486
- Boller et al. (2016) Boller, T., Freyberg, M. J., Trümper, J., Haberl, F., Voges, W., & Nandra, K. 2016, A&A, 588, A103
- Brewer et al. (2016) Brewer, J. M., Fischer, D. A., Valenti, J. A., & Piskunov, N. 2016, ApJS, 225, 32
- Brun et al. (2017) Brun, A. S., et al. 2017, ApJ, 836, 192
- Charbonneau (2020) Charbonneau, P. 2020, Living Reviews in Solar Physics, 17, 4
- Creevey et al. (2017) Creevey, O. L., et al. 2017, A&A, 601, A67
- Curtis et al. (2019) Curtis, J. L., Agüeros, M. A., Douglas, S. T., & Meibom, S. 2019, ApJ, 879, 49
- Curtis et al. (2020) Curtis, J. L., et al. 2020, ApJ, 904, 140
- David et al. (2022) David, T. J., Angus, R., Curtis, J. L., van Saders, J. L., Colman, I. L., Contardo, G., Lu, Y., & Zinn, J. C. 2022, ApJ, accepted, (arXiv:2203.08920)
- Finley & Matt (2018) Finley, A. J., & Matt, S. P. 2018, ApJ, 854, 78
- Gaia Collaboration et al. (2021) Gaia Collaboration et al. 2021, A&A, 649, A1
- Garraffo et al. (2016) Garraffo, C., Drake, J. J., & Cohen, O. 2016, A&A, 595, A110
- Gastine et al. (2014) Gastine, T., Yadav, R. K., Morin, J., Reiners, A., & Wicht, J. 2014, MNRAS, 438, L76
- Hall et al. (2007) Hall, J. C., Henry, G. W., & Lockwood, G. W. 2007, AJ, 133, 2206
- Hall et al. (2021) Hall, O. J., et al. 2021, Nature Astronomy
- Kochukhov et al. (2010) Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5
- Kochukhov et al. (2011) Kochukhov, O., et al. 2011, ApJ, 732, L19
- Li et al. (2012) Li, T. D., Bi, S. L., Liu, K., Tian, Z. J., & Shuai, G. Z. 2012, A&A, 546, A83
- Metcalfe et al. (2016) Metcalfe, T. S., Egeland, R., & van Saders, J. 2016, ApJ, 826, L2
- Metcalfe et al. (2019) Metcalfe, T. S., Kochukhov, O., Ilyin, I. V., Strassmeier, K. G., Godoy-Rivera, D., & Pinsonneault, M. H. 2019, ApJ, 887, L38
- Metcalfe & van Saders (2017) Metcalfe, T. S., & van Saders, J. 2017, Sol. Phys., 292, 126
- Metcalfe et al. (2021) Metcalfe, T. S., et al. 2021, ApJ, 921, 122
- Ó Fionnagáin & Vidotto (2018) Ó Fionnagáin, D., & Vidotto, A. A. 2018, MNRAS, 476, 2465
- Petit et al. (2008) Petit, P., et al. 2008, MNRAS, 388, 80
- Radick et al. (2018) Radick, R. R., Lockwood, G. W., Henry, G. W., Hall, J. C., & Pevtsov, A. A. 2018, ApJ, 855, 75
- Réville et al. (2015) Réville, V., Brun, A. S., Matt, S. P., Strugarek, A., & Pinto, R. F. 2015, ApJ, 798, 116
- Ricker et al. (2014) Ricker, G. R., et al. 2014, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 9143, Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, ed. J. Oschmann, Jacobus M., M. Clampin, G. G. Fazio, & H. A. MacEwen, 914320
- Ryabchikova et al. (2015) Ryabchikova, T., Piskunov, N., Kurucz, R. L., Stempels, H. C., Heiter, U., Pakhomov, Y., & Barklem, P. S. 2015, Phys. Scr, 90, 054005
- See et al. (2019) See, V., et al. 2019, ApJ, 886, 120
- Skumanich (1972) Skumanich, A. 1972, ApJ, 171, 565
- Spada & Lanzafame (2020) Spada, F., & Lanzafame, A. C. 2020, A&A, 636, A76
- Stassun et al. (2017) Stassun, K. G., Collins, K. A., & Gaudi, B. S. 2017, AJ, 153, 136
- Stassun et al. (2018) Stassun, K. G., Corsaro, E., Pepper, J. A., & Gaudi, B. S. 2018, AJ, 155, 22
- Strassmeier et al. (2015) Strassmeier, K. G., et al. 2015, Astronomische Nachrichten, 336, 324
- Torres et al. (2010) Torres, G., Andersen, J., & Giménez, A. 2010, A&A Rev., 18, 67
- Traulsen et al. (2020) Traulsen, I., et al. 2020, A&A, 641, A137
- Valenti & Fischer (2005) Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141
- van Saders et al. (2016) van Saders, J. L., Ceillier, T., Metcalfe, T. S., Silva Aguirre, V., Pinsonneault, M. H., García, R. A., Mathur, S., & Davies, G. R. 2016, Nature, 529, 181
- van Saders et al. (2019) van Saders, J. L., Pinsonneault, M. H., & Barbieri, M. 2019, ApJ, 872, 128
- Wood et al. (2018) Wood, B. E., Laming, J. M., Warren, H. P., & Poppenhaeger, K. 2018, ApJ, 862, 66
- Wood et al. (2021) Wood, B. E., et al. 2021, ApJ, 915, 37