The origin of the metallicity distributions of the NE and W stellar shelves
in the Andromeda Galaxy
Abstract
Tidal streams and stellar shells are naturally formed in galaxy interactions and mergers. The Giant Stellar Stream (GSS), the North-East (NE), and Western (W) stellar shelves observed in Andromeda galaxy (M31) are examples of these structures and were formed through the merger of M31 and a satellite galaxy. Recent observational papers have provided strong evidence that the shells and GSS originate from a single progenitor. In this paper, we investigate the formation of these two stellar shelves and the detailed nature of their relationship to the GSS. We present numerical simulations of tidal disruption of a satellite galaxy assuming that it is a progenitor of the GSS and the shell system. We represent the progenitor as a dwarf spheroidal galaxy with the stellar mass of and evolve its merger with M31 for 3 Gyrs to reproduce the chemodynamical properties of the NE and W shelves. We find that an initial metallicity of the progenitor with a negative radial gradient of FeH = -, successfully reproduces observed metallicities of the NE, W shelves, and the GSS, showing that all these structures can originate from the same merger event.
keywords:
galaxies: interactions – galaxies: dwarf – methods: numerical1 Introduction
The Andromeda Galaxy (M31) is our cosmic neighbour and due to its proximity, it is very important for studying galactic dynamics and evolution. In the hierarchical assembly paradigm of galaxy formation, large mass galaxies, like Andromeda, are formed through mergers of smaller galaxies (White & Rees, 1978; White & Frenk, 1991). Some of the tracers of these mergers are structures strewn through the halos of massive galaxies such as streams and shells (Hernquist & Quinn, 1988; Johnston et al., 2001, 2008).
Many observed structures in the halo of M31 are formed due to merger events of M31 with satellite galaxies. The most prominent is Giant Stellar Steam (GSS) discovered by Ibata et al. (2001). Distances along the GSS were given by McConnachie et al. (2003), Conn et al. (2016), and velocities by Ibata et al. (2004), Guhathakurta et al. (2006), Kalirai et al. (2006), Gilbert et al. (2009). The stellar mass of the stream is (Ibata et al., 2001; Fardal et al., 2006). In the work of Ferguson et al. (2002), the discovery of the North Eastern and Western shelves is presented. By comparing color-magnitude diagrams these two structures probably have the same origin as GSS (Ferguson et al., 2005; Richardson et al., 2008). Further investigations were done in Merrett et al. (2006) and Bhattacharya et al. (2021) where observations of the planetary nebulae in the region of the NE shelf are presented. Using observations from Ferguson et al. (2002), in the work of Fardal et al. (2007) the W shelf is detected. One faint structure, in the southeast, the SE shelf is detected spectroscopically in Gilbert et al. (2007). The observations that unveil the kinematics of RGB stars in the W shelf are given in Fardal et al. (2012). The observational fields of the edges of the shells are given in Fardal et al. (2008). The edge of the NE shelf is placed on the radial distance from the center of M31 of 40 kpc, and the edge of the W shelf at 20 kpc. The consistency of the physical properties based on color-magnitude diagrams and photometric metallicities arises the probability of the same progenitor for these tidal structures (Ferguson et al., 2005; Gilbert et al., 2007; Richardson et al., 2008; Tanaka et al., 2010; Fardal et al., 2012; Bernard et al., 2015). The evidence that tidal structures in M31 halo are related to the GSS is given in Brown et al. (2006, 2008).
In general, the formation of the structures in the halo of the host is discussed in Pillepich et al. (2014), Remus et al. (2016), Karademir et al. (2019), Milošević (2022). The formation of shells is typical for radial mergers (Amorisco, 2015). In the halo of M31, the origin of the GSS and NE and W shelves are discussed in theoretical works of Fardal et al. (2006, 2007); Fardal et al. (2013) Sadoun et al. (2014), Hammer et al. (2010, 2013). In the work of Fardal et al. (2007), it was shown in numerical simulations that the GSS and shelves could have the same progenitor, confirmed in follow-up work by Sadoun et al. (2014). In Fardal et al. (2006, 2007) satellite on very radial orbit forms these substructures in the halo of M31. In our previous paper, Milošević et al. (2022, hereafter Paper I), we also showed that the GSS, the NE, and W stellar shells can all have the same progenitor. The stellar mass of the satellite in Fardal et al. (2006), Sadoun et al. (2014) and Paper I is the same , but in Sadoun et al. (2014) and Paper I there is a 20 times more massive halo of the progenitor galaxy. These minor merger scenarios reproduced the stream and shell system. Unlike minor merger scenarios, the major merger (stellar mass of the progenitor ) was presented in several works (Hammer et al., 2018; D’Souza & Bell, 2018) with less success in reproducing properties of the shelves than minor merger scenarios.
The morphology of the progenitor is still an open question. A disky progenitor was used in models of Fardal et al. (2008), Kirihara et al. (2017), Miki et al. (2016) and dwarf spheroidal galaxy (dSph) in the Sadoun et al. (2014). In Paper I, we also used the dSph model for the progenitor of the GSS and shelves. Both models successfully reproduce these structures, although disky progenitor better reproduces the asymmetric structure of the GSS envelope. In these theoretical works, structures are formed from the same progenitor. Despite the morphology of the progenitor, the NE shelf forms after the second and the W shelf after the third pericentric passage. Recent observational works show strong evidence that the stream and shells have a common origin based on their dynamics (Escala et al., 2022; Dey et al., 2023).
Metallicity values in the region of the halo substructures of M31 were presented in the Elemental Abundances in M31 survey (Gilbert et al., 2019; Escala et al., 2020a, b, 2021). The halo of M31 is also observed in the SPLASH survey, where kinematics and metallicities are given (Kalirai et al., 2006; Gilbert et al., 2007, 2009; Fardal et al., 2012; Wojno et al., 2023). For the GSS are given metallicities along (Conn et al., 2016; Cohen et al., 2018) and across the stream (Guhathakurta et al., 2006; Kalirai et al., 2006; Ibata et al., 2007; Gilbert et al., 2009, 2014). The observed values give two gradients along the stream, where metallicity values increase from -0.7 in the inner part of the GSS to the central part where the value is -0.2, and then in the outer part, metallicity drops off at a value around -0.8. In the direction across the stream, there is a gradient between metal rich core and the envelope of the stream.
In the region of the NE and W shelves, are given metallicities and velocities based on RGB stars observations for several spectroscopic fields. Due to spectroscopic observations, in Fardal et al. (2012) are given velocities and metallicities for several fields in the W shelf. These fields are between 13 and 26 kpc of the projected radius. In the phase space, projected radius vs. line-of-sight velocity (-) the observed sample shows a wedge pattern which is expected for the shells, formed in the almost radial mergers. It is clearly detected in Fardal et al. (2012) and suggested that the W shelf is formed in the third pericentric passage of the same progenitor that formed the GSS in the first passage. The first analysis of the metallicity and kinematics of the RGB stars in the NE shelf is given in Escala et al. (2022). The observed fields for the NE shelf are from 13 to 31 kpc of projected radius. The wedge pattern for the NE shelf is detected supporting that this structure is formed in radial merger in the second pericentric passage. The observed metallicity of the NE shelf is [Fe/H]phot = -0.42, and for the W shelf is [Fe/H]phot = -0.55. The shapes of MDFs are similar between shells and stream supporting the common origin. Without a kinematically observed trace of the core of the progenitor in Escala et al. (2022), it is given more arguments for models with fully disrupted progenitor.
The observed metallicity gradients along and across the GSS unlocked the possibility of testing initial metallicity distributions in the progenitor of the stream (Fardal et al., 2008; Mori & Rich, 2008; Fardal et al., 2013; Miki et al., 2016; Kirihara et al., 2017). In Paper I, we modeled the distribution of the metallicity in the progenitor of the GSS. Radial metallicity gradients in dwarf galaxies can be positive and negative (Koleva et al., 2009b, a; Spolaor et al., 2009) and we showed that negative radial metallicity gradient in progenitor can reproduce final metallicity distribution along and across the GSS. In the theoretical work of Mercado et al. (2021), from FIRE2 simulation, it is also given that dSph galaxies in the Local Group have a linearly decreasing metallicity gradient. Results are compared with observed metallicity profiles from Leaman et al. (2013); Kacharov et al. (2017). Here we calculate the theoretical metallicity in the regions of the NE and W shelves as it is likely that these structures were formed in the same merger event as the GSS. At the same time with known metallicity values it is possible to predict the position of the remnant of the progenitor. Matching the observed metallicity in several fields in the NE shelf, with the theoretical one from the initial distribution in the progenitor, we have an additional test for the initial gradient and connection between the shell system and the GSS.
This paper is organized as follows: In Section 2 we introduce the method and N-body models for M31 and the satellite progenitor of the GSS. Also, we present the MC method for finding the initial metallicity distribution in the dwarf progenitor galaxy. In Section 3 we present the main results based on the comparison of simulations to observations. In Section 4 we discuss our results and conclude.
2 Methods
2.1 N-body models
In the following, we use a N-body model for M31 and the progenitor galaxy. These models are described in detail in Paper I and are similar as given in Geehan et al. (2006a), Fardal et al. (2007), and Sadoun
et al. (2014). For the main morphological parts of M31, we assume a disk, bulge, and dark matter halo and for the progenitor, we assume a spherical baryonic part and dark matter halo. The initial conditions were generated with GalactICs package (Widrow
et al., 2008), which computes the positions and velocities of the particles for a given mass model. We ran our simulation with Gadget2 cosmological TreePM code (Springel, 2005). We assume a total mass of M31 to be .
The bulge is represented with the Prugniel-Simien profile (Widrow
et al., 2008), which is a de-projected Sersic profile. This profile has law:
| (1) |
Here, is the density at , and is a spherical scale radius for the bulge, and the value for is 1.8.
The disk is represented by a combination of two profiles: exponential profile of surface density in the x-y plane and law in the vertical, z-direction. The exponential profile is given with (Geehan et al., 2006a; Sadoun et al., 2014):
| (2) |
Here, is the total mass of the disk, is surface density, and is disk scale radius. In the last two equations, is the spherical radius, and is the cylindrical radius.
The profile is used in vertical (z) direction (Sadoun et al., 2014) and combined profile is given by:
| (3) |
Here, is the scale height of the disk. The inclination of the disk is and the position angle is (Fardal et al., 2007), and the heliocentric distance to Andromeda is taken to be 785kpc.
A spherical dark matter halo is represented with Navarro-Frenk-White profile (Navarro et al., 1996):
| (4) |
where is a characteristic density, and is a characteristic velocity dispersion, is the scale radius. A more general form is given in GalactICS (Widrow et al., 2008) with an additional term for truncation at some point.
| (5) |
Here, is the radius of the halo and the value at which density starts to decrease, is the distance along which density falls to zero, is an exponent in NFW profile, and we took .
The total mass of the halo inside radius is . The values of parameters are used in GalactICS in the way described in Widrow et al. (2008), where N-body models of M31 are presented, to generate initial conditions. Parameters of the M31 galaxy and dwarf galaxy are given in Table 1 and Table 2 respectively.
| component | m [] | N | |||||
| Bulge | 96247 | = 1,23 kpc | 393 km/s | ||||
| Disk | 108929 | = 6.82 | = 0.57 | ||||
| Halo | 261905 | = 122.5 kpc | 8 kpc | = 12 kpc | = 525 km/s |
| component | m [] | N | |||
|---|---|---|---|---|---|
| Baryonic matter | 131072 | 1.03 kpc | 93 km/s | ||
| Dark matter halo | 248809 | 5 kpc | 242 km/s |
We assume that the best timescale for comparison of modeled and observed properties is between 2 and 3 Gyrs (Paper I). That is in agreement with previous results (Sadoun et al., 2014; Hammer et al., 2018). The dwarf spheroidal galaxy starts its very radial orbit with null velocity from a distance of around 200kpc from the center of the M31 galaxy. The dynamical history of the formation of the shells is the same as in the case of the formation of the GSS because we use the same model and the same conditions in N-body simulation as in previous work.
2.2 Metallicity distribution
We used the same model of metallicity distribution in the progenitor galaxy as described in Paper I, assuming a negative gradient from the center of the galaxy in the radial direction. We successfully reproduced metallicity distribution in the GSS with gradient FeH = - and a central metallicity value of -0.2, matching the observed metallicity values for the GSS taken from the Conn et al. (2016) and Cohen et al. (2018). Many theoretical models of the formation of the GSS predict the formation of shells after several orbits (Fardal et al., 2008; Kirihara et al., 2017; Miki et al., 2016). Accordingly, we try with the same model to describe the observed photometric metallicity of the NE and W shelves given in Escala et al. (2022).
We used Monte Carlo (MC) methods to probe the initial metallicity distribution in the progenitor galaxy. The galaxy is divided into spherical shells and for each particle in every shell, we randomly attach the metallicity value from the Gaussian distribution. The central value of the distribution in each shell is picked up from the negative radial metallicity gradient. We also took for the Gaussian distribution of metallicity in the shell. We trace these particles through simulation and calculate final metallicity values in spectroscopic fields from Escala et al. (2022). After 1000 iterations we calculate the mean value and standard deviation of metallicity in each observed field to generate the final distribution.
We took values from 0 to -0.3 in the center of the progenitor and from -1 to -1.8 in the outer part as described in Paper I. These values and metallicity gradient FeH = - we used to describe the final metallicity distribution in the GSS. This distribution was motivated by observed metallicity along the GSS, given in Conn et al. (2016). With fixed all parameters except initial distribution in the progenitor, we investigated the final distribution in the NE and W shelves and compared it with observed values given in the spectroscopic fields from Escala et al. (2022).
3 Results
In the works of Fardal et al. (2008) and Sadoun et al. (2014), and in Paper I, the formation of the shells is represented as the same merger event in which the GSS is formed. Here we present the formation of the NE and W shelves in a similar single merger scenario with modeled metallicity values for these shelves. Also, we analyze the complex kinematical structure of the shell system.
3.1 Formation and kinematics of the NE and W shelves
On almost radial orbit, a satellite of the M31 galaxy experiences tidal disruption and forms the GSS and shell system. In the first pericentric passage, the GSS is formed, in the second the NE shelf, and in the third the W shelf. The NE shelf is formed in front of the M31 galaxy, closer to us, and the GSS and the W shelf are further from us (Ferguson et al., 2005). We presented the formation of the GSS and shelves in Figure 1. Only particles from the progenitor galaxy are presented and M31 particles are omitted for the sake of clarity. We can see formed GSS and observed fields from McConnachie et al. (2003) are given in red crosses and from Conn et al. (2016) in blue dots. Green dots are the edges of the shelves given in Fardal et al. (2008), and black dots observed fields from Fardal et al. (2012) for the W shelf and Escala et al. (2022) for the NE shelf. For these fields, we calculated metallicity from our simulation. The shells presented in coordinates as we see in the sky are not as prominent as the GSS. In the Hammer et al. (2018) the timescale for the merger event and formation of the structures in the halo of M31 is between 2 and 3 Gyrs; in Sadoun et al. (2014) was suggested 2.7 Gyrs for the GSS, and we estimated (Paper I) the best timescale for the formation of the GSS, from the metallicity distribution point of view, which is 2.9 Gyrs. We can see more clearly formed shells in the middle panel, where the surface density plot is given in the - angular coordinates. On the right panel in Figure 1 are presented shells and the stream in the y-z plane, where we can see that particles of the NE shelf are formed closer to us, with negative values of z-coordinate, unlike the W shelf that is further away from us.



We took the particles from the regions of the NE and W shelves and represented them in 3D space in Figure 2 and Figure 3. In Figure 3 are given particles of the NE shelf. We can see the edge of the structure. As suggested in Fardal et al. (2008), the NE shelf is formed closer to us, due to the M31 galaxy. The particles in our simulation will have negative values for the z-coordinate. Unlike the NE shelf, the W shelf will form further away from us, due to M31, in the region of the positive z-coordinate. We cannot detect the remnant of the progenitor in this extracted tidal structure in 3D space.
Structures, such as streams and shells, are better presented in phase-space plots, where the x-axis is given the distance from the center of M31, and the y-axis is given radial velocity relative to M31. In Figure 4 are given phase-space plots for the time interval between 2.3 and 2.8 Gyrs. We can see the formed GSS and the NE and W stellar shelves, and also the remnant of the progenitor is presented in the vicinity of the NE shelf. Although there is no observational evidence for the remnant in Escala et al. (2022), we can see it in phase-space plots clearly, and after 2.6 Gyrs it becomes faint. The reason for that could be complete disruption.

For the shell system, we can see a characteristic wedge pattern in the space of projected radius () vs. . In Figure 5 evolution of this pattern for the NE and W shelves, and the evolution of the GSS over a time interval between 2.3 and 2.8 Gyrs are presented. From Fardal et al. (2008), Fardal et al. (2012) and Escala et al. (2022) the estimated for the NE shelf is 40kpc and for the W shelf is 20 kpc, although some observed fields are beyond these distances. At the moment of 2.4 Gyrs, the tip of the wedge is at 40kpc; after that, the NE shelf is spreading further. The best time scale for forming the NE shelf, based on the shape of the characteristic wedge pattern is 2.4 Gyrs.
In Paper I, we presented the very complex kinematic nature of the GSS, where two main flows are responsible for the observed peaks in the metallicity distribution in the stream. In the works of Fardal et al. (2007); Fardal et al. (2013), a kinematic analysis of the shell system in the halo of M31 and the distribution of the observed stars over velocities were given. Spectroscopic measurements of the W shelf are given in Fardal et al. (2012) which lead to the kinematic structure of the shell as well as metallicity values for the target objects in several fields. Escala et al. (2022) made additional observations of the NE shelf. From these observations, it is found two Kinemacically Cold Components (KCC) in the region of the NE shelf. Similar to the GSS, this shell also has a complex kinematic structure.
To compare with observed data from Escala et al. (2022) we took particles from the region of the NE shelf. The NE shelf region is defined with boundaries and , where is NE major axis (position angle = E of N), and NW minor axis (Escala et al., 2022). In Figure 6 (left panel), the structure shows a wedge shape with the tip of the wedge at 40 kpc. Blue rectangles represent spectroscopic fields from Escala et al. (2022). On the right panel of Figure 6 are given particles from the W shelf with spectroscopic fields also represented with blue rectangles. The part of the NE shelf with positive line-of-sight velocities (), (where systemic velocity of M31 is = -300km/s), the upper envelope, corresponds to the stars moving toward M31, and the lower envelope corresponds to stars that are moving in the opposite direction (Escala et al., 2022). This shows a very complex kinematical picture of the NE shelf. We calculated mean velocities and velocity dispersions in our simulation that correspond to spectroscopic fields given in Escala et al. (2022) and compared them with the observed one in Figure 7. The upper envelope is represented with red color and the lower envelope with blue color. Smaller dots represent our model, and larger dots observed values of . In most of the fields, we can see agreement between modeled and observed values, but there is also mismatching in the first field (=14.4 kpc), where the model failed to explain values for the lower envelope, as well as in the third field (=21.7 kpc).
A similar analysis is done for the W shelf. In Figure 8 we see a comparison between observed and modeled mean velocities and velocity dispersions for the upper and lower envelopes in the W shelf. The upper envelope is represented with red color and the lower with blue. Larger dots are observed values and small dots form our simulation. There is an agreement between these values in all spectroscopic fields.




3.2 Metallicity distribution of the NE and W shelves
In Paper I, we showed how the initial metallicity distribution can explain observed metallicity in the GSS. Observed values were given in the works of Conn et al. (2016) and Cohen et al. (2018). These values are distributed along the GSS, and earlier were published the values of the metallicities across the GSS in several fields (Ibata et al., 2007; Gilbert et al., 2007, 2009). The similar metallicity values of the GSS and the NE and W shelves support the scenario of the formation of these structures in the same merger event. From the metallicity distribution functions (MDF) for the GSS, NE, and W shelves presented in Escala et al. (2022), we can see the distributions are very similar for these three structures. Observed metallicity values are given in five fields for the NE and three radial zones for the W shelf. The observed metallicity values in the GSS and shelves and similarity in the MDFs gave the possibility of probing initial metallicity distribution in the progenitor galaxy.
We investigate the negative metallicity gradient in the progenitor galaxy, the same one we used in Paper I to compare with observed metallicity in Escala et al. (2022). We calculated metallicity in 5 fields for the NE shelf and also in 5 fields for the W shelf. The good agreement is shown in Figure 9 for the NE shelf. Between 2.4 and 2.7 Gyrs we reproduced observed metallicity in all fields except for the first field, where theoretical metallicity is higher than the observed one, probably because of the contamination of the first field by the M31 stars. Based on these fields we cannot see any obvious gradient in the NE shelf as it is clear for the GSS. All values calculated from the model are very close to the mean value of -0.4 given from observations.

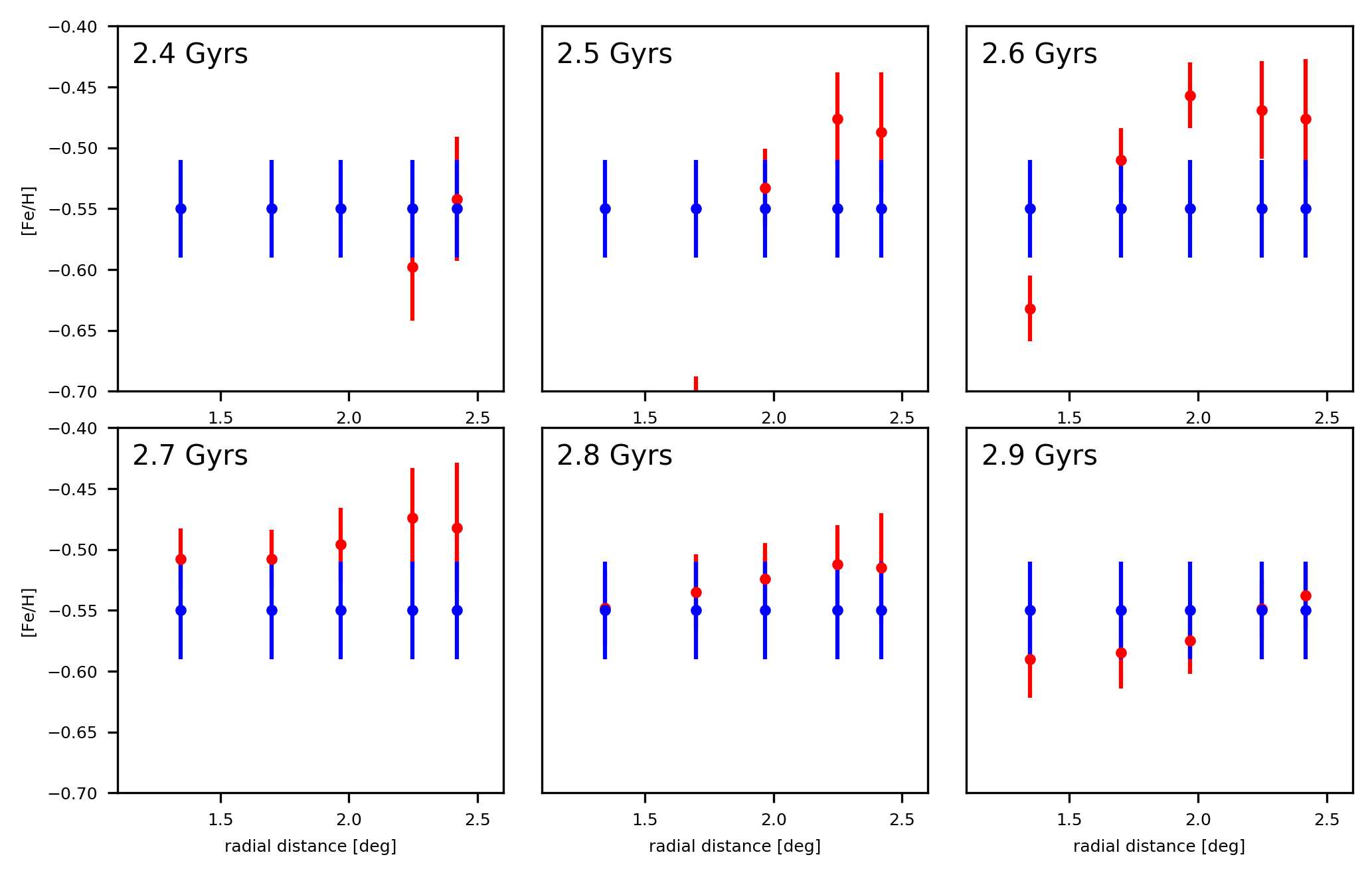
We compare our theoretical metallicity for the W shelf in spectroscopic fields with the mean values given in Escala et al. (2022), so in each field is given mean metallicity for the W shelf from Escala et al. (2022) instead of the observed value, just for the qualitative comparison. These results are presented in Figure 10. The W shelf is more metal-poor than the NE shelf with mean metallicity -0.5. Similar to the NE shelf, we cannot see a gradient in the W shelf. Between 2.7 and 2.9 Gyrs, there is also good agreement between our model and observed metallicity values, suggesting the same progenitor for all three structures.
4 Discussion and conclusions
This paper is a continuation of Paper I, where we investigated metallicity distribution in the GSS. In many theoretical models, these shelves are formed in the same merger scenario as the GSS (e.g. Fardal et al., 2008; Sadoun et al., 2014).
Here, we reproduced the formation of the NE and W shelves using N-body simulations. We used dSph progenitor with a stellar mass of . Based on phase-space plots we found that the best agreement with the observed wedge shape we have for 2.4 Gyrs after the beginning of the simulation. We compared simulated values of mean velocities in the upper and lower envelopes in the NE shelf with observed one from several spectroscopic fields, given in Escala et al. (2022). Our model does not reproduce the values of the mean velocities in the first field at the projected radius of 14.4 kpc, and in the third field at the projected radius of 21.7 kpc for the upper envelope in the NE shelf. In the three other fields, there is an agreement between simulated and observed values for velocities. For the W shelf, our model successfully reproduces observed values from Escala et al. (2022).
We used a negative radial metallicity gradient in the dSph progenitor. In Paper I, with radial metallicity gradient FeH = - and with a central value of -0.2 we reproduced metallicity distribution along the GSS given in Conn et al. (2016). The first observations and analysis for the W shelf were performed by Fardal et al. (2012). We compared our theoretical metallicity with the mean metallicity for the W shelf given in Escala et al. (2022), for the same spectroscopic fields as in Fardal et al. (2012). The simulated metallicity is in agreement with the observed one, except for the innermost field for the NE shelf, where disagreement is probably due to M31 contamination. The theoretical and observed values for the mean metallicity for the NE shelf is and for the W shelf, . From different criteria, the timescale for the formation of the GSS and shell system is between 2.4 and 2.9 Gyrs.
The disruption of the remnant of the progenitor is still an open question and the morphology of the progenitor is as well. We traced the remnant of the progenitor, to 3 Gyrs, which is presented in phase-space plots. After 2.7 Gyrs into the merger, it is hard to locate the remnant. The suggestion from the Escala et al. (2022) is that the remnant is fully disrupted, or it could be located in the region of the disk of M31 (Fardal et al., 2013), which leads to difficulties in observing. Here, we avoided the static potential for the M31 galaxy and used N-body models for both: progenitor and M31. This can affect tidal disruption and dynamic friction as well as the location of the remnant. Major merger scenarios have different predictions for the remnant of the progenitor, a compact dense galaxy like M32 (D’Souza & Bell, 2018), or complete disruption (Hammer et al., 2018).
Our model of the spheroidal progenitor successfully reproduced the observed metallicity of the GSS, represented in the Paper I and NE and W shelves represented in this paper. With a negative radial gradient of initial metallicity in the progenitor, we described metallicity distribution in the GSS and NE shelf and reproduced mean metallicity in the W shelf.
ACKNOWLEDGEMENTS
We thank the anonymous referee for providing important and useful comments that improved this manuscript. This work was supported by the Ministry of Education, and the Ministry of Science, Technological Development and Innovation of the Republic of Serbia, through contracts: 451-03-47/2023-01/200104 and 451-03-47/2023-01/200002.
Data Availability
Data used in the paper will be made available on a reasonable request to the author.
References
- Amorisco (2015) Amorisco N. C., 2015, MNRAS, 450, 575
- Bernard et al. (2015) Bernard E. J., et al., 2015, MNRAS, 446, 2789
- Bhattacharya et al. (2021) Bhattacharya S., Arnaboldi M., Gerhard O., McConnachie A., Caldwell N., Hartke J., Freeman K. C., 2021, A&A, 647, A130
- Brown et al. (2006) Brown T. M., Smith E., Ferguson H. C., Rich R. M., Guhathakurta P., Renzini A., Sweigart A. V., Kimble R. A., 2006, ApJ, 652, 323
- Brown et al. (2008) Brown T. M., et al., 2008, ApJ, 685, L121
- Cohen et al. (2018) Cohen R. E., et al., 2018, AJ, 156, 230
- Conn et al. (2016) Conn A. R., et al., 2016, MNRAS, 458, 3282
- D’Souza & Bell (2018) D’Souza R., Bell E. F., 2018, Nature Astronomy, 2, 737
- Dey et al. (2023) Dey A., et al., 2023, ApJ, 944, 1
- Escala et al. (2020a) Escala I., Gilbert K. M., Kirby E. N., Wojno J., Cunningham E. C., Guhathakurta P., 2020a, ApJ, 889, 177
- Escala et al. (2020b) Escala I., Kirby E. N., Gilbert K. M., Wojno J., Cunningham E. C., Guhathakurta P., 2020b, ApJ, 902, 51
- Escala et al. (2021) Escala I., Gilbert K. M., Wojno J., Kirby E. N., Guhathakurta P., 2021, AJ, 162, 45
- Escala et al. (2022) Escala I., Gilbert K. M., Fardal M., Guhathakurta P., Sanderson R. E., Kalirai J. S., Mobasher B., 2022, AJ, 164, 20
- Fardal et al. (2006) Fardal M. A., Babul A., Geehan J. J., Guhathakurta P., 2006, MNRAS, 366, 1012
- Fardal et al. (2007) Fardal M. A., Guhathakurta P., Babul A., McConnachie A. W., 2007, MNRAS, 380, 15
- Fardal et al. (2008) Fardal M. A., Babul A., Guhathakurta P., Gilbert K. M., Dodge C., 2008, ApJ, 682, L33
- Fardal et al. (2012) Fardal M. A., et al., 2012, MNRAS, 423, 3134
- Fardal et al. (2013) Fardal M. A., et al., 2013, MNRAS, 434, 2779
- Ferguson et al. (2002) Ferguson A. M. N., Irwin M. J., Ibata R. A., Lewis G. F., Tanvir N. R., 2002, AJ, 124, 1452
- Ferguson et al. (2005) Ferguson A. M. N., Johnson R. A., Faria D. C., Irwin M. J., Ibata R. A., Johnston K. V., Lewis G. F., Tanvir N. R., 2005, ApJ, 622, L109
- Geehan et al. (2006a) Geehan J. J., Fardal M. A., Babul A., Guhathakurta P., 2006a, MNRAS, 366, 996
- Geehan et al. (2006b) Geehan J. J., Fardal M. A., Babul A., Guhathakurta P., 2006b, MNRAS, 366, 996
- Gilbert et al. (2007) Gilbert K. M., Fardal M. A., Kalirai J. S., Guhathakurta P., Geha M. C., et al. 2007, ApJ, 668, 245
- Gilbert et al. (2009) Gilbert K. M., Guhathakurta P., Kollipara P., et al. 2009, ApJ, 705, 1275
- Gilbert et al. (2014) Gilbert K. M., Kalirai J. S., Guhathakurta P., et al. 2014, ApJ, 796, 76
- Gilbert et al. (2019) Gilbert K. M., Kirby E. N., Escala I., et al. 2019, ApJ, 883, 128
- Guhathakurta et al. (2006) Guhathakurta P., et al., 2006, AJ, 131, 2497
- Hammer et al. (2010) Hammer F., Yang Y. B., Wang J. L., et al. 2010, ApJ, 725, 542
- Hammer et al. (2013) Hammer F., Yang Y. B., Fouquet S., et al. 2013, MNRAS, 431, 3543
- Hammer et al. (2018) Hammer F., Yang Y. B., Wang J. L., Ibata R., Flores H., Puech M., 2018, MNRAS, 475, 2754
- Hernquist & Quinn (1988) Hernquist L., Quinn P. J., 1988, ApJ, 331, 682
- Ibata et al. (2001) Ibata R., Irwin M., Lewis G., Ferguson A. M. N., Tanvir N., 2001, Nature, 412, 49
- Ibata et al. (2004) Ibata R., Chapman S., Ferguson A. M. N., Irwin M., Lewis G., McConnachie A., 2004, MNRAS, 351, 117
- Ibata et al. (2007) Ibata R., Martin N. F., Irwin M., Chapman S., Ferguson A. M. N., Lewis G. F., McConnachie A. W., 2007, ApJ, 671, 1591
- Johnston et al. (2001) Johnston K. V., Sackett P. D., Bullock J. S., 2001, ApJ, 557, 137
- Johnston et al. (2008) Johnston K. V., Bullock J. S., Sharma S., Font A., Robertson B. E., Leitner S. N., 2008, ApJ, 689, 936
- Kacharov et al. (2017) Kacharov N., et al., 2017, MNRAS, 466, 2006
- Kalirai et al. (2006) Kalirai J. S., Guhathakurta P., Gilbert K. M., et al. 2006, ApJ, 641, 268
- Karademir et al. (2019) Karademir G. S., Remus R.-S., Burkert A., Dolag K., Hoffmann T. L., Moster B. P., Steinwandel U. P., Zhang J., 2019, MNRAS, 487, 318
- Kirihara et al. (2017) Kirihara T., Miki Y., Mori M. e. a., 2017, MNRAS, 464, 3509
- Koleva et al. (2009a) Koleva M., Prugniel P., De Rijcke S., Zeilinger W. W., Michielsen D., 2009a, AN, 330, 960
- Koleva et al. (2009b) Koleva M., de Rijcke S., Prugniel P., Zeilinger W. W., Michielsen D., 2009b, MNRAS, 396, 2133
- Leaman et al. (2013) Leaman R., et al., 2013, ApJ, 767, 131
- McConnachie et al. (2003) McConnachie A. W., Irwin M. J., Ibata R. A., Ferguson A. M. N., Lewis G. F., Tanvir N., 2003, MNRAS, 343, 1335
- Mercado et al. (2021) Mercado F. J., et al., 2021, MNRAS, 501, 5121
- Merrett et al. (2006) Merrett H. R., et al., 2006, MNRAS, 369, 120
- Miki et al. (2016) Miki Y., Mori M., Rich R. M., 2016, ApJ, 827, 82
- Milošević (2022) Milošević S., 2022, Serbian Astronomical Journal,
- Milošević et al. (2022) Milošević S., Mićić M., Lewis G. F., 2022, MNRAS, 511, 2868
- Mori & Rich (2008) Mori M., Rich R. M., 2008, ApJ, 674, L77
- Navarro et al. (1996) Navarro J. F., Frenk C. S., White S. D. M., 1996, ApJ, 462, 563
- Pillepich et al. (2014) Pillepich A., et al., 2014, MNRAS, 444, 237
- Remus et al. (2016) Remus R.-S., Dolag K., Naab T., Burkert A., Hirschmann M., Hoffmann T. L., Johansson P. H., 2016, Monthly Notices of the Royal Astronomical Society, 464, 3742
- Richardson et al. (2008) Richardson J. C., et al., 2008, AJ, 135, 1998
- Sadoun et al. (2014) Sadoun R., Mohayaee R., Colin J., 2014, MNRAS, 442, 160
- Spolaor et al. (2009) Spolaor M., Proctor R. N., Forbes D. A., Couch W. J., 2009, ApJL, 691, L138
- Springel (2005) Springel V., 2005, MNRAS, 364, 1105
- Tanaka et al. (2010) Tanaka M., Chiba M., Komiyama Y., Guhathakurta P., Kalirai J. S., Iye M., 2010, ApJ, 708, 1168
- White & Frenk (1991) White S. D. M., Frenk C. S., 1991, ApJ, 379, 52
- White & Rees (1978) White S. D. M., Rees M. J., 1978, MNRAS, 183, 341
- Widrow et al. (2008) Widrow L. M., Pym B., Dubinski J., 2008, ApJ, 679, 1239
- Wojno et al. (2023) Wojno J. L., et al., 2023, ApJ, 951, 12