The orientations of the binary black holes in GWTC-3

In this Letter we measure the astrophysical distribution of another important extrinsic parameter, the orbital inclination $\theta_{\rm{JN}}$, defined as the angle between the total angular momentum and the line of sight. It might seem obvious that the orientation of BBH orbits should be isotropic, i.e. that $\pi(\theta_{\rm{JN}})\propto\sin\theta_{\rm{JN}}$ [31, 32]. However, several factors may result in detecting a distribution for $\theta_{\rm{JN}}$ which is not isotropic. First, some alternative theories of gravity, e.g. birefringence, predict that the GW power emitted by a merging binary is not symmetric about the orbital plane [33, 34, 35]: this would result in a preference for detecting sources with inclination of e.g. $\pi/6$ over sources with inclination of $\pi-\pi/6$, whereas these two values would be equally detectable in general relativity. Second, the algorithms that search for compact binary coalescences (CBCs) assume that spins are perfectly aligned with the orbital angular momentum, and neglect higher order modes (HOMs) [6]. These approximations have been shown to be sufficient when spins are small or aligned with the orbit, and mass ratios are close to unity. However, their accuracy is also a function of the orbital inclination: indeed, the loss of SNR due to neglecting these effects is maximal when $\theta_{\rm{JN}}=\pi/2$ (“edge-on” orientation). This could result in systematically missing sources with high orbital inclination and hence in a dip in the inferred $\theta_{\rm{JN}}$ distribution at $\theta_{\rm{JN}}=\pi/2$. If this loss of SNR is properly accounted for when calculating selection effects, one should still measure an isotropic distribution. Finally, marginal triggers of non-astrophysical origin (often called glitches) could be mistakenly identified as BBHs, and added in the catalog. It is has been found that that running CBC source characterization algorithms on glitches results in distributions of $\theta_{\rm{JN}}$ peaked at $\pi/2$. A sub-population of glitches in the catalog would thus result in an excess of posterior probability at around $\pi/2$ for $\theta_{\rm{JN}}$. Measuring a distribution of $\theta_{\rm{JN}}$ different from the expected isotropic one could thus indicate problems with our understanding of gravity, with the sensitivity of detection algorithms to highly inclined orbits, or with glitch contamination. Ref. [35] used the sources in GWTC-2 to recast the measured level of symmetry of the inclination angles around $\pi/2$ into constraints on birefringence and Chern-Simons gravity. They did not perform full hierarchical inference on the astrophysical distribution of inclination angles, which is the focus of this work.

In this expression, $\alpha(\vec{\lambda})$ represents the fraction of detectable BBHs given the population parameters $\vec{\lambda}$; $\pi(\vec{\lambda})$ is the population prior and $p(d_{i}|\vec{\lambda})$ is the likelihood of the stretch of data containing the i-th BBH. The likelihood of the individual sources can be written in terms of their posterior distributions by marginalizing over the individual source parameters $\vec{\theta}\equiv(m_{1},m_{2},a_{1},\tau_{1},a_{2},\tau_{2},z,\theta_{\rm{JN}})$. In this expression, $m_{1}$ and $m_{2}$ are the masses of the heavier and lighter black hole in the binary, respectively; $a_{i}$ is the dimensionless spin of the i-th black hole in the binary, and $\tau_{i}$ is the angle between the i-th spin vector and the orbital angular momentum, $z$ is the redshift and $\theta_{\rm{JN}}$ is the orbital inclinations. For the i-th source, one has [39, 38]:

where $p(\vec{\theta}|d_{i}\mathcal{H}_{\mathrm{PE}})$ is the posterior distribution for the source in the i-th stretch of data, and $\mathcal{H}_{\mathrm{PE}}$ symbolizes all of the settings that went into the parameter estimation algorithm used to produce those samples. Similarly, $\pi(\vec{\theta}|\mathcal{H}_{\mathrm{PE}})$ are the priors used when sampling the posterior distribution. Finally, $\pi(\vec{\theta}|\vec{\lambda})$ is the population prior, i.e., our model for how the hyper parameters affect the true underlying distribution of the BBH parameters $\vec{\theta}$. We use the posterior samples of the 69 BBHs reported in GWTC-3, as released by the LVK in Refs [40, 41, 42, 43] and approximate the integral with a discrete sum

where the ${N_{\rm{samples}}}$ samples are drawn from the posterior distribution of the i-th event. We sample the hyper posterior with the GWPopulation algorithm [44], using the dynesty [45] sampler. GWPopulation requires that the same number of ${N_{\rm{samples}}}$ is used for all sources. We are thus limited by the source for which fewest samples were made public. That is GW200129_065458, for which ${N_{\rm{samples}}}=3194$. For the sources reported in GWTC-1, we use the samples labelled IMRPhenomPv2_posterior in the data release; for GWTC-2 we use PublicationSamples; for GWTC-2.1 we use PrecessingSpinIMRHM, and for GWTC-3 we use C01:Mixed.

The detection efficiency $\alpha(\vec{\lambda})$ can also be calculated through an approximated sum starting from a large collection of simulated BBHs for which the SNR (or other detection statistic) is recorded, as described in Ref. [46, 7]. We use the endo3_bbhpop-LIGO-T2100113-v12-
1238166018-15843600.hdf5 sensitivity file released by the LVK [47] to calculate $\alpha(\lambda)$, using a false alarm threshold of 1 per year to identify detectable sources, consistently with [7]. We stress that this file only contains BBHs which would be detectable by GW observatories at O3 sensitivity, whereas our dataset also includes sources detected in O1 and O2. Unfortunately, the sensitivity files released by the LVK in Ref. [48] which also cover GWTC-1 and GWTC-2 do not include the inclination of the simulated sources, and thus cannot be used in this work. We have generated our own sensitivity files which account for the changing sensitivity of the GW network since O1 and verified that the results presented below don’t change significantly. This makes sense because it is only with next-generation detectors that one should expect a different distribution of detectable inclinations [32, 49] and since O3 does dominate the overall surveyed time-volume. To make our findings easy to reproduce, we therefore only present results obtained with the LVK data products. Finally, we have verified that using only GW BBHs from O3 one obtain consistent results, though with larger error bars.

with $B(a,b)\equiv\Gamma(a)\Gamma(b)/\Gamma(a+b)$. For $\alpha_{\theta_{\rm{JN}}}=\beta_{\theta_{\rm{JN}}}$ this distribution is symmetric around $\pi/2$: for $\alpha_{\theta_{\rm{JN}}}=\beta_{\theta_{\rm{JN}}}\simeq 2.15$ it is very similar to $\sin\theta_{\rm{JN}}/2$ (The Jensen–Shannon (JS) divergence [51, 52] between $\sin(\theta_{\rm{JN}})/2$ and $p(\theta_{\rm{JN}}|2.15,2.15)$ is $\sim 5\times 10^{-5}$ bits.), whereas for $\alpha_{\theta_{\rm{JN}}}=\beta_{\theta_{\rm{JN}}}>2.15$ ($\alpha_{\theta_{\rm{JN}}}=\beta_{\theta_{\rm{JN}}}<2.15$) more (less) posterior weight is placed at $\theta_{\rm{JN}}=\pi/2$

For the mass, spin, and redshift hyper parameters we use the same priors used by the LVK, as described in Table VI and Table XII of Ref. [7], with the exception of the two hyper parameters of the spin magnitude beta distribution, for which we used $\alpha_{\chi}:\texttt{Uniform(1,5)}$, $\beta_{\chi}:\texttt{Uniform(1,5)}$. For the inclination model we use the following priors: $\alpha_{\theta_{\rm{JN}}}:\texttt{Uniform(1,8)}$, $\beta_{\theta_{\rm{JN}}}:\texttt{Uniform(1,8)}$, where the model can be normalized.

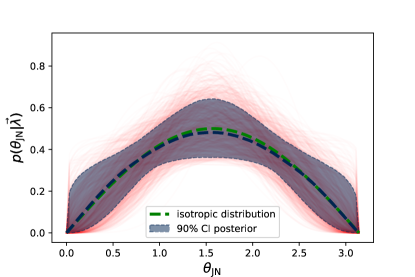
Next, we take 10000 random samples from the hyper posterior and calculate the corresponding $p(\theta_{\rm{JN}}|\alpha_{\theta_{\rm{JN}}},\beta_{\theta_{\rm{JN}}})$, Fig. 2. Each dim red line is an individual draw from the posterior (to enhance visibility, we only show 1000 such draws), whereas the blue band shows the 90% credible interval. The blue thick curve represents the median, which shows remarkable agreement with the expected isotropic distribution (green dashed curve). The JS divergence between the inferred population median and a perfectly isotropic distribution is $1.4\times 10^{-4}$ bits. We stress that this level of agreement is not built-in in our model, nor in the shape or width of the hyper parameters’ priors. This is shown explicitly in Fig. 3: first, we draw 10000 points from the priors of $\alpha_{\theta_{\rm{JN}}}$ and $\beta_{\theta_{\rm{JN}}}$ and plot the resulting 90% credible interval as a grey band, and the median as a dashed grey curve. The posterior 90% credible interval and median from Fig. 2 are also shown in blue. It is apparent that the median and the 90% credible interval are significantly different from the prior.

However, one might still wonder whether the main information extracted from the data is that the distributions should be symmetric, i.e. that $\alpha_{\theta_{\rm{JN}}}\simeq\beta_{\theta_{\rm{JN}}}$. To check whether this is the case, we draw 10000 samples from the prior of $\alpha_{\theta_{\rm{JN}}}$ and then calculate $p(\theta_{\rm{JN}}|\alpha_{\theta_{\rm{JN}}},\beta_{\theta_{\rm{JN}}}=\alpha_{\theta_{\rm{JN}}})$, i.e. we consider the effective prior one would obtain by only considering distributions symmetric around $\pi/2$. The resulting 90% credible interval is shown as a yellow band in Fig. 3, and its median as a dashed yellow curve. Here too it is clear that the measurement is informative, and the data excludes large regions of parameter space. The ratio of the JS divergence between the median obtained with prior draws and a perfectly isotropic distribution and the JS divergence calculated with the population posterior median is 288. Using samples from a prior that has been forced to be symmetric, the ratio is 372.

We have modeled the astrophysical distribution of orbital inclinations as a non-singular beta distribution, and found that the data prefers inclination distributions which are symmetric around $\pi/2$: the skewness of the inclination distribution is reduced by a factor of 5 relative to what would be obtained using prior samples. Furthermore, the inferred distribution for the inclination angle is consistent with being isotropic: the JS divergence between the inferred population median and a perfectly isotropic distribution is $1.4\times 10^{-4}$ bits.

We have only used BBH sources reported by the LVK collaboration because a key part of any hierarchical analysis is a self-consistent evaluation of the selection effects, which is hard to achieve for sources found by other groups. However, we do encourage groups that produce independent catalogs of GW sources to also make public their own sensitivity files, to make this type of analysis possible. As the size of the GW network increases in the next few years, we expect this analyses will yield even stronger constraints, since a larger network can better reveal the polarization content, and hence the inclination angle, of individual sources. The improved inclination measurement for each source, together with the higher detection rates, implies we could set limits on even smaller departures from orientational isotropy, and use more sophisticated models that explicitly allow for these anisotropies. This will be explored in a future paper.