The numerical value for a universal quantity of a two-dimensional dimerized quantum antiferromagnet
Abstract
The numerical value of a universal quantity associated with the quantum critical regime, namely , for a two-dimensional (2D) dimerized spin-1/2 antiferromagnet is calculated using the quantum Monte Carlo simulations (QMC). Here , , and are the uniform susceptibility, the spin-wave velocity, and the temperature, respectively. By simulating large lattices at moderately low temperatures, we find . Our estimation of deviates from the related analytic prediction but agrees with recent numerical calculations of other 2D dimerized spin-1/2 antiferromagnets.
I Introduction
Spatial dimension two is special because of the famous Mermin–Wagner theorem Mer66 . Specifically, continuous symmetry cannot be broken spontaneously (at finite temperature ) in spatial dimension two. As a result, for two-dimensional (2D) quantum antiferromagnets, as rises from zero temperature, one encounters a crossover instead of a phase transition to a unique phase called the quantum critical regime (QCR).
Using the relevant field theory, properties of QCR are investigated Chu94 . In particular, several universal quantities are proposed. Among these quantities, we are especially interested in due to the recently found discrepancy between the analytic prediction and the numerical calculations. Here and are the uniform susceptibility and the spin-wave velocity, respectively.
Analytically, it is predicted that the numerical value of is given by (around) 0.27185. Although this prediction was confirmed by earlier Monte Carlo studies Chu94 ; Tro98 , recent investigations of 2D dimerized bilayer and plaquette spin-1/2 Heisenberg models conclude that Sen15 ; Tan181 . Because of this discrepancy, it will be interesting to conduct a further examination on the numerical value of .
In this study, we perform large-scale Monte Carlo simulations to determine the of a 2D dimerized quantum antiferromagnetic Heisenberg model. By simulating lattices as large as ( is the linear system size), we obtain which matches quantitatively with recent outcomes claimed in Refs. Sen15 ; Tan181 . Our result suggests that a refinement of analytic calculation is needed.
The rest of the paper is organized as follows. After the introduction, the model and the measured observables are described in Sec. II. We then present the obtained results in Sec. III. In particular, the numerical evidence to support is demonstrated. We conclude our investigation in Sec. VI.

II The considered model and observable
The Hamiltonian of the considered 2D spin- dimerized herringbone Heisenberg model takes the following expression
| (1) |
where and are the antiferromagnetic couplings connecting nearest neighbor spins and , respectively, and is the spin- operator at site . A cartoon representation of the studied model is depicted in fig. 1. is set to 1 in our investigation. As the magnitude of increases, a phase transition will occur for a particular value of . This special point in the parameter space is denoted by and is found to be in the literature Pen20 . The investigation presented in this study is conducted at the critical point .
To examine the universal quantity of QCR, the uniform susceptibility and the spin-wave velocity are measured. On a finite lattice of linear size , the uniform susceptibility is defined by
| (2) |
The quantity appearing above is the inverse temperature. The spin-wave velocity for the investigated model is calculated through the temporal and spatial winding numbers squared ( and with ).
III Numerical Results
To conduct the proposed investigation, we have carried out large-scale quantum Monte Carlo calculations (QMC) using the stochastic series expansion algorithm (SSE) with efficent operate-loop update San99 . The obtained outcomes are described in the following subsections.
III.1 The determination of spin-wave velocity
The observable spin-wave velocity is required to compute the numerical value of . Therefore we have calculated this quantity first.
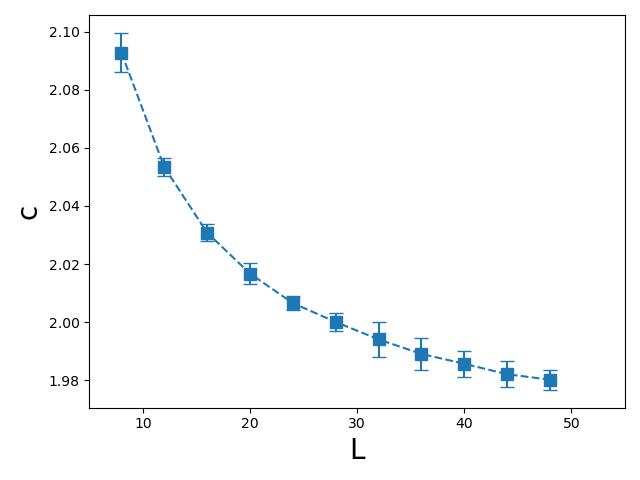
We compute the spin-wave velocity by the method of winding numbers squared Sen15 ; Jia11 . The procedure is as follows. For a given box size and a , the value of is tuned so that and match each other quantitatively. When this condition is fulfilled, the spin-wave velocity associated with this set of and is given by .
It should be pointed out that the existence of long-range antiferromagnetic order is essential to employ this method to calculate . As a result, we conduct the related simulations at which is close to the critical point and is in the antiferromagnetic phase.
III.2 as functions
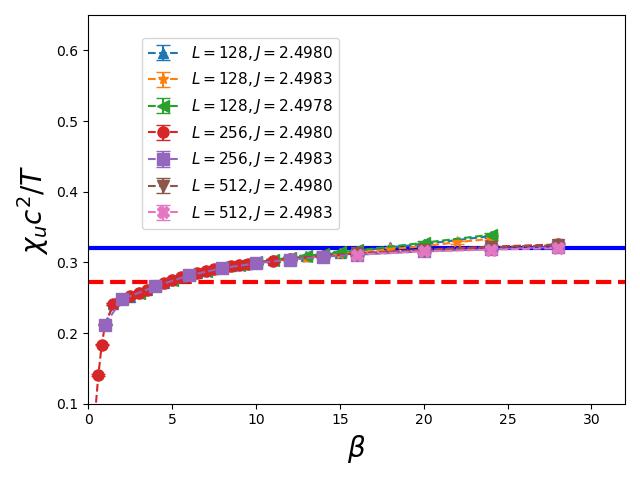
The simulations of calculating are done with , and 512. In addition, the uncertainty of is taken into account in these simulations. Using , the of various and as functions of are shown in fig. 3. The outcomes shown in the figure indicate that as and increase, the value of deviates from its analytic prediction of 0.27185 ( the horizontal dashed line in the figure) and approaches 0.32 (the horizontal solid line in the figure). This result agrees with that of Sen15 and Tan181 .
IV Discussions and Conclusions
In this study, we calculate the numerical value of corresponding to the 2D dimerized quantum herringbone Heisenberg model using QMC. By simulating lattice as large as at moderate low temperatures, we obtain . Our result deviates from the associated analytic prediction but agrees quantitatively with recent numerical calculations of 2D spin-1/2 bilayer and plaquette Heisenberg models. Based on the obtained outcomes in this study, it will be interesting to refine the relevant theoretical calculations.
Acknowledgement
Partial support from National Science and Technology Council (NSTC) of Taiwan is acknowledged (MOST 110-2112-M-003-015 and MOST 111-2112-M-003-011).
Author Contributions
F.J.J proposed the project, conducted the calculations, analyzed the data, and wrote up the manuscript.
Conflict of Interest
The author declares no conflict of interest.
References
- (1) N. D. Mermin and H. Wagner, Phys. Rev. Lett. 17, (1966) 1133.
- (2) A. V. Chubukov, S. Sachdev, and J. Ye, Phys. Rev. B 49, (1994) 11919.
- (3) Jae-Kwon Kim and Matthias Troyer, Phys. Rev. Lett. 80, (1998) 2705.
- (4) A. Sen, H. Suwa, and A. W. Sandvik, Phys. Rev. B 92, (2015) 195145.
- (5) D.-R. Tan and F.-J. Jiang, Phys. Rev. B 98, (2018) 245111.
- (6) J.-H. Peng, D.-R. Tan, and F.-J. Jiang, Phys. Rev. B 102, 214206 (2020).
- (7) A. W. Sandvik, Phys. Rev. B 55, (1999) R14157.
- (8) F.-J. Jiang, Phys. Rev. B 83, (2011) 024419.