\articleinfo

Version of May 6, 2021 ^†^†thanks: This work was supported by JSPS KAKENHI Grant Numbers JP25887038, JP15K17554, JP18K18720 and by the Research Institute for Mathematical Sciences, an International Joint Usage/Research Center located in Kyoto University. \rcvdate \rvsdate

The Laplacian on some self-conformal fractals
and Weyl’s asymptotics for its eigenvalues:
A survey of the analytic aspects

Naotaka Kajino Department of Mathematics, Graduate School of Science, Kobe University
Rokkodai-cho 1-1, Nada-ku, Kobe 657-8501, Japan Research Institute for Mathematical Sciences, Kyoto University
Kitashirakawa-Oiwake-cho, Sakyo-ku, Kyoto 606-8502, Japan [email protected]

Abstract.

This article surveys the analytic aspects of the author’s recent studies on the construction and analysis of a “geometrically canonical” Laplacian on circle packing fractals invariant with respect to certain Kleinian groups (i.e., discrete groups of Möbius transformations on the Riemann sphere $\widehat{\mathbb{C}}=\mathbb{C}\cup\{\infty\}$ ), including the classical Apollonian gasket and some round Sierpiński carpets. The main result on Weyl’s asymptotics for its eigenvalues is of the same form as that by Oh and Shah [Invent. Math. 187 (2012), 1–35, Theorem 1.4] on the asymptotic distribution of the circles in a very large class of such fractals.

Key words and phrases:

Apollonian gasket, Kleinian groups, round Sierpiński carpets, Dirichlet forms, Laplacian, Weyl’s eigenvalue asymptotics

2010 Mathematics Subject Classification:

Primary 28A80, 35P20, 53C23; Secondary 31C25, 37B10, 60J35

1. Introduction

This article, which is a considerable expansion of [12], concerns the author’s recent studies in [11, 14, 15, 16] on Weyl’s eigenvalue asymptotics for a “geometrically canonical” Laplacian defined by the author on circle packing fractals which are invariant with respect to certain Kleinian groups (i.e., discrete groups of Möbius transformations on $\widehat{\mathbb{C}}:=\mathbb{C}\cup\{\infty\}$ ), including the classical Apollonian gasket (Figure 1) and some round Sierpiński carpets (Figure 5). Here we focus on sketching the construction of the Laplacian, the proof of its uniqueness and basic properties, and the analytic aspects of the proof of the eigenvalue asymptotics; the reader is referred to [13] for a survey of the ergodic-theoretic aspects of the proof of the eigenvalue asymptotics.

This article is organized as follows. First in §2 we introduce the Apollonian gasket $K(\mathscr{D})$ and recall its basic geometric properties. In §3, after a brief summary of how the Laplacian on $K(\mathscr{D})$ was discovered by Teplyaev in [34], we give its definition and sketch the proof of the result in [14] that it is the infinitesimal generator of the unique strongly local, regular symmetric Dirichlet form over $K(\mathscr{D})$ with respect to which the inclusion map $K(\mathscr{D})\hookrightarrow\mathbb{C}$ is harmonic on the complement of the three outmost vertices. In §4, we state the principal result in [14] that the Laplacian on $K(\mathscr{D})$ satisfies Weyl’s eigenvalue asymptotics of the same form as the asymptotic distribution of the circles in $K(\mathscr{D})$ by Oh and Shah in [30, Corollary 1.8], and sketch the proof of certain estimates on the eigenvalues required to conclude Weyl’s asymptotics by applying the ergodic-theoretic result explained in [13]. Finally, in §5 we present a partial extension of these results to the case of round Sierpiński carpets which are invariant with respect to certain concrete Kleinian groups.

Notation.

We use the following notation throughout this article.

(0)

The symbols $\subset$ and $\supset$ for set inclusion allow the case of the equality.
(1)

$\mathbb{N}:=\{n\in\mathbb{Z}\mid n>0\}$ , i.e., $0\not\in\mathbb{N}$ .
(2)

$\widehat{\mathbb{C}}:=\mathbb{C}\cup\{\infty\}$ denotes the Riemann sphere.
(3)

$i:=\sqrt{-1}$ denotes the imaginary unit. The real and imaginary parts of $z\in\mathbb{C}$ are denoted by $\mathop{\mathrm{Re}}\nolimits z$ and $\mathop{\mathrm{Im}}\nolimits z$ , respectively.
(4)

The cardinality (number of elements) of a set $A$ is denoted by $\#A$ .
(5)

Let $E$ be a non-empty set. We define $\mathrm{id}_{E}:E\to E$ by $\mathrm{id}_{E}(x):=x$ . For $x\in E$ , we define $\mathbf{1}_{x}=\mathbf{1}_{x}^{E}\in\mathbb{R}^{E}$ by $\mathbf{1}_{x}(y):=\mathbf{1}_{x}^{E}(y):=\bigl{\{}\begin{smallmatrix}1&\textrm{if $y=x$,}\\ 0&\textrm{if $y\not=x$.}\end{smallmatrix}$ For $u:E\to[-\infty,+\infty]$ we set $\|u\|_{\sup}:=\|u\|_{\sup,E}:=\sup_{x\in E}|u(x)|$ .
(6)

Let $E$ be a topological space. The Borel $\sigma$ -field of $E$ is denoted by $\mathscr{B}(E)$ . For $A\subset E$ , its interior, closure and boundary in $E$ are denoted by $\mathop{\mathrm{int}}\nolimits_{E}A$ , $\overline{A}^{E}$ and $\partial_{E}A$ , respectively, and when $E=\mathbb{C}$ they are simply denoted by $\mathop{\mathrm{int}}\nolimits A$ , $\overline{A}$ and $\partial A$ , respectively. We set $\mathcal{C}(E):=\{u\mid\textrm{$u:E\to\mathbb{R}$, $u$ is continuous}\}$ , $\mathop{\mathrm{supp}}\nolimits_{E}[u]:=\overline{u^{-1}(\mathbb{R}\setminus\{0\})}^{E}$ for $u\in\mathcal{C}(E)$ , and $\mathcal{C}_{\mathrm{c}}(E):=\{u\in\mathcal{C}(E)\mid\textrm{$\mathop{\mathrm{supp}}\nolimits_{E}[u]$ is compact}\}$ .
(7)

Let $n\in\mathbb{N}$ . The Lebesgue measure on $(\mathbb{R}^{n},\mathscr{B}(\mathbb{R}^{n}))$ is denoted by $\mathop{\mathrm{vol}}\nolimits_{n}$ . The Euclidean inner product and norm on $\mathbb{R}^{n}$ are denoted by $\langle\cdot,\cdot\rangle$ and $|\cdot|$ , respectively. For $A\subset\mathbb{R}^{n}$ and $f:A\to\mathbb{C}$ we set $\mathop{\mathbf{Lip}}\nolimits_{A}f:=\sup_{x,y\in A,\,x\not=y}\frac{|f(x)-f(y)|}{|x-y|}$ ( $\sup\emptyset:=0$ ). For a non-empty open subset $U$ of $\mathbb{R}^{n}$ and $u:U\to\mathbb{R}$ with $\mathop{\mathbf{Lip}}\nolimits_{U}u<+\infty$ , the first-order partial derivatives of $u$ , which exist $\mathop{\mathrm{vol}}\nolimits_{n}$ -a.e. on $U$ , are denoted by $\partial_{1}u,\ldots,\partial_{n}u$ , and we set $\nabla u:=(\partial_{1}u,\ldots,\partial_{n}u)$ .

2. The Apollonian gasket and its fractal geometry

In this section, we introduce the Apollonian gasket and state its geometric properties needed for our purpose. The same framework is presented also in [13, Section 2], but we repeat it here for the reader’s convenience. The following definition and proposition form the basis of the construction and further detailed studies of the Apollonian gasket.

Definition 2.1 (tangential disk triple).

(0)

We set $S:=\{1,2,3\}$ .
(1)

Let $D_{1},D_{2},D_{3}\subset\mathbb{C}$ be either three open disks or two open disks and an open half-plane. The triple $\mathscr{D}:=(D_{1},D_{2},D_{3})$ of such sets is called a tangential disk triple if and only if $\#(\overline{D_{j}}\cap\overline{D_{k}})=1$ (i.e., $D_{j}$ and $D_{k}$ are externally tangent) for any $j,k\in S$ with $j\not=k$ . If $\mathscr{D}$ is such a triple consisting of three disks, then the open triangle in $\mathbb{C}$ with vertices the centers of $D_{1},D_{2},D_{3}$ is denoted by $\triangle(\mathscr{D})$ .
(2)

Let $\mathscr{D}=(D_{1},D_{2},D_{3})$ be a tangential disk triple. The open subset $\mathbb{C}\setminus\bigcup_{j\in S}\overline{D_{j}}$ of $\mathbb{C}$ is then easily seen to have a unique bounded connected component, which is denoted by $T(\mathscr{D})$ and called the ideal triangle associated with $\mathscr{D}$ . We also set $\{q_{j}(\mathscr{D})\}:=\overline{D_{k}}\cap\overline{D_{l}}$ for each $(j,k,l)\in\{(1,2,3),(2,3,1),(3,1,2)\}$ and $V_{0}(\mathscr{D}):=\{q_{j}(\mathscr{D})\mid j\in S\}$ .
(3)

A tangential disk triple $\mathscr{D}=(D_{1},D_{2},D_{3})$ is called positively oriented if and only if its associated ideal triangle $T(\mathscr{D})$ is to the left of $\partial T(\mathscr{D})$ when $\partial T(\mathscr{D})$ is oriented so as to have $\{q_{j}(\mathscr{D})\}_{j=1}^{3}$ in this order.

Finally, we define

	$\displaystyle\mathsf{TDT}^{+}$	$\displaystyle:=\{\mathscr{D}\mid\textrm{$\mathscr{D}$ is a positively oriented tangential disk triple}\},$
	$\displaystyle\mathsf{TDT}^{\oplus}$	$\displaystyle:=\{\mathscr{D}\mid\textrm{$\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{+}$, $D_{1},D_{2},D_{3}$ are disks}\}.$

The following proposition is classical and can be shown by some elementary (though lengthy) Euclidean-geometric arguments. We set $\mathop{\mathrm{rad}}\nolimits(D):=r$ and $\mathop{\mathrm{curv}}\nolimits(D):=r^{-1}$ for each open disk $D\subset\mathbb{C}$ of radius $r\in(0,+\infty)$ and $\mathop{\mathrm{curv}}\nolimits(D):=0$ for each open half-plane $D\subset\mathbb{C}$ .

Proposition 2.2.

Let $\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{+}$ , set $(\alpha,\beta,\gamma):=\bigl{(}\mathop{\mathrm{curv}}\nolimits(D_{1}),\mathop{\mathrm{curv}}\nolimits(D_{2}),\mathop{\mathrm{curv}}\nolimits(D_{3})\bigr{)}$ and set $\kappa:=\kappa(\mathscr{D}):=\sqrt{\beta\gamma+\gamma\alpha+\alpha\beta}$ .

(1)

Let $D_{\mathrm{cir}}(\mathscr{D})\subset\mathbb{C}$ denote the circumscribed disk of $T(\mathscr{D})$ , i.e., the unique open disk with $\{q_{1}(\mathscr{D}),q_{2}(\mathscr{D}),q_{3}(\mathscr{D})\}\subset\partial D_{\mathrm{cir}}(\mathscr{D})$ . Then $\overline{T(\mathscr{D})}\setminus\{q_{1}(\mathscr{D}),q_{2}(\mathscr{D}),q_{3}(\mathscr{D})\}\subset D_{\mathrm{cir}}(\mathscr{D})$ , $\partial D_{\mathrm{cir}}(\mathscr{D})$ is orthogonal to $\partial D_{j}$ for any $j\in S$ , and $\mathop{\mathrm{curv}}\nolimits(D_{\mathrm{cir}}(\mathscr{D}))=\kappa$ .
(2)

There exists a unique inscribed disk $D_{\mathrm{in}}(\mathscr{D})$ of $T(\mathscr{D})$ , i.e., a unique open disk $D_{\mathrm{in}}(\mathscr{D})\subset\mathbb{C}$ such that $D_{\mathrm{in}}(\mathscr{D})\subset T(\mathscr{D})$ and $\#(\overline{D_{\mathrm{in}}(\mathscr{D})}\cap\overline{D_{j}})=1$ for any $j\in S$ . Moreover, $\mathop{\mathrm{curv}}\nolimits(D_{\mathrm{in}}(\mathscr{D}))=\alpha+\beta+\gamma+2\kappa$ .

The following notation is standard in studying self-similar sets.

Definition 2.3.

(1)

We set $W_{0}:=\{\emptyset\}$ , where $\emptyset$ is an element called the empty word, $W_{m}:=S^{m}$ for $m\in\mathbb{N}$ and $W_{*}:=\bigcup_{m\in\mathbb{N}\cup\{0\}}W_{m}$ . For $w\in W_{*}$ , the unique $m\in\mathbb{N}\cup\{0\}$ satisfying $w\in W_{m}$ is denoted by $|w|$ and called the length of $w$ .
(2)

Let $w,v\in W_{*}$ , $w=w_{1}\ldots w_{m}$ , $v=v_{1}\ldots v_{n}$ . We define $wv\in W_{*}$ by $wv:=w_{1}\ldots w_{m}v_{1}\ldots v_{n}$ ( $w\emptyset:=w$ , $\emptyset v:=v$ ). We also define $w^{(1)}\ldots w^{(k)}$ for $k\geq 3$ and $w^{(1)},\ldots,w^{(k)}\in W_{*}$ inductively by $w^{(1)}\ldots w^{(k)}:=(w^{(1)}\ldots w^{(k-1)})w^{(k)}$ . For $w\in W_{*}$ and $n\in\mathbb{N}\cup\{0\}$ we set $w^{n}:=w\ldots w\in W_{n|w|}$ . We write $w\leq v$ if and only if $w=v\tau$ for some $\tau\in W_{*}$ , and write $w\not\asymp v$ if and only if neither $w\leq v$ nor $v\leq w$ holds.

Proposition 2.2-(2) enables us to define natural “contraction maps” $\Phi_{w}:\mathsf{TDT}^{+}\to\mathsf{TDT}^{+}$ for each $w\in W_{*}$ , which in turn is used to define the Apollonian gasket $K(\mathscr{D})$ associated with $\mathscr{D}\in\mathsf{TDT}^{+}$ , as follows.

Definition 2.4.

We define maps $\Phi_{1},\Phi_{2},\Phi_{3}:\mathsf{TDT}^{+}\to\mathsf{TDT}^{+}$ by

\begin{cases}\Phi_{1}(\mathscr{D}):=(D_{\mathrm{in}}(\mathscr{D}),D_{2},D_{3}),\\ \Phi_{2}(\mathscr{D}):=(D_{1},D_{\mathrm{in}}(\mathscr{D}),D_{3}),\quad\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{+}.\\ \Phi_{3}(\mathscr{D}):=(D_{1},D_{2},D_{\mathrm{in}}(\mathscr{D})),\end{cases}

(2.1)

We also set $\Phi_{w}:=\Phi_{w_{m}}\circ\cdots\circ\Phi_{w_{1}}$ ( $\Phi_{\emptyset}:=\mathrm{id}_{\mathsf{TDT}^{+}}$ ) and $\mathscr{D}_{w}:=\Phi_{w}(\mathscr{D})$ for $w=w_{1}\ldots w_{m}\in W_{*}$ and $\mathscr{D}\in\mathsf{TDT}^{+}$ .

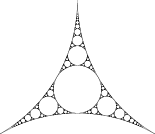
Refer to caption — a Examples without a half-plane

Definition 2.5 (Apollonian gasket).

Let $\mathscr{D}\in\mathsf{TDT}^{+}$ . We define the Apollonian gasket $K(\mathscr{D})$ associated with $\mathscr{D}$ (see Figure 1) by

K(\mathscr{D}):=\overline{T(\mathscr{D})}\setminus\bigcup\nolimits_{w\in W_{*}}D_{\mathrm{in}}(\mathscr{D}_{w})=\bigcap\nolimits_{m\in\mathbb{N}}\bigcup\nolimits_{w\in W_{m}}\overline{T(\mathscr{D}_{w})}.

(2.2)

The curvatures of the disks involved in (2.2) admit the following simple expression.

Definition 2.6.

We define $4\times 4$ real matrices $M_{1},M_{2},M_{3}$ by

M_{1}:=\begin{pmatrix}1&0&0&0\\ 1&1&0&1\\ 1&0&1&1\\ 2&0&0&1\end{pmatrix},\mspace{10.0mu}M_{2}:=\begin{pmatrix}1&1&0&1\\ 0&1&0&0\\ 0&1&1&1\\ 0&2&0&1\end{pmatrix},\mspace{10.0mu}M_{3}:=\begin{pmatrix}1&0&1&1\\ 0&1&1&1\\ 0&0&1&0\\ 0&0&2&1\end{pmatrix}

(2.3)

and set $M_{w}:=M_{w_{1}}\cdots M_{w_{m}}$ for $w=w_{1}\ldots w_{m}\in W_{*}$ ( $M_{\emptyset}:=\mathrm{id}_{4\times 4}$ ). Note that then for any $n\in\mathbb{N}\cup\{0\}$ we easily obtain

M_{1^{n}}=\begin{pmatrix}1&0&0&0\\ n^{2}&1&0&n\\ n^{2}&0&1&n\\ 2n&0&0&1\end{pmatrix},\mspace{10.0mu}M_{2^{n}}=\begin{pmatrix}1&n^{2}&0&n\\ 0&1&0&0\\ 0&n^{2}&1&n\\ 0&2n&0&1\end{pmatrix},\mspace{10.0mu}M_{3^{n}}=\begin{pmatrix}1&0&n^{2}&n\\ 0&1&n^{2}&n\\ 0&0&1&0\\ 0&0&2n&1\end{pmatrix}.

(2.4)

Proposition 2.7.

Let $\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{+}$ , let $\alpha,\beta,\gamma,\kappa$ be as in Proposition 2.2, let $w\in W_{*}$ and $(D_{w,1},D_{w,2},D_{w,3}):=\mathscr{D}_{w}$ . Then

\bigl{(}\mathop{\mathrm{curv}}\nolimits(D_{w,1}),\mathop{\mathrm{curv}}\nolimits(D_{w,2}),\mathop{\mathrm{curv}}\nolimits(D_{w,3}),\kappa(\mathscr{D}_{w})\bigr{)}=(\alpha,\beta,\gamma,\kappa)M_{w}.

(2.5)

Proof.

This follows by an induction in $|w|$ using Proposition 2.2-(2) and Definition 2.4. ∎

We next collect basic facts regarding the Hausdorff dimension and measure of $K(\mathscr{D})$ . For each $s\in(0,+\infty)$ let $\mathscr{H}^{s}:2^{\mathbb{C}}\to[0,+\infty]$ denote the $s$ -dimensional Hausdorff (outer) measure on $\mathbb{C}$ with respect to the Euclidean metric, and for each $A\subset\mathbb{C}$ let $\dim_{\mathrm{H}}A$ denote its Hausdorff dimension; see, e.g., [25, Chapters 4–7] for details. As is well known, it easily follows from the definition of $\mathscr{H}^{s}$ that the image $f(A)$ of $A\subset\mathbb{C}$ by $f:A\to\mathbb{C}$ with $\mathop{\mathbf{Lip}}\nolimits_{A}f<+\infty$ satisfies $\mathscr{H}^{s}(f(A))\leq(\mathop{\mathbf{Lip}}\nolimits_{A}f)^{s}\mathscr{H}^{s}(A)$ for any $s\in(0,+\infty)$ and hence in particular $\dim_{\mathrm{H}}f(A)\leq\dim_{\mathrm{H}}A$ . On the basis of this observation, we easily get the following lemma.

Lemma 2.8.

Let $\mathscr{D},\mathscr{D}^{\prime}\in\mathsf{TDT}^{+}$ . Then there exists $c\in(0,+\infty)$ such that $\mathscr{H}^{s}(K(\mathscr{D}))\leq c^{s}\mathscr{H}^{s}(K(\mathscr{D}^{\prime}))$ for any $s\in(0,+\infty)$ . In particular, $\dim_{\mathrm{H}}K(\mathscr{D})=\dim_{\mathrm{H}}K(\mathscr{D}^{\prime})$ .

Proof.

Let $f_{\mathscr{D}^{\prime},\mathscr{D}}$ denote the unique orientation-preserving Möbius transformation on $\widehat{\mathbb{C}}$ such that $f_{\mathscr{D}^{\prime},\mathscr{D}}(q_{j}(\mathscr{D}^{\prime}))=q_{j}(\mathscr{D})$ for any $j\in S$ . Then $f_{\mathscr{D}^{\prime},\mathscr{D}}(K(\mathscr{D}^{\prime}))=K(\mathscr{D})$ , since a Möbius transformation on $\widehat{\mathbb{C}}$ maps any open disk in $\widehat{\mathbb{C}}$ onto another. Now the assertion follows from the observation in the last paragraph and $\mathop{\mathbf{Lip}}\nolimits_{\overline{D_{\mathrm{cir}}(\mathscr{D}^{\prime})}}f_{\mathscr{D}^{\prime},\mathscr{D}}<+\infty$ . ∎

Definition 2.9.

Noting Lemma 2.8, we define

d_{\mathsf{AG}}:=\dim_{\mathrm{H}}K(\mathscr{D}),\qquad\textrm{where $\mathscr{D}\in\mathsf{TDT}^{+}$ is arbitrary.}

(2.6)

Theorem 2.10 (Boyd [2]; see also [7, 26, 27]).

1.300197<d_{\mathsf{AG}}<1.314534.

(2.7)

Moreover, for the $d_{\mathsf{AG}}$ -dimensional Hausdorff measure $\mathscr{H}^{d_{\mathsf{AG}}}(K(\mathscr{D}))$ of $K(\mathscr{D})$ we have the following theorem, which was proved first by Sullivan [33] through considerations on the isometric action of Möbius transformations on the three-dimensional hyperbolic space, and later by Mauldin and Urbański [26] through purely two-dimensional arguments.

Theorem 2.11 ([33, Theorem 2], [26, Theorem 2.6]).

0<\mathscr{H}^{d_{\mathsf{AG}}}(K(\mathscr{D}))<+\infty\qquad\textrm{for any $\mathscr{D}\in\mathsf{TDT}^{+}$.}

(2.8)

Remark 2.12.

The self-conformality of $K(\mathscr{D})$ is required most crucially in the proof of Theorem 2.11, and is heavily used further to obtain certain equicontinuity properties of $\{\mathscr{H}^{d_{\mathsf{AG}}}(K(\mathscr{D}_{w}))\}_{w\in W_{*}}$ as a family of functions of $\bigl{(}\mathop{\mathrm{curv}}\nolimits(D_{1}),\mathop{\mathrm{curv}}\nolimits(D_{2}),\mathop{\mathrm{curv}}\nolimits(D_{3})\bigr{)}$ , where $(D_{1},D_{2},D_{3}):=\mathscr{D}$ . This equicontinuity is the key to verifying the ergodic-theoretic assumptions of Kesten’s renewal theorem [19, Theorem 2], which is then applied to conclude Theorem 4.4 below.

3. The canonical Dirichlet form on the Apollonian gasket

In this section, we introduce the canonical Dirichlet form on the Apollonian gasket $K(\mathscr{D})$ , whose infinitesimal generator is our Laplacian on $K(\mathscr{D})$ , and state its properties established by the author in [14]; see [6, 4] for the basics of the theory of regular symmetric Dirichlet forms.

Before giving its actual definition, we briefly summarize how it has been discovered. The initial idea for its construction was suggested by the theory of analysis on the harmonic Sierpiński gasket $K_{\mathcal{H}}$ (Figure 2, right) due to Kigami [20, 22]. This is a compact subset of $\mathbb{C}$ defined as the image of a harmonic map $\Phi:K\to\mathbb{C}$ from the Sierpiński gasket $K$ (Figure 2, left) to $\mathbb{C}$ . More precisely, let $V_{0}=\{q_{1},q_{2},q_{3}\}$ be the set of the three outmost vertices of $K$ , let $(\mathcal{E},\mathcal{F})$ be the (self-similar) standard Dirichlet form on $K$ (so that $\mathcal{F}$ is known to be a dense subalgebra of $(\mathcal{C}(K),\|\cdot\|_{\sup})$ ), and let $h^{K}_{1},h^{K}_{2}\in\mathcal{F}$ be $\mathcal{E}$ -harmonic on $K\setminus V_{0}$ and satisfy $\mathcal{E}(h^{K}_{j},h^{K}_{k})=\delta_{jk}$ for any $j,k\in\{1,2\}$ (see [10, Sections 2 and 3] and the references therein for details). Then we can define a continuous map $\Phi:K\to\mathbb{C}$ by $\Phi(x):=\bigl{(}h^{K}_{1}(x),h^{K}_{2}(x)\bigr{)}$ , and its image $K_{\mathcal{H}}:=\Phi(K)$ is called the harmonic Sierpiński gasket.

In fact, Kigami has proved in [20, Theorem 3.6] that $\Phi:K\to K_{\mathcal{H}}$ is injective and hence a homeomorphism, and further in [20, Theorem 4.1] that a one-dimensional, measure-theoretic “Riemannian structure” can be defined on $K$ through the embedding $\Phi$ and the $\mathcal{E}$ -energy measure $\mu$ ¹¹1 $\mu$ was first introduced in [24] and is called the Kusuoka measure on $K$ . of $\Phi$ , which plays the role of the “Riemannian volume measure” and is given by

\mu:=\mu_{\langle h^{K}_{1}\rangle}+\mu_{\langle h^{K}_{2}\rangle}=\textrm{``}|\nabla\Phi|^{2}\,d\mathop{\mathrm{vol}}\nolimits\textrm{''};

(3.1)

here $\mu_{\langle u\rangle}$ denotes the $\mathcal{E}$ -energy measure of $u\in\mathcal{F}$ playing the role of “ $|\nabla u|^{2}\,d\mathop{\mathrm{vol}}\nolimits$ ” and defined as the unique Borel measure on $K$ such that

\int_{K}f\,d\mu_{\langle u\rangle}=\mathcal{E}(fu,u)-\frac{1}{2}\mathcal{E}(f,u^{2})\qquad\textrm{for any $f\in\mathcal{F}$.}

(3.2)

Kigami has also proved in [22, Theorem 6.3] that the heat kernel of $(K,\mu,\mathcal{E},\mathcal{F})$ satisfies the two-sided Gaussian estimate of the same form as for Riemannian manifolds, and further detailed studies of $(K,\mu,\mathcal{E},\mathcal{F})$ have been done in [9, 23, 10]; see [10] and the references therein for details.

As observed from Figures 1 and 2, the overall geometric structure of the Apollonian gasket $K(\mathscr{D})$ resembles that of the harmonic Sierpiński gasket $K_{\mathcal{H}}$ , and then it is natural to expect that the above-mentioned framework of the measurable Riemannian structure on $K$ induced by the embedding $\Phi:K\to K_{\mathcal{H}}$ can be adapted to the setting of $K(\mathscr{D})$ for $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ to construct a “geometrically canonical” Dirichlet form on $K(\mathscr{D})$ . Namely, it is expected that there exists a non-zero strongly local regular symmetric Dirichlet form $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ over $K(\mathscr{D})$ with respect to which the coordinate functions $\mathop{\mathrm{Re}}\nolimits(\cdot)|_{K(\mathscr{D})},\mathop{\mathrm{Im}}\nolimits(\cdot)|_{K(\mathscr{D})}$ are harmonic on $K(\mathscr{D})\setminus V_{0}(\mathscr{D})$ . The possibility of such a construction was first noted by Teplyaev in [34, Theorem 5.17], and in [14] the author has completed the construction of $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ and further proved its uniqueness and concrete identification, summarized as follows. We start with some definitions.

Definition 3.1.

(1)

A subset $C$ of $\mathbb{C}$ is called a circular arc if and only if $C=\{z_{0}+re^{i\theta}\mid\theta\in[\alpha,\beta]\}$ for some $z_{0}\in\mathbb{C}$ , $r\in(0,+\infty)$ and $\alpha,\beta\in\mathbb{R}$ with $\alpha<\beta$ . In this case we set $\mathop{\mathrm{cent}}\nolimits(C):=z_{0}$ , $\mathop{\mathrm{rad}}\nolimits(C):=r$ and $D_{C}:=\mathop{\mathrm{int}}\nolimits\{(1-t)\mathop{\mathrm{cent}}\nolimits(C)+tz\mid\textrm{$z\in C$, $t\in[0,1]$}\}$ .
(2)

For a circular arc $C$ , the length measure on $(C,\mathscr{B}(C))$ is denoted by $\mathscr{H}^{1}_{C}$ , the gradient vector along $C$ at $x\in C$ of a function $u:C\to\mathbb{R}$ is denoted by $\nabla_{C}u(x)$ provided $u$ is differentiable at $x$ , and we set $W^{1,2}(C):=\{u\in\mathbb{R}^{C}\mid\textrm{$u$ is a.c.\ on $C$, $|\nabla_{C}u|\in L^{2}(C,\mathscr{H}^{1}_{C})$}\}$ , where “a.c.” is an abbreviation of “absolutely continuous”.
(3)

We define $h_{1},h_{2}:\mathbb{C}\to\mathbb{R}$ by $h_{1}(z):=\mathop{\mathrm{Re}}\nolimits z$ and $h_{2}(z):=\mathop{\mathrm{Im}}\nolimits z$ .

Definition 3.2.

Let $\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{\oplus}$ . We define

\mathscr{A}_{\mathscr{D}}:=\{\overline{T(\mathscr{D})}\cap\partial D_{j}\mid j\in S\}\cup\{\partial D_{\mathrm{in}}(\mathscr{D}_{w})\mid w\in W_{*}\}

(3.3)

and set $K^{0}(\mathscr{D}):=\bigcup_{C\in\mathscr{A}_{\mathscr{D}}}C$ , so that each $C\in\mathscr{A}_{\mathscr{D}}$ is a circular arc, $\bigcup_{C\in\mathscr{A}_{\mathscr{D}}}D_{C}=\triangle(\mathscr{D})\setminus K(\mathscr{D})$ , $\bigcup_{C,A\in\mathscr{A}_{\mathscr{D}},\,C\not=A}(C\cap A)=\bigcup_{w\in W_{*}}V_{0}(\mathscr{D}_{w})$ , and an induction in $|w|$ easily shows that for any $w\in W_{*}$ ,

\mathscr{A}_{\mathscr{D}_{w}}=\{C\cap K(\mathscr{D}_{w})\mid C\in\mathscr{A}_{\mathscr{D}}\}\setminus\{\emptyset\}.

(3.4)

The canonical Dirichlet form $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ on $K(\mathscr{D})$ and the associated “Riemannian volume measure” similar to (3.1) turn out to be expressed explicitly in terms of the circle packing structure of $K(\mathscr{D})$ , as follows.

Definition 3.3 (cf. [14, Theorems 5.11 and 5.13]).

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ .

(1)

We define a Borel measure $\mu^{\mathscr{D}}$ on $K(\mathscr{D})$ by

$\mu^{\mathscr{D}}:=\sum\nolimits_{C\in\mathscr{A}_{\mathscr{D}}}\mathop{\mathrm{rad}}\nolimits(C)\mathscr{H}^{1}_{C}(\cdot\cap C),$ (3.5)

so that for any $w\in W_{*}$ we have $\mu^{\mathscr{D}}(K(\mathscr{D}_{w}))=2\mathop{\mathrm{vol}}\nolimits_{2}(\triangle(\mathscr{D}_{w}))$ by (3.4), $\bigcup_{C\in\mathscr{A}_{\mathscr{D}_{w}}}D_{C}=\triangle(\mathscr{D}_{w})\setminus K(\mathscr{D}_{w})$ and $\mathop{\mathrm{vol}}\nolimits_{2}(K(\mathscr{D}_{w}))=0$ .

(2)

For each $u\in\mathbb{R}^{K^{0}(\mathscr{D})}$ with $u|_{C}$ a.c. on $C$ for any $C\in\mathscr{A}_{\mathscr{D}}$ , we define a $\mu^{\mathscr{D}}$ -a.e. defined, $\mathbb{R}^{2}$ -valued Borel measurable map $\nabla_{\mathscr{D}}u$ by $(\nabla_{\mathscr{D}}u)|_{C}:=\nabla_{C}(u|_{C})$ for each $C\in\mathscr{A}_{\mathscr{D}}$ , so that $|\nabla_{\mathscr{D}}u|^{2}\,d\mu^{\mathscr{D}}=\sum_{C\in\mathscr{A}_{\mathscr{D}}}|\nabla_{C}(u|_{C})|^{2}\mathop{\mathrm{rad}}\nolimits(C)\,d\mathscr{H}^{1}_{C}$ . Then we further define

\mathcal{F}_{\mathscr{D}}:=W^{1,2}_{\mathscr{D}}:=\biggl{\{}u\in\mathbb{R}^{K^{0}(\mathscr{D})}\biggm{|}\begin{minipage}{138.9pt} $u|_{C}\in W^{1,2}(C)$ for any $C\in\mathscr{A}_{\mathscr{D}}$, $|\nabla_{\mathscr{D}}u|\in L^{2}(K(\mathscr{D}),\mu^{\mathscr{D}})$ \end{minipage}\biggr{\}}

(3.6)

and set $\mathcal{C}_{\mathscr{D}}:=\{u\in\mathcal{C}(K(\mathscr{D}))\mid u|_{K^{0}(\mathscr{D})}\in\mathcal{F}_{\mathscr{D}}\}$ and $\mathcal{C}^{\mathrm{lip}}_{\mathscr{D}}:=\{u\in\mathcal{C}(K(\mathscr{D}))\mid\mathop{\mathbf{Lip}}\nolimits_{K(\mathscr{D})}u<+\infty\}$ , which are considered as linear subspaces of $\mathcal{F}_{\mathscr{D}}$ through the linear injection $\mathcal{C}(K(\mathscr{D}))\ni u\mapsto u|_{K^{0}(\mathscr{D})}\in\mathbb{R}^{K^{0}(\mathscr{D})}$ . Noting that $\langle\nabla_{\mathscr{D}}u,\nabla_{\mathscr{D}}v\rangle\in L^{1}(K(\mathscr{D}),\mu^{\mathscr{D}})$ for any $u,v\in\mathcal{F}_{\mathscr{D}}$ , we also define a bilinear form $\mathcal{E}^{\mathscr{D}}:\mathcal{F}_{\mathscr{D}}\times\mathcal{F}_{\mathscr{D}}\to\mathbb{R}$ on $\mathcal{F}_{\mathscr{D}}$ by

\begin{split}\mathcal{E}^{\mathscr{D}}(u,v):=&\int_{K(\mathscr{D})}\langle\nabla_{\mathscr{D}}u,\nabla_{\mathscr{D}}v\rangle\,d\mu^{\mathscr{D}}\\ =&\sum\nolimits_{C\in\mathscr{A}_{\mathscr{D}}}\int_{C}\langle\nabla_{C}(u|_{C}),\nabla_{C}(v|_{C})\rangle\mathop{\mathrm{rad}}\nolimits(C)\,d\mathscr{H}^{1}_{C}.\end{split}

(3.7)

In particular, setting $d\mu^{\mathscr{D}}_{\langle u\rangle}:=|\nabla_{\mathscr{D}}u|^{2}\,d\mu^{\mathscr{D}}$ for each $u\in\mathcal{F}_{\mathscr{D}}$ , we have $\mu^{\mathscr{D}}=\mu^{\mathscr{D}}_{\langle h_{1}|_{K(\mathscr{D})}\rangle}+\mu^{\mathscr{D}}_{\langle h_{2}|_{K(\mathscr{D})}\rangle}$ as the counterpart of (3.1) for $K(\mathscr{D})$ .

Theorem 3.4 ([14, Theorem 5.18]).

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ and set $\mathcal{F}_{\mathscr{D},0}^{0}:=\{u\in\mathcal{F}_{\mathscr{D}}\mid u|_{V_{0}(\mathscr{D})}=0\}$ . Then $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ is an irreducible, strongly local, regular symmetric Dirichlet form on $L^{2}(K(\mathscr{D}),\mu^{\mathscr{D}})$ with a core $\mathcal{C}^{\mathrm{lip}}_{\mathscr{D}}$ , and

\int_{K(\mathscr{D})}u^{2}\,d\mu^{\mathscr{D}}\leq 40\kappa(\mathscr{D})^{-2}\mathcal{E}^{\mathscr{D}}(u,u)\qquad\textrm{for any $u\in\mathcal{F}_{\mathscr{D},0}^{0}$.}

(3.8)

Moreover, the inclusion map $\mathcal{F}_{\mathscr{D}}\hookrightarrow L^{2}(K(\mathscr{D}),\mu^{\mathscr{D}})$ is a compact linear operator under the norm $\|u\|_{\mathcal{F}_{\mathscr{D}}}:=(\mathcal{E}^{\mathscr{D}}(u,u)+\int_{K(\mathscr{D})}u^{2}\,d\mu^{\mathscr{D}})^{1/2}$ on $\mathcal{F}_{\mathscr{D}}$ .

Theorem 3.5 ([14, Theorem 5.23]).

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ , let $\mu^{\prime}$ be a finite Borel measure on $K(\mathscr{D})$ with $\mu^{\prime}(U)>0$ for any non-empty open subset $U$ of $K(\mathscr{D})$ , and let $(\mathcal{E}^{\prime},\mathcal{F}^{\prime})$ be a strongly local, regular symmetric Dirichlet form on $L^{2}(K(\mathscr{D}),\mu^{\prime})$ with $\mathcal{E}^{\prime}(u,u)>0$ for some $u\in\mathcal{F}^{\prime}$ . Then the following two conditions are equivalent:

(1)

Any $h\in\{h_{1}|_{K(\mathscr{D})},h_{2}|_{K(\mathscr{D})}\}$ is in $\mathcal{F}^{\prime}$ and is $\mathcal{E}^{\prime}$ -harmonic on $K(\mathscr{D})\setminus V_{0}(\mathscr{D})$ , i.e., $\mathcal{E}^{\prime}(h,v)=0$ for any $v\in\mathcal{F}^{\prime}\cap\mathcal{C}(K(\mathscr{D}))$ with $v|_{V_{0}(\mathscr{D})}=0$ .
(2)

$\mathcal{F}^{\prime}\cap\mathcal{C}(K(\mathscr{D}))=\mathcal{C}_{\mathscr{D}}$ and $\mathcal{E}^{\prime}|_{\mathcal{C}_{\mathscr{D}}\times\mathcal{C}_{\mathscr{D}}}=c\mathcal{E}^{\mathscr{D}}|_{\mathcal{C}_{\mathscr{D}}\times\mathcal{C}_{\mathscr{D}}}$ for some $c\in\mathbb{R}$ .

Remark 3.6.

In contrast to the case of $K(\mathscr{D})$ described in Definition 3.3, Theorems 3.4 and 3.5, the standard Dirichlet form $(\mathcal{E},\mathcal{F})$ on the Sierpiński gasket $K$ satisfies $\mu_{\langle u\rangle}(K^{0})=0$ for any $u\in\mathcal{F}$ by [10, Lemma 8.26] and [8, Lemma 5.7], where $K^{0}$ denotes the union of the boundaries of the equilateral triangles constituting $K$ . In particular, $(\mathcal{E},\mathcal{F})$ cannot be expressed as the sum of any weighted one-dimensional Dirichlet forms on $\Phi(K^{0})\subset K_{\mathcal{H}}$ similar to (3.7). The author does not have a good explanation of the reason for this difference, and it would be very nice to give one. A naive guess could be that some sufficient smoothness of the relevant curves might be required for the validity of an expression like (3.7) of a non-zero strongly local regular symmetric Dirichlet form satisfying the analog of Theorem 3.5-(1); indeed, the curves constituting $\Phi(K^{0})$ are $\mathcal{C}^{1}$ but not $\mathcal{C}^{2}$ by [22, Theorem 5.4-(2)], whereas the corresponding curves $C\in\mathscr{A}_{\mathscr{D}}$ in $K(\mathscr{D})$ are circular arcs and therefore real analytic. While this guess itself might well be correct, it would be still unclear how smooth the relevant curves should need to be.

The rest of this section is devoted to a brief sketch of the proof of Theorems 3.4 and 3.5, which is rather long and occupies the whole of [14, Sections 4 and 5]. It starts with identifying what the trace $\mathcal{E}^{\mathscr{D}}|_{V_{m}(\mathscr{D})}$ ,

\mathcal{E}^{\mathscr{D}}|_{V_{m}(\mathscr{D})}(u,u):=\inf_{v\in\mathcal{F}_{\mathscr{D}},\,v|_{V_{m}(\mathscr{D})}=u}\mathcal{E}^{\mathscr{D}}(v,v),\quad u\in\mathbb{R}^{V_{m}(\mathscr{D})},

(3.9)

of $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ to $V_{m}(\mathscr{D}):=\bigcup_{w\in W_{m}}V_{0}(\mathscr{D}_{w})$ should be for any $m\in\mathbb{N}\cup\{0\}$ . In view of the desired properties of $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ in Theorem 3.5, the forms $\{\mathcal{E}^{\mathscr{D}}|_{V_{m}(\mathscr{D})}\}_{m\in\mathbb{N}\cup\{0\}}$ should have the properties in the following theorem.

Theorem 3.7 ([34, Theorem 5.17]).

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ . Then there exists $\{\mathcal{E}^{\mathscr{D}}_{m}\}_{m\in\mathbb{N}\cup\{0\}}$ such that the following hold for any $m\in\mathbb{N}\cup\{0\}$ :

(1)

$\mathcal{E}^{\mathscr{D}}_{m}$ is a symmetric Dirichlet form on $\ell^{2}(V_{m}(\mathscr{D}))$ . $\mathcal{E}^{\mathscr{D}}_{m}(\mathbf{1}_{x},\mathbf{1}_{y})=0=\mathcal{E}^{\mathscr{D}}_{m}(\mathbf{1}_{x},\mathbf{1})$ for any $x,y\in V_{m}(\mathscr{D})$ with $\{\tau\in W_{m}\mid x,y\in V_{0}(\mathscr{D}_{\tau})\}=\emptyset$ .
(2)

Both $h_{1}|_{V_{m}(\mathscr{D})}$ and $h_{2}|_{V_{m}(\mathscr{D})}$ are $\mathcal{E}^{\mathscr{D}}_{m}$ -harmonic on $V_{m}(\mathscr{D})\setminus V_{0}(\mathscr{D})$ .
(3)

$\mathcal{E}^{\mathscr{D}}_{m}(u,u)=\min_{v\in\mathbb{R}^{V_{m+1}(\mathscr{D})},\,v|_{V_{m}(\mathscr{D})}=u}\mathcal{E}^{\mathscr{D}}_{m+1}(v,v)$ for any $u\in\mathbb{R}^{V_{m}(\mathscr{D})}$ .
(4)

$\mathcal{E}^{\mathscr{D}}_{m}(h_{1}|_{V_{m}(\mathscr{D})},h_{1}|_{V_{m}(\mathscr{D})})+\mathcal{E}^{\mathscr{D}}_{m}(h_{2}|_{V_{m}(\mathscr{D})},h_{2}|_{V_{m}(\mathscr{D})})=2\mathop{\mathrm{vol}}\nolimits_{2}(\triangle(\mathscr{D}))$ .

Teplyaev’s proof of Theorem 3.7 in [34] is purely Euclidean-geometric and provides no further information on $\{\mathcal{E}^{\mathscr{D}}_{m}\}_{m\in\mathbb{N}\cup\{0\}}$ . The author has identified it as follows, by applying a refinement of [28, Corollary 4.2].

Theorem 3.8 ([14, Theorem 4.18]).

For each $\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{\oplus}$ , a sequence $\{\mathcal{E}^{\mathscr{D}}_{m}\}_{m\in\mathbb{N}\cup\{0\}}$ as in Theorem 3.7 is unique, and

\mathcal{E}^{\mathscr{D}}_{0}(u,u)=\sum_{j\in S}\frac{\kappa(\mathscr{D})^{2}+\mathop{\mathrm{curv}}\nolimits(D_{j})^{2}}{2\kappa(\mathscr{D})\mathop{\mathrm{curv}}\nolimits(D_{j})}\bigl{(}u(q_{j+1}(\mathscr{D}))-u(q_{j+2}(\mathscr{D}))\bigr{)}^{2}

(3.10)

for any $u\in\mathbb{R}^{V_{0}(\mathscr{D})}$ , where $q_{j+3}(\mathscr{D}):=q_{j}(\mathscr{D})$ for $j\in S$ . Moreover, for any $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ , any $m\in\mathbb{N}\cup\{0\}$ and any $u\in\mathbb{R}^{V_{m}(\mathscr{D})}$ ,

\mathcal{E}^{\mathscr{D}}_{m}(u,u)=\sum\nolimits_{w\in W_{m}}\mathcal{E}^{\mathscr{D}_{w}}_{0}(u|_{V_{0}(\mathscr{D}_{w})},u|_{V_{0}(\mathscr{D}_{w})}).

(3.11)

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ . Theorem 3.7-(3) allows us to apply to $\{\mathcal{E}^{\mathscr{D}}_{m}\}_{m\in\mathbb{N}\cup\{0\}}$ the general theory from [21, Chapter 2] of constructing a Dirichlet form by taking the “inductive limit” of Dirichlet forms on finite sets. Namely, setting $V_{*}(\mathscr{D}):=\bigcup_{m\in\mathbb{N}\cup\{0\}}V_{m}(\mathscr{D})$ , we can define a linear subspace $\mathcal{F}^{\prime}_{\mathscr{D}}$ of $\mathbb{R}^{V_{*}(\mathscr{D})}$ and a bilinear form $\mathcal{E}^{\prime\mathscr{D}}:\mathcal{F}^{\prime}_{\mathscr{D}}\times\mathcal{F}^{\prime}_{\mathscr{D}}\to\mathbb{R}$ on $\mathcal{F}^{\prime}_{\mathscr{D}}$ by

	$\displaystyle\mathcal{F}^{\prime}_{\mathscr{D}}:=\bigl{\{}u\in\mathbb{R}^{V_{*}(\mathscr{D})}\bigm{\|}\lim\nolimits_{m\to\infty}\mathcal{E}^{\mathscr{D}}_{m}(u\|_{V_{m}(\mathscr{D})},u\|_{V_{m}(\mathscr{D})})<+\infty\bigr{\}},$		(3.12)
	$\displaystyle\mathcal{E}^{\prime\mathscr{D}}(u,v):=\lim\nolimits_{m\to\infty}\mathcal{E}^{\mathscr{D}}_{m}(u\|_{V_{m}(\mathscr{D})},v\|_{V_{m}(\mathscr{D})})\in\mathbb{R},\quad u,v\in\mathcal{F}^{\prime}_{\mathscr{D}}.$		(3.13)

The next step of the proof of Theorems 3.4 and 3.5 is the following identification of $(\mathcal{E}^{\prime\mathscr{D}},\mathcal{F}^{\prime}_{\mathscr{D}})$ as $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ , i.e., as given by (3.6) and (3.7).

Theorem 3.9 ([14, Theorem 5.13]).

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ . Then $\mathcal{F}^{\prime}_{\mathscr{D}}=\{u|_{V_{*}(\mathscr{D})}\mid u\in\mathcal{F}_{\mathscr{D}}\}$ , the mapping $\mathcal{F}_{\mathscr{D}}\ni u\mapsto u|_{V_{*}(\mathscr{D})}\in\mathcal{F}^{\prime}_{\mathscr{D}}$ is a linear isomorphism, and $\mathcal{E}^{\prime\mathscr{D}}(u|_{V_{*}(\mathscr{D})},v|_{V_{*}(\mathscr{D})})=\mathcal{E}^{\mathscr{D}}(u,v)$ for any $u,v\in\mathcal{F}_{\mathscr{D}}$ .

Sketch of the proof.

By Theorem 3.7-(2),(3) and (3.12) we have $h_{1}|_{V_{*}(\mathscr{D})},h_{2}|_{V_{*}(\mathscr{D})}\in\mathcal{F}^{\prime}_{\mathscr{D}}$ , which together with (3.12) implies that $\mathcal{C}^{\prime}_{\mathscr{D}}:=\{u\in\mathcal{C}(K(\mathscr{D}))\mid u|_{V_{*}(\mathscr{D})}\in\mathcal{F}^{\prime}_{\mathscr{D}}\}$ is a dense subalgebra of $(\mathcal{C}(K(\mathscr{D})),\|\mspace{-1.35mu}\cdot\mspace{-1.35mu}\|_{\sup})$ with $h_{1}|_{K(\mathscr{D})},h_{2}|_{K(\mathscr{D})}\in\mathcal{C}^{\mathrm{lip}}_{\mathscr{D}}\subset\mathcal{C}^{\prime}_{\mathscr{D}}$ . Hence at this stage we can already define the $\mathcal{E}^{\prime\mathscr{D}}$ -energy measure $\mu^{\prime\mathscr{D}}_{\langle u\rangle}$ of $u\in\mathcal{C}^{\prime}_{\mathscr{D}}$ by (3.2) with $K(\mathscr{D}),\mathcal{E}^{\prime\mathscr{D}},\mathcal{C}^{\prime}_{\mathscr{D}}$ in place of $K,\mathcal{E},\mathcal{F}$ , and the analog of (3.1) by $\mu^{\prime\mathscr{D}}:=\mu^{\prime\mathscr{D}}_{\langle h_{1}|_{K(\mathscr{D})}\rangle}+\mu^{\prime\mathscr{D}}_{\langle h_{2}|_{K(\mathscr{D})}\rangle}$ . Then it follows from Theorem 3.7-(4) and (3.11) that $\mu^{\prime\mathscr{D}}(K(\mathscr{D}_{w}))=2\mathop{\mathrm{vol}}\nolimits_{2}(\triangle(\mathscr{D}_{w}))=\mu^{\mathscr{D}}(K(\mathscr{D}_{w}))$ for any $w\in W_{*}$ , whence $\mu^{\prime\mathscr{D}}=\mu^{\mathscr{D}}$ .

Now that $\mu^{\prime\mathscr{D}}$ has been identified as $\mu^{\mathscr{D}}$ given by (3.5), it is natural to guess²²2This is how the author first came up with the expressions (3.6) and (3.7). that $\mathcal{F}^{\prime}_{\mathscr{D}}\subset\{u|_{V_{*}(\mathscr{D})}\mid u\in\mathcal{F}_{\mathscr{D}}\}$ and that $\mathcal{E}^{\prime\mathscr{D}}(u|_{V_{*}(\mathscr{D})},u|_{V_{*}(\mathscr{D})})=\mathcal{E}^{\mathscr{D}}(u,u)$ for any $u\in\mathcal{F}_{\mathscr{D}}$ with $u|_{V_{*}(\mathscr{D})}\in\mathcal{F}^{\prime}_{\mathscr{D}}$ . This guess is not difficult to verify, first for any piecewise linear $u\in\mathcal{F}_{\mathscr{D}}$ by direct calculations based on Theorem 3.7-(2), (3.10), (3.11) and (3.13), and then for any $u\in\mathcal{F}_{\mathscr{D}}$ with $u|_{V_{*}(\mathscr{D})}\in\mathcal{F}^{\prime}_{\mathscr{D}}$ by using the canonical approximation of $u$ by piecewise linear functions; here $u\in\mathcal{F}_{\mathscr{D}}$ is called $m$ -piecewise linear, where $m\in\mathbb{N}\cup\{0\}$ , if and only if $u|_{K^{0}(\mathscr{D}_{w})}$ is a linear combination of $h_{1}|_{K^{0}(\mathscr{D}_{w})},h_{2}|_{K^{0}(\mathscr{D}_{w})},\mathbf{1}_{K^{0}(\mathscr{D}_{w})}$ for any $w\in W_{m}$ , and piecewise linear if and only if $u$ is $m$ -piecewise linear for some $m\in\mathbb{N}\cup\{0\}$ .

Finally, for any $u\in\mathcal{F}_{\mathscr{D}}$ , some direct calculations using (3.10), (3.7) and (3.4) show that $\mathcal{E}^{\mathscr{D}_{w}}_{0}(u|_{V_{0}(\mathscr{D}_{w})},u|_{V_{0}(\mathscr{D}_{w})})\leq 7\int_{K(\mathscr{D}_{w})}|\nabla_{\mathscr{D}}u|^{2}\,d\mu^{\mathscr{D}}$ for any $w\in W_{*}$ , which together with (3.11) yields $\mathcal{E}^{\mathscr{D}}_{m}(u|_{V_{m}(\mathscr{D})},u|_{V_{m}(\mathscr{D})})\leq\mathcal{E}^{\mathscr{D}}(u,u)$ for any $m\in\mathbb{N}\cup\{0\}$ , whence $u|_{V_{*}(\mathscr{D})}\in\mathcal{F}^{\prime}_{\mathscr{D}}$ by (3.12). ∎

The last main step of the proof of Theorem 3.4 is to prove (3.8), which is based mainly on (3.5), (3.7) and the following lemma.

Lemma 3.10 ([14, Lemma 5.19]).

Let $C\subset\mathbb{C}$ be a circular arc, let $u\in\mathbb{R}^{C}$ satisfy $\mathop{\mathbf{Lip}}\nolimits_{C}u<+\infty$ , and for $a\in\mathbb{R}$ define $\mathcal{I}_{C}^{a}u:\overline{D_{C}}\to\mathbb{R}$ by

\mathcal{I}_{C}^{a}u((1-t)\mathop{\mathrm{cent}}\nolimits(C)+tz):=(1-t)a+tu(z),\quad(t,z)\in[0,1]\times C.

(3.14)

Then for any $a\in[\min_{C}u,\max_{C}u]$ , $\mathop{\mathbf{Lip}}\nolimits_{\overline{D_{C}}}\mathcal{I}_{C}^{a}u\leq\sqrt{5}\mathop{\mathbf{Lip}}\nolimits_{C}u$ and

\frac{2}{21}\int_{D_{C}}\mspace{-3.0mu}|\nabla\mathcal{I}_{C}^{a}u|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}\leq\int_{C}\mspace{-2.0mu}|\nabla_{C}u|^{2}\mathop{\mathrm{rad}}\nolimits(C)\,d\mathscr{H}^{1}_{C}\leq 2\int_{D_{C}}\mspace{-3.0mu}|\nabla\mathcal{I}_{C}^{a}u|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}.

(3.15)

Further, with $\overline{u}^{C}:=\mathscr{H}^{1}_{C}(C)^{-1}\int_{C}u\,d\mathscr{H}^{1}_{C}$ , for any $a\in\{0,\overline{u}^{C}\}$ ,

2\int_{D_{C}}|\mathcal{I}_{C}^{a}u|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}\leq\int_{C}u^{2}\mathop{\mathrm{rad}}\nolimits(C)\,d\mathscr{H}^{1}_{C}\leq 4\int_{D_{C}}|\mathcal{I}_{C}^{a}u|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}.

(3.16)

Combining Lemma 3.10 with (3.5) and (3.7), we obtain the following.

Lemma 3.11 ([14, Lemma 5.21]).

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ and $u\in\mathcal{C}^{\mathrm{lip}}_{\mathscr{D}}$ . Noting $\overline{\triangle(\mathscr{D})}\setminus(K(\mathscr{D})\setminus K^{0}(\mathscr{D}))=\bigcup_{C\in\mathscr{A}_{\mathscr{D}}}\overline{D_{C}}$ , define $\mathcal{I}_{\mathscr{D}}^{0}u\in\mathbb{R}^{\overline{\triangle(\mathscr{D})}}$ by

\mathcal{I}_{\mathscr{D}}^{0}u|_{K(\mathscr{D})}:=u,\quad\mathcal{I}_{\mathscr{D}}^{0}u|_{\overline{D_{C}}}:=\begin{cases}\mathcal{I}_{C}^{0}(u|_{C})&\textrm{if $C\subset\partial T(\mathscr{D})$,}\\ \mathcal{I}_{C}^{\overline{u}^{C}}(u|_{C})&\textrm{if $C\not\subset\partial T(\mathscr{D})$,}\end{cases}\quad C\in\mathscr{A}_{\mathscr{D}}.

(3.17)

If also $u|_{V_{0}(\mathscr{D})}=0$ , then $\mathcal{I}_{\mathscr{D}}^{0}u|_{\partial\triangle(\mathscr{D})}=0$ , $\mathop{\mathbf{Lip}}\nolimits_{\overline{\triangle(\mathscr{D})}}\mathcal{I}_{\mathscr{D}}^{0}u\leq\sqrt{5}\mathop{\mathbf{Lip}}\nolimits_{K(\mathscr{D})}u$ ,

	$\displaystyle\frac{2}{21}\int_{\triangle(\mathscr{D})}\|\nabla\mathcal{I}_{\mathscr{D}}^{0}u\|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}\leq\mathcal{E}^{\mathscr{D}}(u,u)\leq 2\int_{\triangle(\mathscr{D})}\|\nabla\mathcal{I}_{\mathscr{D}}^{0}u\|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2},$		(3.18)
	$\displaystyle 2\int_{\triangle(\mathscr{D})}\|\mathcal{I}_{\mathscr{D}}^{0}u\|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}\leq\int_{K(\mathscr{D})}u^{2}\,d\mu^{\mathscr{D}}\leq 4\int_{\triangle(\mathscr{D})}\|\mathcal{I}_{\mathscr{D}}^{0}u\|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}.$		(3.19)

Sketch of the proof of Theorem 3.4.

Recall the following classical fact implied by [5, Lemma 6.2.1, Theorems 4.5.1, 4.5.3 and 6.1.6]: if $Q$ is an open rectangle in $\mathbb{C}$ whose smaller side length is $\delta\in(0,+\infty)$ , then

\int_{Q}u^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}\leq\frac{\delta^{2}}{\pi^{2}}\int_{Q}|\nabla u|^{2}\,d\mathop{\mathrm{vol}}\nolimits_{2}

(3.20)

for any $u\in\mathbb{R}^{\overline{Q}}$ with $\mathop{\mathbf{Lip}}\nolimits_{\overline{Q}}u<+\infty$ and $u|_{\partial Q}=0$ . Since $\triangle(\mathscr{D})\subset Q$ for some such $Q$ with $\delta=3\kappa(\mathscr{D})^{-1}$ and then each $u\in\mathbb{R}^{\overline{\triangle(\mathscr{D})}}$ with $\mathop{\mathbf{Lip}}\nolimits_{\overline{\triangle(\mathscr{D})}}u<+\infty$ and $u|_{\partial\triangle(\mathscr{D})}=0$ can be extended to $\overline{Q}$ by setting $u|_{\overline{Q}\setminus\triangle(\mathscr{D})}:=0$ so as to satisfy $\mathop{\mathbf{Lip}}\nolimits_{\overline{Q}}u<+\infty$ and $u|_{\partial Q}=0$ , we easily see from Lemma 3.11 and (3.20) that (3.8) holds for any $u\in\mathcal{F}_{\mathscr{D},0}^{0}\cap\mathcal{C}^{\mathrm{lip}}_{\mathscr{D}}$ .

Now, by utilizing the canonical approximation of each $u\in\mathcal{F}_{\mathscr{D}}$ by piecewise linear functions as in the sketch of the proof of Theorem 3.9 above, we can show that (3.8) extends to any $u\in\mathcal{F}_{\mathscr{D},0}^{0}$ , which implies $\mathcal{F}_{\mathscr{D}}\subset L^{2}(K(\mathscr{D}),\mu^{\mathscr{D}})$ , and that the inclusion map $\mathcal{F}_{\mathscr{D}}\hookrightarrow L^{2}(K(\mathscr{D}),\mu^{\mathscr{D}})$ is the limit in operator norm of finite-rank linear operators and hence compact. The rest of the proof is straightforward. ∎

Sketch of the proof of Theorem 3.5.

The implication from (2) to (1) is immediate from Theorem 3.9 and Theorem 3.7-(2),(3). That from (1) to (2) can be shown by defining the trace $\mathcal{E}|_{V_{m}(\mathscr{D})}$ of $(\mathcal{E},\mathcal{F})$ to $V_{m}(\mathscr{D})$ for $m\in\mathbb{N}\cup\{0\}$ in essentially the same way as (3.9), proving that $\{\mathcal{E}|_{V_{m}(\mathscr{D})}\}_{m\in\mathbb{N}\cup\{0\}}$ satisfies Theorem 3.7-(1),(2),(3) by the assumption of (1) and then applying Theorem 3.8 to conclude that $\{\mathcal{E}|_{V_{m}(\mathscr{D})}\}_{m\in\mathbb{N}\cup\{0\}}=\{c\mathcal{E}^{\mathscr{D}}_{m}\}_{m\in\mathbb{N}\cup\{0\}}$ for some $c\in\mathbb{R}$ , which is easily seen to imply (2). ∎

4. Weyl’s eigenvalue asymptotics for the Apollonian gasket

The following proposition is an easy consequence of Theorem 3.4; see also [5, Exercise 4.2, Corollary 4.2.3, Theorems 4.5.1 and 4.5.3].

Proposition 4.1.

Let $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ , let $V$ be a finite subset of $V_{*}(\mathscr{D})$ and set $\mathcal{F}_{\mathscr{D},V}^{0}:=\{u\in\mathcal{F}_{\mathscr{D}}\mid u|_{V}=0\}$ . Then $(\mathcal{E}^{\mathscr{D}}|_{\mathcal{F}_{\mathscr{D},V}^{0}\times\mathcal{F}_{\mathscr{D},V}^{0}},\mathcal{F}_{\mathscr{D},V}^{0})$ is a strongly local, regular symmetric Dirichlet form on $L^{2}(K(\mathscr{D})\setminus V,\mu^{\mathscr{D}})$ , and there exists a unique non-decreasing sequence $\{\lambda^{\mathscr{D},V}_{n}\}_{n\in\mathbb{N}}\subset[0,+\infty)$ such that $-\mathcal{L}_{\mathscr{D},V}\varphi^{\mathscr{D},V}_{n}=\lambda^{\mathscr{D},V}_{n}\varphi^{\mathscr{D},V}_{n}$ for any $n\in\mathbb{N}$ for some complete orthonormal system $\{\varphi^{\mathscr{D},V}_{n}\}_{n\in\mathbb{N}}\subset\mathcal{D}(\mathcal{L}_{\mathscr{D},V})$ of $L^{2}(K(\mathscr{D})\setminus V,\mu^{\mathscr{D}})$ ; here $\mathcal{L}_{\mathscr{D},V}:\mathcal{D}(\mathcal{L}_{\mathscr{D},V})\to L^{2}(K(\mathscr{D})\setminus V,\mu^{\mathscr{D}})$ denotes the Laplacian, i.e., the non-positive self-adjoint operator on $L^{2}(K(\mathscr{D})\setminus V,\mu^{\mathscr{D}})$ , associated with $(\mathcal{E}^{\mathscr{D}}|_{\mathcal{F}_{\mathscr{D},V}^{0}\times\mathcal{F}_{\mathscr{D},V}^{0}},\mathcal{F}_{\mathscr{D},V}^{0})$ . Also, $\lim_{n\to\infty}\lambda^{\mathscr{D},V}_{n}=+\infty$ , and for any $n\in\mathbb{N}$ ,

\lambda^{\mathscr{D},V}_{n}=\min\biggl{\{}\max_{u\in L\setminus\{0\}}\frac{\mathcal{E}^{\mathscr{D}}(u,u)}{\int_{K(\mathscr{D})}u^{2}\,d\mu^{\mathscr{D}}}\biggm{|}\begin{minipage}{90.5pt} $L$ is a linear subspace of $\mathcal{F}_{\mathscr{D},V}^{0}$, $\dim L=n$ \end{minipage}\biggr{\}}.

(4.1)

The proof of the following theorem is the principal aim of [14].

Theorem 4.2 ([14, Theorem 7.1]).

There exists $c_{\mathsf{AG}}\in(0,+\infty)$ such that for any $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ and any finite subset $V$ of $V_{*}(\mathscr{D})$ ,

\lim_{\lambda\to+\infty}\frac{\#\{n\in\mathbb{N}\mid\lambda^{\mathscr{D},V}_{n}\leq\lambda\}}{\lambda^{d_{\mathsf{AG}}/2}}=c_{\mathsf{AG}}\mathscr{H}^{d_{\mathsf{AG}}}(K(\mathscr{D})).

(4.2)

The rest of this section outlines the analytic aspects of the proof of Theorem 4.2. It can be deduced from the following theorem applicable to more general counting functions, including the classical one given by $\#\{w\in W_{*}\mid\mathop{\mathrm{curv}}\nolimits(D_{\mathrm{in}}(\mathscr{D}_{w}))\leq\lambda\}$ , whose asymptotic behavior analogous to (4.2) has been obtained first by Oh and Shah in [30, Corollary 1.8].

Definition 4.3.

(1)

We define $I:=\{j^{n}k\mid\textrm{$j,k\in S$, $j\not=k$, $n\in\mathbb{N}$}\}$ , so that $I\subset W_{*}\setminus\{\emptyset\}$ , $\tau\not\asymp\upsilon$ for any $\tau,\upsilon\in I$ with $\tau\not=\upsilon$ and

K(\mathscr{D})\setminus V_{0}(\mathscr{D})=\bigcup\nolimits_{\tau\in I}K(\mathscr{D}_{\tau})\qquad\textrm{for any $\mathscr{D}\in\mathsf{TDT}^{+}$.}

(4.3)

(2)

We define $\Gamma\subset[0,+\infty)^{4}$ by $\Gamma:=\{(g,\kappa(g))\mid\textrm{$g\in[0,+\infty)^{3}$, $\kappa(g)>0$}\}$ , where $\kappa(g):=\sqrt{\beta\gamma+\gamma\alpha+\alpha\beta}$ for $g=(\alpha,\beta,\gamma)\in[0,+\infty)^{3}$ , and set $\Gamma^{\circ}:=\Gamma\cap(0,+\infty)^{4}$ , which is an open subset of $\Gamma$ ; recall Propositions 2.2 and 2.7 and note that $gM_{w}\in\Gamma$ for any $g\in\Gamma$ and any $w\in W_{*}$ .
(3)

Recalling Theorem 2.11, we set $\mathscr{H}_{\Gamma}(g):=\mathscr{H}^{d_{\mathsf{AG}}}(K(\mathscr{D}))$ for each $g=(\alpha,\beta,\gamma,\kappa)\in\Gamma$ , where we take any $\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{+}$ with $\bigl{(}\mathop{\mathrm{curv}}\nolimits(D_{1}),\mathop{\mathrm{curv}}\nolimits(D_{2}),\mathop{\mathrm{curv}}\nolimits(D_{3})\bigr{)}=(\alpha,\beta,\gamma)$ , which is easily seen to exist. Note that $\mathscr{H}_{\Gamma}(g)=s^{d_{\mathsf{AG}}}\mathscr{H}_{\Gamma}(sg)$ for any $(g,s)\in\Gamma\times(0,+\infty)$ .

Theorem 4.4 ([14]).

Let $\Gamma^{\prime}$ denote either of $\Gamma$ and $\Gamma^{\circ}$ , and for each $n\in\mathbb{N}$ let $\lambda_{n}:\Gamma^{\prime}\to(0,+\infty)$ be continuous and satisfy $\lambda_{n}(sg)=s\lambda_{n}(g)$ for any $(g,s)\in\Gamma^{\prime}\times(0,+\infty)$ . Suppose that $\lambda_{1}(g)=\min_{n\in\mathbb{N}}\lambda_{n}(g)$ and $\lim_{n\to\infty}\lambda_{n}(g)=+\infty$ for any $g\in\Gamma^{\prime}$ , set $\mathscr{N}(g,\lambda):=\#\{n\in\mathbb{N}\mid\lambda_{n}(g)\leq\lambda\}$ for $(g,\lambda)\in\Gamma^{\prime}\times[0,+\infty)$ , and suppose that there exist $\eta\in[0,d_{\mathsf{AG}})$ and $c\in(0,+\infty)$ such that for any $g=(\alpha,\beta,\gamma,\kappa)\in\Gamma^{\prime}$ and any $\lambda\in(0,+\infty)$ ,

\begin{split}&\sum\nolimits_{\tau\in I}\mathscr{N}(gM_{\tau},\lambda)\leq\mathscr{N}(g,\lambda)\\ &\mspace{30.0mu}\leq\sum\nolimits_{\tau\in I}\mathscr{N}(gM_{\tau},\lambda)+c(\min\{\beta+\gamma,\gamma+\alpha,\alpha+\beta\})^{-\eta}\lambda^{\eta}+c.\end{split}

(4.4)

Then there exists $c_{0}\in(0,+\infty)$ such that for any $g\in\Gamma^{\prime}$ ,

\lim_{\lambda\to+\infty}\frac{\mathscr{N}(g,\lambda)}{\lambda^{d_{\mathsf{AG}}}}=c_{0}\mathscr{H}_{\Gamma}(g).

(4.5)

Theorem 4.4 is proved by applying Kesten’s renewal theorem [19, Theorem 2] to the Markov chain on $\widetilde{\Gamma}:=\{g\in\Gamma\mid\mathscr{H}_{\Gamma}(g)=1\}$ , the “space of Euclidean shapes of $\{K(\mathscr{D})\}_{\mathscr{D}\in\mathsf{TDT}^{+}}$ ”, with transition function $\mathscr{P}(g,\cdot):=\sum_{\tau\in I}\mathscr{H}_{\Gamma}(gM_{\tau})\delta_{[gM_{\tau}]_{\Gamma}}$ , where for each $g\in\Gamma$ we set $[g]_{\Gamma}:=\mathscr{H}_{\Gamma}(g)^{1/d_{\mathsf{AG}}}g\in\widetilde{\Gamma}$ and $\delta_{[g]_{\Gamma}}$ denotes the Borel probability measure on $\widetilde{\Gamma}$ with $\delta_{[g]_{\Gamma}}(\{[g]_{\Gamma}\})=1$ ; a brief sketch of the proof of Theorem 4.4 can be found in [13], and the full details will appear in [14, Sections 3 and 7].

Sketch of the proof of Theorem 4.2 under Theorem 4.4.

We define $\mathscr{N}_{\mathscr{D},V}(\lambda):=\#\{n\in\mathbb{N}\mid\lambda^{\mathscr{D},V}_{n}\leq\lambda\}$ , $\mathscr{N}_{\mathscr{D}}(\lambda):=\mathscr{N}_{\mathscr{D},\emptyset}(\lambda)$ and $\mathscr{N}_{\mathscr{D},0}(\lambda):=\mathscr{N}_{\mathscr{D},V_{0}(\mathscr{D})}(\lambda)$ for $\mathscr{D}\in\mathsf{TDT}^{\oplus}$ , each finite subset $V$ of $V_{*}(\mathscr{D})$ and $\lambda\in[0,+\infty)$ . Then for any such $\mathscr{D},V,\lambda$ , as noted in [21, Theorem 4.1.7 and Corollary 4.1.8], we easily see from $\dim\mathcal{F}_{\mathscr{D}}/\mathcal{F}_{\mathscr{D},V}^{0}=\#V$ and (4.1) that $\lambda^{\mathscr{D},\emptyset}_{n}\leq\lambda^{\mathscr{D},V}_{n}\leq\lambda^{\mathscr{D},\emptyset}_{n+\#V}$ for any $n\in\mathbb{N}$ and thereby that

\mathscr{N}_{\mathscr{D},V}(\lambda)\leq\mathscr{N}_{\mathscr{D}}(\lambda)\leq\mathscr{N}_{\mathscr{D},V}(\lambda)+\#V,

(4.6)

so that it suffices to prove (4.2) for $V=V_{0}(\mathscr{D})$ , i.e., for $\mathscr{N}_{\mathscr{D},0}(\lambda)$ .

To apply Theorem 4.4, for each $n\in\mathbb{N}$ and each $g=(\alpha,\beta,\gamma,\kappa)\in\Gamma^{\circ}$ we set $\lambda_{n}(g):=(\lambda^{\mathscr{D},V_{0}(\mathscr{D})}_{n})^{1/2}$ , where we take any $\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{\oplus}$ with $\bigl{(}\mathop{\mathrm{curv}}\nolimits(D_{1}),\mathop{\mathrm{curv}}\nolimits(D_{2}),\mathop{\mathrm{curv}}\nolimits(D_{3})\bigr{)}=(\alpha,\beta,\gamma)$ , so that $\lambda_{n}(g)\geq\lambda_{1}(g)>0$ by $\{u\in\mathcal{F}_{\mathscr{D}}\mid\mathcal{E}^{\mathscr{D}}(u,u)=0\}=\mathbb{R}\mathbf{1}$ and $\lim_{n\to\infty}\lambda_{n}(g)=+\infty$ by Proposition 4.1. We also easily see from Proposition 2.7, (3.5), (3.7) and (4.1) that for any $n\in\mathbb{N}$ , $\lambda_{n}:\Gamma^{\circ}\to(0,+\infty)$ is continuous and satisfies $\lambda_{n}(sg)=s\lambda_{n}(g)$ for any $(g,s)\in\Gamma^{\circ}\times(0,+\infty)$ .

It remains to verify that $\{\lambda_{n}\}_{n\in\mathbb{N}}$ satisfies (4.4). To this end, let $\mathscr{D}=(D_{1},D_{2},D_{3})\in\mathsf{TDT}^{\oplus}$ , $(\alpha,\beta,\gamma,\kappa)=:g$ be as in Proposition 2.2 and $\lambda\in(0,+\infty)$ . Then since $\#\{n\in\mathbb{N}\mid\lambda_{n}(gM_{w})\leq\lambda^{1/2}\}=\mathscr{N}_{\mathscr{D}_{w},0}(\lambda)$ for any $w\in W_{*}$ by Proposition 2.7, (4.4) for $\{\lambda_{n}\}_{n\in\mathbb{N}}$ can be rephrased as

\begin{split}&\sum\nolimits_{\tau\in I}\mathscr{N}_{\mathscr{D}_{\tau},0}(\lambda)\leq\mathscr{N}_{\mathscr{D},0}(\lambda)\\ &\mspace{27.0mu}\leq\sum\nolimits_{\tau\in I}\mathscr{N}_{\mathscr{D}_{\tau},0}(\lambda)+c(\min\{\beta+\gamma,\gamma+\alpha,\alpha+\beta\})^{-\eta}\lambda^{\eta/2}+c,\end{split}

(4.7)

which can be shown with $\eta=1<d_{\mathsf{AG}}$ (recall Theorem 2.10) as follows. Set $c_{g}:=\min\{\beta+\gamma,\gamma+\alpha,\alpha+\beta\}$ and $n_{\lambda}:=\min\{n\in\mathbb{N}\mid c_{g}^{2}n^{2}\geq 40\lambda\}$ . Then for any $n\in\mathbb{N}$ with $n\geq n_{\lambda}$ , any $j\in S$ and any $\tau\in I\cup\{j^{n_{\lambda}}\}$ with $\tau\leq j^{n_{\lambda}}$ , from (3.8), (4.1) and (2.4) we obtain

\mspace{-3.0mu}\mathscr{N}_{\mathscr{D}_{\tau},0}(\lambda)=0\mspace{8.0mu}\textrm{by}\mspace{8.0mu}\lambda^{\mathscr{D}_{\tau},V_{0}(\mathscr{D}_{\tau})}_{1}\geq\frac{\kappa(\mathscr{D}_{\tau})^{2}}{40}\geq\frac{\kappa(\mathscr{D}_{j^{n_{\lambda}}})^{2}}{40}>\frac{c_{g}^{2}n_{\lambda}^{2}}{40}\geq\lambda.\mspace{-5.0mu}

(4.8)

On the other hand, setting $I_{\lambda}:=\{\tau\in I\mid|\tau|\leq n_{\lambda}\}\cup\{j^{n_{\lambda}}\mid j\in S\}$ and $V_{\lambda}:=\bigcup_{\tau\in I_{\lambda}}V_{0}(\mathscr{D}_{\tau})$ , we have $K(\mathscr{D})\setminus V_{\lambda}=\bigcup_{\tau\in I_{\lambda}}(K(\mathscr{D}_{\tau})\setminus V_{0}(\mathscr{D}_{\tau}))$ with the union disjoint, which together with (4.1) and (4.8) easily implies that

\mathscr{N}_{\mathscr{D},V_{\lambda}}(\lambda)=\sum\nolimits_{\tau\in I_{\lambda}}\mathscr{N}_{\mathscr{D}_{\tau},0}(\lambda)=\sum\nolimits_{\tau\in I}\mathscr{N}_{\mathscr{D}_{\tau},0}(\lambda).

(4.9)

Now (4.7) follows from (4.9), $\#V_{\lambda}=9n_{\lambda}-3$ and the fact that $\mathscr{N}_{\mathscr{D},V_{\lambda}}(\lambda)\leq\mathscr{N}_{\mathscr{D},0}(\lambda)\leq\mathscr{N}_{\mathscr{D},V_{\lambda}}(\lambda)+\#V_{\lambda}-3$ by the same proof as (4.6). Theorem 4.4 is thus applicable to $\{\lambda_{n}\}_{n\in\mathbb{N}}$ and yields (4.5), which means (4.2). ∎

5. Kleinian groups with limit sets round Sierpiński carpets

In this last section, we illustrate the possibility of extending the results in §3 and §4 to other circle packing fractals, by presenting the results of the author’s recent study in [16] obtained as the initial step toward developing a rich theory of construction and analysis of “geometrically canonical” Laplacians on more general self-conformal fractals.

Let $\mathop{\mbox{M\"{o}b}}\nolimits(\widehat{\mathbb{C}})$ denote the group of (orientation preserving or reversing) Möbius transformations on $\widehat{\mathbb{C}}$ . A discrete subgroup $G$ of $\mathop{\mbox{M\"{o}b}}\nolimits(\widehat{\mathbb{C}})$ is called a Kleinian group³³3Kleinian groups are usually assumed to consist only of orientation preserving elements, but here we allow them to contain orientation reversing ones., and the smallest closed subset $\partial_{\infty}G$ of $\widehat{\mathbb{C}}$ invariant with respect to the action of $G$ is called the limit set of $G$ . It is known in the theory of Kleinian groups (see, e.g., [3, 17, 18, 36]) that the limit sets of certain classes of Kleinian groups are circle packing fractals, and typical examples of such circle packing fractals are provided in the book [29] together with a number of beautiful pictures of them.

Since the expressions (3.5) of $\mu^{\mathscr{D}}$ and (3.7) of the unique canonical Dirichlet form $(\mathcal{E}^{\mathscr{D}},\mathcal{F}_{\mathscr{D}})$ on $K(\mathscr{D})$ makes sense on a general circle packing fractal, (a candidate of) a “geometrically canonical” Laplacian on it can be defined by (3.5) and (3.7), and it is natural to expect Weyl’s eigenvalue asymptotics to hold when the fractal has some nice self-conformal structure. The author has recently verified this expectation in [15, 16] for the circle packing fractals arising as the limit sets of two specific classes of Kleinian groups, one of which studied in [15] is the double cusp groups on the boundary of Maskit’s embedding of the Teichmüller space of the once-punctured torus treated in detail in [18, 29, 36]. In this case, the limit sets (Figure 4) can be shown to admit a self-conformal cellular decomposition similar to (4.3) which is finitely ramified in the sense that any cell intersects the others only on boundedly many points, and this property makes the proof of Weyl’s asymptotics largely analogous to that of Theorem 4.2; a brief presentation of the precise statements of the results can be found in [11], and the full details will be given in [15].

On the other hand, each Kleinian group in the other class, which has been studied in [16], has as its limit set a round Sierpiński carpet (Figure 5), i.e., a subset of $\widehat{\mathbb{C}}$ homeomorphic to the standard Sierpiński carpet (Figure 4) whose complement in $\widehat{\mathbb{C}}$ consists of disjoint open disks in $\widehat{\mathbb{C}}$ . In particular, this limit set is infinitely ramified, i.e., is not finitely ramified regardless of the choice of a cellular decomposition, which prevents the method of the above proof of (4.7) from applying to it and thereby makes the proof of Weyl’s asymptotics for this case considerably more difficult.

The rest of this section is devoted to a brief summary of the results in [16] for the latter class of Kleinian groups, which are defined as follows. Let $q\in\mathbb{N}$ satisfy $q>6$ . It is a well-known fact from hyperbolic geometry (see, e.g., [31, Theorem 3.5.6]) that by $\frac{\pi}{2}+\frac{\pi}{3}+\frac{\pi}{q}<\pi$ there exists a geodesic triangle with inner angles $\frac{\pi}{2},\frac{\pi}{3},\frac{\pi}{q}$ , unique up to hyperbolic isometry, in the Poincaré disk model $\mathbb{D}:=\{z\in\mathbb{C}\mid|z|<1\}$ of the hyperbolic plane; here we make the following specific choice of such one. The following construction is a slight modification of that given in [3].

Definition 5.1.

(1)

Set $\ell_{1}:=\mathbb{R}$ , $\ell_{3}:=\{te^{i\pi/q}\mid t\in\mathbb{R}\}$ and choose $t_{q},s_{q}\in(0,+\infty)$ so that $\ell_{2}:=\{z\in\mathbb{C}\mid|z-t_{q}e^{i\pi/q}|=s_{q}\}$ is orthogonal to $\partial\mathbb{D}$ and intersects $\ell_{1}$ with angle $\frac{\pi}{3}$ ; there is a unique such choice of $t_{q},s_{q}$ by virtue of $\frac{\pi}{2}+\frac{\pi}{3}+\frac{\pi}{q}<\pi$ . The closed geodesic triangle in $\mathbb{D}$ formed by $\ell_{1},\ell_{2},\ell_{3}$ is denoted by $\triangle_{q}$ , and the subgroup of $\mathop{\mbox{M\"{o}b}}\nolimits(\widehat{\mathbb{C}})$ generated by $\{\mathop{\mathrm{Inv}}\nolimits_{\ell_{k}}\}_{k=1}^{3}$ is denoted by $\Gamma_{q}$ , where $\mathop{\mathrm{Inv}}\nolimits_{\ell}$ denotes the inversion (reflection) in a circle or a straight line $\ell\subset\mathbb{C}$ .
(2)

Choose $r_{q}\in(0,1)$ so that $\ell_{4}:=\{z\in\mathbb{C}\mid|z|=r_{q}\}$ intersects $\ell_{2}$ with angle $\frac{\pi}{3}$ ; it is easy to see that there is a unique such choice of $r_{q}$ . The subgroup of $\mathop{\mbox{M\"{o}b}}\nolimits(\widehat{\mathbb{C}})$ generated by $\{\mathop{\mathrm{Inv}}\nolimits_{\ell_{k}}\}_{k=1}^{4}$ is denoted by $G_{q}$ .

Proposition 5.2.

(1)

$\mathbb{D}=\bigcup_{\tau\in\Gamma_{q}}\tau(\triangle_{q})$ and $\tau(\mathop{\mathrm{int}}\nolimits\triangle_{q})\cap\upsilon(\triangle_{q})=\emptyset$ for any $\tau,\upsilon\in\Gamma_{q}$ with $\tau\not=\upsilon$ .
(2)

$G_{q}$ is a Kleinian group, $\partial_{\infty}G_{q}=\overline{\bigcup_{\tau\in G_{q}}\tau(\partial\mathbb{D})}=\widehat{\mathbb{C}}\setminus\bigcup_{\tau\in G_{q}}\tau(\widehat{\mathbb{C}}\setminus\overline{\mathbb{D}})$ , $D_{1}\cap D_{2}=\emptyset$ for any $D_{1},D_{2}\in\bigl{\{}\tau(\widehat{\mathbb{C}}\setminus\mathbb{D})\bigm{|}\tau\in G_{q}\bigr{\}}$ with $D_{1}\not=D_{2}$ , and $\mathop{\mathrm{int}}\nolimits\partial_{\infty}G_{q}=\emptyset$ . In particular, $\partial_{\infty}G_{q}$ is a round Sierpiński carpet.

Proof.

(1) is immediate from Poincaré’s polygon theorem (see, e.g., [31, Theorem 7.1.3]), which applies to $\triangle_{q}$ since any of its inner angles is a submultiple of $\pi$ , i.e., of the form $\pi/n$ for some $n\in\mathbb{N}\cup\{+\infty\}$ .

For (2), recall (see, e.g., [31, Sections 4.4–4.6]) that $\mathop{\mbox{M\"{o}b}}\nolimits(\widehat{\mathbb{C}})$ is canonically isomorphic to the group of isometries of the upper half-space model $\mathbb{H}^{3}:=\mathbb{C}\times(0,+\infty)$ of the three-dimensional hyperbolic space, where the inversion $\mathop{\mathrm{Inv}}\nolimits_{\ell}$ in a circle or a straight line $\ell\subset\mathbb{C}$ corresponds to the inversion in the sphere or the plane $\widetilde{\ell}$ intersecting $\mathbb{C}$ orthogonally on $\ell$ . Then since the closed polyhedron $\triangle_{q}^{3}$ in $\mathbb{H}^{3}$ formed by $\{\widetilde{\ell_{k}}\}_{k=1}^{4}$ , defined as the part of $\{re^{i\theta}\mid(r,\theta)\in[0,+\infty)\times[0,\frac{\pi}{q}]\}\times(0,+\infty)$ above $\widetilde{\ell_{2}}$ and $\widetilde{\ell_{4}}$ , has only submultiples of $\pi$ as the dihedral angles between its faces, by Poincaré’s polyhedron theorem (see, e.g., [31, Theorem 13.5.2]) applied to $\triangle_{q}^{3}$ we have $\mathbb{H}^{3}=\bigcup_{\tau\in G_{q}}\tau(\triangle_{q}^{3})$ and $\tau(\mathop{\mathrm{int}}\nolimits_{\mathbb{H}^{3}}\triangle_{q}^{3})\cap\upsilon(\triangle_{q}^{3})=\emptyset$ for any $\tau,\upsilon\in G_{q}$ with $\tau\not=\upsilon$ . Now we can obtain the first three assertions from this fact, $\mathop{\mathrm{int}}\nolimits\partial_{\infty}G_{q}=\emptyset$ from [31, Theorem 12.2.7], and the last one from the topological characterization of the Sierpiński carpet in [35]. ∎

Even though in Definition 5.1 we have specifically chosen the unit disk $\mathbb{D}$ and the geodesic triangle $\triangle_{q}$ , a particular choice of a disk $D$ in $\mathbb{C}$ and a geodesic triangle in $D$ should not matter for the desired Laplacian eigenvalue asymptotics. We should note also that the expressions (3.5) and (3.7) do not make perfect sense for the family $\{\tau(\partial\mathbb{D})\mid\tau\in G_{q}\}$ of circles constituting $\partial_{\infty}G_{q}$ , since $\partial\mathbb{D}$ should be treated together with the part $\widehat{\mathbb{C}}\setminus\overline{\mathbb{D}}$ of $\widehat{\mathbb{C}}\setminus\partial_{\infty}G_{q}$ enclosed by $\partial\mathbb{D}$ and thereby considered to be of infinite area and radius, which is incompatible with (3.5) and (3.7). To take care of these issues, we introduce the following definition.

Definition 5.3.

We define $\mathcal{G}:=\bigl{\{}g\in\mathop{\mbox{M\"{o}b}}\nolimits(\widehat{\mathbb{C}})\bigm{|}g^{-1}(\infty)\in\widehat{\mathbb{C}}\setminus\overline{\mathbb{D}}\bigr{\}}$ , and for each $g\in\mathcal{G}$ we set $\mathscr{D}_{g}:=\bigl{\{}g\tau(\widehat{\mathbb{C}}\setminus\overline{\mathbb{D}})\bigm{|}\tau\in G_{q}\bigr{\}}\setminus\bigl{\{}g(\widehat{\mathbb{C}}\setminus\overline{\mathbb{D}})\bigr{\}}$ and $K_{g}:=g(\mathbb{D}\cap\partial_{\infty}G_{q})=g(\mathbb{D})\setminus\bigcup_{D\in\mathscr{D}_{g}}D$ , so that $\mathscr{D}_{g}$ is a family of open disks in $\mathbb{C}$ and $\overline{D_{1}}\subset g(\mathbb{D})\setminus\overline{D_{2}}$ for any $D_{1},D_{2}\in\mathscr{D}_{g}$ with $D_{1}\not=D_{2}$ .

Definition 5.4 ([16]).

Let $g\in\mathcal{G}$ . We define a linear subspace $\mathcal{C}_{g}$ of $\mathcal{C}_{\mathrm{c}}(K_{g})$ by $\mathcal{C}_{g}:=\{u\in\mathcal{C}_{\mathrm{c}}(K_{g})\mid\mathop{\mathbf{Lip}}\nolimits_{K_{g}}u<+\infty\}$ , and also define a finite Borel measure $\mu^{g}$ on $K_{g}$ and a bilinear form $\mathcal{E}^{g}:\mathcal{C}_{g}\times\mathcal{C}_{g}\to\mathbb{R}$ on $\mathcal{C}_{g}$ by

	$\displaystyle\mu^{g}:=\sum\nolimits_{D\in\mathscr{D}_{g}}\mathop{\mathrm{rad}}\nolimits(D)\mathscr{H}^{1}_{\partial D}(\cdot\cap\partial D),$		(5.1)
	$\displaystyle\mathcal{E}^{g}(u,v):=\sum\nolimits_{D\in\mathscr{D}_{g}}\int_{\partial D}\langle\nabla_{\partial D}(u\|_{\partial D}),\nabla_{\partial D}(v\|_{\partial D})\rangle\mathop{\mathrm{rad}}\nolimits(D)\,d\mathscr{H}^{1}_{\partial D}.$		(5.2)

Proposition 5.5 ([16]).

Let $g\in\mathcal{G}$ . Then $(\mathcal{E}^{g},\mathcal{C}_{g})$ is closable in $L^{2}(K_{g},\mu^{g})$ and its smallest closed extension $(\mathcal{E}^{g},\mathcal{F}_{g})$ in $L^{2}(K_{g},\mu^{g})$ is a strongly local, regular symmetric Dirichlet form on $L^{2}(K_{g},\mu^{g})$ . Further, the inclusion map $\mathcal{F}_{g}\hookrightarrow L^{2}(K_{g},\mu^{g})$ is a compact linear operator under the norm $\|u\|_{\mathcal{F}_{g}}:=(\mathcal{E}^{g}(u,u)+\int_{K_{g}}u^{2}\,d\mu^{g})^{1/2}$ on $\mathcal{F}_{g}$ .

Proposition 5.6 ([16]).

Let $g\in\mathcal{G}$ . Then any $h\in\{h_{1}|_{K_{g}},h_{2}|_{K_{g}}\}$ is $\mathcal{E}^{g}$ -harmonic on $K_{g}$ , i.e., $\mathcal{E}^{g}(h,v)=0$ for any $v\in\mathcal{C}_{g}$ , with $\mathcal{E}^{g}(h,v)$ still defined by (5.2).

Proof.

This follows easily by explicit calculations using the Gauss–Green theorem and the fact that $\partial D$ is a circle for any $D\in\mathscr{D}_{g}$ . ∎

The following is the main result of [16]. Note that for any $g\in\mathcal{G}$ and any non-empty open subset $U$ of $K_{g}$ , $d_{q}:=\dim_{\mathrm{H}}\partial_{\infty}G_{q}=\dim_{\mathrm{H}}K_{g}\in(1,2)$ and $\mathscr{H}^{d_{q}}(U)\in(0,+\infty)$ by [32, Theorem 7] and $\mathop{\mathbf{Lip}}\nolimits_{\overline{\mathbb{D}}}g<+\infty$ , and Proposition 5.5 implies the analog of Proposition 4.1 for $(\mathcal{E}^{g,U},\mathcal{F}_{g,U}^{0})$ on $L^{2}(U,\mu^{g}|_{U})$ , where $\mu^{g}|_{U}\mspace{-1.15mu}:=\mspace{-1.15mu}\mu^{g}|_{\mathscr{B}(U)}$ , $\mathcal{F}_{g,U}^{0}\mspace{-1.15mu}:=\mspace{-1.15mu}\overline{\{u\in\mathcal{C}_{g}\mid\mathop{\mathrm{supp}}\nolimits_{K_{g}}[u]\subset U\}}^{\mathcal{F}_{g}}$ and $\mathcal{E}^{g,U}:=\mathcal{E}^{g}|_{\mathcal{F}_{g,U}^{0}\times\mathcal{F}_{g,U}^{0}}$ .

Theorem 5.7 ([16]).

There exists $c_{q}\in(0,+\infty)$ such that for any $g\in\mathcal{G}$ and any non-empty open subset $U$ of $K_{g}$ with $\mathscr{H}^{d_{q}}(\partial_{K_{g}}U)=0$ and $\overline{U}\subset g(\mathbb{D})$ , the eigenvalues $\{\lambda^{g,U}_{n}\}_{n\in\mathbb{N}}$ (repeated according to multiplicity) of the Laplacian on $L^{2}(U,\mu^{g}|_{U})$ associated with $(\mathcal{E}^{g,U},\mathcal{F}_{g,U}^{0})$ satisfy

\lim_{\lambda\to+\infty}\frac{\#\{n\in\mathbb{N}\mid\lambda^{g,U}_{n}\leq\lambda\}}{\lambda^{d_{q}/2}}=c_{q}\mathscr{H}^{d_{q}}(U).

(5.3)

The ergodic-theoretic aspects of the proof of Theorem 5.7 are largely analogous to those of the proof of Theorem 4.2, and in particular the roles played by the self-conformality of $K_{g}$ are similar to those described in Remark 2.12. The most difficult part of the proof of Theorem 5.7 is that of an analog of (4.7), which is achieved by heavy use of heat kernel estimates in combination with the property of $\{\tau(\partial\mathbb{D})\mid\tau\in G_{q}\}$ that they are uniformly relatively separated in the following sense (see [1]):

\inf_{(x,y)\in C_{1}\times C_{2}}|x-y|\geq\varepsilon_{q}\min\{\mathop{\mathrm{rad}}\nolimits(C_{1}),\mathop{\mathrm{rad}}\nolimits(C_{2})\}

(5.4)

for any $C_{1},C_{2}\in\{\tau(\partial\mathbb{D})\mid\tau\in G_{q}\}$ with $C_{1}\not=C_{2}$ for some $\varepsilon_{q}\in(0,+\infty)$ . The full details of the proof of Theorem 5.7 will appear in [16].

References

[1] M. Bonk, Uniformization of Sierpiński carpets in the plane, Invent. Math. 186 (2011), 559–665.
[2] D. W. Boyd, The residual set dimension of the Apollonian packing, Mathematika 20 (1973), 170–174.
[3] S. Bullett and G. Mantica, Group theory of hyperbolic circle packings, Nonlinearity 5 (1992), 1085–1109.
[4] Z.-Q. Chen and M. Fukushima, Symmetric Markov Processes, Time Change, and Boundary Theory, London Math. Soc. Monogr., vol. 35, Princeton Univ. Press, Princeton, NJ, 2012.
[5] E. B. Davies, Spectral Theory and Differential Operators, Cambridge Stud. Adv. Math., vol. 42, Cambridge Univ. Press, Cambridge, 1995.
[6] M. Fukushima, Y. Oshima and M. Takeda, Dirichlet Forms and Symmetric Markov Processes, 2nd ed., de Gruyter Stud. Math., vol. 19, Walter de Gruyter, Berlin, 2011.
[7] K. E. Hirst, The Apollonian packing of circles, J. London Math. Soc. 42 (1967), 281–291.
[8] M. Hino, Energy measures and indices of Dirichlet forms, with applications to derivatives on some fractals, Proc. London Math. Soc. 100 (2010), 269–302.
[9] N. Kajino, Heat kernel asymptotics for the measurable Riemannian structure on the Sierpinski gasket, Potential Anal. 36 (2012), 67–115.
[10] N. Kajino, Analysis and geometry of the measurable Riemannian structure on the Sierpiński gasket, Contemp. Math., vol. 600, 2013, pp. 91–133.
[11] N. Kajino, Weyl’s eigenvalue asymptotics for the Laplacian on circle packing limit sets of certain Kleinian groups, in: Heat Kernels, Stochastic Processes and Functional Inequalities, Oberwolfach Report 55/2016. Available in: https://www.mfo.de/occasion/1648
[12] N. Kajino, The Laplacian on some round Sierpiński carpets and Weyl’s asymptotics for its eigenvalues (in Japanese), RIMS Kôkyûroku 2116 (2019), 47–56.
[13] N. Kajino, The Laplacian on some self-conformal fractals and Weyl’s asymptotics for its eigenvalues: A survey of the ergodic-theoretic aspects, RIMS Kôkyûroku 2176 (2021), in press. arXiv:2001.11354
[14] N. Kajino, The Laplacian on the Apollonian gasket and Weyl’s asymptotics for its eigenvalues, 2021, in preparation.
[15] N. Kajino, Weyl’s eigenvalue asymptotics for the Laplacian on circle packing limit sets of certain Kleinian groups, 2021, in preparation.
[16] N. Kajino, The Laplacian on some round Sierpiński carpets and Weyl’s asymptotics for its eigenvalues, 2021, in preparation.
[17] L. Keen, B. Maskit and C. Series, Geometric finiteness and uniqueness for Kleinian groups with circle packing limit sets, J. Reine Angew. Math. 436 (1993), 209–219.
[18] L. Keen and C. Series, Pleating coordinates for the Maskit embedding of the Teichmüller space of punctured tori, Topology 32 (1993), 719–749.
[19] H. Kesten, Renewal theory for functionals of a Markov chain with general state space, Ann. Probab. 2 (1974), 355–386.
[20] J. Kigami, Harmonic metric and Dirichlet form on the Sierpinski gasket, in: K. D. Elworthy and N. Ikeda (eds.), Asymptotic Problems in Probability Theory: Stochastic Models and Diffusions on Fractals (Sanda/Kyoto, 1990), Pitman Research Notes in Math., vol. 283, Longman Sci. Tech., Harlow, 1993, pp. 201–218.
[21] J. Kigami, Analysis on Fractals, Cambridge Tracts in Math., vol. 143, Cambridge Univ. Press, Cambridge, 2001.
[22] J. Kigami, Measurable Riemannian geometry on the Sierpinski gasket: the Kusuoka measure and the Gaussian heat kernel estimate, Math. Ann. 340 (2008), 781–804.
[23] P. Koskela and Y. Zhou, Geometry and analysis of Dirichlet forms, Adv. Math. 231 (2012), 2755–2801.
[24] S. Kusuoka, Dirichlet forms on fractals and products of random matrices, Publ. Res. Inst. Math. Sci. 25 (1989), 659–680.
[25] P. Mattila, Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability, Cambridge Studies in Advanced Math., vol. 44, Cambridge Univ. Press, Cambridge, 1995.
[26] R. D. Mauldin and M. Urbański, Dimension and measures for a curvilinear Sierpinski gasket or Apollonian packing, Adv. Math. 136 (1998), 26–38.
[27] C. T. McMullen, Hausdorff dimension and conformal dynamics, III: computation of dimension, Amer. J. Math. 120 (1998), 691–721.
[28] R. Meyers, R. Strichartz and A. Teplyaev, Dirichlet forms on the Sierpiński gasket, Pacific J. Math. 217 (2004), 149–174.
[29] D. Mumford, C. Series and D. Wright, Indra’s Pears: The Vision of Felix Klein, Cambridge University Press, Cambridge, 2002.
[30] H. Oh and N. Shah, The asymptotic distribution of circles in the orbits of Kleinian groups, Invent. Math. 187 (2012), 1–35.
[31] J. G. Ratcliffe, Foundations of Hyperbolic Manifolds, 3rd ed., Grad. Texts in Math., vol. 149, Springer, Cham, 2019.
[32] D. Sullivan, The density at infinity of a discrete group of hyperbolic motions, Inst. Hautes Études Sci. Publ. Math. 50 (1979), 171–202.
[33] D. Sullivan, Entropy, Hausdorff measures old and new, and limit sets of geometrically finite Kleinian groups, Acta Math. 153 (1984), 259–277.
[34] A. Teplyaev, Energy and Laplacian on the Sierpiński gasket, in: M. L. Lapidus and M. van Frankenhuijsen (eds.), Fractal Geometry and Applications: A Jubilee of Benoît Mandelbrot, Proc. Sympos. Pure Math., vol. 72, Part 1, Amer. Math. Soc., Providence, RI, 2004, pp. 131–154.
[35] G. T. Whyburn, Topological characterization of the Sierpiński curve, Fund. Math. 45 (1958), 320–324.
[36] D. Wright, Searching for the cusp, in: Y. Minsky, M. Sakuma and C. Series (eds.), Spaces of Kleinian Groups, London Math. Soc. Lecture Note Ser., vol. 329, Cambridge University Press, Cambridge, 2005, pp. 301–336.

The Laplacian on some self-conformal fractals and Weyl’s asymptotics for its eigenvalues: A survey of the analytic aspects

Abstract.

Key words and phrases:

2010 Mathematics Subject Classification:

1. Introduction

Notation.

2. The Apollonian gasket and its fractal geometry

Definition 2.1 (tangential disk triple).

Proposition 2.2.

Definition 2.3.

Definition 2.4.

Definition 2.5 (Apollonian gasket).

Definition 2.6.

Proposition 2.7.

Proof.

Lemma 2.8.

Proof.

Definition 2.9.

Theorem 2.10 (Boyd [2]; see also [7, 26, 27]).

Theorem 2.11 ([33, Theorem 2], [26, Theorem 2.6]).

Remark 2.12.

3. The canonical Dirichlet form on the Apollonian gasket

Definition 3.1.

Definition 3.2.

Definition 3.3 (cf. [14, Theorems 5.11 and 5.13]).

Theorem 3.4 ([14, Theorem 5.18]).

Theorem 3.5 ([14, Theorem 5.23]).

Remark 3.6.

Theorem 3.7 ([34, Theorem 5.17]).

Theorem 3.8 ([14, Theorem 4.18]).

Theorem 3.9 ([14, Theorem 5.13]).

Sketch of the proof.

Lemma 3.10 ([14, Lemma 5.19]).

Lemma 3.11 ([14, Lemma 5.21]).

Sketch of the proof of Theorem 3.4.

Sketch of the proof of Theorem 3.5.

4. Weyl’s eigenvalue asymptotics for the Apollonian gasket

Proposition 4.1.

Theorem 4.2 ([14, Theorem 7.1]).

Definition 4.3.

Theorem 4.4 ([14]).

Sketch of the proof of Theorem 4.2 under Theorem 4.4.

5. Kleinian groups with limit sets round Sierpiński carpets

Definition 5.1.

Proposition 5.2.

Proof.

Definition 5.3.

Definition 5.4 ([16]).

Proposition 5.5 ([16]).

Proposition 5.6 ([16]).

Proof.

Theorem 5.7 ([16]).

References

The Laplacian on some self-conformal fractals
and Weyl’s asymptotics for its eigenvalues:
A survey of the analytic aspects