The kinetic theory of ultra-subsonic fermion systems and applications to flat band magic angle twisted bilayer graphene
Abstract
The only kinematically-allowed phonon-scattering events for bands of subsonic fermions () are interband transitions, leading to different low- transport physics than in the typical supersonic case. We apply a kinetic theory of phonon-limited transport to a generic two-band system of subsonic fermions, deriving formulae for relaxation times and resistivity that are accurate in the limit of close bands and small . We predict regimes of , , and perfect conductivity. Our theory predicts linear-in- resistivity down to a crossover temperature that is suppressed from its supersonic analogue by a factor of , offering a new explanation for low- “strange metal” behavior observed in flat band systems.
Rapid progress in the fabrication and manipulation of layered two-dimensional van der Waals heterostructures has lead to an unprecedented ability to engineer nearly flat band (NFB) electronic systems, which have already displayed a wealth of exotic phenomena Geim and Grigorieva (2013); Novoselov et al. (2006); Bistritzer and MacDonald (2011); Morell et al. (2010); Li et al. (2019); Kim et al. (2017); Cao et al. (2018a, b, 2020a, 2021); Yankowitz et al. (2019); Kerelsky et al. (2019); Lu et al. (2019); Stepanov et al. (2020); Sharpe et al. (2019); Chen et al. (2020); Rozen et al. (2021); Zhou et al. (2022, 2021a, 2021b); Serlin et al. (2020); Wu et al. (2018, 2019a); Tschirhart et al. (2022); Polshyn et al. (2020); Jaoui et al. (2021); Polshyn et al. (2019); Cao et al. (2020b); Sarma and Wu (2022); Zhang et al. (2022); Polski et al. (2022); Xie and MacDonald (2020); Andrei and MacDonald (2020); Li et al. (2021); Ghiotto et al. (2021); Pan et al. (2020); Pan and Sarma (2021); Morales-Durán et al. (2021); Ahn and Sarma (2022); Kerelsky et al. (2021); Khalaf et al. (2019); Arora et al. (2020). However, all solid state systems contain phonons. To understand observations of novel physics in solid state NFB systems, it is important to understand how phonons interact with NFB fermions. This work focuses on one aspect: when the fermions in question are subsonic (), kinematics requires that all single-phonon scattering processes are interband transitions, with consequences on the low- transport physics.
The prime example of the NFB systems is magic angle twisted bilayer graphene (MATBLG). MATBLG has been found to exhibit SC proximate to strongly correlated insulating states Cao et al. (2018a, b, 2020a, 2021); Yankowitz et al. (2019); Kerelsky et al. (2019); Lu et al. (2019); Wu et al. (2018) and has been reported to exhibit a linear-in- “strange metal”-like resistivity over a large range of dopings and temperatures Jaoui et al. (2021); Polshyn et al. (2019); Cao et al. (2020b); Sarma and Wu (2022), sometimes down to temperatures as low as Jaoui et al. (2022). These phenomena have inspired analogy between MATBLG and the cuprate high- SCs, as well as speculation that SC in MATBLG might be driven by strong correlation physics. However, phonon-based theories of SC Wu et al. (2019b); Li et al. (2020) and high- transport Wu et al. (2019b); Davis et al. (2023a); Sarma and Wu (2022) in MATBLG have been put forth that give generally good quantitative agreement with experiment. These results - along with many others Stepanov et al. (2020); Saito et al. (2020) - suggest an alternative physical picture in which MATBLG hosts standard, phonon-driven BCS-style SC that competes with interaction-driven insulating orders at commensurate filling fractions of the NFBs Lu et al. (2019). It is thus imperative to understand whether low-, linear-in- transport in MATBLG is indeed arising from a strange metal state.
The standard kinetic theory of acoustic phonon scattering is exceptionally accurate in describing transport in layered graphene systems (as well as in normal metals and semiconductors) at temperatures above a few Kelvin Hwang and Das Sarma (2008); Wu et al. (2019b); Davis et al. (2023b, a), and accurately describes TBLG transport away from the magic angle Wu et al. (2019b); Davis et al. (2023a). In this work, we apply the same framework to NFB systems at asymptotically low , extending the kinetic theory well beyond its regime of proven validity. Remarkably, the familiar theory predicts qualitatively different low- transport physics for subsonic fermions than it does for the supersonic alternative, due entirely to the kinematic differences between the two limits.
We develop a transport theory for an “ultrasubsonic” (USS) two-band fermion system, which is accurate in the asymptotic double-limit of small and small band separation. Our main results are analytical formulae for relaxation times and for the resistivity of a general USS system, with transparent dependencies on temperature and doping level. We show that the interband nature of subsonic fermion scattering manifests an exponentially divergent relaxation time at low temperatures, in contrast with the familiar Bloch-Grüneisen (BG) power law applicable to supersonic fermions. The divergence in relaxation time is capable of perfectly balancing the thermodynamic suppression of states away from the Fermi level, leading to a non-intuitive physical picture in which states far from the Fermi level contribute meaningfully to transport. This scenario predicts a linear-in- resistivity over a wide range of , and down to a temperature much lower than the BG paradigm of supersonic fermion bands would suggest possible. The divergence in relaxation time can also drive the system to perfect conductivity at asymptotically low , mimicking a SC transition. We also note that the geometry of isolated NFBs can manifest a mid- power law. All these features are consistent with the hitherto unexplained phenomenology of MATBLG transport.
There are reasons to suspect that the standard kinetic theory of acoustic-phonon-limited-transport may not apply to NFB systems. Kinetic theory replaces the interacting Hamiltonian with a Markovian collision integral, and is thus incapable of treating emergent physics due to strong correlations, which many expect to be important in NFB systems. Further, vertex corrections to the electron-phonon coupling could become important in the absence of Migdal’s theorem. Nevertheless, it is important to understand the predictions of naive kinetic theory for NBF systems. The fact that our theory gives a simple and concrete mechanism for robust linear-in- resistivity is noteworthy, given that this is the primary signature of the “strange metal” state. Further, it is interesting that phonon scattering in subsonic fermion bands can also generate regimes of resistivity - often assumed to arise from electron-electron scattering in Fermi liquids - and regimes of perfect conductivity that mimic the behavior of superconductivity. While a realistic treatment of NFB electron-phonon physics is beyond reach, it is possible that the atypical kinematics of subsonic fermions is a key ingredient to understanding transport in NFB systems, which our approach is able to fully capture.
Although our theory has MATBLG in mind, we work with a general USS model. Our transport theory could apply to a system with renormalized fermion and phonon band structures and a renormalized deformation potential coupling in a theory that has already taken interaction-induced corrections into account. This, in fact, is the standard transport theory in normal metals where electron-electron interactions generally do not affect transport in the phonon-dominated regime. Further, in addition to providing an alternative explanation for experimental transport observations in MATBLG, our results could find application generally in all subsonic band systems, including other flat band systems generated by layered 2D heterostructures and heavy fermion systems. It is also noteworthy that strange metallicity is ubiquitous in heavy fermion compounds, which also manifest flat bands (i.e. heavy mass) and multiple bands near the Fermi surface, indicating a possible role for our proposed subsonic transport mechanism.
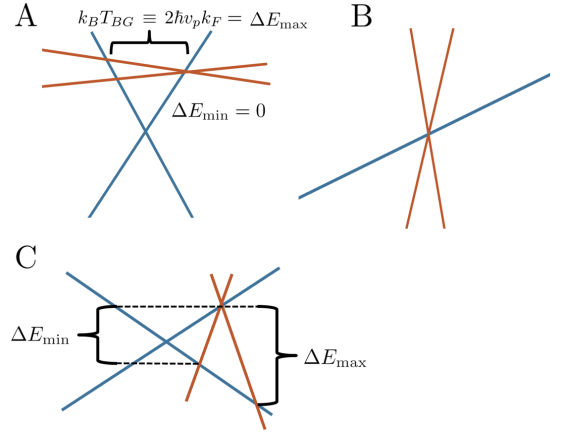
Phonon scattering of supersonic and subsonic fermions.—In an electron-phonon scattering process, conservation of energy and momentum define a “scattering manifold” of kinematically allowed Bloch states that an electron can scatter to. The maximum energy difference between a Bloch state on the scattering manifold and the initial state defines the Bloch-Grüneisen temperature, Hwang and Sarma (2019). For example, in an isotropic system, we simply have [Fig.1 (A)]. When , enough phonon modes will be populated that all kinematically allowed scattering events are possible. This is the so-called “equipartition regime”, which is characterized by a linear-in- scattering rate for each Bloch state. This is universal in kinetic theory and usually (but not always Davis et al. (2023b, a)) gives a linear-in- resistivity above . On the other hand, when , only low-energy phonon modes are available and scattering is restricted to a small neighborhood of the initial state. This is what gives rise to the famous low- power law in the Bloch-Grüneisen regime (where is the spatial dimension). Crucially, when the electrons are supersonic, the scattering manifold is smoothly connected to the original state, allowing arbitrarily small-momentum scattering events. As a result, the BG regime holds all the way to zero temperature. In single-layer graphene and in normal metals, or larger. (We also note that in many normal metals, the Debye temperature is lower than , in which case the BG crossover takes place at the Debye temperature Hwang and Sarma (2019).)
However, when the Bloch state in question is subsonic, the scattering manifold determined by energy-momentum conservation is necessarily disconnected from the original state. Similarly, in a band made entirely of subsonic Bloch states, all phonon scattering processes in subsonic fermion systems are interband processes. This implies that the scattering manifold also has a minimum allowed energy transfer [see Fig. 1 (C)], defining another temperature scale applicable for subsonic scattering, Below we expect an crossover to a regime in which the entire scattering manifold is inaccessible. That is, all thermally populated phonons are too low-energy to satisfy the conservation laws of an electron-phonon scattering event. Intuitively, we expect that below , the relaxation time of the Bloch state diverges exponentially as (instead of as in the supersonic BG regime).
Basic kinetic theory.—We first review the fundamental equations for phonon-limited resistivity in the Boltzmann framework Davis et al. (2023b, a). The resistivity is given in terms of the relaxation times :
| (1) |
where is the area of the system and is the Fermi velocity of the state . The relaxation times are determined from a self-consistent integral equation, derived from the Boltzmann equation. In the case of longitudinal acoustic phonons, in the Debye approximation, which couple to the fermions via the deformation potential, this takes the form
| (2) |
Above, is the mass density of the system, is the deformation potential, and is the phonon velocity. The function enforces the conservation of energy and momentum and defines the scattering manifold, while are “matrix elements” encoding geometric wavefunction overlap data Hwang and Das Sarma (2008); Wu et al. (2019b); Davis et al. (2023b, a). The dependencies on temperature and chemical potential are contained in , which encodes the thermal occupation data for the fermion and phonon states. These are given explicitly in the SM SM (Please see Supplemental Material for the microscopic model, additional details on Boltzmann kinetic theory and derivations of ultrasubsonic transport theory results, an analysis of the applicability of our theory to MATBLG, and a treatment of the ultrasubsonic Dirac cone). On a finite momentum grid, Eq. (2) is a matrix inversion problem that can be solved for the relaxation times, . Equation (1) then gives the resistivity.
Equipartition regime: .—When (equipartition regime), the inverse relaxation times scale linearly with temperature:
| (3) |
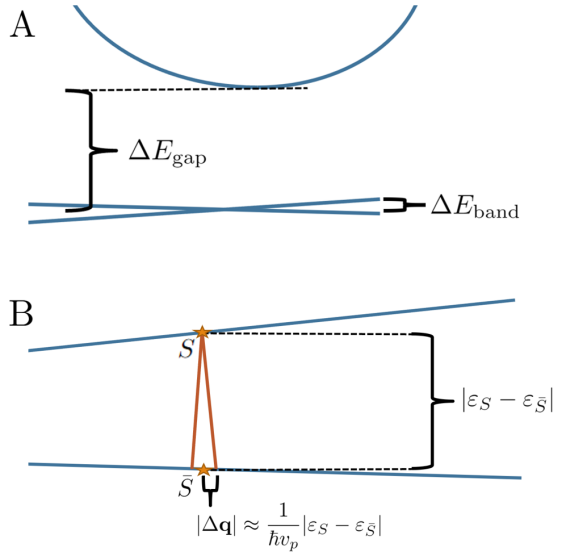
for some -independent proportionality constants that depend on the details of the system. In the case of NFBs separated from all other bands by a large energy gap, there is a mid- regime in which is larger than the NFB bandwidth, yet is still small compared to the gap between the NFBs and the other bands [Fig. 2 (A)]. In this case, we may neglect bands other than the NFBs, apply the equipartition scaling for the relaxation times [Eq. (3)], and expand the thermal weighting functions () in the formula for the resistivity [Eq. (1)], giving
| (4) |
We thus find a mid-, scaling regime due entirely to phonon scattering. This is noteworthy since scaling is generally seen as the hallmark of transport dominated by electron-electron scattering in a Fermi liquid Ashcroft and Mermin (1976); Ziman (1960); Coleman (2015), but the “mid-” regime generated by NFB phonon scattering has exactly the same dependence.
Ultrasubsonic kinetic theory.—We now consider electron-phonon scattering in a limit that allows transparent analytical results. We consider a two-band model in the double-limit of small and small band separation, which we call the “ultrasubsonic (USS) limit” [see Fig. 2 (B)]. For a given Bloch state (, with energy ), its scattering manifold is a small loop on the opposite band, surrounding its “compliment”, the point on the opposite band with the same momentum as the original state (, with energy ). In the USS limit, the scattering manifold is well-approximated by a circle of radius , centered at . The energy variation along the scattering manifold is then roughly which is double-suppressed in the USS limit. We thus make the approximations and for along the scattering manifold, approximating the relaxation times and the thermal occupancy function along the scattering manifold by their values at the compliment point.
Using the approximations discussed above and taking the thermodynamic limit (continuum limit in momentum space) of Eq. (2), we have
| (5) |
where the -independent factors and encode wavefunction overlap and band geometry data. They are given in the SM SM (Please see Supplemental Material for the microscopic model, additional details on Boltzmann kinetic theory and derivations of ultrasubsonic transport theory results, an analysis of the applicability of our theory to MATBLG, and a treatment of the ultrasubsonic Dirac cone). We may combine Eq. (5) for the state with its analogue for the compliment state , into a 2x2 matrix equation determining both and , which we solve analytically for the USS relaxation times:
| (6) |
Combining the relaxation time formula [Eq. (6)] with the resistivity formula [Eq. (1)] gives the master formula for the resistivity of the ultra-subsonic fermion system. We present this in the SM SM (Please see Supplemental Material for the microscopic model, additional details on Boltzmann kinetic theory and derivations of ultrasubsonic transport theory results, an analysis of the applicability of our theory to MATBLG, and a treatment of the ultrasubsonic Dirac cone). In the case of a particle-hole (PH) symmetric system, the formulae for the USS resistivity simplifies:
| (7) |
In the limit , expanding the factor in Eq. (6) gives the expected scattering rate of the equipartition regime. However, when , instead of the usual crossover to a power law, we find an exponential blow up of the relaxation times, in line with the physical picture in which the entire scattering manifold becomes thermally inaccessible.
Extreme low- limit.—In the PH symmetric case [Eq. 7], the only -dependent factor in the Brillouin zone summations is is the kernel
| (8) |
This factor represents the competition at low- between the divergence of the relaxation times and the thermodynamic suppression of states far from the Fermi level. In the extreme low- limit, where all the and functions blow up exponentially, we simply have
| (9) |
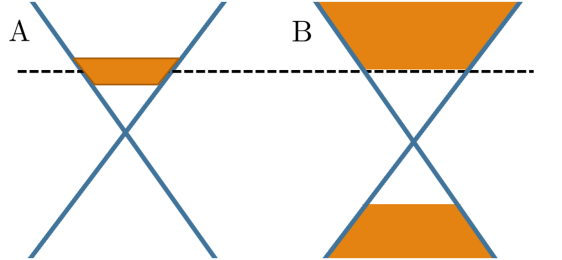
The thermal kernel determines which Bloch states meaningfully contribute to transport. Equation (9) suggests that all states with contribute equally, while states with do not contribute, even though they may be close to the Fermi energy. We emphasize that this is radically different than the usual paradigm, where low- transport is almost entirely determined by states in the immediate vicinity of the Fermi level. This is depicted in Fig. 3.
Applying Eq. (9), the two summations in Eq. (7) are simply -independent constants (, ), and the extreme low- expression for the resistivity is
| (10) |
From Eq. (10), it is apparent that at the charge neutrality point (), we have purely linear-in- phonon-induced resistivity down to . On the other hand, when , then the low- resistivity is proportional to the factor , and is exponentially suppressed when , giving a crossover to perfect conductivity. Comparing this with the physics of supersonic fermions, we find
| (11) |
where gives the traditional lower bound for the regime of linear-in- resistivity based on the usual Bloch-Grüneisen paradigm. The crossover temperature is parametrically suppressed by the small parameter, . The subsonic case is thus expected to host linear-in- resistivity scaling down to a significantly lower temperature than one would estimate based on intuition from supersonic fermion scattering.
Concluding discussion.—Phonon scattering processes in subsonic fermion systems are necessarily interband transitions, implying the existence of a nonzero, minimum energy transfer allowed by kinematics. At temperatures below this energy scale, phonon scattering is suppressed and Bloch states become long-lived, with important effects on the low- transport physics. Applying standard Boltzmann kinetic theory of acoustic phonon scattering to nearly flat band (NFB) systems, we find that this underlies a robust, linear-in- scaling of the resistivity down to temperatures far lower than the Bloch-Grüneisen paradigm of supersonic fermion scattering would suggest. This result provides a concrete mechanism for the linear-in- resistivity over a wide range of temperatures based only on familiar concepts of solid state physics and the distinct kinematics of NFB systems. In particular, it provides an alternative theoretical explanation for low- “strange metal” resistivity scaling in NFB systems. Our theory also predicts regimes of perfect conductivity and scaling which compete with the regime, which are not commonly associated with phonon physics. Both and low- behaviors are reported in MATBLG Jaoui et al. (2022). Thus, low- , , and perfect conductivity regimes may all arise in NFB systems from the same universal phonon-scattering physics, providing a possible explanation for these reported observations in MATBLG.
Our theory of USS fermion transport is general and could apply widely to NFB systems in other 2D heterostructures or heavy fermion materials. However, our results are particularly germane to the ongoing debate on the presence of a strange metal state in MATBLG. Using the Bistritzer-MacDonald (BM) model for the non-interacting band structure of MATBLG, we see that much of the band is made up of subsonic states (). Large sections of the NFBs have small band separation () and small (), rendering USS theory highly applicable. We discuss this more quantitatively in the SM SM (Please see Supplemental Material for the microscopic model, additional details on Boltzmann kinetic theory and derivations of ultrasubsonic transport theory results, an analysis of the applicability of our theory to MATBLG, and a treatment of the ultrasubsonic Dirac cone). We emphasize that a direct quantitative application of USS theory to the BM model could be of limited utility since the bands are expected to be renormalized by interaction effects, strain, and twist disorder.
Acknowledgements.
We thank Fengcheng Wu for helpful discussions. This work is supported by the Laboratory for Physical Sciences.References
- Geim and Grigorieva (2013) A. K. Geim and I. V. Grigorieva, Nature 499, 419 (2013), URL https://doi.org/10.1038%2Fnature12385.
- Novoselov et al. (2006) K. S. Novoselov, E. McCann, S. V. Morozov, V. I. Fal’ko, M. I. Katsnelson, U. Zeitler, D. Jiang, F. Schedin, and A. K. Geim, Nature Physics 2, 177 (2006), URL https://doi.org/10.1038%2Fnphys245.
- Bistritzer and MacDonald (2011) R. Bistritzer and A. H. MacDonald, Proceedings of the National Academy of Sciences 108, 12233 (2011), URL https://doi.org/10.1073%2Fpnas.1108174108.
- Morell et al. (2010) E. S. Morell, J. D. Correa, P. Vargas, M. Pacheco, and Z. Barticevic, Physical Review B 82 (2010), URL https://doi.org/10.1103%2Fphysrevb.82.121407.
- Li et al. (2019) X. Li, F. Wu, and A. H. MacDonald, Electronic structure of single-twist trilayer graphene (2019), URL https://arxiv.org/abs/1907.12338.
- Kim et al. (2017) K. Kim, A. DaSilva, S. Huang, B. Fallahazad, S. Larentis, T. Taniguchi, K. Watanabe, B. J. LeRoy, A. H. MacDonald, and E. Tutuc, Proceedings of the National Academy of Sciences 114, 3364 (2017), URL https://doi.org/10.1073%2Fpnas.1620140114.
- Cao et al. (2018a) Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, et al., Nature 556, 80 (2018a), URL https://doi.org/10.1038%2Fnature26154.
- Cao et al. (2018b) Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, and P. Jarillo-Herrero, Nature 556, 43 (2018b), URL https://doi.org/10.1038%2Fnature26160.
- Cao et al. (2020a) Y. Cao, D. Chowdhury, D. Rodan-Legrain, O. Rubies-Bigorda, K. Watanabe, T. Taniguchi, T. Senthil, and P. Jarillo-Herrero, Phys. Rev. Lett. 124, 076801 (2020a), URL https://link.aps.org/doi/10.1103/PhysRevLett.124.076801.
- Cao et al. (2021) Y. Cao, J. M. Park, K. Watanabe, T. Taniguchi, and P. Jarillo-Herrero, Nature 595, 526 (2021).
- Yankowitz et al. (2019) M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young, and C. R. Dean, Science 363, 1059 (2019), URL https://doi.org/10.1126%2Fscience.aav1910.
- Kerelsky et al. (2019) A. Kerelsky, L. J. McGilly, D. M. Kennes, L. Xian, M. Yankowitz, S. Chen, K. Watanabe, T. Taniguchi, J. Hone, C. Dean, et al., Nature 572, 95 (2019), URL https://doi.org/10.1038%2Fs41586-019-1431-9.
- Lu et al. (2019) X. Lu, P. Stepanov, W. Yang, M. Xie, M. A. Aamir, I. Das, C. Urgell, K. Watanabe, T. Taniguchi, G. Zhang, et al., Nature 574, 653 (2019), URL https://doi.org/10.1038%2Fs41586-019-1695-0.
- Stepanov et al. (2020) P. Stepanov, I. Das, X. Lu, A. Fahimniya, K. Watanabe, T. Taniguchi, F. H. Koppens, J. Lischner, L. Levitov, and D. K. Efetov, Nature 583, 375 (2020).
- Sharpe et al. (2019) A. L. Sharpe, E. J. Fox, A. W. Barnard, J. Finney, K. Watanabe, T. Taniguchi, M. A. Kastner, and D. Goldhaber-Gordon, Science 365, 605 (2019), URL https://doi.org/10.1126%2Fscience.aaw3780.
- Chen et al. (2020) G. Chen, A. L. Sharpe, E. J. Fox, Y.-H. Zhang, S. Wang, L. Jiang, B. Lyu, H. Li, K. Watanabe, T. Taniguchi, et al., Nature 579, 56 (2020), URL https://doi.org/10.1038%2Fs41586-020-2049-7.
- Rozen et al. (2021) A. Rozen, J. M. Park, U. Zondiner, Y. Cao, D. Rodan-Legrain, T. Taniguchi, K. Watanabe, Y. Oreg, A. Stern, E. Berg, et al., Nature 592, 214 (2021).
- Zhou et al. (2022) H. Zhou, L. Holleis, Y. Saito, L. Cohen, W. Huynh, C. L. Patterson, F. Yang, T. Taniguchi, K. Watanabe, and A. F. Young, Science 375, 774 (2022), URL https://doi.org/10.1126%2Fscience.abm8386.
- Zhou et al. (2021a) H. Zhou, T. Xie, T. Taniguchi, K. Watanabe, and A. F. Young, Nature 598, 434 (2021a), URL https://doi.org/10.1038%2Fs41586-021-03926-0.
- Zhou et al. (2021b) H. Zhou, T. Xie, A. Ghazaryan, T. Holder, J. R. Ehrets, E. M. Spanton, T. Taniguchi, K. Watanabe, E. Berg, M. Serbyn, et al., Nature 598, 429 (2021b), URL https://doi.org/10.1038%2Fs41586-021-03938-w.
- Serlin et al. (2020) M. Serlin, C. L. Tschirhart, H. Polshyn, Y. Zhang, J. Zhu, K. Watanabe, T. Taniguchi, L. Balents, and A. F. Young, Science 367, 900 (2020), URL https://doi.org/10.1126%2Fscience.aay5533.
- Wu et al. (2018) F. Wu, A. MacDonald, and I. Martin, Physical Review Letters 121 (2018), URL https://doi.org/10.1103%2Fphysrevlett.121.257001.
- Wu et al. (2019a) F. Wu, T. Lovorn, E. Tutuc, I. Martin, and A. H. MacDonald, Phys. Rev. Lett. 122, 086402 (2019a), URL https://link.aps.org/doi/10.1103/PhysRevLett.122.086402.
- Tschirhart et al. (2022) C. L. Tschirhart, E. Redekop, L. Li, T. Li, S. Jiang, T. Arp, O. Sheekey, T. Taniguchi, K. Watanabe, K. F. Mak, et al., Intrinsic spin hall torque in a moire chern magnet (2022), URL https://arxiv.org/abs/2205.02823.
- Polshyn et al. (2020) H. Polshyn, J. Zhu, M. A. Kumar, Y. Zhang, F. Yang, C. L. Tschirhart, M. Serlin, K. Watanabe, T. Taniguchi, A. H. MacDonald, et al., Nature 588, 66 (2020), URL https://doi.org/10.1038%2Fs41586-020-2963-8.
- Jaoui et al. (2021) A. Jaoui, I. Das, G. Di Battista, J. Díez-Mérida, X. Lu, K. Watanabe, T. Taniguchi, H. Ishizuka, L. Levitov, and D. K. Efetov, Quantum critical behavior in magic-angle twisted bilayer graphene (2021), URL https://arxiv.org/abs/2108.07753.
- Polshyn et al. (2019) H. Polshyn, M. Yankowitz, S. Chen, Y. Zhang, K. Watanabe, T. Taniguchi, C. R. Dean, and A. F. Young, Nature Physics 15, 1011 (2019).
- Cao et al. (2020b) Y. Cao, D. Chowdhury, D. Rodan-Legrain, O. Rubies-Bigorda, K. Watanabe, T. Taniguchi, T. Senthil, and P. Jarillo-Herrero, Phys. Rev. Lett. 124, 076801 (2020b), URL https://link.aps.org/doi/10.1103/PhysRevLett.124.076801.
- Sarma and Wu (2022) S. D. Sarma and F. Wu, Physical Review Research 4 (2022), URL https://doi.org/10.1103%2Fphysrevresearch.4.033061.
- Zhang et al. (2022) Y. Zhang, R. Polski, A. Thomson, . Lantagne-Hurtubise, C. Lewandowski, H. Zhou, K. Watanabe, T. Taniguchi, J. Alicea, and S. Nadj-Perge, Spin-orbit enhanced superconductivity in bernal bilayer graphene (2022), URL https://arxiv.org/abs/2205.05087.
- Polski et al. (2022) R. Polski, Y. Zhang, Y. Peng, H. S. Arora, Y. Choi, H. Kim, K. Watanabe, T. Taniguchi, G. Refael, F. von Oppen, et al., Hierarchy of symmetry breaking correlated phases in twisted bilayer graphene (2022), URL https://arxiv.org/abs/2205.05225.
- Xie and MacDonald (2020) M. Xie and A. MacDonald, Physical Review Letters 124 (2020), URL https://doi.org/10.1103%2Fphysrevlett.124.097601.
- Andrei and MacDonald (2020) E. Y. Andrei and A. H. MacDonald, Nature Materials 19, 1265 (2020), URL https://doi.org/10.1038%2Fs41563-020-00840-0.
- Li et al. (2021) T. Li, S. Jiang, L. Li, Y. Zhang, K. Kang, J. Zhu, K. Watanabe, T. Taniguchi, D. Chowdhury, L. Fu, et al., Nature 597, 350 (2021), URL https://doi.org/10.1038%2Fs41586-021-03853-0.
- Ghiotto et al. (2021) A. Ghiotto, E.-M. Shih, G. S. S. G. Pereira, D. A. Rhodes, B. Kim, J. Zang, A. J. Millis, K. Watanabe, T. Taniguchi, J. C. Hone, et al., Nature 597, 345 (2021), URL https://doi.org/10.1038%2Fs41586-021-03815-6.
- Pan et al. (2020) H. Pan, F. Wu, and S. D. Sarma, Physical Review B 102 (2020), URL https://doi.org/10.1103%2Fphysrevb.102.201104.
- Pan and Sarma (2021) H. Pan and S. D. Sarma, Physical Review Letters 127 (2021), URL https://doi.org/10.1103%2Fphysrevlett.127.096802.
- Morales-Durán et al. (2021) N. Morales-Durán, A. H. MacDonald, and P. Potasz, Physical Review B 103 (2021), URL https://doi.org/10.1103%2Fphysrevb.103.l241110.
- Ahn and Sarma (2022) S. Ahn and S. D. Sarma, Physical Review B 105 (2022), URL https://doi.org/10.1103%2Fphysrevb.105.115114.
- Kerelsky et al. (2021) A. Kerelsky, C. Rubio-Verdú, L. Xian, D. M. Kennes, D. Halbertal, N. Finney, L. Song, S. Turkel, L. Wang, K. Watanabe, et al., Proceedings of the National Academy of Sciences 118 (2021).
- Khalaf et al. (2019) E. Khalaf, A. J. Kruchkov, G. Tarnopolsky, and A. Vishwanath, Phys. Rev. B 100, 085109 (2019), URL https://link.aps.org/doi/10.1103/PhysRevB.100.085109.
- Arora et al. (2020) H. S. Arora, R. Polski, Y. Zhang, A. Thomson, Y. Choi, H. Kim, Z. Lin, I. Z. Wilson, X. Xu, J.-H. Chu, et al., Nature 583, 379 (2020), URL https://doi.org/10.1038%2Fs41586-020-2473-8.
- Jaoui et al. (2022) A. Jaoui, I. Das, G. D. Battista, J. Díez-Mérida, X. Lu, K. Watanabe, T. Taniguchi, H. Ishizuka, L. Levitov, and D. K. Efetov, Nature Physics 18, 633 (2022), URL https://doi.org/10.1038%2Fs41567-022-01556-5.
- Wu et al. (2019b) F. Wu, E. Hwang, and S. Das Sarma, Phys. Rev. B 99, 165112 (2019b), URL https://link.aps.org/doi/10.1103/PhysRevB.99.165112.
- Li et al. (2020) X. Li, F. Wu, and S. Das Sarma, Phys. Rev. B 101, 245436 (2020), URL https://link.aps.org/doi/10.1103/PhysRevB.101.245436.
- Davis et al. (2023a) S. M. Davis, F. Wu, and S. D. Sarma, Acoustic phonon contribution to the resistivity of twisted bilayer graphene (2023a), eprint 2302.07275.
- Saito et al. (2020) Y. Saito, J. Ge, K. Watanabe, T. Taniguchi, and A. F. Young, Nature Physics 16, 926 (2020).
- Hwang and Das Sarma (2008) E. H. Hwang and S. Das Sarma, Phys. Rev. B 77, 115449 (2008), URL https://link.aps.org/doi/10.1103/PhysRevB.77.115449.
- Davis et al. (2023b) S. M. Davis, Y.-Z. Chou, F. Wu, and S. Das Sarma, Phys. Rev. B 107, 045426 (2023b), URL https://link.aps.org/doi/10.1103/PhysRevB.107.045426.
- Hwang and Sarma (2019) E. H. Hwang and S. D. Sarma, Physical Review B 99 (2019), URL https://doi.org/10.1103%2Fphysrevb.99.085105.
- SM (Please see Supplemental Material for the microscopic model, additional details on Boltzmann kinetic theory and derivations of ultrasubsonic transport theory results, an analysis of the applicability of our theory to MATBLG, and a treatment of the ultrasubsonic Dirac cone) (Please see Supplemental Material for the microscopic model, additional details on Boltzmann kinetic theory and derivations of ultrasubsonic transport theory results, an analysis of the applicability of our theory to MATBLG, and a treatment of the ultrasubsonic Dirac cone).
- Ashcroft and Mermin (1976) N. W. Ashcroft and N. D. Mermin, Solid State Physics (Harcourt College Publishers, 1976), ISBN 9780030839931.
- Ziman (1960) J. M. Ziman, Electrons and Phonons (Oxford University Press, 1960), ISBN 9780198507796.
- Coleman (2015) P. Coleman, Introduction to Many-Body Physics (Cambridge University Press, 2015), ISBN 9780521864886.