The Interval function, Ptolemaic, distance hereditary, bridged graphs and axiomatic characterizations

Transit functions on discrete structures were introduced by Mulder [15] to generalize some basic notions in discrete geometry, amongst which convexity, interval and betweenness. A transit function on a non-empty set $V$ is a function $R:V\times V$ to $2^{V}$ on $V$ satisfying the following three axioms:

$(t1)$

$u\in R(u,v)$, for all $u,v\in V$,

$(t2)$

$R(u,v)=R(v,u)$, for all $u,v\in V$,

$(t3)$

$R(u,u)=\{u\}$, for all $u\in V$.

If $V$ is the vertex set of a graph $G$, then we say that $R$ is a transit function on $G$. Throughout this paper, we consider only finite, simple and connected graphs. The underlying graph $G_{R}$ of a transit function $R$ on $V$ is the graph with vertex set $V$, where two distinct vertices $u$ and $v$ are joined by an edge if and only if $R(u,v)=\{u,v\}$.

A $u,v$ - shortest path in a connected graph $G=(V,E)$ is a $u,v$-path in $G$ containing the minimum number of edges. The length of a shortest $u,v$-path $P$ (that is, the number of edges in $P$) is the standard distance in $G$. The interval function $I_{G}$ of a connected graph $G$ is the function $I_{G}$ defined with respect to the standard distance $d$ in $G$ as

$I_{G}(u,v)=\{w\in V$: $w$ lies on some shortest $u,v$ - path in $G\}=\{w\in V:d(u,w)+d(w,v)=d(u,v)\}$

The interval function $I_{G}$ is a classical example of a transit function on a graph ( we some times denote $I_{G}$ by $I$, if there is no confusion for the graph $G$). It is easy to observe that the underlying graph $G_{I_{G}}$ of $I_{G}$ is isomorphic to $G$. The term interval function was coined by Mulder in [14], where it is extensively studied using an axiomatic approach.
Nebeský initiated a very interesting problem on the interval function $I$ of a connected graph $G=(V,E)$ during the 1990s. The problem is the following: “ Is it possible to give a characterization of the interval function $I_{G}$ of a connected graph $G$ using a set of simple axioms (first - order axioms) defined on a transit function $R$ on $V$?” Nebeský [17, 18] proved that there exists such a characterization for the interval function $I(u,v)$ by using first - order axioms on an arbitrary transit function $R$. In further papers that followed [19, 20, 21, 22], Nebeský improved the formulation and the proof of this characterization. Also, refer Mulder and Nebeský [16]. In [8], the axiomatic characterization of $I_{G}$ is extended to that of a disconnected graph. In all these characterizations, five essential axioms known as classical axioms are always required. These five classical axioms are $(t1)$ and $(t2)$ and three additional $(b2)$, $(b3)$, and $(b4)$ defined as follows:

The notation $x\in R(u,v)$ can be interpreted as $x$ is in between $u$ and $v$. For example, the axiom $(b2)$ can be interpreted as: if $x$ is between $u$ and $v$, and $y$ is between $u$ and $x$, then $y$ is between $u$ and $v$. Similarly we can describe all other axioms. Hence we use the terminology of betweeness for an axiom on a transit function $R$. The above interpretation was the motivation for the concept of betweenness in graphs using transit functions. It was formally introduced by Mulder in [15] as those transit function that satisfy axioms $(b1)$ and $(b2)$. Here the axiom $(b1)$ is defined for every $u,v\in V$ and a transit function $R$ as follows:
$(b1)$ $x\in R(u,v),x\neq v\Rightarrow v\not\in R(u,x)$

The following implications can be easily verified for a transit function $R$ among axioms $(t1),(t2),(t3),(b1),(b3)$ and $(b4)$.

• 1.

  Axioms $(t1)$ and $(b4)$ implies axiom $(t3)$.

• 2.

  Axioms $(t1),(t2),(t3)$ and $(b3)$ implies axiom $(b4)$ which implies axiom $(b1)$ ( that is , for a transit function $R,(b3)$ implies $(b4)$ implies $(b1)$)

The converse of the above implications need not hold. A transit function $R$ satisfying axioms $(b2)$ and $(b3)$ is known as a geometric transit function.

The problem of characterizing the interval function of an arbitrary graph can be adopted for different graph classes; viz., characterizing the interval function of special graph classes using a set of first - order axioms on an arbitrary transit function. Such a problem was first attempted by Sholander in [24] with a partial proof for characterizing the interval function of trees. Chvátal et al. [11] obtained the completion of this proof. Further new characterizations of the interval function of trees and block graphs are discussed in [1]. Axiomatic characterization of the interval function of median graphs, modular graphs, geodetic graphs, (claw, paw)-free graphs and bipartite graphs are respectively described in [9, 10, 14, 16, 19].

In this paper, we continue the approach of characterizing the interval function of some related classes of graphs, namely, distance hereditary graphs, Ptolemaic graphs and bridged graphs. We fix the graph theoretical notations and terminology used in this paper. Let $G$ be a graph and $H$ a subgraph of $G$. $H$ is called an isometric subgraph of $G$ if the distance $d_{H}(u,v)$ between any pair of vertices, $u,v$ in $H$ coincides with that of the distance $d_{G}(u,v)$. $H$ is called an induced subgraph if $u,v$ are vertices in $H$ such that $uv$ is an edge in $G$, then $uv$ must be an edge in $H$ also. A graph $G$ is said to be $H$-free, if $G$ has no induced subgraph isomorphic to $H$. Let $G_{1},G_{2},\ldots,G_{k}$ be graphs. For a graph $G$, we say that $G$ is $G_{1},G_{2},\ldots,G_{k}$-free if $G$ has no induced subgraph isomorphic to $G_{i}$, $i=1,\ldots,k$. Chordal graph is an example of a graph $G$ which is defined with respect to an infinite number of forbidden induced subgraphs ($G$ is chordal if $G$ have no induced cycles $C_{n}$ with length $n$ more than three). There are several graphs that can be defined or characterized by a list of forbidden induced subgraphs or isometric subgraphs. See the survey by Brandstädt et al. [3] and the information system [12], for such graph families. A graph $G=(V,E)$ is a bridged graph if $G$ has no isometric cycles of length greater than $3$. Clearly the family of bridged graphs contain the family of chordal graphs. The graph $G$ is distance hereditary if the distances in any connected induced subgraph $H$ of $G$ are the same as in $G$. Thus, any induced subgraph $H$ inherits the distances of $G$. The graph $G$ is a Ptolemaic graph if $G$ is both chordal and distance hereditary. Both Ptolemaic graphs and distance hereditary graphs possess a characterization in terms of a list of forbidden induced subgraphs, while bridged graphs by definition itself possess an infinite list of forbidden isometric subgraphs. In this paper, our idea is to find suitable axioms that fail on every forbidden induced subgraph for the Ptolemaic and distance hereditary graphs, while that for the bridged graph is to find an axiom that fails on all of its forbidden isometric subgraphs, namely on all isometric cycles $C_{n},n>3$.

In addition to the geometric axioms $(b3)$ and $(b2)$, we consider the following betweenness axioms $(J0),(J2),(J2^{\prime})$ and $(J3^{\prime})$ for a transit function $R$ on $V$ for proving the characterizations of these classes of graphs.

• $(J{0})$

  : For any pair of distinct vertices $u,v,x,y\in V$ we have $x\in R(u,y),y\in R(x,v)\Rightarrow x\in R(u,v)$.

• $(J{0^{\prime}})$

  : $x\in R(u,y),y\in R(x,v),R(u,y)\cap R(x,v)\subseteq\{u,x,y,v\}\Rightarrow x\in R(u,v)$.

• $(J{2})$

  : $R(u,x)=\{u,x\},R(x,v)=\{x,v\},R(u,v)\neq\{u,v\}\implies x\in R(u,v)$.

• $(J{2^{\prime}})$

  : $x\in R(u,y),y\in R(x,v),R(u,x)=\{u,x\},R(x,y)=\{x,y\},R(y,v)=\{y,v\},R(u,v)\neq\{u,v\}\Rightarrow x\in R(u,v)$

• $(J{3^{\prime}})$

  : $x\in R(u,y),y\in R(x,v),R(x,y)\neq\{x,y\},R(u,v)\neq\{u,v\}\Rightarrow x\in R(u,v)$.

From the definition of the axioms, we observe the following. The axiom $(J2)$ is a simple betweenness axiom which is always satisfied by the interval function $I$. The axiom $(J2^{\prime})$ is a natural extension of $(J2)$. We provide examples in the respective sections for the independence of the axioms $(J2^{\prime})$ and $(J3^{\prime})$ and $(J0^{\prime})$. The axioms $(J2^{\prime})$ and $(J3^{\prime})$ were first considered in [6] and later in [4]. The axiom $(J0)$ first appeared in [24] for characterizing the interval function of trees. The axiom is discussed in [4] for characterizing the interval function of a Ptolemaic graph $G$. We may observe that both the family of bridged graphs $\mathcal{BG}$ and distance hereditary graphs $\mathcal{DH}$ is a strict super class of the family of Ptolemaic graphs,$\mathcal{PG}$, that is, $\mathcal{PG}\subsetneq\mathcal{DH}$ and $\mathcal{PG}\subsetneq\mathcal{BG}$ and $\mathcal{BG}$ and $\mathcal{DH}$ coincide only in $\mathcal{PG}$. But, $\mathcal{BG}\nsubseteq\mathcal{DH}$ and $\mathcal{DH}\nsubseteq\mathcal{BG}$, This relation is also reflected in the implications between the axioms $(J0),(J2^{\prime}),(J3^{\prime})$ and $(J0^{\prime})$. From the definitions, we have the axiom $(J0)$ implies axioms $(J2^{\prime})$ and $(J3^{\prime})$, and also $(J0)$ implies $(J0^{\prime})$, while the reverse implications are not true. In other words, axioms $(J2^{\prime}),(J3^{\prime})$ and $(J0^{\prime})$ are weaker axioms than $J(0)$ and hence graphs whose interval function satisfy axioms $(J2^{\prime})$ and $(J3^{\prime})$ will be a super class of graphs whose interval function satisfies $(J0)$. Similarly graphs whose interval function satisfies axiom $(J0^{\prime})$ will be a super class of graphs whose interval function satisfies $(J0)$. See Figure 1 for the relationships between the family $\mathcal{PG}$, $\mathcal{DH}$ and $\mathcal{BG}$.

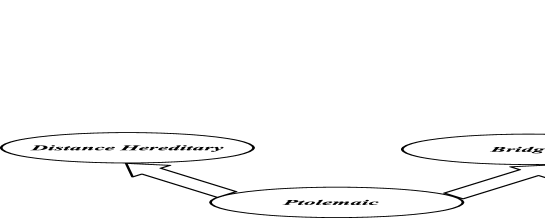
We organize the results as follows. In Section 2, we characterize the interval function of a distance hereditary graph, Ptolemaic graph in Section 3, bridged graph in Section 4 and in Section  5, a discussion of the so called induced path transit function for the distance hereditary graphs respectively.

For the axiomatic characterization of the interval function of distance hereditary graphs, we require the axioms $(J2^{\prime})$ and $(J3^{\prime})$. First we show that these axioms are independent with the Examples 1 and 2 below. Also it is clear from the Figures 2 and 3 that the axioms $(J2^{\prime})$ and $(J3^{\prime})$ are independent. The interval function $I_{G}$ doesn’t satisfy axiom $(J2^{\prime})$, while $I_{G}$ satisfy axiom $(J3^{\prime})$ for the graphs in Figure 2. Also $I_{G}$ doesn’t satisfy axiom $(J3^{\prime})$, while $I_{G}$ satisfy axiom $(J2^{\prime})$ for the graphs in Figure 3. By an $HHD3$ - fan - free graph $G$, we mean that $G$ is free from the House graph, the Hole graph (cycles $C_{n}$, $n\geq 5$), the Domino graph and the $3$-fan (See the Figures 2 and 3 for these graphs).

The following results are proved in [4] and [6].

Bandelt and Mulder obtained a forbidden induced subgraph characterization of distance hereditary graphs in [2]. We quote the theorem as

We state a related result from [4] using the axiom $(J3)$ defined for a transit function $R$ as

Note that a $P$ graph is the graph obtained by adding a pendent edge on an induced 4-cycle, $C_{4}$. It follows from the definition that axiom $(J3)$ implies both the axioms $(J2^{\prime})$ and $(J3^{\prime})$, but the reverse implications are not true. We quote the result.

It may be observed that a $P$ graph is a distance hereditary graph and hence the class of $HHP3$ - fan - free graphs is a proper subclass of the class of $HHD3$ - fan - free graphs (distance hereditary graphs). The proof of the next theorem characterizing the class of distance hereditary graphs follows the same lines of ideas as in the proof of Theorem 2 with modifications since the axioms $(J2^{\prime})$ and $(J3^{\prime})$ are weaker axioms than the axiom $(J3)$.

We need the following Lemma

For the axiomatic characterization of $I_{G}$ of a Ptolemaic graph $G$, the essential axiom is $(J0)$. Ptolemaic graphs are chordal graphs that are $3$ - fan - free. Changat et al. in [4] characterized the graphs for which the interval function satisfies the axiom $(J0)$ as follows.